7竖向荷载作用
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
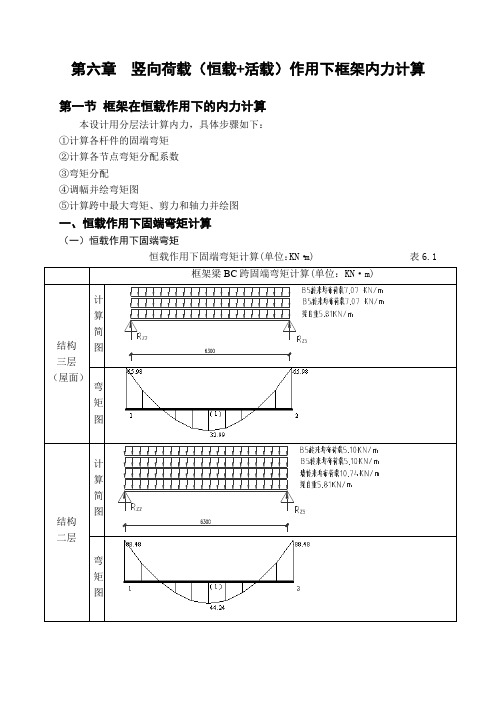
第六章竖向荷载（恒载+活载）作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力，具体步骤如下：①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算（一）恒载作用下固端弯矩恒载作用下固端弯矩计算(单位：KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2（二）计算各节点弯矩分配系数用分层法计算竖向荷载，假定结构无侧移，计算时采用力矩分配法，其计算要点是：①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层，各层梁跨度及柱高与原结构相同，柱端假定为固端。
③计算梁、柱线刚度。
对于柱，假定分层后中间各层柱柱端固定与实际不符，因而，除底层外，上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁，宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中，可近似按下式计算梁的截面惯性矩：一边有楼板：I=1.5Ir两边有楼板：I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3，底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
（1）计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度（2）计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0（三）分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图（KN·m）（四）框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量，在竖向荷载作用下可以考虑竖向内力重分布，主要是降低支座负弯矩，以减小支座处的配筋，跨中则应相应增大弯矩。
高层建筑结构的荷载和地震作用
4、风振系数 z
１）风速特点： 风速的变化可分为两部分：一种是长周期的成分，其值一般在10min以上；另一种 是短周期成分，一般只有几秒左右。因此，为便于分析，通常把实际风分解为平均风 （稳定风）和脉动风两部分。稳定风周期长，对结构影响小；脉动风周期短，对结构 影响大。
２）风的动力效应：对于高度较大、刚度较小的高层建筑，脉动风压会产生不可
2）定义：风荷载体型系数是指风作用在建筑物表面所引起的压力(吸力)与原 始风速算得的理论风压的比值。
3）特点：风荷载体型系数一般都是通过实测或风洞模拟试验的方法确定，它 表示建筑物表面在稳定风压作用下的静态压力分布规律，主要与建筑物的体型与尺 度有关。
3.2 风荷载
+0.8 －(0.48+0.03H/L)
0.8+1.2/n1/2
3）计算：在计算风荷载对建筑物的整体作用时，只需按各个表面的平 均风压计算，即采用各个表面的平均风荷载体型系数计算。
4）风荷载体型系数的确定：根据设计经验和风洞试验 （１）单体风压体型系数
例:
-0.6
当表面粗糙时取μs = 0.8
-0.6
3.2 风荷载
（2）群体风压体型系数 对建筑群，尤其是高层建筑群，当房屋相互间距较近时，由于漩涡
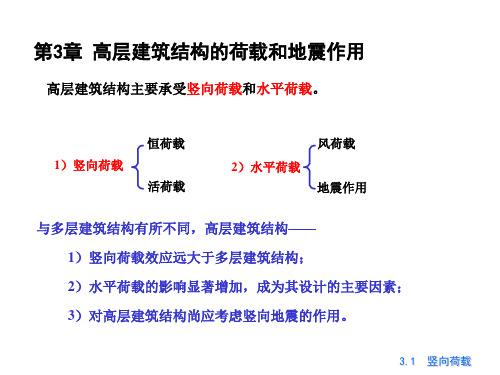
第3章 高层建筑结构的荷载和地震作用
高层建筑结构主要承受竖向荷载和水平荷载。
1）竖向荷载
恒荷载 活荷载
2）水平荷载
风荷载 地震作用
与多层建筑结构有所不同，高层建筑结构—— 1）竖向荷载效应远大于多层建筑结构； 2）水平荷载的影响显著增加，成为其设计的主要因素； 3）对高层建筑结构尚应考虑竖向地震的作用。
3.1 竖向荷载
3.1 恒荷载
框架在竖向荷载作用下内力计算
A2
q1=10kN/m
B2
ic2 1
ib 0.777 ic2 1
A1
B1
8000
A 2
B 2
ic2 1
ic2 1
q 1 = 8 k N / m
A 1
B 1
ib 0.777
ic1 0.801
ic1 0.801
A 0
8 0 0 0
B 0
3、用力矩分配法计算第二层开口框架
（1）计算分配系数：
➢ 根据算得的各杆端弯矩值，作最后的弯矩图并求得 相应的剪力图和轴力图。
例题：
1882 12
42.667kNgm
(3)循环过程:A1
B1
用力矩分配法计算顶层开口框架
（1）计算分配系数：
A 2结 点
S A 2 A1 4 (0 .9 ic 2 )
S A 2 B 2 4 ib
S 4 (0 .9 ic 2 ib ) 4 1 .6 7 7
A2
A 2 A 1
S A 2 A1 S
6、计算梁跨中弯矩，计算梁剪力，绘制框架M、V图
例题：
用分层法计算 图示框架的内力
1、计算梁柱线刚度
Ic
bh3 12
1 12
0.4 0.553
1 12
0.0666
Ib
bh3 12
1 12
0.3
0 .7 3
1 12
0 .1 0 2 9
ic1
EIc H1
1 1 5 12
0.0666 E
1 12
1 2
，以作校核；
' ik
1 2
iik iik
(i)
➢ 计算荷载作用下各杆端产生的固端弯矩MFik，并写在相 应的各杆端部，求出汇交于每一节点的各杆固端弯矩之 和MFi，把它写在该节点的内框中；
竖向荷载的计算方法
竖向荷载的计算方法竖向荷载呢，简单说就是垂直方向作用在结构上的力。
在建筑结构里，这可是个很重要的事儿。
那咱们先来说说恒载的计算。
恒载就是那些固定不变的重量，像建筑物的自重啦。
比如说楼板，你就可以根据楼板的厚度、材料的密度来算出它的重量。
如果是混凝土楼板，混凝土的密度大概是一个固定的值，你量出楼板的面积和厚度，一乘就大概能知道这楼板自身的重量啦。
这就像是一个人本身的体重，稳稳地压在结构上，不会变来变去的。
墙的重量计算也类似哦，根据墙的类型，是砖墙还是混凝土墙，然后算出每立方米的重量，再乘以墙的体积就妥了。
再说说活载的计算。
活载可就调皮一些啦，它是可变的荷载。
像咱们人在建筑物里走来走去，家具的摆放啥的。
不同的建筑功能，活载取值可不一样呢。
比如说住宅里，按照规范呢，每平方米的活载取值有个大概的范围。
但是你要是在商场里，那活载取值就要大很多啦，毕竟商场里人多，而且可能还会有一些较重的货物临时堆放啥的。
计算活载的时候，就是用规定的活载取值乘以相应的面积。
就好像是根据不同的活动场景，预估会有多少“活动的重量”压在结构上。
还有雪荷载呢。
这雪荷载就看老天爷的心情啦。
不同地区的雪荷载标准值不一样哦。
在北方那些经常下雪的地方，雪荷载可能就比较大。
计算雪荷载的时候，也是根据当地的雪荷载标准值和屋面的面积来计算。
这就像是大自然偶尔给建筑物戴上的一顶“雪帽子”，不过这“帽子”的重量可得算清楚，不然结构可能就会被压得“喘不过气”啦。
总的来说，竖向荷载的计算虽然有点小复杂，但是只要咱们把各个部分的荷载计算清楚，再把它们加起来，就能知道结构到底承受了多少竖向的压力啦。
宝子们，是不是感觉也没有那么难呢？。
竖向极限承载力标准值
竖向极限承载力标准值竖向极限承载力标准值是指在竖向荷载作用下，材料或结构体所能承受的最大力量。
这一数值对于工程设计和结构安全至关重要，因此在工程实践中，需要对竖向极限承载力标准值进行准确的计算和评估。
首先，竖向极限承载力标准值的计算需要考虑材料的强度和稳定性。
材料的强度是指材料在受力作用下的抗压、抗拉等能力，而稳定性则是指材料在受力作用下的变形和破坏情况。
在计算竖向极限承载力标准值时，需要综合考虑材料的强度和稳定性，确保结构在受力作用下不会发生失稳和破坏。
其次，竖向极限承载力标准值的计算还需要考虑结构的几何形状和支座条件。
不同形状和支座条件的结构，在受到相同荷载作用下，其竖向极限承载力标准值会有所不同。
因此，在进行计算时，需要充分考虑结构的几何形状和支座条件，确保计算结果的准确性和可靠性。
另外，竖向极限承载力标准值的计算还需要考虑结构的荷载组合和荷载效应。
在实际工程中，结构往往同时受到多种不同方向和大小的荷载作用，因此在计算竖向极限承载力标准值时，需要综合考虑不同荷载的组合和效应，确保结构在受到复合荷载作用下的安全性和稳定性。
最后，竖向极限承载力标准值的计算需要遵循相关的设计规范和标准。
不同的材料和结构，在计算竖向极限承载力标准值时，需要遵循不同的设计规范和标准，确保计算结果符合国家和行业的要求。
因此，在进行计算时，需要充分了解和掌握相关的设计规范和标准，确保计算结果的准确性和合理性。
综上所述，竖向极限承载力标准值的计算是一个复杂而又重要的工作，需要综合考虑材料的强度和稳定性、结构的几何形状和支座条件、荷载组合和荷载效应，以及相关的设计规范和标准。
只有在充分考虑以上因素的基础上进行计算，才能得到准确可靠的竖向极限承载力标准值，确保工程设计和结构安全的可靠性和稳定性。
高层建筑 第三章荷载作用与组合
(3) 偶然荷载：在结构使用期间不一定出现，一旦出现， 其量值很大且持续时间较短的荷载。如地 震、爆炸力、撞击力等。 按作用方向：(1) 竖向荷载：荷载作用方向沿垂直方向的 荷载。如结构自重、楼屋面活荷载等。 (2)水平荷载：荷载作用方向沿水平方向的荷 载。如风荷载、水平地震作用等。 与多层建筑相比，高层建筑层数多、高度较大，其竖向荷 载的影响是与建筑高度成正比的线性关系，而水平作用所 产生的作用效应随建筑高度成非线性的增长。并逐渐成为 设计控制指标。 三、荷载代表值 荷载代表值是指为了方便设计给荷载规定以一定的量值。 包括：标准值、组合值、频遇值和准永久值。 其中标准值指正常情况下在设计基准期（如50年）内可能 出现的最不利荷载值，是荷载的基本代表值，而其他代表
离地面或海 平面高度
A 5 1.09 1.00 0.65 10 1.28 1.00 0.65 20 1.52 1.23 0.74 30 1.67 1.39 0.88 40 1.79 1.52 1.00 50 1.89 1.62 1.10 60 1.97 1.71 1.20 70 2.05 1.79 1.28 80 2.12 1.87 1.36 90 2.18 1.93 1.43 100 2.23 2.00 1.50 150 2.46 2.25 1.79 200 2.64 2.46 2.03
值是采用相应的系数乘以其标准值得出。系数查现行《建 筑结构荷载规范》（GB50009-2012）。 永久荷载应采用标准值作为代表值；可变荷载应根据设 计要求采用标准值、组合值、频遇值或准永久值作为代表 值；偶然荷载应按建筑结构使用特点确定其代表值。 建筑结构设计应根据使用过程中在结构上可能同时出现 的荷载，按承载能力极限状态和正常使用极限状态分别进 行荷载组合，并应取各自的最不利的效应组合进行设计。 对于承载能力极限状态，应按荷载效应的基本组合或偶 然组合进行荷载组合。对于正常使用极限状态，应根据不 同的设计要求，采用荷载的标准组合或偶然组合、频遇组 合或准永久组合进行荷载组合。
不同竖向荷载作用下低_中_高压缩性土固结系数大小的统计分析_吕永高
2 .70 24 .4 15 .1
0.06
2 .71 23 .5 14 .3
0.08
2 .70 22 .3 15 .4
0.09
表 6 低压缩性土在不同载荷下的固结系数 (单位 :cm2·s -1)
土样号
200 kPa
400 kPa
921620
3 .0 ×10-3
2 .3 ×10 -3
971001
3 .7 ×10-3
第一作者通讯地址 :山东 省烟台市莱山区清泉路 32 号 , 烟台 大学土木工程系 邮编 :264005
图 3 低压缩土 Cv -P 变化
64
0.51
土样号 971004 35 .3
18 .5 2 .70 0 .975 24 .5 16 .3
0.52
土样号 971005 36 .0
18 .9 2 .70 0 .943 22 .5 15 .3
0.53
表 2 高压缩性土在不同载荷下的固结系数 (单位 :cm2·s -1)
土样号
200 kPa
2 .71 21 .7 13 .5
0.22
2 .70 21 .2 13 .5
0.38
2 .70 24 .6 16 .2
0.45
表 4 中压缩性土在不同载荷下的固结系数 (单位 :cm2·s -1)
土样号
200 kPa
400 kPa
971002 971013 971017
1 .7 ×10-3 3 .5 ×10-3 1 .8 ×10-3
1 .8 ×10 -3 3 .3 ×10 -3 1 .8 ×10 -3
〔收稿日期〕 2002 -06 -10
63
检测与分析
竖向荷载内力计算方法
竖向荷载内力计算方法我折腾了好久竖向荷载内力计算方法，总算找到点门道。
我一开始接触这个的时候，真的是两眼一抹黑，完全不知道从哪儿下手。
我就先从最基础的书本知识看起，那书上的公式啊，密密麻麻的。
我记得有个弯矩分配法的公式，看起来好复杂。
我最初尝试用这个方法的时候，就老是把那些系数搞混。
比如说这个节点的分配系数，我就经常错算成另一个的。
这就像是你去菜市场买菜，以为黄瓜的价格是西红柿的，结果结账的时候就发现错得离谱。
那我的计算结果也是错得一塌糊涂。
后来我发现，这种计算就像是搭积木，每一个数据和步骤都是一块积木块，少了或者错放了一块，整个“建筑”就塌了。
我开始非常仔细地对照书本上的例题来做。
每一步都要反复确认。
然后我又试了迭代法。
这个方法一开始用起来更头疼。
就好像你在一片黑暗里找东西，每走一步都好像要撞到墙上。
我找不到合适的初始值，计算得到的结果就是乱的。
我试了好些不同的初始值，有时候纯粹就是瞎猜一个数字。
但经过很多次失败后，我发现有些规律了。
你得结合结构的特性和一些已知的条件去选初始值，不能随便乱写。
我还自己做了一些小的结构模型示例，来验证这些计算方法。
像简单的梁结构或者小的框架结构。
这就有点像你学做菜，先从简单的番茄炒鸡蛋开始，再去尝试更复杂的菜。
通过这些自己做的小模型，我能更直观地看到内力的分布和计算结果是否合理。
对了，在计算过程中，数据的准确性也非常重要。
有次我因为在计算中把一个荷载数值写错了一位小数点，整个计算结果都是错的。
这就告诉我在计算的时候要打起一百二十分的精神，每个数据都要多次检查。
要是你正在路上走，不小心走错了一个路口，那最后到达的可能就是完全不同的地方，计算也是如此。
还有啊，画受力图也是个很关键的步骤。
很多时候我光看着文字描述很难想象出结构怎么受力的，但一旦画出来就清晰多了。
这就好比你要拼一个特别复杂的拼图，你得先有个完整的图在脑海里才好下手，受力图就给我提供了这样一个在脑海里的清晰结构。
第七章 竖向荷载作用下框架内力计算
第七章 竖向荷载作用下横向框架结构的内力计算7.1 计算单元取3轴线横向框架进行计算，计算单元宽度为7.5m ，如图所示，由于房间内直接传给该框架的楼面荷载如图中的水平阴影线所示，计算单元内的其余楼面荷载则通过纵向框架梁以集中力的形式传给横向框架，作用于各节点上。
7.2 荷载计算节点集中荷载1P ： 边纵梁传来：(a)屋面自重(三角形部分)：N k 78.56298.423.3.26.3=⨯⨯⨯(b)边纵梁自重： 5.709⨯6.0＝43.73kN 女儿墙自重： kN 87.330.6312.3=⨯合计： 1P ＝ 154.32kN节点集中荷载2P ：纵梁传来（a ）屋面自重(三角形部分)：KN 12.27298.40.326.3=⨯⨯⨯（b ）走道屋面板自重0.5⨯（6.0+6.0-3）⨯1.5⨯4.98=58.79KN纵梁自重： 5.709⨯6.0＝43.73kN合计： 2P ＝ 170.55kN对于1～4层，计算的方法基本与第五层相同，计算过程如下： 1 5.709/q kN m =1q '＝3.46/kN/mm KN q /99.103.333.32=⨯= m KN q /99.74.233.32=⨯=节点集中荷载1P ：纵梁自重： 5.709⨯6.0＝43.73kN外墙自重：()88.76KN 68.37.03.3225.00.6=⨯-⨯⨯-）（ 来纵梁传楼面自重（三角形部分）： (0.5 3.60.5 3.6 3.33)221.58kN ⨯⨯⨯⨯⨯= 扣窗面积墙重加窗重： 2 2.4 2.0 3.682 2.1631.01kN -⨯⨯⨯+⨯=-合计： 174.24kN节点集中荷载2P ：纵梁自重： 5.709⨯7.2＝41.10kN 内墙自重： 71.50kN 纵梁传来(a)楼面自重（三角形部分）：()KN5.0=⨯0.3⨯⨯5.0⨯⨯66.233.3780.3（b）走道楼面板自重（梯形部分）()KN⨯5.0=⨯5.7⨯+-48.9333.30.38.15.7扣窗面积墙重加窗重： 2.412 3.6820.4816.10kN-⨯⨯⨯+⨯=-合计： 152.58kN 7.2.2活荷载计算：活荷载作用下各层框架梁上的荷载分布如图：合计： 7.99KNP：节点集中荷载2屋面活载（三角形部分）：2⨯（0.5⨯3.0⨯0.5⨯3.0⨯0.5）=2.72KN走道传来屋面荷载（梯形部分）： ()KN 05.45.05.14.20.60.621=⨯⨯-+合计： 12.04KN 对于1～4层，m KN /6.60.30.2q 2=⨯= m KN q /64.25.2'2=⨯= 节点集中荷载1P ： 楼面活载（三角形部分）：2⨯（0.5⨯3.30.5⨯3.3⨯2）＝10.89KN合计： 31.97KN中节点集中荷载2P ： 楼面活载（三角形部分）：2⨯（0.5⨯3.30.5⨯3.3⨯2）＝10.89KN走道传来屋面荷载（梯形部分）：()KN 25.205.25.14.20.60.621=⨯⨯-+ 纵梁传来的屋面活载（梯形部分）：()KN 08.2128.10.35.75.75.0=⨯⨯-+⨯ 合计： 52.22KN7.2.3．屋面雪荷载标准值：同理，在屋面雪荷载作用下KN/m 16.10.335.0q 2=⨯= m KN q /84.04.235.0'2=⨯=节点集中荷载1P ： 屋面雪载（三角形部分）：2⨯（0.5⨯3.3⨯0.5⨯3.3⨯0.35）=2.08KN纵梁传来的屋面雪载（梯形部分）()KN 69.335.08.16.35.75.75.0=⨯⨯-+⨯ 合计： 5.77KN中节点集中荷载2P ： 屋面雪载（三角形部分）：2⨯（0.5⨯3.3⨯0.5⨯3.3⨯0.35）=2.08KN走道传来屋面雪载（梯形部分）： ()KN 835.235.05.14.25.75.721=⨯⨯-+纵梁传来的屋面雪载（梯形部分）： 3.97KN 合计： 8.72KN 1～4层,雪荷载作用下的节点集中力同屋面活荷载作用下的。
第六章-框架在竖向荷载作用下的内力分析
第六章框架在竖向荷载作用下的内力分析（采用弯矩二次分配法）6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法，因为框架结构对称，荷载对称；又属于奇数跨，故在对称轴上梁的截面只有竖向位移（沿对称轴方向）没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法，即将各节点的不平衡弯矩同时作分配和传递，并以两次分配为限。
（取一榀横向框架）2. 荷载传递路线2700对于边跨板，为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板，为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载： 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载：0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载： 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载： 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重： 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为：屋面梁：恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁：恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载： 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载：0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载： 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载： 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重： 3.9kN/mB-C 轴间框架梁均布荷载为：屋面梁：恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁：恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正，反之为负。
吊车荷载
用在左因右为两吊侧车的轮吊压车Pma梁x和上P，min当同一时侧出柱现由，P且ma分x产别生作最 大竖向荷载标准值时，另一侧柱则相应地由Pmin产 生最小竖向荷载标准值Dmink，由影响线可得吊车 竖向荷载的设计值计算公式：
式中
a 腹板横向加劲肋的间距，可取a hw 2hw k 腹板在纯剪切荷载作用下的屈曲系数，
当不设中间加劲肋时取为5.34。
3、腹板的有效宽度
当工字形截面梁、柱构件的腹板受弯及受压板幅利 用屈曲后强度时，应按有效宽度计算其截面几何 特性。有效宽度取为：
腹板全部受压 he hw 腹板部分受拉 he hc 式中：he—腹板受压区有效宽度。
Ns V 0.9hwtw cr
0.8w 1.25时， cr 1 0.8w 0.8 fv
w
1.25时，
cr
fv
/ 2w
式中
Ns — 拉力场产生的压力；
cr — 利用拉力场时腹板的屈曲剪应力； w — 参数，参考前面公式。
加劲肋稳定性验算按GB50017规定进行，计算长度取腹板
工字形截面构件腹板的受剪板幅，当腹板的高度变化不超过 60mm/m时，其抗剪承载力设计值可按下列公式计算：
其中：
Vd
hwtw
f
' v
当w 0.8时 当0.8 w 1.4时 当w 1.4时
式中
f
' v
fv
f
' v
[1
桩基础竖向承载力力学特性及影响因素研究
- 114 -工 程 技 术桩基础由于承载力大和变形小的优点被广泛应用于工程建设中。
研究表明，桩基础可以有效控制上部结构的变形从而保证结构的稳定性。
针对桩基础竖向承载力力学特性，邓小雪[1]基于有限元方法研究了竖向荷载作用下复杂群桩的变形及荷载分布规律。
结果表明，超长群桩的Q-S 曲线呈缓变特征，桩身轴力在中桩最大，角桩最小，桩身的压缩沉降量随桩长增加而减少。
刘祥沛等[2]基于室内模型试验和数值模拟研究了桩基础破坏特征。
结果表明，当桩基础破坏时桩顶位移会迅速增加，破坏时桩底反力出现突变。
秋仁东等[3]基于大比例模型试验研究了长群桩基础承载力性状。
结果表明，群桩基础存在明显的硬化效应，端阻力在桩距较近的条件下提高幅度较大。
此外，群桩承台反力随沉降的增加而变大。
在其他条件相同的情况下，承台反力随桩距增加而变大。
考虑目前桩基础承载力计算不精确，桩基工程经常出现质量问题，造成人员和财产的损失。
本文采用数值模拟对桩的承载力特性及基础参数进行优化。
为相关工程设计及施工提供借鉴。
1 工况概况与数值模拟本文研究的桩基础属于桥梁桩基础，桩基础采用钻孔灌注桩，桩身混凝土强度均采用C 30混凝土浇筑。
预估单桩承载力特征值为2000kN 。
静载试验采用竖向承载力压桩试验，每根试验桩设计4根反力锚桩。
根据现场钻孔资料显示，研究区土体自上而下为素填土，颜色褐色-黄褐色，稍密，物理力学性质一般。
黏土，呈浅灰色，湿，稍密，局部相变为黏土，平均标贯击数N ＝6.6击，物理力学性质一般。
粉砂，中砂层呈灰色-灰黑色，颗粒大部分分散小部分胶结，粒径＞2mm 的颗粒含量占总质量的25％~50％，稍湿~饱和，中密状态。
根据勘查报告显示，现场地基属于软土地基，压缩性较大。
为保证基础承载力及变形要求，采用钻孔灌注桩进行施工。
本次压桩试验采用分级加载方式，每级荷载为200kN ，最终荷载为2000kN 。
为进一步研究桩土相互作用，本文采用ABAQUS 数值模拟建立不同桩长及不同桩径的有限元数值模型，以便系统分析桩基的竖向承载力特性，并选出最优桩基础设计方案。
第7章--桩基础
第7章--桩基础第7章桩基础桩基础由设置于土中的基桩和承接结构荷载的承台共同组成如图7－1所示，根据承台的位置高底，可分为低承台桩基础和高承台桩基础两种。
若桩身全部埋入土中，承台底面土体接触则称为高承台桩基础;若桩身上部露出地面面承台底面位于地面以上则称为高承台桩基础。
由于承台位置的不同，两种桩基础中基桩的力、变形情况也不一样，因而其设计方法也不相同。
建筑物桩基础通常为低承台桩基础，而码头、桥梁等构筑物经常采用高承台桩基础。
基桩是指群桩基础中的单桩，群桩基础是由两根以上基桩组成的桩基础；单桩基础是采用一根桩（通常为大直径桩）承受和传递上部结构（通常为柱）荷载的独立基础。
桩基础的功能及适用条件1、桩基础的功能桩基础的主要功能是将上部结构的荷载传至地下较深的密实或低压缩性的土层中，以满足承载力和沉降的要求。
桩基础也可用来承受上拔力、水平力，或承受垂直、水平、上拔荷载的共同作用以及机器产生的振动和动力作用等。
2、适用条件桩基础的适用条件主要根据场地的工程地质条件、设计方案的技术经济比较以及施工条件而定。
与其它深基础相比，桩基础的适用范围最广，一般来说，在下列情况下可考虑选用桩基础方案：（1）高、重建筑物下的浅层地基土承载力与变形不能满足要求时；（2）地基软弱，而采用地基加固措施在技术上不可行或经济上不合理时，或地基土性特殊，如液化土、湿陷性黄土、膨胀土、季节性冻土等特殊土时；（3）除了存在较大的垂直荷载外，还有较大的偏心荷载、水平荷载、动力荷载及周期性荷载作用时；（4）上部结构对基础的不均匀沉降相当敏感，或建筑物受相邻建筑或大面积地面荷载的影响时；（5）对精密或大型的设备基础需要减少基础振幅，减弱基础振动对结构的影响，或应控制基础沉降和沉降速率时；（6）地下水位很高，采用其它基础形式施工困难，或位于水中的构筑物基础，如桥梁、码头、采油钻井平台等；（7）需要长期保存、具有重要历史意义的建筑物。
7-1桩基础的类型根据桩的不同分类标准，桩基础有不同的分类。
2016高层大作业答案
一、概念选择题1、高层建筑结构的受力特点是（ B ）：A 竖向荷载为主要荷载，水平荷载为次要荷载B 水平荷载为主要荷载，竖向荷载为次要荷载C 竖向荷载和水平荷载均为主要荷载D 不一定2、多遇地震作用下层间弹性变形验算的重要目的是下列所述的哪种? ( C ) A ．防止结构倒塌； B ．防止结构发生破坏； C ．防止非结构部分发生过重的破坏； D ．防止使人们惊慌。
3、框架结构中柱子的抗侧刚度修正系数α与梁柱相对刚度有关，梁刚度愈小，则α（ A ）。
A 、愈小B 、愈大C 、不变D 、不一定4、剪力墙高宽比H ／B<1.5，墙体易发生（ C ）。
A ．弯曲破坏B ．弯剪破坏C ．剪切破坏D ．弯压破坏5、当剪力墙的整体系数满足（A ），可不考虑连梁的约束作用，各墙肢分别按独立的悬臂墙计算。
A ．1<α B ．101<≤α C ．10≥α D ．与α没有关系6、墙肢的轴向变形，随着层数增大，其影响就( A )。
A ．越大 B ．与高宽比无关 C ．越小 D ．不变7、竖向荷载作用下剪力墙内力的计算，不考虑结构的连续性，可近似认为各片剪力墙只承受( C )。
A ．弯矩 B ．剪力 C ．轴向力 D ．弯矩和轴向力8、计算框架结构梁截面惯性矩I 时考虑楼板影响，0I 为按矩形截面计算的梁截面惯性矩，中框架梁取I=（ D ）。
A 、I 0B 、1.2I 0C 、1.5I 0D 、2I 09、以下平面形状的建筑物中，哪一种风荷载的体型系数最小（ B ）。
A. 正多边形B. 圆形C.矩形D. 风车形二、简答题1、画出如图1所示荷载作用下框架结构的弯矩图（只画形状，不必标大小）。
图1结构中水平荷载是如何分配的？(1)平面抗侧力结构将高层建筑结构沿两个正交主轴方向划分为若干榀平面抗侧力结构，然后分别对作用在这两个方向上的水平荷载进行分析。
每一个方向上的水平荷载，仅由该方向上的平面抗侧力结构承受，垂直于水平荷载方向的抗侧力结构不参加抵抗水平荷载的工作。
7 竖向荷载作用下框架的内力分析
7 竖向荷载作用下框架的内力分析本框架结构对称、荷载对称、三跨，可取半结构结构计算。
计算简图如图7.1所示。
图7.1 半结构计算简图7.1 计算方法竖向荷载作用下框架的内力可以采用分层法进行简化计算。
1）关于分层法①基本原理：假定作用在某一层框架梁上的荷载（竖向的）只对本楼层的梁及与本层梁相连的框架柱产生弯矩和剪力，而对其他楼层的框架梁及隔层的框架柱都不产生弯矩和剪力。
②修正：由于除底层外，其余各层柱端并非如该方法所假设的完全固端（有转角产生），对此应做以下修正：a)除底层以外的其他各层柱的线刚度均乘以0.9的系数；b)除底层以外的其他各层柱的弯矩传递系数取为1/3；③若欲提高精度，可对节点，特别是边节点的不平衡弯矩再做一次分配，予以修正。
——摘录至《混凝土结构·中册》中国建筑工业出版社2）各类荷载作用下内力分析① 均布荷载作用下q q ql M M B A 7075.2127.5*1222-=-=-=-= q q ql V V B A 85.227.5*2===-=（简支时） q q ql M 061.487.5*822===跨中（简支时）② 梯形及三角形荷载作用(i)梯形荷载作用276.057001575===l a α q q ql M M B A 352.2)276.0276.021(127.5*)21(12322322-=+⨯--=+--=-=αα q q ql V V B A 063.2)276.01(27.5*)1(2=-=-=-=α（简支时） q q ql M 649.3)276.043(247.5*)43(242222=⨯-=-=α跨中（简支时）(ii) 三角形荷载作用（半跨）q q ql M A 5672.085365.185322-=⨯-=⨯-=q q ql M B 2836.0215672.08562-=⨯-=⨯-=(iii) 三角形荷载作用（全跨） q q ql V V B A 825.05.023.3*2=⨯==-=α（简支时）q q ql M 9075.0)5.043(243.3*)43(242222=⨯-=-=α跨中（简支时）3）计算各节点上各杆件的线刚度、转动刚度与节点弯矩分配系数，详见图7.1.1、图7.1.2所示。
竖向荷载作用下结构水平位移分析
竖向荷载作用下结构水平位移分析向需文谢伟平王国波于艳丽(武汉理工大学土木工程与建筑学院武汉430070)摘要：结构不发生侧移的临界位置称为位移平衡点。
本文利用虚功原理、力法等结构力学基本原理，并结台定性结构力学的分析判断，推导、证明了单跨刚架在左右两柱刚度变化时位移平衡点的变化规律，并将这两个结论推广到多跨多层NⅡ架结构。
理论推导和算例分析表明：(1)位移平衡点偏向于柱子刚度弱小的一侧；(2)单跨刚架在竖向荷载作用下，刚架侧移的方向与荷载绕位移平衡点转动的方向相反。
论文分析结果可为高层建筑结构的初步定性设计提供参考。
关键词：剐架位移平衡点刚架侧移虚功原理定性结构力学图1(a)为在梁跨中作用竖向荷载的刚架，各杆EI 1引言(抗弯刚度)一样，左边铰支，右边固支，显然一般情况近年来国内外土木工程事业蓬勃发展，高层建筑下不通过计算是很难判断出该刚架侧移方向的，所以不断涌现n．：，，而水平侧移一直是高层结构设计中需要必须要对模型进行简化。
本文利用虚功原理将竖向荷控制的重要设计指标。
但是结构的水平位移通常被认为是由水平荷载引起的，实际上竖向荷载也同样能引载作用下的水平侧移问题转化为分析水平荷载作用下起结构的水平位移。
对于一些结构，尤其是以动力响梁的变形问题。
应为主的结构，设计时要特别考虑这种水平位移‰被由虚功原理”一：称为‘'wobbl yBridge'’的伦敦千禧桥就曾在人群行走过FxA。
=PxA，(1)程中出现了明显的水平振动韩国首尔一高楼因数人其中，F表示作用在刚架上的水平荷载，P表示齐练健身操导致大楼产生摇晃。
所以研究结构在竖向作荷载作用下的侧移很有必要。
但是当下研究竖向荷载用在刚架上的竖向荷载，△；是P作用下刚架的水平侧下结构水平位移的文献并不多见，本文拟在前人的研移，表△示F作用下在对应P处的竖向位移。
究基础上对结构的一般性结论进行推广，并得出快速若F=P，有△产△，，即竖向荷载作用下刚架的水平判断结构在竖向荷载作用下侧移方向的方法。
竖向荷载的原理
竖向荷载的原理竖向荷载是指作用在建筑物或结构物上方向垂直于地面的荷载力。
对于建筑物或结构物而言，竖向荷载是其设计和施工过程中必须重视的重要因素之一。
竖向荷载的原理是指竖向荷载产生的原因及其作用机理。
竖向荷载可以由多种原因产生，其中包括自重、活载、雪载、风载、地震荷载等。
自重是建筑物或结构物自身重量所产生的竖向荷载，是任何建筑结构所必须考虑的基本荷载。
活载是指人员、家具、机器设备等临时负荷对建筑物或结构物所产生的额外竖向荷载。
雪载是指在寒冷地区或高海拔地区，积雪所产生的竖向荷载。
风载是指气象风力作用于建筑物或结构物表面所产生的竖向荷载。
地震荷载是指地震作用于建筑物或结构物的水平位移所产生的竖向荷载。
这些竖向荷载都会对建筑物或结构物产生一定的影响，因此在设计和施工过程中需要进行精确计算和合理考虑。
竖向荷载的作用机理是指竖向荷载对建筑物或结构物的影响和作用方式。
竖向荷载会通过传递和分布作用于建筑物或结构物的各个部位。
在竖向荷载的作用下，建筑物或结构物的不同部位会受到不同程度的应力和变形。
这些应力和变形会引起建筑物或结构物的变形和变形，从而影响其力学性能和安全性能。
竖向荷载的作用机理可以通过弹性力学原理进行分析和计算。
弹性力学原理是研究弹性体在外力作用下的应力与应变关系的理论基础。
基于弹性力学原理，可以将竖向荷载作用下的建筑物或结构物看作是弹性体，在不同部位受到不同程度的应力和变形。
通过对建筑物或结构物进行应力分析和变形分析，可以评估其受力性能和变形性能，从而确保其设计合理和施工安全。
在竖向荷载的作用下，建筑物或结构物通常会发生竖向位移和变形。
竖向位移是指建筑物或结构物整体沿竖直方向的位移，通常由荷载作用导致的竖向应力引起。
竖向变形是指建筑物或结构物各部位相对运动造成的形状变化，也是由荷载作用导致的应力和变形引起。
建筑物或结构物的竖向位移和变形对其结构的安全和稳定性具有重要影响，因此在设计和施工过程中需要充分考虑和控制。
高层结构设计第3章 高层建筑的荷载和地震作用
3、抗震设防目标
具体通过“三水准”的抗震设防要求和 “两阶段”的抗震设计方法实现。
三水准地震作用的标定
三水准：“小震”“中震”“大震” 地震影响 众值烈度（多遇地震）小震 基本烈度（设防烈度地震）中震 罕遇烈度（罕遇地震）大震 50年超越概率 63.2% 10% 2-3% 地震重现期 50年 475年 1642-2475年
：空气密度
2014-11-16
15
（2）风荷载体型系数 s 风对建筑表面的作用力并不等于基本风压值，而是随建筑物的 体型、尺度、表面位臵等而改变，其大小由实测或风洞试验确定 s =垂直于建筑表面的平均风作用力/基本风压值
2014-11-16
16
（2）风荷载体型系数 s 风对建筑表面的作用力并不等于基本风压值，而是随建筑物的 体型、尺度、表面位臵等而改变，其大小由实测或风洞试验确定 s =垂直于建筑表面的平均风作用力/基本风压值
吸力
2014-11-16
27
4、总风荷载
各个表面承受风力的合力，沿高度变化的分布荷载
Z Z 0 (1 B1 cos1 Zn Bn cos n )
α2 =900 α1=0 μs= +0.8 B1 wind B4
μs=-0.6
2014-11-16 28
μs=-0.6
4、地震作用计算原则
一般情况下，计算两个主轴方向的地震作用；有斜交抗 侧力构件（角度大于 15 度）时应分别计算各抗侧力构件 方向的地震作用 质量与刚度分布明显不对称、不均匀的结构，应计算双 向水平地震作用下的扭转影响，其他情况应计算单向地 震作用下的扭转影响 8 度和 9 度抗震设计时，高层建筑中的大跨度和长悬臂结 构应考虑竖向地震作用 9度抗震设计时应计算竖向地震作用
混凝土结构设计复习题
混凝土结构设计复习题三、填空题1.大偏心受压构件破坏相当于受弯构件（适筋）梁的破坏；而小偏心构件破坏相当于（超筋）梁的破坏。
2.大偏心受压截面的破坏特征是（1受拉钢筋屈服后混凝土被压碎2压碎区较小3拉区裂缝较宽）。
小偏心受压截面的破坏特征是（1截面全部或大部受压2压碎区较大3距轴力较远一侧钢筋一般均未达到屈服）。
3.矩形截面大偏心受压构件强度计算公式的适用条件是（ξ≤ξb）和（某≥2a’）。
4.钢筋混凝土偏心受压构件截面承载能力Np—Mp的关系是：当发生“受压破坏”时，随着弯矩的（增大），构件的抗压能力（减小）；当发生“受拉破坏”时，随着轴力的（增大），抗弯能力（增大）。
5.大偏心受压柱的截面强度，当弯矩M一定，轴力N愈大截面愈（安全）；小偏心受压柱截面强度，当弯矩M一定，轴力N愈大截面愈（危险）。
6.在大偏压柱中，最危险的内力组合是：当M相近时，N愈（小），愈危险，或当N相近时，M愈（大）愈危险。
7.大偏心受压柱的判别式是（某≤ξbh0）。
8.轴心受压构件纵向弯曲系数随长细比的增大而（减小）。
9.偏心受压构件的破坏形态分为（受压破坏）和（受拉破坏）。
应根据（ξ）来判断。
10.偏心受压构件破坏形态有受拉破坏和受压破坏，受拉破坏混凝土压碎区较受压破坏压碎区（小）。
11.偏心受压构件除应计算弯矩作用平面的强度以外，尚应按（轴心受压构件）验算出垂直于弯矩平面的强度。
12.预应力混凝土中，混凝土强度等级一般不宜低于（C30），当采用高强度钢丝、钢铰线时，混凝土强度等级不宜低于（C40）。
13.钢筋混凝土构件中，受拉区混凝土即将开裂时的受拉钢筋应力大致是（20-30）N/mm2左右。
14.对构件施加预应力能推迟（裂缝）的出现，提高构件（抗裂度）和（刚度）。
15.对锚具的要求主要为（安全可靠）、（预应力损失小）、（构造简单）、（施工方便）。
16.先张法预应力构件是靠（粘结力）来传递预应力的，而后张法是靠（锚固）来保持预应力的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
9竖向荷载作用下结构的内力分析9.1竖向荷载作用下框架内力分析1荷载及计算简图⑴计算方法框架在竖向荷载作用的内力计算可采用精确法(如弯矩分配法),也可采用近似法(如分层法).由于在竖向荷载作用下框架侧移很小,而且各层荷载对其他层杆件内力影响不大,本本工程手算采用弯矩二次分配法.⑵荷载计算计算以1轴为设计对象,板的受力计算简图如图①屋面梁的均布线荷载恒载计算------屋面板传来的梯型恒载0.5*3.6*5.5=9.90KN/m梁自重0.25*0.60*25=3.75KN/m女儿墙自重1.72*1.2=2.064KN/m活载计算------屋面板传来的梯型活载0.5*3.6*2.0=3.6KN/m②5~12层梁的均布线荷载恒载计算-------板传来的梯型恒载0.5*2.0*2.95=2.95KN/m0.5*3.6*2.95=5.31KN/m梁自重0.25*0.6*25=3.75KN/m外墙自重1.72*2.4=4.13KN/m集中力31.05KN活载计算------板传来的梯型活载0.5*2.0*2.0=2.0 KN/m0.5*3.6*2.0=3.6KN/m集中力 4.75KN③2~3层梁的均布线荷载恒载计算------板传来的梯型恒载0.5*3.6*2.95=5.31KN/m梁自重0.25*0.60*25=3.75KN/m外墙自重1.72*2.7=4.644KN/m 活载计算------板传来的梯型活载0.5*3.6*2.0=3.6KN/m 则1轴的横向框架恒荷载及活荷载分布如图:恒荷载示意图活载示意图⑶计算跨度框架梁、柱用轴线表示,节点间的水平距离为梁的计算跨度.柱计算高度对一般层可取层高,对底层取基础顶面与上层楼板顶面之间的高度.2内力计算⑴恒载作用下杆端弯矩计算 ① 框梁固端弯矩 屋顶框梁:Ⅰ梁自重、女儿墙自重1g =3.75+2.064=5.814KN/m2/ql R R B A ===5.814/2=2.907KNm KN ql M M B A .07.231290.6814.51222-=⨯-=-==Ⅱ板传来的梯型恒载m KN g /90.92=KN q a l R R B A 25.2590.928.19.62=⨯-=-== m KN l a l a ql M M B A .63.34)9.68.19.68.121(1290.69.9)21(123322233222-=+⨯-⨯⨯-=+--==4~12层框梁:Ⅰ梁自重、外墙自重1g =3.75+4.13=7.88KN/m2/ql R R B A ===7.88/2=3.94KNm KN ql M M B A .26.311290.688.71222-=⨯-=-==Ⅱ板传来的梯型恒载m KN g /31.52=KNc bc l c b l b lqc R A 36.4)458.148.17.529.68.17.5129.67.518(9.6128.131.5)45421218(12322323322323=⨯-⨯⨯-⨯+⨯-⨯⨯⨯⨯=--+-= mKN c l c bc ab lqc M A .725.3)158.129.68.18.17.537.52.118(9.6368.131.5)152318(363222232222-=⨯-⨯+⨯⨯-⨯⨯⨯⨯-=-+--= mKN c l c bc ab l qc M B .978.3)158.129.68.128.17.537.52.118(9.6368.131.5)1522318(363222232222-=⨯+⨯⨯-⨯⨯+⨯⨯⨯⨯-=+-+-=KN c bc l c b l b lqc R B 25.2)458.148.14.229.68.13.3129.63.318(9.6128.131.5)45421218(12322323322323=⨯-⨯⨯-⨯+⨯-⨯⨯⨯⨯=--+-= KN R qc R B A 53.225.228.131.52=-⨯=-=mKN c l c bc ab lqc M A .869.3)158.129.68.128.13.333.36.318(9.6368.131.5)1522318(363222232222-=⨯+⨯⨯-⨯⨯+⨯⨯⨯⨯-=+-+-=mKN c l c bc ab lqc M B .563.2)158.129.68.18.13.333.36.318(9.6368.131.5)152318(363222232222-=⨯-⨯+⨯⨯-⨯⨯⨯⨯-=-+--=KN bc l c b l b l qc R A 58.3)9.065.429.69.065.489.665.412(9.649.031.5)2812(42232322323=⨯⨯-⨯+⨯-⨯⨯⨯⨯=-+-⨯=KN R qc R B B 199.158.39.031.5=-⨯=-=m KN l c bc ab l qc M A .836.4)9.69.09.065.4365.425.212(9.61290.031.5)312(1222222222-=⨯+⨯⨯-⨯⨯⨯⨯-=+--= m KN l c bc ab l qc M B .885.4)9.69.029.065.4365.425.212(9.61290.031.5)2312(1222222222-=⨯⨯-⨯⨯+⨯⨯⨯⨯-=⨯-+-= 板传来的梯型恒载m KN g /95.22'=KNc bc l c b l b l qc R A 23.0)450.140.173.129.60.173.1129.673.118(9.6120.195.2)45421218(12322323322323=⨯-⨯⨯-⨯+⨯-⨯⨯⨯⨯=--+-= mKN c l c bc ab l qc M A .466.0)150.129.60.10.173.1373.117.518(9.6360.195.2)152318(363222232222-=⨯-⨯+⨯⨯-⨯⨯⨯⨯-=-+--= mKN c l c bc ab l qc M B .465.0)150.129.60.120.173.1373.117.518(9.6360.195.2)1522318(363222232222-=⨯+⨯⨯-⨯⨯+⨯⨯⨯⨯-=+-+-=KN c bc l c b l b l qc R B 43.1)450.140.123.629.60.123.6129.623.618(9.6120.195.2)45421218(12322323322323=⨯-⨯⨯-⨯+⨯-⨯⨯⨯⨯=--+-= KN R qc R B A 05.043.120.195.22=-⨯=-=mKN c l c bc ab l qc M A .814.0)150.129.60.120.123.6323.667.018(9.6360.195.2)1522318(363222232222-=⨯+⨯⨯-⨯⨯+⨯⨯⨯⨯-=+-+-= mKN c l c bc ab l qc M B .785.0)150.129.60.10.123.6323.667.018(9.6360.195.2)152318(363222232222-=⨯-⨯+⨯⨯-⨯⨯⨯⨯-=-+--=KN bc l c b l b l qc R A 10.0)4.02.129.64.02.189.62.112(9.644.095.2)2812(42232322323=⨯⨯-⨯+⨯-⨯⨯⨯⨯=-+-⨯=KN R qc R B B 08.110.04.095.2=-⨯=-=m KN l c bc ab l qc M A .205.0)9.64.04.02.132.17.512(9.6124.095.2)312(1222222222-=⨯+⨯⨯-⨯⨯⨯⨯-=+--=m KN l c bc ab l qc M B .202.0)9.64.024.02.132.17.512(9.61240.095.2)2312(1222222222-=⨯⨯-⨯⨯+⨯⨯⨯⨯-=⨯-+-= Ⅲ次梁传来的集中力F=31.05KNKN b a l Pb R A 66.8)4.25.43(9.64.205.31)3(3232=+⨯⨯=+= m KN l Pab M A .904.169.64.25.405.312222-=⨯⨯-=-=m KN l b Pa M B .696.319.64.25.405.312222-=⨯⨯-=-= 2~3层框梁Ⅰ梁自重、女儿墙自重1g =3.75+4.644=8.394KN/m96.282/9.6394.82/=⨯===ql R R B A KNm KN ql M M B A .303.331290.6394.81222-=⨯-=-==Ⅱ板传来的梯型恒载m KN g /31.52=KN q a l R R B A 54.1331.528.19.62=⨯-=-== mKN l a l a ql M M B A .574.18)9.68.19.68.121(1290.631.5)21(123322233222-=+⨯-⨯⨯-=+--==活载产生的梁固端弯矩(计算方法同上) 同上计算结果列于力矩二次分配法表中.⑵根据梁、柱线刚度,计算各节点弯矩分配系数 顶层(12层)边框架边节点13A ：13131313131213131313131244219130.39110.609444(2191334200)A B A B AA ABA B A A i i i μμμ⨯====-=+⨯+注:AiBi μ为i 层梁板框架梁A 节点分配系数,1-AiBi μ为i 层梁板框架柱A 节点分配系数.11层~9层边框架边节点10~12A121212121213121112121211121344219130.2420.3794444(21913342002)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯+⨯8层边框架边节点9A :999991098999109844234780.2090.3040.4874444(234783420054705)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯++7层~5层边框架边节点6~8A :8888898788898744234780.1760.4124444(23478254705)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯+⨯4层边框架边节点5A :5555565455565444246520.1600.3540.4864444(246525470575144)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯++3~2层边框架边节点3~4A :4444454344454344246520.1400.4304444(24652275144)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯+⨯1层边框架边节点2A :2222232122232144246520.1860.5670.2474444(246527514432844)A B A B A A A A A B A A A A i i i i μμμ⨯=====++⨯++⑶纵向框梁产生的柱轴力R 及柱偏心弯矩M纵向框梁,按简支梁计算的支反力R 反向作用于柱上 恒载:1g --梁自重; 2g --板传来的; 3g --墙自重屋面:KN R A 88.13=; 5~12: KN R A 62.15= 2~4: KN R A 55.16= 屋面:m KN M A .74.1125.088.13=⨯= 9~12:m KN M A .95.1125.062.15=⨯= 5~8: m KN M A .34.215.062.15=⨯= 2~4: m KN M A .90.2175.055.16=⨯= 活载:m KN q l q o /8.12==; KN lqR 62.12==9~屋面: m KN M A .20.0125.062.1=⨯= 5~8: m KN M A .24.015.062.1=⨯= 2~4: m KN M A .29.0175.062.1=⨯=⑷弯矩二次分配①恒载作用下弯矩二次分配②活载作用下弯矩二次分配恒载作用下框架弯矩图M(kN m)活载作用下框架弯矩图M(kN m)⑸梁端剪力及柱轴力计算对与梁剪力的求解要根据以上梁实际受荷情况梁已求的梁端弯矩，再由实际受荷与弯矩求剪力。