RLC串联电路教案
电工基础教案12RLC串联电路

RLC串联电路授课教案课题模块三正弦交流电路课题四RLC串联电路授课班级授课时间教学目的1.会计算RLC串联电路的电压、电流及功率2.会计算功率因数教学重点及难点重点:RLC串联电路的电压、电流及功率的计算难点:提高功率因数的方法教学内容纲要教学方法一、RLC串联电路的分析与计算1.推导:如图 3-1 所示 R 、 L 、 C 串联电路。
根据 KVL 可得:由R、L、C三元件的伏安关系图 3-1。
可得即图 3-2式中称为复阻抗。
以电流相量为参考相量,作相量图如图3-2 所示。
从相量图可见,三者组成一个直角三角形,称为电压三角形,三者之间满足2.复阻抗的计算1 )直接计算式中图 3-3之间符合阻抗三角形关系,见图 3-32 )间接计算阻抗三角形即阻抗模是电压有效值与电流有效值的比,它的幅角等于电压与电流的相位差。
3 .阻抗角与电路性质①当时,电压超前电流,电路呈感性;②当时,电流超前电压,电路呈容性;③ 当时,电压与电流同相,电路呈电阻性;注:特例1 . R-L 串联2 . R-C 串联例1 :R 、 L 、 C 串联电路中,已知电源频率。
试求电路复阻抗 Z 。
若电源频率,重求复阻抗 Z 。
解:①当时②当时图 3-4例2 :电路如图 3-4(a) 所示,,电源频率,求:①电流及总复阻抗 Z ;②总电压、电感及电容电压的有效值;③ 画相量图。
解:①求总电流及复阻抗;②求各电压;③ 画相量图,见图 3-4(b) 。
例3 :移相电路如图 3-5 所示,,欲使输入电压滞后输出电压,求电感量 L 及输出电压。
图3-5解:设电流相量为,电路为 RL 串联电路,电压超前电流。
因此作相量图如图 3-5( b )所示。
根据题意则电路的复阻抗阻抗角因此由构成的直角三角形可知二、功率因数1、有功功率(平均功率)瞬时功率的平均值称为平均功率,也称有功功率,用 P 表示,单位为瓦( W )。
2、无功功率正弦稳态二端网络电路内部与外部能量交换的最大速率定义为无功功率,用字母Q 表示,单位为乏。
RLC串联电路教案(可打印修改)
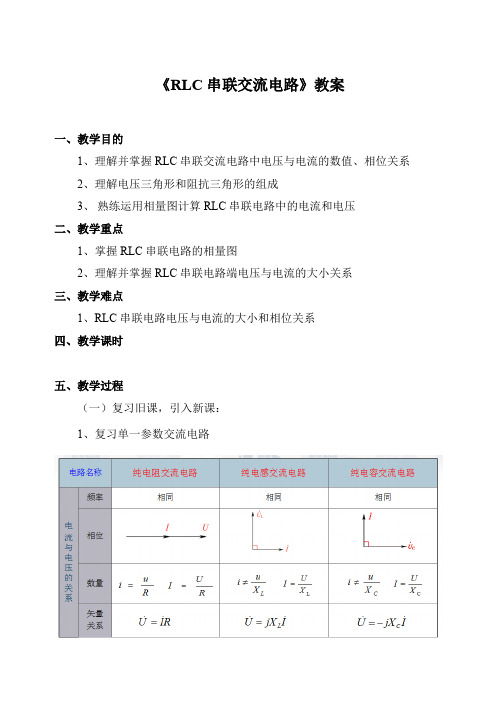
《RLC串联交流电路》教案一、教学目的1、理解并掌握RLC串联交流电路中电压与电流的数值、相位关系2、理解电压三角形和阻抗三角形的组成3、熟练运用相量图计算RLC串联电路中的电流和电压二、教学重点1、掌握RLC串联电路的相量图2、理解并掌握RLC串联电路端电压与电流的大小关系三、教学难点1、RLC串联电路电压与电流的大小和相位关系四、教学课时五、教学过程(一)复习旧课,引入新课:1、复习单一参数交流电路2、引出问题正弦交流电路一定是单一参数特性吗?分析:1、实际电路往往由多种元件构成,不同元件性质不同。
例如,荧光灯电路2、交流电路中的实际元件往往有多重性质,如电感线圈存在一定的电阻, 匝与匝之间还有电容效应因此,单一参数交流电路知识一种理想情况,具有多元件、多参数的电路模型更接近于实际应用的电路。
3、新的学习任务研究多元件、多参数的交流电路(二)新课讲授图1 RLC 串联交流电路1、电压与电流的关系以电流作为参考,设表达式为则由基尔霍夫第二定律可知,CL R u u u u ++=)90sin()90sin(sin ︒︒-+++=t X I t X I t R I u C m L m m ωωω同频率正弦量的和仍为同频率的正弦量,因此电路总电压u 也是频率为的正弦量。
正弦量可以用矢量表示,则(1)式为:CL R U U U U &&&&++=[]Z I I jX R I X X j R U CL &&&&=+=-+=)()(这是RLC 串联电路中总电压和总电流的关系,形式和欧姆定律类似,所以也称 相量形式的欧姆定律。
RLC 串联电路中总电压和总电流的数值关系:22)(C L R U U U U -+=22)(C L X X R I -+=Z I =RLC 串联电路中电压电流的相位关系RX X U U U C LR C L -=-=arctan arctan ϕ上述分析过程,我们用矢量表示正弦量,根据复数运算的相关知识进行分析得出了结论。
RLC串联电路谐振条件和谐振频率
平山县职业教育中心教案首页编号:_10_号授课教师:___宋翠平_____授课时间:_5_月____步骤教学内容教学方法教学手段学生活动时间分配明确目标一、明确目标:教师解读学习目标二、引入任务1:在无线电技术中常应用串联谐振的选频特性来选择信号。
收音机通过接收天线,接收到各种频率的电磁波,每一种频率的电磁波都要在天线回路中产生相应的微弱的感应电流。
为了达到选择信号的目的,通常在收音机里采用如图1所示的谐振电路。
讲授(口述)演示启发提问讨论展示实物展示课件板书个别回答小组讨论代表发言7分钟操作示范一、教师讲解RLC串联电路谐振条件和谐振频率1、谐振条件——电阻、电感、电容串联电路发生谐振的条件是电路的电抗为零,即:0=-=CLXXX。
则电路的阻抗角为:。
φ=0说明电压与电流同相。
我们把RLC串联电路中出现的阻抗角φ=0,电流和电压同相的情况,称作串联谐振。
2、谐振频率——RLC串联电路发生谐振时,必须满足条件:教师示范课件演示教师提问课件板书演示学生抢答小组抢答10分钟分析上式,要满足谐振条件,一种方法是改变电路中的参数L或C,另一种方法是改变电源频率。
则,对于电感、电容为定值的电路,要产生谐振,电源角频率必须满足下式:谐振时的电压频率为:谐振频率f0仅由电路参数L和C决定,与电阻R的大小无关,它反映了电路本身的固有特性,f0叫做电路的固有频率。
合作学习任务2学生分析讨论试做下面习题:在电阻、电感、电容串联谐振电路中,L=0.05mH,C=200pF,品质因素Q=100,交流电压的有效值U=1mV,试求:(1)电路的谐振频率f0;(2)谐振时电路中的电流I0;(3)电容上的电压UC。
解:(1)电路的谐振频率为:f0=1/〔2π(LC)1/2〕= 1/〔2×3.14×(0.05×10-3×200×10-12)1/2〕≈1.59MHz(2)由于品质因素Q=(L/C)1/2/R 则R=(L/C)1/2/Q=(5×10-5/2×10-10)1/2/100=5Ω谐振时,电路中的电流为:I0=U/R=1×10-3/5=0.2mA(3)电容两端的电压是电源电压的Q倍:UC=QU=100×1×10-3=0.1V启发诱导重点讲解个别指导课件板书个人操作小组操作20分钟任务3学生分析讨论串联谐振电路的通频带实际应用中,既要考虑到回路选择性的优劣,又要考虑到一定范围内回路允许信号通过的能力,规定在谐振曲线上,所包含的频率范围叫做电路的通频带,用字BW表示,如图2所示。
实验十__RLC串联谐振电路PPT教案

360
4、RLC串联电路幅频特性
Z R j(L 1 ) c
(1)谐振条件
当XL=XC时电路谐振.1
谐振频率:
f0
2 LC
(2)电路串联谐振的特点:
①阻抗最小. Z = R. (输入端电压最小) Q测量值和计算值不同
②电流最大. I0 = U/R. (UR上电压最大)
③Φωi(相位) = 0.
Q:回路品质因数,一般情况下
R 0CR R
Q>>1
RLC串联谐振电路 R=0 和 R=20欧姆测两次
(3)UC~f曲线和UL~f曲线 (L、C上电压随频率变化的关系)
当保持信号电压U不
变而改变信号频率时 UL UC
1
因,此L、我C们上可电使压用随点频测率
UC
UL
法改测变量。输出电压幅频
特要性求的信方号法源测是量恒其压频源 0 率,特所性以。在测量过程中
实验日期
班级 姓名 学号
数据处理 f 0
1
2 LC
Q0 = UC/U = ? Q20= UC/U = ?
实验考核: RLC串联谐振电路 实验日期
班级 姓名 学号
绘图:
绘图:
数据处理
1
标
标
f0
2 LC
注
注
Q0 = UC/U = ?
Q20= UC/U = ?
四、回答问题(不作)
(1)谐振时,电阻R两端电压为 什么与电源电压不相等?电容两 端的电压是否等于电感两端的电 压? (2)为什么做串联谐振电路实 验时,在谐振频率附近信号源输 出电压显著下降? (3)用一只标准电容器,应用 谐振原理,设计测量未知电感的
f 2 1 ~ 相频特性
RLC串联谐振电路

RLC串联谐振电路(1)实验目的:1.加深对串联谐振电路条件及特性的理解。
2.掌握谐振频率的测量方法。
3.理解电路品质因数的物理意义和其测定方法。
4.测定RLC串联谐振电路的频率特性曲线。
(2)实验原理:RLC串联电路如图所示,改变电路参数L、C或电源频率时,都可能使电路发生谐振。
该电路的阻抗是电源角频率ω的函数:Z=R+j(ωL-1/ωC) 当ωL-1/ωC=0时,电路中的电流与激励电压同相,电路处于谐振状态。
谐振角频率ω0 =1/LC,谐振频率f0=1/2πLC。
谐振频率仅与原件L、C的数值有关,而与电阻R和激励电源的角频率ω无关,当ω<ω0时,电路呈容性,阻抗角φ<0;当ω>ω0时,电路呈感性,阻抗角φ>0。
1、电路处于谐振状态时的特性。
(1)、回路阻抗Z0=R,| Z0|为最小值,整个回路相当于一个纯电阻电路。
(2)、回路电流I0的数值最大,I0=U S/R。
(3)、电阻上的电压U R的数值最大,U R =U S。
(4)、电感上的电压U L与电容上的电压U C数值相等,相位相差180°,U L=U C=QU S。
2、电路的品质因数Q电路发生谐振时,电感上的电压(或电容上的电压)与激励电压之比称为电路的品质因数Q,即:L/Q=U L(ω0)/ U S= U C(ω0)/ U S=ω0L/R=1/R*C(3)谐振曲线。
电路中电压与电流随频率变化的特性称频率特性,它们随频率变化的曲线称频率特性曲线,也称谐振曲线。
在U S 、R 、L 、C 固定的条件下,有I=U S /22)C 1/-L (ωω+RU R =RI=RU S /22)C 1/-L (ωω+R U C =I/ωC=U S /ωC 22)C 1/-L (ωω+R U L =ωLI=ωLU S /22)C 1/-L (ωω+R改变电源角频率ω,可得到响应电压随电源角频率ω变化的谐振曲线,回路电流与电阻电压成正比。
交流电路RLC串联教案

课内试验项目:RLC串联电路试验
提示注意事项,并重点讲解本次双踪示波器的使用方法。做好电
学生回答共同分析
第1页
教学
过程
教师活动
学生活动
导学达标
路图的连接示范,按照试验操作单对试验项目进行连接测试并作好记录。
二、结果分析与结论:(先提问1~2人)
为什么U≠UR+UL+ UC?
指导学生在示波器测出 的基础上画出电压相量三角形(假设:XL>XC):
电压相量三角形的画图步骤:
设以电流相量为基准
已知电阻上的电压与电流同相位,满足欧姆定律即
观察电感上的电压波形,得其波形超前电流波形约90O,其数值大小应为 ,相量关系为 。
观察电容上的电压波形,其波形落后电流约90O,其数值大小应为 ,相量关系为 。
进行相量合成,得如下图所示的相量图
理解掌握共同分析
共同分析
第3页
教学
过程
教师活动
学生活动
达标导学
2、RLC串联电路电流和电压相位关系:从双踪示波器上明显可以看出:在电阻R上,UR与i同相;在电感L上UL与i相差90度(超前);在电容C上Uc与i也相差90度(滞后)
3、从阻抗Z看电路性质:
由式:
可作出一个阻抗三角形。它与电压三角形相似,电压三角形的每边乘以电流即可得功率三角形。从阻抗三角形可得出:
三、R、L串联电路的功率关系和功率因数
将电压三角形的三边乘上I,就可得到各功率之间的关系,称“功率三角形”如下图所示:
从功率三角形可以得到三个功率之间的关系式:
S为视在功率,其单位为V· A(伏安)
其中:
从功率三角形还可以得到:
P=UIcosΦ
2020RLC串联电路教案

课时教案科目电工电子技术与技能第 1 周第课时 2020 年 2 月日课题复习3.3RLC串联电路授课班级教学目标知识与技能目标1、了解RLC串联电路。
2、掌握RL、RLC串联电路电压和阻抗的计算。
3、掌握RL,RLC串联电路功率的计算。
4、掌握RLC串联谐振电路产生的条件4过程与方法目标1.培养学生的理解能力。
2.培养学生解决实际问题的能力。
情感态度与价值观培养学生温故知新的学习习惯,学习适应网络教学模式,培养学生勇于面对挫折的精神重点RL,RLC串联电路的电压和电流的关系以及电路中的功率问题。
难点理解掌握RL,RLC串联电路的功率的计算。
教学方法网络直播,讲授,练习课型复习课教具资源笔记本电脑,手机,腾讯课堂,问卷星,云班课教学实施(仿此格式填写)内容安排时间安排教师活动学生活动设计意图复习导入5min ◆利用腾讯课堂播放PPT回顾总结纯电阻、纯电感和纯电容电路。
◆利用大学慕课播放RLC串联电路的授课视频。
【设备】腾讯课堂通过手机或者是电脑登入腾讯课堂熟悉上课软件一、RLC 串联电路的电压关系由电阻、电感、电容相串联构成的电路称为 RLC 串联电路。
各电压之间的大小关系为:22)(C L R U U U U -+=ZI X X R I U U U U C L C L R =-+=-+=2222)()(R-L-C 串联电路的欧姆定律表达式ZU I =2222)(X R X X R I UZ C L +=-+==阻抗:|Z |称为电路的阻抗,单位:欧姆 电抗:X = XL - XC 叫做电抗二、 R-L-C 串联电路的电压与电流的相位关系阻抗角:Φ 叫做阻抗角,体现了总电压与总电流之间的相位关系R X X R XC L arctan arctan-==ϕ(1)当C L X X >时,X > 0,0>ϕ,电路呈感性。
(2)当C L X X <时,X < 0,0<ϕ,电路呈容性。
电工电子教案2.5 RLC串联电路

C=32μF,电源电压为 u 220 2 sin(314t π)V
试求:
3
(1)电路中的电流;
(2)电压与电流的相位差;
(3)电阻、电感和电容的电压。
二、串联谐振
1.串联谐振
➢在RLC串联电路中,发生总电压和电流同相的现 象称为串联谐振;
➢串联谐振的条件为:X L X C
➢串联谐振频率(固有频率)为: 1
f0 2π LC
[动画演示]:串联谐振电路
二、串联谐振
2.串联谐振特点
(1)阻抗最小,且为纯电阻,即 Z =R; (2)电路中的电流最大,且与电压同相,即:
U I0 R
(3)电感与电容两端的电压相等,其大小为
总电压的Q倍,即:
UL
U C
QU
XL R
U
XC RU来自Q称为串联谐振电路的品质因数
➢电压和电流有效值之间仍符合欧姆定律,即:
IU Z
➢ Z 体现了电路对电流的阻碍作用,称为阻抗, 其单位仍为欧姆(Ω)。
Z R2 (XL XC )2
[动画演示]:RLC串联电路的特点
一、电流与电压的关系
1.数值关系
各电压之间关系为:
u uR uL uC
U UR UL UC
S P2 (QL QC )2
第五节 RLC串联电路
【课后作业】 1.教材中复习思考题第6、8题; 2.《电工电子技术及应用学习指导与练习》 第二章 填空题:17、18、19、20、21; 单项选择题:13、14、19、21、23、24、 25、26; 判断题:14、17、18、20; 计算题:2、3、4、7
三、电路的功率
3. 无功功率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《RLC串联交流电路》教案
一、教学目的
1、理解并掌握RLC串联交流电路中电压与电流的数值、相位关系
2、理解电压三角形和阻抗三角形的组成
3、熟练运用相量图计算RLC串联电路中的电流和电压
二、教学重点
1、掌握RLC串联电路的相量图
2、理解并掌握RLC串联电路端电压与电流的大小关系
三、教学难点
1、RLC串联电路电压与电流的大小和相位关系
四、教学课时
五、教学过程
(一)复习旧课,引入新课:
1、复习单一参数交流电路
2、引出问题
正弦交流电路一定是单一参数特性吗?
分析:
1、实际电路往往由多种元件构成,不同元件性质不同。
例如,荧光灯电路
2、交流电路中的实际元件往往有多重性质,如电感线圈存在一定的电阻,匝与匝之间还有电容效应
因此,单一参数交流电路知识一种理想情况,具有多元件、多参数的电路模型更接近于实际应用的电路。
3、新的学习任务
研究多元件、多参数的交流电路
(二)新课讲授
图1 RLC 串联交流电路
1、电压与电流的关系
以电流作为参考,设表达式为
则
由基尔霍夫第二定律可知,
C
L
R
u
u
u
u+
+
=
)
90
sin(
)
90
sin(
sin︒
︒-
+
+
+
=t
X
I
t
X
I
t
R
I
u
C
m
L
m
m
ω
ω
ω
同频率正弦量的和仍为同频率的正弦量,因此电路总电压u也是频率为的正弦量。
+uR-+uL-+uC-
R LC
B
A
+-
u
i i
正弦量可以用矢量表示,则(1)式为:
C
L
R
U
U
U
U
+
+
=
[]Z I
I
jX
R
I
X
X
j
R
U
C
L
=
+
=
-
+
=)
(
)
(
这是RLC串联电路中总电压和总电流的关系,形式和欧姆定律类似,所以也称相量形式的欧姆定律。
RLC串联电路中总电压和总电流的数值关系:
2
2)
(
C
L
R
U
U
U
U-
+
=
2
2)
(
C
L
X
X
R
I-
+
=
Z
I
=
RLC串联电路中电压电流的相位关系
R
X
X
U
U
U
C
L
R
C
L
-
=
-
=arctan
arctan
ϕ
上述分析过程,我们用矢量表示正弦量,根据复数运算的相关知识进行分析得出了结论。
由于相量图可以更直观地描述正弦交流电中的数值和相位关系,我们来尝试画出。
图2 RLC串联电路的相量图
(C)
XL>XCX
L<XCXL=XC
电压三角形
2
2
)(C L R U U U U -+=
2
2
)(C L X X R I -+= R
C
L U U U -=arctan
ϕ
电压三角形各条边同除以电流有效值I , 可得到一个阻抗三角形:
阻抗三角形
2222)(X R I X X R I Z C L +=-+=
R
X X C
L -=arctan
ϕ
2、RLC 串联电路的性质
a 、X L >X C ,则U L >U C ,电压比电流超前Φ,电路呈电感性,称电感性电路。
b 、X L <X C , 则U L <U C ,电压比电流滞后Φ,电路呈电容性,称电容性电路。
c 、X L =X C , 则U L =U C ,电压和电流同相,电路呈电阻性,称电阻性电路。
3、课堂练习
例 1 在图1所示RLC 串联电路中,已知V t u )60314sin(2220︒+=,
F C mH L R μ40,12730==Ω=,。
求:
(1)电路中的总电流 i
(2)各元件两端的电压C L R u u u 、、
4、课堂小结 到现在为止,我们通过层层的分析,探索出了RLC 交流电路分析计算方法,明确了RLC 串联电路中总电压、总电流之间的关系,会通过电抗来判断电路的
性质。
在这个过程中,我们灵活运用了正弦交流电的三种表示方法瞬时值表达式、矢量、相量图,扬长避短,避免复杂的计算,能较直观地得出结论。
这启发我们,在进行研究和学习的时候,要注意根据研究对象的特点,合理地选取恰当的方法和工具。
善于思考的同学可能会发现新的问题:如果RLC三种元件不是串联而是并联,电路中的电压电流关系和电路性质又如何?下次课我们一起来讨论这个问题,请同学们课下做好预习。
5、作业布置:
课后习题。
