学海导航高三数学人教B版文科第一轮总复习课件10.55直线与圆、圆与圆的位置关系
2024届新高考一轮复习人教B版 主题三 第八章 第4节 直线与圆、圆与圆的位置关系 课件(36张)

4
3
2
.
.
1
0
1.圆的切线方程常用结论
(1)过圆x2+y2=r2(r>0)上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.
(2)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为
x0x+y0y=r2.
2.当两圆外切时,两圆有一条内公切线,该公切线垂直于两圆圆心的连线;当两
(-) + ( + ) = ,r1+r2=3,r2-r1=1,所以 r2-r1<|O1O2|<r1+r2,即两圆的
位置关系为相交.
5.圆(x-2)2+y2=4与圆x2+(y-2)2=4的公共弦所在直线的方程为
解析:根据题意(x-2)2+y2=4,
即x2+y2-4x=0,①
x2+(y-2)2=4,即x2+y2-4y=0.②
|-+-| |+|
+
=
+
=
++
+
=
判断直线与圆的位置关系的常见方法
(1)几何法:利用d与r的关系.
(2)代数法:联立方程之后利用Δ判断.
(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.
弦长问题
[例2] 过点(-4,0)作直线l与圆(x+1)2+(y-2)2=25交于A,B两点,如果|AB|=8,求
直线l的方程.
解:圆(x+1)2+(y-2)2=25 的圆心坐标是(-1,2),半径 r=5.
【优化设计】高考数学(人教版,文科)一轮总复习精品课件:8.4 直线与圆、圆与圆的位置关系(共28张PPT)

-1144-
考点一 直线与圆的位置关系及其应用
【例 1】点 M(a,b)是圆 x2+y2=r2 内异于圆心的一点,则直线 ax+by=r2 与圆的交点个数为(A)
A.0
B.1
C.2
D.需要讨论确定
解析:由题意知 a2+b2<r2,所以圆心(0,0)到直线 ax+by-r2=0 的距离 d= ������2 >r,
8-8-
基础自测
1.直线 x-y+1=0 与圆(x+1)2+y2=1 的位置关系是(B)
A.相切
B.直线过圆心
C.直线不过圆心,但与圆相交
D.相离
解析:∵圆心(-1,0)到直线 x-y+1=0 的距离 d=|-1-02+1|=0, ∴直线过圆心.
8.4 直线与圆、圆与圆的位置关系 第八章
9-9-
2.圆 x2+y2-4x=0 在点 P(1, 3)处的切线方程为(D)
(2)若求出的切线条数与判断不一致,则可能漏掉了切线斜率不 存在的情况.
8.4 直线与圆、圆与圆的位置关系 第八章
5-5-
(3)直线与圆相交:
直线与圆相交时,若 l 为弦长,d 为弦心距,r 为半径,则有
r2=
d2+
������ 2
2
,即 l=2 ������2-������2,求弦长或已知弦长求其他量的值,一般
用此公式.
2.圆与圆的位置关系
(1)圆与圆的位置关系可分为五种: 相离 、 外切 、 相交 、
内切 、 内含 .
(2)判断圆与圆的位置关系常用方法:
①几何法:设两圆圆心分别为 O1,O2,半径为 r1,r2(r1≠r2),则
学海导航高三数学人教B版文科第一轮总复习课件10.56椭圆

一
椭圆的定义及标准方程
【例 1】已知点 P 在以坐标轴为对称轴的椭圆上,且 P
到两焦点的距离分别为 5、3,过 P 且与长轴垂直的直线恰 过椭圆的一个焦点,求椭圆的方程.
x2 y2 解析:(方法一)设所求的椭圆方程为 2+ 2=1(a>b a b y2 x2 >0)或 2+ 2=1(a>b>0), a b
x2 y2 解析:(1)设椭圆的方程为 2+ 2=1(a>b>0), a b |PF1|=m,|PF2|=n. 在△PF1F2 中,由余弦定理可知,4c2=m2+n2-2mncos 60° . 因为 m+n=2a, 所以 m2+n2=(m+n)2-2mn=4a2-2mn, 所以 4c2=4a2-3mn,即 3mn=4a2-4c2. m+n 2 2 又 mn≤( ) =a (当且仅当 m=n 时取等号). 2 2 c 1 1 2 2 2 所以 4a -4c ≤3a ,所以 2≥ ,即 e≥ . a 4 2 1 又 0<e<1,所以 e 的取值范围是[ ,1). 2
b= 3 c 1 解析:依题设e= = a 2 2 2 2 a =b +c
a=2 ,解得 . b= 3
x2 y2 又椭圆焦点在 y 轴上,故其方程为 + =1. 3 4
x2 y2 3.椭圆25+169=1的焦点坐标是( C ) A.(± 5,0) C.(0,± 12) B.(0,± 5) D.(± 12,0)
解析:c= 169-25=12,因为椭圆的焦点在 y 轴上,所 以椭圆的焦点坐标为(0,± 12),故选 C.
x2 y2 4.已知椭圆a2+b2=1的左焦点F1,右顶点A,上顶点 B且∠F1BA=90° ,则椭圆的离心率是( A ) 5-1 A. 2 3 C. 2 3-1 B. 2 1 D.2
2023年高考数学(文科)一轮复习讲义——直线与圆、圆与圆的位置关系
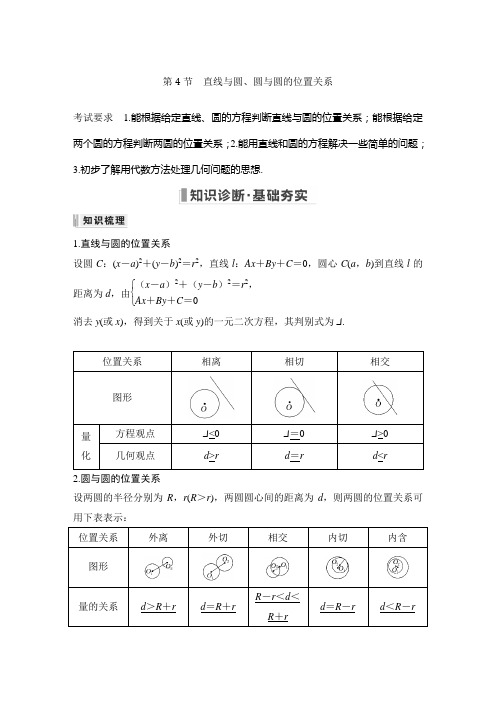
第4节 直线与圆、圆与圆的位置关系考试要求 1.能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系;2.能用直线和圆的方程解决一些简单的问题;3.初步了解用代数方法处理几何问题的思想.1.直线与圆的位置关系设圆C :(x -a )2+(y -b )2=r 2,直线l :Ax +By +C =0,圆心C (a ,b )到直线l 的距离为d ,由⎩⎨⎧(x -a )2+(y -b )2=r 2,Ax +By +C =0消去y (或x ),得到关于x (或y )的一元二次方程,其判别式为Δ.位置关系相离相切相交图形量化方程观点 Δ<0 Δ=0 Δ>0 几何观点d >rd =rd <r2.圆与圆的位置关系设两圆的半径分别为R ,r (R >r ),两圆圆心间的距离为d ,则两圆的位置关系可用下表表示: 位置关系 外离外切相交内切内含图形量的关系d >R +rd =R +rR -r <d <R +rd =R -rd <R -r公切线条数432101.圆的切线方程常用结论(1)过圆x2+y2=r2上一点P(x0,y0)的圆的切线方程为x0x+y0y=r2.(2)过圆(x-a)2+(y-b)2=r2上一点P(x0,y0)的圆的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.(3)过圆x2+y2=r2外一点M(x0,y0)作圆的两条切线,则两切点所在直线方程为x0x +y0y=r2.2.直线被圆截得的弦长的求法(1)几何法:运用弦心距d、半径r和弦长的一半构成的直角三角形,计算弦长|AB|=2r2-d2.(2)代数法:设直线y=kx+m与圆x2+y2+Dx+Ey+F=0相交于点M,N,将直线方程代入圆的方程中,消去y,得关于x的一元二次方程,求出x M+x N和x M·x N,则|MN|=1+k2·(x M+x N)2-4x M·x N.1.思考辨析(在括号内打“√”或“×”)(1)“k=1”是“直线x-y+k=0与圆x2+y2=1相交”的必要不充分条件.()(2)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.()(3)如果两圆的圆心距小于两圆的半径之和,则两圆相交.()(4)若直线平分圆的周长,则直线一定过圆心.()答案(1)×(2)×(3)×(4)√解析(1)“k=1”是“直线x-y+k=0与圆x2+y2=1相交”的充分不必要条件;(2)除外切外,还有可能内切;(3)两圆还可能内切或内含.2.(2021·绍兴一模)设m∈R,则“1≤m≤2”是“直线l:x+y-m=0和圆C:x2+y 2-2x -4y +m +2=0有公共点”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件 答案 A解析 圆C :(x -1)2+(y -2)2=3-m ,圆心为(1,2),半径r =3-m (m <3).若直线l 与圆C 有公共点,则圆心(1,2)到直线l 的距离d =|3-m |2≤3-m ,解得1≤m <3. 因为{m |1≤m ≤2}{m |1≤m <3},所以“1≤m ≤2”是“直线l :x +y -m =0和圆C :x 2+y 2-2x -4y +m +2=0有公共点”的充分不必要条件.3.(2022·全国百校联盟质检)已知直线l :x -2y +6=0与圆C :x 2+y 2-4y =0相交于A ,B 两点,则CA →·CB →=( ) A.165 B.-165 C.125 D.-125 答案 D解析 由圆的一般方程x 2+y 2-4y =0得标准方程为x 2+(y -2)2=4,故可得圆心C (0,2),半径r =2, 联立得⎩⎪⎨⎪⎧x -2y +6=0,x 2+y 2-4y =0,解得⎩⎪⎨⎪⎧x =-2,y =2或⎩⎪⎨⎪⎧x =65,y =185.不妨设A (-2,2),B ⎝ ⎛⎭⎪⎫65,185,则CA →=(-2,0),CB →=⎝ ⎛⎭⎪⎫65,85,所以CA →·CB →=-2×65+0×85=-125.4.(2021·洛阳模拟)若圆x 2+y 2=a 2与圆x 2+y 2+ay -6=0的公共弦长为23,则a =________. 答案 ±2解析 两圆方程作差得公共弦所在直线方程为a 2+ay -6=0,原点到a 2+ay -6=0的距离为d =⎪⎪⎪⎪⎪⎪6a -a .∵公共弦长为23, ∴a 2=(3)2+⎪⎪⎪⎪⎪⎪6a -a 2,∴a 2=4,a =±2.5.(易错题)若半径为r ,圆心为(0,1)的圆和定圆(x -1)2+(y -2)2=1相切,则r 的值等于________. 答案2+1或2-1解析 由题意,定圆(x -1)2+(y -2)2=1的圆心为A (1,2),半径R =1,半径为r 的圆的圆心为B (0,1), 所以|AB |=(1-0)2+(2-1)2= 2.因为两圆相切,所以|AB |=|R -r |或|AB |=|R +r |, 即|1-r |=2或 |1+r |=2, 解得r =1±2或r =-1±2. 因为r >0,所以r=2+1或r=2-1.6.(易错题)过点A(3,5)作圆O:x2+y2-2x-4y+1=0的切线,则切线的方程为________________.答案5x-12y+45=0或x-3=0解析化圆x2+y2-2x-4y+1=0为标准方程得(x-1)2+(y-2)2=4,其圆心为(1,2),半径为2.∵|OA|=(3-1)2+(5-2)2=13>2,∴点A(3,5)在圆外.显然,当切线斜率不存在时,直线与圆相切,即切线方程为x-3=0.当切线斜率存在时,可设所求切线方程为y-5=k(x-3),即kx-y+5-3k=0.又圆心为(1,2),半径r=2,而圆心到切线的距离d=|3-2k|k2+1=2,即|3-2k|=2k2+1,∴k=512,故所求切线方程为5x-12y+45=0或x-3=0.考点一直线与圆的位置关系1.若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是()A.[-3,-1]B.[-1,3]C.[-3,1]D.(-∞,-3]∪[1,+∞)答案 C解析由题意可得,圆的圆心为(a,0),半径为2,∴|a-0+1|12+(-1)2≤2,即|a+1|≤2,解得-3≤a ≤1.2.(2022·成都诊断)直线l :mx -y +1-m =0与圆C :x 2+(y -1)2=5的位置关系是( ) A.相交 B.相切 C.相离D.不确定答案 A解析 法一 (代数法)由⎩⎪⎨⎪⎧mx -y +1-m =0,x 2+(y -1)2=5,消去y ,整理得(1+m 2)x 2-2m 2x +m 2-5=0,因为Δ=16m 2+20>0,所以直线l 与圆相交.法二 (几何法)由题意知,圆心(0,1)到直线l 的距离d =|-m |m 2+1<1<5,故直线l 与圆相交.法三 易得直线l 过定点(1,1), 把点(1,1)代入圆的方程有1+0<5, ∴点(1,1)在圆的内部,故直线l 与圆C 相交.3.“a =3”是“直线y =x +4与圆(x -a )2+(y -3)2=8相切”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件 答案 A解析 若直线y =x +4与圆(x -a )2+(y -3)2=8相切,则有|a -3+4|2=22,即|a +1|=4,所以a =3或-5.故“a =3”是“直线y =x +4与圆(x -a )2+(y -3)2=8相切”的充分不必要条件.感悟提升判断直线与圆的位置关系的常见方法(1)几何法:利用d与r的关系.(2)代数法:联立方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交. 上述方法中最常用的是几何法,点与圆的位置关系法适用于动直线问题.考点二圆的弦长问题例1 (1)(2022·河南名校联考)已知圆C:(x-a)2+y2=4(a≥2)与直线x-y+22-2=0相切,则圆C与直线x-y-4=0相交所得弦长为()A.1B. 2C.2D.2 2(2)已知圆x2+y2-6x=0,过点(1,2)的直线被该圆所截得的弦的长度的最小值为()A.1B.2C.3D.4答案(1)D(2)B解析(1)根据题意,圆C:(x-a)2+y2=4的半径r=2.圆C:(x-a)2+y2=4(a≥2)与直线x-y+22-2=0相切,则圆心C到直线x-y+22-2=0的距离为2,即|a+22-2|2=2,解得a=2或a=2-42(舍去),所以圆C的方程为(x-2)2+y2=4,则圆心C(2,0)到直线x-y-4=0的距离d=|2-4|2=2,所以圆C与直线x-y-4=0相交所得弦长为222-d2=2 2.(2)圆的方程可化为(x-3)2+y2=9,故圆心的坐标为C(3,0),半径r=3.如图,记点M(1,2),则当MC与直线垂直时,直线被圆截得的弦的长度最小,此时|MC |=22, 弦的长度l =2r 2-|MC |2=29-8=2.感悟提升 弦长的两种求法(1)代数方法:将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系,根据弦长公式求弦长. (2)几何方法:若弦心距为d ,圆的半径长为r ,则弦长l =2r 2-d 2.训练1 (2022·南昌摸底测试)若直线x +ay -a -1=0与圆C :(x -2)2+y 2=4交于A ,B 两点,当|AB |最小时,劣弧AB 的长为( ) A.π2 B.πC.2πD.3π答案 B解析 圆C :(x -2)2+y 2=4的圆心为C (2,0),半径r =2.直线的方程可化为x -1+a (y -1)=0,可知直线恒过点D (1,1). 因为点D (1,1)的坐标满足(1-2)2+12<4, 所以点D (1,1)恒在圆C 内,且|CD |=2,易知,当CD ⊥AB 时,|AB |取得最小值,且最小值为2r 2-|CD |2=2 2.此时,劣弧AB 对应的圆心角为π2,所以劣弧AB 对应的弧长为π2×2=π. 考点三 圆的切线问题例2 (经典母题)过点P (2,4)引圆C :(x -1)2+(y -1)2=1的切线,则切线方程为________________.答案 x =2或4x -3y +4=0解析 当直线的斜率不存在时,直线方程为x =2,此时,圆心到直线的距离等于半径,直线与圆相切,符合题意;当直线的斜率存在时,设直线方程为y -4=k (x -2),即kx -y +4-2k =0.∵直线与圆相切,∴圆心到直线的距离等于半径,即d=|k -1+4-2k |k 2+(-1)2=|3-k |k 2+1=1,解得k =43,∴所求切线方程为43x -y +4-2×43=0, 即4x -3y +4=0.综上,切线方程为x =2或4x -3y +4=0.迁移1 在例2中,若点P 坐标变为⎝ ⎛⎭⎪⎫22+1,22+1,其他条件不变,求切线方程.解 易知点P ⎝ ⎛⎭⎪⎫22+1,22+1在圆C :(x -1)2+(y -1)2=1上,则k PC =22+1-122+1-1=1,∴所求切线方程的斜率为-1,则切线方程为y -⎝ ⎛⎭⎪⎫22+1=-⎣⎢⎡⎦⎥⎤x -⎝ ⎛⎭⎪⎫22+1,即x +y -2-2=0.迁移2 在例2中,已知条件不变,设两个切点为A ,B ,求切点弦AB 所在的直线方程.解 由题意得,点P ,A ,C ,B 在以PC 为直径的圆上,此圆的方程为(x -2)(x -1)+(y -4)(y -1)=0,整理得x 2+y 2-3x -5y +6=0.①圆C :(x -1)2+(y -1)2=1展开得x 2+y 2-2x -2y +1=0,② 由②-①得x +3y -5=0,即为直线AB 的方程.感悟提升 求过某点的圆的切线问题时,应首先确定点与圆的位置关系,再求切线方程.若点在圆上(即为切点),则过该点的切线只有一条;若点在圆外,则过该点的切线有两条,此时注意斜率不存在的切线.训练2 (1)过直线y =2x +3上的点作圆C :x 2+y 2-4x +6y +12=0的切线,则切线长的最小值为( )A.19B.2 5C.21D.555(2)(2021·晋中模拟)过点P (2,3)作圆C :x 2+y 2-2x =0的两条切线,切点分别为A ,B ,则P A →·PB →=________.答案 (1)A (2)32解析 (1)圆的方程可化为(x -2)2+(y +3)2=1,要使切线长最小,只需直线y =2x +3上的点和圆心之间的距离最短,此最小值即为圆心(2,-3)到直线y =2x +3的距离d ,d =|2×2+3+3|5=25,故切线长的最小值为d 2-r 2=19.(2)由x 2+y 2-2x =0得(x -1)2+y 2=1,所以圆心C (1,0),半径为1,所以|PC |=2,|P A |=|PB |=3,∠APB =60°, 所以P A →·PB →=|P A →||PB →|cos 60°=32. 考点四 圆与圆的位置关系例3 已知两圆x 2+y 2-2x -6y -1=0,x 2+y 2-10x -12y +m =0. (1)m 取何值时两圆外切? (2)m 取何值时两圆内切?(3)当m =45时,求两圆的公共弦所在直线的方程和公共弦的长. 解 因为两圆的标准方程分别为 (x -1)2+(y -3)2=11, (x -5)2+(y -6)2=61-m ,所以两圆的圆心分别为(1,3),(5,6),半径分别为11,61-m ,(1)当两圆外切时,由(5-1)2+(6-3)2=11+61-m ,得m =25+1011.(2)当两圆内切时,因为定圆半径11小于两圆圆心之间的距离5,所以61-m -11=5,解得m=25-1011.(3)由(x2+y2-2x-6y-1)-(x2+y2-10x-12y+45)=0,得两圆的公共弦所在直线的方程为4x+3y-23=0,故两圆的公共弦的长为2(11)2-(|4×1+3×3-23|42+32)2=27.感悟提升 1.判断两圆的位置关系时常用几何法,即利用两圆圆心之间的距离与两圆半径之间的关系,一般不采用代数法.2.若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差消去x2,y2项得到.训练3 (1)已知圆M:x2+y2-2ay=0(a>0)截直线x+y=0所得线段的长度是22,则圆M与圆N:(x-1)2+(y-1)2=1的位置关系是()A.内切B.相交C.外切D.相离(2)(2022·东北三省三校联考)圆x2-4x+y2=0与圆x2+y2+4x+3=0的公切线共有()A.1条B.2条C.3条D.4条答案(1)B(2)D解析(1)由题意得圆M的标准方程为x2+(y-a)2=a2,圆心(0,a)到直线x+y=0的距离d=a2,所以2a2-a22=22,解得a=2.圆M,圆N的圆心距|MN|=2小于两圆半径之和1+2,大于两圆半径之差1,故两圆相交.(2)x2-4x+y2=0⇒(x-2)2+y2=22,圆心坐标为(2,0),半径为2;x2+y2+4x+3=0⇒(x+2)2+y2=12,圆心坐标为(-2,0),半径为1,圆心距为4,两圆半径和为3.因为4>3,所以两圆的位置关系是外离,故两圆的公切线共有4条.阿波罗尼斯圆公元前3世纪,古希腊数学家阿波罗尼斯(Apollonius)在《平面轨迹》一书中,曾研究了众多的平面轨迹问题,其中有如下结果:到两定点距离之比等于已知数的动点轨迹为直线或圆.如图,点A ,B 为两定点,动点P 满足|P A |=λ|PB |.则λ=1时,动点P 的轨迹为直线;当λ>0且λ≠1时,动点P 的轨迹为圆,后世称之为阿波罗尼斯圆.证明:设|AB |=2m (m >0),|P A |=λ|PB |,以AB 的中点为原点,直线AB 为x 轴,线段AB 的垂直平分线为y 轴,建立平面直角坐标系(图略),则A (-m ,0),B (m ,0).又设P (x ,y ),则由|P A |=λ|PB |得(x +m )2+y 2=λ(x -m )2+y 2, 两边平方并化简整理得(λ2-1)x 2-2m (λ2+1)x +(λ2-1)y 2=m 2(1-λ2).当λ=1时,x =0,轨迹为线段AB 的垂直平分线;当λ>0且λ≠1时,⎝ ⎛⎭⎪⎪⎫x -λ2+1λ2-1m 2+y 2=4λ2m 2(λ2-1)2,轨迹为以点⎝ ⎛⎭⎪⎪⎫λ2+1λ2-1m ,0为圆心,⎪⎪⎪⎪⎪⎪2λm λ2-1为半径的圆. 例1 如图所示,在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4,设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程;(2)若圆C 上存在点M ,使|MA |=2|MO |,求圆心C 的横坐标a 的取值范围.解 (1)联立⎩⎪⎨⎪⎧y =x -1,y =2x -4,得圆心为C (3,2). 由题意知切线的斜率存在,设切线方程为y =kx +3,圆心C 到切线的距离d =|3k +3-2|1+k2=r =1,得k =0或k =-34. 故所求切线方程为y =3或3x +4y -12=0.(2)设点M (x ,y ),由|MA |=2|MO |, 知x 2+(y -3)2=2x 2+y 2,化简得x 2+(y +1)2=4,即点M 的轨迹为以(0,-1)为圆心,2为半径的圆,可记为圆D .又因为点M 也在圆C 上,故圆C 与圆D 的关系为相交或相切,故1≤|CD |≤3,其中|CD |=a 2+(2a -3)2, 解得0≤a ≤125. 即圆心C 的横坐标a 的取值范围是⎣⎢⎡⎦⎥⎤0,125. 例2 在平面直角坐标系xOy 中,设点A (1,0),B (3,0),C (0,a ),D (0,a +2),若存在点P ,使得|P A |=2|PB |,|PC |=|PD |,则实数a 的取值范围是________. 答案 [-22-1,22-1]解析设P(x,y),则(x-1)2+y2=2·(x-3)2+y2,整理得(x-5)2+y2=(22)2,即动点P在以(5,0)为圆心,22为半径的圆上运动. 另一方面,由|PC|=|PD|知动点P在线段CD的垂直平分线y=a+1上运动,因而问题就转化为直线y=a+1与圆(x-5)2+y2=(22)2有交点.所以|a+1|≤2 2.故实数a的取值范围是[-22-1,22-1].1.(2022·兰州质检)“k=33”是“直线l:y=k(x+2)与圆x2+y2=1相切”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件答案 A解析若直线l与圆相切,则有|2k|k2+1=1,解得k=±33,所以“k=33”是“直线l:y=k(x+2)与圆x2+y2=1相切”的充分不必要条件.2.(2021·福州调研)已知圆x2+y2+2x-2y+a=0截直线x+y+2=0所得的弦的长度为4,则实数a的值是()A.-2B.-4C.-6D.-8答案 B解析将圆的方程化为标准方程为(x+1)2+(y-1)2=2-a,所以圆心为(-1,1),半径r=2-a,圆心到直线x+y+2=0的距离d=|-1+1+2|2=2,故r2-d2=4,即2-a-2=4,所以a=-4.3.圆x2+2x+y2+4y-3=0上到直线x+y+1=0的距离为2的点共有()A.1个B.2个C.3个D.4个答案 C解析圆的方程可化为(x+1)2+(y+2)2=8,圆心(-1,-2)到直线的距离d=|-1-2+1|=2,半径是22,结合图形(图略)可知有3个符合条件的点.24.(2021·南昌模拟)已知圆O:(x-1)2+(y-1)2=1,则下列选项所对应的图形中,与圆O相切的是()A.x2+y2=1B.(x-4)2+(y-5)2=16C.x+y=1D.x-y=2答案 B解析圆O:(x-1)2+(y-1)2=1的圆心坐标为(1,1),半径r=1.对于选项A,x2+y2=1表示的是圆心坐标为(0,0),半径r1=1的圆,此圆与圆O的圆心距为12+12=2<r+r1=2,所以两圆不相切,不符合题意.对于选项B,(x-4)2+(y-5)2=16表示的是圆心坐标为(4,5),半径r2=4的圆,此圆与圆O的圆心距为(4-1)2+(5-1)2=5=r+r2=5,所以两圆相切.对于选项C,圆心(1,1)到直线x+y=1的距离为22<1,故直线x+y=1与圆O 相交.对于选项D,圆心(1,1)到直线x-y=2的距离为2>1,故直线x-y=2与圆O 相离.5.过点P(1,-2)作圆C:(x-1)2+y2=1的两条切线,切点分别为A,B,则AB 所在直线的方程为()A.y=-34 B.y=-12C.y=-32 D.y=-14答案 B解析由题意知,点P,A,C,B在以PC为直径的圆上,易求得这个圆为(x-1)2+(y+1)2=1,此圆的方程与圆C的方程作差可得AB所在直线的方程为y=-12.6.(2022·宜宾诊断)已知直线l:y=3x+m与圆C:x2+(y-3)2=6相交于A,B 两点,若∠ACB=120°,则实数m的值为()A.3+6或3- 6B.3+26或3-2 6C.9或-3D.8或-2答案 A解析由题意知圆心C(0,3)到直线l的距离d=|0-3+m|3+1=|m-3|2.因为∠ACB=120°,所以|m-3|2×2=6,解得m=3±6.7.已知圆C的圆心坐标是(0,m),半径长是r.若直线2x-y+3=0与圆C相切于点A(-2,-1),则m=________,r=________.答案-2 5解析根据题意画出图形,可知A(-2,-1),C(0,m),B(0,3),则|AB|=(-2-0)2+(-1-3)2=25,|AC|=(-2-0)2+(-1-m)2=4+(m+1)2,|BC |=|m -3|.∵直线2x -y +3=0与圆C 相切于点A ,∴∠BAC =90°,∴|AB |2+|AC |2=|BC |2.即20+4+(m +1)2=(m -3)2,解得m =-2.因此r =|AC |=4+(-2+1)2= 5.8.(2021·长春模拟)已知点P (1,2)和圆C :x 2+y 2+kx +2y +k 2=0,过点P 作圆C 的切线有两条,则实数k 的取值范围是________.答案 ⎝⎛⎭⎪⎫-233,233 解析 因为C :x 2+y 2+kx +2y +k 2=0为圆, 所以k 2+4-4k 2>0,解得-233<k <233.又过点P 作圆C 的切线有两条,所以点P 在圆的外部,故1+4+k +4+k 2>0,解得k ∈R ,综上可知-233<k <233.故k 的取值范围是⎝⎛⎭⎪⎫-233,233. 9.在圆x 2+y 2-2x -6y =0内,过点E (0,1)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为______.答案 10 2解析 圆的标准方程为(x -1)2+(y -3)2=10,则圆心(1,3),半径r =10,圆心(1,3)与E (0,1)距离(1-0)2+(3-1)2=5.由题意知AC ⊥BD ,且|AC |=210,|BD |=210-5=25,所以四边形ABCD 的面积为S =12|AC |·|BD |=12×210×25=10 2.10.已知圆M :x 2+y 2-2ax +10ay -24=0,圆N :x 2+y 2+2x +2y -8=0,且圆M 上任意一点关于直线x +y +4=0的对称点都在圆M 上.(1)求圆M 的方程;(2)证明圆M 和圆N 相交,并求两圆公共弦的长度l .(1)解 圆M :x 2+y 2-2ax +10ay -24=0的圆心为M (a ,-5a ),∵圆M 上任意一点关于直线x +y +4=0的对称点都在圆M 上,∴直线x +y +4=0经过M ,则a -5a +4=0,解得a =1.∴圆M 的方程为x 2+y 2-2x +10y -24=0.(2)证明 ∵圆M 的圆心M (1,-5),半径r 1=52,圆N 的圆心N (-1,-1),半径r 2=10,∴|MN |=(1+1)2+(-5+1)2=2 5.∵52-10<25<52+10,∴圆M 和圆N 相交.由圆M ,圆N 的方程左右两边分别相减,得x -2y +4=0,∴两圆公共弦的直线方程为x -2y +4=0.∵M 到直线x -2y +4=0的距离d =|1+10+4|5=35, ∴公共弦长度l =2h 2-d 2=2 5.11.已知圆C 经过(2,4),(1,3)两点,圆心C 在直线x -y +1=0上,过点A (0,1)且斜率为k 的直线l 与圆C 相交于M ,N 两点.(1)求圆C 的方程;(2)①请问AM →·AN →是否为定值,若是,求出该定值,若不是,请说明理由;②若OM →·ON →=12(O 为坐标原点),求直线l 的方程.解 (1)设圆C 的方程为(x -a )2+(y -b )2=r 2,依题意,得⎩⎪⎨⎪⎧(2-a )2+(4-b )2=r 2,(1-a )2+(3-b )2=r 2,a -b +1=0,解得⎩⎪⎨⎪⎧a =2,b =3,r =1,∴圆C 的方程为(x -2)2+(y -3)2=1.(2)①AM →·AN →为定值,理由如下:过点A (0,1)作直线AT 与圆C 相切,切点为T ,易得|AT |2=7,∴AM →·AN →=|AM →|·|AN →|cos 0°=|AT |2=7.根据圆的弦切角定理及相似三角形,∴AM →·AN →为定值,且定值为7.②依题意可知,直线l 的方程为y =kx +1,设M (x 1,y 1),N (x 2,y 2),将y =kx +1代入(x -2)2+(y -3)2=1,并整理,得(1+k 2)x 2-4(1+k )x +7=0,∴x 1+x 2=4(1+k )1+k 2,x 1x 2=71+k 2, ∴OM →·ON →=x 1x 2+y 1y 2=(1+k 2)x 1x 2+k (x 1+x 2)+1=4k (1+k )1+k 2+8=12,即4k (1+k )1+k 2=4,解得k =1.又当k =1时,Δ>0,∴k =1,∴直线l 的方程为y =x +1.12.(2022·宝鸡模拟)过点P (x ,y )作圆C 1:x 2+y 2=1与圆C 2:(x -2)2+(y -2)2=1的切线,切点分别为A ,B ,若|P A |=|PB |,则x 2+y 2的最小值为( )A. 2B.2C.2 2D.8 答案 B解析 由(x 2+y 2-1)-(x 2+y 2-4x -4y +7)=0得x +y -2=0,则P 点在直线l :x +y -2=0上,原点到直线l 的距离d =2,所以(x 2+y 2)min =d 2=2.13.(2022·南阳联考)阿波罗尼斯(约公元前262~公元前190年)证明过这样一个命题:平面内到两定点距离之比为常数k (k >0,且k ≠1)的点的轨迹是圆,后人将此圆称为阿氏圆.若平面内两定点A ,B 间的距离为4,动点P 满足|P A ||PB |=3,则动点P 的轨迹所围成的图形的面积为________;P A →·PB →的最大值是________. 答案 12π 24+16 3解析 以直线AB 为x 轴,线段AB 的垂直平分线为y 轴,建立平面直角坐标系, 则A (-2,0),B (2,0).设P (x ,y ),∵|P A ||PB |=3,∴(x +2)2+y 2(x -2)2+y 2=3,得x 2+y 2-8x +4=0,即(x -4)2+y 2=12,所以点P 的轨迹为圆,其面积为12π.P A →·PB →=(-2-x ,-y )·(2-x ,-y )=x 2-4+y 2=|OP |2-4,如图,当P 位于点D 时,|OP |2最大,|OP |2的最大值为(4+23)2=28+163, 故P A →·PB →的最大值是24+16 3.14.(2021·北京海淀区模拟)已知A (2,0),直线4x +3y +1=0被圆C :(x +3)2+(y -m )2=13(m <3)所截得的弦长为43,且P 为圆C 上任意一点.(1)求|P A |的最大值与最小值;(2)圆C 与坐标轴相交于三点,求以这三个点为顶点的三角形的内切圆的半径. 解 (1)∵直线4x +3y +1=0被圆C :(x +3)2+(y -m )2=13(m <3)所截得的弦长为43,∴圆心到直线的距离d =|-12+3m +1|5=(13)2-(23)2=1.∵m <3,∴m =2,∴|AC |=(-3-2)2+(2-0)2=29, ∴|P A |的最大值与最小值分别为29+13,29-13.(2)由(1)可得圆C 的方程为(x +3)2+(y -2)2=13,令x =0,得y =0或4; 令y =0,得x =0或-6,∴圆C 与坐标轴相交于三点M (0,4),O (0,0),N (-6,0),∴△MON为直角三角形,斜边|MN|=213,∴△MON内切圆的半径为4+6-2132=5-13.。
直线与圆、圆与圆的位置关系课件-2025届高三数学一轮复习

≤ + ,解得−
≤≤
.
−−
+
=
+
≤ ,即
考点二 直线与圆位置关系的应用
角度1 圆的切线问题(链接高考)
例2 (2023·新课标Ⅰ卷)过点 , − 与圆 + − − = 相切的两条直
(2)过圆 + = 外一点 , 作圆的两条切线,则两切点所在
直线方程为 + = .
2.圆与圆的位置关系的常用结论
(1)两圆相交时,其公共弦所在的直线方程由两圆方程相减得到.
(2)两个圆系方程
①过直线 + + = 与圆 + + + + = 交点的圆系方
(其中不含圆 ,所以注意检验 是否满足题意,以防丢解).
1.若经过点 −, − 的直线与圆 + = 相切,则该直线在轴上的截
距为(
A.
)
√
C.−
B.5
解析:选C.因为 −
+ −
D.−
= ,所以点在圆上,
所以切线方程为− − = ,令 = 得 =
+ − − = 相交.
方法三:圆的方程可化为 −
+ = ,
所以圆的圆心为 , ,半径为3.
圆心到直线 − + − = 的距离为
+−
+
=
+
≤ < ,所以直线与圆相交.故选C.
学海导航人教版高三第一轮复习课件文科数学第57讲 直线与圆、圆与圆的位置关系

答案:C
复习目标 课前预习 高频考点 课时小结
直线与圆的位置关系
有关弦长问题 圆与圆的位置关系
复习目标
课前预习
高频考点
课时小结
考点一· 直线与圆的位置关系
【例1】过点M(2,4)向圆(x-1)2+(y+3)2=1引切线,则 切线方程为____________.
复习目标
课前预习
高频考点
课时小结
解:因为(2-1)2+(4+3)2>1,所以M在圆外. 若切线的斜率存在, 设过M的切线斜率为k,则切线方程为y-4=k(x- 2). |k+3+4-2k| 24 由已知,有 =1,所以k= 7 . 2 k +1 24 故切线方程为y-4= 7 (x-2). 又切线斜率不存在时,直线x=2也满足条件. 故所求切线方程为24x-7y-20=0或x=2. 答案:24x-7y-20=0或x=2
复习目标
课前预习
高频考点
课时小结
【变式探究】
1.(2015·山东卷)一条光线从点(-2,-3)射出,经y 轴反射后与圆(x+3)2+(y-2)2=1相切,则反射光线所在直 线的斜率为( ) 3 2 B.-2或-3 4 3 D.-3或-4 5 3 A.-3或-5 5 4 C.-4或-5
复习目标
课前预习
复习目标
课前预习
高频考点
课时小结
解:因为所求直线与直线2x+y+1=0平行, 所以设所求的直线方程为2x+y+m=0. 因为所求直线与圆x2+y2=5相切, 所以 |m| = 5,所以 m=± 5. 1+4
即所求的直线方程为2x+y+5=0或2x+y-5=0.
答案:A
复习目标
课前预习
高频考点
课时小结
【学海导航】2015届高三数学(文)(人教版B)第一轮总复习同步训练:第10单元《解析几何》
第十单元 解析几何第52讲 直线的方程1.直线x tan π7+y =0的倾斜角是( ) A .-π7 B.π7C.5π7D.6π72.已知直线l 过点O (0,0)和点P (2+3cos α,3sin α),则直线l 的斜率的最大值为( )A.12B.33C.32D. 3 3.已知直线l 1的方程是ax -y +b =0,l 2的方程是bx -y -a =0(ab ≠0,a ≠b ),则下列各示意图形中,正确的是( )4.直线x -2y +2k =0与两坐标轴所围成的三角形面积不大于1,那么k 的范围是( )A .k ≥-1B .k ≤1C .-1≤k ≤1且k ≠0D .k ≤-1或k ≥15.若直线(a 2+2a )x -y +1=0的倾斜角为钝角,则实数a 的取值范围是________.6.已知点A (-2,0),B (1,3)是圆x 2+y 2=4上的定点,经过点B 的直线与该圆交于另一点C ,当△ABC 面积最大时,直线BC 的方程是________.7.直线3x -4y +k =0在两坐标轴上的截距之和为2,则实数k =________.8.在△ABC 中,已知点A (5,-2)、B (7,3),且边AC 的中点M 在y 轴上,边BC 的中点N 在x 轴上.(1)求点C 的坐标;(2)求直线MN 的方程.9.已知O 为平面直角坐标系的原点,过点M (-2,0)的直线l 与圆x 2+y 2=1交于P ,Q 两点.(1)若OP →·OQ →=-12,求直线l 的方程; (2)若△OMP 与△OPQ 的面积相等,求直线l 的斜率.第53讲 两直线的位置关系与对称问题1.“a =3”是“直线ax +2y +2a =0和直线3x +(a -1)y -a +7=0平行”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分又不必要条件2.过点A (2,3)且垂直于直线2x +y -5=0的直线方程为( )A .x -2y +4=0B .2x +y -7=0C .x -2y +3=0D .x -2y +5=03.过点(5,2),且在y 轴上的截距是在x 轴上的截距的2倍的直线方程是( )A .2x +y -12=0B .2x +y -12=0或2x -5y =0C .x -2y -1=0D .x -2y -1=0或2x -5y =04.在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,则直线x sin A +ay +c =0与直线bx -y sin B +sin C =0的位置关系是( )A .平行B .垂直C .重合D .相交但不垂直5.若函数y =ax +8与y =-12x +b 的图象关于直线y =x 对称,则a +b =______. 6.已知直线3x +4y -3=0与直线6x +my +14=0平行,则它们之间的距离是 .7.已知点P (4,a )到直线4x -3y -1=0的距离不大于3,则a 的取值范围是________.8.已知两直线l 1:x +m 2y +6=0,l 2:(m -2)x +3my +2m =0,当m 为何值时,l 1与l 2:(1)相交;(2)平行;(3)重合?9.已知线段PQ 两端点的坐标分别为(-1,1)、(2,2),若直线l :x +my +m =0与线段PQ 有交点,求m 的范围.第54讲 圆的方程1.圆x 2+y 2-4x +6y =0的圆心坐标是( )A .(2,3)B .(-2,3)C .(-2,-3)D .(2,-3)2.已知倾斜角为60°的直线l 过圆C :x 2+2x +y 2=0的圆心,则此直线l 的方程是( ) A.3x +y +1=0 B .x -3y +1=0C .x +3y +1=0 D.3x -y +3=0 3.曲线y =-4-x 2(x ≤0)的长度为( )A.2π3B.3π2C .2πD .π4.已知圆的方程为(x -a )2+(y -b )2=r 2(r >0),下列结论错误的是( )A .当a 2+b 2=r 2时,圆必过原点B .当a =r 时,圆与y 轴相切C .当b =r 时,圆与x 轴相切D .当b <r 时,圆与x 轴相交5.设P 为圆x 2+y 2=1上的动点,则点P 到直线3x -4y -10=0的距离的最小值为______.6.已知点P (1,4)在圆C :x 2+y 2+2ax -4y +b =0上,点P 关于直线x +y -3=0的对称点也在圆C 上,则a = ,b =______.7.已知圆的半径为10,圆心在直线y =2x 上,圆被直线x -y =0截得的弦长为42,则圆的标准方程为______________________.8.已知实数x 、y 满足方程x 2+y 2-4x +1=0.求y x的最大值和最小值.9.在平面直角坐标系xOy 中,已知圆P 在x 轴上截得线段长为22,在y 轴上截得线段长为2 3.(1)求圆心P 的轨迹方程;(2)若P 点到直线y =x 的距离为22,求圆P 的方程.第55讲 直线与圆、圆与圆的位置关系1.若直线3x +y +a =0过圆x 2+y 2+2x -4y =0的圆心,则a 的值为( )A .-1B .1C .3D .-32.直线tx +y -t +1=0(t ∈R )与圆x 2+y 2-2x +4y -4=0的位置关系为( )A .相交B .相切C .相离D .以上都有可能3.直线x +y -1=0被圆(x +1)2+y 2=3截得的弦长等于( ) A. 2 B .2C .2 2D .44.直线3x +y -23=0与圆O :x 2+y 2=4交于A 、B 两点,则OA →·OB →=( )A .2B .-2C .4D .-45.设直线x -my -1=0与圆(x -1)2+(y -2)2=4相交于A ,B 两点,且弦AB 的长为23,则实数m 的值是 .6.若圆C :x 2+y 2+2x -4y +3=0关于直线2ax +by +6=0对称,则由点(a ,b )向圆所作的切线长的最小值是 .7.经过点P (2,-3),作圆x 2+2x +y 2=24的弦AB ,使得点P 平分弦AB ,则弦AB 所在直线的方程为________________________________________________________________________.8.如图,在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程;(2)若圆C 上存在点M ,使MA =2MO ,求圆心C 的横坐标a 的取值范围.9.在平面直角坐标系xOy 中,已知圆x 2+y 2-12x +32=0的圆心为Q ,过点P (0,2)且斜率为k 的直线l 与圆Q 相交于不同的两点A ,B .(1)求k 的取值范围;(2)是否存在常数k ,使得向量OA →+OB →与PQ →共线?如果存在,求k 的值;如果不存在,请说明理由.第56讲 椭 圆1.已知F 1(-1,0),F 2(1,0)是椭圆C 的两个焦点,过F 2且垂直于x 轴的直线交于A ,B 两点,且|AB |=3,则C 的方程为( )A.x 22+y 2=1B.x 23+y 22=1C.x 24+y 23=1D.x 25+y 24=1 2.已知F 1、F 2是椭圆x 216+y 29=1的两个焦点,过F 1的直线与椭圆交于M 、N 两点,则△MNF 2的周长为( )A .8B .16C .25D .323.椭圆x 225+y 29=1的左焦点为F 1,点P 在椭圆上,若线段PF 1的中点M 在y 轴上,则|PF 1|=( )A.415B.95C .6D .74.直线y =-3x 与椭圆C :x 2a 2+y 2b 2=1(a >b >0)交于A ,B 两点,以线段AB 为直径的圆恰好经过椭圆的右焦点,则椭圆C 的离心率为( ) A.32 B.3-12C.3-1 D .4-2 35.如果方程x 2+ky 2=2表示焦点在y 轴的椭圆,那么实数k 的取值范围是________.6.若椭圆x 22+y 2m =1的离心率为12,则实数m 等于 .7.如图,在平面直角坐标系xOy 中,椭圆x 2a 2+y 2b2=1(a >b >0)被围于由4条直线x =±a ,y =±b 所围成的矩形ABCD 内,任取椭圆上一点P ,若OP →=m ·OA →+n ·OB →(m ,n ∈R ),则m ,n 满足的一个等式是__________. 8.设x 、y ∈R ,i 、j 为直角坐标平面内x 、y 轴正方向上的单位向量,若向量a =x i +(y +2)j ,b =x i +(y -2)j ,且|a|+|b|=8.求点M (x ,y )的轨迹C 的方程.9.已知椭圆C:x2a2+y2b2=1(a>b>0)的焦距为4,且过点P(2,3).(1)求椭圆C的方程;(2)设Q(x0,y0)(x0y0≠0)为椭圆C上一点,过点Q作x轴的垂线,垂足为E.取点A(0,22),连接AE,过点A作AE的垂线交x轴于点D.点G是点D关于y轴的对称点,作直线QG,问这样作出的直线QG是否与椭圆C一定有唯一的公共点?并说明理由.第57讲 双曲线1.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的离心率为52,则C 的渐近线方程为( ) A .y =±14x B .y =±13x C .y =±12x D .y =±x 2.双曲线x 2m 2+12+y 2m 2-4=1的焦距是( ) A .2 2 B .4C .8D .与m 有关3.过点(2,-2)且与双曲线x 22-y 2=1有公共渐近线的双曲线方程是( ) A.y 22-x 24=1 B.x 24-y 22=1 C.y 24-x 22=1 D.x 22-y 24=1 4.设P 是双曲线x 2a 2-y 29=1上一点,双曲线的一条渐近线方程为3x -2y =0,F 1、F 2分别是双曲线的左、右焦点.若|PF 1|=3,则|PF 2|等于( )A .1或5B .6C .7D .95.设F 1,F 2是双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的两个焦点,若在C 上存在一点P ,使PF 1⊥PF 2,且∠PF 1F 2=30°,则C 的离心率为________. 6.设双曲线x 2a 2-y 2b2=1(a >0,b >0)的离心率e ∈[2,2],则两条渐近线夹角的取值范围是__________.7.△PF 1F 2的一个顶点P (7,12)在双曲线x 2-y 2b2=1上,另外两个顶点F 1,F 2为该双曲线的左,右焦点,则△PF 1F 2的内心的横坐标为______.8.已知双曲线的方程是16x 2-9y 2=144.(1)求这双曲线的焦点坐标、离心率和渐近线方程;(2)设F 1和F 2是双曲线的左、右焦点,点P 在双曲线上,且|PF 1|·|PF 2|=32,求∠F 1PF 2的大小.9.已知双曲线C 的中心在坐标原点O ,对称轴为坐标轴,点(-2,0)是它的一个焦点,并且离心率为233.(1)求双曲线C 的方程;(2)已知点M (0,1),设P (x 0,y 0)是双曲线C 上的点,Q 是点P 关于原点的对称点,求MP →·MQ →的取值范围.第58讲 抛物线1.在抛物线y 2=2px 上横坐标为4的点到焦点的距离为5,则p 的值为( ) A.12B .1C .2D .42.抛物线y 2=8x 的焦点到直线x -3y =0的距离是( ) A .2 3 B .2 C. 3 D .13.已知双曲线x 2a 2-y 2b2=1的一个焦点与抛物线y 2=4x 的焦点重合,且该双曲线的离心率为5,则该双曲线的渐近线方程为( )A .y =±12x B .y =±2xC .y =±2xD .y =±22x4.抛物线y =4x 2上一点到直线l :y =4x -5的距离最短,则该点的坐标是( )A .(12,1) B .(0,0)C .(1,2)D .(1,4)5.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是________.6.直线y =x -1被抛物线y 2=4x 截得线段的中点坐标是________.7.双曲线x 23-16y 2p2=1的左焦点在抛物线y 2=2px 的准线上,则p 的值为______.8.已知斜率为1的直线l 过抛物线y 2=2px (p >0)的焦点F ,且与抛物线交于A ,B 两点. (1)求直线l 的方程(用p 表示);(2)若设A (x 1,y 1),B (x 2,y 2),求证:|AB |=x 1+x 2+p ;(3)若|AB |=4,求抛物线方程.9.已知抛物线C 的顶点为原点,其焦点F (0,c )(c >0)到直线l :x -y -2=0的距离为322.设P 为直线l 上的点,过点P 作抛物线C 的两条切线P A ,PB ,其中A ,B 为切点.(1)求抛物线C 的方程;(2)当点P (x 0,y 0)为直线l 上的定点时,求直线AB 的方程.第59讲 直线与圆锥曲线的位置关系1.抛物线y =-x 2上的点到直线4x +3y -8=0距离的最小值是( ) A.43 B.75 C.85D .3 2.在同一坐标系中,方程x 2a 2+y 2b2=1与bx 2=-ay (a >b >0)表示的曲线大致是( )3.过椭圆C :x 2a 2+y2b2=1(a >b >0)的左顶点A 且斜率为k 的直线交椭圆C 于另一个点B ,且点B 在x 轴上的射影恰好为右焦点F ,若13<k <12,则椭圆离心率的取值范围是( )A .(14,94)B .(23,1)C .(12,23)D .(0,12)4.双曲线x 2-y 2=1的左焦点为F ,点P 为左支下半支上任意一点(异于顶点),则直线PF 的斜率的变化范围是( )A .(-∞,0)B .(1,+∞)C .(-∞,0)∪(1,+∞)D .(-∞,-1)∪(1,+∞)5.以曲线y 2=8x 上的任意一点为圆心作圆与直线x +2=0相切,则这些圆必过一定点,则这一定点的坐标是______.6.直线y =x +b 与抛物线x 2=2y 交于A ,B 两点,O 为坐标原点,且OA ⊥OB ,则b =______.7.已知直线l 1:y =kx 和l 2:y =k ′x 分别与抛物线W :y 2=2x 和抛物线M :y 2=4x 交于A ,B ,C ,D 四点(如图),则S △OACS △OBD=________.8.已知中心在坐标原点,焦点在x轴上的椭圆C,其长轴长等于4,离心率为2 2.(1)求椭圆C的标准方程;(2)若点E(0,1),问是否存在直线l:y=kx+m与椭圆C交于M,N两点,且|ME|=|NE|?若存在,求出k的取值范围;若不存在,请说明理由.9.已知椭圆x2a2+y2b2=1(a>b>0)的左焦点F1(-1,0),长轴长与短轴长的比是2∶ 3.(1)求椭圆的方程;(2)过F1作两直线m,n交椭圆于A,B,C,D四点,若m⊥n,求证:1|AB|+1|CD|为定值.第60讲 轨迹问题1.若动点P 到定点F (1,-1)的距离与到直线l :x -1=0的距离相等,则动点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .直线2.方程(x -y )2+(xy -1)2=0表示的曲线是( ) A .一条直线和一条双曲线 B .两条双曲线 C .两个点 D .以上答案都不对3.已知两定点F 1(5,0),F 2(-5,0),曲线上的点P 到F 1,F 2的距离之差的绝对值是6,则该曲线的方程为( )A.x 29-y 216=1B.x 216-y 29=1 C.x 225-y 236=1 D.y 225-x 236=1 4.已知双曲线的两个焦点为F 1(-5,0),F 2(5,0),P 是此双曲线上的一点,且PF 1⊥PF 2,|PF 1|·|PF 2|=2,则该双曲线的方程是( )A.x 22-y 23=1B.x 23-y 22=1 C.x 24-y 2=1 D .x 2-y 24=1 5.已知动点M (x ,y )到直线l :x = 4的距离是它到点N (1,0)的距离的2倍,则动点M 的轨迹C 的方程为 .6.已知A (0,7),B (0,-7),C (12,2),以C 为一个焦点作过A ,B 的椭圆,椭圆的另一个焦点F 的轨迹方程是 .7.在直角坐标系中,△ABC 的两个顶点A ,B 坐标分别为A (-1,0),B (1,0),平面内两点G ,M 同时满足下列条件:①GA →+GB →+GC →=0; ②MA =MB =MC ; ③GM →∥AB →.则△ABC 的另一个顶点C 的轨迹方程为__________________________.8.设点P (x ,y )(y ≥0)为平面直角坐标系xOy 中的一个动点(其中O 为坐标原点),点P到定点M (0,12)的距离比点P 到x 轴的距离大12.(1)求点P 的轨迹方程;(2)若直线l :y =kx +1与点P 的轨迹相交于A ,B 两点,且|AB |=26,求k 的值.9.已知定点F (0,1)和直线l 1:y =-1,过定点F 与直线l 1相切的动圆的圆心为点C . (1)求动点C 的轨迹方程;(2)过点F 的直线l 2交轨迹于两点P ,Q ,交直线l 1于点R ,求RP →·RQ →的最小值.第61讲 圆锥曲线的综合应用1.若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p =( )A .4B .2C .-4D .-22.与曲线x 224+y 249=1共焦点,而与曲线x 236-y 264=1共渐近线的双曲线方程为( )A.y 216-x 29=1B.x 216-y29=1 C.y 29-x 216=1 D.x 29-y 216=1 3.椭圆x 24+y23=1上有n 个不同的点P 1,P 2,…,P n (n ∈N *),F 是右焦点,{|P n F |}组成公差d >1100的等差数列,则n 的最大值为( )A .99B .100C .199D .2004.双曲线x 26-y 23=1的渐近线与圆(x -3)2+y 2=r 2(r >0)相切,则r 等于( )A. 3 B .2 C .3 D .65.若曲线C 1:x 2+y 2-2x =0与曲线C 2:y (y -mx -m )=0有4个不同的交点,则实数m 的取值范围为______________________.6.若F 1,F 2分别为双曲线C :x 29-y 227=1的左,右焦点,点A 在双曲线C 上,点M的坐标为(2,0),AM 为∠F 1AF 2的平分线.则|AF 2|的值为 .7.若椭圆x 2a 2+y 2b2=1(a >b >0)的左,右焦点分别为F 1,F 2,线段F 1F 2被抛物线y 2=2bx的焦点分成5∶3两段,则此椭圆的离心率为______.8.已知椭圆C 的焦点在x 轴上,它的一个顶点恰好是抛物线y =14x 2的焦点,离心率为255. (1)求椭圆C 的标准方程.(2)过椭圆C 的右焦点F 作直线l 交椭圆C 于A ,B 两点,交y 轴于点M ,若MA →=λ1AF →,MB →=λ2BF →,求λ1+λ2的值.9.在平面直角坐标系xOy中,点E到两点F1(-1,0),F2(1,0)的距离之和为22,设点E的轨迹为曲线C.(1)求C的方程;(2)设过点F2(1,0)且斜率为k(k≠0)的直线l与曲线C交于不同的两点M,N,点P在y 轴上,且|PM|=|PN|,求点P纵坐标的取值范围.第十单元 解析几何 第52讲 直线的方程1.D k =-tan π7=tan(π-π7)=tan 6π7,且6π7∈[0,π),所以倾斜角为6π7.2.D 因为动点P (2+3cos α,3sin α)的轨迹方程为圆C :(x -2)2+y 2=3,所以当直线l 与圆C 相切时,斜率取得最值,此时,k max =322-(3)2=3,故选D.3.D4.C 令x =0,得y =k ;令y =0,得x =-2k .所以三角形面积S =12|xy |=k 2.又S ≤1,即k 2≤1,所以-1≤k ≤1. 又因为k =0时不合题意,故选C. 5.(-2,0) 此题倾斜角为钝角等价于斜率小于0,从而得到a 2+2a <0,解之得-2<a <0. 6.x =1 AB 的长度恒定,故△ABC 面积最大,只需要C 到直线AB 的距离最大即可.此时,C 在AB 的中垂线上,AB 的中垂线方程为y -32=-3(x +12),代入x 2+y 2=4得C (1,-3)或C (-1,3)(舍去),所以直线BC 的方程是x =1.7.-24 令x =0,得y =k 4;令y =0,得x =-k3,则有k 4-k3=2,所以k =-24.8.解析:(1)设点C (x ,y ),由题意得5+x 2=0,3+y2=0,得x =-5,y =-3.故所求点C 的坐标是(-5,-3).(2)点M 的坐标是(0,-52),点N 的坐标是(1,0),直线MN 的方程是y -0-52-0=x -10-1,即5x -2y -5=0.9.解析:(1)依题意,直线l 的斜率存在.因为直线l 过点M (-2,0),可设直线l :y =k (x +2). 因为P ,Q 两点在圆x 2+y 2=1上,所以|OP →|=|OQ →|=1,因为OP →·OQ →=-12,所以OP →·OQ →=|OP →|·|OQ →|·cos ∠POQ =-12,所以∠POQ =120°,所以O 到直线l 的距离等于12.所以|2k |k 2+1=12,得k =±1515.所以直线l 的方程为x -15y +2=0或x +15y +2=0. (2)因为△OMP 与△OPQ 的面积相等,所以MQ →=2MP →.设P (x 1,y 1),Q (x 2,y 2),所以MQ →=(x 2+2,y 2),MP →=(x 1+2,y 1).所以⎩⎪⎨⎪⎧ x 2+2=2(x 1+2)y 2=2y 1,即⎩⎪⎨⎪⎧x 2=2(x 1+1)y 2=2y 1,(*)因为P ,Q 两点在圆上,所以⎩⎪⎨⎪⎧x 21+y 21=1x 22+y 22=1,把(*)代入,得⎩⎪⎨⎪⎧x 21+y 21=14(x 1+1)2+4y 21=1,所以⎩⎨⎧x 1=-78y 1=±158.所以直线l 的斜率k =k MP =±159,即k =±159. 第53讲 两直线的位置关系与对称问题1.A a =3代入⇒直线ax +2y +2a =0和直线3x +(a -1)y -a +7=0平行,反之直线ax +2y +2a =0和3x +(a -1)y -a +7=0平行⇒a (a -1)=2×3≠2a (-a +7),a =3或a =-2,所以“a =3”是“直线ax +2y +2a =0和直线3x +(a -1)y -a +7=0平行”的充分而不必要条件.2.A 根据已知直线方程知所求直线的斜率为12,所以所求直线方程为y -3=12(x -2),即x -2y +4=0,故选A.3.B 当直线过原点时方程为2x -5y =0,不过原点时,可设出其截距式为x a +y2a=1再由过点(5,2)即可解出.4.B 由正弦定理,得a sin A =bsin B,即-sin A a ·b sin B =-1,而-sin A a 与b sin B分别为两条直线的斜率,故两条直线垂直,故选B.5.2 易知,点(0,8)在直线y =ax +8上,则点(8,0)必在直线y =-12x +b 上,则b =4.同理,(0,4)在直线y =-12x +b 上,则点(4,0)必在直线y =ax +8上,则a =-2,所以a +b=2.6.2 由已知两条直线平行得-34=-6m,解得m =8,所以直线6x +my +14=0为3x +4y +7=0,故两平行线间的距离为|-3-7|32+42=2.7.[0,10] 由题意得,点到直线的距离为 |4×4-3×a -1|5=|15-3a |5.又|15-3a |5≤3,即|15-3a |≤15,解之得0≤a ≤10,所以a ∈[0,10].8.解析:当m =0时,l 1:x +6=0,l 2:x =0,所以l 1∥l 2. 当m =2时,l 1:x +4y +6=0,l 2:3y +2=0, 所以l 1与l 2相交.当m ≠0且m ≠2时,由1m -2=m 23m,得m =-1或m =3.由1m -2=62m,得m =3. 故(1)当m ≠-1,m ≠3且m ≠0时,l 1与l 2相交; (2)当m =-1或m =0时,l 1∥l 2;(3)当m =3时,l 1与l 2重合.9.解析:(方法一)直线x +my +m =0恒过点A (0,-1).k AP =-1-10+1=-2,k AQ =-1-20-2=32,则-1m ≥32或-1m ≤-2,所以-23≤m ≤12且m ≠0.又m =0时直线x +my +m =0与线段PQ 有交点,故所求m 的范围是[-23,12].(方法二)过P 、Q 两点的直线方程为y -1=2-12+1(x +1),即y =13x +43,代入x +my +m =0,整理得x =-7mm +3,由已知-1≤-7m m +3≤2,解得-23≤m ≤12.第54讲 圆的方程1.D 圆方程化为(x -2)2+(y +3)2=13,圆心(2,-3),故选D. 2.D 3.D 化为x 2+y 2=4(x ≤0,y ≤0),表示在第三象限的四分之一圆弧,长度=14·2π·2=π.4.D 已知圆的圆心坐标为(a ,b ),半径为r ,当b <r 时,圆心到x 轴的距离为|b |,只有当|b |<r 时,才有圆与x 轴相交,而b <r 不能保证|b |<r ,故D 是错误的.故选D.5.1 圆心(0,0)到直线3x -4y -10=0的距离d =|-10|5=2.再由d -r =2-1=1,知最小距离为1.6.-1 1 点P (1,4)在圆C :x 2+y 2+2ax -4y +b =0上, 所以2a +b +1=0,①点P 关于直线x +y -3=0的对称点也在圆C 上, 所以圆心(-a,2)在直线x +y -3=0上, 即-a +2-3=0,②由①②解得a =-1,b =1.7.(x -2)2+(y -4)2=10或(x +2)2+(y +4)2=10 解析:圆心在直线y =2x 上,设圆心为(a,2a ),圆心到直线y =x 的距离d =r 2-(l2)2,得d =(10)2-(422)2=2,2=|a -2a |12+12⇒a =±2.所以圆的标准方程为(x -2)2+(y -4)2=10或(x +2)2+(y +4)2=10.8.解析:如图,方程x 2+y 2-4x +1=0表示以点(2,0)为圆心,以3为半径的圆. 设yx =k ,即y =kx ,由圆心(2,0)到y =kx 的距离为半径时直线与圆相切,斜率取得最大、最小值.由|2k -0|k 2+1=3,解得k 2=3.所以k max =3,k min =- 3.(也可由平面几何知识,有OC =2,CP =3,∠POC =60°,直线OP 的倾斜角为60°,直线OP ′的倾斜角为120°解之)9.解析:(1)设P (x ,y ),圆P 的半径为r . 由题意y 2+2=r 2,x 2+3=r 2, 从而y 2+2=x 2+3.故P 点的轨迹方程为y 2-x 2=1.(2)设P (x 0,y 0),由已知得|x 0-y 0|2=22,又点P 在双曲线y 2-x 2=1上,从而得⎩⎪⎨⎪⎧|x 0-y 0|=1y 20-x 20=1.由⎩⎪⎨⎪⎧x 0-y 0=1y 20-x 20=1⇒⎩⎪⎨⎪⎧ x 0=0y 0=-1,此时,圆P 的半径r =3; 由⎩⎪⎨⎪⎧x 0-y 0=-1y 20-x 20=1⇒⎩⎪⎨⎪⎧x 0=0y 0=1,此时,圆P 的半径r = 3. 故圆P 的方程为x 2+(y -1)2=3或x 2+(y +1)2=3. 第55讲 直线与圆、圆与圆的位置关系1.B 因为圆x 2+y 2+2x -4y =0的圆心为(-1,2),由直线3x +y +a =0过圆x 2+y 2+2x -4y =0的圆心得:a =1.2.A 圆心坐标为(1,-2),半径为3,圆心到直线的距离d =|t -2-t +1|t 2+1=1t 2+1≤1<3, 所以直线与圆一定相交.3.B 求圆的弦长利用勾股定理,弦心距d =2,r =3,r 2=d 2+l 24,l =23-2=2,选B.4.A 直线3x +y -23=0与圆O :x 2+y 2=4交于A (1,3),B (2,0),OA →·OB →=2.5.±33由条件可知圆心(1,2)到直线x -my -1=0的距离为d =4-3=1,所以|1-2m -1|1+m 2=1,所以m =±33.6.4 直线2ax +by +6=0过圆心C (-1,2),a -b -3=0, 当点M (a ,b )到圆心距离最小时,切线长最短; |MC |=(a +1)2+(b -2)2=2a 2-8a +26, a =2时最小,b =-1,此时切线长等于4.7.x -y -5=0 点P 在圆内,则过点P 且被点P 平分的弦所在的直线和圆心与P 的连线垂直,又圆心与P 的连线的斜率是-1,则所求直线的斜率为1,且过点P (2,-3),则所求直线方程是x -y -5=0.8.解析:(1)由题设,圆心C 是直线y =2x -4和y =x -1的交点, 解得点C (3,2),于是切线的斜率必存在. 设过A (0,3)的圆C 的切线方程为y =kx +3.由题意,|3k +1|k 2+1=1,解得k =0或-34.故所求切线方程为y =3或3x +4y -12=0. (2)因为圆心在直线y =2x -4上,所以圆C 的方程为(x -a )2+[y -2(a -2)]2=1. 设点M (x ,y ),因为MA =2MO , 所以x 2+(y -3)2=2x 2+y 2,化简得x 2+y 2+2y -3=0,即x 2+(y +1)2=4,所以点M (x ,y )在以D (0,-1)为圆心,2为半径的圆上. 由题意,点M (x ,y )在圆C 上,所以圆C 与圆D 有公共点, 则|2-1|≤CD ≤2+1,即1≤a 2+(2a -3)2≤3. 由5a 2-12a +8≥0,得a ∈R ,由5a 2-12a ≤0,得0≤a ≤125.所以点C 的横坐标a 的取值范围为[0,125].9.解析:(1)圆的方程可化为(x -6)2+y 2=4,可得圆心为Q (6,0),半径为2,设直线l 的方程为y =kx +2.(方法一)将直线方程代入圆方程得x 2+(kx +2)2-12x +32=0, 整理得(1+k 2)x 2+4(k -3)x +36=0.① 直线与圆交于两个不同的点A ,B 等价于Δ=[4(k -3)]2-4×36(1+k 2)=42(-8k 2-6k )>0,解得-34<k <0,即k 的取值范围为(-34,0).(方法二)直线l 与圆(x -6)2+y 2=4交于两个不同的点A ,B 等价于|6k -0+2|k 2+1<2, 化简得-8k 2-6k >0,解得-34<k <0,即k 的取值范围为(-34,0).(2)设A (x 1,y 1),B (x 2,y 2),则OA →+OB →=(x 1+x 2,y 1+y 2),由方程①,x 1+x 2=-4(k -3)1+k 2,②又y 1+y 2=k (x 1+x 2)+4.③而P (0,2),Q (6,0),PQ →=(6,-2).所以OA →+OB →与PQ →共线等价于-2(x 1+x 2)=6(y 1+y 2),将②③代入上式,解得k =-34.由(1)知k ∈(-34,0),而k =-34∉(-34,0).故没有符合题意的常数k .第56讲 椭 圆1.C 由题意得,c =1,2b 2a=3,又a 2-b 2=c 2,解得a =2,b 2=3,故选C.2.B 由题知|MN |+|MF 2|+|NF 2|=|MF 1|+|NF 1|+|MF 2|+|NF 2|=4a =16.故选B. 3.A 因为线段PF 1的中点M 在y 轴上,故可知P (c ,±b 2a )=(4,±95),所以|PF 1|=10-95=415,选A.4.C 设椭圆的左,右焦点分别为F 1,F 2. 由题意可得OF 2=OA =OB =OF 1=c .又y =-3x 得∠AOF 2=2π3,∠AOF 1=π3.所以|AF 2|=3c ,|AF 1|=c .由椭圆定义知,|AF 1|+|AF 2|=2a ,所以c +3c =2a ,所以e =ca =3-1.5.0<k <1 椭圆方程化为x 22+y 22k=1.焦点在y 轴上,则2k>2,即k <1.又k >0,所以0<k <1.6.32或83 由已知m >0且m ≠2,若0<m <2,e =2-m 2=12,得m =32,若m >2,则e =m -2m =12,得m =83. 7.m 2+n 2=12设P (x ,y ),由OP →=m ·OA →+n ·OB →⇒(x ,y )=m (a ,b )+n (-a ,b )=(am -an ,bm +bn )⇒⎩⎪⎨⎪⎧x =a (m -n )y =b (m +n )⇒⎩⎨⎧xa =m -n y b=m +n⇒(m -n )2+(m +n )2=x 2a 2+y 2b 2=1⇒m 2+n 2=12.8.解析:(方法一)因为a =x i +(y +2)j ,b =x i +(y -2)j ,且|a|+|b|=8, 所以点M (x ,y )到两个定点F 1(0,-2),F 2(0,2)的距离之和为8.所以轨迹C 为以F 1,F 2为焦点的椭圆,方程为x 212+y 216=1.(方法二)由题知,x 2+(y +2)2+x 2+(y -2)2=8, 移项,得x 2+(y +2)2=8-x 2+(y -2)2,两边平方,得x 2+(y +2)2=x 2+(y -2)2-16x 2+(y -2)2+64, 整理,得2x 2+(y -2)2=8-y ,两边平方,得4[x 2+(y -2)2]=(8-y )2,展开,整理得x 212+y 216=1.9.解析:(1)因为焦距为4,所以a 2-b 2=4,又因为椭圆C 过点P (2,3),所以2a 2+3b2=1,故a 2=8,b 2=4.从而椭圆C 的方程为x 28+y 24=1.(2)由题意,各点的坐标如下图所示.则QG 的直线方程:y -0y 0=x -8x 0x 0-8x 0,化简得x 0y 0x -(x 20-8)y -8y 0=0.又x 20+2y 20=8,所以x 0x +2y 0y -8=0,代入x 28+y 24=1,求得最后Δ=0,所以直线QG 与椭圆只有一个公共点. 第57讲 双曲线1.C 由题知,c a =52,即54=c 2a 2=a 2+b2a2,所以b 2a 2=14,所以b a =12,所以C 的渐近线方程为y =±12x ,故选C.2.C3.A 可设所求双曲线方程为x 22-y 2=λ,把(2,-2)点坐标代入方程得λ=-2.4.C 由渐近线方程y =32x ,且b =3,所以a =2.据定义有|PF 2|-|PF 1|=4,所以|PF 2|=7.5.3+1 在Rt △F 1F 2P ,设2c =F 1F 2=2,则PF 2=1, PF 1=3⇒2a =PF 1-PF 2=3-1⇒e =c a =23-1=3+1.6.[π3,π2]7.1 因P (7,12)在双曲线x 2-y2b2=1上,故72-122b2=1,所以b 2=3,a 2=1.如图,|P A |=|PB |, 2a =|PF 1|-|PF 2|=|P A |+|AF 1|-|PB |-|BF 2| =|AF 1|-|BF 2|.因为|AF 1|=|F 1C |,|BF 2|=|CF 2|, 所以|F 1C |-|CF 2|=2a ,又|F 1C |+|CF 2|=2c ,所以|F 1C |=a +c ,|CF 2|=c -a , 所以C (a,0),所以C 点的横坐标为1.8.解析:(1)由16x 2-9y 2=144得x 29-y 216=1,所以a =3,b =4,c =5.焦点坐标F 1(-5,0),F 2(5,0),离心率e =53,渐近线方程为y =±43x .(2)||PF 1|-|PF 2||=6,cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1||PF 2|=(|PF 1|-|PF 2|)2+2|PF 1||PF 2|-|F 1F 2|22|PF 1||PF 2|=36+64-10064=0.所以∠F 1PF 2=90°.9.解析: (1)设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0),半焦距为c ,则c =2,又由c a =233,得a =3,b 2=c 2-a 2=1,故所求双曲线C 的方程为x 23-y 2=1.(2)依题意有:Q (-x 0,-y 0),所以MP →=(x 0,y 0-1),MQ →=(-x 0,-y 0-1),所以MP →·MQ →=-x 20-y 20+1,又x 203-y 20=1,所以MP →·MQ →=-43x 20+2,由x 203-y 20=1可得,x 20≥3, 所以MP →·MQ →=-43x 20+2≤-2,故MP →·MQ →的取值范围是(-∞,-2]. 第58讲 抛物线1.C 抛物线的准线方程为x =-p 2,由抛物线的定义知4+p2=5,解得p =2.2.D 抛物线的焦点F (2,0),则距离d =22=1,故选D.3.C 因为抛物线y 2=4x 的焦点是(1,0),所以c a =1a =5,所以a =55,b =255,所以该双曲线的渐近线方程为y =±bax =±2x .4.A 设平行于直线l 且与抛物线相切的方程为y =4x +b ,联立y =4x 2,令Δ=0,得b =-1,可得交点为(12,1),故选A.5.-1≤k ≤1 因为y 2=8x ,所以Q (-2,0)(Q 为准线与x 轴的交点),设过Q 点的直线l 方程为y =k (x +2).因为l 与抛物线有公共点, ⎩⎪⎨⎪⎧y 2=8x y =k (x +2)有解,即k 2x 2+(4k 2-8)x +4k 2=0有解. 所以Δ=(4k 2-8)2-16k 4≥0,即k 2≤1.所以-1≤k ≤1.6.(3,2) 将y =x -1代入抛物线y 2=4x ,经整理得x 2-6x +1=0.由韦达定理得x 1+x 2=6,x 1+x 22=3,y 1+y 22=x 1+x 2-22=6-22=2.所以所求点的坐标为(3,2). 7.4 双曲线的左焦点坐标为(-3+p 216,0), 抛物线的准线方程为x =-p2,所以-3+p 216=-p2,所以p 2=16,又p >0,所以p =4.8.解析:(1)因为抛物线的焦点F 的坐标为(p2,0),又因为直线的斜率为1,所以直线l 的方程为:y =x -p2.(2)证明:过点A ,B 分别作准线的垂线AA ′,BB ′,交准线于A ′,B ′,则由抛物线的定义得:|AB |=|AF |+|BF | =|AA ′|+|BB ′|=x 1+p 2+x 2+p 2=x 1+x 2+p .(3)由|AB |=4,得x 1+x 2+p =4,直线y =x -p2与抛物线方程联立,⎩⎪⎨⎪⎧y =x -p 2y 2=2px⇒x 2-3px +p 24=0,由韦达定理,x 1+x 2=3p ,解得p =1, 抛物线方程为y 2=2x .9.解析:(1)依题意d =|0-c -2|2=322,解得c =1(负根舍去).所以抛物线C 的方程为x 2=4y .(2)设点A (x 1,y 1),B (x 2,y 2),P (x 0,y 0).由x 2=4y ,即y =14x 2,得y ′=12x .所以抛物线C 在点A 处的切线P A 的方程为y -y 1=x 12(x -x 1),即y =x 12x +y 1-12x 21.因为y 1=14x 21,所以y =x 12x -y 1.因为点P (x 0,y 0)在切线l 1上,所以y 0=x 12x 0-y 1.①同理,y 0=x 22x 0-y 2.②综合①②得,点A (x 1,y 1),B (x 2,y 2)的坐标都满足方程y 0=x2x 0-y .因为经过A (x 1,y 1),B (x 2,y 2)两点的直线是唯一的.所以直线AB 的方程为y 0=x2x 0-y ,即x 0x -2y -2y 0=0.第59讲 直线与圆锥曲线的位置关系1.A 由y =-x 2可得y ′=-2x ,而直线4x +3y -8=0的斜率为-43,令y ′=-2x=-43,得x =23.代入y =-x 2得y =-49,故距离d min =|4×23+3×(-49)-8|32+42=43.2.B3.C 由题意B (c ,b 2a ),所以k =b 2ac +a=a -c a =1-e ,所以13<1-e <12,所以12<e <23.4.C 数形结合法,与渐近线斜率比较. 5.(2,0) 6.27.14 由⎩⎪⎨⎪⎧ y =kx y 2=2x )知x A =2k 2,由⎩⎪⎨⎪⎧y =k ′x y 2=4x),知x B =4k ′2, 所以|OA |=1+k 2·x A ,|OB |=1+k 2·x B , 故OA OB =x A x B =12,同理OC OD =x C x D =12. 所以S △OAC S △OBD =12|OA ||OC |sin ∠AOC12|OB ||OD |sin ∠BOD =14.8.解析:(1)由题意可设椭圆的标准方程为x 2a 2+y 2b2=1(a >b >0).则由长轴长等于4,即2a =4,所以a =2.又e =22,所以c = 2.又由于b 2=a 2-c 2=2,所以所求椭圆C 的标准方程为x 24+y 22=1.(2)假设存在这样的直线l :y =kx +m ,设M (x 1,y 1),N (x 2,y 2),MN 的中点为F (x 0,y 0). 因为|ME |=|NE |,所以MN ⊥EF ,所以y 0-1x 0·k =-1,①(ⅰ)其中若x 0=0,则k =0,显然直线y =m (-2<m <2)符合题意; (ⅱ)下面仅考虑k ≠0的情形:由⎩⎪⎨⎪⎧y =kx +m x 24+y 22=1,得(1+2k 2)x 2+4kmx +2m 2-4=0, Δ=16k 2m 2-4(1+2k 2)(2m 2-4)>0, 得4k 2+2>m 2,②则x 0=x 1+x 22=-2km 1+2k 2,y 0=kx 0+m =m1+2k 2.代入①式,即m1+2k 2-1-2km 1+2k 2·k =-1,解得m =-1-2k 2.代入②式得4k 2+2>(-1-2k 2)2,得-22<k <22(k ≠0).综上(ⅰ)(ⅱ)可知,存在这样的直线l ,其斜率k 的取值范围是(-22,22). 9.解析:(1)由已知得⎩⎪⎨⎪⎧2a ∶2b =2∶3c =1a 2=b 2+c 2,解得a =2,b = 3.故所求椭圆方程为x 24+y 23=1.(2)证明:由(1)知F 1(-1,0).当直线m 斜率存在时,设直线m 的方程为:y =k (x +1)(k ≠0).由⎩⎪⎨⎪⎧y =k (x +1)x 24+y 23=1), 得(3+4k 2)x 2+8k 2x +4k 2-12=0.由于Δ>0,设A (x 1,y 1),B (x 2,y 2),则有x 1+x 2=-8k 23+4k 2,x 1x 2=4k 2-123+4k 2,|AB |=(1+k 2)[(x 1+x 2)2-4x 1x 2]=(1+k 2)[(-8k 23+4k 2)2-4×4k 2-123+4k 2]=12(1+k 2)3+4k 2.同理|CD |=12(1+k 2)3k 2+4.所以1|AB |+1|CD |=3+4k 212(1+k 2)+3k 2+412(1+k 2)=7(1+k 2)12(1+k 2)=712.当直线m 斜率不存在时,此时|AB |=3,|CD |=4, 1|AB |+1|CD |=13+14=712. 综上,1|AB |+1|CD |为定值712.第60讲 轨迹问题1.D 因为定点F (1,-1)在直线l :x -1=0上,所以轨迹为过F (1,-1)与直线l 垂直的一条直线,故选D.2.C (x -y )2+(xy -1)2=0⇔⎩⎪⎨⎪⎧x -y =0xy -1=0,所以⎩⎪⎨⎪⎧ x =1y =1或⎩⎪⎨⎪⎧x =-1y =-1. 3.A4.C 设双曲线的方程为x 2a 2-y 2b2=1.由题意||PF 1|-|PF 2||=2a ,|PF 1|2+|PF 2|2=(25)2.又因为|PF 1|·|PF 2|=2,所以a =2,b =1.故双曲线方程为x 24-y 2=1. 5.x 24+y 23=1 点M (x ,y )到直线x =4的距离,是到点N (1,0)的距离的2倍,则 |x -4|=2(x -1)2+y 2⇒x 24+y 23=1. 所以,动点M 的轨迹为椭圆,方程为x 24+y 23=1. 6.y 2-x 248=1(y ≤-1) 解析:由题意知|AC |=13,|BC |=15,|AB |=14,又|AF |+|AC |=|BF |+|BC |,所以|AF |-|BF |=|BC |-|AC |=2,故点F 的轨迹是以A ,B 为焦点,实轴长为2的双曲线的下支.又c =7,a =1,b 2=48,所以点F 的轨迹方程为y 2-x 248=1(y ≤-1). 7.x 2+y 23=1(y ≠0) 解析:由①GA →+GB →+GC →=0,知G 为三角形△ABC 的重心.由②MA =MB =MC ,知M 为三角形△ABC 的外心.设M (x 0,y 0),C (x ,y ),则G (x 3,y 3). 由②MA =MB =MC 知,(x 0+1)2+y 20=(x 0-1)2+y 20=(x 0-x )2+(y 0-y )2,得x 0=0,1+y 20=x 2+(y -y 0)2,(*)则M (0,y 0),GM →=(-x 3,y 0-y 3),AB →=(2,0), 由GM →∥AB →知2(y 0-y 3)=0,即y 0=y 3,将其代入(*),化简得x 2+y 23=1. 又因为C 不能在x 轴上,所以C 的轨迹方程为x 2+y 23=1(y ≠0). 8.解析:(1)过P 作x 轴的垂线且垂足为N ,由题意可知|PM |-|PN |=12, 而y ≥0,所以|PN |=y , 所以x 2+(y -12)2=y +12, 化简得x 2=2y (y ≥0)为所求的方程.(2)设A (x 1,y 1),B (x 2,y 2),联立⎩⎪⎨⎪⎧y =kx +1x 2=2y , 得x 2-2kx -2=0,所以x 1+x 2=2k ,x 1x 2=-2.|AB |=1+k 2(x 1+x 2)2-4x 1x 2=1+k 24k 2+8=26,所以k 4+3k 2-4=0,而k 2≥0,所以k 2=1,所以k =±1.9.解析:(1)由题设知点C 到点F 的距离等于它到l 1的距离,所以点C 的轨迹是以F 为焦点,l 1为准线的抛物线,所以动点C 的轨迹方程为x 2=4y .(2)由题意知,直线l 2的方程可设为y =kx +1(k ≠0),与抛物线方程联立消去y ,得x 2-4kx -4=0.设P (x 1,y 1),Q (x 2,y 2),则x 1+x 2=4k ,x 1x 2=-4.又易得点R 的坐标为(-2k,-1),所以 RP →·RQ →=(x 1+2k ,y 1+1)·(x 2+2k,y 2+1) =(x 1+2k )(x 2+2k)+(kx 1+2)(kx 2+2) =(1+k 2)x 1x 2+(2k +2k )(x 1+x 2)+4k 2+4 =-4(1+k 2)+4k (2k +2k )+4k 2+4 =4(k 2+1k 2)+8. 因为k 2+1k 2≥2,当且仅当k 2=1时取等号, 所以RP →·RQ →≥4×2+8=16,即RP →·RQ →的最小值为16.第61讲 圆锥曲线的综合应用1.A 2.A3.D d =|P n F |-|P 1F |n -1(n ≥2). 因为d >1100,所以|P n F |-|P 1F |n -1>1100(n ≥2), 进而有:n <100(|P n F |-|P 1F |)+1(n ≥2),若使n 的值最大,只需100(|P n F |-|P 1F |)+1(n ≥2)最大,即使|P n F |-|P 1F |最大,而(|P n F |-|P 1F |)max =3-1=2,所以n <201,所以n 的最大值为200,故选D.4.A 双曲线x 26-y 23=1的渐近线方程为y =±22x ,因与圆(x -3)2+y 2=r 2(r >0)相切,故圆心(3,0)到直线y =±22x 的距离等于r ,则r =|2×3-2×0|2+4= 3. 5.(-33,0)∪(0,33) 解析:注意到曲线C 1:(x -1)2+y 2=1表示的是以点(1,0)为圆心,1为半径的圆,曲线C 2:y (y -mx -m )=0表示的直线y -mx -m =0,即y =m (x +1),注意到直线y =0与曲线C 1有两个不同的交点,因此要使曲线C 1与C 2有4个不同的交点,须要直线y =m (x +1)与曲线C 1有两个不同的交点,且这两个交点与点(0,0),(2,0)不重合,结合图形观察分析可知,满足题意的直线y =m (x +1)的斜率m 应在区间(-33,33)内,且不等于零,即实数m 的取值范围是(-33,0)∪(0,33).6.6 由双曲线方程知a =3,c =6.令|AF 1|=r 1,|AF 2|=r 2,由AM 为∠F 1AF 2的角平分线,得r 1r 2=S △AF 1M S △AF 2M =|F 1M ||F 2M |=84=2 ⇒r 1=2r 2,而r 1-r 2=2a =6⇒2r 2-r 2=6⇒r 2=6. 7.255 根据题意,可得⎩⎪⎨⎪⎧ 3(b 2+c )=5(c -b 2)a 2=b 2+c 2,解得e =c a =255. 8.解析:(1)抛物线y =14x 2的焦点坐标为(0,1), 设椭圆C 的标准方程为:x 2a 2+y 2b2=1(a >b >0),则b =1. 所以c a =255,所以c 2a 2=45,所以a 2-b 2a 2=45,a 2=5, 所以椭圆C 的标准方程为:x 25+y 2=1. (2)设A (x 1,y 1),B (x 2,y 2),M (0,y 0),则由MA →=λ1AF →,得x 1=2λ11+λ1,y 1=y 01+λ1, 所以15(2λ11+λ1)2+(y 01+λ1)2=1,所以λ21+10λ1+5-5y 20=0, 同理可得:λ22+10λ2+5-5y 20=0,所以λ1,λ2是方程x 2+10x +5-5y 20=0的根,所以λ1+λ2=-10.9.解析:(1)由题设知|EF 1|+|EF 2|=22>|F 1F 2|, 根据椭圆的定义,E 的轨迹是以F 1,F 2为焦点,长轴长为22的椭圆,设其方程为x 2a 2+y 2b2=1(a >b >0), 则c =1,a =2,b =1,所以C 的方程为x 22+y 2=1. (2)依题设直线l 的方程为y =k (x -1),将y =k (x -1)代入x 22+y 2=1并整理得, (2k 2+1)x 2-4k 2x +2k 2-2=0,Δ=8k 2+8>0.设M (x 1,y 1),N (x 2,y 2),则x 1+x 2=4k 22k 2+1,x 1x 2=2k 2-22k 2+1. 设线段MN 的中点为Q ,则x Q =2k 22k 2+1,y Q =k (x Q -1)=-k 2k 2+1, 即Q (2k 22k 2+1,-k 2k 2+1). 因为k ≠0,所以直线MN 的垂直平分线的方程为y +k 2k 2+1=-1k (x -2k 22k 2+1), 令x =0,解得y P =k 2k 2+1=12k +1k, 当k >0时,因为2k +1k ≥22,所以0<y P ≤24;当k <0时,因为2k +1k ≤-22,所以-24≤y P <0. 综上得点P 的纵坐标的取值范围是[-24,0)∪(0,24].。
学海导航高三数学人教B版文科第一轮总复习训练10.55直线与圆、圆与圆的位置关系(含答案详析)
第55讲 直线与圆、圆与圆的位置关系1.若直线3x +y +a =0过圆x 2+y 2+2x -4y =0的圆心,则a 的值为( )A .-1B .1C .3D .-32.直线tx +y -t +1=0(t ∈R )与圆x 2+y 2-2x +4y -4=0的位置关系为( )A .相交B .相切C .相离D .以上都有可能3.直线x +y -1=0被圆(x +1)2+y 2=3截得的弦长等于( ) A. 2 B .2C .2 2D .44.直线3x +y -23=0与圆O :x 2+y 2=4交于A 、B 两点,则OA →·OB →=( )A .2B .-2C .4D .-45.设直线x -my -1=0与圆(x -1)2+(y -2)2=4相交于A ,B 两点,且弦AB 的长为23,则实数m 的值是 .6.若圆C :x 2+y 2+2x -4y +3=0关于直线2ax +by +6=0对称,则由点(a ,b )向圆所作的切线长的最小值是 .7.经过点P (2,-3),作圆x 2+2x +y 2=24的弦AB ,使得点P 平分弦AB ,则弦AB 所在直线的方程为________________________________________________________________________.8.如图,在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程;(2)若圆C 上存在点M ,使MA =2MO ,求圆心C 的横坐标a 的取值范围.9.在平面直角坐标系xOy 中,已知圆x 2+y 2-12x +32=0的圆心为Q ,过点P (0,2)且斜率为k 的直线l 与圆Q 相交于不同的两点A ,B .(1)求k 的取值范围;(2)是否存在常数k ,使得向量OA →+OB →与PQ →共线?如果存在,求k 的值;如果不存在,请说明理由.第55讲 直线与圆、圆与圆的位置关系1.B 因为圆x 2+y 2+2x -4y =0的圆心为(-1,2),由直线3x +y +a =0过圆x 2+y 2+2x -4y =0的圆心得:a =1.2.A 圆心坐标为(1,-2),半径为3,圆心到直线的距离d =|t -2-t +1|t 2+1=1t 2+1≤1<3, 所以直线与圆一定相交.3.B 求圆的弦长利用勾股定理, 弦心距d =2,r =3,r 2=d 2+l 24,l =23-2=2,选B. 4.A 直线3x +y -23=0与圆O :x 2+y 2=4交于A (1,3),B (2,0),OA →·OB →=2.5.±33由条件可知圆心(1,2)到直线x -my -1=0的距离为d =4-3=1, 所以|1-2m -1|1+m 2=1,所以m =±33. 6.4 直线2ax +by +6=0过圆心C (-1,2),a -b -3=0,当点M (a ,b )到圆心距离最小时,切线长最短;|MC |=(a +1)2+(b -2)2=2a 2-8a +26,a =2时最小,b =-1,此时切线长等于4.7.x -y -5=0 点P 在圆内,则过点P 且被点P 平分的弦所在的直线和圆心与P 的连线垂直,又圆心与P 的连线的斜率是-1,则所求直线的斜率为1,且过点P (2,-3),则所求直线方程是x -y -5=0.8.解析:(1)由题设,圆心C 是直线y =2x -4和y =x -1的交点,解得点C (3,2),于是切线的斜率必存在.设过A (0,3)的圆C 的切线方程为y =kx +3.由题意,|3k +1|k 2+1=1,解得k =0或-34. 故所求切线方程为y =3或3x +4y -12=0.(2)因为圆心在直线y =2x -4上,所以圆C 的方程为(x -a )2+[y -2(a -2)]2=1.设点M (x ,y ),因为MA =2MO ,所以x 2+(y -3)2=2x 2+y 2,化简得x 2+y 2+2y -3=0,即x 2+(y +1)2=4,所以点M (x ,y )在以D (0,-1)为圆心,2为半径的圆上.由题意,点M (x ,y )在圆C 上,所以圆C 与圆D 有公共点,则|2-1|≤CD ≤2+1,即1≤a 2+(2a -3)2≤3.由5a 2-12a +8≥0,得a ∈R ,由5a 2-12a ≤0,得0≤a ≤125. 所以点C 的横坐标a 的取值范围为[0,125]. 9.解析:(1)圆的方程可化为(x -6)2+y 2=4,可得圆心为Q (6,0),半径为2,设直线l 的方程为y =kx +2.(方法一)将直线方程代入圆方程得x 2+(kx +2)2-12x +32=0,整理得(1+k 2)x 2+4(k -3)x +36=0.①直线与圆交于两个不同的点A ,B 等价于Δ=[4(k -3)]2-4×36(1+k 2)=42(-8k 2-6k )>0,解得-34<k <0,即k 的取值范围为(-34,0).(方法二)直线l 与圆(x -6)2+y 2=4交于两个不同的点A ,B 等价于|6k -0+2|k 2+1<2, 化简得-8k 2-6k >0,解得-34<k <0, 即k 的取值范围为(-34,0). (2)设A (x 1,y 1),B (x 2,y 2),则OA →+OB →=(x 1+x 2,y 1+y 2),由方程①,x 1+x 2=-4(k -3)1+k 2,② 又y 1+y 2=k (x 1+x 2)+4.③而P (0,2),Q (6,0),PQ →=(6,-2).所以OA →+OB →与PQ →共线等价于-2(x 1+x 2)=6(y 1+y 2),将②③代入上式,解得k =-34. 由(1)知k ∈(-34,0),而k =-34∉(-34,0).故没有符合题意的常数k .。
学海导航高三数学人教B版文科第一轮总复习课件9.47空间点、线、面的位置关系
三
求异面直线所成的角
【例3】(1)如图,在长方体ABCDA1B1C1D1中,AA1=AB=
2,AD=1,点E,F,G分别是DD1,AB,CC1的中点,则异面 直线A1E与GF所成角的余弦值为( A.1 15 B. 5 10 C. 5 D.0 )
(2)(2011· 全国卷)已知正方体 ABCDA1B1C1D1 中,E 为 C1D1 的中点, 则异面直线 AE 与 BC 所成角的余弦值为____________.
⑤长方体 ABCDA1B1C1D1 中, 平面 ABCD 与平面 A1BC1 只有一个公共点 B; ⑥直线 a、b、c,若 a⊥c,b⊥c,则 a∥b. 其中真命题的个数是: 平面几何的知识向立体几何推广的时候,要 慎重.在直线与直线的位置关系中,空间中多了一种全新 的异面关系,复习时应借助熟悉的空间几何图形,理解这 种关系.
解析:将平面展开图还原成几何体,易知 AB 与 CD 所成 的角为 60° ,故选 D.
3.若直线 l(在平面 α 之外)上有两点到平面 α 的距离相 等,则直线 l 与平面 α 的关系是 .
解析:当这两点在 α 的同侧时,l 与 α 平行;当这两点在 α 异侧时,l 与 α 相交.
4.在空间四边形 ABCD 的边 AB、BC、CD、DA 上分别 取 E、F、G、H 四点,如果 EF 与 HG 交于点 M,那么( A ) A.M 一定在直线 AC 上 B.M 一定在直线 BD 上 C.M 可能在直线 AC 上,也可能在直线 BD 上 D.M 既不在直线 AC 上,也不在直线 BD 上
解析:(1)如图所示,连接 B1G、B1F,由 A1E∥B1G 可得, ∠B1GF 就是异面直线 A1E 与 GF 所成的角. 由 B1F= 5,B1G= 2,FG= 3,可得 B1G⊥FG, 即异面直线 A1E 与 GF 所成角的余弦值为 0,故选 D.
学海导航数学(理)总复习(第1轮)课件 第55讲 圆的方程
3.(2011·中山月考)圆 x -2x+y -3=0 的圆心到直 线 x- 3y-3=0 的距离为 1 .
2
2
【解析】圆 x2-2x+y2-3=0 可转化为(x-1)2
+y2=4,故圆心坐标为 (1,0),圆心到直线 x- 3y |1- 3· 0-3| -3=0 的距离为 2 =1,故填 1. 1+ 3
1当D 2 E 2 4 F ④ ___ 0时,表示圆;
D E ); 2 当D E 4 F ⑤ ___ 0时,表示一个点( , 2 2 3当D 2 E 2 4 F ⑥ ___ 0时,不表示任何图形.
2 2
3.确定圆的方程的方法和步骤 确定圆的方程的主要方法是待定系数法, 大致步骤为:⑦ ______________ ; ⑧ ______________ ;⑨ ____________ . 4.点与圆的位置关系 点和圆的位置关系有三种:设圆的标准方程 为 x a y b r 2,点M ( x0,y0 ).
掌握圆的标准方程和一般方程,能根据 条件用待定系数法求得圆的方程,并能 应用圆的方程知识解决简单的问题.
1.圆的标准方程为① __________ ,其中圆心 为(a,b),半径为r (r>0).特别地,圆心在原点, 半径为r的圆的方程为x 2 y 2 r 2 . 2.圆的一般方程为x 2 y 2 Dx Ey F 0 ( D 2 E 2 4 F>0),圆心为② __________ , 半径r ③ ____________ >0. 注意:
4.过点 A(1,-1),B(-1,1),且圆心在直线 x +y-2=0 上的圆的方程是 (x-1)2+(y-1)2=4 .
【解析】AB 的垂直平分线为 y=x,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【拓展演练1】(1)任意的实数k,直线y=kx+1与圆x2+ y2=2的位置关系一定是( A.相离 B.相切 C.相交但直线不过圆心 D.相交且直线过圆心 )
解析:(1)直线y=kx+1恒过定点(0,1),定点到圆心的距 离d=1< 2 ,即定点在圆内部,所以直线y=kx+1与圆相交 但直线不过圆心,故选C.
4.直线y=2x+3被圆x2+y2-6ห้องสมุดไป่ตู้-8y=0所截得的弦 长等于 .
解析:圆的标准方程为(x-3)2+(y-4)2=25,圆心(3,4), |2×3-4+3| 半径 R=5, 圆心 O 到直线 y=2x+3 的距离 d= = 4+1 5,弦长为 2 r2-d2=4 5.
5.圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关 系为( B ) B.相交 D.相离
(3)已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线, 则( ) A.l与C相交 C.l与C相离 B.l与C相切 D.以上三个选项均有可能
解析:(3)圆的方程可化为(x-2)2+y2=4,易知圆心 为(2,0),半径为2,圆心到点P的距离为1,所以点P在圆 内,所以直线与圆相交,故选A.
二
圆与圆的位置关系
【例2】两个圆C1:x2+y2+2x+2y-2=0,C2:x2+y2-
4x-2y+1=0的公切线的条数为( A.1条 C.3条
) B.2条 D.4条
解析:C1:(x+1)2+(y+1)2=4, C2:(x-2)2+(y-1)2=4. 圆心距 d=|C1C2|= 2+12+1+12= 13. |r1-r2|<d<r1+r2, 所以两圆 C1 与 C2 相交,有两条公切线,故选 B.
A.内切 C.外切
解析:两圆的圆心分别为(-2,0),(2,1), 半径分别为 r=2,R=3. 两圆的圆心距离为 -2-22+0-12= 17, 则 R-r< 17<R+r,所以两圆相交,故选 B.
一
直线与圆的位置关系
【例1】(1)若直线x-y+1=0与圆(x-a)2+y2=2有公
共点,则实数a的取值范围是( A.[-3,-1] B.[-1,3] C.[-3,1] D.(-∞,-3]∪[1,+∞)
(2)“a=3”是“直线y=x+4与圆(x-a)2+(x-3)2=8相 切”的( ) B.必要不充分条件 D.既不充分也不必要条件
A.充分不必要条件 C.充要条件
|a-3+4| 解析:(2)若直线与圆相切,则 =2 2 ,a=3或 2 a=-5,所以“a=3”是“直线y=x+4与圆(x-a)2+(x- 3)2=8相切”的充分不必要条件,故选A.
|3×2-4×-1+5| 解析:r= =3,故选 C. 2 2 3 +-4
3.直线 x+2y=0 被圆 C:x2+y2-6x-2y-15=0 所截得 的弦长等于 .
解析:由已知,圆心 C(3,1),半径 r=5.又圆心 C 到直线 |3+2| l 的距离 d= = 5,则弦长=2 r2-d2=4 5. 5
第55讲
直线与圆、圆与圆的位置关系
1.直线4x+3y=40和圆x2+y2=100的位置关系是( A ) A.相交 C.相切 B.相离 D.无法确定
40 解析:因为 d= =8<10=r,所以直线与圆相交. 5
2.以点(2,-1)为圆心,且与直线 3x-4y+5=0 相切 的圆的方程为( C ) A.(x-2)2+(y+1)2=3 B.(x+2)2+(y-1)2=3 C.(x-2)2+(y+1)2=9 D.(x+2)2+(y-1)2=9
解析:(2)设直线斜率为k, 则直线方程为y-2=k(x-2), 即kx-y+2-2k=0, |k+2-2k| 圆心(1,0)到直线的距离 = 5, 2 k +1 |2-k| 1 即 2 = 5,解得k=-2. k +1 因为直线与直线ax-y+1=0垂直, 1 1 所以k=-a=-2,即a=2,选C.
当 l 的斜率存在时,设所求直线 l 的斜率为 k, 则直线 l 的方程为 y-5=kx,即 kx-y+5=0. |-2k-6+5| 由点 C 到直线 AB 的距离 =2, 2 k +1 3 得 k= ,此时直线 l 的方程为 3x-4y+20=0. 4 又直线 l 的斜率不存在时,也满足题意,此时方程为 x= 0. 所以所求直线 l 的方程为 x=0 或 3x-4y+20=0.
【拓展演练 2】 若⊙O:x2+y2=5 与⊙O1:(x-m)2+y2=20(m∈R)相交 于 A、B 两点,且两圆在点 A 处的切线互相垂直,则线段 AB 的长度是 .
解析:由题意知,O(0,0),O1(m,0),且 5<|m|<3 5. 因为两圆在点 A 处的切线互相垂直, 所以 OA⊥O1A, 所以有 m2=( 5)2+(2 5)2=25⇒m=± 5, 5× 20 所以|AB|=2× =4. 5
三
圆的弦长、中点弦问题
【例3】已知点P(0,5)及圆C:x2+y2+4x-12y+24=0. (1)若直线l过点P且被圆C截得的线段长为4 3 ,求l的方
程; (2)求过点P的圆C的弦的中点的轨迹方程.
解析:(1)如图所示,AB=4 3,D 是线段 AB 的中点,CD ⊥AB,AD=2 3,AC=4,在 Rt△ACD 中,可得 CD=2.
(3)过点(-1,2)的直线l被圆x2+y2-2x-2y+1=0截得的 弦长为 2,则直线l的斜率为 .
解析:(3)设直线的斜率为k,则直线方程为:y-2= k(x+1);圆的圆心坐标为(1,1),半径为1,所以圆心到直 |2k+1| |2k+1| 2 22 线的距离d= 2 ,所以( 2 ) +( 2 ) =1,解得k= 1 +k 1+k 1 -1或k=-7.
)
解析:(1)圆(x-a)2+y2=2 的圆心 C(a,0)到直线 x-y |a+1| +1=0 的距离为 d,则 d≤r= 2⇔ ≤ 2⇔|a+1|≤2 2 ⇔-3≤a≤1,故选 C.
(2)已知过点P(2,2)的直线与圆(x-1)2+y2=5相切,且 与直线ax-y+1=0垂直, 则a=( 1 A.-2 C.2 ) B.1 1 D. 2
