正弦量与相量法基本概念共25页
合集下载
【第8章】 相量法

实轴 +1
复数在复平面上可 以用向量表示。
0
a1
2. 复数的四种表示形式
⑴ 表达式 ① 代数形式 A= a1+ ja2 +j a2 A
② 极坐标形式
③ 三角函数式 ④ 指数形式
0 模 幅角 A a cos j + j a sin j
A aj
a φ
a1 +1
A ae jj
(由欧拉公式e jφ = cos φ + jsin φ得到) ⑵ 四种表达式关系
I e jy i I y I m m m i
复振幅与正弦量的一一对应关系: 复振幅的模是正弦量的最大值 复振幅的幅角为正弦量的初相位
jy i I Ie Iy i 复有效值
复有效值与正弦量的一一对应关系: 复有效值的模是正弦量的有效值 复有效值的幅角为正弦量的初相位
同样可以建立正弦电压与相量的对应关系:
φ =0,同相; i i1
0 i2
φ = (180o) ,反相; i i1 i2
wt
0 i i1
wt
φ = /2,正交;
i2
wt 因为规定了: |φ| (180°)。 0 所以,我们说i1 领先 i2 /2, 而不说i2落后i1 3 /2
注:我们此处比较的是两个电流的相位差,那么,我们是 否可以比较一个电压和一个电流的相位差?在今后的分析 中可以利用电压和电流的相位差来判断电路的性质。
线圈从中性面开始转过了ωt 时,导线切割磁 力线的速度是ωr SIN ωt
可见:交流电是电流的大小和方向都随时间做周期 性变化的电流。
交流电有许多优点: •交流电可以用变压器升高或降低电压, •交流电可以驱动结构简单,运行可靠的交流 感应电动机,交流电是廉价的动力或能量来源。
复数在复平面上可 以用向量表示。
0
a1
2. 复数的四种表示形式
⑴ 表达式 ① 代数形式 A= a1+ ja2 +j a2 A
② 极坐标形式
③ 三角函数式 ④ 指数形式
0 模 幅角 A a cos j + j a sin j
A aj
a φ
a1 +1
A ae jj
(由欧拉公式e jφ = cos φ + jsin φ得到) ⑵ 四种表达式关系
I e jy i I y I m m m i
复振幅与正弦量的一一对应关系: 复振幅的模是正弦量的最大值 复振幅的幅角为正弦量的初相位
jy i I Ie Iy i 复有效值
复有效值与正弦量的一一对应关系: 复有效值的模是正弦量的有效值 复有效值的幅角为正弦量的初相位
同样可以建立正弦电压与相量的对应关系:
φ =0,同相; i i1
0 i2
φ = (180o) ,反相; i i1 i2
wt
0 i i1
wt
φ = /2,正交;
i2
wt 因为规定了: |φ| (180°)。 0 所以,我们说i1 领先 i2 /2, 而不说i2落后i1 3 /2
注:我们此处比较的是两个电流的相位差,那么,我们是 否可以比较一个电压和一个电流的相位差?在今后的分析 中可以利用电压和电流的相位差来判断电路的性质。
线圈从中性面开始转过了ωt 时,导线切割磁 力线的速度是ωr SIN ωt
可见:交流电是电流的大小和方向都随时间做周期 性变化的电流。
交流电有许多优点: •交流电可以用变压器升高或降低电压, •交流电可以驱动结构简单,运行可靠的交流 感应电动机,交流电是廉价的动力或能量来源。
正弦量与相量法的基本概念

正弦量与相量法的基本概念
目
CONTENCT
录
• 正弦量定义与性质 • 相量法基础 • 正弦量与相量法的转换 • 交流电路中的相量法应用 • 相量法在电机控制中的应用 • 正弦量与相量法的实验验证
01
正弦量定义与性质
定义
总结词
正弦量是随时间按正弦规律变化的量 ,通常用复数表示。
详细描述
正弦量是随时间变化的物理量,如交 流电电压、电流等。在数学上,正弦 量通常用复数表示,其实部表示幅值 大小,虚部表示相位。
THANK YOU
感谢聆听
相量法在电机控制中的应用
利用相量法可以简化电机控制中的数学模型,方便分析和 设计控制策略。通过将交流电机等效为直流电机,可以使 用成熟的直流电机控制方法进行控制。
控制算法
利用相量法,可以设计出各种控制算法,如PI控制器、模 糊控制器等,实现对电机的精确控制。
案例分析:无刷直流电机控制
无刷直流电机
无刷直流电机是一种采用电子换向器的直流电机,具有高效、调速范围宽、维护方便等优 点。
乘法运算
两个正弦量的乘法运算可以通 过复数乘法实现,即对应相量 直接相乘。
除法运算
两个正弦量的除法运算可以通 过复数除法实现,即对应相量 直接相除。
运算规则
在进行相量运算时,应遵循复 数的运算法则和运算顺序。
03
正弦量与相量法的转换
转换公式
正弦量与相量法转换公式
$I = I_m angle theta$,其中 $I$ 是 正弦量,$I_m$ 是相量,$theta$ 是 初相角。
信号处理
在信号处理领域,相量法可用 于分析信号的频谱和滤波器的 设计。
04
交流电路中的相量法应用
目
CONTENCT
录
• 正弦量定义与性质 • 相量法基础 • 正弦量与相量法的转换 • 交流电路中的相量法应用 • 相量法在电机控制中的应用 • 正弦量与相量法的实验验证
01
正弦量定义与性质
定义
总结词
正弦量是随时间按正弦规律变化的量 ,通常用复数表示。
详细描述
正弦量是随时间变化的物理量,如交 流电电压、电流等。在数学上,正弦 量通常用复数表示,其实部表示幅值 大小,虚部表示相位。
THANK YOU
感谢聆听
相量法在电机控制中的应用
利用相量法可以简化电机控制中的数学模型,方便分析和 设计控制策略。通过将交流电机等效为直流电机,可以使 用成熟的直流电机控制方法进行控制。
控制算法
利用相量法,可以设计出各种控制算法,如PI控制器、模 糊控制器等,实现对电机的精确控制。
案例分析:无刷直流电机控制
无刷直流电机
无刷直流电机是一种采用电子换向器的直流电机,具有高效、调速范围宽、维护方便等优 点。
乘法运算
两个正弦量的乘法运算可以通 过复数乘法实现,即对应相量 直接相乘。
除法运算
两个正弦量的除法运算可以通 过复数除法实现,即对应相量 直接相除。
运算规则
在进行相量运算时,应遵循复 数的运算法则和运算顺序。
03
正弦量与相量法的转换
转换公式
正弦量与相量法转换公式
$I = I_m angle theta$,其中 $I$ 是 正弦量,$I_m$ 是相量,$theta$ 是 初相角。
信号处理
在信号处理领域,相量法可用 于分析信号的频谱和滤波器的 设计。
04
交流电路中的相量法应用
正弦量的三要素及相量表示法基尔霍夫

第五章
正弦电流电路导论
内容提要
1.正弦量的相量表示法; 2.两类约束的相量形式; 3.正弦电流电路的分析计算; 4.正弦电流电路的功率。
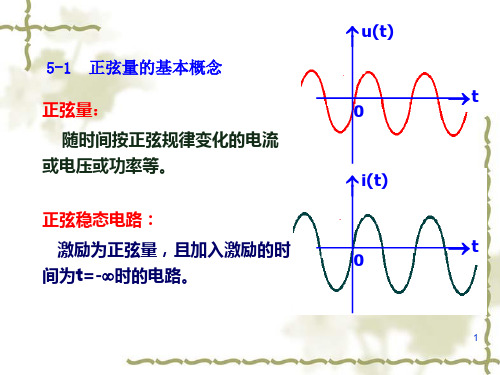
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流:随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值:时变电压和电流在任一时刻的数值,用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解:
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω:每秒变化的弧度。单位:弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系:
1 f T
2 2 f T
* 电网频率(工频):我国:50Hz;美国和日本:60Hz * 无线通信频率: 30 kHz ~ 30GMHz ◆ 相位和初相位 ①相位:正弦波的 (ωt ψ ) 。 ②初相位 :t =0 时的相位。 ③规定:初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量:表示正弦量的复数称为相量。
相量表示法:用模值等于正弦量的最大值(或有效值)、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即:相量 Im (或 I )
j
模用最大值表示时,为最 I ψ 大值相量,即 I m m
正弦电流电路导论
内容提要
1.正弦量的相量表示法; 2.两类约束的相量形式; 3.正弦电流电路的分析计算; 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流:随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值:时变电压和电流在任一时刻的数值,用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解:
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω:每秒变化的弧度。单位:弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系:
1 f T
2 2 f T
* 电网频率(工频):我国:50Hz;美国和日本:60Hz * 无线通信频率: 30 kHz ~ 30GMHz ◆ 相位和初相位 ①相位:正弦波的 (ωt ψ ) 。 ②初相位 :t =0 时的相位。 ③规定:初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量:表示正弦量的复数称为相量。
相量表示法:用模值等于正弦量的最大值(或有效值)、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即:相量 Im (或 I )
j
模用最大值表示时,为最 I ψ 大值相量,即 I m m
正弦量的相量表示方法

电工基础
正弦量的相量表示方法
正弦量的表示方法有: 数学表达式、波形图、 相量表达式
1.1 复数及四则运算
1.复数
在数学中常用 A a bi 表示复数,其中a为实部,b为虚部,i 1
称为虚单位。在电工技术中,为区别于电流的符号,虚单位常用j表示。
+j
3
A
+j
b
P
r
O
4
+1
O
a +1
图4.7 复数在复平面上的表示 图4.8 复数的矢量表示
解
A B (8 j6) (6 j8) 14 j2
A B (8 j6)(6 j8) 10 36.9 10 53.1 100 16.2
正弦量的相量表示方法
1.2 正弦量的相量表示法
给出一个正弦量 u U m sin(t ) 在复平面上作一矢量,如图4.10所示。
(1)矢量的长度按比例等于振幅值U m
(在第四象限)
A1 5 36.9
A2的模 r2 (3)2 42 5
辐角2
arctan
4 3
126.9
则 A2 极坐标形式为
A2 5 126.9
(在第二象限)
正弦量的相量表示方法
例 4.7 写出复数 A 220 60 的三角形式和代数形式。
解 三角形式 A 220(cos60 jsin 60)
u2 2U 2 sin(t 2 ) 40 sin(100t 30) V
电工基础
(2) 复数的三角形式
A r cos jr sin
(3) 复数的指数形式
A re j
(4) 复数的极坐标形式
A r
正弦量的相量表示方法
例4.6 写出复数 A1 4 j3 A2 3 j4 的极坐标形式。 解 A1 的模 r1 42 (3)2 5
正弦量的相量表示方法
正弦量的表示方法有: 数学表达式、波形图、 相量表达式
1.1 复数及四则运算
1.复数
在数学中常用 A a bi 表示复数,其中a为实部,b为虚部,i 1
称为虚单位。在电工技术中,为区别于电流的符号,虚单位常用j表示。
+j
3
A
+j
b
P
r
O
4
+1
O
a +1
图4.7 复数在复平面上的表示 图4.8 复数的矢量表示
解
A B (8 j6) (6 j8) 14 j2
A B (8 j6)(6 j8) 10 36.9 10 53.1 100 16.2
正弦量的相量表示方法
1.2 正弦量的相量表示法
给出一个正弦量 u U m sin(t ) 在复平面上作一矢量,如图4.10所示。
(1)矢量的长度按比例等于振幅值U m
(在第四象限)
A1 5 36.9
A2的模 r2 (3)2 42 5
辐角2
arctan
4 3
126.9
则 A2 极坐标形式为
A2 5 126.9
(在第二象限)
正弦量的相量表示方法
例 4.7 写出复数 A 220 60 的三角形式和代数形式。
解 三角形式 A 220(cos60 jsin 60)
u2 2U 2 sin(t 2 ) 40 sin(100t 30) V
电工基础
(2) 复数的三角形式
A r cos jr sin
(3) 复数的指数形式
A re j
(4) 复数的极坐标形式
A r
正弦量的相量表示方法
例4.6 写出复数 A1 4 j3 A2 3 j4 的极坐标形式。 解 A1 的模 r1 42 (3)2 5
7 正弦量与相量

+jຫໍສະໝຸດ C=A*B+j
C B
ϕb ϕb ϕa + ϕb A
C=A/B
+j
A
B
B jA A
-jB
+1 O C
+1
ϕ a- ϕ b
O 旋转因子示意 +1
O 复数的乘法
复数的除法
7.4 正弦量的相量表示法
一、正弦稳态电路的特点
1、角频率不变性:在线性电路中,如 角频率不变性:在线性电路中, 果电路的所有激励都是同频率的正弦量, 果电路的所有激励都是同频率的正弦量, 激励都是同频率的正弦量 则电路中各支路的稳态响应也为同频率 稳态响应也为 则电路中各支路的稳态响应也为同频率 的正弦量。 ( P208) 的正弦量。 2、计算的复杂性:在列写VCR、KCL、 计算的复杂性:在列写VCR、KCL、 KVL方程的时候会遇到微分、积分和 KVL方程的时候会遇到微分、积分和和 方程的时候会遇到微分 差化积的问题 的问题。 差化积的问题。
二、复数的四则运算
1、加减运算 1)定量运算 1)定量运算------用代数形式计算 定量运算------用代数形式计算
F1 ± F2 = (a1 + jb1 ) ± (a2 + jb2 ) = (a1 ± a2 ) + j (b1 ± b2 )
法则:实部加减,虚部加减。 法则:实部加减,虚部加减。
7 正弦量与相量
重点
1、正弦量的三要素 2、复数的几种表示形式的转换及计算 3、 KCL、KVL 、VCR的相量表示 KCL、 VCR的相量表示
难点
相量图的绘制
本章作业
P217 7.1 7.2 7.5 7.7 7.10 7.12
C B
ϕb ϕb ϕa + ϕb A
C=A/B
+j
A
B
B jA A
-jB
+1 O C
+1
ϕ a- ϕ b
O 旋转因子示意 +1
O 复数的乘法
复数的除法
7.4 正弦量的相量表示法
一、正弦稳态电路的特点
1、角频率不变性:在线性电路中,如 角频率不变性:在线性电路中, 果电路的所有激励都是同频率的正弦量, 果电路的所有激励都是同频率的正弦量, 激励都是同频率的正弦量 则电路中各支路的稳态响应也为同频率 稳态响应也为 则电路中各支路的稳态响应也为同频率 的正弦量。 ( P208) 的正弦量。 2、计算的复杂性:在列写VCR、KCL、 计算的复杂性:在列写VCR、KCL、 KVL方程的时候会遇到微分、积分和 KVL方程的时候会遇到微分、积分和和 方程的时候会遇到微分 差化积的问题 的问题。 差化积的问题。
二、复数的四则运算
1、加减运算 1)定量运算 1)定量运算------用代数形式计算 定量运算------用代数形式计算
F1 ± F2 = (a1 + jb1 ) ± (a2 + jb2 ) = (a1 ± a2 ) + j (b1 ± b2 )
法则:实部加减,虚部加减。 法则:实部加减,虚部加减。
7 正弦量与相量
重点
1、正弦量的三要素 2、复数的几种表示形式的转换及计算 3、 KCL、KVL 、VCR的相量表示 KCL、 VCR的相量表示
难点
相量图的绘制
本章作业
P217 7.1 7.2 7.5 7.7 7.10 7.12
第19讲_正弦量与相量法的基本概念[1]
![第19讲_正弦量与相量法的基本概念[1]](https://img.taocdn.com/s3/m/c2ecab4ae518964bcf847c13.png)
第19讲 正弦量与相量法的基本概念
学习重点: 1、正弦量三要素的概念,周期、频率与角频率的关系; 2、相位差及其物理含义; 3、正弦量的有效值及其物理含义; 4、振幅相量、有效值相量的概念;
5、正弦量的相量运算。
一. 正 弦量(P145)
电路中凡是按正弦(余弦)规律随时间作周期变化的电压或电 流称为正弦电压或正弦电流,统称为正弦量。它可以用正弦函 数表示,也可以用余弦函数表示。本课程用余弦函数表示,即
u, i u
i
u i
0
t
特殊相位关系:
= 0, 同相:
u, i u i
= ( 180o ) ,反相:
u, i
i
0
u
0 u, i
u
t
t
= 90°正交
i
0
t
u 领先 i 90° 或 i 落后 u 90° 不说 u 落后 i 270° 或i 领先 u 270°
规定: | | (180°)
= Re( 2 U 1 e
j t
) + Re( 2 U 2 e
j t
)
= Re( 2 U 1 e
j t
+
2U
2
e
j t
)
= R e [ 2 (U 1 + U 2 ) e
U
j t
]
得:
U = U1 + U 2
(2) 正弦量的微分、积分运算
i I
di dt j I
复常数包含了I , 。
称 I = I 为正弦量 i(t) 对应的有效值相量。
i(t ) =
学习重点: 1、正弦量三要素的概念,周期、频率与角频率的关系; 2、相位差及其物理含义; 3、正弦量的有效值及其物理含义; 4、振幅相量、有效值相量的概念;
5、正弦量的相量运算。
一. 正 弦量(P145)
电路中凡是按正弦(余弦)规律随时间作周期变化的电压或电 流称为正弦电压或正弦电流,统称为正弦量。它可以用正弦函 数表示,也可以用余弦函数表示。本课程用余弦函数表示,即
u, i u
i
u i
0
t
特殊相位关系:
= 0, 同相:
u, i u i
= ( 180o ) ,反相:
u, i
i
0
u
0 u, i
u
t
t
= 90°正交
i
0
t
u 领先 i 90° 或 i 落后 u 90° 不说 u 落后 i 270° 或i 领先 u 270°
规定: | | (180°)
= Re( 2 U 1 e
j t
) + Re( 2 U 2 e
j t
)
= Re( 2 U 1 e
j t
+
2U
2
e
j t
)
= R e [ 2 (U 1 + U 2 ) e
U
j t
]
得:
U = U1 + U 2
(2) 正弦量的微分、积分运算
i I
di dt j I
复常数包含了I , 。
称 I = I 为正弦量 i(t) 对应的有效值相量。
i(t ) =
第二节正弦量的相量表示法第三节电阻元件伏安关系的向
i(t) 11.18 2 cos(t 10.3) 21
例2 图示电路,已知:
+ u1(t) -
u1(t) 6 2 cos(t 30)
-
u2 (t) 4 2 cos(t 60)
u3(t)Biblioteka u2(t)+
求 u3(t)
解: 正弦量以相量表示,有
•
U1 630
•
U2 460
•
••
U3 U1 U2 (5.19 j3) (2 j3.45)
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2)平均功率: P 1
T
p(t)dt
T0
0
p(t)
UI
3)无功功率: Q UI
X
LI
2
U X
2 L
(Var)
0
意义:反映电感元件与电源进行能量交换的最大速率.
t
12
i(t) 2I cos(t i )
u(t) 2U cos(t u )
p(t) 2U cos(t u ) 2I cos(t i )
UI cos(2t 90)
2)平均功率: P 1
T
p(t)dt
T0
0
3)无功功率: Q UI
XCI 2
U2 XC
(Var)
p(t)
UI
0
意义:反映电容元件与电源进行能量交换的最大速率.
3 j4
8 j6
例2:写出下列正弦量的时域形式:
•
U1 3 j4
•
U 2 8 j6
u1(t) 5 2 cos(t 126.9)
电工学第8章正弦量与相量

除法:模相除,角相减。
例1.
547 10 25 ?
5 47 10 25 ( 3 . 41 j 3 . 657 ) ( 9 . 063 j 4 . 226 ) 解
12.47 j 0.569 12.48 2.61
例2.
解
(17 j9) (4 j6) 220 35 ? 20 j5 19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04 180.2 j126.2 6.72870.16
故 +j, –j, -1 都可以看成旋转因子。
3. 正弦量的相量表示
构造一个复函数
无物理意义
j( wt Y )
A(t ) 2Ie
2Icos(wt Y ) j 2Isin( wt Ψ )
对A(t)取实部:
是一个正弦量 有物理意义
Re[A(t )] 2Icos( w t Ψ ) i(t)
例
100 50
i
已知正弦电流波形如图,w=103rad/s, (1)写出i(t)表达式; (2)求最大值发生的时间t1
t
t1
解 i ( t ) 100 cos(103 t y )
0
t 0 50 100 cosy
由于最大值发生在计时起点右侧
i ( t ) 100 cos(103 t
A | A | e
j
A | A | e j
| A | (cos j sin ) a jb
A | A | e j | A |
两种表示法的关系:
复数也是矢量 直角坐标表示 极坐标表示
例1.
547 10 25 ?
5 47 10 25 ( 3 . 41 j 3 . 657 ) ( 9 . 063 j 4 . 226 ) 解
12.47 j 0.569 12.48 2.61
例2.
解
(17 j9) (4 j6) 220 35 ? 20 j5 19.24 27.9 7.21156.3 原式 180.2 j126.2 20.6214.04 180.2 j126.2 6.72870.16
故 +j, –j, -1 都可以看成旋转因子。
3. 正弦量的相量表示
构造一个复函数
无物理意义
j( wt Y )
A(t ) 2Ie
2Icos(wt Y ) j 2Isin( wt Ψ )
对A(t)取实部:
是一个正弦量 有物理意义
Re[A(t )] 2Icos( w t Ψ ) i(t)
例
100 50
i
已知正弦电流波形如图,w=103rad/s, (1)写出i(t)表达式; (2)求最大值发生的时间t1
t
t1
解 i ( t ) 100 cos(103 t y )
0
t 0 50 100 cosy
由于最大值发生在计时起点右侧
i ( t ) 100 cos(103 t
A | A | e
j
A | A | e j
| A | (cos j sin ) a jb
A | A | e j | A |
两种表示法的关系:
复数也是矢量 直角坐标表示 极坐标表示
