2016年秋北师大版八年级上2.1认识无理数(1)教案
北师大版八年级数学上册第二章实数第1节认识无理数优秀教学案例

2.案例分析:让学生分析一些实际问题,如测量物体长度、计算圆的面积等,运用无理数解决实际问题。
3.小组分享:各小组向全班分享自己的讨论成果和案例分析,促进学生之间的交流和合作。
(四)总结归纳
1.无理数的定义和性质:引导学生总结无理数的定义和性质,加深学生对无理数概念的理解。
北师大版八年级数学上册第二章实数第1节认识无理数优秀教学案例
一、案例背景
本节内容是北师大版八年级数学上册第二章实数的第一节——认识无理数。在学习了有理数的基础上,本节课引导学生认识无理数,理解无理数的概念和性质,体会数学的广泛应用。无理数是数学中的一个重要概念,它在生活中和学科领域中有着广泛的应用。如圆周率π就是一个无理数,它在几何学、物理学等领域有着重要应用。另外,无理数在数学分析、高等数学等领域也是基本概念。因此,本节课对于学生理解和掌握数学知识体系,培养学生的数学思维能力具有重要意义。
5.注重学生的反思与评价:在教学过程中,我注重学生的反思与评价,及时反馈,指导学生的改进方向。通过引导学生进行自我反思和相互评价,我帮助学生检查自己对无理数概念的理解和掌握程度,发现自己的不足,明确改进的方向。这种教学方式能够培养学生的评价能力和批判性思维,提高学生的自我认知和自我改进能力。
作为一名特级教师,我深知教学案例亮点的重要性。在教学过程中,我努力将教学内容与学生的生活实际和学科领域相结合,采用多种教学方法和手段,关注学生的个体差异,创设生动有趣的情境,引导学生在问题导向的过程中自主探究和合作交流,培养学生的数学思维能力和问题解决能力。同时,我注重学生的反思与评价,及时反馈,调整教学策略,以达到最佳教学效果。
(二)讲授新知
1.无理数的定义:详细讲解无理数的定义,并通过实例进行说明,让学生理解和掌握无理数的概念。
北师大版八年级上册2.1认识无理数 教案
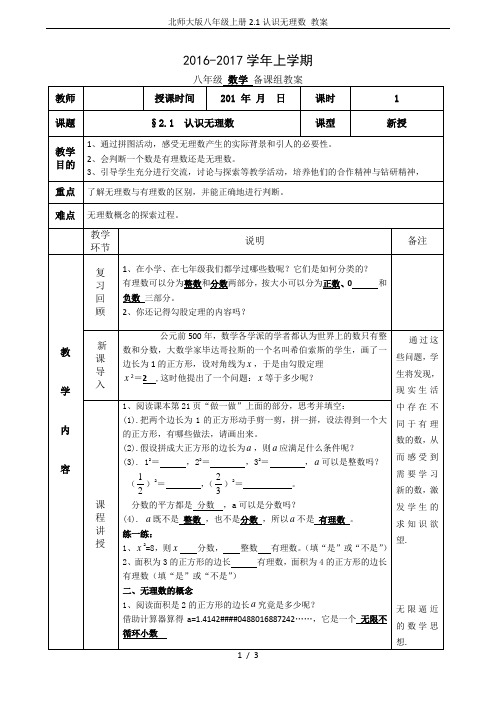
1、阅读面积是2的正方形的边长 究竟是多少呢?
借助计算器算得a=1.4142####0488016887242……,它是一个无限不循环小数
2、把下列和数化成小数: =, =
我们发现分数可以化成有限小数或是无限循环小数。
3、概念:无限不循环小数叫做无理数.
总结:.所有的无理数都不能转化成分数,但所有的有理数都可以转化成分数。
2=2,这时他提出了一个问题: 等于多少呢?
通过这些问题,学生将发现,现实生活中存在不同于有理数的数,从而感受到需要学习新的数,激发学生的求知识欲望.
无限逼近的数学思想.
通过练习,巩固新知,同时也让学生感受到新数的运用。
课
程
讲
授
1、阅读课本第21页“做一做”上面的部分,思考并填空:
(1).把两个边长为1的正方形动手剪一剪,拼一拼,设法得到一个大的正方形,有哪些做法,请画出来。
无理数一般有以下几种类型:
(1)一般的无限不循环小数。例:0.1237486…
(2)看似循环实际不循环的小数。例:5.3040040004…
(3)具有特定意义的数。如:圆周率π=3.14159265…也是一个无限不循环小数,故π是无理数
【例题精析】
下列数哪些是有理数?哪些是无理数?
0.351,- , ,-0.202 002 0002···(相邻两个2之间0断题
(1)有限小数是有理数;()(2)无限小数都是无理数;()
(3)无理数都是无限小数;()(4)有理数是有限小数.()
(5)无限不循环小数是无理数. ( )(6)有理数与无理数的差都是有理数。()(7)两个无理数的和不一定是无理数()
4、在3.141 59,-1,-π,0,2, ,- ,1.234 567 891 011 12···(由相继的正整数组成), , ,0.458 3,3.7,18,5.411 010 010 001···(相邻两个1之间0的个数逐次加1)中,是有理数的有个,是无理数的有个。
北师大版八年级数学上册:2.1《认识无理数》教学设计

北师大版八年级数学上册:2.1《认识无理数》教学设计一. 教材分析《认识无理数》是北师大版八年级数学上册第二章的第一节内容。
本节内容是在学生学习了实数、有理数的基础上,引入无理数的概念,使学生了解无理数在生活中的应用和实际意义,培养学生运用数学解决实际问题的能力。
教材通过丰富的实例和探究活动,让学生感受无理数的存在,体验数的概念的扩展,培养学生的数感。
二. 学情分析八年级的学生已经学习了实数和有理数,对数的概念有一定的了解。
但是,学生对无理数的理解可能还比较模糊,需要通过具体的实例和实践活动来加深对无理数概念的理解。
此外,学生可能对无理数的存在感到困惑,需要教师通过讲解和引导,让学生逐渐接受无理数的存在。
三. 教学目标1.了解无理数的概念,理解无理数的存在和实际意义。
2.能够识别常见的无理数,如π、√2等。
3.能够运用无理数解决实际问题,提高运用数学解决实际问题的能力。
4.培养学生的数感,提高学生的数学思维能力。
四. 教学重难点1.重点:无理数的概念和实际意义的理解。
2.难点:无理数的识别和运用。
五. 教学方法1.实例教学法:通过具体的实例,让学生感受无理数的存在和实际意义。
2.实践活动法:通过实践活动,让学生加深对无理数概念的理解。
3.问题驱动法:通过提问和引导,让学生主动探索无理数的性质和运用。
六. 教学准备1.教材和教案。
2.投影仪和教学课件。
3.练习题和测试题。
七. 教学过程1.导入(5分钟)利用投影仪展示生活中的实例,如圆的周长和面积的关系,引出无理数的概念。
2.呈现(10分钟)讲解无理数的定义,通过具体的实例,让学生感受无理数的存在。
如π、√2等。
3.操练(10分钟)让学生进行练习,识别常见的无理数,加深对无理数概念的理解。
4.巩固(10分钟)讲解无理数的性质和运用,让学生通过实践活动,加深对无理数概念的理解。
5.拓展(10分钟)引导学生思考无理数在生活中的应用和实际意义,培养学生的数感。
八年级数学上册2.1认识无理数教学设计 (新版北师大版)

八年级数学上册2.1认识无理数教学设计(新版北师大版)一. 教材分析《八年级数学上册2.1认识无理数》这一节,主要让学生了解无理数的概念,掌握无理数的性质,以及学会用有理数和无理数表示实数。
教材通过生活中的实例引入无理数的概念,接着引导学生通过观察、思考、探究,掌握无理数的性质。
在这一过程中,学生需要理解无理数与有理数的区别,以及无理数在实际生活中的应用。
二. 学情分析八年级的学生已经学习了有理数的概念和性质,具备一定的数学基础。
但是,对于无理数这一概念,学生可能较为陌生,难以理解。
因此,在教学过程中,教师需要结合学生的实际情况,从生活实例出发,引导学生逐步理解无理数的概念,并掌握无理数的性质。
三. 教学目标1.让学生了解无理数的概念,知道无理数是一种实数。
2.让学生掌握无理数的性质,能够辨别一个数是有理数还是无理数。
3.让学生理解无理数在实际生活中的应用,提高学生运用数学知识解决问题的能力。
四. 教学重难点1.重难点:无理数的概念和性质。
2.难点:理解无理数在实际生活中的应用。
五. 教学方法1.情境教学法:通过生活实例引入无理数的概念,让学生在实际情境中感受无理数。
2.启发式教学法:引导学生观察、思考、探究,从而掌握无理数的性质。
3.小组合作学习:让学生在小组讨论中,共同解决问题,提高学生的合作能力。
六. 教学准备1.教学课件:制作课件,展示无理数的定义、性质和实际应用。
2.教学素材:准备一些生活中的实例,用于引入无理数的概念。
3.练习题:准备一些有关无理数的练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)教师通过展示一些生活中的实例,如圆的周长、声音的频率等,引导学生思考这些实例与数学的关系。
进而提出问题:“你知道无理数吗?无理数是什么?”让学生分享自己对无理数的理解。
2.呈现(15分钟)教师利用课件,详细讲解无理数的定义、性质和特点。
同时,通过展示一些实际应用的例子,让学生了解无理数在生活中的重要作用。
北师大版八年级数学上册2.1认识无理数优秀教学案例

1.分组讨论:将学生分成若干小组,针对问题进行讨论、交流。
2.讨论内容:让学生结合所学知识,运用逼近法估算无理数的大小,如估算π的值。
3.讨论过程:引导学生通过观察、分析、归纳等数学思维方法,探索无理数的性质,提高学生的逻辑思维能力。
(四)总结归纳
1.学生总结:让学生根据自己的学习体会,总结本节课所学的无理数的性质和估算方法。
3.小组评价:引导学生对其他小组的汇报进行评价,提高学生的评价能力和批判性思维。
(四)反思与评价
1.引导学生对自己的学习过程进行反思,总结学习方法和经验,提高学生的自我监控能力。
2.学生互评:学生之间相互评价,培养学生的评价能力和批判性思维。
3.教师评价:教师对学生的学习过程和成果进行评价,及时反馈,指导学生的学习。
教学重点:无理数的概念和性质,逼近法估算无理数的大小。
教学难点:无理数的概念理解,逼近法的运用。
二、教学目标
(一)知识与技能
1.让学生理解无理数的概念,掌握无理数的性质,能正确识别和表示无理数。
2.让学生学会运用逼近法估算无理数的大小,提高学生的数学运算能力。
3.培养学生运用数学知识解决实际问题的能力,提高学生的数学应用意识。
5.教学内容的总结与作业的布置:教师针对学生的学习情况进行总结,强调本节课的重点和难点,布置有关无理数的练习题,巩固所学知识,要求学生运用所学知识,独立完成作业,提高学生的动手操作能力。同时,教师对学生的作业进行批改,及时反馈,指导学生的学习,使学生能够更好地掌握无理数的相关知识。
(二)讲授新知
1.无理数的概念:讲解无理数的定义,通过具体例子让学生理解无理数的特点。
2.无理数的性质:讲解无理数的性质,如无限不循环小数、不能精确表示等,引导学生通过观察、分析、归纳等数学思维方法,探索无理数的性质。
北师大版数学八年级上册2.1认识无理数第1课时优秀教学案例

二、教学目标
(一)知识与技能
1.让学生理解无理数的概念,知道无理数的特点,能够识别生活中的无理数实例。
2.使学生掌握无理数的性质,了解无理数与有理数的区别,能够运用性质进行简单的论证和判断。
2.教师对学生的学习情况进行评价,关注他们的个体差异,实施差异化教学,使每个学生都能得到有效的锻炼。
3.总结本节课的主要内容,强调无理数的概念、性质和运算方法。
(五)作业小结
1.布置课后作业,让学生运用所学知识解决实际问题,提高他们的实践能力。
2.通过作业的完成情况,了解学生对课堂所学知识的掌握程度,为今后的教学提供参考。
五、案例亮点
(二)讲授新知
1.引导学生提出问题:“无理数有什么特点?”,“无理数与有理数有什么区别?”等,激发他们的思考。
2.组织学生进行小组讨论,鼓励他们发表自己的观点和看法,培养他们的团队合作精神。
3.教师通过讲解,引导学生自主探究无理数的性质,如不能表示为两个整数的比值,不能精确表示等。
4.利用多媒体课件展示无理数的性质,让学生直观地感受无理数的特点。
3.鼓励学生在课后进行深入研究,拓展知识面,提高他们的创新能力。
五、教学反思
本节课通过生活实例引入无理数的概念,引导学生探究无理数的性质和运算方法,注重培养学生的实践能力和创新能力。在教学过程中,关注学生的个体差异,实施差异化教学,使每个学生都能得到有效的锻炼。同时,注重启发式教学,培养学生主动探究、积极思考的能力。但在时间安排上,可以更加合理,确保学生有足够的时间进行小组讨论和作业练习。
北师大版八年级上册2.1认识无理数教学设计

三、教学重难点和教学设想
(一)教学重难点
1.无理数概念的理解:无理数对于学生来说是新的数学概念,理解无理数的本质和特点是一大难点。学生需要从具体的例子中抽象出无理数的定义,并理解其与有理数的区别。
2.无理数的运算:无理数的运算规则与有理数不同,如何进行无理数的近似计算、比较大小等是教学的另一个重点和难点。
2.自主探究,合作交流:鼓励学生在小组内或全班范围内进行讨论,通过自主探究和合作交流,发现无理数的性质和规律。在此过程中,教师应适时引导,帮助学生突破难点。
3.利用多媒体,直观演示:运用多媒体教具和软件,如几何画板、计算器等,直观演示无理数在数轴上的位置、无理数的运算过程等,增强学生的直观体验。
4.分层教学,因材施教:针对不同学生的学习水平和能力,设计不同难度的例题和练习,使每个学生都能在原有基础上得到提高。
(1)已知某正方形的对角线长为10cm,求该正方形的面积。
(2)计算圆的周长与直径的比值,并说明这个比值为什么是一个无理数。
4.探究题:小组合作,探究以下问题:
(1)无理数在数轴上的位置关系。
(2)如何用数轴上的点来表示一个无理数。
5.思考题:让学生思考以下问题,并用自己的语言总结:
(1)无理数与有理数的区别和联系。
(2)无理数在数学和其他学科中的应用。
作业要求:
1.学生需独立完成基础练习题和提高题,确保对无理数的概念、性质和运算有深刻的理解。
2.应用题和探究题要求学生在小组内合作完成,培养团队合作精神和解决问题的能力。
3.思考题要求学生在完成作业后进行总结,提高自己的数学思维能力。
4.作业完成后,学生需认真检查,确保解答过程正确、清晰。
2.1认识无理数教学设计北师大版八年级数学上册

4.目标确定(根据课程标准和学生实际,指向学科素养和思政育人,描述学生经历学习过程后应达成的
目标) 1.了解数学史上的第一次危机,体会数学家对探索数学真相的无畏精神,树立敢于质疑、敢于追求
质的两个整数"的假设矛盾。
8.作业与拓展学习设计(关注作业的针对性、预计完成时间,发挥作业对复习巩固、引导学生深
入学习的作用)
一.必做题
1.下列数中是无理数的是( )
A.2π
B.3.1415926
C. 11 3
D.﹣3.6
2.已知 2<m<3,且 m 是无理数,请写出一个符合要求的 m 的值
.
3.下列各数中:12, 22 , ,|﹣1|,0.1010010001…(每两个 1 之间的 0 依次加 1),其中,无理数 73
拓展 1:在右 1 的正方形网格中,画出 3 条不相等且
长度都是无理数的线段
拓展 2:请你在方格纸上按照如下要求设计直角三角 形: (1)使它的三边中有一边边长不是有理数; (2)使它的三边中有两边边长不是有理数; (3)使它的三边都不是有理数。
设计意图
前两个例题巩固无理数的概念,加深对概念的理解;拓展问题旨在提升学生解决问题的能力。
所以 1.375<a<1.4375
估算 6:因为1.406252 1.9775390625,
所以 1.40625<a<1.4375
......
问题 5:还可以继续算下去吗?会不会算到某一
次,这个数的平方恰好等于 2?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
希伯索斯学习,学习他为捍卫真理而勇于献身的精神
.
三、课堂练习
(一 )课本随堂练习 如图,正三角形 ABC 的边长为 2,高为 h, h 可能是整数吗?可能是分数吗?
解:由正三角形的性质可知 可能是分数 .
BD=1,在 Rt△ABD 中,由勾股定理得 h2=3. h 不可能是整数,也不
2.1 认识有理数 (1)
教学目标 知识与技能
1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性
.
2.能判断给出的数是否为有理数;并能说出现由 . 过程与方法
1.让学生亲自动手做拼图活动,感受无理数存在的必要性和合理性,培养大家的动手能力和合 作精神 .
2.通过回顾有理数的有关知识,能正确地进行推理和判断,识别某些数是否为有理数,训练他 们的思维判断能力 . 情感与价值观
[生丙]因为没有一个整数或分数的平方为
5,所以 5 不是有理数 .
[师]大家分析得很准确,像上面讨论的数
a, b 都不是有理数,而是另一类数——无理数 .关
于无理数的发现是付出了昂贵的代价的 .早在公元前,古希腊数学家毕达哥拉斯认为万物皆“数”
,
即“宇宙间的一切现象都能归结为整数或整数之比”
,也就是一切现象都可用有理数去描述 .后来,
(二 )补充练习 为了加固一个高 2 米、宽 1 米的大门,需要在对角线位置加固一条木板,设木板长为
则由勾股定理得 a2=1 2+22,即 a2=5, a 的值大约是多少?这个值可能是分数吗? 解: a 的值大约是 2.2,这个值不可能是分数 .
a 米,
四、课堂小结
1.通过拼图活动,经历无理数产生的实际背景,让学生感受有理数又不够用了
a
2
=2.
a 是整数吗? a
是分数吗?请大家分组讨论后回答 . [生甲]我们组的结论是:因为
之间,故 a 不可能是整数 .
12=1,22=4,32=9, , 整数的平方越来越大,所以
a 应在 1 和 2
[生乙]因为 1 1
1,2 2
4,1 1
1
, , 两个相同因数的乘积都为分数,所以
2 2 43 3 93 3 9
[师]现在我们一齐把大家的做法总结一下:
下面请大家思考一个问题,假设拼成大正方形的边长为
a,则 a 应满足什么条件呢?
[生甲] a 是正方形的边长,所以 a 肯定是正数 .
[生乙]因为两个小正方形面积之和等于大正方形面积,所以根据正方形面积公式可知 [生丙]由 a2=2 可判断 a 应是 1 点几 . [师]大家说得都有道理,前面我们已经总结了有理数包括整数和分数,那么
a 不可
能是分数 .
[师]经过大家的讨论可知,在等式 a2=2 中, a 既不是整数,也不是分数,所以 a 不是有理数,
但在现实生活中确实存在像 a 这样的数,由此看来,数又不够用了 .
2.做一做 投影片
(1) 在下图中,以直角三角形的斜边为边的正方形的面积是多少?
(2) 设该正方形的边长为 b,则 b 应满足什么条件? b 是有理数吗?
这个学派中的一个叫希伯索斯的成员发现边长为
1 的正方形的对角线的长不能用整数或整数之比来
表示,这个发现动摇了毕达哥拉斯学派的信条,据说为此希伯索斯被投进了大海,他为真理而献出
了宝贵的生命,但真理是不可战胜的,后来古希腊人终于正视了希伯索斯的发现
.也就是我们前面谈
过的 a2=2 中的 a 不是有理数 . 我们现在所学的知识都是前人给我们总结出来的,我们一方面应积极地学习这些经验,另一方
1.问题的提出 [师]请大家四个人为一组,拿出自己准备好的两个边长为 动手剪一剪,拼一拼,设法得到一个大的正方形,好吗?
1 的正方形和剪刀,认真讨论之后,
[生]好 .( 学生非常高兴地投入活动中 ).
[师]经过大家的共同努力,每个小组都完成了任务,请各组把拼的图展示一下
.
同学们非常踊跃地呈现自己有理数 .
五、课后作业:见作业本。
1.激励学生积极参与教学活动,提高大家学习数学的热情
.
2.引导学生充分进行交流,讨论与探索等教学活动,培养他们的合作与钻研精神
.
3.了解有关无理数发现的知识,鼓励学生大胆质疑,培养他们为真理而奋斗的精神
.
教学重点
1.让学生经历无理数发现的过程 .感知生活中确实存在着不同于有理数的数 . 2.会判断一个数是否为有理数 . 教学难点
[师]请大家先回忆一下勾股定理的内容 .
[生]在直角三角形中,若两条直角边长为
a, b,斜边为 c,则有 a2+b2=c2.
[师]在这题中,两条直角边分别为
1 和 2,斜边为 b,根据勾股定理得
b2=1
2
+2
2,即
b
2
=5
,则
b 是有理数吗?请举手回答 . [生甲]因为 22=4,32=9, 4< 5< 9,所以 b 不可能是整数 . [生乙]没有两个相同的分数相乘得 5,故 b 不可能是分数 .
1.把两个边长为 1 的正方形拼成一个大正方形的动手操作过程 . 2.判断一个数是否为有理数 . 教学方法
教师引导,主要由学生分组讨论得出结果 . 教学过程
一、创设问题情境 ,引入新课
[师]同学们 ,我们学过不计其数的数 ,概括起来我们都学过哪些数呢 ? [生]在小学我们学过自然数、小数、分数 . [生]在初一我们还学过负数 . [师]对,我们在小学学了非负数,在初一发现数不够用了,引入了负数,即把从小学学过的 正数、零扩充到有理数范围,有理数包括整数和分数,那么有理数范围是否就能满足我们实际生活 的需要呢?下面我们就来共同研究这个问题 . 二、讲授新课
