回归方程公式详解
标准曲线回归方程公式
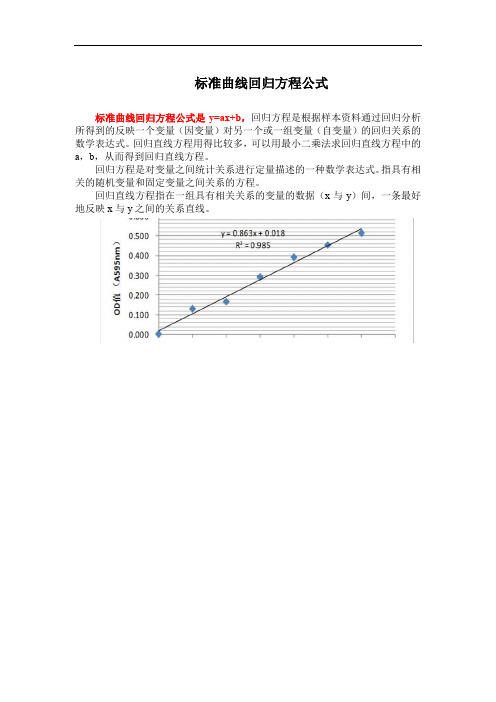
标准曲线回归方程公式
标准曲线回归方程公式是y=ax+b,回归方程是根据样本资料通过回归分析所得到的反映一个变量(因变量)对另一个或一组变量(自变量)的回归关系的数学表达式。
回归直线方程用得比较多,可以用最小二乘法求回归直线方程中的a,b,从而得到回归直线方程。
回归方程是对变量之间统计关系进行定量描述的一种数学表达式。
指具有相关的随机变量和固定变量之间关系的方程。
回归直线方程指在一组具有相关关系的变量的数据(x与y)间,一条最好地反映x与y之间的关系直线。
直线回归法计算公式

直线回归法计算公式
直线回归法是一种常用的统计学方法,用于分析两个变量之间的关系。
在实际应用中,直线回归法被广泛应用于数据分析、市场研究、经济预测等领域。
本文将介绍直线回归法的计算公式及其应用。
一、直线回归法的基本原理
直线回归法是通过一条直线来描述两个变量之间的关系。
在这条直线上,每个点的纵坐标值都可以通过一个与横坐标值相关的数学公式来计算得到。
这个数学公式就是直线回归方程,也称为最小二乘法方程。
二、直线回归方程的计算公式
直线回归方程的计算公式如下:
y = a + bx
其中,y表示因变量,x表示自变量,a表示截距,b表示斜率。
直线回归方程的本质就是在寻找一条直线,使得所有点到这条直线的距离之和最小。
三、直线回归法的应用
直线回归法的应用非常广泛。
在市场研究中,我们可以通过对销售数据进行直线回归分析来预测未来的销售趋势;在经济学中,我们可以通过对经济数据进行直线回归分析来预测未来的经济发展趋势;在医学研究中,我们可以通过对临床数据进行直线回归分析来探究疾病发展规律。
总之,直线回归法是一种非常实用的统计学方法,它可以帮助我们更好地理解和分析数据之间的关系。
(完整word版)线性回归方程的求法(需要给每个人发)

耿老师总结的高考统计部分的两个重要公式的具体如何应用ˆ+a ˆ=bx ˆ的求法:第一公式:线性回归方程为y(1)先求变量x 的平均值,既x =(2)求变量y 的平均值,既y =1(x 1+x 2+x 3+⋅⋅⋅+x n )n 1(y 1+y 2+y 3+⋅⋅⋅+y n )n ˆ,有两个方法(3)求变量x 的系数bˆ=法1b∑(x -x )(y -y )iii =1n∑(x -x )ii =1n(题目给出不用记忆)2(x1-x )(y 1-y )+(x 2-x )(y 2-y )+...+(x n-x )(y n-y )][(需理解并会代入数据)=222⎡⎤(x -x )+(x -x )+...+(x -x )2n ⎣1⎦nˆ=法2b∑(x -x )(y -y )iii =1∑(x -x )ii =1n(题目给出不用记忆)2=[x 1y1+x 2y 2+...x ny n]-nx ⋅y,(这个公式需要自己记忆,稍微简单些)2222⎡⎣x 1+x 2+...+x n ⎤⎦-nx ˆˆ=y -bx ˆ,既a (4)求常数aˆ+a ˆ-a ˆ=bx ˆ。
可以改写为:y =bx ˆ(y ˆ与y 不做区分)最后写出写出回归方程y例.已知x ,y 之间的一组数据:x0123y1357求y 与x 的回归方程:解:(1)先求变量x 的平均值,既x =(2)求变量y 的平均值,既y =1(0+1+2+3)=1.541(1+3+5+7)=44ˆ,有两个方法(3)求变量x 的系数b2222⎡⎤(x -x )+(x -x )+(x -x )+(x -x )1234⎣⎦ˆ法1b=(0-1.5)(1-4)+(1-1.5)(3-4)+(2-1.5)(5-4)+(3-1.5)(7-4)5==22227⎡⎣(0-1.5)+(1-1.5)+(2-1.5)+(3-1.5)⎤⎦(x1-x )(y 1-y )+(x 2-x )(y 2-y )+(x 3-x )(y 3-y )+(x 4-x )(y 4-y )][=ˆ=法2b[x 1y1+x 2y 2+...x ny n]-nx ⋅y=[0⨯1+1⨯3+2⨯5+3⨯7]-4⨯1.5⨯4=52222⎡⎤x +x +...+x -nx 12n ⎣⎦2222⎡⎤0+1+2+3⎣⎦7ˆ=4-ˆ=y -bx ˆ,既a (4)求常数aˆ+a ˆ=bx ˆ=最后写出写出回归方程y第二公式:独立性检验两个分类变量的独立性检验:525⨯1.5=77525x +77y1a ca +cy2b d总计x 1a +b c +d a +b +c +d注意:数据a 具有两个属性x 1,y 1。
线性回归公式

线性回归公式
线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。
线性回归方程是利用数理统计中的回归分析,来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法之一,应用十分广泛。
线性回归方程中变量的相关关系最为简单的是线性相关关系,设随机变量与变量之间存在线性相关关系,则由试验数据得到的点,将散布在某一直线周围。
因此,可以认为关于的回归函数的类型为线性函数。
分析按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
回归性方程

回归性方程
回归方程是根据样本资料通过回归分析所得到的反映一个变量(因变量)对另一个或一组变量(自变量)的回归关系的数学表达式。
回归直线方程用得比较多,可以用最小二乘法求回归直线方程中的a,b,从而得到回归直线方程。
原理
对变量之间统计关系进行定量描述的一种数学表达式。
指具有相关的随机变量和固定变量之间关系的方程。
回归直线方程指在一组具有相关关系的变量的数据(x与Y)间,一条最好地反映x与y之间的关系直线。
离差作为表示Xi对应的回归直线纵坐标y与观察值Yi的差,其几何意义可用点与其在回归直线竖直方向上的投影间的距离来描述。
数学表达:Yi-y^=Yi-a-bXi.
总离差不能用n个离差之和来表示,通常是用离差的平方和,即(Yi-a-bXi)^2计算。
线性回归方程的公式为:b=(x1y1+x2y2+…xnyn-nxy)/(x1+x2+…xnNX)。
线性回归方程是数理统计中使用回归分析来确定两个或多个变量之间定量关系的统计分析方法之一。
线性回归方程公式_数学公式

线性回归方程公式_数学公式线性回归方程公式线性回归方程公式:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)。
线性回归方程公式求法:第一:用所给样本求出两个相关变量的(算术)平均值:x_=(x1+x2+x3+...+xn)/ny_=(y1+y2+y3+...+yn)/n第二:分别计算分子和分母:(两个公式任选其一)分子=(x1y1+x2y2+x3y3+...+xnyn)-nx_Y_分母=(x1^2+x2^2+x3^2+...+xn^2)-n__x_^2第三:计算b:b=分子/分母用最小二乘法估计参数b,设服从正态分布,分别求对a、b的偏导数并令它们等于零。
其中,且为观测值的样本方差.线性方程称为关于的线性回归方程,称为回归系数,对应的直线称为回归直线.顺便指出,将来还需用到,其中为观测值的样本方差。
先求x,y的平均值X,Y再用公式代入求解:b=(x1y1+x2y2+...xnyn-nXY)/(x1+x2+...xn-nX)后把x,y的平均数X,Y代入a=Y-bX求出a并代入总的公式y=bx+a得到线性回归方程(X为xi的平均数,Y为yi的平均数)线性回归方程的应用线性回归方程是回归分析中第一种经过严格研究并在实际应用中广泛使用的类型。
这是因为线性依赖于其未知参数的模型比非线性依赖于其位置参数的模型更容易拟合,而且产生的估计的统计特性也更容易确定。
线性回归有很多实际用途。
分为以下两大类:如果目标是预测或者映射,线性回归可以用来对观测数据集的和X的值拟合出一个预测模型。
当完成这样一个模型以后,对于一个新增的X值,在没有给定与它相配对的y的情况下,可以用这个拟合过的模型预测出一个y值。
给定一个变量y和一些变量X1,...,Xp,这些变量有可能与y相关,线性回归分析可以用来量化y与Xj之间相关性的强度,评估出与y不相关的Xj,并识别出哪些Xj的子集包含了关于y的冗余信息。
回归经验方程公式

回归经验方程公式
回归经验方程公式是一种用来建模和预测现象或事件的数学表达式。
它基于经验数据和统计方法,通过拟合数据点到一个数学函数或曲线上,以确定变量之间的关系。
回归经验方程公式的一般形式可以表示为:
Y = β0 + β1X1 + β2X2 + ... + βnXn + ε
其中,Y表示因变量(要预测的变量),X1、X2、...、Xn表示自变量(用来预测的变量),β0、β1、β2、...、βn表示回归系数,ε表示误差项。
回归经验方程公式的建立过程通常分为以下几个步骤:
1. 数据收集:收集与研究对象相关的数据,包括因变量和自变量的观测值。
2. 数据预处理:对数据进行清洗、缺失值处理、异常值处理等。
3. 模型选择:根据研究问题和数据特点选择适当的回归模型,如线性回归、多项式回归、逻辑回归等。
4. 模型拟合:利用统计方法,对选定的回归模型进行参数估计和模型拟合,即确定回归系数。
5. 模型评估:通过检验回归模型的合理性和拟合效果,评估模型的准确性和可靠性。
6. 预测和应用:利用建立的回归经验方程公式,对未知自变量的值进行预测,以便进行决策和应用。
回归经验方程公式在许多领域都有广泛的应用,包括经济学、金融学、市场营销、医学、工程等。
它可以帮助我们了解变量之间的关系,预测未来的趋势和结果,为决策提供科学依据。
同时,回归经验方程公式也有其局限性,如对数据的依赖性较强、模型假设的前提条件等,需要在实际应用中慎重考虑和验证。
一元线性回归方程r公式
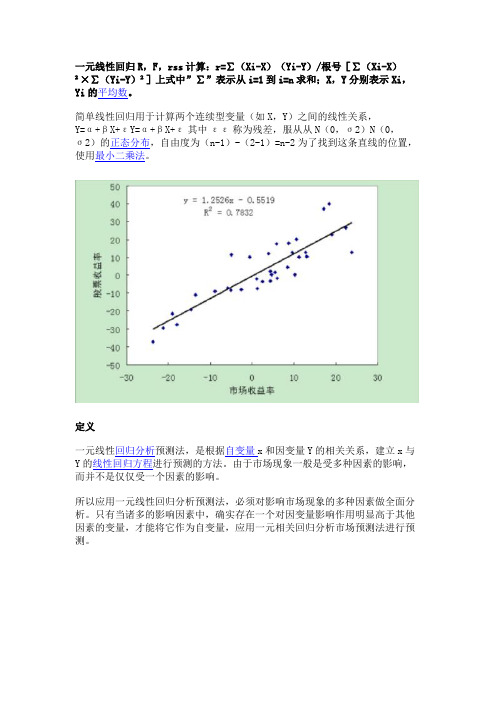
一元线性回归R,F,rss计算:r=∑(Xi-X)(Yi-Y)/根号[∑(Xi-X)
²×∑(Yi-Y)²]上式中”∑”表示从i=1到i=n求和;X,Y分别表示Xi,Yi的平均数。
简单线性回归用于计算两个连续型变量(如X,Y)之间的线性关系,
Y=α+βX+εY=α+βX+ε其中εε称为残差,服从从N(0,σ2)N(0,
σ2)的正态分布,自由度为(n-1)-(2-1)=n-2为了找到这条直线的位置,使用最小二乘法。
定义
一元线性回归分析预测法,是根据自变量x和因变量Y的相关关系,建立x与Y的线性回归方程进行预测的方法。
由于市场现象一般是受多种因素的影响,而并不是仅仅受一个因素的影响。
所以应用一元线性回归分析预测法,必须对影响市场现象的多种因素做全面分析。
只有当诸多的影响因素中,确实存在一个对因变量影响作用明显高于其他因素的变量,才能将它作为自变量,应用一元相关回归分析市场预测法进行预测。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回归方程公式详解
回归方程(Regression Equation)是统计学中用来描述自变量与因变量之间关系的数学公式。
回归方程可以通过分析数据得到,并用于预测未来观测值或者理解变量之间的关系。
一般来说,回归方程的形式为:
Y = β0 + β1X1 + β2X2 + ... + βnXn + ε
其中,
Y 是因变量(被预测的变量);
X1, X2, ..., Xn 是自变量(影响因变量的变量);
β0, β1, β2, ..., βn 是回归系数(或称为斜率),表示每个自变量对因变量的影响;
ε是误差项(残差),表示不能被自变量解释的随机误差。
回归方程的目标是通过估计回归系数,找到最佳的拟合线来描述因变量和自变量之间的关系。
在实际应用中,可以使用不同的回归方法,如线性回归、多项式回归、逻辑回归等,具体选择取决于数据的性质和研究问题的需求。
对于线性回归模型(最常见的一种回归模型),回归方程的形式简化为:Y = β0 + β1X1 + ε
其中,Y 和X1 是一维变量(向量),β0 和β1 是回归系数,ε 是误差项。
线性回归的目标是找到最佳的拟合直线,使得观测数据点与该直线的拟合误差最小。
需要注意的是,回归方程所估计的系数可以提供关于自变量与因变量之间的定量关系和影响程度的信息。
此外,回归方程的使用也需要考虑一些假设和前提条件,如线性性、独立性、常态性、同方差性等。
在实际应用中,可以使用统计软件(如Python中的scikit-learn、R语言中的lm函数等)进行回归分析,从而得到具体的回归方程和系数。
