博弈论书pdf
博弈论(第三章)
劳资博弈
先由工会决定工资率，再由厂商决定雇用多少劳动力
max π (W , L ) = max [ R ( L ) − WL ]
L≥0 L≥0
max u[W , L* (W )]
W ≥0
R
斜率为W R(L) WL
W
W*
0
L (W )
厂商的反应函数
*
L
0
L* (W * )
L* (W )
u3 u2 u1 u0
第三节 子博弈和子博弈完美（精炼）纳什均衡 子博弈
A
借
B
不借 (1,0)
还 (2,2)
不还 起诉
A 不起诉
(1,0)
(0,4)
第三节 子博弈和子博弈完美（精炼）纳什均衡 子博弈精炼纳什均衡
如果在一个完美信息的动态博弈中，各博弈方 的策略构成的一个策略组合满足，在整个动态博弈 及它的所有子博弈中都构成纳什均衡，那么这个策 略组合称为该动态博弈的一个“子博弈精炼纳什均 衡”。
无不确定性的委托人—代理人模型
1
委托 不委托
代理人的选择
激励相容约束：
w(E)-E> w(S)-S w(E)> w(S)+E-S
2
接受
拒绝
[R(0),0]
2
努力 偷懒
[R(0),0]
[R(E)-w(E), w(E)-E]
[R(S)-w(S), w(S)-S]
参与约束：
2
接受 [R(E)-w(E), w(E)-E]
第四节 经典动态博弈模型
斯塔克博格模型（ Stackelberg）
和古诺模型双方产量均为2的产量，总量为4相比 较，斯塔克博格模型中两厂商的产量较高。厂商1的得 益4.5大于古诺模型中厂商1的得益4，但厂商2的得益 2.25小于国内模型中厂商2的得益4。 *在动态博弈中，有先动优势，也有后动优势。信 息多了，可能结果好，但也可能结果更糟。
第11章-博弈论教材全篇
田忌
齐王 b1 b2 b3 b4 b5 b6
a1
3 1 1 1 1 1
a2
1 3 1 1 1 1
a3
1 1 3 1 1 1
a4 1 1 1 3 1 1
a5
1 1 1 1 3 1
a6
1 1 1 1 1 3
2－2 具有鞍点的博弈
通过下面的例3说明，什么是局中人的最优纯策略， 如何求出这个纯策略以及博弈解和博弈值的概念。
博弈的三个要素的矩阵表示（局中人A的收益）
局中人B
局中人A
策
a1
a2
略
am
b1
c11 c21
cm1
策
b2
c12 c22
cm 2
略
bn
c1n c2 n
cmn
局中人A的收益函数可用如下的矩阵表示：
c11
A
c21
cm1
c12 c22
cm 2
c1n c2n
cmn
二人零和博弈也称为矩阵博弈。
博弈论的研究建立在下述假设前提下：即参与博弈 的各局中人都是理性的。
“博弈中一个理性的决策必定建立在预测其他局中人 的反应之上。一个局中人将自己置身于其他局中人的 位置，并为他着想从而预测其他局中人将选择的行为， 在这个基础上该局中人决定自己最理想的行动。”
博弈的三个要素，即局中人，策略集和收益函数 构成了博弈信息，根据不同信息可对博弈做如下 分类：
同样乙方应从收益表中每列找出最大正数（恰为乙 方输掉的数值），为了减少损失，应从这些数字中 求出最小数，它所对应的列策略为乙方的最优纯策 略。
计算过程如下：
对局中人甲，先从每一行中求出最小值
min6,1, 8 8，min3, 2,6 2， min3,0, 4 3，再求出其中的最大值 max8, 2, 3 2。数字2对应的行策略
博弈论囚徒困境的四种形式 PDF
�p� 1 徒囚性理非
�所表下如衡均 seyaB 练精的弈 博复重次三�赖抵择选段阶二第 2 徙囚�下件条的 2�l≥P 定给在以所�弈博段阶两的示所 4 表是段阶的后随即�段阶三第和二第入进弈博么那�形情的”赖抵“择选都方双看先 。)白坦择选 2 徒囚� ”赖抵“择选 l 徒因(能可 的作合不有也�)”赖抵“选都方双(能可的作合有段阶一第�言而 2 和 1 徒囚的性理就 。)白坦�白坦�赖抵(是略策段阶三的 1 徒的性 理以所�利有为更将这疑无�付支的 0 得获段阶二第�付支的) 1- (得获段阶一第在能可么那 �赖抵择选�况情实真的己自藏隐果如反相�付支的)3-(得获能只大最段阶二第在 1 徒囚的 性理�白坦择选段阶二第在 2 徒因是于�方弈博的性理是已自示显 2 徒囚向疑无但�罚惩于 免能可白坦择选段阶一第 1 徒囚管尽 �作合行进赖抵择选会将段阶一第在 1 徒囚性理明说要 面下。白坦择选会仍故�择选的段阶一下在 2 徒囚变改会不择选的段阶本在己自�的性理是 2 徒囚道知 l 徒囚的性理于由�段阶二第在�白坦择选会机作合的续后有没为因会 2 徒囚和 1 徒囚的性理段阶三第在。况情的次三复重弈膊本基虑考步一进� 下件条的 2�1≥ P � ”赖抵“=X 择选会将 2 徒囚�2�1≥P 即 �6-p3≥8-p7 果如 。6-p3=])3-(+)3-([) p-1( +])3-( +0[p �是付支望期的时此 2 徒囚 �时 ”白坦“ =X 当 ;8-p7 = ]) 3- ( + ) 5- ( [ ) p-1( +]0 +) 1- ([p�是付支望期的 2 徒囚�时”赖抵“=X 当 �4 表� 白坦 白坦 2=t X X 白坦 赖抵 1=t �p-1� 1 徒囚性理 2 徒囚
博弈论-蒋文华-浙江大学
博弈论-蒋⽂华-浙江⼤学第⼀讲、博弈论概述献给诸位知⼈者智，⾃知者明；胜⼈者⼒，⾃胜者强；⼩胜者术，⼤胜者德。
第⼀章何为“博弈”博：博览全局弈：对弈棋局→谋定⽽动是指在⼀定的游戏规则约束下，基于直接相互作⽤的环境条件，各参与⼈依据所掌握的信息，选择各⾃的策略（⾏动），以实现利益最⼤化的过程。
第⼀节从⼀个简单的故事说起博弈时要搞清楚对⼿是谁！博弈时要搞清楚和别⼈⽐什么！⾏为选择既跟对⼿的情况有关，⼜跟所遇到的外部环境的变化有关。
特别提⽰：博弈既可以是竞争，也可以是合作！特别提⽰：博弈，必须学会换位思考！特别提⽰：博弈，只需领先⼀步，⾼⼈⼀筹！博弈就是你中有我，我中有你。
由于直接相互作⽤（互动），每个博弈参与者的得益不仅取决于⾃⼰的策略（⾏动），还取决于其他参与者的策略（⾏动）。
博弈的核⼼在于整体思维基础上的理性换位思考，⽤他⼈的得益去推测他⼈的策略（⾏动），从⽽选择最有利于⾃⼰的策略（⾏动）。
特别提⽰：站在别⼈的⽴场上想⼀想，就是为⾃⼰未来的遭遇着想。
——⽶兰·昆德拉特别提⽰：如果因为对⽅眼中的你的傻，⽽让对⽅更愿意和你合作，何乐⽽不为呢？（⼤智若愚）特别提⽰：请不要在⼀个充分竞争的市场去追求成功！特别提⽰：选对市场（对⼿）⽐选对策略更重要！特别提⽰：在博弈之前，博弈就已经开始了！第⼆节博弈的渊源⼀、中国的理解博+弈=下围棋略观围棋，法于⽤兵，怯者⽆功，贪者先亡。
----汉代刘向，《围棋赋》⼆、西⽅的理解game(规则)费厄泼赖（fair play）第三节学习博弈论的收益⼀、当局者清更有利的选择更快速的反应⼆、旁观者更清理解历史与现实预测未来的发展三、提出完善游戏规则（制度）的建议第⼆章发展简史第⼀节最初的探索和应⽤⼀、古诺模型参加博弈的双⽅以各⾃在同⼀时间内相互独⽴的产量作为决策的变量，是⼀个产量竞争模型。
⼆、伯川德模型该模型与古诺模型的不同之处在于，企业把其产品的价格⽽不是产量作为竞争⼿段和决策变量，通过制定⼀个最优的销售价格来实现利润最⼤化。
博弈论完整版
ke 第1次作业1、考虑一个工作申请的博弈。
两个学生同时向两家企业申请工作，每家企业只有一个工作岗位。
工作申请规则如下：每个学生只能向其中一家企业申请工作；如果一家企业只有一个学生申请，该学生获得工作；如果一家企业有两个学生申请，则每个学生获得工作的概率为1/2。
现在假定每家企业的工资满足：W1/2<W2<2W1，则问：a ．写出以上博弈的战略式描述b ．求出以上博弈的所有纳什均衡（包括混合策略均衡） 解：a ．写出以上博弈的战略式描述学生B学生Ab ．求出以上博弈的所有纳什均衡（包括混合策略均衡）①存在两个纯战略纳什均衡： （企业1，企业2），收益为)2,1(W W ;（企业2，企业1），收益为)1,2(W W 。
②存在一个混合策略均衡：学生A 选择企业1的概率为p ，选择企业2的概率为p -1;学生B 选择企业1的概率为q ，选择企业2的概率为q -1。
当学生A 以)1,(p p -的概率选择时，学生B 选择企业1的期望收益应该与选择企业2的期望收益相等，同时当学生B 以)1,(q q -的概率选择时，学生A 选择企业1与选择企业2的期望收益相等，即：221).1(2.1)1(121.W p W p W p W p -+=-+ 221).1(2.1)1(121.W q W q W q W q -+=-+ 解得：21212W W W W p +-=,211221W W W W p +-=-；21212W W W W q +-=,211221W W W W q +-=-所以，混合策略纳什均衡为：学生A 、B 均以)21122,21212(W W W W W W W W +-+-的概率选择企业1，企业2。
2、两个厂商生产一种完全同质的商品，该商品的市场需求函数为P Q -=100，设厂商1和厂商2都没有固定成本。
若他们在相互知道对方边际成本的情况下，同时作出产量决策是分别生产20单位和30单位。
博弈论基础3
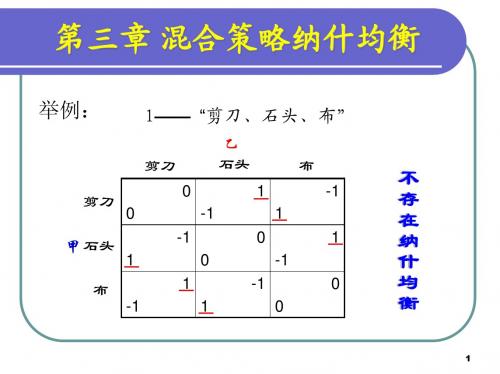
举例：
1—— “剪刀、石头、布”
剪刀 剪刀 甲 石头 布 -1 0 0 -1 1 1 1 0 -1 0 -1 0 -1 0 乙 石头 1 1 1 布 -1
不 存 在 纳 什 均 衡
1
第三章 混合策略纳什均衡
举例：
“2——扑克牌对色游戏”
红 红 甲 黑 -1 -1 1 -1 乙 1 1 1 黑 -1
(0.5 × 0.5) × 5 + (0.5 × 0.5 + 0.5 × 0.5) × 5 + (0.5 × 0.5) × 5
期望支付= 期望支付
11
二、期望支付
在博弈中，当局中人并不清楚其他局中人的 实际策略选择时，他的支付便具有了不确 定性，只能使用期望支付的方式来预测自 己的得益情况，进而确定自己的策略选择
情 侣 博 弈
1
何 敏
[0,1]
0
1 如果 p > 4 1 如果 p = 4 1 如果 p < 4
26
第二节 反应函数法
p
王军反应函数 （1,1）
1
情 侣 博 弈
何敏反应函数
（1/4,3/4）
1/4
（0,0）
0 3/4 1
纳什均衡
q
27
第二节 反应函数法
纳什均衡 情 侣 博 弈
（电影，电影） （足球，足球） 王军以25%的概率选择电影， 何敏以75%的概率选择电影
U g (1/ 4,3 / 4) = 1/ 2
31
一、帕累托优势标准
按照支付大小筛选出来的纳什均衡，比其他纳什 均衡具有帕累托优势。 这种按照支付大小筛选纳什均衡的标准，称为
帕累托优势标准。
高级运筹学（博弈论书稿）-周晶
第章博弈论(对策论)第一节引言1.1博弈行为和博弈论在日常生活中，经常会看到一些相互之间具有斗争或竞争性质的行为。
譬如，两个人下棋，任何一个人在走某一步之前，都需要考虑对方是怎么走的，以及对方在他走了一步之后会怎么走，以至无穷。
高手与俗手的区别往往就在于高手能够考虑10步甚至20步以后的变化，最终的输赢不仅取决于你的决策，而且取决于你对手的决策，这就是博弈。
博弈与决策的根本区别在于是否考虑对方的行为，具有竞争或对抗性质的行为称为博弈行为。
在这类行为中，参加斗争或竞争的各方各自具有不同的目标和利益。
为了达到各自的目标和利益，各方必须考虑对手的各种可能的行动方案，并力图选取对自己最有利或最合理的方案。
比如战争活动中的双方，都力图选取对自己最有利的策略，千方百计去战胜对方；还比如在政治方面，国际间的谈判、各种政治力量间的较量、各国际集团之间的角逐等都无一不具有对抗性质；在经济活动中，各国之间、各公司企业之间的经济谈判，企业之间为争夺市场而进行的竞争等，举不胜举。
博弈论(game theory)，就是研究决策主体的行为发生直接相互作用时候的决策以及这种决策的均衡问题的理论与方法，即研究博弈行为中竞争各方是否存在着最合理行动方案，以及如何找到最合理行动方案的数学理论和方法。
也就是说，当一个主体，好比说一个人或一个企业的选择受到其他人、其他企业选择的影响，而且反过来影响到其他人、其他企业选择时的决策问题和均衡问题。
博弈论应是一种分析问题的方法，它被设计用来帮助我们理解所观察到的决策主体相互作用时的现象，其应用范围涉及经济学、政治学、犯罪学、军事、外交、国际关系、公共选择等各个领域。
博弈论思想的主要特征是各参与人所实施的行为方案(策略)相互依存，各方在冲突或合作后所实现的损益得失结果不仅取决于自己所采取的行为方案，同时也依赖于其他参与方所实施的行为方案，是各参与方行为方案组合的函数。
所以，博弈论在我国也被称为“对策论”。
博弈论（哈佛大学原版教程）
博弈论（哈佛⼤学原版教程）Lecture XIII:Repeated GamesMarkus M.M¨o biusApril19,2004Gibbons,chapter2.3.B,2.3.COsborne,chapter14Osborne and Rubinstein,sections8.3-8.51IntroductionSo far one might get a somewhat misleading impression about SPE.When we?rst introduced dynamic games we noted that they often have a large number of(unreasonable)Nash equilibria.In the models we’ve looked at so far SPE has’solved’this problem and given us a unique NE.In fact,this is not really the norm.We’ll see today that many dynamic games still have a very large number of SPE.2Credible ThreatsWe introduced SPE to rule out non-credible threats.In many?nite horizon games though credible threats are common and cause a multiplicity of SPE.Consider the following game:1actions before choosing the second period actions.Now one way to get a SPE is to play any of the three pro?les above followed by another of them (or same one).We can also,however,use credible threats to get other actions played inperiod1,such as:Play(B,R)in period1.If player1plays B in period1play(T,L)in period2-otherwise play (M,C)in period2.It is easy to see that no single period deviation helps here.In period2a NE is played so obviously doesn’t help.In period1player1gets4+3if he follows strategy and at most5+1 if he doesn’t.Player2gets4+1if he follows and at most2+1if he doesn’t. Therefore switching to the(M,C)equilibrium in period2is a credible threat.23Repeated Prisoner’s DilemmaNote,that the PD doesn’t have multiple NE so in a?nite horizon we don’t have the same easy threats to use.Therefore,the? nitely repeated PD has a unique SPE in which every player defects in eachperiod.In in?nite other types of threats are credible.Proposition1In the in?nitely repeated PD withδ≥12there exists a SPEin which the outcome is that both players cooperate in every period. Proof:Consider the following symmetric pro?le:s i(h t)=CIf both players have played C in everyperiod along the path leading to h t.D If either player has ever played D.To see that there is no pro?table single deviation note that at any h t such that s i(h t)=D player i gets:0+δ0+δ20+..if he follows his strategy and1+δ0+δ20+..if he plays C instead and then follows s i.At any h t such that s i(h t)=C player i gets:1+δ1+δ21+..=1 1?δ3if he follows his strategy and2+δ0+δ20+..=2if he plays D instead and then follows s i.Neither of these deviations is worth while ifδ≥12.QEDRemark1While people sometimes tend to think of this as showing that people will cooperate in they repeatedly interact ifdoes not show this.All it shows is that there is one SPE in which they do.The correct moral to draw is that there many possible outcomes.3.1Other SPE of repeated PD1.For anyδit is a SPE to play D every period.2.Forδ≥12there is a SPE where the players play D in the?rst periodand then C in all future periods.3.Forδ>1√2there is a SPE where the players play D in every evenperiod and C in every odd period.4.Forδ≥12there is a SPE where the players play(C,D)in every evenperiod and(D,C)in every odd period.3.2Recipe for Checking for SPEWhenever you are supposed to check that a strategy pro?le is an SPE you should?rst try to classify all histories(i.e.all information sets)on and o?the equilibrium path.Then you have to apply the SPDP for each class separately.Assume you want to check that the cooperation with grim trigger pun-ishment is SPE.There are two types of histories you have to check.Along the equilibrium path there is just one history:everybody coop-erated so far.O?the equilibrium path,there is again only one class: one person has defected.4Assume you want to check that cooperating in even periods and defect-ing in odd periods plus grim trigger punishment in case of deviation by any player from above pattern is SPE.There are three types of his-tories:even and odd periods along the equilibrium path,and o?the equilibrium path histories.Assume you want to check that TFT(’Tit for Tat’)is SPE(which it isn’t-see next lecture).Then you have you check four histories:only the play of both players in the last period matters for future play-so there are four relevant histories such as player1and2both cooperated in the last period,player1defected and player2cooperated etc.1Sometimes the following result comes in handy.Lemma1If players play Nash equilibria of the stage game in each period in such a way that the particular equilibrium being played in a period is a function of time only and does not depend on previous play,then this strategy is a Nash equilibrium. The proof is immediate:we check for the SPDP.Assume that there is a pro?table deviation.Such a deviation will not a?ect future play by assump-tion:if the stage game has two NE,for example,and NE1is played in even periods and NE2in odd periods,then a deviation will not a?ect future play.1 Therefore,the deviation has to be pro?table in the current stage game-but since a NE is being played no such pro?table deviation can exist.Corollary1A strategy which has players play the same NE in each period is always SPE.In particular,the grim trigger strategy is SPE if the punishment strategy in each stage game is a NE(as is the case in the PD). 4Folk TheoremThe examples in3.1suggest that the repeated PD has a tremendous number of equilibria whenδis large.Essentially,this means that game theory tells us we can’t really tell what is going to happen.This turns out to be an accurate description of most in?nitely repeated games.1If a deviation triggers a switch to only NE1this statement would no longer be true.5Let G be a simultaneous move game with action sets A1,A2,..,A I and mixed strategy spacesΣ1,Σ2,..,ΣI and payo?function?u i.De?nition1A payo?vector v=(v1,v2,..,v I)? I is feasible if there exists action pro?les a1,a2,..,a k∈A and non-negative weightsω1,..,ωI which sum up to1such thatv i=ω1?u ia1+ω2?u ia2+..+ωk?u ia k+De?nition2A payo?vector v is strictly individually rational ifv i>v i=minσ?i∈Σ?imaxσi(σ?i)∈Σiu i(σi(σ?i),σ?i)(1)We can think of this as the lowest payo?a rational player could ever get in equilibrium if he anticipates hisopponents’(possibly non-rational)play.Intuitively,the minmax payo?v i is the payo?player1can guarantee to herself even if the other players try to punish her as badly as they can.The minmax payo?is a measure of the punishment other players can in?ict. Theorem1FolkTheorem.Suppose that the set of feasible payo?s of G is I-dimensional.Then for any feasible and strictly individually rational payo?vector v there existsδ<1such that for allδ>δthere exists a SPE x?of G∞such that the average payo?to s?is v,i.e.u i(s?)=v i 1?δThe normalized(or average)payo?is de?ned as P=(1?δ)u i(s?).It is the payo?which a stage game would have to generate in each period such that we are indi?erent between that payo?stream and the one generates by s?:P+δP+δ2P+...=u i(s?)4.1Example:Prisoner’s DilemmaThe feasible payoset is the diamond bounded by(0,0),(2,-1),(-1,2) and(1,1).Every point inside can be generated as a convex combina-tions of these payo?vectors.6The minmax payofor each player is0as you can easily check.The other player can at most punish his rival by defecting,and each playerthat the equilibria I showed before generate payo?s inside this area.4.2Example:BOSConsiderHere each player can guarantee herself at least payo?23which is the pay-o?from playing the mixed strategy Nash equilibrium.You can check that whenever player2mixes with di?erent probabilities,player1can guarantee herself more than this payo?by playing either F or O all the time.4.3Idea behind the Proof1.Have players on the equilibrium path play an action with payo?v(oralternate if necessary to generate this payo?).22.If some player deviates punish him by having the other players for Tperiods chooseσ?i such that player i gets v i.3.After the end of the punishment phase reward all players(other than i)for having carried out the punishment by switching to an action pro?lewhere player i gets v Pij+ .2For example,in the BoS it is not possible to generate32,32in the stage game evenwith mixing.However,if players alternate and play(O,F)and then(F,O)the players can get arbitrarily close for largeδ. 8。
博弈论(浙江大学,汪淼军)
( ) UI (σ ) = ∑σi (Ci ) ⋅Ui σ −i , [ci ]
——所有参与人所有偏离都是无利于图的
5
3.纳什定理 ——任何一个有博弈都存在至少一个纳什均衡纳什均衡 证明
——如果 S 是非空紧集凸集，F 是从 S 到 S 连续函数，则至少存在一个 X ，
8
a.一阶条件分析
qi ∈ arg max qi ×[a − c − qi − q j ] 一阶条件为：
a − c − 2qi − q j = 0
所以纳什均衡为： qi = q j = (a − c) / 3
b.剔除严格劣战略
qi
≤
a
− 2
c
⇒
qj
>
a−c 4
依次反复可得：
qi
=
qj
=
a
−c 3
(讨论)
x
A
y
B
x
A
x → y,
y A B
A
x'→ y'
17
3.相互转换 ..性别战
（足,足） （足,芭） （芭,足） （芭,芭）
性别战
足球 1,3 1,3 0,0 0,0
C2 芭蕾 0,0 3,1 0,0 3,1
..赌博博弈
C2
C1
M
P
Rr
0,0
1,-1
Rf
0.5,-0.5
0,0
Fr
-0.5,0.5
1,-1
a. c1 > c2
b. qi = a − pi + bi p j c.生产能力 K 受限， K < a / 2
吉本斯博弈论基础pdf
吉本斯博弈论基础pdf
吉本斯博弈论基础主要包括以下几个方面：
1.参与者：在博弈论中，参与者是决策的主体，可以是个人、组织或国家等。
在吉本斯博弈论中，参与者通常被视为具有有限理性的个体，他们根据自身的利益和偏好进行决策。
2.战略：战略是参与者在博弈中的选择，可以是合作或竞争等不同的行为方式。
在吉本斯博弈论中，战略的制定需要考虑对手的反应和预期，以达到最优的决策效果。
3.收益：收益是参与者在博弈中的结果，可以是经济利益、社会地位等。
在吉本斯博弈论中，收益的分配取决于参与者的策略选择和博弈规则的设定。
4.均衡：均衡是博弈中的一种状态，指所有参与者的最优策略组合。
在吉本斯博弈论中，均衡的概念非常重要，它是分析博弈结果和预测未来行为的基础。
5.动态博弈：动态博弈是指参与者的决策和行动有先后顺序，后行动者可以根据先行动者的行为做出最优的决策。
在吉本斯博弈论中，动态博弈的分析需要考虑时间因素和信息不完全等因素。
总的来说，吉本斯博弈论基础主要包括参与者、战略、收益、均衡和动态博弈等几个方面。
这些基础概念和分析方法构成了吉本斯博弈论的基本框架，为研究决策制定和行为模式提供了重要的理论支持。
博弈论
三、双寡头削价竞争
问两寡头最终的策略是什么？
寡 头 2
寡 头 1 高价 低价
高价
低价
100，100
150，20
10，150
70，70
§2.2 基本概念
一、定义
博弈即一些个人，队组或其他组织，面对一定的环境 条件，在一定的规则下，同时或先后，一次或多次，从各 允许选择的行为或策略中进行选择并加以实施，各自取得 相应的结果的过程。
四、博弈的过程
博弈过程也是博弈结构的重要方面。虽然我 们前面介绍的大多数博弈例子，都是几个博弈方 一次性同时进行决策选择的，但事实上社会经济 活动中也有许多策略较量的博弈问题，是先后、 反复或者重复的策略对抗。例如寡头削价竞争就 完全可能是先后进行的而不是同时进行的。博弈 过程的这种差异对博弈的结果和博弈分析也有非 常重大的影响，因此需要注意它们的区别，分类 进行研究。根据博弈过程方面的这些差异，博弈 问题通常分为“静态博弈”、“动态博弈”和 “重复博弈”几个大类。
博弈论（Game Theory)
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 引论 基本概念 完全信息静态博弈 完全信息动态博弈 不完全信息静态博弈 不完全信息动态博弈 合作博弈 演化博弈
第一章 引论
研究对象：冲突、竞争现象的定量分析理论。 对策： 参加竞争的各方为了获胜而需研究出一组对付对方的策略。 历史沿革：（1）我国古代围棋、国际象棋（印度）等； （2）1912年，数学家翟墨罗把对策从模拟模型抽象为数学模 型； （3）第一次、第二次世界大战，军事对策应用于战役和战 略研究； （4）1944年，冯· 诺意曼、摩根斯特合写了“博弈论和经济 行 为”，推动了博弈论在经济管理中的应用； （5）近年来，由于纳什、泽尔腾、海萨尼获诺贝尔经济学奖 （1994），进一步推动了博弈论的研究。
博弈论-8
11
不完全信息古诺模型
22
此时卖者认为买者的期望报价
1 ab cb ps xdx cb E[ pb (vb ) pb (vb ) ps ] P pb (vb ) ps 1 ( ps ab cb ) 2
卖者目标函数
1 max[ ( ps E[ pb (vb ) pb (vb ) ps ]) vs ] P[ pb (vb ) ps ] ps 2
第5章 不完全信息静态博弈
1
本章概要
不完全信息博弈 海萨尼转换 不完全信息静态博弈的战略式表述 贝叶斯均衡 贝叶斯均衡与混合战略 机制设计理论初步 显示原理
2
不完全信息博弈 古诺博弈
企业1和2的成本可能高（cH），也可能低（cL） 企业1和2互不知道对方边际成本的情况下进行产量竞 争
问题——双方如何报价？如何成交？
18
分析过程
P(b j bi ) P[V (b j ) V (bi )]
当参与人i叫价bi时，获胜的概率是对方叫价低于bi的概率 ，或者等价地说，是对方的保留价格低于V (bi)的概率。 由于参与人对该物品的保留价格是 [0，1]上的均匀分布， 这一概率就等于V (bi)。所以，一个具有保留价格vi、叫价 bi的参与人的期望支付为： V (bi) ×(vi-bi)+[(1-V (bi)] ×0 从而他的目标是: max V (bi )(vi - bi ) 一阶条件
博弈论1 (2)全篇
6
四、古典博弈论的三个基本假设：参与人是理性的；他们有 这些理性的共同知识；他们知道博弈规则。
理性的三个基本内涵：理性的局中人具有关于博弈的完全知 识；可以确切知道整个状态空间；具有相对无限的逻辑能力。
五、博弈的典型例子
1 ．囚徒困境 坦白
坦白
不坦白
-6，-6 -1，-8
3
2、博弈与一般决策的区别
二、博弈模型要素
1、参与人：博弈中的决策主体。他的目的是通过选择策 略以最大化自己的支付（效用）水平。
虚拟参与人（自然）：指决定外生的随机变量的概率分布 的机制。自然作为虚拟参与人没有自己的支付与目标函数， 即所有的结果对它都是无差异的。
2、策略：参与人在给定信息集（信息集包含了一个参与人有关 其他参与人之前行动的知识，可理解为参与人在特定时刻有关 变量值的知识。一个参与人无法准确知道的变量全体属于一个 信息集）的情况下的行动规则。它规定参与人在什么时候选择 什么行动。[策略是可供局中人选择对付其它局中人的完整行动 方案。]
21
例 某个地方的居民均匀地环绕一个圆形湖居 住。两小贩来此地推销商品。1）若居民都选 择离自己较近的小贩购买商品，问小贩选择推 销地点博弈的NE是什么？2）若有三个小贩同 时到此地推销商品，则推销地点博弈的NE又是 什么？3）若圆形湖的周长是1（千米），居民 的购买量是Q=1-D，D为居民与小贩推销点距 离，则两个和三个小贩博弈的NE各是什么？
14
例6 设 s1 [10,0] s2 [3,0]
u1 (s) 10s1 7s1s2 s12
u2 s 15s2 5s1s2 s22
求NE。
15
例7 设 s1 [10,0] s2 [3,0]
第十章---博弈论初步精选全文完整版
甲 (式乙)
p.61
p.42
A B
混合策略组合及其支付也就有无限多的可能。
q.31 C 4，6 7，3
乙
.q72 D 9，1 2，8 9
不存在纯策略均衡时的混合策略均衡3
• 条件混合策略：参与人在假定其他参与人按某一概率选择某一策略
的条件下设计的对自己而言具有相对优势的（即期望支付最大的）混合 策略，称为“条件混合策略”。
• 对乙而言，如果假定甲合作，那么乙合作的支付为6，比不合作的支付 多1，因此合作是甲合作条件下乙的条件策略；假定甲不合作，那么乙的 条件策略是也不合作，乙若合作支付只有1，不合作则可得到3。
• 条件策略组合：参与人以其他参与人选择某一策略为条件的条件策略与
作为它的条件的对方策略之间的组合，称为“条件优势策略组合”或
• 假q2=定1-（q1p代1，入p甲2）与、乙（各q自1，的q2期）望的支取付值表从达0到式1有无，限经多整可理能可，得把：p2=1-p1和 E甲= p1（7－10q1）+5q1+2（式1）； E乙= 5q1（2p1－1）－7p1+8（式2）
• 每个参与人需要确定，在另一参与人为其混合策略选择某个概率值时， 己方混合策略的概率向量应怎样取值，才能使自己的期望支付最大。
e点的坐标是p1=0.5，q1=0.7，则纳什均衡 时p2=0.5，q2=0.3 。
q1 1
本题中混合策略的纳什均衡还可表示为：
((p1 , p2)，(q1 ,q2) )= ((0.5 , 0.5)，(0.7 , 0.3) )。 0.7 本题中，只有唯一的这个纳什均衡点。
1
q1＜0.7
p1= [0,1] q1 = 0.7
博弈论
12 完全信息静态博弈2 完全信息静态博弈2.1 基本分析思路和方法2.2 纳什均衡2.3 无限策略博弈分析和反应函数2.4 混合策略和混合策略纳什均衡2.5 纳什均衡的存在性2.6 纳什均衡的选择和分析方法扩展囚徒困境-3，-30，-5-5，0-1，-1坦白抵赖坦白抵赖甲乙上策：如果不管其他博弈方选择什么策略，一个博弈方的某个策略给他带来的得益始终高于其他策略，至少不低于其他策略，那么这个策略就是该博弈方的上策。
-3大于-50大于-1坦白是甲的上策坦白是乙的上策在乙选择坦白的情况下——甲选择坦白在乙选择抵赖的情况下——甲选择坦白严格上策的严格上策。
就称为博弈方那么，都有以及任一使得对任何，，博弈方存在策略合个博弈方的任何策略组如果对其他i s s s u s s u s s s s s s s s s n i i i i i i i i i i i n i i i ****111)(),(),,,,,(1−−−+−−′>≠′=−L L例1:博弈G 的得益矩阵如图所示：7，36，62，23，7上下左右甲乙。
“右”是乙的严格上策，“上”是甲的严格上策证明==*2*1:s s如果一个博弈的某个策略组合中的所有策略都是各个博弈方各自的上策，那么这样的策略组合就是该博弈的一个上策均衡。
（1）上策均衡如囚徒困境-3,-30,-5-5, 0-1,-1坦白抵赖坦白抵赖甲乙衡坦白，坦白）：上策均策略组合(*=s 均衡——稳定的博弈结果（策略组合）严格上策均衡都成立。
对所有策略组合，不等式对于任何一个博弈方一个严格上策均衡：的为博弈满足以下条件，就称它，的一个策略组合。
如果；人博弈是设),,,(),,,,,(),,,,,,(},,2,1{),,(},,,{),,,(211111*11**2*1*1121**2*1*n n i i i i n i i i i n n n n n s s s s s s s s u s s s s s u n i G s s s s u u S S G n S S S s s s s L L L L L L L L L L L +−+−>∈==××∈=例1:7，36，62，23，7上下左右甲乙。
第三讲博弈论战略分析.pdf
继续
占优战略的存在以及它与合作解相悖的事实是导致社 会两难的根本原因。例如，在囚徒困境的例子中，两 个罪犯肯定愿意协调他们的战略，拒绝认罪，这样每 人只需服刑一年。警察把他们关在不同的牢房，就是 为了防止他们协调双方的战略。 在广告博弈中，合作解是不做广告。当政府宣称要实 施一项广告禁令时，遵守这一禁令可以让烟草公司获 得利润，因为在政府的强制之下，两家企业都会不做 广告。在军力调拨博弈中，和平是合作解。 然而，由于对重型大炮和铁路运输的依赖性所造成的 时间限制，使得双方不可能协调他们的战略。
继续
假定有两个候选人：参议院布兰克先生和地方官员 格雷先生。虽然他们在政治立场上没什么个人偏 好，但身为民主党的布兰克持左翼立场要比身为共 和党的格雷更加具有信服力。 相反，如果持右翼立场，格雷比布兰克更具有信服 力。持左翼立场还是右翼立场是他们可以选择的两 种战略。 此外，他们还有第三个可供选择的战略：持中立立 场。
继续
当一个博弈中的每一位 参与者都选择了各自的 占优战略时，相应的博 弈结果就是占优战略均 衡。 我们也可以说，“倾倒”战 略占优于“雇卡车”战略。 如果无论对手选择哪种 战略，一个战略的收益 总是高于另一个战略， 我们就说，第二个战略 被第一个战略占优，第 二个战略被称为劣战略 (dominated strategy)。 在该博弈中，“雇卡车”战 略就是一个劣战略。
3.1垃圾处理博弈
在探讨这个 博弈之前， 我们先来看 一个故事。 故事的主人 公是两所房 屋的主人， 琼斯先生和 史密斯先 生。两人各 在郊区拥有 一套周末别 墅，该地区 不提供垃圾 日常处理服 务。
他们可以共同雇一 辆卡车处理垃圾，但 收费很高，每人每年 需支付500美元。此 外，他们还有另一个 选择，琼斯可以将垃 圾倒在史密斯房子旁 边的一块属于自己的 空地上，史密斯则可 以将垃圾倒在琼斯房 子旁边的一块属于自 己的空地上。（如图 3.1）
范里安第二十一章博弈论
(-1,1)
(1,-1)
背面
(1,-1)
(-1,1)
23
纳什均衡
混合战略
参与者i的一个混合战略是指在其纯战略空间 Si 中的一个概率分布。
——确定选采取某一个纯战略的概率。 纯战略空间： S 混合战略：
i
{正面，背面}
i ( p,1 p)
p [0,1]
24
纳什均衡
纳什均衡：
29
完全信息动态博弈
例：敲诈博弈 参与者1的战略空间：{给，不给}
参与者2的战略空间：{(R,R),(R,L),(L,R),(L,L)} R:不拉；L：拉
参与者2 (R,L) 给 (0,1000) (R,R) (0,1000) (1000,0) (L,R) (L,L)
(,)
(1000,0)
si S i ，对于其他参与者的每一个 s i 的收益都不小于选择 的收
si Si , si S i
, s i ) ui (s , s i ) u ( s i i
——理性的参与者一定会选择占优战略
10
纳什均衡
占优战略
（招认，招认） 囚徒困境
囚徒2
沉默 招认
混合战略
参与者 i 选择正面的概率为P 参与者 j 选择正面的概率为q 正面(z) 参与者1 背面(f) 参与者1的期望收益： 猜硬币 参与者2 正面(z) 背面(f)
(-1,1)
(1,-1)
(1,-1)
(-1,1)
u1 ( p, q) pqu1 (z, z ) p(1 q)u1 (z, f )
G (T ) 有限次重复博弈 由唯一的子博弈精练均衡 :即 将阶段博弈的纳什均衡在每阶段重复进行。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
博弈论书pdf
摘要：
1.博弈论概述
2.博弈论的基本概念
3.博弈论的应用领域
4.博弈论的发展历程
5.如何学习和应用博弈论
6.博弈论书的推荐
正文：
一、博弈论概述
博弈论，又称为对策论，是一种研究决策制定的数学工具。
它主要研究多个决策者在特定规则下进行策略选择，并分析各种策略带来的结果。
博弈论旨在解决在竞争、合作、冲突等场景中，决策者如何做出最优选择以实现自身目标的问题。
二、博弈论的基本概念
1.参与者：博弈中的决策者，可以是个人、组织或国家等。
2.策略：参与者可选择的行动方案。
3.收益：参与者采取某策略后所获得的利益或损失。
4.博弈：参与者之间根据特定规则进行策略选择与收益分配的过程。
5.纳什均衡：一种特殊的博弈均衡状态，指参与者在不知道其他参与者策略选择时，自己的最优策略不依赖于其他参与者的选择。
三、博弈论的应用领域
博弈论广泛应用于经济学、社会学、政治学、军事战略、人工智能等领域。
其中，最著名的应用案例是囚徒困境博弈和拍卖理论。
四、博弈论的发展历程
博弈论的发展可以追溯到20 世纪初。
1944 年，美国数学家诺曼·兰恩·库珀发表了关于博弈论的论文，标志着博弈论的正式诞生。
此后，约翰·福布斯·纳什、莱昂纳德·达维多维奇和罗杰·巴纳生机等人的研究使博弈论得到了迅速发展。
近年来，博弈论在人工智能、网络经济等领域的应用也取得了显著成果。
五、如何学习和应用博弈论
学习和应用博弈论需要掌握基本的数学知识，了解相关的理论模型，并通过实践案例加深理解。
以下是一些建议：
1.阅读经典教材，如《博弈论与经济行为》、《博弈论与信息经济学》等。
2.学习博弈论软件，如Axelrod、Netlogo 等，模拟实际问题进行博弈分析。
3.参加相关课程和研讨会，了解博弈论的前沿动态。
4.多做案例分析，提高博弈思维能力。