高一实验班分班考试数学试题
2023北师大实验中学新高一分班考试数学真题

2023北师大实验中学新高一分班考试数学真题第一部分选择题(共30题,每题2分,满分60分)1. 若a > 0,b < 0,c > 0,则(a+b) c = ____- A) ac + bc- B) - ac + bc- C) ac - bc- D) - ac - bc2. 设函数f(x) = x^2 + 3x - 2,则f(0) + f(1) + f(2)的值为____- A) 6- B) 8- C) 14- D) 16(以下省略28题)第二部分解答题(共2题,每题20分,满分40分)1. 设函数y = ax^2 + bx + c,其中a ≠ 0,给出如下条件:- 当x = 1时,y = 4;- 当x = -2时,y = 9。
求函数的解析式。
2. 若a、b、c都是非零实数,且满足方程ax^2 + bx + c = 0有两个不相等的实数根,则称这样的二次方程为“标准二次方程”。
给出如下条件:- 二次方程x^2 - 4x + c = 0是标准二次方程;- 对于任意非零实数m,二次方程mx^2 - (m+1)x + c = 0都不是标准二次方程。
求a、b、c的取值范围。
第三部分简答题(共2题,每题20分,满分40分)1. 在笛卡尔坐标系中,求方程y = 2x^2 + 3x - 4的对称轴和顶点坐标。
2. 已知函数f(x) = ax^2 + bx + c是单调递增的,且f(-1) = f(1) = 4,求三个参数a、b、c的取值情况。
第四部分计算题(共2题,每题20分,满分40分)1. 已知函数y = 2x^3 - 3x^2的图像上有两点A(1, -1)和B(-2, -12),求曲线与x轴交点的坐标。
2. 若两个正数的和为8,求它们的乘积的最大值。
总分:满分180分以上为2023北师大实验中学新高一分班考试数学真题,希望能对你有所帮助。
2022新高一入学分班考数学试卷12套(含答案)

D.不能确定
α
β
B
D
C
10.如图为由一些边长为 1cm 正方体堆积在桌面形成的立方体的三视图,则该立方体露在外面部分的表面积是
________ cm2。
正视图 A. 11 B.15
左视图 C.18
俯视图 D.22
第Ⅱ卷(答卷)
二. 填空题(本大题共 5 小题, 小题 4 分,共 20 分)
11.函数 y
形 S3 ,以此类推,则 S2006 为(
A.是矩形但不是菱形; C.既是菱形又是矩形;
) B. 是菱形但不是矩形; D.既非矩形又非菱形.
9.如图 ,D 是直角△ABC 斜边 BC 上一点,AB=AD,记∠CAD= ,∠ABC= .若 10 ,则 的度数是 (
)
A
A.40
B. 50
C. 60
W=
20 30
2x 1 x
8
1 x 82
82
12
14
8
1 8
x
82
2x
40
1 x 6 6 x 11 12 x 16
化简得
W=
1 18
x2 x2
14 2x
1
26
x 6 6 x
11
………………10
分
8
1 8
x2
4x
48
12 x 16
①当 W= 1 x 2 14 时,∵ x ≥0,函数 y 随着 x 增大而增大,∵1≤ x ≤6 8
4
1
5
2
x
①
2 x 1 6 x
②
由①得:x>-1
由②得: x 4
所以原不等式组的解集为: 1 x 4
2024年秋季新高一入学分班考试模拟卷数学答案(广东版)

2024年秋季高一入学分班考试模拟卷(广东专用)(02) 数 学答案及评分标准一、单选题(本大题共10小题,每小题3分,共30分) 1 2 3 4 5 6 7 8 9 10 DACBDAABAA二、填空题(本大题共8小题,每小题3分,共24分)11.7 12.4 13. 30 25 14.(3,4]15.0或1或12 16.1− 18.120212 三、解答题 19.(10分)【详解】(1)由交集的定义可知,{}5A B = ;由并集的定义可知,{}2,3,4,5,7A B ∪=; (2)由补集定义可知,{}2,3,6U A = ,(){}2,3U A B ∩=. 20.(10分)【详解】22332428x x x x x x ++−−− ()22324(2)(2)24xx x x x x x x ++=−−−++3122x x =−−− 22x =−, 当3x =时,原式2232==−. 21.(10分)【详解】(1)解:若命题p 为真命题,即命{}620x x x ∃∈≤≤∣,2x a <,所以62a <,所以3a >, 若命题q 为真命题,即R x ∀∈,220x x a +−>,所以2240a ∆=+<,解得1a <−, 因为命题p 和命题q ¬有且只有一个为假命题,当命题p 为假,命题q ¬为真时31a a ≤≥− ,解得13a −≤≤;当命题p 为真,命题q ¬为假时31a a > <− ,所以a ∈∅; 所以[]1,3a ∈−;(2)解:若命题p 和命题q 都为假命题,则31a a ≤ ≥−,即13a −≤≤;因为命题p 和命题q 至少有一个为真命题,所以3a >或1a <−,即()(),13,a ∞∞∈−−∪+; 22.(10分)【详解】设甲地销售了x ()110,N x x ≤≤∈辆,则乙地销售了()10x −辆,总利润设为y 万元, 故()44341040y x x x x x=−+−=−++,根据基本不等式,44x x +≥=,当且仅当4x x =,即2x =时,等号成立,故44040436y x x=−++≤−=故最大利润为36(万元). 23.(12分)【详解】(1)当2x =−时,()222211y =−−+×−+=,所以m =1, 故答案为:1;(2)根据表格数据,描点画图如下:(3)根据图象可知,函数具有如下性质:①函数的最大值是2,没有最小值;②当x >1时,y 随x 的增大而减小;(答案不唯一)(4)①由图象可知:函数图象与x 轴有两个交点, 所以方程﹣x 2+2|x |+1=0有2个实数根, 故答案为:2;②方程﹣x 2+2|x |+1=a 有4个实数根时, 即表示y =a 与图象有4个交点,故由图象可知,a 的取值范围是:1<a <2. 故答案为:1<a <2. 24.(12分)【详解】(1)连接OA ,过O 作OE ⊥AB 于E , 因为粒子注入和引出路径都与圆O 相切, 所以∠EAO =90°-905337α=°−°=°, 因为OE ⊥AB ,OE 所在的是直径,AB 为弦, 所以AE =BE =18km 2AB =,则tan ∠EAO =8OE OEAE =, 所以38tan 37864OE =°≈×=km ,所以AO 10≈=km , 所以圆O 的直径为2×10=20 km ;(2) CD的长l =90105km 180ππ×=, 因为 3.2π<,所以55 3.2=16π<×, 则AB 的长度更长. 25.(16分)【详解】(1)260x x −−=①,所以(2)(3)0x x +−=, 所以12x =−,23x =,215x x −=,故①不是“邻根方程”;2210x −+=②,所以21142x x =⇒=± ,所以122111122x x x x −−,,,故②是 “邻根方程”; (2)因为方程2(1)0x m x m −−−=(m 是常数)是“邻根方程”, 所以方程必有两不相等实根,即22(1)4(1)0m m m ∆=−+=+>,记12x x <,由求根公式有:12x x =所以12111x x m −===⇒+=,解得:0m =或2m =−;(3)因为方程210ax bx ++=是“邻根方程”, 记12x x <,所以122214x x b a a −=⇒=+,所以22281(4)126t a a a a b =−+=−=−+−, 所以当4a =时,t 的最大值为16. 26.(16分)【详解】(1)ACE △为等腰三角形,理由如下:对于直线13:34=+l y x , 令0x =,可得3y =,令0y =,可得4x =−,即()()4,0,0,3A B −; 将点()2,0C ,()0,6D 代入直线2:l y kx b =+, 可得206k b b +== ,解得36k b =− = ,则直线2:36l y x =−+, 联立方程33436y x y x =+=−+ ,解得45185x y= =,即418,55E ,可得6,6AE CE AC ==,即AEAC CE =≠,所以ACE △为等腰三角形. (2)①当P 、Q 在CE 上时,如图1,此时OPC OPQ ≅ ,则2OQOC ==,设(3),6Q m m −+, 又因为(2,0)C ,则()222362m m +−+=,解得85m =或2m =(舍去), 所以86,55Q;②P 在CE 上,Q 在AE 上时,如图2,此时OPC POQ ≅ ,则,2POC OPQ PQ OC ==∠=∠,可知PQ OC ∥, 设3,34Q n n + ,则32,34P n n ++,代入36y x =−+得()333264n n +=−++,解得45n =−, 所以412,55Q−;③P 在AE 上,Q 在CE 上时,如图3,此时OPC OPQ ≅ ,则2OQOC ==,可知(2,0)Q −; ④P 在AC 上,Q 与点E 重合时,如图4,此时OPC POQ ≅ ,则2,PQOC POC OPQ ∠∠===, 可得AOD APO =∠∠,AP PQ AO OC AC AE +=+==, 所以Q 与点E 重合,即418,55Q;综上所述:点Q 在坐标为86,55 ,412,55 − ,(2,0)−,418,55.。
高一实验班分班考试数学试题

高一实验班分班考试数学试题高一实验班分班考试数学试题时量:120分钟分钟 满分:120分一、填空题(每小题4分,本题满分32分)分)1、在△ABC 中,∠C=90°,cosB=32,a=3,则b= 。
2、同时抛掷两枚正方体骰子,所得点数之和为7的概率是的概率是 。
3、设a>b>0,a 2+b 2=4ab ,则a ba b+-的值等于的值等于 。
4、如图,在△ABC 中,AB=AC ,∠BAD=30°,且AE=AD ,则∠CDE= 。
5、已知实数x ,y 满足x 2-2x+4y=5,则x+2y 的最大值为的最大值为 。
6、等腰三角形ABC 中,BC=8,AB 、AC 的长是关于x 的方程x 2-10x+m=0的两根,则m 的值为的值为 。
7、以A(2,3)为圆心的圆与两坐标轴共有三个公共点,☉A 的半径是的半径是 。
8、如右图所示:一张长方形纸片ABCD ,其长AD 为a ,宽AB 为b (a>b ),在BC 边上选取一点M ,将△ABM 沿AM 翻折后B 至B ’的位置,若B ’为长方形纸片ABCD 的对称中心,则a b的值为 。
二、选择题:(每小题4分,本题满分32分)分)9、为筹备班级的初中毕业联欢晚会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是调查,那么最终买什么水果,下面的调查数据中最值得关注的是 ( )A 、众数 B 、平均数、平均数C 、中位数、中位数D 、方差、方差10、某市“旧城改选”中计划在市内一块如右图所示的三角形空地上种植某种草皮以美化环境,已知种植草皮每平方米售价a 元,则购买这种草皮至少需元,则购买这种草皮至少需 ( ) A 、450a B 、225a C 、150a D 、300a 11、如下图是由一些相同的小正方体构成的几何体的三视图,则构成这个几何体的小正方体的个数是 ( )A 、5 B 、6 C 、7 D 、8 12、如右上图:D 是ABC 的边AB 上的一点,ADC Ð=BCA Ð,AC=6,DB=5,ABC 的面积是S ,则BCD 的面积是的面积是 ( )A 、35S B 、47S C 、59S D 、611S 13、如图,将矩形ABCD 分成15个大小相等的正方形,E 、F 、G 、H 分别在AD 、AB 、BC 、CD 边上,且是某个小正方形的顶点若四边形EFGH 的面积为1,刚矩形ABCD 的面积是的面积是 ( )A 、52B 、53C 、32D 、15814、若关于X 的不等式组{232x a x a ³+-有解,则函数21(3)4y a x x =---图象与X 轴的交点个数为轴的交点个数为 ( )A 、0 B 、1 C 、2 D 、1或2 15、若P 1(X 1,Y 1),P 2(X 2,Y 2)是二次函数2(0)y ax bx c abc =++¹的图象上的两点,且Y 1=Y 2,则当12x x x =+时,Y 的值为的值为 ( )A 、0 B 、C C 、ba-D 、244ac b a-16、如图,A 是半径为1的◎O 外的一点,OA=2,AB 是◎O 的切线,B 是切点,弦//BC OA ,连接AC ,则阴影部分的面积等于则阴影部分的面积等于 ( )A 、29pB 、6pC 、368p+D 、348p-三、解答题:(共六大题,满分56分)分)17、(8分)已知:如图,ABC 中,AC=BC ,090ACB Ð=,D 是AC 上一点,AE BD ^交BD 的延长线于E ,且12AE BD =。
区高一新生入学分班考试数学试题及答案

区高一新生入学分班考试数学试题及答案高一新生入学分班考试数学试题总分:150分,时长:120分钟第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列运算正确的是()。
A。
a·a=aB。
a÷a4=a2C。
a3+a3=2a6D。
(a3)2=a62.一元二次方程2x2-7x+k=0的一个根是x1=2,则另一个根和k的值是()A。
x2=1,k=4B。
x2=-1,k=-4C。
x2=2/3,k=6D。
x2=-2/3,k=-63.如果关于x的一元二次方程x-kx+2=0中,k是投掷骰子所得的数字(1,2,3,4,5,6),则该二次方程有两个不等实数根的概率P=()A。
2/3B。
1/2C。
1/3D。
1/64.二次函数y=-x2-4x+2的顶点坐标、对称轴分别是()A。
(-2,6),x=-2B。
(2,6),x=2C。
(2,-6),x=-2D。
(-2,-6),x=25.已知关于x的方程5x-4+a=0无解,4x-3+b=0有两个解,3x-2+c=0只有一个解,则化简a-c+c-b-a-b的结果是()A。
2aB。
2bC。
2cD。
06.在物理实验课上,XXX用弹簧称将铁块A悬于盛有水的水槽中,然后匀速向上提起,直至铁块完全露出水面一定高度,则下图能反映弹簧称的读数y(单位N)与铁块被提起的高度x(单位cm)之间的函数关系的大致图象是()见原图)7.下列图中阴影部分的面积与算式|3/1|+(4/2)+2-1的结果相同的是(见原图)8.已知四边形S1的两条对角线相等,但不垂直,顺次连结S1各边中点得四边形S2,顺次连结S2各边中点得四边形S3,以此类推,则S2006为()A。
是矩形但不是菱形;B。
是菱形但不是矩形;C。
既是菱形又是矩形;D。
既非矩形又非菱形。
9.如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β。
杭州西湖区高一实验班分班考试数学试卷

杭州西湖区高一实验班分班考试数学试卷第一部分:选择题(共60分,每小题3分)1. 设f(x) = 3x - 5,则f(2)的值为()。
A. -1B. 1C. 2D. 32. 已知集合A = {x | x < 5},集合B = {x | x > 3},则A∩B的值为()。
A. {1, 2, 3, 4}B. {2, 3, 4, 5}C. {3, 4, 5, 6}D. {4, 5, 6, 7}3. 若2sinθ = √3,则tanθ的值为()。
A. -√3B. -1C. 1D. √34. 如果 x^2 + 5x + 6 = 0 的根是α和β,则α+β的值为()。
A. -6B. -5C. -4D. -35. 已知函数f(x) = 2x^2 - 3x + 1,g(x) = 3x + 2,求f(x) + g(x)的值。
A. 5x^2 - 2x + 3B. 5x^2 + x + 3C. 5x^2 - 2x - 1D. 5x^2 - x + 36. 对于任意实数x,(3x + 2)^2的值为()。
A. 9x^2 + 12x + 4B. 9x^2 + 2x + 4C. 9x^2 + 4D. 9x^2 + 12...第二部分:解答题(共40分)1. 求下列方程的解:2x + 5 = 10解:将式子两边同时减去5,得到2x = 5,再除以2,得到x = 2.5。
所以该方程的解为x = 2.5。
2. 已知函数f(x) = 3x + 2,求f(4)的值。
解:将x替换为4,得到f(4) = 3(4) + 2 = 14。
所以f(4)的值为14。
...总结本文档为杭州西湖区高一实验班分班考试数学试卷,共包含60分的选择题和40分的解答题。
选择题部分涵盖了各类数学知识点,考察学生对基础概念和计算能力的掌握。
解答题部分要求学生运用所学的数学知识解答具体问题。
该试卷旨在评估学生在数学方面的能力和水平。
请学生们仔细阅读题目要求,准确回答问题。
高一新生分班考试数学试卷含答案
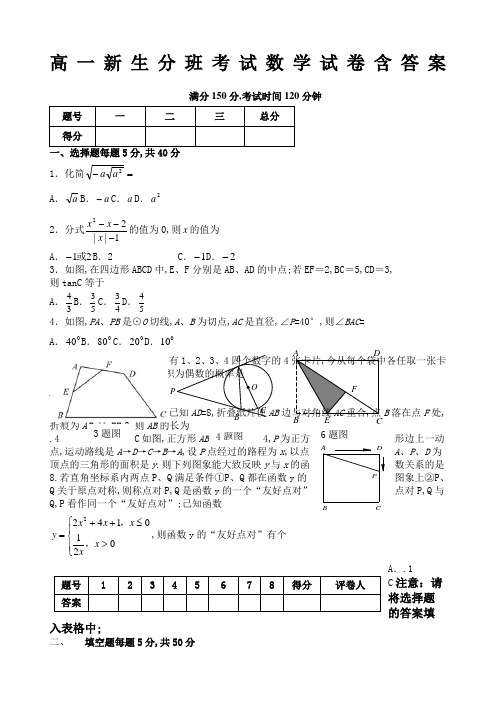
P DCB A 高一新生分班考试数学试卷含答案满分150分,考试时间120分钟题号 一二三总分得分一、选择题每题5分,共40分 1.化简=-2a a A .a B .a -C .a D .2a2.分式1||22---x x x 的值为0,则x 的值为A .21或-B .2C .1-D .2-3.如图,在四边形ABCD 中,E 、F 分别是AB 、AD 的中点;若EF =2,BC =5,CD =3, 则tanC 等于A .43B .35C .34D .454.如图,PA 、PB 是⊙O 切线,A 、B 为切点,AC 是直径,∠P =40°,则∠BAC = A .040B .080C .020D .0105.在两个袋内,分别装着写有1、2、3、4四个数字的4张卡片,今从每个袋中各任取一张卡片,则所取两卡片上数字之积为偶数的概率是A .21B .165C .167D .43 6.如图,矩形纸片ABCD 中,已知AD =8,折叠纸片使AB 边与对角线AC 重合,点B 落在点F 处,折痕为AE ,且EF =3,则AB 的长为.4 C 如图,正方形ABCD 的边长为4,P 为正方形边上一动点,运动路线是A →D →C →B →A ,设P 点经过的路程为x ,以点A 、P 、D 为顶点的三角形的面积是y .则下列图象能大致反映y 与x 的函数关系的是8.若直角坐标系内两点P 、Q 满足条件①P 、Q 都在函数y 的图象上②P 、Q 关于原点对称,则称点对P,Q 是函数y 的一个“友好点对”点对P,Q 与Q,P 看作同一个“友好点对”;已知函数⎪⎩⎪⎨⎧>≤++=02101422x xx x x y ,,,则函数y 的“友好点对”有个 A ..1 C 注意:请将选择题的答案填入表格中;二、 填空题每题5分,共50分题号 12345678得分评卷人答案4题图 O C B A P6题图 AB CDF E 3题图9.已知a 、b 是一元二次方程2210x x --=的两个实数根,则代数式()()2a b a b ab -+-+的值等于10.有一个六个面分别标上数字1、2、3、4、5、6的正方体,甲、乙、丙三位同学从不同的角度观察的结果如图所示.如果记2的对面的数字为m ,3的对面的数字为n ,则方程1x m n +=的解x 满足1+<<k x k ,k 为整数,则k =11.如图,直角梯形纸片ABCD中,AD y x ()f x 2y x =2()f x x =1x =(1)1f =||)(x x x f =c b a >>0=++c b a 0≠b )()()(c f b f a f ++111C B A ABC-2,1==BC AB 31=AA M 1BB 1MC AM +BM 图,AB 是半圆O 的直径,四边形CDMN 和DEFG 都是正方形,其中C,D,E 在AB 上,F,N 在半圆上;若AB=10,则正方形CDMN 的面积与正方形DEFG 的面积之和是 16.如图,CD 为直角ΔABC 斜边AB 上的高,BC 长度为1,DE ⊥AC;设ΔADE,ΔCDB,ΔABC 的周长分别是12,,p p p ;当12p p p+取最大值时,AB=17.如图放置的等腰直角∆ABC 薄片2,900==∠AC ACB 沿x 轴滚动,点A 的运动轨迹曲线与x 轴有交点,则在两个相邻交点间点A 的轨迹曲线与x 轴围成图形面积为___ 18.如图是一个数表,第1行依次写着从小到大的正整数,然后把每行相邻的两个数的和写在这两数正中间的下方,得到下一行,数表从上到下与从左到右均为无限项,则这个数表中的第11行第7个数为用具体数字作答1234567… … 4… … 486480…注意:请将填空题的答案填在下面的横线上; 三、解答题共60分19.本小题满分12分如图,抛物线1417452++-=x x y 与y 轴交于A 点,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C 3,0. 1求直线AB 的函数关系式;2动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动,过点P 作PN ⊥x 轴,交直线AB 于点M ,交抛物线于点N ;设点P 移动的时间为t 秒,MN 的长度为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;3设在2的条件下不考虑点P 与点O ,点C 重合的情况,连接CM ,BN ,当t 为何值时,四边形BCMN 为平行四边形 问对于所求的t 值,平行四边形BCMN 能否为菱形 请说明理由.20.本小题满分12分函数)(x f ,若自变量x 00(,)x x 为坐标的点为函数()f x 得分 评卷人11题图B CE D AF 5 23 3 2 1 2 6 1 甲 乙 丙10题图 oxy C AB题图17ABC M1A 1B 1C 题图141若函数bx ax x f ++=3)(有两个关于原点对称的不动点,求a,b 应满足的条件; 2在1的条件下,若a=2,直线1)1(:-+-=b x a y l 与y 轴、x 轴分别相交于A 、B 两点,在xb y =的图象上取一点PP 点的横坐标大于2,过P 作PQ ⊥x 轴,垂足是Q ,若四边形A BQP 的面积等于2,求P 点的坐标3定义在实数集上的函数)(x f ,对任意的x 有)()(x f x f -=-恒成立;下述命题“若函数)(x f 的图像上存在有限个不动点,则不动点有奇数个”是否正确 若正确,给予证明;若不正确,举反例说明;21.本小题满分12分已知圆O轴于A 点,交y 轴正半轴于B 点 1求BAO ∠2设圆O 与x 轴的两交点是12,F F ,1F 射出经反射到2F 经过的路程3点P 是x 轴负半轴上一点,从点P 发出的光线经l 反射后与圆O 相切.若光线从射出经反射到相切经过的路程最短,求点P 的坐标 22.本小题满分12分在金融危机中,某钢材公司积压了部分圆钢,经清理知共有2009根.现将它们堆放在一起. 1若堆放成纵断面为正三角形每一层的根数比上一层根数多1根,并使剩余的圆钢尽可能地少,则剩余了多少根圆钢2若堆成纵断面为等腰梯形每一层的根数比上一层根数多1根,且不少于七层, Ⅰ共有几种不同的方案Ⅱ已知每根圆钢的直径为10cm ,为考虑安全隐患,堆放高度不得高于4m ,则选择哪个方案,最能节省堆放场地23.本小题满分12分试求出所有正整数a 使得关于x 的二次方程22(21)4(3)0ax a x a +-+-=至少有一个整数根.数学试卷答案一、选择题每题5分,共40分三、 填空题每题5分,共50分 9.1-10.011.612.1或-113.614.115.2516.217.24+π18.12288 三、解答题共60分19.解:1易知A0,1,B3,,可得直线AB 的解析式为y =121+x ……………3分2)121(1417452+-++-=-==t t t MP NP MN s)30(415452≤≤+-=t t t ………………6分3若四边形BCMN 为平行四边形,则有MN =BC ,此时,有25415452=+-t t ,解得11=t ,22=t 所以当t =1或2时,四边形BCMN 为平行四边形.………………8分①当t =1时,23=MP ,4=NP ,故25=-=MP NP MN ,又在Rt △MPC中,2522=+=PC MP MC ,故MN =MC ,此时四边形BCMN 为菱形…………10分②当t =2时,2=MP ,29=NP ,故25=-=MP NP MN ,又在Rt △MPC中,522=+=PC MP MC ,故MN ≠MC ,此时四边形BCMN 不是菱形.…………12分 20.解:1由题得x bx ax =++3有两个互为相反数的根0x ,0x -)0(0≠x 即)(0)3(2b x a x b x -≠=--+有两个互为相反数的根0x ,0x -……1分根带入得⎪⎩⎪⎨⎧=---+=--+0))(3(0)3(020020a x b x a x b x ,两式相减得0)3(20=-x b ,3=∴b ……3分方程变为)3(02-≠=-x a x 90≠>∴a a 且…………4分 2由1得3,2==b a ,所以2:+-=x y l ,即A0,2B2,0……5分设x y 3=上任意一点)2)(3,(>t tt P ,所以)2)(0,(>t t Q ……6分 又因为2-=∆AOB AOQP S S 四边形,所以22221)32(21=⨯⨯-+t t 25=∴t ……8分)56,25(P ∴……………………9分3正确①在)()(x f x f -=-令0=x 得)0()0(f f -=所以0)0(=f所以)0,0(为函数的不动点……………………10分 ②设00(,)x x 为函数()f x 图像上的不动点,则00)(x x f = 所以000)()(x x f x f -=-=-,所以),(00x x --也为函数()f x 图像上的不动点……………………12分 21.解:1由题|OA|=4,|OB|=334,所以33tan =∠BAO ,所以030=∠BAO 2分 2如图1由对称性可知,点1F 关于l 的对称点/1F 在过点()4,0A -且倾斜角为060的直线/l 上在/21AF F ∆中,0'160=∠AO F ,3811'1=-==O F AO AF AF ,3162=AF所以/21AF F ∆为直角三角形,02'190=∠F AF ;所以光线从1F 射出经反射到2F 经过的路程为3382'12'121==+=+F F MF M F MF M F …………………………6分 2如图2由对称性可知,点P 关于l 的对称点'P 在过点()4,0A -且倾斜角为060的直线/l 上Q P MQ M P MQ PM ''=+=+,所以路程最短即为/l 上点/P 到切点Q 的切线长最短; 连接',OP OQ ,在'OQP Rt ∆中,只要'OP 最短,由几何知识可知,/P 应为过原点O 且与/l 垂直的直线与/l 的交点,这一点又与点P 关于l 对称,∴260cos 0'===AO AP AP ,故点P 的坐标为()2,0-……………12分22.解:1设纵断面层数为n ,则321++即20092)1(≤+n n ,040182≤-+n n ,当62=n 时,此时剩余的圆钢为562)162(622009=+-2当纵断面为等腰梯形时,设共堆放n 层)1(.....)2()1(=-+++++++n x x x x 即4177220092)12(⨯⨯⨯=⨯=-+n x n ,……………………6分因1-n 与n 的奇偶性不同,所以12-+n x 与n 的奇偶性也不同,且12-+<n x n ,从而由上述等式得:⎩⎨⎧=-+=574127n x n 或⎩⎨⎧=-+=2871214n x n 或⎩⎨⎧=-+=981241n x n 或⎩⎨⎧=-+=821249n x n ,所以共有4种方案可供选择;-----------------------------8分3因层数越多,最下层堆放得越少,占用面积也越少,所以由2可知:若41=n ,则29=x ,说明最上层有29根圆钢,最下层有69根圆钢,两腰之长为400cm,上下底之长为280cm 和680cm,从而梯形之高为3200cm, 而400103200<+,所以符合条件;………………10分若49=n ,则17=x ,说明最上层有17根圆钢,最下层有65根圆钢,两腰之长为480cm,上下底之长为160cm 和640cm,从而梯形之高为3240cm, 显然大于4m,不合条件,舍去;综上所述,选择堆放41层这个方案,最能节省堆放场地………………12分 23.解:原方程可化为122)2(2+=+x a x ,易知2-≠x ,此时2)2(122++=x x a ……2分 因为a 是正整数,即1)2(1222≥++x x 为正整数;又0)2(2>+x ,则122)2(2+≤+x x 即0822≤-+x x ,解得24≤≤-x ;因为2-≠x 且x 是整数,故x 只能取-4,-3,-1,0,1,2,…………………………6分依次带入a 的表达式得⎩⎨⎧=-=14a x ⎩⎨⎧=-=63a x ⎩⎨⎧=-=101a x ⎩⎨⎧==3a x 从而满足题意的正整数a 的值有4个,分别为1,3,6,10…………………………12分。
2024年秋季高一入学分班考试数学试题与答案

(考试时间:120分钟 试卷满分:1502024年秋季高一入学分班考试数学试题分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.若集合{}1,2,3A =,{}2,3,4B =,则A B = ( ) A .{}1,2,3,4 B .{}1,4C .{}2,3D .∅22x =−,则x 的值可以是( )A .2−B .1−C .1D .23.“2x =”是“24x =”的( ) A .充分必要条件 B .充分不必要条件 C .必要不充分条件D .既不充分也不必要条件4.已知二次函数2y ax bx c ++的图象的顶点坐标为(2,1)−,与y 轴的交点为(0,11),则( )A .3,12,11a b c ==−=B .3,12,11a b c === C .3,6,11a b c ==−= D .1,4,11a b c ==−= 5.把2212x xy y −++分解因式的结果是( ) A .()()()112x x y x y +−++ B .()()11x y x y ++−− C .()()11x y x y −+−−D .()()11x y x y +++−6.已知命题p :1x ∃>,210x ,则p ¬是( ) A .1x ∀>,210x B .1x ∀>,210x +≤ C .1x ∃>,210x +≤ D .1x ∃≤,210x +≤7.函数y =) A .[]3,3−B .()3,1(1,3)−∪C .()3,3−D .()(),33,−∞−+∞8.若实数a b ,且a ,b 满足2850a a −+=,2850b b −+=,则代数式1111b a a b −−+−−的值为( ) A .-20B .2C .2或-20D .2或20二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分. 9.下列坐标系中的曲线或直线,能作为函数()y f x =的图象的是( )A .B .C .D .10.下列命题中是全称量词命题并且是真命题的是( ) A .x ∀∈R ,2210x x ++≥ B .x ∃∈N ,2x 为偶数 C .所有菱形的四条边都相等 D .π是无理数11.下列结论中,错误的结论有( )A .()43y x x =−取得最大值时x 的值为1 B .若1x <−,则11x x ++的最大值为-2C .函数()f x =的最小值为2D .若0a >,0b >,且2a b +=,那么12a b+的最小值为3+三、填空题:本题共3小题,每小题5分,共15分.12.若多项式3x x m ++含有因式22x x −+,则m 的值是 .13.不等式20ax bx c ++>的解集是(1,2),则不等式20cx bx a ++>的解集是(用集合表示) . 14.对于每个x ,函数y 是16y x =−+,22246y x x =−++这两个函数的较小值,则函数y 的最大值是 .四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤. 15.(13分)解下列不等式:(1)2320x x −+−≥; (2)134x x −+−≥; (3)11.21x x −≤+16.(15分)设全集R U =,集合{}|15Ax x =≤≤,集合{|122}B x a x a =−−≤≤−.(1)若“x A ∈”是“x B ∈”的充分不必要条件,求实数a 的取值范围; (2)若命题“x B ∀∈,则x A ∈”是真命题,求实数a 的取值范围.17.(15分)已知集合{}{}210,20A x ax B x x x b =−==−+=.(1)若{}3A B ∩=,求实数,a b 的值及集合,A B ; (2)若A ≠∅且A B B ∪=,求实数a 和b 满足的关系式.18.(17分)已知22y x ax a =−+.(1)设0a >,若关于x 的不等式23y a a <+的解集为{},12|A Bx x =−≤≤,且x A ∈的充分不必要条件是x B ∈,求a 的取值范围;(2)方程0y =有两个实数根12,x x , ①若12,x x 均大于0,试求a 的取值范围;②若22121263x x x x +=−,求实数a 的值.19.(17分)我国是用水相对贫乏的国家,据统计,我国的人均水资源仅为世界平均水平的14.因此我国在制定用水政策时明确提出“优先满足城乡居民生活用水”,同时为了更好地提倡节约用水,对水资源使用进行合理配置,对居民自来水用水收费采用阶梯收费.某市经物价部门批准,对居民生活用水收费如下:第一档,每户每月用水不超过20立方米,则水价为每立方米3元;第二档,若每户每月用水超过20立方米,但不超过30立方米,则超过部分水价为每立方米4元;第三档,若每户每月用水超过30立方米,则超过部分水价为每立方米7元,同时征收其全月水费20%的用水调节税.设某户某月用水x立方米,水费为y元.(1)试求y关于x的函数;(2)若该用户当月水费为80元,试求该年度的用水量;(3)设某月甲用户用水a立方米,乙用户用水b立方米,若,a b之间符合函数关系:247530=−+−.则当b a a两户用水合计达到最大时,一共需要支付水费多少元?一、单项选择题:本题共8小题,每小题5分,共402024年秋季高一入学分班考试数学答案分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1 2 3 4 5 6 7 8 CDBADBCA二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9 10 11 BDACABCD三、填空题:本题共3小题,每小题5分,共15分. 12.2 13.1|12x x <<6四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤. 16.(13分)【解析】(1)2320x x −+−≥可化为2320,(1)(2)0x x x x −+≤∴−−≤, 所以解为1 2.x ≤≤(3分)(2)当1x <时,不等式可化为134x x −+−+≥,此时不等式解为0x ≤; 当13x ≤≤时,不等式可化为134x x −−+≥,此时不等式无解; 当3x >时,不等式可化为134x x −+−≥,此时不等式解为4x ≥; 综上:原不等式的解为0x ≤或4x ≥.(9分) (3)原不等式可化为211021x x x +−+≥+,(11分)与()()2120210x x x ++≥+≠同解, 所以不等式的解为:2x ≤−或12x >−.(13分)16.(15分)【解析】(1)由“x A ∈”是“x B ∈”的充分不必要条件,得A B ,(2分)又{}|15Ax x =≤≤,{|122}B x a x a =−−≤≤−,因此12125a a −−< −≥ 或12125a a −−≤ −> ,解得7a ≥,所以实数a 的取值范围为7a ≥.(7分)(2)命题“x B ∀∈,则x A ∈”是真命题,则有B A ⊆,(9分) 当B =∅时,122a a −−>−,解得13a <,符合题意,因此13a <;(11分)当B ≠∅时,而{}|15{|122}A x x B x a x a =≤≤=−−≤≤−,, 则11225a a ≤−−≤−≤,无解,(14分) 所以实数a 的取值范围13a <.(15分)17.(15分)【解析】(1)若{}3∩=A B , 则{}{}2310,320x ax x x x b ∈−=∈−+=,(2分) 所以310,960a b −=−+=,解得1,33a b ==−,(4分) 所以{}{}{}{}2110103,2301,33A x ax x x B x xx =−==−===−−==−,综上:1,33a b ==−,{}{}3,1,3A B ==−;(7分)(2)若A ≠∅,则0a ≠,此时{}110A x ax a=−==,(9分) 又A B B ∪=,所以A B ⊆, 即{}2120x x x b a ∈−+=,(12分)所以2120440b a ab −+= ∆=−≥ , 所以实数a 和b 满足的关系式为212b a a=−+.(15分)18.(17分)【解析】(1)由23y a a <+,得2223x ax a a a −+<+, 即22230x ax a −−<,即()()30x a x a −+<, 又0a >,∴3a x a −<<,即{}|3A x a x a =−<<,(3分)∵x A ∈的充分不必要条件是x B ∈,∴B 是A 的真子集,则0132a a a >−<− > ,解得0123a a a> > >,则1a >, 即实数a 的取值范围是1a >.(6分) (2)方程为220y x ax a =−+=, ①若12,x x 均大于0则满足21212440200a a x x a x x a ∆=−≥ +=> => ,解得10a a a a ≥≤> > 或, 故1a ≥,即a 的取值范围为1a ≥.(10分)②若22121263x x x x +=−,则()2121212263x x x x x x +−=−, 则()21212830x x x x +−+=,即24830a a −+=,(13分) 即()()21230a a −−=,解得12a =或32a =, 由0∆≥,得1a ≥或0a ≤. 所以32a =,即实数a 的值是32.(17分)19.(17分)【解析】(1)因为某户该月用水x 立方米, 按收费标准可知, 当020x <≤时,3y x =;当2030x <≤时,()203420420y x x ×+−−;当30x >时,[2034(3020)7(30)] 1.28.4132y x x =×+×−+−×=−.(5分)所以3,020420,20308.4132,30x x y x x x x <≤=−<≤ −>(6分)(2)由题可得,当该用户水费为80元时,处于第二档,所以42080x −=, 解得25x =. 所以该月的用水量为25立方米.(10分) (3)因为247530b a a =−+−,所以()2248530244646a b a a a +=−+−=−−+≤.(13分)当24a =时,()46max a b +=,此时22b =.(15分)所以此时两户一共需要支付的水费是4242042220144y =×−+×−=元.(17分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一实验班分班考试数学试题
第Ⅰ卷(90分)
一、选择题(共10小题,每小题6分,满分60分.每小题均给出了代号为A ,B ,C ,D 的四个选项,其中只有一个是正确的.请将正确选项的代号填入Ⅱ卷的答题卡内.) 1. 5个相异自然数的平均数为12,中位数为17,这5个自然数中最大一个的可能值的最
大值是
(A )21 (B )22 (C )23 (D )24 2. 如图,长方形ABCD 恰好可分成7个形状大小相同的小长
方形,如果小长方形的面积是3,则长方形ABCD 的周长是 (A )17 (B )18 (C )19 (D )317 3.化简2
2y x x
8)x y x 4y x x 2(
-÷--+得 3333()
()()()
4
4
4
4
x y x y x y x y
A B C D ++++-
-
4.若a ,b ,c 是非零实数,且a+b+c=O ,那么
|
|||||||abc abc c c b b a a +++的所有可能的值为 (A )0 (B )1或-1 (C )2或-2 (D )0或-2 5.如图,已知AB=10,P 是线段AB 上任意一点,在AB 的同侧分别以AP 和PB 为边作等边△APC 和等边△BPD.则CD 长度的最小值是
(A )4 (B )5 (C )6 (D )5(5 —1) (第5题图) 6.如果两圆的公切线只有两条,那么这两个圆的位置关系是
(A) 相交 (B) 外离
(C) 内切
(D) 外切
7.在全体实数中引进一种新的运算*,其规定如下:
(1)对任意实数a 、b ,有a*b=(a+1)·(b -1);(2)对任意实数a ,有a *2
==a*a 当x=2时,[3*(x *2
)]-2*x+1的值为
(A) 34 (B) 16 (C) 12 (D)6 8.若不等式|x+l|+|x-3|≤a 有解,则a 的取值范围是
A
D
B
C
(第2题)
(A) 0<a≤4 (B) a≥4 (C) O<a≤2 (D) a≥2
9.关于x 的不等式组⎪⎪⎩⎪⎪⎨
⎧+<+->+a x x x x 2
35
3
3
2只有5个整数解.则a 的取值范围是 (A) -5<a<-92 (B) -5≤a<-92 (C) -5<a≤-92 (D) -5≤a ≤-92
10.观察右图,根据规律,则从 2004到2006,箭头方向依次为
(A) ↓→ (B) →↑
(C) ↑→
(D) →↓
二、填空题(共5小题,每小题6分,满分30分。
请将正确答案填入Ⅱ卷的答题表内,不要答在横线上)
11. 如果一个两位数5X 与三位数3YZ 的积是29400,那么X+Y+Z 的值是 。
12.如图,AB 为半⊙O 的直径,C 为半圆弧的三等分点, 过B ,C 两点的半⊙O 的切线交于点P ,若AB 的长是2a , 则PA 的长是 .
13.从等边三角形内一点向三边作垂线,已知这三条垂线 的长分别为1,3,5.则这个等边三角形的面积是 .
14.设x 1,x 2是方程x 2
-2(k+1)x+k 2
+2=0的两个实数根,且(x 1+1)(x 2+1)=8,则k 的值是 。
15.右下图是由9个等边三角形拼成的图形,
已知中间最小的等边三角形的边长是1,求这个六边形的周长是 。
3 → 4
7 → 8
11 → …
↓ ↑ ↓ ↑ ↓ ↑ … 1 → 2
5 → 6
9 → 10 …
A
B O
C (第12题)
高一实验班分班考试
数学试题
选择题、填空题答题表
题
型 选择题(60分)
填空题(30分)
题
号 1 2
3
4
5
6
7
8
9
10 11 12 13 14 15
答
案
得分栏
题型 选择题 填空题
解答题 总分
16
17 18 19 20 得分
第Ⅱ卷(60分)
三、解答题(共5个小题,满分60分。
解答每一题应写出必要的演算步骤或证明过程。
) 16.求值(本题满分为12分)
1
99.89.255 2.5
15514()1611688634
⨯+÷---+⨯÷
17.如图,反比例函数y=-8
x
与一次函数y=-x+2的图象交于A 、B 两点.
(1)求 A 、B 两点的坐标;(本小题满分为6分) (2)求△AOB 的面积.(本小题满分为6分)
18. 如图,两圆同心,大圆的弦AD 交小圆于B 、C 两点,AE 切小圆于点E ,连结CE ,直线BE 交大圆于P 、Q 两点,已知BE =AE =b ,AB =a.
(1) 求证CD 、CE 的长是方程ax a b x ab 2
2
2
2
0-++=()的两个根;(本小题满分为6分) (2)求PB 的长。
(本小题满分为6分)
Q
19.关于x 的方程kx 2
-(k-1)x+l=0有有理根,求整数k 的值.(本题满分为12分) 20.已知0<a <1,且满足183029302301=⎥⎦⎤⎢⎣
⎡+++⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡
+
a a a ,求[]a 10的值. (其中[]x 表示不超过x 的最大整数) (本题满分为12分)
高一实验班分班考试
考试数学试题(答案)
选择题、填空题答题表
案
1
99.89.255 2.5
15514()16
11688634
9.25(9.80.2) 2.515102()16 (42716161634)
92.5 2.5716 (89164)
733............⨯+÷---+⨯÷+-=--+⨯÷-=-⨯-=分
分
=40.........................................................12分
17.解:⑴解方程组82
y x y x ⎧
=-
⎪⎨⎪=-+⎩ 得121242;24x x y y ==-⎧⎧⎨⎨=-=⎩⎩ 所以A 、B 两点的坐标分别为A (-2,4)B(4,-2)………6分
(2)因为直线y=-x+2与y 轴交点D 坐标是(0, 2), 所以1
1222,24422
AOD BOD S S ∆∆=⨯⨯==⨯⨯=
所以246AOB S ∆=+=………………………………………12分
18.解: (1)依题意,可证⊿ACE ∽⊿AEB 得CE =AC 。
由切割线定理,得2
b a AC =⋅,即CE
AC b a
==
2
又CD =AB =a
∴+=+=+⋅=⋅=⎧⎨⎪⎪⎩
⎪⎪CD CE a b a a b a CD CE a b a b 2222
2………………………………………………3分
∴CD CE 、的长是方程ax
a b x ab 2
2220-++=()的两个根…………………6分
(2)由相交弦定理,得PB BQ AB BD ⋅=⋅
即PB PB b a b a
()+=⋅
2
………………………………………………………………9分
解得
PB b =-
+51
2
(不合题意,舍去) ∴=
-PB b 51
2
…………………………………………………………………12分 19.解:
(1) 当k=0时,x=-1,方程有有理根。
(3)
(2) 当k ≠0时,因为方程有有理根,而k 是整数,则△=(k-1)2-4k=k 2
-6k+1必为完全平
方数,即存在非负整数m ,使k 2-6k+1=m 2
,……………………………………………………….6分
配方,得(k-3)2-m 2
=8即(k-3+m)(k-3-m)=8 由于k-3+m, k-3-m 是奇偶性相同的整数,其积为8,所以它们均是偶数。
又k-3+m ≥ k-3-m ,从而有
34,32,323 4.
k m k m k m k m -+=-+=-⎧⎧⎨
⎨--=--=-⎩⎩ 或 …………………………………..9分
解得=6或=0(舍
去)……………………………………………………………………………………11分
综合(1)、(2)知方程kx 2
-(k-1)x+l=0有有理根时,k=6或k=0……………………………….12分
20.解:因为0<230
29302301<+<<+<+a a a ,
所以⎥⎦
⎤⎢⎣⎡+301a ,⎥⎦⎤⎢⎣⎡+302a ,…,⎥⎦⎤⎢⎣⎡+3029a 等于0或1……………3分 由题设知,其中有18个等于1,所以
⎥⎦⎤⎢⎣⎡
+==⎥⎦⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+3011302301a a a =0,………………….6分 ⎥⎦
⎤⎢⎣⎡+==⎥⎦
⎤⎢⎣⎡+=⎥⎦⎤⎢⎣⎡+302930133012a a a =1,…………………..9分 所以 130
110<+<a ,1≤3012+a <2. 故18≤30a <19,于是6≤10 a <3
19,所以[]a 10=6.…………………………..12分。
