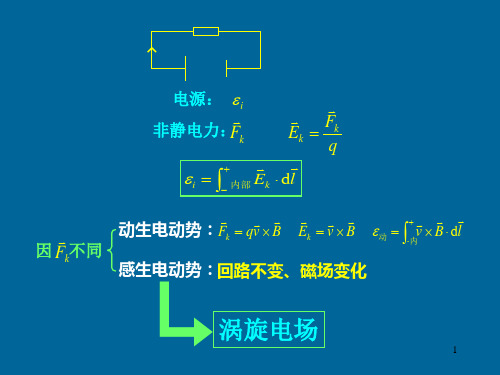
第五节感生电动势涡旋电场
感生电动势
E涡
B t
5
9-3 感生电动势 B 线圈在磁场中不动 B
B 若 0， t 则Er 沿顺时针方向。
方 向 说 明
Er 的方向就是感生电动势 的方向。 一般地，感生电场或感生电动势的方 向直接用楞次定律判断。
B 若 0， t 则Er 沿逆时针方向。
E感 只有以螺线管轴线为中心的圆周切向分量
B r R L
12
9-3
感生电动势
感生电场线是在垂直于轴线平面内， 以轴线为中心的一系列同心圆。 作如图环路
B r d d 2 E dl ( B S ) ( B r ) l 涡 R L dt dt
Байду номын сангаас
rR
9-3
感生电动势
dB 2 R E d l 涡 L dt dB 2 E涡 2r R dt
B
S S
L
R
r
B t
R 2 dB E涡 2r d t
方向：逆时针方向
15
E涡
9-3
感生电动势
E涡
R 2 dB 2r d t
rR rR
6
B ε E感 dl dS L s t
9-3
感生电动势
上式表明感生电场的环流不等于0，说 明感生电场是有旋场。 感生电场的性质和稳恒电流的磁场的 性质十分相似。 如果说，电流是磁场的涡旋中心，那么 变化的磁场就是感生电场的涡旋中心。 感生电场的电力线类似于磁力线，是无 头无尾的闭合曲线，呈涡旋状，所以称之为 涡旋电场。 感生电场也是无源场。
d l E涡 dl dt
第二十六讲：§感生电动势和感生电场
第二十六讲： §7.3感生电动势和感生电场一、感生电动势 涡旋电场1、感生电动势：由于dtm φd 所产生的感应电动势。
2、感生电场（涡旋电场）：变化的磁场所激发的电场为感生电场。
其特点：①感生电场是非保守场；②电场线是闭合的。
3、感生电场与静电场的比较①相同点：都是电场（物理场，物质性，具有能量，即对电荷有电场力的作用）。
②不同点：⑴激发方式不同，感生电场是由变化的磁场激发的；静电场是由相对观察者静止的带电体激发的。
⑵感生电场电场线是闭合的，静电场电场线是非闭合的。
⑶感生电场是非保守场，静电场是保守场。
因为静电力是保守力，故而静电场力沿闭合路径的积分等于零， 由0W =⋅=⋅=⎰⎰ d q d 静静 ⑴看出， ∵ 0≠q ∴ 0=⋅⇒⎰d 静 静电场为保守场。
由0≠-=⋅=⎰dt d d m i φε 涡看出， 当 0dtd ≠m φ为变化的磁场， 则 0≠⋅⇒⎰ d 涡 也可推出0≠⋅=⇒⎰ d q W 涡⑵比较⑴、⑵式可推出感生电场是非保守场。
4、感生电场与磁场的关系式d m ⋅=⎰φ ； d dtd dt d m ⋅=⎰φ ; d t d S i ⋅∂∂-=⋅=⎰⎰ 涡ε ☆ 5、与涡E 、()i i I ε方向的确定注意：与绕行方向满足右手螺旋法则 当0d dt B 时，0 dS dtdB S i ⎰-=⇒ε i ε与绕行方向相反； 当0d dt B 时，0 dS dtdB S i ⎰-=⇒ε i ε与绕行方向相同。
P264例题7-5已知：如图所示，R,=dt B d 正常数 求：⑴1涡；⑵2E 涡解： ⑴∵d td S i ⋅∂∂-=⋅=⎰⎰ 涡ε R r 21r 2r t B E ππ∂∂-=⋅⇒涡 tB E ∂∂=⇒2r -1涡 R r 22r 2R t B E ππ∂∂-=⋅⇒涡 tB r E ∂∂=⇒2R -22涡 涡电场线绕行方向相反，如上图所示。
P264例题7-6 已知：0d dtB ，L ab = ，h 求：ab ε解：解法一：利用法拉第电磁感应定律S d t dt d S m ⋅∂∂-=-=⎰B i φεtB hL S t B t B i ∂∂=⋅∂∂=⋅∂∂=⎰2ε∵Oa 和Ob 沿径向，而涡E 与径向垂直。
电磁学13-涡旋电场-自感
• 互感系数可正可负，取决于两线圈之间的位置和 电流环绕的正方向
– 一般的，对每个载流线圈，其磁通的正方向规定为和 线圈中电流的正方向成右手螺旋关系。若来自其他线 圈的磁场的正方向与此正向相符，则M>0;反之，M<0
图中标示的 是正方向
Ψ 1
Ψ2
Ψ 1Βιβλιοθήκη Ψ2i1 线圈1 i2 线圈2 M >0
i1 线圈1
电感的充放电过程(1)
• 考虑电阻和电感串联的电路，如图
(1)开关拨向1，开始充电过程（电能转化成线圈的磁场能）
ε
2 1 R L
u L (t ) + u R (t ) = ε iR (t ) = iL (t )
微分方程的解 考虑初条件
ε
R
t
iL (t ) =
di (t ) + R ⋅ i (t ) = ε L dt R − t ε L
线圈2 i2
M <0
互感器的电路方程
• 互感器：用于电路中的互感元件。
– 理想互感器模型：只有自感和互感效应而没 有电阻、电容效应的互感器。只考虑互感器 中线圈之间的互感，而不考虑电路其他部分 对互感器的电磁感应。
• 在电路中，互感器是四端元件，其电路 方程为
i1
u1
L1
L2
i2
u2
di2 (t ) di1 (t ) +M u1 (t ) = L1 dt dt di1 (t ) di2 (t ) +M u 2 (t ) = L2 dt dt
ε
R
ε
R
e
−
t
τ
u L (t ) = −ε e
u L (t )
11-2动生电动势和感生电动势 涡旋电场
L
ω+ a
+ + b + + dl + +
v
l+ + +
+ + + +
+ + + +
ε ab < 0 ，说明动生电动势的方向由 指 说明动生电动势的方向由b指
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
a、b之间的电压就等于εab。 、 之间的电压就等于 例11-4 法拉第曾利用圆盘发 电机来演示感应电动势的产 生，金属圆盘在磁场中转动 时能在连接电流计的回路中 产生感应电流。如图所示， 产生感应电流。如图所示， 设圆盘半径R=0.20m，转速为 设圆盘半径 ， 50转/秒，匀强磁场的磁感应 转秒 强度B=0.70T，求盘心与盘边 强度 ， 缘之间的电势差U。 缘之间的电势差 。
设杆长为 l
∫
l
0
v B d l = v Bl
dε i = (v × B) ⋅ dl
第十一章 电磁场的统一理论
1111-2 动生电动势和感生电动势 涡旋电场
二
动生电动势的计算 动生电动势的产生不要求导体必须是回路， 动生电动势的产生不要求导体必须是回路，一段 电源。 在磁场中运动的导体就像一个电动势为εi的电源。如 果是闭合回路，则会在回路中产生感应电流。 果是闭合回路，则会在回路中产生感应电流。 1) 利用电磁感应定律计算 dΦ dΨ εi = − 或 εi = − dt dt 如果运动导体不是闭合的， 如果运动导体不是闭合的，可以设想一个包含运动 导体的闭合回路，添加的回路的部分最好是静止的。 导体的闭合回路，添加的回路的部分最好是静止的。 2) 利用动生电动势计算公式 电动势的方向是 v× B 的 方向
感生电动势 涡旋电场
（2）. 同一条 E线v 上，E大v 小处处相同，方向沿切线方向（左旋）
（3）.
Ev存在于整个空间（管内、外）
6
2.
Ev的分布：
L
Ev
dl
d m dt
（1）. r < R 取电力线为回路，
I
R
L Ev
正 方向如图 dl Ev 2 r
d dt
(B
r2)
Ev
L
L
Ev
r 2
dB dt
与L反向
2. 涡旋电场的电力线成闭合线， B和
左旋关系
t
成Ev
B t
Ev
左旋关系
电场有2种： 电荷激发的电场静电场
E
F
E线有源，保守场
q
变化磁场激发的电场涡旋电场
Ev
Fv q
Ev线无源，非保守场
3
三. Ev的性质
客观存在的物质，具有能量、动量，满足叠加原理，对
场中的带电粒子有力的作用。
高斯定理：
b
3. 感应电动势分成动生、感生两种，这种分法 在特殊情况下只有相对意义，如：
但在普遍情况下，不可能通过参照系变换使之互换 N 1v2
P459 变压器铁芯（涡流） 由于变化磁场激起感生电场，则在导体内产生感应电流。 这些感应电流的流线呈闭合的涡旋状，故称涡电流(涡流)
交变电流
交变电流
整块铁芯
彼此绝缘的薄片
由于大块金属电阻很小，形成涡流很大，金属易 被加热到很高温度。涡流的热效应常被用于真空提纯 金属和半导体材料，以及冶炼难溶金属等；而在电机 和变压器等通有交流电的电器设备中，为减少热能损 耗，通常采用叠片式铁芯来减少涡流。
P459 阻尼摆，P461 电子感应加速器——自己选看
人教版物理选修3-2 第4章第5节 电磁感应现象的两类情况
高中物理选修3-2课件
则金属棒 ab 接入回路的 bc 部分切割磁感线产生的 感应电动势为： E＝Bv0 bc ＝Bv20ttan30° 在回路 bOc 中，回路总感应电动势具体由导体 bc 部分产生，因此，回路内总的感应电动势为：E 总 ＝E＝ 3Bv20t/3.
高中物理选修3-2课件
核心要点突破
一、感生电动势 1．产生机理 如图4－5－1所示，当磁场变化时，产生的感生电 场的电场线是与磁场方向垂直的曲线．如果空间存 在闭合导体，导体中的自由电荷就会在电场力的作 用下定向移动，而产生感应电流，或者说导体中产 生了感应电动势．
高中物理选修3-2课件
图4－5－1
高中物理选修3-2课件
【答案】 E＝ 33Bv20t
【规律总结】 由 E＝Blv 计算导体切割磁感线产 生的动生电动势问题，若 l 不变，当 v 是瞬时速度 时，可求 E 的瞬时值，当 v 是平均速度时，可求平 均感应电动势．若 l 变化，求瞬时值时，需用该时 刻的 l 及 v 代入；而求平均值通常由 E＝nΔΔΦt 求得．
图4－5－2
高中物理选修3-2课件
2．特点 (1)感生电场是一种涡旋电场，电场线是闭合的. (2)感生电场的产生跟空间中是否存在闭合电路无 关. 3．方向判定 感生电场的方向根据闭合电路(或假想的闭合电路) 中感应电流的方向确定，即利用楞次定律判断.
高中物理选修3-2课件
即时应用 (即时突破，小试牛刀) 1．某空间出现了如图4－5－3所示的磁场，当磁感 应强度变化时，在垂直于磁场的方向上会产生感生 电场，有关磁感应强度的变化与感生电场的方向关 系描述正确的是( )
【思路点拨】 回路中原磁场方向向下，且磁通 量增加，由楞次定律可以判知，感应电流的磁场 方向向上，根据安培定则可以判知，ab中的感应 电流的方向是a→b，由左手定则可知，ab所受安 培力的方向水平向左，从而向上拉起重物．
12.3 感生电动势涡旋电场
M
o
N
B B MN oMN s ( s s扇） t t B 1 R 2 1 2 ( .R R ( ) R 2 ) t 2 2 12 B 3 2 2 ( R R ) t 4 12
12
例6）AB、BC、CA棒组成外切三角形，求AB棒上 的感生电动势。 A 1 1 B AB ABC s 3 3 t 1 B 2 R o 3 t C B
讨论
9
d L dB L 2 i R dt 2 dt 2
2
例3）在螺线管截面上放置金属棒oA，则oA棒上 产生的感应电动势。
i
o
E感
E感 dl E感 dl 0 oA 0
A
10
例5）求在螺线管中的横载面内，放置有一直金 属棒MN，求MN＝2R上产生的感生电动势？ 1 1 B 已知： , , 3 6 t 求： iMN o d m 利用 i感 dt N M 作三角形回路）OMN 三角形回路中的感应电动势即导线MN上的感 生电动势，因在OM，ON上产生的电势为零。 11
R dB 2 dt
dB 2 E感 2r R dt R2 dB 1 所以 E感 2r dt r
o
R
r
7
E感分布曲线
例2：圆形均匀分布的磁场半径为 R，磁场随时间均匀
dB k ，在磁场中放置一长为 L 的导体棒，求 dt 棒中的感生电动势。 解： E感作用在导体棒上，使导体棒 R
第五节法拉第电磁感应定律的应用
2、导体棒一直运动下去，自 由电荷是否也会沿着导体棒 一直运动下去?为什么?
分析与解答: 2、自由电荷不会一直运动下去. 因为C、D两端聚集电荷越来越 多，在CD棒间产生的电场越来 越强,当电场力等于洛伦兹力时, 自由电荷不再定向运动.
X X
X X
C X
X
F洛 X X X LX X X V F
X X X
感生电动势 闭合回路的任何部分都不 动，空间磁场变化导致回 路中磁通量变化
由于S变化引起 回路中变化
非静电力是洛仑兹力的 分力，由洛仑兹力对运 动电荷作用而产生电动 势 楞次定律或右手定则
由于B变化引起 回路中变化
变化磁场在它周围空间激发 感生电场，非静电力是感生 电场力，由感生电场力对电 荷做功而产生电动势 楞次定律
感生电场
磁场变强
一、感生电场与感生电动势 1、感生电场
(1)定义:变化的磁场在周围空间激发的 电场叫感生电场(涡旋电场). (2)方向:就是感生电流的方向. 用楞次定律判断. (3) 电场线:是闭合的曲线.
磁场变强
一、感生电场与感生电动势 2、感生电动势：
由感生电场产生的感应电动势.
感生电动势所对应的非静电力是 感生电场对自由电荷的作用.
感生电场是产生 感生电动势的原因.
3、应用实例---电子感应加速器
电子感应加速器是用感生电场来加速电子 的一种设备。 铁芯
线圈 电子束 环形真空 管 道
它的柱形电磁铁在两极间产生磁场。在磁 场中安置一个环形真空管道作为电子运行的轨 道。当磁场发生变化时，就会沿管道方向产生 感生电场。射入其中的电子就受到感生电场的 持续作用而不断加速。
F洛 X X X LX X X V F
X X X
大学物理 感应电场
r B E感 2 t
方向：逆时针方向
讨论
负号表示 E感与 B t 反号， 由此可据 B t 的正
r
B t
B
负 来确定 E感的方向。
R L
（1）
B
，则
B
t 0
E感
0
E感与 L 积分方向切向同向。
（2）
B
，则
B
t 0 E感
0
E感
与
L
积分方向切向相反。
rR
B
L E感 • dl S t • dS
库仑电场：由电荷按库仑定律 激发的电场
感生电场：由变化磁场激发的电场
感生电动势 非静电力 感生电场力 （作用于单位电荷上的感生电场力的功就是感生电动势）
一般空间中既可存在电荷又可存在变化的磁场。 所以空间中既存在库仑电场又存在感生电场。
E E库 E感
二、感生电动势
由电动势的定义：
i E感 • dl
L
i
由法拉第电磁感应定律：
dm dt
L
dm dt
dt
dm
感
•
dl
线积分的方向应与的 m
正方向成右手螺旋关系
d dt
(
S
•
dS )
S
B t
•
dS
B
i L E感 • dl S t • dS
B
L E感 • dl S t • dS
讨论
1. 此式反映变化磁场和感生电场的相互关系，
即感生电场是由变化的磁场产生的。
d E感
htg,
•
dl
dl
r B
h2sect
dl cos
d,
大学物理电磁学部分19感生电动势涡旋电场解读
EK dl ，
在限定导体回路不运动的情况及回路面积不变的情况下， 有： B d d i E感 dl m B dS dS S t dt s dt
E感 •感生电场的电力线类似于磁力线，是无头无尾的闭合 曲线，呈涡旋状，所以 称之为涡旋电场。 •涡旋电场永远和磁感应强度矢量的变化连在一起。
L
E静 dl 0
E E静 E感
B 在稳恒条件下，一切物理量不随时间变化， 0 t 静电场的环路定理 E dl 0
L
5
dB 增加 k ，求空间的感生电场的分布情况。 dt 解： 由于磁场均匀增加，圆形磁场区 R 域内、外 E感 线为一系列同心圆； 1. r < R 区域： 作半径为 r 的环形路径; o r 设涡旋电场的绕向也为逆时针方向。 B dB B E感 dl S t dS S dt dS
B 由此得到方程： E感 dl d S S
t
dB 0 dt
3
感生电场与静电场的区别 感生电场 E感 静电场 E
起源 由静止电荷激发 由变化的磁场激发
电 力 线 形 状
电 场 的 性 质
电力线为非闭合曲线
电力线为闭合曲线 dB 0 E感 dt
E感
R dB 2 dt
dB 2 E 感 2r R dt R 2 dB 1 所以 E 感 2r dt r
o
R
r
7
E感分布曲线
例2：圆形均匀分布的磁场半径为 R，磁场随时间均匀
dB k ，在磁场中放置一长为 L 的导体棒，求 dt 棒中的感生电动势。 解： R E感作用在导体棒上，使导体
5、感生电动势和动生电动势解析
留意: (1)将电压表并联在待测电路两端.
(2)量程应大于小灯泡两端电压的估量值. (3)红表笔接高电势,黑表笔接低电势.
(4)读数时先看量程再看小格,要正视表针.
(二)使用
2.测量电流 怎样用多用电表测量通过 小灯泡的电流?测量中应 步留骤意:什((12么))选测?档量;;
a
解析：以a表示金属杆运动的加速度，在t时刻，金属杆 与初始位置的距离L＝at2/2，此时杆的速度v＝at 这时，杆与导轨构成的回路的面积S=Ll 回路中的感应电动势E＝SΔB/Δt＋Blv
B k t B B (t t) B tk
t t
回路的总电阻 R＝2Lr0 回路中的感应电流 I=E/R
F 3k 2l 2 t
作用于杆的安培力F＝BIl 代入数据为F＝1.44×10-3N
2r0
学 问 回
1.如何把电流表改装成电压表?
Ig
Rg
分压电阻 R
IR R
分流电阻
忆
Ug
UR
I
Ig Rg
U
Ug
Ig
V
I
A
U
Ug
2.如何把电流表改装成量程较大的电流表?
能否把电流表改装成直接测量电阻的
欧姆表?
例 题
r，其余局部电阻不计．开头磁感强度为B0．
〔1〕假设从t=0时刻起，磁感强度均匀增加，每秒增量为
k，同时棒保持静止．求棒中的感应电流．在图上标出感
应电流的方向；
〔2〕在上述〔1〕状况中，始终保持棒静止，当t=t1末时
需加的垂直于棒的水平拉力为多大？ 〔3〕假设t=0时刻起，磁感强度渐
e
a
f
渐减小，当棒以恒定速度v向右做
《大学物理》感生电动势
× × × ×
ε 已知：h、L 、
求： 解一：CD E感 =
B t
r 2
方向如图.
B t
L×
×× ××
× × ×
× ×B × ×t
×
××
εd =E 感.d l
=
r 2
B t
dl
cosθ
B× × × × × E感
× hθ r θ
C
D
×× ×× ×× ××
=
h 2
B t
dl
l dl L
ε=
h 2
B t
l
E 感.d l
=
s
B t
.
dS
l
E 感.d l
=
s
B t
.
dS
3. 式中的S是以 l 为周界的任意曲面。
S l
l
E 感.d l
=
s
B t
.
dS
3. 式中的S是以 l 为周界的任意曲面。
4. E 感 与
B t
构成左旋关系。
S
B
E
t
l
感
5. 感生电场与静电场比较：
5. 感生电场与静电场比较： a. 静电场是有势无旋场，感生电场是有 旋无势场;
L×
××
× ×
× ×
×B ×t
×
B×
×
× ×
× ×
× ×
× ×
E感
× hθ r θ
×× ×× ×× ××
l dl L
解二：l =htgθ , d l =h secθ2 dθ , r = h sec2θ-3-5
εd
=
E
12-(3)感生电动势-涡旋电场
B
2 大小：
L Ek dl
S
ds t
3 感应电场方向： 左手螺旋法则
dB 0
dt
Ek
9
五 电磁感应的应用
将导体放入变化的磁场中时，由于 在变化的磁场周围存在着涡旋的感生 电场，感生电场作用在导体内的自由 电荷上，使电荷运动，形成涡电流。
涡电流的应用 利 & 弊 抽真空
6
四 涡旋电场的性质 -- 与静电场相比
涡旋电场
起源
无源场
Ek ds 0
变化磁场 有旋场 非保守力场
L
S E
k
dl
dΦm dt
B
×
Ek
dB 0
dt
感应电场线
对电荷有力的作用 ＋ 具有质量、能量
静电场
起源
有源场
S
E
ds
q
0
静止电荷 无旋场 保守力场
dI dt
K
0
)，求：螺线管内外涡
自右向左
B
I
× × ×
×B × R ×
×××
×××
B感
B 0nI
dI 0 dt
dB 0 dt
顺时针为正
12
求：螺线管内外涡旋电场的分布 B 0nI dI dt K 0
解：螺线管内涡旋电场的分布 ( r <R )
方向： 由楞次定律或左手螺旋关系知
涡流损耗
dB 0 dt
坩埚 冶金工业
电磁炉
10
发电机的原理 i NBS sint
令 m NBS
电磁感应现象的两类情况
（1） a 1.5V
（2）0.1N 0.1J
v
R
B
r
（3）0.1J
P
b
Q
小结
感 生 电 动 势 和 动 生 电 动 势
感应电场:由变化的磁场激发的电场.
感生电动势:由感生电场产生的感应 电动势称为感生电动势.
动生电动势:由于导体运动而产生的 感应电动势.
理论分析
导体CD在匀强磁场B中以速度V向右运动,并且导线CD 与B、V的方向相垂直,由于导体中的自由电子随导体一 起运动.因此每个电子受到的洛伦兹力为F洛=eVB,F洛方 向向下．在力Ｆ的作用下，自由电子沿导体向下运动， 使导体下端出现过剩的负电荷, 导体上端出现过剩的正 电荷．结果使导体上端C的电势高于下端D的电势,出现 由C指向D的静电场,此时电场对自由电子的作用力是向 上,与洛伦兹力方向相反,当二力互相平衡时，ＣＤ两端 C 便产生一个稳定的电势差。
F洛 F vB e
于是动生电动势就是
E FL BLv
与法拉第电磁感应定律得到的结果一致.
问题：洛伦兹力总与电荷的运动方向垂直.因此,洛伦兹力对电荷不做功.但 是动生电动势又等于洛伦兹力搬运单位正电荷所做的功,两者是否矛盾？
其实并不矛盾．运动导体中的自由电子，不仅随导体以速度v运动，而且还沿导体 v‘做定向运动，正是这个定向运动产生感应电流．因此导体中电子的合速度是Ｖ ＝ v＋ v‘，电子所受的总的洛伦兹力为Ｆ＝eＶＢ．Ｆ与合速度v垂直，它对电子 不做功．Ｆ的一个分量是Ｆ１=evB,这个分力对电子做功，产生电动势．Ｆ的另 一个分量是Ｆ２＝ev’B，Ｆ２的方向与v方向相反，是阻碍导体运动的，做负 功．可以证明两个分力Ｆ１和Ｆ２所做的功代数和为零．结果仍然是洛伦兹力并不 提供能量，而只是起到传递能量的作用，即外力克服洛伦兹力的一个分量Ｆ２所做 的功，通过另一个分量Ｆ１转化为感应电流的能量． X X
电磁学6章(2-5)
导线中的感应电动势。
解：1）设直导线中通有电流 I1 。建立坐标系
I1 在 x 处产生的B为：
B 0I1 2x
x
d
o
通过面元 l dx 的磁通为：dΨ 0I1 l d x
2x
I
l a
dx
x
Ψ da 0I1 l d x 0I1l ln d a
d 2x
2
d
M Ψ 0l ln d a
I1 2
二、感生电动势: 导体或导体回路不动，由于磁场随时间变化，
导体或导体回路内产生的感应电动势。
1、感生电动势： 由法拉第电磁感应定律：
E
dΦ
d
Bd S
dt
dt S
S 不 变 ， 只 有B 随 时 间 变 化:
设 B BeB d
e
B是沿
B方向的单位矢量
B
E
dt
Bd S
S
S
t eB dS
B
r
R
O
r
E感 d l E感 2r
E感 d l E
L
B
d
S
S t
B d S B r 2
S t
t
L
2rE感
B t
r 2
B
∴
r B E感 2 t
“-”号表示场强的方向与 t 成左螺旋关系。 与选定正方向相反。沿逆时针方向。
2）在螺线管外（ r > R ）
取半径为r 的同心圆L 作为积分路径，选顺时针方向作为
变换统一起来。
同一问题在不同参考系中可以得到完全相反的结论。
如图：在 S 系中导体沿 x 轴运动，均匀
静止磁场沿 z 轴的负方向，a 端有正电荷
物理学下17-感生电动势
张宏浩
1
二、感生电动势和感生电场
1、感生电动势 由于磁场发生变化而 激发的电动势
S N G
动生电动势
电磁感应 感生电动势
非静电力 非静电力
洛仑兹力
?
2、 麦克斯韦假设： 变化的磁场在其周围空间会激发一种涡旋状的电场，
称为涡旋电场或感生电场。记作 E 涡或 E 感
L
?
r B B R R
L S B t S
dt dB 2 E涡 2r R dt R 2 dB E涡 2r d t
L
dB 2 B R dS S t dt dB 2 R E涡 dl
解： r R B B E d l d S 涡 r l S t B 0 0 R E dl cos 0 dS cos 0 L 涡 l S
t
求： 圆柱内、外的 E 涡 分布。
B t
r dB dB 2 E涡 2r r E涡 2 dt dt
S
S 的法线方向应选得与曲线 L
的积分方向成右手螺旋关系
S
L
B 是曲面上的任一面元上磁感应强度的变化率 t
不是积分回路线元上的磁感应强度的变化率
3）
E涡
B 与 构成左旋关系。 t
B t
B L E涡 dl S t dS
E涡
利用涡旋电场对电子进行加速
f
电子束
感生电动势与涡旋电场
例：正弦交流电B求：任意时刻的电动势解：t ωθ=⎰⋅⨯=L l d B V)(ε θcos BS m =Φ =t BS ωcost NBS dtd N m mi ωωεsin ==Φ-=ωεNBS m =，转速n ：转/分(r/min)，)/(602s rad nπω= 例：磁通计的原理 Bdtd m i Φ-=ε感应电流 i εdt d R R i m i Φ-==1ε t →0感生电量m t m m t t Rd R dt dt d R idt q m m ∆Φ-=Φ-=Φ-==⎰⎰⎰ΦΦ111)()0(00 m q ∆Φ∝，Rq m =∆Φif ，0)0(=Φm ，Rq t m =Φ)(：磁通计原理测量磁场，若线圈面积较小，且线圈平面B⊥，S t B m /)(Φ=可测：时变磁场、恒定磁场 对于恒定磁场B例：洛仑兹力是否作功？洛仑兹力对电荷永远不作功洛仑兹力是产生动生电动势的非静电力 B v q F⨯=：产生动生电动势B u q f⨯=：对动生电动势无贡献 B u q B v q f F F m ⨯+⨯=+=外 =B u v q⨯+)(=B V q ⨯u v V+=V F m ⊥，0=⋅V F mF、f 分别对电荷作功洛仑兹力不提供能量，它只是转化和传递能量第3节感生电动势与涡旋电场一、涡旋电场假说例：求矩形回路中的感生电动势解：⎰⎰=⋅=ΦSSmdSBS dBtθcos)(=dxlxt Ilrr122)(⎰+πμ，It Iωs i n)(==rlrtl I210lnsin2+ωπμ，rlrtl Idtdmi210lncos2+-=Φ-=ωωπμε产生电动势的非静电力是什么力？从哪里来的？涡旋电场假说：变化的磁场⇒具有闭合力线的电场：涡旋电场（感应电场），场强VE，非静电场一段导线：⎰⋅=L Vil dEε，闭合回路：⎰Φ-=⋅=LmVi dtdl dEε静电场涡旋电场产生原因静电荷变化的磁场电力线不闭合闭合环路定理0=⋅⎰L l dE⎰Φ-=⋅=LmVi dtdl dEε保守场、电势非保守场，电势高斯定理∑⎰=⋅内iSqS dE1ε=⋅⎰S V S dE对q的作用力EqF=VEqF=⎰Φ-=⋅LmV dtdl dE=0<⋅∂∂-⋅-⎰⎰S dtBS dBdtdSS固定回路，LVEVEtB∂∂二、 涡旋电场的计算⎰Φ-=⋅L mV dt d l d E =⋅⎰L l d H ∑内传I例：半径为R 的无限长 直螺线管内有均匀磁场B设磁场以恒定速率增加，0>∂∂t B求：V E（1）R r <，沿电力线积分，n向外2)(2cos r tB BS dt d dt d r E dl E l d E L m V L VV ππθ∂∂=--=Φ-===⋅⎰⎰ r tB E V ∂∂=21（2）R r > V E ⎰Φ-==⋅Lm V V dt d r E l d E π2 22)(R t B R B dt d ππ∂∂=--=rR t B E V 1212∂∂= R r例：无限长直螺线管（R 、、0>∂∂tB）求：直导线ab 解：⎰⎰⎰∂∂==⋅=b a L b L a V b L a V ab dl rhr t B dl E l d E 21cos )()()(θε =0)2/(212122>-∂∂=∂∂l R l t Bhl t B ，方向b a →，b 端电势高 讨论：（1）对于涡旋电场不能引入电势概念，为什么说b 端 电势高？答：b 端积累正电荷，a 端积累负电荷电势概念是针对积累电荷的静电场引入的（2）直导线ab 向上平移ab ε如何变化？答：hl tBab ∂∂=21ε，ab 向上平移，↓h ，↓ab ε 直导线通过O 点，0=h ，ab ε=0⎰⋅=baV L ab l d E )(ε，V E l d ⊥，ab ε=0（3）BO a b l ab bO ab O a O abO εεεεε=++=hl t B hl B dt d dt d m OabO ab 21)21(∂∂=--=Φ-==εε （4）I 、 MN 中有无电动势？II 、 G 中有无电流？ B0/≠∂∂t B III 、N M ''中有无电动势？ M NIV 、G '中有无电流？M ' N 'G '计算电动势的小结：（1）磁场恒定，回路或其一部分运动：动生电动势一段导线：l d B V bL a ab ⋅⨯=⎰)()(ε闭合回路：⎰⋅⨯=L l d B V )(ε，dtd mi Φ-=ε（2）磁场变化，回路不动：感生电动势一段导线：⎰⋅=LV i l d Eε闭合回路：⎰⋅=L V i l d E ε，dtd mi Φ-=ε（3）磁场变化，且回路或其一部分又运动：既有感生电动势，又有动生电动势，最好使用：dtd mi Φ-=εG h第4节 自感一、 自感现象及其规律I B ∝，I m ∝Φ，LI m =ΦL :L ：自感（系数），SI ：亨利（H ） dt d m L Φ-=ε=dtdI L I dt dL LI dt d --=-)(如果L 恒定，=L εdtdIL - L ε L εL ε：自感电动势 自感电动势总是阻碍电流变化 I I。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B t
πr
2
××
×L × n×
× ×× ×
B × ×t
× ××
××R
E感 =
rB 2t
×××××
× E感
B
式中负号表示 E感 的方向
×× ×× ×× ××
和所设的 E 感方向相反
在圆域外 ( r >R )
× × × ×
2-3-5
B
t
× n×
× ××
L ×× × × ×
×××× r
RB
在圆域外 ( r >R )
××
×L × n×
× ×× ×
B × ×t
× ××
××R
× × × ×
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. . l ES cos 0o
× × × ×
E感
l
dl
=
E感 2π r =
B t
s dS
B t
ε . i = l E 感 d l
l
E 感.d l
=
s
B t
.
dS
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由电动势的定义：
ε . i = l E 感 d l
l
E 感.d l
=
s
B t
.
dS
讨论： 1. 此式反映变化磁场和感生电场的相互
关系，即感生电场是由变化的磁场产生的。
=
s
B t
.
dS
l
E 感.d l
=
s
B t
.
dS
3. 式中的S是以 l 为周界的任意曲面。
S l
l
E 感.d l
=
s
B t
.
dS
3. 式中的S是以 l 为周界的任意曲面。
4. E 感 与
B t
构成左旋关系。
S
B
E
t
l
感
5. 感生电场与静电场比较：
5. 感生电场与静电场比较： a. 静电场是有势无旋场，感生电场是有 旋无势场;
第五节 感生电动势
涡旋电场
一、涡旋电场 感生电动势
2-3-5
一、涡旋电场 感生电动势
当回路 1中电流
1
发生变化时，在回路
2中出现感应电动势。
ε
2-3-5
Φm 2
G
R
一、涡旋电场 感生电动势
当回路 1中电流
1
发生变化时，在回路
2中出现感应电动势。
ε 产生感应电动势
的非静电力是什么？
R
2-3-5
Φm 2
5. 感生电场与静电场比较：
a. 静电场是有势无旋场，感生电场是有
旋无势场;
l
E 静.d l
=0
5. 感生电场与静电场比较：
a. 静电场是有势无旋场，感生电场是有
旋无势场;
l
E 静.d l
=0
l
E 感.d l
=
s
B t
.
dS
=
0
5. 感生电场与静电场比较：
a. 静电场是有势无旋场，感生电场是有
πr
2
××
×L × n×
× ×× ×
B × ×t
× ××
××R
E感 =
rB 2t
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. . l E感 d lcos 0o=
s
B t
dS cos 0o
× × × ×
E感
l
dl
=
E感 2π r =
B t
s dS
G
一、涡旋电场 感生电动势
当回路 1中电流
1
发生变化时，在回路
2中出现感应电动势。
ε 产生感应电动势
的非静电力是什么？
2-3-5
Φm 2
G
麦克斯韦假设：
R
在变化磁场的周围将产生电场，称这种
电场为感生电场，或涡旋电场。
一、涡旋电场 感生电动势
当回路 1中电流
1
发生变化时，在回路
2中出现感应电动势。
旋无势场;
l
E 静.d l
=0
l
E 感.d l
=
s
B t
.
dS
=
0
b. 静电场的电力线是“有头有尾”的， 感生电场的电力线是一组闭合曲线。
5. 感生电场与静电场比较：
a. 静电场是有势无旋场，感生电场是有
旋无势场;
l
E 静.d l
=0
l
E 感.d l
=
s
B t
.
dS
=
0
b. 静电场的电力线是“有头有尾”的， 感生电场的电力线是一组闭合曲线。
ε 产生感应电动势
的非静电力是什么？
2-3-5
Φm 2
G
麦克斯韦假设：
R
在变化磁场的周围将产生电场，称这种
电场为感生电场，或涡旋电场。
问题： E 感 = ？
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
由法拉第电磁感应定律：
B × ×t
× ××
××R
×××××
×
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
× × × ×
××
×L × n×
× ×× ×
B × ×t
× ××
××R
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. . l E感 d lcos 0o=
s
B t
dS cos 0o
B × × × ×t
×L × n×
× ××
× ×× × × × R
× × × ×
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. l E感 d l cos 0o=
s
B t
dS cos 0o
E感
l
dl
=
B t
s dS
B
× × × ×t
×L × n×
× ××
× ×× × × × R
× × × ×
×××××
× E感
B
×× ×× ×× ××
l E 感.d l =
s
B t
.
dS
设E感与dl 方向一致。
. . l E感 d lcos 0o=
s
B t
dS cos 0o
E感
l
dl
=
E感 2π r =
B t
s dS
B t
πr
2
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由电动势的定义：
ε . i = l E 感 d l
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由电动势的定义：
由法拉第电磁感应定律：
2-3-5
εi =
dΦ dt
=
d dt
s
B
.dS
=
s
B t
.
dS
由电动势的定义：
ε . i = l E 感 d l
l
E 感.d l
=
s
B t
.
dS
讨论： 1. 此式反映变化磁场和感生电场的相互
关系，即感生电场是由变化的磁场产生的。 2. 这是电磁场基本方程之一。
l
E 感.d l
c. 静电场是由静止电荷产生的，感生电 场是由变化磁场产生的。
[例1]电子感应加速器。在涡旋电场作用下， 电子可以被加速到 10---100MeV。 已知： B ，求：感生电场场强。
t 铁芯
磁场 B 线圈
电 子束
环形 真空室
l E 感.d l =
s
B t
.
dS
× × × ×
××
×L × n×
× ×× ×