辽宁省大连市普通高中2013-2014学年高二上学期期末考试(数学文)
2013-2014学年第一学期期末考试成绩册(登分版) (2)paiming (1)
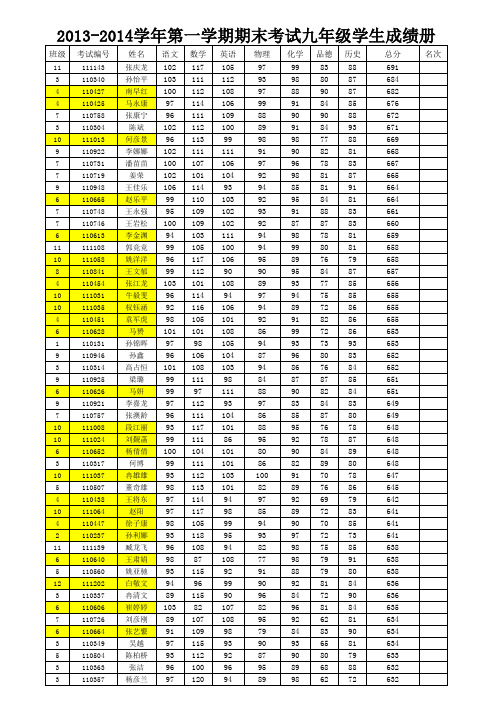
品德 83 80 90 84 90 84 77 82 78 81 81 84 88 87 78 80 76 84 77 75 72 82 72 73 80 76 87 82 84 87 76 78 84 89 70 76 69 72 70 72 75 79 79 81 72 81 62 83 65 80 68 62
名次
3 2 6 12 10 8 5 3 6 3 2 5 10 9 5 9 7 4 3 2 11 10 9 9 6 2 3 7 5 5 10 7 3 4 8 2 7 1 5 3 5 4 4 4 3 12 11 4 9 1 8 5 1 4 1
110305 110217 110615 111240 111042 110805 110562 110321 110605 110316 110241 110543 111057 110958 110565 110918 110754 110422 110320 110257 111147 111046 110963 110930 110617 110210 110350 110767 110546 110518 111019 110717 110356 110405 110802 110260 110713 110104 110550 110335 110508 110437 110444 110446 110327 111233 111115 110434 110957 110123 110814 110564 110143 110417 110146
88 88 90 88 92 98 90 90 82 91 91 76 85 82 90 96 89 88 87 93 87 77 67 90 89 94 92 86 87 75 94 94 89 84 89 94 89 91 79 94 88 90 83 88 92 84 89 82 82 88 91 77 91 83 84
【新课标版】2013-2014学年高二上学期期末考试数学文Word版含答案

2013-2014学年度上学期期末考试高二数学(文)试题【新课标】一、选择题:(每题5分,共60分)1. 若复数是虚数单位)是纯虚数,则实数a 的值为( )A .-3B .3C .-6D .62. 用反证法证明:若整系数一元二次方程ax 2+bx +c =0(a ≠0)有有理数根,那么a 、b 、c 中至少有一个是偶数.用反证法证明时,下列假设正确的是( )A .假设a 、b 、c 都是偶数B .假设a 、b 、c 都不是偶数C .假设a 、b 、c 至多有一个偶数D .假设a 、b 、c 至多有两个偶数3. 分析法又称执果索因法,若用分析法证明:“设a >b >c ,且a +b +c =0”,求证 “b 2-ac <3a ”索的因应是( )A .a -b >0B .a -c >0C .(a -b )(a -c )>0D .(a -b )(a -c )<04.4. 给出下面类比推理命题(其中Q 为有理数集,R 为实数集,C 为复数集):①“若a ,b ∈R ,则a -b =0⇒a =b ”类比推出“若a ,b ∈C ,则a -b =0⇒a =b ”;②“若a ,b ,c ,d ∈R ,则复数a +b i =c +d i ⇒a =c ,b =d ”类比推出“若a ,b ,c ,d ∈Q ,则a +b =c +d ⇒a =c ,b =d ”;③若“a ,b ∈R ,则a -b >0⇒a >b ”类比推出“若a ,b ∈C ,则a -b >0⇒a >b ”. 其中类比结论正确的个数是( )A .0B .1C .2D .35.推理“①矩形是平行四边形;②三角形不是平行四边形;③三角形不是矩形”中的小前提是( )A .①B .②C .③D .①和②6.复数 ( )A .B .C .D .7. 函数的单调递增区间是( )A. B. (0,3) C. (1,4) D.8. 抛物线的焦点坐标是( )A .B .C .D .9. 设双曲线的虚轴长为2,焦距为,则双曲线的渐近线方程为( )A. B. C. D.10. 设函数在区间[1,3]上是单调函数,则实数a 的取值范围是( )A .B .C .D .11. 为了表示个点与相应直线在整体上的接近程度,我们常用( )表示A. B. C. D.12. 过双曲线的左焦点作圆的切线,切点为E ,延长FE 交抛物线于点P ,若E 为线段FP 的中点,则双曲线的离心率为( )A .B .C .D .二、填空题:(每题5分,共20分)13.双曲线的一个焦点是,则m 的值是_________.14.曲线在点(1,3)处的切线方程为___________________.15. 已知回归直线的斜率的估计值是 1.23,样本点的中心为(4,5),则回归直线的方程是________________.16. 设n 为正整数,f (n )=1+12+13+…+1n ,计算得f (2)=32,f (4)>2,f (8)>52,f (16)>3,观察上述结果,可推测一般的结论为_______________________________.三、解答题:17.(本题满分12分)在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.(1)求抛物线C的标准方程;(2)设直线l是抛物线的准线,求证:以AB为直径的圆与准线l相切.18.(本题满分12分)某校为了探索一种新的教学模式,进行了一项课题实验,乙班为实验班,甲班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,成绩如下表(总分:150分):(1)现从甲班成绩位于内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果;(2)根据所给数据可估计在这次测试中,甲班的平均分是101.8,请你估计乙班的平均分,并计算两班平均分相差几分;(3)完成下面2×2列联表,你认为在犯错误的概率不超过0.025的前提下,“这两个班19.(本题满分12分)已知函数,其图象在点(1,)处的切线方程为(1)求a,b的值;(2)求函数的单调区间,并求出在区间[—2,4]上的最大值。
2013-2014学年高二上学期期末联考数学(文)试题

学校 姓名 联考证号2013-2014学年高二上学期期末联考数学(文)试题(A )注意事项:1.答题前,考生务必用蓝、黑色墨水笔或圆珠笔将学校名称、姓名、班级、联考证号、座位号填写在试题和试卷上。
2.请把所有答案做在试卷上,交卷时只交试卷,不交试题,答案写在试题上无效。
3.满分150分,考试时间120分钟。
一.选择题(本大题共12个小题,每小题5分,共60分,在每个小题给出的四个选项中,只有一项是符合题目要求的)1.设集合M ={1, 2, 4, 8},N ={x |x 是4的正约数},则M ∩N =A .{2,4}B .{1,2,4}C .{2,4,8}D .{1,2,8} 2. 直线过点)2,1(--且与直线0432=+-y x 垂直,则的方程为A .3x +2y +1=0B .0532=+-y xC .3x +2y +7=0D .0832=+-y x3.已知两个球的表面积之比为l : 9,则这两个球的半径之比为A .1 : 3B .1 : 3C .1 : 9D .1 : 814.tan240︒=A .33B .22C .1D . 35. 双曲线221169x y -=的渐近线方程为 A. x y 916±= B. x y 169±= C. x y 43±= D. x y 34±= 6. 等差数列{a n }中,a 2=2,a 3=4,则a 10=A .12B .14C .16D .187.曲线y =x 2-x +4上一点P 处的切线的斜率为5,则点P 处的切线方程为A .5x -y -5=0B .5x -y +5=0C .5x -y -53=0D .5x -y +53=08.阅读右图所示的程序框图,运行相应的程序,输出的结果是、A .676B .26C .5D .29.下列函数中,值域是[0,)+∞的函数为A .||2()3x y -= B .11x y x -=+ C .2|log (1)|y x =+ D .21y x x =++10.设变量x ,y 满足约束条件1,40,340,x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数z =3x -y 的最大值为A .4-B .0C .43D .4 11.一个体积为123的正三棱柱(即底面为正三角形,侧棱垂直于底面的三棱柱)的三视图如图所示,则这个三棱柱的侧视图的面积为A .12B .8C.D.12.过抛物线y 2=2px (p >0)的焦点作倾斜角为30︒的直线l 与抛物线交于P ,Q 两点,分别作PP '、QQ '垂直于抛物线的准线于P '、Q ',若|PQ |=2,则四边形PP 'Q 'Q 的面积为A .1B .2C . 3D .3二.填空题(本大题共4小题,每小题5分,共20分,把答案填在答卷纸的相应位置上)13.在∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且B =30︒,C =45︒,1c =,则b= ▲ .14.过原点且倾斜角为60°的直线被圆0422=-+x y x 所截得的弦长为 ▲ .15.函数()(2)xf x x e =-在区间[0,2]上的最大值为 ▲ .16.给出下列四个命题:①命题“∀x ∈R ,x 2+1>0”的否定是“∃x 0∈R ,x 20+1≤0”; ②曲线22184x y k k +=-+是椭圆的充要条件是48k -<<; ③命题“若22am bm <,则a b <”的逆命题是真命题;④若∀x ∈R ,4x 2+4(a -2)x +1>0,则1<a <3.其中正确的命题为 ▲ (只填正确命题的序号).三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤,并把解答写在答卷纸的相应位置上)17.(本题满分10分)已知y (0,1)x p a a a =>≠: 且在R 上为增函数,q :直线3x +4y +a =0与圆x 2+y 2=1相交.若p 真q 假,求实数a 的取值范围.18.(本题满分12分)已知f (x )=sin x +3cos x (x ∈R ).(Ⅰ)求函数f (x )的周期和最大值;(Ⅱ)若f (A +π6)=23,求cos2A 的值.19.(本题满分12分)对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M 名学生作为样本,得到这M 名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:(Ⅰ)求出表中M ,P 及图中a 的值;(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间[25,30)内的概率.20.(本题满分12分)如图,在四棱锥P —ABCD 中,底面ABCD 为直角梯形,AD ∥BC ,∠BAD =90︒,PA ⊥底面ABCD ,且PA =AD =AB =2BC =2,M 、N 分别为PC 、PB 的中点.(Ⅰ)求证:PB ⊥平面ADMN ;(Ⅱ)求四棱锥P -ADMN 的体积.21.(本题满分12分)已知椭圆C 的两焦点是)1,0(),1,0(21F F -,离心率21=e . (Ⅰ)求椭圆C 的方程;(Ⅱ)若P 在椭圆C 上,且121=-PF PF ,求∆PF 1F 2的面积.22.(本题满分12分)设函数c bx ax x x f ++-=23)((a >0,b ,c ∈R ),曲线)(x f y =在点P (0,f (0))处的切线方程为1=y .(Ⅰ)试确定b 、c 的值;(Ⅱ)是否存在实数a 使得过点(0,2)可作曲线)(x f y =的三条不同切线,若存在,求出a 的取值范围;若不存在,请说明理由.。
辽宁省大连市普通高中2013-2014学年高二数学上学期期末考试试题 文 新人教B版

2013~2014学年第一学期期末考试试卷高二数学(文科)本试卷分第I 卷〔选择题〕和第II 卷〔非选择题〕两局部.考生作答时,将答案答在答题卡和答题纸上,在本试卷上答题无效.第I 卷一、选择题:本大题共12小题,每一小题5分,共60分.在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的.1.抛物线24y x =的焦点为〔 〕〔A 〕〔0,1〕 〔B 〕〔1,0〕 〔C 〕(0,1)- 〔D 〕(1,0)- 2.(2,0)M -,(2,0)N ,||3|PM PN|-=,如此动点P 的轨迹是〔 〕〔A 〕双曲线〔B 〕圆 〔C 〕椭圆 〔D 〕抛物线3. 命题p :R ∀∈x ,cos 1≤x ,如此p ⌝是〔 〕〔A 〕∈∃0x R,1cos 0≥x 〔B 〕∈∀x R,1cos ≥x〔C 〕∈∀x R,1cos >x 〔D 〕∈∃0x R,1cos 0>x4.函数()f x 的导函数()f x '的图象如图所示,那么函数()f x 的图象最有可能的是〔 〕5.设,R a b ∈,那么“>1a b〞是“>>0a b 〞的( ) 〔A 〕充分不必要条件 〔B 〕必要不充分条件〔C 〕充要条件 〔D 〕既不充分也不必要条件6.可导函数在闭区间的最大值必在〔 〕取得〔A 〕极值点 〔B 〕导数为0的点〔C 〕极值点或区间端点 〔D 〕区间端点7. )()()(0000lim x f x x f x x f x '=∆-∆+→∆,其中x ∆〔 〕 〔A 〕恒取正值或恒取负值 〔B 〕有时可以取0〔C 〕恒取正值 〔D 〕可以取正值和负值,但不能取08. 如下说法正确的答案是〔 〕〔A 〕0R x ∃∈,00xe ≤〔B 〕对,a b ∀>如此2ab =,22min ()4a b += 〔C 〕1a >,1b >是1ab >的充分条件〔D 〕0a b +=的充要条件是1a b=- 9.设等比数列{}n a 的公比2q =,前n 项和为n S ,如此24a S 的值为〔 〕 〔A 〕154 〔B 〕152〔C 〕74 〔D 〕7210.12(1,0),(1,0)F F -是椭圆的两个焦点,过1F 的直线l 交椭圆于,M N 两点,假设2MF N ∆的周长为8,如此椭圆方程为〔 〕〔A 〕13422=+y x 〔B 〕13422=+x y 〔C 〕1151622=+y x 〔D 〕1151622=+x y 11.函数32()f x x bx cx d =+++的大致图象如图所示,如此2212x x +等于〔 〕〔A 〕89 〔B 〕109〔C 〕169〔D 〕28912.直线kx y =交双曲线22:143x y C -=于,A B 两点,P 为双曲线C 上异于,A B 的任意一点,如此直线,PA PB 的斜率之积为( )〔A 〕43 〔B 〕34〔C 〕233 〔D 〕32 第II 卷二、填空题:本大题共4小题,每一小题5分,共20分.13.双曲线22149x y -=的渐近线方程是. 14. n S 为等差数列{}n a 的前n 项和,266a a +=,如此=7S .15.曲线ln y x =在点〔1,0〕处的切线方程为.16. 双曲线:C 2221(0,1)y x b b b-=>≠的左右焦点为12F F ,,过点1F 的直线与双曲线C 左支相交于,A B 两点,假设22||||2||AF BF AB +=,如此||AB 为.三、解答题:本大题共小6题,共70分,解答应写出文字说明、证明过程或演算步骤.17.〔本小题总分为10分〕a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,A 为B ,C 的等差中项.(Ⅰ)求A ;(Ⅱ)假设a =2,△ABC 的面积为3,求b ,c 的值.18.(本小题总分为12分)不等式260x x --≤解集为M ,不等式2280x x +->解集为N ,不等式22320x ax a -+<)0(>a 解集为P .(Ⅰ) 求M N ;(Ⅱ)假设“M N 〞是“P 〞的充分条件,求实数a 的取值范围.19.(本小题总分为12分)函数32()23128f x x x x =--+.(Ⅰ)求函数()f x 的单调区间;(Ⅱ)假设[2,3]x ∈-,求函数()f x 的值域.20.〔本小题总分为12分〕离心率2e =的椭圆2222:1(0)x y C a b a b+=>>一个焦点为(-1,0). (Ⅰ)求椭圆C 的方程;(Ⅱ) 假设斜率为1的直线l 交椭圆C 于,A B 两点,且||AB =l 方程.21.〔本小题总分为12分〕抛物线的顶点在坐标原点O ,对称轴为x 轴,焦点为F ,抛物线上一点A 的横坐标为2,且16=⋅OA FA 。
2013-2014学年第二学期高二数学(文)期末试卷(答案)

2013-2014学年第二学期高二数学(文)期末试卷(答案) 考试时间:120分钟一.选择题(每小题5分,共60分) 1.设全集U 是实数集R ,{}{}2|4,|13M x x N x x =>=<<,则=⋂N M C U )(( )A .{}|21x x -≤<B .{}|12x x <≤C .{}|22x x -≤≤ D .{}|2x x <2.已知()f x 是R 上的奇函数,对x R ∈都有(4)()(2)f x f x f +=+成立,若(1)2f =, 则(2005)f 等于 ( )A.2005B.2C.1D.1a >3.对于任意的,x y R ∈,不等式y y x x 2222-≥-恒成立,则当 14x ≤≤时,yx 的取值范围是 ( )A .1[,1)4-B . 1[,1]4-C .1(,1]2-D .1[,1]2-4.已知平面向量a =(1,3)-,(4,2)b =-,若a b λ-与a 垂直,则λ= ( ) A.-1 B.1 C.-2 D.25.如图,函数)(x f y =的图象是中心在原点,焦点在x 轴上的椭圆的两段弧,则不等式xx f x f +-<)()(的解集为( )A.{}22,02|≤<<<-x x x 或B.{}22,22|≤<-<≤-x x x 或C.⎭⎬⎫≤<⎩⎨⎧-<≤-222,222|x x x 或 D.{}0,22|≠<<-x x x 且 6.半径为4的球面上有A 、B 、C 、D 四点,且AB ,AC ,AD 两 两互相垂直,则ABC ∆、ACD ∆、ADB ∆面积之和ABC ACD ADB S S S ∆∆∆++的最大值为( )A .8B .16C .32D .647.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:根据上表可得回归直线方程,据此模型预报身高为172 cm 的高三男生的体重为 ( )A. 70.09B. 70.12C. 70.55D. 71.058.已知某个几何体的三视图如下,根据图中标出的尺寸 单位:cm. ,可得这个几何体的体积是 ( )A. 383cmB. 343cmC. 323cmD. 313cm9.命题p :函数2212-+-=||)(x x x f 不具有奇偶性;命题q :当121<<c 时,函数x c y )12(-=为减函数.对于以上两个命题,下列结论中正确的是 ( )A.命题“p 或q ”为假B.命题“p 或q ”为真C.命题“p ⌝且q ”为假D.命题“非q ”为真 10.右图是统计高三年级1000名同学某次数学考试成绩的程序框图,若输出的结果是720,则这次考试数学分数不低 于90分的同学的频率是 ( ) A.0.28 B.0.38 C.0.72 D.0.6211.函数()3sin 2f x x π⎛⎫=- ⎪3⎝⎭的图象为C ,① 图象C 关于 直线1112x =π对称; ②函数()f x 在区间5ππ⎛⎫-⎪1212⎝⎭,内是 增函数;③由3sin 2y x =的图象向右平移π3个单位长度可以得到图象C .以上三个论断中,正确论断的个数是 ( ) A.0 B.1 C.2 D.3 12.已知椭圆)0,0(1)0(122222222>>=->>=+n m n y m x b a b y a x 与双曲线有相同的焦点(-c ,0)和(c ,0),若c 是a 、m 的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率是 ( )A.33B.22C.41D.21二.填空题(每小题5分,共20分)13.若定义运算c a bc ad d b -=,则符合条件2iz 1-i 24+=的复数z 为 .14.从[0,1]之间选出两个数,这两个数的平方和小于0.25的概率是 ____________.15.数列{}n a 中,352,1,a a ==如果数列1{}1n a +是等差数列,则11a =___________.16.定义一种运算“*”对于正整数满足以下运算性质:(1)220061*=;(2)(22)20063[(2)2006]n n +*=⋅*,则20082006*的值是 ___ .三.解答题17.(本小题满分12分)在三角形ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若B c a C b cos )2(cos -=21世纪教育网(1)求∠B 的大小; (2)若,4,7=+=c a b 求三角形ABC 的面积.18.(本小题满分12分)一汽车厂生产A,B,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表所示(单位:辆),若按A,B,C 三类用分层抽样的方法在这个月生产的轿车中抽取50辆,则A 类轿车有10辆.(Ⅰ)求z 的值;(Ⅱ)用随机抽样的方法从B 类舒适型轿车中抽取8辆,经检测它们的得分如下: 9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2. 把这8辆轿车的得分看作一个总体,从中任取一个分数a .记这8辆轿车的得分的平均数为x ,定义事件E ={0.5a x -≤,且函数()2 2.31f x ax ax =-+没有零点},求事件E 发生的概率.z19.(本小题满分12分)如图,已知三棱锥A —BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 中点,D 为PB 中点,且△PMB为正三角形。
辽宁省大连市2014-2015学年高二数学上学期期末考试试题 文

2014~2015学年第一学期期末考试试卷高二数学(文科)本试卷分第I 卷〔选择题〕和第II 卷〔非选择题〕两局部.考生作答时,将答案答在答题卡和答题纸上,在本试卷上答题无效.第I 卷一、选择题:本大题共12小题,每一小题5分,共60分.在每一小题给出的四个选项中,只有一项为哪一项符合题目要求的.1.“1x >〞是“2x x >〞的 〔 〕 A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不必要也不充分条件2.等差数列{}n a 的前n 项和为n S ,假设1910a a +=,如此9S 的值为 ()A .30B .45 C.90D .1803.椭圆192522=+y x 上一点M 到椭圆的一个焦点的距离等于4,那么点M 到另一个焦点的距离等于 〔 〕 A. 6 B. 5 C. 3 D. 14. 如下命题错误的答案是...... 〔 〕 A .命题“假设p 如此q 〞与命题“假设q ⌝,如此p ⌝〞互为逆否命题 B .命题“∈∃x R,02>-x x 〞的否认是“∈∀x R,02≤-x x 〞C .∀0>x 且1≠x ,都有21>+xx D .“假设b a bm am <<则,22〞的逆命题为真5.研究x 与Y 之间关系的一组数据如表1所示,如此Y 对x 的回归直线方程a bx y+=ˆ必过点 〔 〕A .(2,2)B .3(,0)2C .(1,2)D .3(,4)2表16. 变量,x y 满足约束条件241y x y x y ≤⎧⎪+≥⎨⎪-≤⎩,如此3z x y =+的最大值为( )A.12B.11C.3D.-17.设抛物线28y x =上一点P 到y 轴距离是6,如此点P 到该抛物线焦点的距离是 〔 〕A .12B .8C .6D .48.双曲线322=-y x 的渐近线方程为 〔 〕A.x y ±=B.3y x =±C.x y 3±=D. x y 33±= 9.设函数()ln =f x x x ,如此()f x 的极小值为 〔 〕A. e -B.1eC. 2e D. 1e-10. 设0,0a b >>,是33a b与的等比中项,如此11a b+的最小值为 〔 〕 A. 8 B. 4 C. 1 D. 1411.假设函数()3221f x x x mx =+++在(,)-∞+∞内单调递增,如此m 的取值范围是( )A .34≥m B .34>m C .34≤m D .34<m 12.12,F F 分别是双曲线()222210,0x y a b a b-=>>的左、右焦点,P 是以12F F 为直径的圆与该双曲线的一个交点,且12212PF F PF F ∠=∠,如此这个双曲线的离心率是 〔 〕A.2221第II 卷二、填空题:本大题共4小题,每一小题5分,共20分.13.不等式09xx<-的解集为.〔用区间表示〕 14. 曲线2122y x x =-在点3(1,)2-处的切线方程为__________________.15. 等差数列{}n a 、{}n b 满足3423++=n n b a n n (n N *),且前n 项和分别为,n n A B , 如此55A B 的值为. 16.函数()sin cos f x x x x =-,假设存在()0,x π∈,使得()f x x λ'>成立,如此实数λ的取值范围是.三、解答题:本大题共小6题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.〔本小题总分为10分〕在对人们的休闲方式的一次调查中,共调查了130人,其中女性70人,女性中有40人主要的休闲方式是看电视;男性中有35人主要的休闲方式是运动. (Ⅰ)根据以上数据完善如下2×2列联表〔表2〕; (Ⅱ)能否有95%的把握认为休闲方式与性别有关. 表2参考公式()21122122121212n n n n n n n n n χ++++-=表318.〔本小题总分为12分〕等差数列{}n a 的公差为2,假设1413,,a a a 成等比数列,数列{}n a 前n 项和为n S . 〔Ⅰ〕求n a 和n S ; 〔Ⅱ〕求数列⎭⎬⎫⎩⎨⎧n S 1的前n 项和n T . 19.〔本小题总分为12分〕 函数()32245f x x x x =+-+.〔Ⅰ〕求()f x 的单调区间;〔Ⅱ〕求()f x 在[3,1]-上的最大值和最小值.20.〔本小题总分为12分〕动点M 到点()4,0的距离比它到直线:3l x =-的距离多1. 〔Ⅰ〕求动点M 的轨迹C 的方程;〔Ⅱ〕求过点)0,4(且倾斜角为︒30的直线被曲线C 所截得线段的长度.21.〔本小题总分为12分〕 函数()()xf x x a e =+,(∈a R ).〔Ⅰ〕假设函数()f x 在区间[3,)-+∞上是增函数,求实数a 的取值范围; 〔Ⅱ〕假设2()x f x e ≥在[0,2]x ∈时恒成立,求实数a 的取值范围.22.〔本小题总分为12分〕椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为()()12,0,,0F c F c -,椭圆上两点B ,A 坐标分别为()(),0,0,A a B b ,假设2ABF ∆,02120BF A ∠=.〔Ⅰ〕求椭圆C 的标准方程;〔Ⅱ〕过点O 作两条互相垂直的射线,与椭圆C 分别交于,M N 两点,证明:点O 到直线MN 的距离为定值.2014~2015学年第一学期期末考试答案高二数学〔文科〕1~12 CBADD BBADB AC13. ()()∞+∞-,90, == 14. 2210x y ++= 15. 111516.1λ< 17.解〔1〕〔2〕22130(25303540)653.095 3.841607013013021χ⨯-⨯==≈<⨯⨯⨯ ∴没有95%的把握认为休闲方式与性别有关. ············· 10分18.解:〔1〕:1413,,a a a 成等比数列,24113,a a a ∴=即()()2111312a d a a d ∴+=+又2d =,解得13a = 如此21n a n =+(n 2)n S n =+ ············· 6分〔2〕11111()(n 2)22n s n n n ==-++ 11111111[(1)+()()()]2324112n T n n n n =--+++++-++1111(1)2212n n =+--++⎪⎭⎫⎝⎛+++-=21112143n n ························ 12分19. 解:〔1〕f (x )=x 3+2x 2-4x +5,∴f ′(x )=3x 2+4x -4 ························ 2分 令0)(>'x f ,如此2-<x 或32>x ,令0)(<'x f ,如此322<<x -, 所以增区间为()),,(,∞+∞322--,减区间为),(322- ··········· 6分 〔2〕令f ′(x )=0,得x =-2或x =23,∴2-=x 为极大值点,32=x 为极小值点, 又f (-3)=8,f (-2)=13,f ⎝ ⎛⎭⎪⎫23=9527,f (1)=4,∴y =f (x )在[-3,1]上的最大值为13,最小值为9527. ·········· 12分20. 解:〔1〕由题意易知,动点M 到点()0,4的距离与到直线4-=x 的距离相等,故M 点的轨迹为以()0,4为焦点,4-=x 为准线的抛物线,此抛物线方程为216y x = ··· 4分(2)设直线与抛物线交点为B A ,,直线AB 方程为)4(330-=-x y , 即33433-=x y·············· 6分将直线方程与抛物线方程联立⎪⎩⎪⎨⎧=-=x y x y 16334332,得016562=+-x x ,故16,56=⋅=+B A B A x x x x64856=+=++=p x x AB B A············· 12分〔其他方法请酌情给分〕21.解:〔1〕'()(+1)e x f x x a =+,x ∈R .因为函数()f x 是区间[3,)-+∞上的增函数, 所以'()0f x ≥,即10x a ++≥在[3,)-+∞上恒成立.因为1y x a =++是增函数,所以满足题意只需310a -++≥,即2a ≥. ···· 6分(2)x x e e x f 2)(≥,即()x x e e a x 2≥+,x e a x-≥在[0,2]x ∈时恒成立,即max )(x e a x -≥设x e x g x -=)(,1)(-='x e x g ,易知01)(≥-='xe x g ,在[0,2]x ∈上恒成立,2)2()(2max -==∴e g x g ,22-≥∴e a············· 12分22.解:(1)由题意,易知c b c a 3,2==,23233)2(2122==⨯-⨯=∆c c c c S ABF 3,2,1===∴b a c ,∴椭圆方程为13422=+y x ············· 4分(2)设),(),,(2211y x N y x M ,当直线MN 的斜率不存在时,x MN ⊥轴,MNO ∆为等腰直角三角形,11x y =∴,又1342121=+y x ,解得72127121==x , 即O 到直线MN 的距离7212=d ···················· 6分 当直线的斜率存在时,直线MN 的方程为m kx y +=,与椭圆13422=+y x 联立消去y 得012)2(432222=-+++m km x k x ,222122143124,438k m x x k km x x +-=+-=+∴ON OM ⊥ 02121=+∴y y x x , 0))((2121=+++∴m kx m kx x x即0)()1(221212=++++m x x km x x k043843124)1(2222222=++-+-+∴m km k k m k , 整理得)1(12722+=k m∴O 到直线MN 的距离721271212==+=km d ··········· 12分。
辽宁省大连市2012-2013学年高二数学上学期期末考试试题 文 新人教A版
2012——2013学年度第一学期期末测试卷高二数学(文科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.考生作答时,将答案答在答题卡上,在本试卷上答题无效.考试结束后,将本试卷和答题卡一并交回.第I 卷一.选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知向量=(-3,2)a ,=(,-4)x b ,若a ∥b ,则x 的值为( ) (A )4 (B )5 (C )6 (D ) 7 2.ABC ∆中,“6A π>”是“1sin 2A >”的( ) (A )必要不充分条件 (B )充分必要条件(C )充分不必要条件 (D ) 既不充分也不必要条件 3.函数x x y cos sin =是( )(A )最小正周期为π的奇函数 (B )最小正周期为π的偶函数 (C )最小正周期为π2的奇函数 (D )最小正周期为π2的偶函数4. 若抛物线28y x =上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是( ) (A) 4 (B) 6 (C) 8 (D) 125. 已知{}n a 是等比数列,22a =,514a =,则公比q 的值为( ) (A) 12- (B)2- (C)2 (D)126.等差数列{}n a 中,51130a a +=,47a =,则12a 的值为( ) (A) 15 (B)23(C)25(D)377.若双曲线22221x y a b-=的两条渐近线互相垂直,则该双曲线的离心率是( )(A) 3(B)32(C)2(D) 28. 已知0a b <<,则下列不等式一定成立的是( )(A)2a ab < (B)110a b<< (C)||||a b < (D)11()()22a b <9.函数sin()(0,)2y x πωϕωϕ=+><的图象一部分如右图所示,则ω、ϕ的值分别是( )(A )1,3π(B )1,3π-(C )2, 3π(D )2, 3π-10.如图,在平面直角坐标系xoy 中,两个非零向量,OA OB 与x 轴正半轴的夹角分别为6π和23π,向量OC 满足OA OB OC ++=0,则OC 与x 轴正半轴夹角取值范围是( )(A )0,3π⎛⎫ ⎪⎝⎭ (B )5,36ππ⎛⎫⎪⎝⎭(C )2,23ππ⎛⎫ ⎪⎝⎭(D )25,36ππ⎛⎫⎪⎝⎭ 11.过椭圆22165x y +=内的一点(2,1)P -的弦,恰好被P 点平分,则这条弦所在的直线方程是( )(A )53130x y --= (B )53130x y +-= (C )53130x y -+= (D )53130x y ++=12.对于任意的R x ∈,不等式222130x a x -++>恒成立.则实数a 的取值范围是( )(A )22a <(B )22a ≤(C )3a <(D )3a ≤第II 卷二、填空题:本大题共4小题,每小题5分,共20分.13. 已知椭圆22194x y +=的左右焦点分别为1F 、2F ,经过1F 的直线交椭圆于A 、B 两点,则△2ABF 的周长为 . 14.不等式(1)(1)0x x x+-<的解集为____________.15.设变量,x y 满足约束条件⎪⎩⎪⎨⎧≥≤+-≥-241y y x y x 则目标函数24z x y =+的最大值为 .16. 已知椭圆12222=+by a x )0(>>b a ,A 为左顶点,B 为短轴端点,F 为右焦点,且BF AB ⊥,则这个椭圆的离心率等于 .三.解答题:本大题共6题,共70分,解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)解关于x 的不等式2(1)1ax -<.18.(本小题满分12分)已知函数()sin()(0,||)f x x ωϕωϕπ=+><的图象如图所示. (Ⅰ)求,ωϕ的值;(Ⅱ)设()()()4g x f x f x π=-,求函数()g x19.(本小题满分12分)在数列{}n a 中,13a =,1133n n n a a ++=+.(Ⅰ)设3nn n a b =.证明:数列{}n b 是等差数列; (Ⅱ)求数列{}n a 的前n 项和n S .20.(本小题满分12分)21.(本小题满分12分)在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,满足sin 25A =,且ABC ∆的面积为2.求(Ⅰ)求bc 的值;(Ⅱ)若6=+c b ,求a 的值.22.(本小题满分12分)设1F 、2F 分别是椭圆C :22221(0)x y a b a b 的左、右焦点,P 是C 上的一个动点,且124PF PF +=,C 的离心率为12. (Ⅰ)求C 方程;(Ⅱ)是否存在过点2F 且斜率存在的直线l 与椭圆交于不同的两点C 、D ,使得|F 1C|=|F 1D|.若存在,求直线l 的方程;若不存在,请说明理由.2012——2013学年度第一学期期末测试卷 高二数学(文科)参考答案与评分标准说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答末改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分. 一.选择题1.C ;2. C ;3.A ;4. B ;5.D ;6.B ;7.D ;8. B ;9.C ;10.B ;11.A ;12.C . 二、填空题13. 13;14.(,1)(0,1)-∞-; 15.13;16.12. 三.解答题17.解:由2(1)1ax -< 得22211a x ax -+<,即(2)0ax ax -<. 2分(1)当0a =时,不等式转化为00<,故x 无解. ·············· 4分 (2)当0a <时,不等式转化为(2)0x ax ->,即2()0x x a-<.∵20a <,∴不等式的解集为2|0x x a ⎧⎫<<⎨⎬⎩⎭. ·············· 6分 (3)当0a >时,不等式转化为(2)0x ax -<, 又20a >,∴不等式的解集为2|0x x a ⎧⎫<<⎨⎬⎩⎭. ············· 8分 综上所述:当0a =时,不等式解集为φ; 当0a <时,不等式解集为2|0x x a ⎧⎫<<⎨⎬⎩⎭; 当0a >时,不等式解集为2|0x x a ⎧⎫<<⎨⎬⎩⎭. ············· 10分 18.解:(Ⅰ)由图可知πππ=-=)42(4T ,22==Tπω, 2分又由1)2(=πf 得,1)sin(=+ϕπ,又(0)1f =-,得sin 1ϕ=-πϕ<||2πϕ-=∴, ························· 4分(Ⅱ)由(Ⅰ)知:x x x f 2cos )22sin()(-=-=π. ··········· 6分因为()(cos 2)[cos(2)]cos 2sin 22g x x x x x π=---=1sin 42x =. ····· 8分 所以,24222k x k ππππ-≤≤+,即 (Z)2828k k x k ππππ-≤≤+∈. ··· 10分故函数()g x 的单调增区间为[,] (Z)2828k k k ππππ-+∈. ········· 12分19.解: (Ⅰ)1133n n n a a ++=+,∴ 11133n n n na a ++=+,于是11n nb b +=+,∴{}n b 为首项和公差为1的等差数列. ·················· 4分 (Ⅱ)由 11b =,n b n = 得,3n na n =.∴3nn a n =⨯. ·········· 6分 1211323(1)33n n n S n n -=⨯+⨯++-⨯+⨯, 23131323(1)33n n n S n n +=⨯+⨯++-⨯+⨯,两式相减,得11223(333)n n n S n +=⨯-+++, ············ 10分解出113()3n n nS +=-+. ····················· 12分 分分分 分分 1423AB d =⨯分 ,552sin =A 25∴4sin 2sin cos 225A A A ==. ···················· 4分 ∵2sin 21==∆A bc S ABC ,∴5=bc . ··············· 6分 (Ⅱ)∵,552sin=A ∴532sin 21cos 2=-=A A . ············ 8分 ∵5=bc ,6=+c b ,∴A bc c b a cos 2222-+=)cos 1(2)(2A bc c b +-+=20=. ···· 10分∴52=a . ·························· 12分 22.解:(Ⅰ)因为124PF PF +=,所以2a =,········· ····· 2分 因为离心率为12,所以1c =,所以b = 所以椭圆方程为22143x y +=.· 4分(Ⅱ)假设存在满足条件的直线l ,易知点2F 在椭圆的内部,直线l 与椭圆一定有两个交点,设直线l 斜率为k ,点C 11(,)x y ,点D 22(,)x y直线l 的方程为(1)y k x =-, 由方程组22143(1)x y y k x ⎧+=⎪⎨⎪=-⎩. ·· 5分2222(43)84120k x k x k +-+-=得.··6分则22121202284,43243x x k k x x x k k ++===++,2002243(1)(1).4343k ky k x k k k -∴=-=-=++··8分又11F D FC =,所以1F 在CD 的垂直平分线上,又CD 的垂直平分线上方程为222314()4343k k y x k k k +=--++,所以222314(1)4343k k k k k =---++. 10分所以2530k +=,不成立, 所以不存在直线l ,使得11F D FC =. 综上所述,不存在直线l ,使得11F D FC = . ········ ·· 12分。
2013-2014学年第二学期高二数学(文)期末试卷(含答案)
2013-2014学年第二学期高二数学(文)期末试卷(含答案)(满分150 分,时间120 分钟)注意事项:1.考生应把班级、姓名、学号,写在密封线以内,写在密封线以外的无效。
2.请用钢笔、中型笔或圆珠笔把答案写在答题卡上。
3.考试结束后只上交答题卡,原试卷自己保存。
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中只有一项是符合题目要求的 )1.设集合{1,2}A =,则满足{1,2,3}A B ⋃=的集合B 的个数是( ) A .1 B .3 C .4 D .82.下列函数中,在其定义域内既是奇函数又是减函数的是( )A .R x x y ∈-=,3B .R x x y ∈=,sinR x x y ∈=, D .1(),2x y x R =∈ 3、设13log 5a =,153b =,0.315c ⎛⎫= ⎪⎝⎭,则有 ( ) A .a b c << B .c b a << C .c a b << D .b c a <<4.若lg a +lg b =0(其中a ≠1,b ≠1),则函数f (x )=a x 与g (x )=b x 的图象( )A .关于直线y =x 对称B .关于x 轴对称C .关于y 轴对称D .关于原点对称5.幂函数的图象过点(2,41),则它的单调增区间是( ) A .),0(+∞ B .),0[+∞ C .),(+∞-∞ D .)0,(-∞6、若函数()3222f x x x x =+--的一个正数零点附近的函数值用二分法逐次计那么方程32220x x x +--=的一个近似根(精确到0.1)为( )A .1.2B .1.3C .1.4D .1.57. “032>x ”是“0<x ”成立的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既非充分也非必要条件8.下列命题中是假命题的是 ( )A .(0,),>2x x sin x π∀∈ B .000,+=2x R sin x cos x ∃∈ C . ,3>0x x R ∀∈ D .00,=0x R lg x ∃∈9.设集合{|0},,A x x B =>=R 则从集合A 到集合B 的映射f 只可能是 ( )A.||x y x =→B. x y x 2=→C. x y x 2log =→D. )1(log 2+=→x y x10.给出如下四个命题①若“p 且q ”为假命题,则p 、q 均为假命题②命题“若b a >,则122->b a ”的否命题为“若b a ≤,则122-≤b a ” ③“11,2≥+∈∀x R x ”的否定是“11,2≤+∈∃x R x ”④在∆ABC 中,“B A >”是“B A sin sin >”的充要条件其中不正确...的命题的个数是( ) A .4 B .3 C .2 D .111.函数)10(||<<=a x xa y x的图象的大致形状是 ( )12、如果偶函数()f x 在区间[]1,6上是增函数且最大值是8,则()f x 在[]6,1-- 上是( )A .增函数,最大值8-B .增函数,最小值8-C .减函数,最大值8D .减函数,最小值8二、填空题:(5'×4=20')13、已知集合}1,1{-=A ,}1|{==mx x B ,且A B A =⋃,则m 的值为 。
辽宁省大连市第二十高级中学1415学年度高二上学期期末
辽宁省大连市第二十高级中学2014—2015学年度上学期期末考试高二数学文试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、设集合则“”是“”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件2、函数-的导数是()A、2-1x2B、-1x2C、x-1x2D、1 x23、若,则等于()A.B.C.D.4、已知为等比数列,,,则()A、B、C、D、5、设,则函数的最小值是()A、12B、27C、6D、306、已知抛物线过点A(1,2),设抛物线的焦点为F,则|FA|等于()A、6B、7C、5D、27、已知双曲线的一个焦点与抛物线的焦点重合,且双曲线的渐近线方程为,则该双曲线的方程为()A、B、C、D、8、已知为等差数列,其公差为-2,且是与的等比中项,为的前项和,,则的值为()A.-110 B.-90 C.90 D.1109、直线被椭圆所截的弦的中点坐标是()A、(, -)B、(-,)C、(, -)D、(-,)10、曲线在处的切线平行于直线,则点的坐标为()A.B.C.和D.和11、已知点P为椭圆上的一点,是椭圆的焦点,且,则的面积为()A、B、C、2 D、12、若直线l被圆所截的弦长不小于2,则l与下列曲线一定有公共点的是( )A 、B . C. D .卷Ⅱ二.填空题: 本大题共4小题,每小题5分,满分20分.13、曲线在点处的切线方程为__________;14、若实数y x ,满足⎪⎩⎪⎨⎧≥++≤-≥+-020022y x y x y x ,则的最大值为_______,最小值为______ .15、已知双曲线的两条渐近线的夹角为,则双曲线的离心率为16、已知椭圆22221,(0)x y a b a b+=>>与抛物线有一个公共的焦点,且两曲线的一个交点为,若,则椭圆方程为三、解答题:本大题共6题,共70分,解答应写出文字说明、证明过程或演算步骤17、(本小题满分10分)求抛物线过点的切线方程18、(本小题满分12分)已知f(x)=,(1)若函数有最大值178,求实数的值;(2)若不等式>对一切实数恒成立,求实数的取值范围;19、(本小题满分12分)已知数列为等差数列,,,数列的前项和为,且有(1)求、的通项公式;(2)若,的前项和为,求;20、(本小题满分12分)已知函数-的图象在=1处的切线为l ,求l 与两坐标轴围成的三角形面积的最小值.21、(本小题满分12分)如图,为抛物线的焦点,A (4,2)为抛物线内一定点,P 为抛物线上一动点,且的最小值为8。
2013-2014学年上学期期末考试高二数学试题及答案
2013—2014学年上学期期终考试试卷2012级数学试卷一、填空题:(每题3分,共24分)1. 过点(1,3)且与直线1y -=x 平行的直线方程是2. 过圆4x 22=+y 上一点)1,3(-P 的切线方程是3. 点A(-2,1)到直线0243:=--y x l 的距离为4. 已知直线a ∥b ,且a ∥平面α,则b 与平面α的位置关系是5. 平行于同一平面两条直线的位置关系为6. 在60°的二面角βα--m 的面α内有一点A 到面β的距离为3,A 在β上的射影为A ′,则A ′到面α的距离为7. 用一个平面截半径为25cm 的球,截面面积是π492cm ,则球心到截面的距离为 8.抛掷两颗骰子,则“两颗骰子点数相同”的概率为二、选择题(每题3分,共30分)1.若直线0=++c by ax 通过第一、三、四象限,则 ( ) A. 0,0>>bc ab B. 0,0<>bc ab C. 0,0><bc ab D. 0,0<<bc ab2. 若直线02x =++ay 和02x 3=-y 互相垂直,则a 等于 ( )A. 23-B. 32- C. 32 D. 233. 方程04222=++-+m y x y x 表示一个圆,则 ( ) A. 5≤m B. 5m < C. 51<mD. 51≤m4. 空间中与同一条直线都垂直的两条直线的位置关系是 ( ) A.平行 B.相交 C.异面 D.以上都可能5.如果平面的一条斜线长是它在这个平面上的射影长的3倍,则这条斜线与平面所成角的余弦值为 ( )A .31 B.322 C.22 D.326. 长方体一个顶点上的三条棱长分别是a ,b ,c ,那么长方体的全面积是( ) A. ca bc ab ++ B. 222c b a ++ C. abc 2 D. )(2ca bc ab ++7.已知两球的球面面积比为4︰9 ,则两个球的体积比为 ( ) A. 2︰3 B. 4︰9 C. 8︰27 D. 4︰278.一副扑克牌有黑、红、梅、方各13张,大小王各1张,从中任取一张,则不同取法的种数是 ( ) A. 4 B. 54 C. 413 D. 1349.由1,2,3,4,5五个数字组成 个没有重复数字的三位数偶数( ) A. 12 B. 24 C. 36 D. 4810.某校对全校3000名学生的肺活量进行调查,准备抽取500名学生作为调查对象,则上面所述问题中的总体是 ( ) A.3000名学生 B.3000名学生的肺活量 C.500名学生 D.500名学生的肺活量 三、计算题:(共24分)1.已知点()5,3A 是圆0808422=---+y x y x 的一条弦的中点,求这条弦所在直线方程.(8分)2.求圆2x 22=+y 上的点到直线03=--y x 的最长距离。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页 共7页2013~2014学年第一学期期末考试试卷高二数学(文科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分.考生作答时,将答案答在答题卡和答题纸上,在本试卷上答题无效.第I 卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.抛物线24y x =的焦点为( ) (A )(0,1) (B )(1,0) (C )(0,1)- (D )(1,0)-3. 已知命题:,,则是( ) (A )∈∃0x R,1cos 0≥x (B )∈∀x R,1cos ≥x(C )∈∀x R,1cos >x (D )∈∃0x R,1cos 0>x4. 已知函数()f x 的导函数()f x '的图象如图所示,那么函数()f x 的图象最有可能的是( )5.设,R a b ∈,那么“>1ab”是“>>0a b ”的( ) (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 6.可导函数在闭区间的最大值必在( )取得(A )极值点 (B )导数为0的点 (C )极值点或区间端点 (D )区间端点 7.)()()(0000limx f xx f x x f x '=∆-∆+→∆,其中x ∆( )(A )恒取正值或恒取负值 (B )有时可以取0(C )恒取正值 (D )可以取正值和负值,但不能取08. 下列说法正确的是( )(A )0R x ∃∈,00xe≤(B )对,a b ∀>则2ab =,22min ()4a b +=第2页 共7页(C )1a >,1b >是1ab >的充分条件 (D )0a b +=的充要条件是1ab=- 9.设等比数列{}n a 的公比2q =,前n 项和为n S ,则24a S 的值为( ) (A )154 (B )152 (C )74 (D )7210.已知12(1,0),(1,0)F F -是椭圆的两个焦点,过1F 的直线l 交椭圆于,M N 两点,若2MF N ∆的周长为8,则椭圆方程为( )(A )13422=+y x (B )13422=+x y (C )1151622=+y x (D )1151622=+x y 11.函数32()f x x bx cx d =+++的大致图象如图所示,则2212x x +等于( )(A )89(B )109(C )169(D )28912. 直线kx y =交双曲线22:143x y C -=于,A B 两点,P 为双曲线C 上异于,A B 的任意一点,则直线,PA PB 的斜率之积为( )(A )43 (B )34 (C)3 (D)2第II 卷二、填空题:本大题共4小题,每小题5分,共20分.13.双曲线22149x y -=的渐近线方程是 . 14. n S 为等差数列{}n a 的前n 项和,266a a +=,则=7S . 15.曲线ln y x =在点(1,0)处的切线方程为 .16. 已知双曲线:C 2221(0,1)y x b b b-=>≠的左右焦点为12F F ,,过点1F 的直线与双曲线C左支相交于,A B 两点,若22||||2||AF BF AB +=,则||AB 为 .三、解答题:本大题共小6题,共70分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分10分)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,A 为B ,C 的等差中项. (Ⅰ)求A ;(Ⅱ)若a =2,△ABC 的面积为3,求b ,c 的值.第3页 共7页18.(本小题满分12分)不等式260x x --≤解集为M ,不等式2280x x +->解集为N ,不等式22320x ax a -+<)0(>a 解集为P . (Ⅰ) 求M N I ;(Ⅱ)若“M N I ”是“P ”的充分条件,求实数a 的取值范围.19.(本小题满分12分)已知函数32()23128f x x x x =--+. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若[2,3]x ∈-,求函数()f x 的值域. 20.(本小题满分12分)已知离心率e =2222:1(0)x y C a b a b +=>>一个焦点为(-1,0). (Ⅰ)求椭圆C 的方程;(Ⅱ) 若斜率为1的直线l 交椭圆C 于,A B 两点,且||AB =l 方程.第4页 共7页21.(本小题满分12分)已知抛物线的顶点在坐标原点O ,对称轴为x 轴,焦点为F ,抛物线上一点A 的横坐标为2,且16=⋅。
(Ⅰ)求抛物线的方程;(Ⅱ)过点)0,8(M 作直线l 交抛物线于B ,C 两点,求证:OC OB ⊥ . 22.(本小题满分12分)已知函数21()ln 2f x x a x =+(0a <). (Ⅰ)若1a =-,求函数()f x 的极值;(Ⅱ)若0x ∀>,不等式()0f x ≥恒成立,求实数a 的取值范围.2013~2014学年第一学期期末考试参考答案与评分标准高二数学(文科)说明:一、本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制订相应的评分细则.二、对解答题,当考生的解答在某一步出现错误时,如果后继部分的解答未改变该题的内容和难度,可视影响的程度决定后继部分的给分,但不得超过该部分正确解答应得分数的一半;如果后继部分的解答有较严重的错误,就不再给分.三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分.一、选择题1.B ;2.A ;3.D ;4. A ;5.B ;6.C ;7. D ;8.C ;9.B ;10.A ;11.C ;12. B . 二、填空题 13.x y 23±=;14.21;15.1y x =-;16.4. 三、解答题17.解:(Ⅰ)∵A 为B ,C 的等差中项, 2A B C =+,2分 ······································第5页 共7页∵A B C π++=,∴A =π3. ····························································································· 4分(Ⅱ)△ABC 的面积S =12bc sin A =3,故bc =4. ····························································· 6分而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. ·········································································· 8分 解得b =c =2. ················································································································ 10分18.解:(Ⅰ)∵ 260x x --≤,∴{|23}M x x =-≤≤. ············································································ 2分 ∵2280x x +->,∴{|2N x x =>或4}x <-. ··················································································· 4分 ∴实数M N I 为{|23}x x <≤. ·····························································································································5分 (Ⅱ)由22430x ax a -+<得()(2)0x a x a --<,又0a >,∴{|2}P x a x a =<<, ··········································································································· 7分 又“M N I ”是“P ”的充分条件,∴ ⎩⎨⎧>≤,32,2a a . ············································································ 9分∴实数a 的取值范围]2,23(.······················································································································· 12分19.解:(Ⅰ)2()=6612f x x x --, . 当()0f x >,时,2x >或1x <-; ····························································································································· 2分 当()0f x <,时, 12x -<<. ······································································································································· 4分 ∴函数()f x 的单调增区间为(,1)-∞-和(2,)+∞; 函数()f x 的单调减区间为(1,2)-。
