简化真值表
电动机控制逻辑简化真值表

电动机控制逻辑简化真值表•PLC的控制程序可使用类似数字电路的功能块图实现。
LQD30A48-3V31V5REJ根据控制要求:在停机状态下按下正转启动按钮SB1,则电动机正转启动并保持正转状态;在停机状态下按下反转启动按钮SB2,则电动机反转启动并保持反转状态;在任何状态下按停止按钮SB3,则电动机立即停机。
•由此可列出电动机控制逻辑简化真值表,如表I-l所列。
其中,“1”表示PLC“软元件”的状态•为1,即触点闭合或线圈得电;“O”表示PLC“软元件”的状态为0,即触点断开或线圈失电;“T”表示输出元件操作前的状态现态;“T+l”表示输出元件操作完成后的状态(次态)。
•在STEP 7环境下,FBD语言的逻辑“与”指令及逻辑“或”指令与数字电路中所讲的逻辑“与门”及逻辑“或门”的符号及意义相同,FBD语言的赋值指令用方框内的“一”表示。
由此可画出电动机正、反转控制功能块图FBD 语言程序,如图1-37所示。
•图1-36正、反转控制逻辑图图1-37正、反转控制FBD语言程序•当然,在STEP 7的梯形图LAD语言环境下,也可以用若干个触点(或逻辑块)的串联来表示其逻辑“与”的关系(逻辑“与”指令),用若干个触点(或逻辑块)的并联来表示其逻辑“或”的关系(逻辑“或”指令),用一对圆括弧“()”表示逻辑输出(赋值指令)。
•一个完整的逻辑关系必须从左边一条母线开始向右绘制,逻辑赋值指令必须与最右边一条母绒相连,能流只能通过左母线、经状态为1的触点和赋值指令到右母线形成能流回路。
按照这种方法可画出电动机正、反转控制梯形图LAD语言程序,如图1-38所示。
其中的常开触点和常闭触点的符号及意义与继电接触式控制系统中的常开触点和常闭触点的符号及意义相同。
数字逻辑基础卡诺图化简
101
0
110
0
1 2020/8/14 1 1
1
14
练习:三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
111
1
2020/8/14
15
(2)从最小项表达式画卡诺图 把表达式中所有的最小项在对应的小方块中填
入1,其余的小方块中填入0。
例4: 画出函数Y(A、B、C、D)= ∑m(0,3,5,7,9,12,15) 的卡诺图。
① 无关项的概念
对应于输入变量的某些取值下,输出函数的值可 以是任意的(随意项、任意项),或者这些输入变量的 取值根本不会(也不允许)出现(约束项),通常把这 些输入变量取值所对应的最小项称为无关项或任意项, 在卡诺图中用符号“×”表示,在标准与或表达式中用 ∑d( )表示。
例:当8421BCD码作为输入变量时,禁止码1010~ 1111这六种状态所对应的最小项就是无关项。
相邻 相邻
② 几何相邻的必须
逻辑相邻:变量的 取值按00、01、11、 10的顺序(循环码 ) 排列 。
图1-11 三变量卡诺图的画法
2020/8/14
12
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”: 上下相邻,左右相 邻,并呈现“循环 相邻”的特性,它 类似于一个封闭的 球面,如同展开了 的世界地图一样。
复习:
真值表--逻辑表达式(化简)--逻辑电路图
例:三变量表决逻辑 Y=? 逻辑图?
2020/8/14
简化命题逻辑中的真值表应用

简化命题逻辑中的真值表应用命题逻辑是数理逻辑的一个分支,研究命题之间的逻辑关系。
在命题逻辑中,真值表是一种常用的工具,用于确定命题的真值。
然而,当命题逻辑问题变得复杂时,真值表的应用变得繁琐且易错。
因此,简化命题逻辑中的真值表应用成为了一个重要的课题。
简化命题逻辑中的真值表应用可以通过引入真值表的规则和技巧来实现。
首先,我们可以利用真值表的对称性质来简化计算。
例如,当命题的真值表中有对称的命题时,我们可以利用对称性质将这些命题合并为一个命题,从而减少真值表的大小。
这种简化方法可以大大减少计算量,提高计算效率。
其次,我们可以利用真值表的重复性质来简化计算。
当命题的真值表中有重复的命题时,我们可以利用重复性质将这些命题合并为一个命题,从而减少真值表的大小。
这种简化方法可以减少计算步骤,提高计算速度。
另外,我们还可以利用真值表的规律性质来简化计算。
例如,当命题的真值表中存在某种规律时,我们可以利用这种规律来推导出其他命题的真值,从而减少计算步骤。
这种简化方法可以提高计算的准确性和可靠性。
除了利用真值表的规则和技巧来简化计算,我们还可以借助计算机技术来简化命题逻辑中的真值表应用。
计算机可以高效地处理大量的数据和复杂的计算,因此可以用来自动化地生成和简化真值表。
通过编写相应的程序,我们可以将命题逻辑问题转化为计算机程序,并利用计算机的计算能力来简化真值表的生成和计算过程。
简化命题逻辑中的真值表应用不仅可以提高计算效率和准确性,还可以帮助我们更好地理解和应用命题逻辑。
通过简化真值表的过程,我们可以深入理解命题之间的逻辑关系,发现其中的规律和特点。
这些规律和特点不仅可以帮助我们更好地解决命题逻辑问题,还可以为我们在其他领域中应用逻辑思维提供指导和启示。
总之,简化命题逻辑中的真值表应用是一个重要的课题。
通过引入真值表的规则和技巧,借助计算机技术,我们可以简化真值表的生成和计算过程,提高计算效率和准确性。
这不仅可以帮助我们更好地解决命题逻辑问题,还可以深入理解和应用命题逻辑的规律和特点。
逻辑符号及真值表

逻辑符号及真值表
这些逻辑符号可以用于构建命题逻辑中复杂命题的逻辑结构,从而方便我们进行推理和论证。
在使用逻辑符号时,通常会用到真值表来验证命题的逻辑结构。
真值表是一种用来列出命题不同取值组合的表格。
在真值表中,每一行代表一种取值组合,每一列代表一个命题变量或逻辑符号。
通过对每个命题变量进行相应的逻辑运算,可以得出最终命题的真值(T 或F)。
例如,在合取命题p ∧ q中,p和q为命题变量,∧为逻辑符号。
我们可以列出如下的真值表:
p | q | p ∧ q
--|---|------
T | T | T
T | F | F
F | T | F
F | F | F
从表中可以看出,在p为真、q为真的情况下,p ∧ q的真值为真(T)。
而在其他情况下,其真值为假(F)。
通过使用逻辑符号和真值表,我们可以更加清晰地理解和分析命题逻辑中的复杂结构,从而更加准确地进行推理和论证。
- 1 -。
简化真值表方法

简化真值表方法简化真值表方法是一种用于简化布尔函数的方法,通过构建真值表并进行逐行比较,逐步确定布尔函数的简化形式。
本文将介绍简化真值表方法的基本原理和步骤,并通过一个例子详细说明该方法的具体应用。
简化真值表方法的基本原理是将布尔函数的真值表按照输出结果的不同进行分类,并将相同输出结果的行合并为一个组。
首先,我们需要根据布尔函数的输入变量的个数,构建一个包含所有可能输入组合的真值表。
然后,根据布尔函数的输出结果,将真值表的行分为不同的组。
接下来,我们逐个比较组内的行,找出其中的共同特征,并将其表示为布尔函数的简化形式。
最后,将简化形式表示为布尔函数的逻辑表达式或真值表。
下面,我们通过一个例子来详细说明简化真值表方法的具体步骤。
假设我们有一个布尔函数f(A, B, C),其真值表如下:```A B C | f(A,B,C)0 0 0 | 00 0 1 | 00 1 0 | 10 1 1 | 11 0 0 | 01 0 1 | 11 1 0 | 11 1 1 | 1```我们可以将真值表的行按照输出结果的不同进行分类,得到以下四个组:```组1:A=0, B=0, C=0, f(A,B,C)=0组2:A=0, B=0, C=1, f(A,B,C)=0组3:A=1, B=0, C=0, f(A,B,C)=0组4:A=0, B=1, C=0, f(A,B,C)=1A=0, B=1, C=1, f(A,B,C)=1A=1, B=0, C=1, f(A,B,C)=1A=1, B=1, C=0, f(A,B,C)=1A=1, B=1, C=1, f(A,B,C)=1```接下来,我们逐个比较组内的行,找出其中的共同特征。
对于组1,所有行的输出结果均为0,因此可以将其简化为A'BC'。
同样地,对于组2、组3和组4,我们可以得到以下简化形式:```组1:A'BC'组2:A'BC组3:ABC'组4:BC```我们将简化形式表示为布尔函数的逻辑表达式或真值表。
命题公式真值表
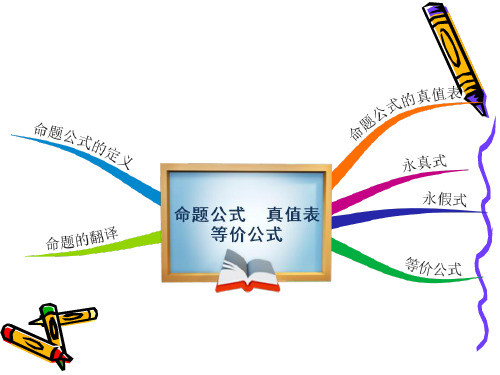
定义 1-3.1 命题演算的合式公式,规定为: (1)单个命题变元本身是一个合式公式; (2)如果 A 是合式公式,那么 A 是合式公式; (3)如果 A 和 B 是合式公式,那么
A B , A B , A B , A B 是合式公式;
(4)当且仅当能够有限次地应用(1)、(2)、(3) 所得到的包含命题变元,联结词和括号的字符串 是合式公式.
T F F T
1-4 真值表与等价公式
(5) ( P Q) (P Q) 的真值表为:
P
Q
PQ
P
Q
( P Q)
P Q
( P Q) (P Q)
T T F F
T F T F
T F F F
F F T T
F T F T
F T T T
F T T T
T T T T
1-4 真值表与等价公式
1.真值表
定义1-4.1 在命题公式中,对于分量指派真值的各种可能 组合,就确定了这个命题公式的各种真值情况,把它汇列成 表,就是命题公式的真值表.
例 2 构造下列命题公式的真值表: (1) P Q ; (3) ( P Q) P ; (5) ( P Q) (P Q) . (2) P Q ; (4) ( P Q) (P Q) ;
1-4 真值表与等价公式
解 (1)
P Q 的真值表为:
P
Q
P Q
T T F F
T F T F
T F T T
(2)
P Q 的真值表为:
P
Q
P Q
T T F F
T F T F
T F T T
1-4 真值表与等价公式
第三节 逻辑函数的图解化简法
A 0 B 0 C 0 D 0 0 0 0 1 0 0 1 1 0 0 1 0 0 1 1 0 0 1 1 1 0 1 0 1 0 1 0 0 1 1 0 0 1 1 0 1 1 1 1 1 1 1 1 0 1 0 1 0 1 0 1 1 1 0 0 1 1 0 0 0
5 变量卡诺图 变量数 n = 5 在卡诺图 上有 25 = 32 个小方格,对 应32个最小项。每个小方格 有5个相邻格。
3、 将每个与项相加,得到化简后的函数。
F BC C D AB D ABD ABCD
例2:化简
F m 2,3,5,7,8,10,12,13
本题直接给出最小项之和地形式,因此,在卡诺图 对应小方格处直接填“1”。 解: AB AB
CD 00
00
01
11
10
1 1 1 1 1 1
0
1 1 1
1
1 0 0
1
1 1
1
0 0
1
1 0
A 4 变量卡诺图 A AB 变量数 n = 4 在卡诺图上有 CD 00 01 11 10 ABC D ABC D ABC D ABC D 4 2 = 16 个小方格,对应十六个 00 m0 m4 m12 m8 最小项。每个小方格有四个相邻 C ABCD ABCD ABCD ABCD 01 m1 m5 m13 m9 格。 DD ABCD ABCD ABCD ABCD m0 和m1、m2、m4 、m8 相邻。 11 m m m15 m11 7 3 m5 和m1、m4、m7 、m13 相邻。 C ABC D ABC D ABCD ABC D 10 m m m14 m10 2 6 m9 和m1、m8、m11 、m13 相邻。 B 四变量格雷码排列:
命题逻辑的真值表和范式
命题逻辑的真值表和范式命题逻辑是研究命题(陈述句)之间的逻辑关系的一种逻辑学分支。
在命题逻辑中,我们使用真值表和范式来表示和分析命题的逻辑结构。
本文将介绍真值表和范式在命题逻辑中的重要性和应用。
一、真值表真值表是用来表示和计算命题的真假值情况的一种工具。
它列举了命题中每个命题变量的可能取值情况,并根据命题之间的逻辑运算规则计算出整个命题的真假值。
真值表通常由命题变量和逻辑运算符组成。
例如,对于两个命题变量P和Q,我们可以构建如下的真值表:P | Q | P∧Q | P∨Q | P→Q | P↔Q----------------------T | T | T | T | T | T----------------------T | F | F | T | F | F----------------------F | T | F | T | T | F----------------------F | F | F | F | T | T在真值表中,"T"代表命题的真值为真,"F"代表命题的真值为假。
通过观察真值表,并根据命题之间的逻辑运算规则,我们可以推断出命题之间的逻辑关系。
例如,P∧Q表示P与Q的合取,只有当P和Q 都为真时,合取才为真。
类似地,P∨Q表示P与Q的析取,只要P和Q中至少有一个为真,析取就为真。
真值表为我们提供了一种清晰的逻辑分析工具,能够帮助我们理解和推理命题之间的逻辑关系。
二、范式范式是用来简化和表示复杂命题的一种方法。
它将命题表示为若干个简单命题之间的逻辑连接,并以逻辑运算符为界限构成。
在命题逻辑中,最常见的范式有析取范式(DNF)和合取范式(CNF)。
析取范式将命题表示为若干个合取式之间的析取,而合取范式将命题表示为若干个析取式之间的合取。
例如,对于命题P、Q和R,我们可以将它们表示为析取范式和合取范式。
析取范式(DNF):(P∧Q∧¬R)∨(¬P∧Q∧R)∨(¬P∧¬Q∧R)合取范式(CNF):(P∨¬Q∨¬R)∧(¬P∨Q∨¬R)∧(¬P∨Q∨R)范式的使用可以帮助我们简化和理解复杂的逻辑表达式。
简化真值表
简化真值表
真值表是逻辑学中的重要工具,用于描述逻辑运算中各个输入变量对应的输出值。
但是,对于较为复杂的逻辑运算,真值表往往过于繁琐,难以阅读和分析。
因此,简化真值表的方法成为逻辑学研究的一个重要课题。
简化真值表的基本思路就是寻找逻辑运算中的规律和重复的模式,以此将多个输入变量对应的输出值合并为一个表项。
其中,最常见的简化方法是使用卡诺图法,将真值表中的所有表项按照相邻和重叠的方式进行组合,以得到最简化的逻辑表达式。
除了卡诺图法,还有一些其他的简化方法,例如奎因-麦克拉斯基方法和Petrick方法等。
这些方法不同于卡诺图法,其基本思路是将真值表中的所有表项转化为逻辑方程,并对方程进行简化。
简化真值表的方法可以大大缩减真值表的大小,从而使得逻辑运算更加清晰明了。
同时,简化后的逻辑表达式也更加精简,便于进行逻辑设计和优化。
因此,简化真值表是逻辑学研究中不可或缺的重要内容。
- 1 -。
简化真值表方法
简化真值表方法简化真值表方法是一种用于简化逻辑函数的方法。
逻辑函数可以用真值表来表示,真值表是根据逻辑变量的取值情况列出的函数的取值情况。
简化真值表方法通过对真值表中具有相同取值的项进行合并,从而得到简化后的逻辑函数。
本文将介绍10条关于简化真值表方法的方法,并展开详细描述。
希望通过本文的介绍,读者能够更好地了解和应用简化真值表方法。
1. 真值表的排列:将逻辑函数的输入变量和输出变量的可能取值列出,并按照字典序的方式排列。
这个排列是为了后续的分组和合并做准备。
2. 真值表的展开:将逻辑函数的真值表完全展开,即将逻辑函数的所有输入变量的所有可能取值与对应的输出变量的取值都列出。
这样可以清楚地了解逻辑函数的取值情况,并对后续的分组和合并操作有所准备。
3. 相同取值项的合并:观察真值表中具有相同取值的项,将它们合并成一个项。
合并后的项的取值为相同的取值,合并后的项的对应输出取值为原始相同取值项的输出取值的共同取值。
4. 不变项的提取:观察真值表中取值始终不变的输入项,将它们提取出来作为不变项。
不变项的取值与输出变量的取值无关,可以直接确定其输出取值。
5. 组合合并:将合并后的项按照输入变量的排列方式进行组合合并。
将具有相同输入变量取值的项进行合并,合并后的项的输出变量取值为合并前的项中输出变量取值的共同取值。
6. 重复步骤4和步骤5:重复执行步骤4和步骤5,直到不能再进行合并为止。
每一次合并都会减少项的数量,使得逻辑函数得到更简化的形式。
7. 零项和全项的处理:观察真值表中的全0项和全1项,将它们提取出来作为零项和全项。
全0项的输出取值为0,全1项的输出取值为1。
8. Minterm的提取:观察真值表中输出变量为1的项,将它们提取出来作为Minterm。
Minterm的输出变量为1,其他输入变量的取值与Minterm一致。
9. Maxterm的提取:观察真值表中输出变量为0的项,将它们提取出来作为Maxterm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简化真值表方法(归谬赋值法)
1.转换:把推理式转换成蕴涵式。 • p→q, p ├ q → , • (p→q) ∧ p → q → 2.假设:假设该蕴涵式为假。 (p→q) ∧ p → q → 0
3.赋值:以蕴涵为假为条件,逐层赋 值。 注意:赋值过程中,要尽可能使假 设成立,即尽可能使前件真后件假成 立。
简化真值表方法(归谬赋值法)
• • • • 原理——归谬法 p →q ∧¬ ├ ¬p ∧¬q p→q, p→¬ ├ ¬p →¬q → →¬ 归谬赋值法以假设一推理无效为出发点(即p)。 p) 然后对表示一推理的蕴涵式赋值。 • 1.若赋值过程中未出现矛盾,则表示假设成立, 可判定该推理无效。 • 2.若赋值过程中出现矛盾(即q ∧¬ ),则表示假 ∧¬q 设不成立,假设被否定,可判定该推理有效。
用简化真值表方法检验下 ¬r) ├ (q ∧ s) ,→ , ¬ ∨ (¬p∨q) ∧(r→ s) ∧¬ (¬p∨ ¬r) → (q ∧ s) ¬ → ¬ ∨ • 0 100 • 001 • 000
赋值技巧
1 变项赋值一般从结论(后件)开始。理由: 结论为假,容易赋值; 结论为一个命题,相对较简单。 2 若结论为假有不止一种赋值,则要进行每一种 赋值的推演: ① 若每一种推演都有效,则可判定该推理有效。 ② 只要有一种推演无效,则可判定该推理无效。
简化真值表
• ├与→ 前提├ 结论 件→ 件 真 真
• 必然性推理 • 蕴 • 共同
推理式转换成蕴涵式
• • • • • • • p→q, p ├ q → , (p→q) ∧ p → q → 在真值表上看该式是否是永真式。 在真值表上看该式是否是永真式。 是: 有效 前件(前提) 后件(结论)必真。 前件(前提)真,后件(结论)必真。 不是: 不是:无效 前件(前提) 后件(结论)不必真。 前件(前提)真,后件(结论)不必真。
判定:产生矛盾,假设不成立,该推理有效。
p→q , ¬ q→ p├ ¬ (p ∀q)
(p→q )∧ (¬ q→ p)→ ¬ (p ∀ q) 110 1 1 0110 0 1 1 0 0 (p→q )∧ (¬ q→ p)→ ¬ (p ∀ q) 011 1 0 110 0 0 0 1 1
判定:不产生矛盾,假设成立,该推理无 效。
习题
一、填空 1. 若p取值为假,q取值为真 ,则p→q取值为 , ¬ p→¬q取值为 。 ,q取值 2. 若“p→q”取值为假,则p取值为 为 。 3. 若p→q取值为假, p∀q取值为真 ,则p取值 为 ,q取值为 。 必真。 4. 若p∧q取值为假, p ∨ q取值为真 ,则 ∧ • ⑴ p←q∨p ⑵ q→¬p∧q ⑶ ¬p→q∨¬p • ⑷ ¬p∧(q← p) ⑸ p↔(¬p∧q) ⑹ p←q∨¬p • ⑺q ∨p←p ⑻ ¬p←q∧p 5.与”要么鱼死,要么网破。“等值的命题是 (三个不同形式的命题) 。
真值表检验推理的有效性
p 1 1 0 0 q 1 0 1 0 (p→q) ∧ p → 1 0 0 0 → 1 1 1 1 q 1 0 1 0
真值表检验推理的有效性
p 1 1 0 0 q 1 0 1 0 (p→q) ∧ ¬ p → 0 0 1 1 → ¬q 1 1 0 1 0 1 0 1
真值形式中真值联结词的结合力
复习
不相容选言命题的定义、联结词、形式、 逻辑特性。(有且只有一真为真;其余为假。 引申:∀ 为真,选言肢有且只有一真, ∀ 为 假,选言肢全假或有二个以上为真。 有效推理式和推理规则: 1.否定肯定式(否肯式) p∀q, ¬ p ┣ q 2.肯定否定式(肯否式) p∀q,p ┣ ¬q 推理规则: 否定一部分肢,则可肯定另一部分肢。 肯定一部分肢,则可否定另一部分肢。
二、检验下列推理是否有效
• • • • p→(q→r), q→(p→r) ┣ (p∨q)→r ¬p∨q∨r, ¬r ┣ ¬p∧q ¬q→¬p, r→s, (s∨q)→t, ¬t ┣ ¬(p∨r) r→s, q→p, p→¬s ┣ ¬(¬q→¬r)
1
(p→q) ∧ p → (p→q) → (p→q) → 1 (p→q) → 10 (p→q) → 010
简化真值表方法的检验过程
→ q 0 ∧p → q 1 0 0 ∧ p → q 1 1 0 0 ∧ p → q 11 0 0 ∧ p → q 1 1 0 0
2 3 4 5
(p→q) ∧ p → q → 110 1 1 0 0 0 判定:产生矛盾,假设不成立,该推理有效。 即:p、q无论如何赋值,该推理都能保证前提真、结论必真。 6
1 (p→q) ∧ p → → 0 → 0 q
2 (p→q) ∧ p → 1
q 0
简化真值表方法的检验过程
→ ¬q 0 2 (p→q) ∧ ¬ p → ¬ q → 1 0 0 3 (p→q) ∧ ¬ p → ¬ q → 1 1 1 0 0 1 4 (p→q) ∧ ¬ p → ¬ q → 11 1 10 0 01 5 (p→q) ∧ ¬ p → ¬ q → 011 110 0 0 1 判定:无矛盾,假设成立,该推理无效。 即:当p赋值为假,q赋值为真时,该推理不能保证前提真、 结论必真。 1 (p→q) ∧ ¬ p →
习题
一、填空 1. 若p取值为假,q取值为真 ,则p→q取值为 1 , ¬ p→¬q取值为 0 。 2. 若“p→q”取值为假,则p取值为 1 ,q取值为 0 。 3. 若p→q取值为假, p∀q取值为真 ,则p取值为 1 ,q取值为 0 。 4. 命题“并非如果买股票,就会发大财。”的命题 形式是 并非如果p,那么q , 真值形式是 ¬( p→q) 。 5.与”要么鱼死,要么网破。“等值的命题是 或者鱼死,或者网破,但不会鱼也死,网也破 。 或者鱼死但网不破,或者鱼不死但网破。 鱼死当且仅当网不破。
形式证明的方法
严格析取定义律 ┣ (p ∀ q) ↔ (p ∧ ¬q) ∨ (¬p ∧ q) ┣ (p ∀ q) ↔ (p ∨ q) ∧ ¬ (p ∧ q) 否定严格析取律 ┣ ¬ (p∀q) ↔ (p ∧ q) ∨ (¬p ∧ ¬q) ∀ ┣ ¬ (p∀q) ↔ (p↔q)
复习
充分条件假言命题的定义、联结词、形式、逻辑 特性。(前真后假为假;其余为真。引申:前真后 必真,后假前必假。) 有效推理式和推理规则: 1.肯定前件式(肯前式) p→q, p ┣ q 2.肯定否定式(肯否式) p→q, ¬ q ┣ ¬p 推理规则: 1.肯定前件就要肯定后件,肯定后件不能肯定或否定 肯定前件就要肯定后件, 肯定前件就要肯定后件 前件; 前件; 2.否定后件就要否定前件,否定前件不能肯定或否定 否定后件就要否定前件, 否定后件就要否定前件 后件。 后件。
简化真值表方法的检验过程
1 2 3 4 4 (p→q) ∧(r→ s) ∧(p∨ r) → (q∨s) → → ∨ ∨ 0 (p→q) ∧(r→ s) ∧(p∨ r) → (q∨s) → → ∨ ∨ 1 1 0 0 (p→q) ∧(r→ s) ∧(p∨ r) → (q∨s) → → ∨ ∨ 1 1 1 1 1 0 000 (p→q) ∧(r→ s) ∧(p∨ r) → (q∨s) → → ∨ ∨ 0 1 0 1 0 1 0 1 1 10 0 000 (p→q) ∧(r→ s) ∧(p∨r) → (q∨s) → → ∨ ∨ 0 1 0 1 0 1 0 1 0 10 0 000 0
• ¬、∧、∨、∀、→、←、↔的结合力依次减 → 。(… 最强。 弱。(…)最强。 • 1+2*3=7 • 1+(2*3)=7 • p→¬ ∧p∨r ↔q∀ →¬ ∧q →¬q∧ ↔q∀r→¬ →¬p∧ • 省去的括号如下: 省去的括号如下: • (p→¬ ∧p∨r) ↔(q∀r→¬ ∧q) →¬q∧ →¬p∧ ) →¬ • (p→((¬q∧p)∨r)) ↔((q∀r)→(¬p∧q)) (p→ ¬ ∧ ((q → ¬ ∧
6.充分条件假言推理的规则是 1.肯定前件就 肯定前件就 要肯定后件, 要肯定后件,肯定后件不能肯定或否定前 否定后件就要否定前件, 件;2.否定后件就要否定前件,否定前件 否定后件就要否定前件 不能肯定或否定后件。 不能肯定或否定后件。 7.蕴涵定义律和否定蕴涵律的表达式是 p→q ↔ ¬ p∨q和 ¬(p→q) ↔ p∧¬q。 → ∨ → ∧ 8与命题“如果人没有自知之明,就要犯错 误。”矛盾的合取命题是虽然人没有自知 之明,但不犯错误。 与之等值的析取命题 是或者人有自知之明,或者要犯错误。
