小学六年级数学圆的周长和面积提高练习题
小学六年级圆环的练习题

小学六年级圆环的练习题圆环是小学六年级数学学习中的重点内容之一。
通过练习圆环题目可以帮助学生巩固对圆环的认识和运用,提高数学思维和解题能力。
本文将为大家提供一些小学六年级圆环的练习题,以帮助学生更好地理解和应用相关知识。
1. 题目一:已知圆的半径为3cm,求其周长和面积。
解析:周长的公式为C=2πr,面积的公式为S=πr²。
将半径r=3cm 代入公式中计算即可得到结果。
周长C=2π×3≈18.85cm,面积S=π×3²≈28.27cm²。
2. 题目二:已知一个圆的周长为25.12cm,求其半径和面积。
解析:已知周长C=25.12cm,我们可以通过周长的公式推导出半径的计算公式r=C/(2π)。
将周长C=25.12cm代入计算可得半径r≈4cm。
接下来,我们可以通过半径的公式S=πr²求得面积S≈50.27cm²。
3. 题目三:一个圆的直径等于另一个圆的半径的两倍,如果小圆的周长为18.84cm,求大圆的周长和面积。
解析:我们设小圆的半径为r,由题意可知大圆的半径为2r。
已知小圆的周长C=18.84cm,我们可以通过周长的公式求得小圆的半径r≈3cm。
而大圆的半径为2r≈6cm。
再利用周长的公式C=2πr,我们可以求得大圆的周长C=2π×6≈37.7cm。
同样,根据面积的公式S=πr²,大圆的面积S=π×6²≈113.1cm²。
4. 题目四:已知一个圆的周长与直径的比值为π,求其半径和面积。
解析:已知周长与直径的比值C/d=π,我们可以推导出周长与半径的比值C/r=2π。
由于周长与半径的比值为常数,我们可以设周长为C,半径为r,则C/r=2π。
根据题意,可以得到周长C=r×2π,将此式代入C/r=2π中可得r×2π/r=2π,即2π=2π,该等式恒成立。
因此,我们无法求出具体的半径和面积。
(完整)六年级数学圆的面积与周长练习题

(完整)六年级数学圆的面积与周长练习题圆的练题一、选择题1、圆周率π的值()。
A等于3.14 B大于3.14 C小于3.142、一个圆的半径2米,那么它的周长和面积相比,()。
A面积大B周长大C同样大D无法比较3、把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长()。
A等于圆周长B大于圆周长C小于圆周长D无法比较4、圆的直径扩大2倍,它的面积扩大()。
A 2倍B 4倍C 6倍D无法确定5、圆中最长的线段是圆的()。
A周长B直径C半径D无法确定6、周长相等的两个圆的面积()。
A相等B不相等C无法比较7、一个正方形和一个圆的周长相等,它们的面积相比()。
A正方形大B圆大C相等D无法比较8、画圆时,()决定圆的位置,()决定圆的大小。
A圆规B半径C圆心D无法确定9、周长相称的长方形、正方形和圆,()面积最大。
A长方形B正方形C圆D无法确定10、小圆半径4厘米,大圆半径6厘米,大、小圆直径的比是();大、小圆周长的比是();大、小圆面积的比是()。
A 2:3B 3:2C 4:9D 9:411、一个圆的半径扩大a倍,直径扩大()倍,周长扩大()倍,面积扩大()倍。
A 2B aC 2a D∏E 2∏F a215、圆的大小与下面哪个条件无关。
()A半径B直径C周长D圆心的位置16、下面的图形只有两条对称轴的是()A长方形B正方形C等边三角形D圆17、在一个长5厘米、宽3厘米的长方形中画一个最大的圆,它的半径是()。
A 5厘米B 3厘米C 2.5厘米D 1.5厘米18、一个直径1厘米的圆与一个边长1厘米的正方形相比,它们的面积()。
A圆的面积大B正方形的面积大C一样大D无法比较二、判断题:1、一个圆的直径扩大2倍,它的半径扩大()倍,它的周长扩大()倍。
2、两个圆的半径的比是2:3,它们直径的比是(),周长的比是()。
3、一个圆的直径扩大4倍,半径扩大()倍,周长扩大()倍。
4、画一个周长12.56厘米的圆,圆规两脚间的距离是()厘米。
小学六年级圆数学练习题

小学六年级圆数学练习题
在小学六年级的数学学习中,练习题是巩固和运用所学知识的重要方式之一。
下面将给出一些小学六年级圆数学练习题,供同学们进行练习和巩固。
练习题1:圆的性质
1. 已知一个圆的半径为5cm,求该圆的直径和周长。
2. 一个圆的半径为8cm,求该圆的面积。
练习题2:圆的直径、半径与周长的关系
1. 一个圆的直径为12cm,求该圆的半径和周长。
2. 已知一个圆的周长为20π cm,求该圆的半径和直径。
练习题3:圆的面积
1. 一个圆的半径为6cm,求该圆的面积。
2. 已知一个圆的面积为36π cm²,求该圆的半径。
练习题4:圆的运算
1. 一个圆的直径为10cm,求该圆的周长和面积。
2. 已知一个圆的周长为24π cm,求该圆的直径和面积。
练习题5:圆与其他几何图形的关系
1. 一个正方形的边长为8cm,将该正方形的四个顶点与圆心连接,求圆的半径和周长。
2. 一个长方形的长为10cm,宽为6cm,将该长方形的四个顶点与圆心连接,求圆的半径和面积。
练习题6:圆的综合运用
1. 一个圆的半径为12cm,在该圆内画一个直径为10cm的圆,求两个圆的面积差。
2. 一个圆的直径为16cm,从该圆的外切正方形上剪去一个内切正方形,剩下的图形的面积是多少?
以上是一些小学六年级圆的数学练习题,同学们可以按照自己的学习进度和能力进行解答。
通过练习与巩固,相信大家能更好地掌握圆的性质和运用技巧,提升数学水平。
祝同学们学习进步!。
小学六年级《圆的面积》练习题及答案(基础+提升)

小学六年级《圆的面积》练习题一.选择题(共6题,共12分)1.钟楼上的大钟分针长1米,分针针尖60分钟走了()米。
A.3.14B.6.28C.12.562.一个圆的周长是15.7厘米,那么它的半圆的周长是()厘米。
A.7.85B.10.35C.12.853.如图,盒子内刚好放下5瓶罐头,每瓶罐头瓶底的半径为3cm,盒子的长为()cm。
A.15B.25C.30D.204.一个圆,半径扩大2倍,那么周长()。
A.不变B.也扩大2倍C.扩大4倍5.车轮转动一周所行的路程是车轮的()。
A.半径B.直径C.周长D.面积6.大圆的圆周率()小圆的圆周率。
A.大于B.等于C.小于二.判断题(共6题,共12分)1.一个圆的周长总是直径的3.14倍。
()2.任意两个圆的圆周长与直径的比都相等。
()3.半径相等的两个圆,它们的周长也一定相等。
()4.两个半圆可以拼成一个整圆。
()5.圆的周长等于直径乘圆周率。
()6.圆的半径是4厘米,则圆内最长的线段长8厘米。
()三.填空题(共8题,共22分)1.把一个圆平均分成若干(偶数)等份,剪开后可以拼成一个近似的(),这个长方形的长相当于圆的(),宽相当于圆的()。
2.画圆时,用到的常规工具有()。
3.看图填空(单位:厘米)。
图1:d=()cm 图2:d=()cm图3:r=()cm 图4:d=()cm4.通过圆心并且两端都在圆上的线段叫做()。
一般用字母()表示。
()是一个圆内最长的线段。
5.用圆规画出圆以后,针尖固定的一点就是(),通常用字母()表示,()决定圆的位置。
6.做 r =20cm的铁圈100个,需要铁丝()米。
列式:()。
7.圆的周长总是直径长度的()倍多一些。
这个倍数是个固定的数,我们把它叫做(),用字母()表示。
8.一个圆形粮仓的半径是3米,它的直径是()厘米,周长是()厘米。
四.计算题(共2题,共12分)1.求出下面图形的周长和面积。
(单位:厘米)(π=3.14)2.求下图中阴影部分的面积。
六年级数学圆的周长和面积专项练习

圆的周长和面积专项练习一.填空1、圆周率表示一个圆的()和()的倍数关系。
2、一个圆的直径是20厘米,它的面积是()。
3、用圆规画一个周长是25.12厘米的圆,那么圆规两脚之间的距离应为( )厘米。
4、有一个半圆形的铁板,它的半径是a厘米,那么这块铁板的周长是()厘米,面积是()厘米。
(用含π的式子表示)5、在一张长9厘米,宽6厘米的长方形纸上画一个尽可能大的圆,则圆规两脚间的距离不能超过()厘米,所画圆的面积是()平方厘米。
6、大圆的半径相当于小圆的直径,已知大圆面积比小圆面积多9.42平方分米,大圆面积是()平方分米。
7、在一个正方形里剪一个最大的圆,这个圆的周长是6.28厘米,这个正方形的面积是()平方厘米。
剩下的面积是()平方厘米。
8、用一根长12.56厘米铁丝围成一个正方形,这个正方形的面积是()平方厘米;如果用这根铁丝围成一个圆,圆的面积是()平方厘米。
9、一个挂钟的时针长5厘米,一昼夜这根时针的尖端走了()厘米,时针扫过的面积是()平方厘米。
10、如图,把一个圆平均分成若干等分,拼成一个近似长方形。
已知长方形的宽是10厘米,长是()厘米,圆面积是()平方厘米。
二.判断题1.两端在圆上的线段直径最长。
()2.一个扇形的两半径的夹角 120,它的面积是这个圆的面积的31。
( ) 3.圆的周长是6.28分米,那么半圆的周长就是3.14分米。
( )4.画一个直径是4厘米的圆,圆规两脚应叉开4厘米。
( )5.π=3.14。
( )6.圆的所有半径都相等,所有的直径也相等。
( )7.半径一定等于直径的21。
( ) 8.面积相等的两个圆,它们的半径和直径也一定相等。
( )9.圆的半径扩大4倍,圆的周长和面积也扩大4倍。
( )10.一端在圆里,另一端在圆上的线段是半径。
( )三.选择题1.一个半圆的周长是20.56分米,这个半圆的面积是( )平方分米。
A .113.04B .50.24C .25.122.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为( )平方厘米。
圆的面积和周长练习题

圆的周长提高练习题(4)一、填空1.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是 3米。
这只羊可以吃到()平方米地面的草。
2.一根 2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()3.用一根 10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()4.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()5.大圆的半径等于小圆的直径,大圆的面积是小圆面积的() 20.一个圆的周长扩大3倍,面积就扩大()倍。
6.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大。
7.一种钟表的分针长5cm,1小时分针尖端走过的距离是()分米,分针所扫过的面积()平方分米。
二、解决问题1、一个圆形花圃直径8米,用四分之三种兰花,兰花的种植面积是多少?2、一个圆形花坛的半径是10米,沿着花坛的周围每隔5米种一盆花,一共可以种盆花?3、阿姨要用藤条做5个圆环,每隔圆环的直径是20分米,5个圆环的接头处共需要10分米。
30米的藤条够用吗?4、一种零件的横截面是一个圆环,外圈半径是0.5米,内圈半径是0.4米.这种零件横截面的面积是多少平方米?5、有一个圆形拱门,门高2米。
这个拱门的门框是多少米?拱门的面积是多少平方米?6、一个花坛的周长是47.1米。
小明在花坛周围滚铁环,铁环直径是30厘米,围着花坛转一周,铁环要转多少圈?《圆的面积》教学设计教学内容:六年级数学上册第67-68页圆的面积。
教学目标:1:认知目标理解圆的面积的含义;理解和掌握圆的面积公式。
2:过程与方法目标经历圆的面积公式的推导过程,体验实验操作,逻辑推理的学习方法。
3:情感目标引导学生进一步体会“转化”的数学思想,初步了解极限思想;体验发现新知识的快乐,增强学生的合作交流意识和能力,培养学生学习数学的兴趣。
教学重点:正确掌握圆面积的计算公式。
圆的练习题六年级免费

圆的练习题六年级免费圆是我们学习数学的重要内容之一,六年级的学生们需要通过练习题来巩固和提高对圆的理解和运用能力。
本篇文章将为大家带来一些免费的圆的练习题,希望能够帮助六年级的学生们更好地掌握圆的知识。
练习题一:求圆的面积1. 已知一个圆的半径为5cm,求其面积。
2. 已知一个圆的直径为12cm,求其面积。
解答:1. 圆的面积公式为:面积= π × 半径的平方。
代入半径的值计算,得到面积 = 3.14 × 5 × 5 = 78.5 平方厘米。
2. 根据题意可知,直径 = 2 ×半径,所以半径为 12 ÷ 2 = 6cm。
代入半径的值计算,得到面积 =3.14 × 6 × 6 = 113.04 平方厘米。
练习题二:求圆的周长1. 已知一个圆的半径为8cm,求其周长。
2. 已知一个圆的直径为14cm,求其周长。
解答:1. 圆的周长公式为:周长= 2 × π × 半径。
代入半径的值计算,得到周长 = 2 × 3.14 × 8 = 50.24 厘米。
2. 根据题意可知,直径 = 2 ×半径,所以半径为 14 ÷ 2 = 7cm。
代入半径的值计算,得到周长 = 2 ×3.14 × 7 = 43.96 厘米。
练习题三:判断几何图形与圆的关系根据给出的几何图形,判断它们与圆的关系,是内切、外切、相交还是相离。
解答:1. 一个正方形内切于一个圆,它们的四条边与圆的切点在一个相同的平面上,且正方形的四个顶点位于圆上,所以此时圆与正方形是内切关系。
2. 一个长方形外切于一个圆,它们的四个角点位于圆上,且长方形的四个顶点联成一个矩形,此时圆与长方形是外切关系。
3. 一个三角形的外接圆,即通过三角形的三个顶点构造一个圆,使得圆与三角形的三条边相切,此时圆与三角形是外切关系。
人教版六年级上册数学 圆的周长与面积专题练习
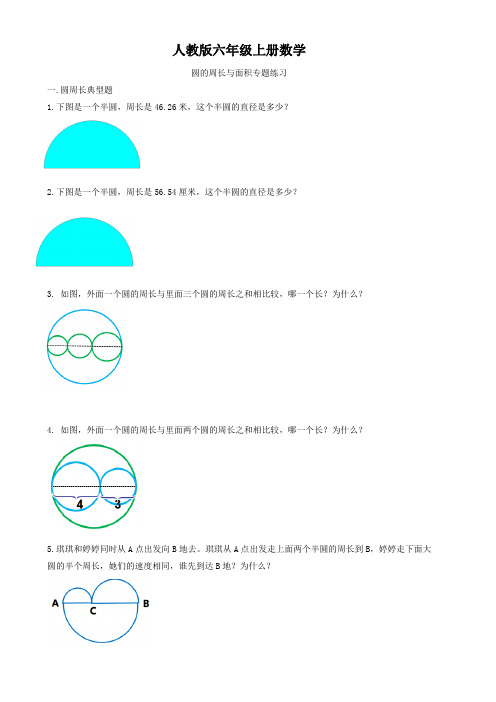
人教版六年级上册数学圆的周长与面积专题练习一.圆周长典型题1.下图是一个半圆,周长是46.26米,这个半圆的直径是多少?2.下图是一个半圆,周长是56.54厘米,这个半圆的直径是多少?3. 如图,外面一个圆的周长与里面三个圆的周长之和相比较,哪一个长?为什么?4. 如图,外面一个圆的周长与里面两个圆的周长之和相比较,哪一个长?为什么?5.琪琪和婷婷同时从A点出发向B地去。
琪琪从A点出发走上面两个半圆的周长到B,婷婷走下面大圆的半个周长,她们的速度相同,谁先到达B地?为什么?二.圆面积典型题(反推半径再求面积)1.已知圆的周长是31.4厘米,那么圆的面积是多少平方厘米?2.如图,在一块面积为12.56平方厘米的圆纸板中,裁出了2个同样大小的圆纸板。
请问:余下的纸板的总面积是多少平方厘米?三.“总-空白”法求阴影的面积1. 图中四个半圆的直径恰好在一个边长为6厘米的正方形的四条边上,如果每个半圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?2. 如图,一个正方形内包含一个半圆和两个完全相同的扇形,正方形的边长为6厘米,求图中阴影部分的面积。
1.如图,图中的三角形都是等腰直角三角形,求各图中阴影部分的面积。
2.图中的4个圆的圆心恰好是正方形的4个顶点,如果每个圆的半径都是1厘米,阴影部分的总面积是多少平方厘米?五.“组合法”求阴影的面积1. 如图所示,直角三角形的三条边长分别为6厘米、8厘米、10厘米,三个顶点分别是三个等圆的圆心,那么阴影部分的面积和是多少平方厘米?2. 如图所示,直角梯形梯形的上底为8厘米,下底为12厘米,高为4厘米,四个顶点分别是四个等圆的圆心,那么阴影部分的面积和是多少平方厘米?1. 已知正方形的面积是9,那么阴影部分的面积是多少?2. 如图求阴影部分的面积。
3.已知正方形的面积是25,那么阴影部分的面积是多少?4.如图,是由一个圆与一个直角扇形重叠组成的,其中圆的直径与扇形的半径都是4厘米,图中阴影部分的面积是多少?5. 周长为9.42分米的圆,面积是多少平方分米?6. 面积为12.56平方厘米的圆,周长是多少厘米?7.如图:长度单位厘米,阴影部分的面积是多少平方厘米?8. 求阴影部分面积(单位:厘米)9. 如图三个圆的周长都是25.12厘米,不用测量计算出图中阴影的总面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学六年级数学(圆的周长和面积(20151006))
1、把4个啤酒瓶扎在一起(如图所示),捆4圈至少用绳子多少厘米?
2、计算下图中阴影部分的周长。
(单位:厘米)
3、一个街心花园如下图的形状,中间正文形的边长是20米,四周为半圆形,这
个街心花园的周长是多少米?
4、在学校200米的跑道中,每条跑道宽1.2米。
由于有弯道,为了公平,外道和内道选手的起跑线不在同一地点。
如:A点处是小明的起跑线,B点处是小强的起跑线(如下图所示)那么,,A、B两点的距离是多少米?
5、如下图,从点A到点B沿着大圆周走和沿着中、小圆周走的路程相同吗?
6、下图中,从A点到B点沿着大圆周走和沿着小圆周走,路程相同吗?
1
7、已知AB=50厘米,求图中各圆的周长总和。
8、已知一个大圆中紧紧地排列着三个半径不同的小圆(如图),并且这四个圆的圆心恰好在同一条直线上。
如果大圆的周长是30厘米,那么三个小圆的周长之和是多少?
9、将半径分别是3厘米和2厘米的两个半圆如下图形状放置,求阴影部分的周
长。
10、一个半圆的周长是20.56分米,这个半圆的直径是多少厘米?
11、以B与C为圆心的两个半圆的直径都是4分米,求阴影部分的周长。
12、下图中圆的面积等于长方形的面积,已知圆的周长是36厘米,那么图中的
阴影部分的周长是多少厘米?
2
13、如下图,是由正方形和半圆组成的图形,其中P点为半圆的中点,Q点为正方形一边上的中点,那么阴影部分的面积是多少?(单位:厘米)
14、求下图中阴影部分的面积。
(单位:厘米)
15、下图小半圆的半径为4厘米,求阴影部分面积。
16、下图中三角形的面积是12平方厘米,求阴影部分的面积是多少?
这些小圆的圆心在大圆的同一直径上,(如图),一个大圆内有三个大小不等的小圆17、厘米,求这三个小圆的周长20连同大圆在内每相邻的两个圆相切,已知
大圆的周长是之和是多少?
3
18、有8个半径为2厘米的小圆,用它们的圆周的一部分连成一个花瓣图形,图中正方形的边的交点为这些圆的圆心,那么这个花瓣图形的周长是多少厘米?
19、有7根直径都是2分米的圆柱形木棍,想用一根绳子把它们捆成一捆,最短需要多少米长的绳子?(打结用的绳子不计)
20、三角形的边长都为3厘米,现将三角形ABC沿着一条直线翻滚三次(如图),求A点经过的路程的长。
21、求下图中外围的周长。
(单位:厘米)
4
22、正方形ABCD的边长为1厘米,依次以A、B、C、D为圆心,以AD、BE、CF、DG为半径画出扇形,求阴影部分的周长。
0的位置,求图ACAB60厘米的半圆绕A逆时针旋转到达,使323、下图中,直
径为中阴影部分的周长。
24、根据右下图中条件,求阴影部分的面积。
(单位:厘米)
25、右下图中阴影部分的面积是40平方厘米,那么环形的面积是多少平方厘米?
26、如下图,三个圆的周长都是25.12厘米,求阴影部分的面积。
(单位:厘米)
5
27、在长方形ABCD中,AB=6厘米,BC=4厘米,扇形ABE的半径AE=6厘米,扇形CBF的半径CF=4厘米,求图中阴影部分的面积。
1,BCDE是正方形,AFBG也是正方形,则图28、如下图,扇形AFB恰为一个圆的 4 中阴影部分的面积是多少?(单位:厘米)
29、求下图中阴影部分的面积。
(单位:厘米)
厘米,求中间阴影部分的面积。
、下图正方形的边长是304
0,阴影部BOA=90分别是小半圆的直径,且OA=OB=6厘米,∠OBOA31、如下图,、分的面积是多少平方厘米。
6
32、求下图中阴影部分的面积。
(单位:厘米)
33、求下图中阴影部分的面积。
(单位:厘米)
34、如下图,半径分别为2,3,4厘米的同心圆被八等分,求阴影部分的面积。
35、已知正方形的边长为10厘米,以两条边长为直径作两个半圆(如下图),求
出阴影部分的面积。
36、求下图中阴影部分的面积。
(单位:厘米)
37、求下图中阴影部分的面积。
(单位:厘米)
38、下图正方形边长为6厘米,求阴影部分面积。
39、下图中两块阴影部分的面积相等,三角形ABC是直角三角形,BC是直径,
长40厘米,求AB的长度。
40、下图三角形ABC是直角三角形,阴影(Ⅰ)比阴影(Ⅱ)的面积小23平方
米,BC的长度是多少米?
41、在下图中,直角三角形ABC的直角边AB是圆的直径,且AB=20厘米,如果阴影(Ⅰ)的面积比阴影(Ⅱ)的面积大7平方厘米,求BC的长。
42、在下图中长方形的宽为1厘米,以B点和C点为圆心,以宽为半径的扇形相交于G,形成两个阴影部分。
已知两个阴影部分的面积相等,求长方形的长是
多少厘米?
8
43、求下面各图中阴影部分的面积。
(单位:厘米)(1)(2)
(3)(4)
d= 4
44厘米,宽是32厘米,求阴影部分的面积。
、下图长方形的长是
45、下图三角形ABC是等腰直角三角形,腰长为8厘米,求阴影部分的面积?
9
46、下图中阴影甲的面积比阴影乙的面积多28平方厘米,AB=40厘米,CB垂
直于AB,求BC的长。
0,以AO为直径画半圆交OD于E,如果图中①的面积为47、下图中,∠BOA=901平方厘米,求阴影部分的面积。
48、下图中三个圆的半径都是5厘米,三个圆两两相交于圆心。
求阴影部分的面积和。
49、求下面各图中阴影部分的面积。
(单位:厘米)(1)(2)
10
11。
