第三章 资产组合理论
合集下载
3资产组合理论

负相关:ij 0 then wiwj 0
【例】如果 i 1,2 12 1, i , wi 1/ 2
则
2 p
12 12 12 12
4444
0
1、资产组合中的风险分散
投资组合方差的一般公式:
nn
2 p
wi w jCov ri , rj
【应用】市场指数基金
25
二、关于资产组合风险问题的讨论
不相关风险的分散:i j 0
如果 i , wi 1/ n
n
则
2 p
wi2
2 i
2
/n
2
i 1
且 lim 2 / n 0 n
【例】股票数量对收益波动性的影响
相关风险的对冲
正相关:ij 0 then wiwj 0
rp
rF
rT rF
T
p
15
加入风险资产后的有效投资组合
r
T:最优风险组合点
风险
rF
资产
有效
前沿
0
16
4.1 两种风险资产最优组合的计算 r
w1 w2 1
rP w1r1 w2r2
2 P
w1212
w22
2 2
2w1w212
max
{w1,w2 }
sP
rP rF
包括两种风险资产的投资组合的风险-收益关系
rp wDrD wErE
2 p
wD2
2 D
wE2
投资学第三章 资产组合理论 练习题
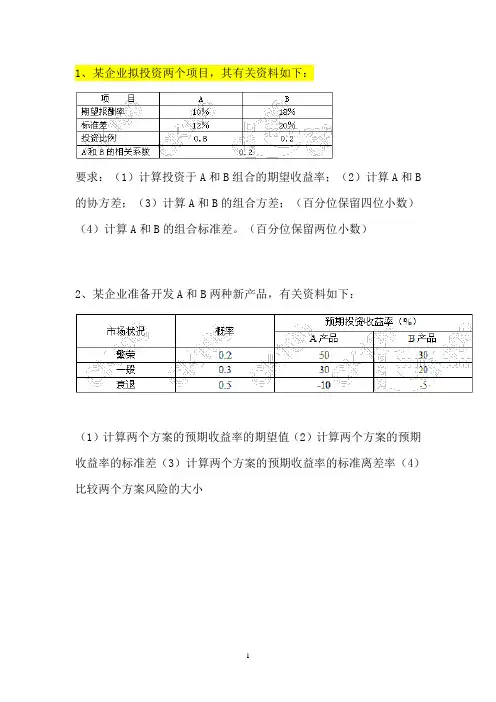
1、某企业拟投资两个项目,其有关资料如下:
要求:(1)计算投资于A和B组合的期望收益率;(2)计算A和B 的协方差;(3)计算A和B的组合方差;(百分位保留四位小数)(4)计算A和B的组合标准差。
(百分位保留两位小数)
2、某企业准备开发A和B两种新产品,有关资料如下:
(1)计算两个方案的预期收益率的期望值(2)计算两个方案的预期收益率的标准差(3)计算两个方案的预期收益率的标准离差率(4)比较两个方案风险的大小
3、某企业准备投资开发一种新产品甲,现有ABC三个方案可供选择,经预测ABC三个方案的预期收益及概率如下表示:
要求:(1)计算三个方案预期收益的期望值;(2)计算三个方案预期收益率的标准离差;(3)如果企业管理层是风险回避者,企业应试选择哪个方案
4、已知:A、B两种证券构成证券投资组织。
A证券的预期收益率10%,方差是0.0144,投资比重为80%;B证券的预期收益率为18%,方差是0.04,投资比重为20%;A证券收益率与B证券收益率的协方差是0.0048。
要求:(1)计算下列指标:①该证券投资组织的预期收益率;②A证券的标准差;③B证券的标准差;④A证券与B证券的相关系数;⑤该证券投资组合的标准差。
(2)当A证券与B证券的相关系数为0.5时,投资组合的标准差为12.11%,结合(1)的计算结果回答以下问题:①相关系数的大小对投资组织收益率有没有影响?②相关系数的大小对投资组合风险有什么样的影响?。
投资学 第三章 资产组合选择理论 均值方差方法

对外经济贸易大学金融学院 《投资学》
12
规则5 由两个资产构成的组合的回报率是构 成资产组合的每个资产的回报率的加权平 均值,资产组合的构成比例为权重。
E(rp ) w 1E(r1 ) w 2E(r2 ) E(rp ) w i E(ri ) i
1
n
2018-3-25
对外经济贸易大学金融学院 《投资学》
2018-3-25 对外经济贸易大学金融学院 《投资学》 16
贝斯特凯迪公司的股票价值对糖的价格很敏感。多年以来, 加勒比海糖产量下降时,糖的价格便猛涨,而贝斯特凯迪 公司便会遭到巨大的损失。下表为公司的股票价值变化情 况:
糖生产的正常年份 股市的牛市 概率 收益率% 股市的熊市 异常年份 糖的生产 危机
对外经济贸易大学金融学院 《投资学》 26
无差异曲线
无差异曲线为水平线,表示风险中性者,对投资风险的大小毫不 在意,他们只关心期望收益率的大小。 无差异曲线为垂直线,表示投资者只关心风险,风险越小越好, 对期望收益率毫不在意,是完全保守的投资者。 对风险厌恶者而言,风险越大,对风险的补偿要求越高,因此, 无差异曲线表现为一条向右凸的曲线。曲线越陡,投资者对风险 增加要求的收益补偿越高,投资者对风险的厌恶程度越强烈;曲线 越平坦,投资者的风险厌恶程度越弱。
s
2018-3-25
对外经济贸易大学金融学院 《投资学》
9
规则3 协方差是两个随机变量相互关系的一 种统计测度,即它测度两个随机变量,如 证券A和B的收益率之间的互动性。
AB cov(rA , rB ) E (rA E (rA ))( rB E (rB ))
2018-3-25
投资组合理论的基本思想:通过分散化的投 资来对冲掉一部分风险。 ——“Don’t put all eggs into one basket”
第3章 资产组合理论

第三章 资产组合理论(1)
第一节 投资的收益与风险
▪ 引子:如证券A可无风险地获得10%的 回报率,证券B以50%的概率获得20% 的收益,50%的概率的收益为0,你将 选择哪一种证券?
2020/7/22
引言
投资学的基本指导理念:风险与收益的最优匹配 对一个理性投资者而言,所谓风险与收益的最
2020/7/22
r ( 1 ) ( 1 4 0 1 0 0 4 )/1 0 0 4 4 %
2020/7/22
三、投资组合的期望收益和方差
2020/7/22
基金资产配置表
2020/7/22
基金持股的行业分布
2020/7/22
基金持有的债券分布
2020/7/22
(一)资产组合的收益
▪ 1、假设组合的收益为rp,组合中包含n种证券, 每种证券的收益为ri,它在组合中的权重是wi, 则组合收益为:
风险的含义
➢ 指收益(或未来结果)的不确定性
虽然结果是不确定的,但每种结果本身和出现的 客观概率是已知的或可估计的
➢ 所谓不确定就是偏离预期的可能性,方差是 最好的衡量工具
2020/7/22
(二)风险的类别
▪ 与证券投资相关的所有风险称为总风险, 总风险可分为系统风险和非系统风险。
➢ 系统性风险 ➢ 非系统性风险
2020/7/22
2020/7/22
协方差与组合风险
▪ 不仅每种资产的风险会影响组合的风险, 资产间的相互关系也会对组合风险产生影 响
▪ 资产间的相互关系可用协方差来表示
➢ 协方差是衡量两个随机变量间互动性的统计 量
2020/7/22
相关系数与组合风险
▪ 资产间的相互关系还可用另一个统计量—相关 系数来表示
第一节 投资的收益与风险
▪ 引子:如证券A可无风险地获得10%的 回报率,证券B以50%的概率获得20% 的收益,50%的概率的收益为0,你将 选择哪一种证券?
2020/7/22
引言
投资学的基本指导理念:风险与收益的最优匹配 对一个理性投资者而言,所谓风险与收益的最
2020/7/22
r ( 1 ) ( 1 4 0 1 0 0 4 )/1 0 0 4 4 %
2020/7/22
三、投资组合的期望收益和方差
2020/7/22
基金资产配置表
2020/7/22
基金持股的行业分布
2020/7/22
基金持有的债券分布
2020/7/22
(一)资产组合的收益
▪ 1、假设组合的收益为rp,组合中包含n种证券, 每种证券的收益为ri,它在组合中的权重是wi, 则组合收益为:
风险的含义
➢ 指收益(或未来结果)的不确定性
虽然结果是不确定的,但每种结果本身和出现的 客观概率是已知的或可估计的
➢ 所谓不确定就是偏离预期的可能性,方差是 最好的衡量工具
2020/7/22
(二)风险的类别
▪ 与证券投资相关的所有风险称为总风险, 总风险可分为系统风险和非系统风险。
➢ 系统性风险 ➢ 非系统性风险
2020/7/22
2020/7/22
协方差与组合风险
▪ 不仅每种资产的风险会影响组合的风险, 资产间的相互关系也会对组合风险产生影 响
▪ 资产间的相互关系可用协方差来表示
➢ 协方差是衡量两个随机变量间互动性的统计 量
2020/7/22
相关系数与组合风险
▪ 资产间的相互关系还可用另一个统计量—相关 系数来表示
投资学之资产组合理论(PPT 40页)

第三章 资产组合理论
第一节 风险与风险偏好
一、风险概述
(一)金融风险的内涵 金融市场是一个若干状态变量构成的复杂多变性 随机系统,这种金融系统中状态变量的事前不确 定性就是风险。 从整个金融经济学框架看,其核心在于如何分 散风险以及如何确定风险的合理价格。 对于投资学而言,其核心在于如何对资产定价 以及对不同风险资产进行优化配置。
i
其中,n代表证券组合中所包含资产类别的数
量; ri 代表第 i 种资产的期望收益率;wi 代
表第 i 种资产的投资比重。
(二)资产组合的方差计算
1、直接法 n 2 pi [ri E(r)]2 i 1
2、间接法
2 p
wA2
2 A
wB2
2 B
2wAwB A,B
资产 A、B 以及三种组合的收益率
n
2 pi [ri E(r)]2 i 1
标准差(standard deviation):方差的平方根。
n
[ pi (ri r )2 ]1/2 i 1
二、风险资产之间的关联性——协方差和 相关系数
协方差(covariance)和相关系数分别从绝对和 相对角度来测算两个随机变量之间相互关系。 风险资产之间的协方差:
n
E[U ( X )] PiU ( Xi ) i 1
不同风险态度示意图
u(E(x)) E(u(x)) u(E(x)) E(u(x)) u(E(x)) E(u(x))
U (b) U (a)
ab
U (b)
U (b)
U (a)
U (a)
ab
ab
投资者风险类型及行为特征
(1)风险厌恶型(Risk Averse):不喜欢风险, 承担风险必须相应的风险补偿。相对期望受益, 则选择风险较小的资产;或相同的风险,选择 收益最大资产。
第一节 风险与风险偏好
一、风险概述
(一)金融风险的内涵 金融市场是一个若干状态变量构成的复杂多变性 随机系统,这种金融系统中状态变量的事前不确 定性就是风险。 从整个金融经济学框架看,其核心在于如何分 散风险以及如何确定风险的合理价格。 对于投资学而言,其核心在于如何对资产定价 以及对不同风险资产进行优化配置。
i
其中,n代表证券组合中所包含资产类别的数
量; ri 代表第 i 种资产的期望收益率;wi 代
表第 i 种资产的投资比重。
(二)资产组合的方差计算
1、直接法 n 2 pi [ri E(r)]2 i 1
2、间接法
2 p
wA2
2 A
wB2
2 B
2wAwB A,B
资产 A、B 以及三种组合的收益率
n
2 pi [ri E(r)]2 i 1
标准差(standard deviation):方差的平方根。
n
[ pi (ri r )2 ]1/2 i 1
二、风险资产之间的关联性——协方差和 相关系数
协方差(covariance)和相关系数分别从绝对和 相对角度来测算两个随机变量之间相互关系。 风险资产之间的协方差:
n
E[U ( X )] PiU ( Xi ) i 1
不同风险态度示意图
u(E(x)) E(u(x)) u(E(x)) E(u(x)) u(E(x)) E(u(x))
U (b) U (a)
ab
U (b)
U (b)
U (a)
U (a)
ab
ab
投资者风险类型及行为特征
(1)风险厌恶型(Risk Averse):不喜欢风险, 承担风险必须相应的风险补偿。相对期望受益, 则选择风险较小的资产;或相同的风险,选择 收益最大资产。
第三章资产组合理论

的风险,还要考虑资产收益率相互之间的关系。
例:某投资公司已将50%的资金投资于A公司的股票,剩下50%的投资,投资经理决定在A 公司、B公司股票和无风险资产(收益率为3%)之间选择其一,哪一种选择更有利?A、 B公司的收益分布如下表所示。
原料生产的正常年份 股市的牛市 概率 A公司 B公司 无风险资产 收益率(%) 收益率(%) 收益率(%) 0.5 20 2 3 股市的熊市 0.3 10 -10 3 0.2 -20 40 3 原料生产危机年份
资产1所占 资产2所占 比重(W1) 比重(W2) ρ=+1 ρ=0 ρ=-1
r
σ
r
σ
r
σ
1.00 0.65 0.50 0.25 0.00
0.00 0.35 0.50 0.75 1.00
5.00 5.75 6.50 7.25 8.00
4.00 5.50 7.00 8.50 10.0
5.00 5.75 6.50 7.25 8.00
在马克维茨的投资组合理论中,投资组合的风险用投资组合的方差来衡量。 由两种资产组成的投资组合的方差为:
2 2 2 2 2 Var A B A W W WAWBCOVAB B A A BB 2
式(3.8)
包含n种资产的投资组合的方差为:
2 Var RP P
14
3.3 资产组合的收益和风险
经计算,三种选择方案投资组合的预期收益率和风险如下表示:
资产组合 全部投资于A公司股票 A、B公司股票各投资50% 预期收益率(%) 9 7.5 方差 0.0229 0.002425
A公司股票与无风险资产各投资50%
6
0.005725
以上的例子说明,尽管B公司股票本身波动性很大,但根据均值—方差决 策准则,由A、B股票构成的资产组合显然比A与无风险资产构成的组合具有优 势,原因是显而易见的,A公司与B公司的收益率是呈反方向波动的。因此,度 量资产组合的风险必须要考虑到各资产收益间的关系。
3章资产组合理
n
p i i
i 1
i 是在第 i 个资产上的 个资产的期望收益率, 投资额占总投资额的比重。
E (r )是组合中第i E (rp )为投资组合的期望收益率,
i
• 3.3.2 风险的度量
– 风险的度量方法
• 概率(probability)
– 度量风险事件发生或者造成损失的可能性。
• 期望值(expected value)
– 在不确定条件下,所有可能结果的加权平均值
• 方差(variance)
– 每一种结果的取值与期望值之差平方的加权平均数
• 标准差(standard deviation),
– 方差的平方根
• 离散系数(deviation coefficient)
– 标准差与期望值的比值,衡量的是单位期望值的风险
• 偏度(Skewness)亦称偏态、偏态系数
信用风险
又称违约风险,是企业在债务到期时无意愿或 者无力还本付息而产生的风险。
流动性风险
流动性风险有两层含义:一个是资产变现的速 度;二是资产在变现过程中价值的减少程度。 市场流动性 融资流动性
经营风险
由于企业经营方面的问题造成盈利水平的不确定性而 给投资者带来的风险。
政治及政策风险
两种以上证券的组合不是落在线段 上。所有的组合可能落在一个平面 中。
• 3.4.1 风险资产与无风险资产的投资组合
– 从风险收益的角度,将所有金融资产分为:
• 风险资产 • 无风险资产 – 包含一种风险资产与一个无风险资产的投资组合的期望 收益为:
E (rp ) E (r ) (1 )rf
• 2.投资学中单个资产的风险度量 – 风险的度量的含义
• 估计实际收益率与预期收益率之间可能的偏离程 度。
p i i
i 1
i 是在第 i 个资产上的 个资产的期望收益率, 投资额占总投资额的比重。
E (r )是组合中第i E (rp )为投资组合的期望收益率,
i
• 3.3.2 风险的度量
– 风险的度量方法
• 概率(probability)
– 度量风险事件发生或者造成损失的可能性。
• 期望值(expected value)
– 在不确定条件下,所有可能结果的加权平均值
• 方差(variance)
– 每一种结果的取值与期望值之差平方的加权平均数
• 标准差(standard deviation),
– 方差的平方根
• 离散系数(deviation coefficient)
– 标准差与期望值的比值,衡量的是单位期望值的风险
• 偏度(Skewness)亦称偏态、偏态系数
信用风险
又称违约风险,是企业在债务到期时无意愿或 者无力还本付息而产生的风险。
流动性风险
流动性风险有两层含义:一个是资产变现的速 度;二是资产在变现过程中价值的减少程度。 市场流动性 融资流动性
经营风险
由于企业经营方面的问题造成盈利水平的不确定性而 给投资者带来的风险。
政治及政策风险
两种以上证券的组合不是落在线段 上。所有的组合可能落在一个平面 中。
• 3.4.1 风险资产与无风险资产的投资组合
– 从风险收益的角度,将所有金融资产分为:
• 风险资产 • 无风险资产 – 包含一种风险资产与一个无风险资产的投资组合的期望 收益为:
E (rp ) E (r ) (1 )rf
• 2.投资学中单个资产的风险度量 – 风险的度量的含义
• 估计实际收益率与预期收益率之间可能的偏离程 度。
资产组合理论
---
8)/12.83
组合标准差
两个投资组合的方差报酬率之差为 SA -SB = 0.1,意味着每增加一个百分点的标准
差,组合B对应的预期收益率要比组合A 高10个基点(0.1%)。
包含无风险资产的最优风险组合
对资产分配问题进行扩展,在股票和债券的风险组合中,加入收益率为 8%的无风险国库券。Ƿ=0.2
-116.7 14.3*8.2
= -0.99
相关系数介于-1与+1之间:
相关系数= -1,完全负相关关系,即收益率变动趋势完全相反; 相关系数= 0,表明两种资产之间的收益率没有关系; 相关系数= 1,完全正相关。
2020/3/5
2.两种风险资产组合的三个规则 (股票比例w B ,债券wS )
规则1—组合的收益率是构成组合所有证券收益率的加权平均,权数 是组合中证券的投资比例。
25 20.14 15.75 13.87 10.8(方差最小组合) 12.0
S=25% BS =0
2020/3/5
E(rP)
组合S,股票
组合A,方差最小的组合
组合B,债券
P
图1 股票于债券的投资机会组合
投资机会组合是由于投资比例不同所生成的组合风险和组合收益率之间的 关系。根据理性投资者的行为特征和决策方法,位于风险最小的组合(组合A)下 方的投资组合是无效的,应当被排除在选择范围之外。而位于组合A上方的曲线 上组合之间的比较则不太明显,这些组合之间的选择取决于投资者的风险厌恶程 度。
2020/3/5
表3列举了等权重组合在每种场景下收益率、预期收益率、方 差、标准差。应当注意的是组合的预期收益率是两种预期收益率 的平均值,组合的标准要略小于两种的标准差的平均值。
第3章资产组合理论
1
对于上述带有约束条件的优化问题,可引入拉格朗日乘 子λ 和μ 来解决。(求条件极值)
构造拉格朗日辅助函数如下:
nn
n
n
L
wiwj ij ( wiri c) ( wi 1)
i1 j1
i 1
i 1
上式分别对wi求导数,令其一阶导数为0,得到方程组:
rp
p 1
r1
(1 p 1
)rf=rf
(r1 rf
1
)
p
可以发现这是一条以rf
为截距,以
r1
rf
1
为斜率的直线。
命题成立,证毕。
2019/12/25
资投本资学配第4置章 线的斜率称为报酬与 波动性比率,即风险的边际收益
(二)存在无风险资产时的有效边界
原有效边界凸向纵轴,因此存在唯一的 切点R
2019/12/25
投资学第4章
2019/12/25
投资学第4章
命题3.3:一种无风险资产与一个风险组合构成 的新组合的结合线为一条直线
2019/12/25
投资学第4章
组合的标准差为
一种风险资产与无风险资产构 成的组合,其标准差是风险资 产的权重与标准差的乘积。
p w11
(2)
由(1)和(2)可得
i1
wi ri
c
n
wi 1
i 1
投资学第4章
上述方程是线性方程组,可通过线性代数加 以解决。
例:假设三项不相关的资产,其均值分别为1, 2,3,方差都为1,若要得到期望收益为2的 该三项资产的最优组合,求解权重。
2019/12/25
第3章资产组合理论与因素模型
E(Ri ) Rj
E
(R
j
)
i1
i1 j1 i j
N
NN
Wi2 E Ri E(Ri )2
WiWj E Ri E(Ri ) R j E(R j )
i1
i1 j1
i j
N
NN
Wi
2
2 i
WiW j ij
i 1
i1 j1
NN
i j
上式也可化为
2 p
WiW j ij
i1 j 1
第3章 资产组合理论与因素模型
3.1 现代资产组合理论的基本思想 3.2 资产组合的收益与风险 3.3 最佳资产组合的确定 3.4 因素模型
1
证券投资理论与实务(第二版)
2020/9/2
3.1.1 马克维茨资产组合分析
资产组合分析的起点:单个证券的信息。 一方面是来自于单个证券过去的历史表现;一方面
4
证券投资理论与实务(第二版)
2020/9/2
3.1.2 投资者的期望效用
马克维茨在资产组合可行集的基础上,设立了区别
有效资产组合与无效资产组合的准则。有效集具备
的条件:第一,必须是可行的;第二,如果存在比
该组合更大期望收益的组合,那么更大期望收益的
组合的方差也应更高;第三,如果存在比该组合更
低方差的组合,那么更低方差组合的期望收益也应
2 p
Rp
R2
R2
1
R1
2
2 p
两证券完全负相关时
Rp
R2
R1
1
R2
2
2 p
Rp
R2
R1
1
R2
2
2 p
11
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
WA
$113,400 0.54 $210,000
WB
$96,600 $210 ,00
0.46
无风险资产与风险资产组合的配置
• 用P表示风险投资组合在完整资产组合 中的比重,用y表示风险投资的比重,用 (1-y) 表示无风险投资的比重:
y $210,000 0.7 $300,000
(w
A
A
-
wB
)2
B
完全负相关
-1 1
•相关系数
ρ=1
ρ=-1
························· ·
ρ=0
二、资产组合的方差
(二)单一风险资产与单一无风险资产的组合
若某投资者仅投资于风险资产A和无风险资产 短期国库券两种,设投资于风险资产的比重为y, 则投资于无风险资产的比重为1-y,则有:
利率波动造成资产价格波动的风险 ——反向影响
如: 利率波动对股票的影响 利率波动对债券的影响
汇率风险
汇率的波动使资产价格发生变化的风险
对本国外贸企业的影响
通货膨胀风险
也称购买力风险 对货币购买力的影响
违约风险
也称财务风险 企业无法偿还债务可能导致破产
经营风险
企业生产经营过程中遇到的问题 产业景气状况 公司管理能力 生产成本变化
例
• 某股票期望收益率为20%,标准差为30%, 同时无风险资产收益率为7%。
• 风险溢价为多少?
风险溢价 20% - 7% 13%
资产组合的收益率与方差 一、资产组合收益率
E(r) wr
w为 各 项 资 产 的 比 重 r为 各 项 资 产 的 期 望 收 益率
例
• 某投资者投资3000元于利率为5%的短期国 库券,投资7000于期望收益率为20%股票,
投资学
主讲:王增泉
第三章 资产组合理论
风险-收益的数学度量
(一)持有期收益率 r P1 P0 I P0
P1为期末价格 P0为期初价格 I为股利 r为持有期收益率
例
现以100元每股购买某股票若干股,一年 后以110元出售,期间分到股利4元。
求持有期收益率。
r P1 P0 I 110 100 4 14%
• 资产组合收益率为多少?
国库券的比重为 3000 0.3 3000 7000
股票的比重为 7000 0.7 3000 7000
组合期望收益率rp 0.3 5% 0.7 20% 15.5%
二、资产组合的方差
(一)协方差与相关系数 若投资于A,B两种证券,则有:
COV (r , r )称为证券A与证券B的协方差 AB
r
rA 20% rP 15.5%
rf 5%
0
资本配置线
资本配置线 风险溢价
A 15%
P
10.5%
资本配置线与夏普比率
资本配置线表示对投资者而言所有可能的风 险收益组合,
其斜率为夏普比率
也称报酬——波动性比率
夏普比率的意义:每增加一单位风险而增加
的期望收益率
夏普比率S
n
E(r) ri pi i 1
(三)风险度量——方差与标准差
1.方差 是估计资产实际收益率与期望收益率可能偏 离的测度方法
n
2 pi[ri E(r)]2 i1
方差
例:若投资于某期货1000元,一年后有 概率 期货价值 收益 收益率 0.4 1800 800 80% 0.6 600 -400 -40%
经营正常时持有期收益率为:1080-1000 20 10% 1000
经营好时持有期收益率为:1180-1000 20 20% 1000
E(r) 0.2 0% 0.5 10% 0.3 20% 11%
2 0.2(0% 11%)2 0.5(10% 11%)2 0.3(20% 11%)2
风险溢价 资产组合标准差
rP
rf
P
上例中夏普比率S
风险溢价 组合方差
15% 15%
1
风险最优方案
由
U E(r) 1 A 2
2
2 y 2 2
P
A
得
U
rf
y(rA
rf )
1 2
A
y2
P2
使y的一阶导数为0,则有:
y
rA rf
A A2
效用值关于风险资产比例y的函数
2 0.11 0.07, 所 以 投 资 者 选 择 股 票 。
三、承担风险的回报——风险溢价
对于风险厌恶的投资者而言,资产本身隐含 的风险愈多,相应地必须能提供更多的预期 报酬作为投资者承担风险的补偿,这一补偿 成为风险溢价,或风险报酬(risk premium)
风险溢价=风险期望资产收益率-无风险资产收益率
(3)风险偏好型(Risk Seeker):这类投资者 喜欢风险,享受风险带来的乐趣,为获取高收 益而甘愿承担高风险。赌博者、彩票者,投资 ST、垃圾股票。
效用函数
U = 效用值
E ( r ) = 某一资产或
资产组合期望收
益
U E(r) 1 A 2
A = 风险厌恶系数
2
2 = 收益的方差
期望收益率为:0.480% 0.6 (40%) 8%
2 0.4 (80% 8%)2 0.6 (40% 8%)2 34.56%
(三)风险度量——方差与标准差
2.标准差 也是估计资产实际收益率与期望收益率可能 偏离的测度方法,为方差的开方。
2
综合题
2.对A
2投资者,y
r r
A
f
A A2
20% 7% 13% 72% 2 (30%)2 2 9%
无风险资产与风险资产组合的配置
总市值 无风险的短期国库券 股票A 股票B 所有的风险资产
$300,000 $90,000 $113,400 $96,600 $210,000
对于投资学而言,其核心在于如何对资产定价 以及对不同风险资产进行优化配置。
(二)证券市场风险的种类
市场风险 利率风险 汇率风险 通胀风险 财务(违约)风险 经营风险 流动性风险
系统风险 非系统风险
市场风险
影响所有资产或投资工具报酬的非预期事件 如: 1998年亚洲金融风暴 2008年次贷危机
利率风险
即 2 0。 U E(r) 1 A 2 E(r)
2
例
• 某股票期望收益率为20%,标准差为30%, 同时无风险资产收益率为7%。
• 一个风险厌恶系数A=4的投资者会在二者之 间如何选择?
• 风险厌恶系数A=2的投资者呢?
答案
无 风 险 资 产 效 用U rf 7% 0.07
比重
期望收益
标准差
A
0.4
15%
10%
B
0.6
20%
15%
• 资产组合标准差为多少?
组合方差 2 w 2 2 w 2 2 2w w
P
AA
BB
AB
AB
0.42 0.12 0.62 0.152 2 0.4 0.6 0.5 0.1 0.15
1.对A 4投 资 者 ,U E(r) 1 A 2
2 20% 1 4 (30% )2 0.2 0.18 0.02
2 0.02 0.07, 所 以 投 资 者 选 择 无 风 险资 产 。
2.对A 2投 资 者 ,U E(r) 1 A 2
2 20% 1 2 (30% )2 0.2 0.09 0.11
称为证券A与证券B的相关系数
且COV (rA, rB ) A B
组合方差
2 P
w 2 2 AA
w 2 2 BB
2wA wB
COV (rA , rB )
w 2 2 AA
w 2 2 BB
2wA wB
A B
例
• 某投资者欲投资相关系数为0.5的两证券
组合期望收益率rP y rA (1 y) rf
组合
方差
2 P
w A2 A2
wB 2 B 2
2wAwB
A B
w A2 A2 y 2 A2
组合标准差 P y2 A2 y A
例
• 某投资者投资3000元于利率为5%的短期国库券, 投资7000于期望收益率为20%,标准差为15%的股 票,
0.0133
组合标准差 0.0133 0.1153 11.53%
•相关系数
– 相关系数是判定两证券收益之间的关联强度 的统计指标。
当
1时, P2
(w
A
A
wB
)2
B
完全正相关
当
0时, P2
w 2 2 AA
w 2 2 BB
完全不相关
当
-1时, P2
1 y $90,000 0.3 $300,000
A : $113,400 0.378 B : $96,600 0.322
$300,000
$300,000
投资组合分散
通常而言,在投资组合中加入新的资产会使投资 组合收益的方差下降,这个过程称为分散化 (diversification)。这也反映了我们所熟悉的一 句格言:“不要把所有的鸡蛋放在一个篮子里”。
