灰色理论系统预测
灰色理论关联度与预测,数学建模必备知识,很实用哦

X m {xm ( jm )} | jm 1, 2,..., nm} 比较序列
灰色关联分析3
设x0(k)为X0(为参考序列)的第k个数;xi(k) 为Xi(比较序列)的第k个数;
则比较序列Xi对参考序列X0的灰色关联度为:
(X0 ,
Xi )
1 n
n k 1
r(x0 (k),
度,根据经验,当ρ=0.5时,关联度大于0.6便 满意了。
回总目录 回本章目录
(3)后验差检验 a.计算原始序列标准差:
X 0 i X 0 2
S1
n 1
回总目录 回本章目录
b. 计算绝对误差序列的标准差:
0 i 0 2
S2
X 0 t ,
3
X 0 t ,...,
n
X 0 t
t1
t 1
t 1
t 1
目录
基本概念 灰色关联分析 灰色预测模型
灰色关联分析1
基本特征
建立的模型属于非函数形式的序列模型 计算方便易行 对样本数量多寡没有严格要求 不要求序列数据必须符合正态分布 不会产生与定性分析大相径庭的结论
n 1
c. 计算方差比:
C S2 S1
回总目录 回本章目录
d. 计算小误差概率:
P P 0i 0 0.6745S1
令: 则:
ei 0i 0 , S0 0.6745S1 P Pei S0
P >0.95 >0.80 >0.70 ≤0.70
灰色关联分析3
灰色关联度的数学模型
X 0 {x0 ( j0 )} | j0 1, 2,..., n0} X1 {x1( j1)} | j1 1, 2,..., n1} X 2 {x2 ( j2 )} | j2 1, 2,..., n2}
灰色系统理论在市场预测中的应用

灰色系统理论在市场预测中的应用绪论市场预测一直是商业决策的重要组成部分。
在过去,市场预测更多依靠主观经验、历史趋势和数据分析等方法。
但是随着大数据、人工智能和数学方法的发展,灰色系统理论开始在市场预测中得到应用。
灰色系统理论是20世纪80年代由我国学者建立的一种数学模型和分析方法,因其高效可靠性以及能够有效处理不规则数据而在市场预测、经济决策等领域得到广泛应用。
一、灰色系统理论的概念灰色系统理论是从一个灰色系统的角度出发,在统计学的基础上发现系统规律,揭示系统内部关系的一种理论。
与其他数学方法相比,灰色系统理论更加强调系统的分析与描述,以此更好地理解和解决现实问题。
灰色系统理论通常基于少量的数据样本建立灰色模型,然后利用该模型进行预测。
与其他模型不同的是,灰色系统理论不需要数据服从一定的分布,可以利用少量的样本数据进行分析。
二、灰色系统理论可以有效地应用于市场预测,尤其是预测不稳定、非线性、不规则的情况。
市场中存在许多因素导致的波动,灰色系统理论通过建立灰色模型,可以更好地把握市场的变化趋势,从而为商业决策提供可靠的依据。
在市场营销中,灰色系统理论在目标市场、销售策略和产品定价等方面得到了广泛应用。
一个关键性质是灰色系统理论在市场预测中对样本数据量的要求相对较低,而在实际应用中可以通过大量数据的自动化集成快速获得准确的预测结果,因此受到越来越多的关注和借鉴。
三、灰色系统理论的实践案例1. 物流配送中心的配送效率评估,基于灰色系统理论对仓储数据和大量的交通数据进行分析,确定最佳的时间和路线,大大提升了物流配送效率。
2. 汽车市场的销售预测,利用灰色模型对市场数据和销售趋势进行预测,为企业提供了更精准的决策依据。
3. 大型游戏的用户活跃度预测,通过对用户行为数据的灰色分析,得出用户活跃度的预测结果,并据此制定广告、营销策略。
四、灰色系统理论的优势和局限性灰色系统理论与其他数学方法相比,具有明显的优势:1. 数据要求相对较低:灰色系统理论适用于不规则、少量的数据样本。
灰色理论预测模型
灰⾊理论预测模型灰⾊理论通过对原始数据的处理挖掘系统变动规律,建⽴相应微分⽅程,从⽽预测事物未来发展状况。
优点:对于不确定因素的复杂系统预测效果较好,且所需样本数据较⼩;缺点:基于指数率的预测没有考虑系统的随机性,中长期预测精度较差。
灰⾊预测模型在多种因素共同影响且内部因素难以全部划定,因素间关系复杂隐蔽,可利⽤的数据情况少下可⽤,⼀般会加上修正因⼦使结果更准确。
灰⾊系统是指“部分信息已知,部分信息未知“的”⼩样本“,”贫信息“的不确定系统,以灰⾊模型(G,M)为核⼼的模型体系。
灰⾊预测模型建模机理灰⾊系统理论是基于关联空间、光滑离散函数等概念,定义灰导数与会微分⽅程,进⽽⽤离散数据列建⽴微分⽅程形式的动态模型。
灰⾊预测模型实验以sin(pi*x/20)函数为例,以单调性为区间检验灰⾊模型预测的精度通过实验可以明显地看出,灰⾊预测对于单调变化的序列预测精度较⾼,但是对波动变化明显的序列⽽⾔,灰⾊预测的误差相对⽐较⼤。
究其原因,灰⾊预测模型通过AGO累加⽣成序列,在这个过程中会将不规则变动视为⼲扰,在累加运算中会过滤掉⼀部分变动,⽽且由累加⽣成灰指数律定理可知,当序列⾜够⼤时,存在级⽐为0.5的指数律,这就决定了灰⾊预测对单调变化预测具有很强的惯性,使得波动变化趋势不敏感。
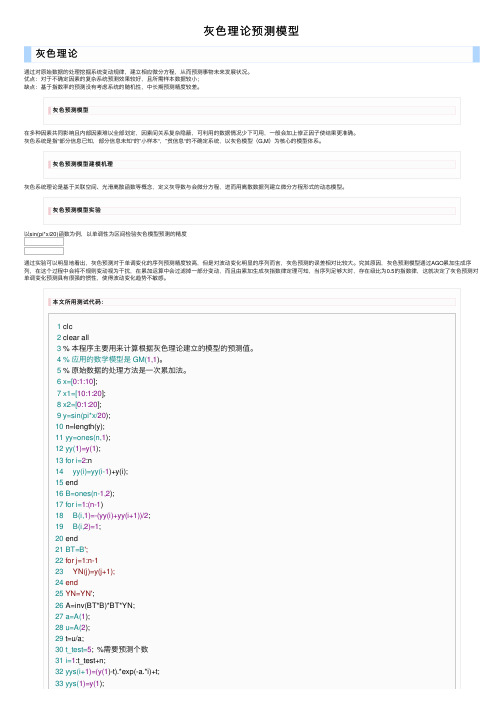
本⽂所⽤测试代码:1 clc2 clear all3 % 本程序主要⽤来计算根据灰⾊理论建⽴的模型的预测值。
4 % 应⽤的数学模型是 GM(1,1)。
5 % 原始数据的处理⽅法是⼀次累加法。
6 x=[0:1:10];7 x1=[10:1:20];8 x2=[0:1:20];9 y=sin(pi*x/20);10 n=length(y);11 yy=ones(n,1);12 yy(1)=y(1);13 for i=2:n14 yy(i)=yy(i-1)+y(i);15 end16 B=ones(n-1,2);17 for i=1:(n-1)18 B(i,1)=-(yy(i)+yy(i+1))/2;19 B(i,2)=1;20 end21 BT=B';22 for j=1:n-123 YN(j)=y(j+1);24 end25 YN=YN';26 A=inv(BT*B)*BT*YN;27 a=A(1);28 u=A(2);29 t=u/a;30 t_test=5; %需要预测个数31 i=1:t_test+n;32 yys(i+1)=(y(1)-t).*exp(-a.*i)+t;33 yys(1)=y(1);34 for j=n+t_test:-1:235 ys(j)=yys(j)-yys(j-1);36 end37 x=1:n;38 xs=2:n+t_test;39 yn=ys(2:n+t_test);40 det=0;41 for i=2:n42 det=det+abs(yn(i)-y(i));43 end44 det=det/(n-1);4546 subplot(2,2,1),plot(x,y,'^r-',xs,yn,'b-o'),title('单调递增' ),legend('实测值','预测值');47 disp(['百分绝对误差为:',num2str(det),'%']);48 disp(['预测值为: ',num2str(ys(n+1:n+t_test))]);495051 %递减52 y1=sin(pi*x1/20);53 n1=length(y1);54 yy1=ones(n1,1);55 yy1(1)=y1(1);56 for i=2:n157 yy1(i)=yy1(i-1)+y1(i);58 end59 B1=ones(n1-1,2);60 for i=1:(n1-1)61 B1(i,1)=-(yy1(i)+yy1(i+1))/2;62 B1(i,2)=1;63 end64 BT1=B1';65 for j=1:n1-166 YN1(j)=y1(j+1);67 end68 YN1=YN1';69 A1=inv(BT1*B1)*BT1*YN1;70 a1=A1(1);71 u1=A1(2);72 t1=u1/a1;73 t_test1=5; %需要预测个数74 i=1:t_test1+n1;75 yys1(i+1)=(y1(1)-t1).*exp(-a1.*i)+t1;76 yys1(1)=y1(1);77 for j=n1+t_test1:-1:278 ys1(j)=yys1(j)-yys1(j-1);79 end80 x21=1:n1;81 xs1=2:n1+t_test1;82 yn1=ys1(2:n1+t_test1);83 det1=0;84 for i=2:n185 det1=det1+abs(yn1(i)-y1(i));86 end87 det1=det1/(n1-1);8889 subplot(2,2,2),plot(x1,y1,'^r-',xs1,yn1,'b-o'),title('单调递增' ),legend('实测值','预测值');90 disp(['百分绝对误差为:',num2str(det1),'%']);91 disp(['预测值为: ',num2str(ys1(n1+1:n1+t_test1))]);9293 %整个区间93 %整个区间94 y2=sin(pi*x2/20);95 n2=length(y2);96 yy2=ones(n2,1);97 yy2(1)=y2(1);98 for i=2:n299 yy2(i)=yy2(i-1)+y2(i);100 end101 B2=ones(n2-1,2);102 for i=1:(n2-1)103 B2(i,1)=-(yy2(i)+yy2(i+1))/2;104 B2(i,2)=1;105 end106 BT2=B2';107 for j=1:n2-1108 YN2(j)=y2(j+1);109 end110 YN2=YN2';111 A2=inv(BT2*B2)*BT2*YN2;112 a2=A2(1);113 u2=A2(2);114 t2=u2/a2;115 t_test2=5; %需要预测个数116 i=1:t_test2+n2;117 yys2(i+1)=(y2(1)-t2).*exp(-a2.*i)+t2;118 yys2(1)=y2(1);119 for j=n2+t_test2:-1:2120 ys2(j)=yys2(j)-yys2(j-1);121 end122 x22=1:n2;123 xs2=2:n2+t_test2;124 yn2=ys2(2:n2+t_test2);125 det2=0;126 for i=2:n2127 det2=det2+abs(yn2(i)-y2(i));128 end129 det2=det2/(n2-1);130131 subplot(2,1,2),plot(x2,y2,'^r-',xs2,yn2,'b-o'),title('全区间' ),legend('实测值','预测值'); 132 disp(['百分绝对误差为:',num2str(det2),'%']);133 disp(['预测值为: ',num2str(ys2(n2+1:n2+t_test2))]);。
灰色预测理论详解

单序列灰色预测模型
灰色系统理论认为:系统的行为现象尽管朦胧,数据尽管 复杂,但它必然是有序的,都存在着某种内在规律。不过 这些规律被纷繁复杂的现象所掩盖,人们很难直接从原始 数据中找到某种内在的规律. 灰色生成:建立灰色模型之前,需要对原始时间序列按照 某种要求进行预处理,得到有规律的时间序列数据—生成 列。即对原始数据的生成就是企图从杂乱无章的现象中去 发现内在规律. 常用的灰色系统生成方式有: 累加生成,累减生成,均值生 成,级比生成等,下面对这几种生成做简单介绍:
灰色预测理论
胡亚飞 彭
敬
李云飞
吕连磊 苗成林
沈 聪
目录
灰色系统理论简介以及发展 灰色预测理论 —灰色预测简介 —灰色预测类型 —灰色预测模型 —灰色预测检验 案例以及软件实现
灰色系统理论简介
灰色系统理论是由我国著名学者邓聚龙教授于1982年 创立的“以部分信息已知,部分信息未知的小样本、贫信 息”不确定系统为研究对象的一门系统科学新学科,具有 原创性的科学意义,是我国对系统科学的新贡献,目前已 受到国内外学术界的广泛重视,并在农业科学、经济管理、 环境科学、医药卫生、矿业工程、教育科学、水利水电、 图像信息、生命科学、控制科学、航空航天等众多领域中 得到了广泛的应用,解决了许多过去难以解决的实际问题。
(1)
k
累加生成的作用:通过累加生成可以看出灰量积累过程的发展态 势,使离乱的原始数据中蕴含的积分特性或规律加以显化。 2.累减生成 对数列求相邻两数值的差,是累加生成的逆运算。 记原始序列为 X(1)=(x(1)(1), x(1)…(2),…),x(1)(n)) 一次累减生成序列为 X(0)=(x(0)(1), x(0)(2),…,x(0)(n)) 其中,x(0)(k)=x(1)(k)-x(1)(k-1) 累减生成的作用 累减生成可将累加生成还原为非生成数列,在建模 方 程用来获得增量信息。
基于灰色系统理论的股票市场预测研究

基于灰色系统理论的股票市场预测研究随着社会发展和经济全球化的趋势,股票市场已成为投资者关注的一个热门话题。
对于投资者来说,股票市场预测是一件非常重要的事情。
股票市场投资存在着较大的风险,利用科学的方法对市场进行预测,可以提高投资的准确率,降低风险。
而基于灰色系统理论的股票市场预测方法,已经在近年来获得了广泛的应用。
本文将对基于灰色系统理论的股票市场预测进行探讨。
一、灰色系统理论基本概念灰色系统理论是一种新兴的系统科学理论,它的基本思想是通过研究数据的内部联系和规律,对未知信息进行推断。
灰色系统理论的核心是灰色预测模型。
灰色预测模型是一种通过揭示时间序列数据的内在规律,对未来数据进行预测的模型。
在灰色预测模型中,数据通过建模、生成灰色预测模型、预测和检验等步骤实现。
二、基于灰色系统理论的股票市场预测原理基于灰色系统理论的股票市场预测,是指通过收集股票市场中的时间序列数据进行建模,利用灰色预测模型对未来股票市场价格进行预测。
灰色系统理论认为,任何一个时间序列数据都有其发展规律和内在联系。
通过建立灰色预测模型,可以利用数据的内在联系和规律,对未来股票市场进行预测。
建立灰色预测模型的过程主要包括以下几个步骤:1.数据预处理在建立灰色预测模型之前,需要对时间序列数据进行预处理。
预处理过程包括数据清洗、数据平稳化、数据标准化等步骤。
这些步骤的目的是消除时间序列数据中的异常值、趋势和周期性等因素,使其成为符合灰色预测模型建立要求的时间序列。
2.建立灰色模型建立灰色预测模型的第一步是确定模型类型。
灰色预测模型包括GM(1,1)模型、GM(2,1)模型等多种类型。
在确定模型类型之后,需要对数据进行一阶差分并求累加生成相应的矩阵序列,利用矩阵序列进行参数估计和模型检验,得到一个可靠的灰色预测模型。
3.模型预测在建立灰色预测模型之后,即可以利用该模型对未来股票市场价格进行预测。
预测过程包括两个部分:一是模型参数预测,二是数据预测。
灰色预测理论-定义

什么是灰色预测法?灰色预测是就灰色系统所做的预测。
所谓灰色系统是介于白色系统和黑箱系统之间的过渡系统,其具体的含义是:如果某一系统的全部信息已知为白色系统,全部信息未知为黑箱系统,部分信息已知,部分信息未知,那么这一系统就是灰色系统。
一般地说,社会系统、经济系统、生态系统都是灰色系统。
例如物价系统,导致物价上涨的因素很多,但已知的却不多,因此对物价这一灰色系统的预测可以用灰色预测方法。
灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测。
尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
其用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
简言之,灰色预测模型是通过少量的、不完全的信息,建立灰色微分预测模型,对事物发展规律作出模糊性的长期描述(模糊预测领域中理论、方法较为完善的预测学分支)。
灰色系统的概念是由邓聚龙教授于1982年提出的,它描述部分信急己知,部分未知介于黑白系统之间的系统。
GM(1,1)模型是灰色理论中较常用的预测方法,它以定性分析为先导,定量与定性结合,对离散序列建立微分方程以及白化方程,一般要经历思想开发、因素分析、量化、动态化、优化五个步骤。
灰色系统通过对原始数据的整理来寻求其变化规律,这是一种就数据寻找数据的现实规律的途径,称为灰色序列的生成。
生成数通过对原始数据的整理寻找数的规律,分为三类:a、累加生成:通过数列间各时刻数据的依个累加得到新的数据与数列。
灰色预测理论详解
xN(0) (1), xN(0) (2),...,xN(0) (n)
为Z1相(1) 关为因X1素(1)序的列紧。邻X生i(成1) 为序列X i(,0) 的则1称-AGO序列 i 1,2,...,,N
N
x (0) 1
(k
)
az1(1)
(k )
bi xi (1) (k )
i2
为GM(1,N)灰色微分方程。
灰色预测
灰色预测是对既含有已知信息又含有不确定信息 的系统进行预测,就是对在一定范围内变化的、 与时间有关的灰色过程进行预测。
通过对原始数据的生成处理来和灰色模型的建立, 挖掘、发现、掌握寻求系统变动的规律。生成数 据序列有较强的规律性,可以用它来建立相应的 微分方程模型,从而预测事物未来的发展趋势和 未来状态,对系统的未来状态做出科学的定量分 析。
x (1)(k 1) (x(1) (1) b )eak b
还原到原始数据
a
a
x (0)(k 1) x(1) (k 1) x(k)
DGM(1,1)模型
X(1() 1) 1
B
X(1() 1)
1
X(1() n
-
1 )1
GM(1,1)和DGM(1,1)的关系
灰色生成:建立灰色模型之前,需要对原始时间序列按照 某种要求进行预处理,得到有规律的时间序列数据—生成 列。即对原始数据的生成就是企图从杂乱无章的现象中去 发现内在规律.
常用的灰色系统生成方式有: 累加生成,累减生成,均值生 成,级比生成等,下面对这几种生成做简单介绍:
1.累加生成 通过数列间时刻各数据的依个累加以得到新的数据与数 列,累加所得的新数列叫做累加生成数列。
灰色预测模型理论及其应用
灰色预测模型理论及其应用灰色系统理论认为对既含有已知信息又含有未知或非确定信息的系统进行预测,就是对在一定方位内变化的、与时间有关的灰色过程的预测. 尽管过程中所显示的现象是随机的、杂乱无章的,但毕竟是有序的、有界的,因此这一数据集合具备潜在的规律,灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测.灰色预测模型只需要较少的观测数据即可,这和时间序列分析,多元回归分析等需要较多数据的统计模型不一样. 因此,对于只有少量观测数据的项目来说,灰色预测是一种有用的工具.本文主要围绕灰色预测GM(1,1)模型及其应用进行展开。
一、灰色系统及灰色预测的概念1.1灰色系统灰色系统产生于控制理论的研究中。
若一个系统的内部特征是完全已知的,即系统的信息是充足完全的,我们称之为白色系统。
若一个系统的内部信息是一无所知,一团漆黑,只能从它同外部的联系来观测研究,这种系统便是黑色系统。
灰色系统介于二者之间,灰色系统的一部分信息是已知的,一部分是未知的。
区别白色和灰色系统的重要标志是系统各因素间是否有确定的关系。
特点:灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”不确定型系统的研究对象。
1.2灰色预测灰色系统分析方法是通过鉴别系统因素之间发展趋势的相似或相异程度,即进行关联度分析,并通过对原始数据的生成处理来寻求系统变动的规律。
生成数据序列有较强的规律性,可以用它来建立相应的微分方程模型,从而预测事物未来的发展趋势和未来状态。
灰色预测是用灰色模型GM(1,1)来进行定量分析的,通常分为以下几类:(1) 灰色时间序列预测。
用等时距观测到的反映预测对象特征的一系列数量(如产量、销量、人口数量、存款数量、利率等)构造灰色预测模型,预测未来某一时刻的特征量,或者达到某特征量的时间。
(2) 畸变预测(灾变预测)。
通过模型预测异常值出现的时刻,预测异常值什么时候出现在特定时区内。
(3) 波形预测,或称为拓扑预测,它是通过灰色模型预测事物未来变动的轨迹。
灰色预测模型原理
灰色预测模型原理灰色预测模型(Grey Prediction Model)是一种基于灰色系统理论和数学建模方法的预测模型。
灰色系统理论是我国学者黄金云教授于1982年提出的一种系统理论,它是研究非确定性和不完备信息系统的一种新方法,可用于研究多变量、小样本和非线性系统。
灰色预测模型主要基于灰色数学建模方法,通过对已知的部分序列数据进行建模和预测,来推测未知的序列数据趋势。
它适用于研究数据量小、信息不完备、非线性关系复杂的系统。
下面将简要介绍灰色预测模型的原理、模型建立过程以及一些应用案例。
1. 灰色预测模型的原理灰色预测模型的核心思想是通过对已知数据进行灰色关联度的度量,从而建立出合适的数学模型,进行未来数据的预测。
其基本原理可以概括为以下五个步骤:(1)建立灰色微分方程:根据原始数据的特点,确定合适的灰色微分方程,通常使用一阶或高阶灰色微分方程。
(2)求解灰色微分方程:根据所选择的灰色微分方程,求解其参数,得到模型的特征参数。
(3)模型检验:检验所建立的灰色预测模型的拟合程度和误差是否符合要求。
(4)进行灰色关联度分析:根据已知数据的变化规律,计算各个因素的灰色关联度,确定相关因素的重要性。
(5)进行预测:利用建立好的灰色预测模型,对未来的数据进行预测和分析,得出预测值。
2. 模型建立过程灰色预测模型的建立过程中,通常包括以下几个步骤:(1)数据的建立与处理:对原始数据进行筛选、预处理和归一化处理,以满足模型的要求。
(2)建立灰色微分方程:从已知数据中提取主要特征,并根据数据的特点选择合适的灰色微分方程。
(3)求解灰色微分方程:根据所选的灰色微分方程,通过累加生成序列、求解参数等方法,得到模型的特征参数。
(4)模型的检验:根据已知数据的拟合程度和误差范围,评估所建立的灰色预测模型的准确性和可靠性。
(5)模型的应用与预测:利用已建立的模型进行未来数据的预测和分析,得出预测结果。
3. 应用案例灰色预测模型在实际应用中具有广泛的应用范围,以下是一些常见的应用案例:(1)经济领域:用于对经济指标、市场需求、价格变动等进行预测,为经济决策提供参考。
灰色理论系统预测
灰色系统预测重点内容:灰色系统理论的产生和发展动态,灰色系统的基本概念,灰色系统与模糊数学、黑箱方法的区别,灰色系统预测GM (1,1)模型,GM(1,N)模型,灰色系统模型的检验,应用举例。
1灰色系统理论的产生和发展动态1982邓聚龙发表第一篇中文论文《灰色控制系统》标志着灰色系统这一学科诞生。
1985灰色系统研究会成立,灰色系统相关研究发展迅速。
1989海洋出版社出版英文版《灰色系统论文集》,同年,英文版国际刊物《灰色系统》杂志正式创刊。
目前,国际、国内200多种期刊发表灰色系统论文,许多国际会议把灰色系统列为讨论专题。
国际著名检索已检索我国学者的灰色系统论著500多次。
灰色系统理论已应用范围已拓展到工业、农业、社会、经济、能源、地质、石油等众多科学领域,成功地解决了生产、生活和科学研究中的大量实际问题,取得了显著成果。
2灰色系统的基本原理2.1灰色系统的基本概念我们将信息完全明确的系统称为白色系统,信息未知的系统称为黑色系统,部分信息明确、部分信息不明确的系统称为灰色系统。
系统信息不完全的情况有以下四种:1.元素信息不完全2.结构信息不完全3.边界信息不完全4.运行行为信息不完全2.2灰色系统与模糊数学、黑箱方法的区别主要在于对系统内涵与外延处理态度不同;研究对象内涵与外延的性质不同。
灰色系统着重外延明确、内涵不明确的对象,模糊数学着重外延不明确、内涵明确的对象。
“黑箱”方法着重系统外部行为数据的处理方法,是因果关系的两户方法,使扬外延而弃内涵的处理方法,而灰色系统方法是外延内涵均注重的方法。
2.3灰色系统的基本原理 公理1:差异信息原理。
“差异”是信息,凡信息必有差异。
公理2:解的非唯一性原理。
信息不完全,不明确地解是非唯一的。
公理3:最少信息原理。
灰色系统理论的特点是充分开发利用已有的“最少信息”。
公理4:认知根据原理。
信息是认知的根据。
公理5:新信息优先原理。
新信息对认知的作用大于老信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
灰色系统预测重点内容:灰色系统理论的产生和发展动态,灰色系统的基本概念,灰色系统与模糊数学、黑箱方法的区别,灰色系统预测GM(1,1)模型,GM(1,N)模型,灰色系统模型的检验,应用举例。
1灰色系统理论的产生和发展动态1982邓聚龙发表第一篇中文论文《灰色控制系统》标志着灰色系统这一学科诞生。
1985灰色系统研究会成立,灰色系统相关研究发展迅速。
1989海洋出版社出版英文版《灰色系统论文集》,同年,英文版国际刊物《灰色系统》杂志正式创刊。
目前,国际、国内200多种期刊发表灰色系统论文,许多国际会议把灰色系统列为讨论专题。
国际著名检索已检索我国学者的灰色系统论著500多次。
灰色系统理论已应用范围已拓展到工业、农业、社会、经济、能源、地质、石油等众多科学领域,成功地解决了生产、生活和科学研究中的大量实际问题,取得了显著成果。
2灰色系统的基本原理2.1灰色系统的基本概念我们将信息完全明确的系统称为白色系统,信息未知的系统称为黑色系统,部分信息明确、部分信息不明确的系统称为灰色系统。
系统信息不完全的情况有以下四种:1.元素信息不完全2.结构信息不完全3.边界信息不完全4.运行行为信息不完全2.2灰色系统与模糊数学、黑箱方法的区别主要在于对系统内涵与外延处理态度不同;研究对象内涵与外延的性质不同。
灰色系统着重外延明确、内涵不明确的对象,模糊数学着重外延不明确、内涵明确的对象。
“黑箱”方法着重系统外部行为数据的处理方法,是因果关系的两户方法,使扬外延而弃内涵的处理方法,而灰色系统方法是外延内涵均注重的方法。
2.3灰色系统的基本原理公理1:差异信息原理。
“差异”是信息,凡信息必有差异。
公理2:解的非唯一性原理。
信息不完全,不明确地解是非唯一的。
公理3:最少信息原理。
灰色系统理论的特点是充分开发利用已有的“最少信息”。
公理4:认知根据原理。
信息是认知的根据。
公理5:新信息优先原理。
新信息对认知的作用大于老信息。
公理6:灰性不灭原理。
“信息不完全”是绝对的。
2.4灰色系统理论的主要内容灰色系统理论经过10多年的发展,已基本建立起了一门新兴学科的结构体系,其主要内容包括以“灰色朦胧集”为基础的理论体系、以晦涩关联空间为依托的分析体系、以晦涩序列生成为基础的方法体系,以灰色模型(G,M)为核心的模型体系。
以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系。
灰色关联分析灰色统计灰色聚类3灰色系统预测模型灰色预测方法的特点表现在:首先是它把离散数据视为连续变量在其变化过程中所取的离散值,从而可利用微分方程式处理数据;而不直接使用原始数据而是由它产生累加生成数,对生成数列使用微分方程模型。
这样,可以抵消大部分随机误差,显示出规律性。
3.1灰色系统理论的建模思想下面举一个例子,说明灰色理论的建模思想。
考虑4个数据,记为)4(),3(),2(),1()0()0()0()0(X X X X上图表明原始数据)0(X 没有明显的规律性,其发展态势是摆动的。
如果将原始数据作累加生成,记第K 个累加生成为)()1(K X ,并且1)1()1()0()1(==X X321)2()1()2()0()0()1(=+=+=X X X5.45.121)3()2()1()3()0()0()0()1(=++=++=X X X X5.735.121)4()3()2()1()4()0()0()0()0()1(=+++=+++=X X X X X上图表明生成数列X 是单调递增数列。
3.2灰色系统预测模型建立 1. 数列预测GM (1,1)模型灰色系统理论的微分方程成为Gm 模型,G 表示gray (灰色),m 表示model (模型),Gm (1,1)表示1阶的、1个变量的微分方程模型。
Gm (1,1)建模过程和机理如下: 记原始数据序列)0(X 为非负序列其中,n k k x ,,2,1,0)()0( =≥ 其相应的生成数据序列为)1(X其中,n k i x k xki ,,2,1,)()(1)0()1( ==∑=为)1(X 的紧邻均值生成序列 {})(,),2(),1()1()1()1()1(n z z z Z =其中,n k k x k x k Z ,2,1),1(5.0)(5.0)()1()1()1(=-+=称b k az k x =+)()()1()0(为Gm(1,1)模型,其中a ,b 是需要通过建模求解的参数,若T =),(b a a 为参数列,且()()()()()()()()(){}n x x x x X 00000,...,3,2,1=()()()()()()()()(){}n x x x x X 11111,..,.3,2,1=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=)()3()2()0()0()0(n x x x Y ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=)5(1)4(1)3(1)2()1()1()1()1(z z z z B则求微分方程b k az k x =+)()()1()0(的最小二乘估计系数列,满足Y B B B aT T 1)(ˆ-=称b ax dtdx =+)1()1(为灰微分方程,b k az k x =+)()()1()0(的白化方程,也叫影子方程。
如上所述,则有1.白化方程b ax dtdx =+)1()1(的解或称时间响应函数为 abe a b x t xat +-=-))0(()(ˆ)1()1( 2.Gm(1,1)灰微分方程b k az k x =+)()()1()0(的时间响应序列为n k abe a b x k xak ,,2,1,))0(()1(ˆ)1()1( =+-=+- 3.取)1()0()0()1(x x =,则n k abe a b x k xak ,,2,1,))1(()1(ˆ)0()1( =+-=+- 4.还原值n k k x k x k x,,2,1),(ˆ)1(ˆ)1(ˆ)1()1()0( =-+=+ 2. 系统综合预测GM (1,N )模型P1344灰色系统模型的检验 定义1. 设原始序列{})(,),2(),1()0()0()0()0(n x x x X = 相应的模型模拟序列为{})(ˆ,),2(ˆ),1(ˆˆ)0()0()0()0(n x x x X= 残差序列{})(),2(),1()0(n εεεε ={})(ˆ)(,),2(ˆ)2(),1(ˆ)1()0()0()0()0()0()0(n x n x x x xx ---= 相对误差序列⎭⎬⎫⎩⎨⎧=∆)()(,,)2()2(,)1()1()0()0()0(n x n x x εεε{}nk 1∆=1.对于k <n,称)()()0(k x k k ε=∆为k 点模拟相对误差,称)()()0(n x n n ε=∆为滤波相对误差,称∑=∆=∆nk k n 11为平均模拟相对误差;2.称∆-1为平均相对精度,n ∆-1为滤波精度;3.给定α,当α<∆,且α<∆n 成立时,称模型为残差合格模型。
定义2设)0(X 为原始序列,)0(ˆX为相应的模拟误差序列,ε为)0(X 与)0(ˆX的绝对关联度,若对于给定的00,0εεε>>,则称模型为关联合格模型。
定义3设)0(X 为原始序列,)0(ˆX为相应的模拟误差序列,)0(ε为残差序列。
∑==n k k x n x 1)0()(1为)0(X 的均值, 21)0(21))((1x k x n s n k -=∑=为)0(x 的方差,∑==nk k n 1)(1εε为残差均值, ∑=-=n k k n s 1222))((1εε为残差方差,1.称12s sc =为均方差比值;对于给定的00>c ,当0c c <时,称模型为均方差比合格模型。
2.称()16745.0)(s k p p <-=εε为小误差概率,对于给定的00>p ,当0p p >时,称模型为小误差概率合格模型。
5应用举例 例 1 设原始序列{})5(),4(),3(),2(),1()0()0()0()0()0()0(x x x x x X =()679.3,390.3,337.3,278.3,874.2=建立Gm(1,1)模型,并进行检验。
解:1)对)0(X 作1-AGO ,得[D 为)0(X 的一次累加生成算子,记为1-AGO ,A cumulated Generating Operator] {})5(),4(),3(),2(),1()1()1()1()1()1()1(x x x x x X =()558.16,579.12,489.9,152.6,874.2=2)对)1(X 作紧邻均值生成,令)1(5.0)(5.0)()1()1()1(-+=k x k x k Z{})5(),4(),3(),2(),1()1()1()1()1()1()1(z z z z z Z =()718.14,84.11,820.7,513.4,874.2=于是,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=1718.14184.111820.71513.41)5(1)4(1)3(1)2()1()1()1()1(z z z z B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=679.3390.3337.3278.3)5()4()3()2()0()0()0()0(x x x x Y ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----•⎥⎦⎤⎢⎣⎡----=T 1718.14184.111820.71513.41111718.14184.11820.7513.4B B⎥⎦⎤⎢⎣⎡--=4235.38235.38221.423 ⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡--=--T832371.11665542.0165542.0017318.04235.38235.38221.423)(11B B ⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⨯=221.423235.38235.384969.2301221.423235.38235.384235.384221.42312 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎦⎤⎢⎣⎡----•⎥⎦⎤⎢⎣⎡==T -T 679.3390.3337.3278.31111718.14184.11820.7513.4832371.11665542.0165542.0017318.0)(ˆ1Y B B B a⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•⎥⎦⎤⎢⎣⎡---=679.3390.3337.3278.3604076.10019051.0537833.0085280.1089344.0028143.0030115.0087386.0 ⎥⎦⎤⎢⎣⎡-=065318.3037156.0 3)确定模型065318.3037156.0)1()1(=-x dtdx及时间响应式 abe a b x k xak +-=+-))1(()1(ˆ)0()1(4986.823728.85037156.0-=k e4)求)1(X 的模拟值{})5(ˆ),4(ˆ),3(ˆ),2(),1(ˆˆ)1()1()1()1()1()1(x x x xx X ==(2.8740,6.1058,9.4599,12.9410,16.5538) 5)还原出)0(X 的模拟值,由)(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+ 得 {})5(ˆ),4(ˆ),3(ˆ),2(ˆ),1(ˆˆ)0()0()0()0()0()0(x x x x x X ==(2.8740,3.2318,3.3541,3.4811,3.6128) 6)误差检验[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡•==T )5()4()3()2()5()4()3()2(εεεεεεεεεεs []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--•--=0662.00911.00171.00462.00662.00911.00171.00462.0 =0.0151085平均相对误差%)80.1%69.2%51.0%41.1(414151+++=∆=∆∑=k k =1.0625%计算X 与Xˆ的灰色关联度 ))1()5((21)1()((42x x x k x S k -+-=∑==)874.2679.3(21)874.2390.3()874.2337.3()874.2278.3(-+-+-+-0.40250.5160.4630.404+++==1.7855)1(ˆ)5(ˆ(21)1(ˆ)(ˆ(ˆ42x x x k x Sk -+-=∑= )874.26128.3(21)874.24811.3()874.23541.3()874.22318.3(-+-+-+-=3694.06071.04801.03578.0+++==1.8144[][]∑=---+---=-42))1(ˆ)5(ˆ())1()5((21))1(ˆ)(ˆ())1()((ˆk x x x x x k x x k x S S)4025.03694.0(21)516.06071.0()463.04801.0()404.03578.0(-+-+-+-=01655.0091.00171.00462.0-++-==0.0453564525.45999.404535.08144.17855.118144.17855.11ˆˆ1ˆ1=+++++=-+++++=S S SS S S ε=0.9902>0.90精度为一级,可以用4986.823728.85)1(ˆ037156.0)1(-=+k e k x)(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+预测。
