单级倒立摆经典控制系统
单级倒立摆系统
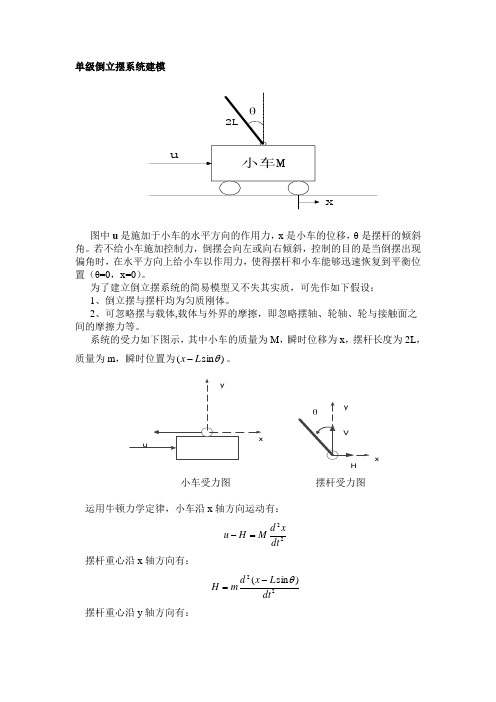
单级倒立摆系统建模图中u 是施加于小车的水平方向的作用力,x 是小车的位移,θ是摆杆的倾斜角。
若不给小车施加控制力,倒摆会向左或向右倾斜,控制的目的是当倒摆出现偏角时,在水平方向上给小车以作用力,使得摆杆和小车能够迅速恢复到平衡位置(θ=0,x=0)。
为了建立倒立摆系统的简易模型又不失其实质,可先作如下假设: 1、倒立摆与摆杆均为匀质刚体。
2、可忽略摆与载体,载体与外界的摩擦,即忽略摆轴、轮轴、轮与接触面之间的摩擦力等。
系统的受力如下图示,其中小车的质量为M ,瞬时位移为x ,摆杆长度为2L ,质量为m ,瞬时位置为)sin (θL x -。
Hx小车受力图 摆杆受力图运用牛顿力学定律,小车沿x 轴方向运动有:22dtxd M H u =-摆杆重心沿x 轴方向有:22)sin (dtL x d m H θ-= 摆杆重心沿y 轴方向有:22)cos (dtL d m mg V θ=- 摆杆围绕其重心的转动运动可用力矩方程来描述:θθθcos sin HL VL I += 式中,2231)2(121mL L m I ==为摆杆围绕其重心的转动惯量。
控制中要求θ小于5弧度,即在θ很小时,θθ≈sin ,1cos ≈θ,将方程在平衡点(θ=0,x=0)附近线性化处理。
则以上各式变为:xM H u =- ① )(θL x m H -= ② 0=-mg V ③HL VL I +=θθ④ 由式①和式②得:u mL xm M =++θ )( ⑤ 由式②、③和④得:θθmgL xmL mL I =++ )(2 ⑥ 由式⑤和式⑥可得单级倒立摆方程:u MmLI m M mL MmL I m M gL M m m 22)()()(++++++=θθu MmLI m M mL I MmL I m M gL m x 22222)()(++++++=θ 对以上两式进行拉氏变换,整理得以u 为输入量,以摆杆摆角θ为输出量得传递函数G(s)=gL m M m s MmL I m M mLs U s )(])[()()(22+-++=θ控制指标共有4个,即单级倒立摆的摆角θ、摆速θ、小车位置x 、小车速度x。
单级倒立摆稳定控制

单级倒立摆稳定控制摘要单级倒立摆是一种受控系统,在工业控制和机器人技术中有着广泛的应用。
这篇文档将介绍单级倒立摆的结构、原理和控制方法,特别是借助PID控制系统来实现单级倒立摆的稳定控制。
单级倒立摆是一种类人形机器人,它通常由一个水平旋转的轮子和一个通过电机传动的滑移杆组成,最后再由摆杆上的陀螺控制实现倒立。
这种结构使得单级倒立摆成为了机器人应用领域中的一个挑战问题。
为了实现单级倒立摆的稳定控制,需要在控制系统中引入一个合适的控制机制。
PID控制算法是一种最为通用的控制算法之一,常被用于像单级倒立摆这样的机器人平衡控制。
PID控制PID控制是一种基于反馈的控制系统,在工业和机器人技术中得到了广泛的应用。
PID控制通过比较实际的输出值与期望的输入值之间的差异,来作出对输出值的控制。
PID控制可以对输出值的稳定性、可靠性和精度进行控制,适用于不同类型的工业和机器人控制系统。
PID控制通常由三个部分组成:比例(P)、积分(I)和微分(D)控制。
比例控制反馈调整输出值,使得实际输出值逼近期望输入值。
积分控制记录过去所有误差,并将这些误差相乘来调整输出值。
微分控制通过记录过去的误差变化率,来防止输出值的快速变化。
在单级倒立摆稳定控制中,采用PID控制可以较好地解决因摩擦力、惯性、重心偏移等因素导致的系统不稳定问题,进而实现系统的平衡控制。
单级倒立摆的稳定控制实现单级倒立摆的稳定控制需要进行以下步骤:步骤1:系统建模将单级倒立摆系统建模,根据运动学和动力学原理,得到系统的运动方程。
步骤2:PID参数调节通过对PID控制算法中比例、积分、微分三个部分的参数进行调整,得到较好的控制效果。
步骤3:PID控制实现将PID控制器与单级倒立摆系统进行连接,实现单级倒立摆的稳定控制。
本文档介绍了单级倒立摆的结构、原理和控制方法,分析了PID控制算法在单级倒立摆稳定控制中的应用。
通过对步骤进行深入的解析,得到了单级倒立摆的稳定控制方法。
基于双闭环PID控制的一阶倒立摆控制系统设计

基于双闭环PID控制的一阶倒立摆控制系统设计一阶倒立摆是一种常见的控制系统,它由一个旋转臂和一个悬挂在旋转臂末端的摆杆组成。
控制目标是使摆杆保持垂直位置并保持在指定的角度范围内。
本文将基于双闭环PID控制设计一阶倒立摆控制系统,并对其进行详细的分析和讨论。
首先,我们需要明确控制系统的结构。
一阶倒立摆控制系统可以分为两个闭环:内环和外环。
内环用于控制旋转臂的角度,并将输出作为外环的输入。
外环用于控制摆杆的角度,并根据测量的摆杆角度和设定的目标角度来调整内环的输入。
在进行控制系统设计之前,我们需要先建立一阶倒立摆的数学模型。
假设倒立摆的质量集中在摆杆的一端,摆杆的长度为L,质量为m,摩擦系数为b,重力加速度为g。
通过应用牛顿第二定律,可以得到如下动力学方程:mL²θ¨ + bLθ˙ + mgLsinθ = u其中,θ是旋转臂的角度,u是旋转臂的扭矩。
为了简化方程,我们进行恒定参数修正和线性化处理,得到线性方程:θ¨ + 2ξωnθ˙ + ωn²θ = kru其中,ξ是阻尼比,ωn是无阻尼自然频率,kr是旋转臂的增益。
接下来,我们将按照以下步骤设计基于双闭环PID控制的一阶倒立摆控制系统:1.内环设计:-选择合适的内环闭环控制器类型。
对于一阶倒立摆,可以选择PID控制器。
-根据倒立摆的特性和性能要求,选择合适的PID参数。
可以使用试错法、经验法、系统辨识等方法进行参数调整。
-将PID控制器的输入设置为旋转臂角度误差,输出为旋转臂的扭矩。
2.外环设计:-选择合适的外环闭环控制器类型。
对于一阶倒立摆,可以选择PID控制器。
-根据倒立摆的特性和性能要求,选择合适的PID参数。
-将PID控制器的输入设置为摆杆角度误差,输出为旋转臂的角度设定值。
3.进行系统仿真和调试:-使用MATLAB等仿真工具建立一阶倒立摆的数学模型,并将设计的控制器与模型进行集成。
-调整控制器的参数,以满足性能指标和系统稳定性的要求。
一级倒立摆【控制专区】系统设计
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
二、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
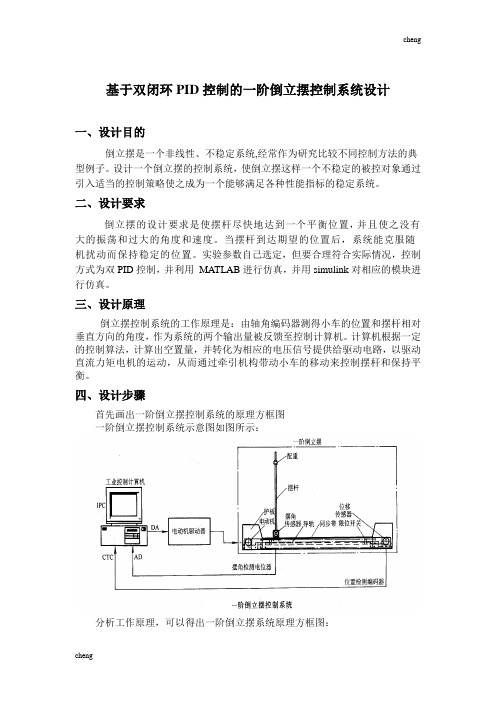
三、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:分析工作原理,可以得出一阶倒立摆系统原理方框图:一阶倒立摆控制系统动态结构图下面的工作是根据结构框图,分析和解决各个环节的传递函数!1.一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中: M :小车质量 m :为摆杆质量 J :为摆杆惯量 F :加在小车上的力 x :小车位置θ:摆杆与垂直向上方向的夹角 l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知: (1) 摆杆绕其重心的转动方程为(2) 摆杆重心的运动方程为得sin cos ..........(1)y x J F l F l θθθ=-2222(sin ) (2)(cos ) (3)x y d F m x l d td F mg m l d t θθ=+=-(3)小车水平方向上的运动为22..........(4)x d xF F M d t-=联列上述4个方程,可以得出一阶倒立精确气模型:()()()()()()()2222222222222222sin .sin cos cos cos .sin cos .lg sin cos J ml F ml J ml m l g x J ml M m m l ml F m l M m m m l M m J ml θθθθθθθθθθθθ⎧+++-⎪=++-⎪⎨+-+⎪=⎪-++⎩式中J 为摆杆的转动惯量:32ml J =若只考虑θ在其工作点附近θ0=0附近(︒︒≤≤-1010θ)的细微变化,则可以近似认为:⎪⎩⎪⎨⎧≈≈≈1cos sin 02θθθθ ⎪⎪⎩⎪⎪⎨⎧++-+=++-+=2..2222..)(lg )()()(Mml m M J mlF m m M Mml m M J g l m F ml J x θθθ 若取小车质量M=2kg,摆杆质量m=1kg,摆杆长度2 l =1m,重力加速度取g=2/10s m ,则可以得 一阶倒立摆简化模型:....0.44 3.330.412x F F θθθ⎧=-⎪⎨⎪=-+⎩即 G 1(s)= ; G 2(s)=一阶倒立摆环节问题解决!2.电动机驱动器选用日本松下电工MSMA021型小惯量交流伺服电动机,其有关参数如下:222()0.4()12() 1.110()s F s s x s s s s θθ-⎧=⎪-⎪⎨-+⎪=⎪⎩驱动电压:U=0~100V 额定功率:PN=200W 额定转速:n=3000r/min 转动惯量:J=3×10-6kg.m2 额定转矩:TN=0.64Nm 最大转矩:TM=1.91Nm 电磁时间常数:Tl=0.001s 电机时间常数:TM=0.003s经传动机构变速后输出的拖动力为:F=0~16N ;与其配套的驱动器为:MSDA021A1A ,控制电压:UDA=0~±10V 。
一阶倒立摆控制系统设计matlab

一阶倒立摆控制系统设计matlab一、控制系统简介控制系统是指通过对某些物理系统或过程的改变以获取期望输出或行为的一种系统。
其中涉及到了对系统的建模、分析以及控制方法的选择和设计等多方面的问题。
控制系统可以通过标准的数学和物理模型来描述,并可以通过物理或者仿真实验进行验证。
本文将围绕一阶倒立摆控制系统设计和仿真展开。
主要内容包括:1.一阶倒立摆系统简介2.系统建模3.系统分析4.设计控制器5.仿真实验及结果分析一阶倒立摆(controlled inverted pendulum)是一种比较常见的控制系统模型。
它的系统模型简单,有利于系统学习和掌握。
一般而言,一阶倒立摆系统是由一个竖直的支杆和一个质量为$m$的小球组成的。
假设球只能在竖直方向上运动,当球从垂直平衡位置偏离时,支杆会向相反的方向采取动作,使得小球可以回到平衡位置附近。
为了控制一阶倒立摆系统,我们首先需要对其进行建模。
由于系统并不是非常复杂,所以建模过程相对简单。
假设支杆长度为$l$,支杆底端到小球的距离为$h$,支杆与竖直方向的夹角为$\theta$,小球的质量为$m$,地球重力为$g$,该系统的拉格朗日方程可以表示为:$L =\frac{1}{2}m\dot{h}^{2}+\frac{1}{2}ml^{2}\dot{\theta}^{2}-mgh\cos{\theta}-\frac{1}{2}I\dot{\theta}^{2}$$I$表示支杆的惯性矩,它可以通过支杆的质量、长度以及截面积等参数计算得出。
$h$和$\theta$分别表示小球和支杆的位置。
我们可以通过拉格朗日方程可以得出系统的动力学方程:$b$表示摩擦系数,$f_{c}$表示对支杆的控制力。
由于一阶倒立摆会发生不稳定的倾斜运动,即未受到外部控制时会继续倾斜。
我们需要对系统加上控制力,使得系统保持在稳定的位置上。
在进行控制器设计之前,我们需要对系统进行分析,以便更好地了解系统在不同条件下的特性表现。
直线一级倒立摆系统实验报告

直线一级倒立摆系统实验报告1. 实验目的:通过对直线一级倒立摆系统进行分析,掌握系统的基本原理、参数设置和控制策略;提高学生实际动手能力和科学实验能力。
2. 实验内容:(1)搭建直线一级倒立摆系统实验平台;(2)设置系统的动力学模型,采集系统的状态变量;(3)根据系统的特性设计控制策略,实现系统的稳定控制;(4)记录实验数据,并进行数据处理和分析。
3. 实验原理:直线一级倒立摆系统是一种经典的非线性控制系统,其原理和稳定性分析可以使用动力学建模方法来描述。
系统由直线弹簧、质量块、直线导轨和质量块的摆杆组成。
当摆杆处于垂直状态时,系统处于平衡状态;当摆杆被扰动后,系统进入不稳定状态,需要通过控制策略来实现其稳定控制。
在实验中,我们选取了单摆系统作为直线一级倒立摆系统的原形。
单摆系统由一个质点和一个线性弹簧组成,其状态变量为质点的位置和速度。
当质点处于平衡位置时,系统拥有稳定状态;当质点被扰动后,系统进入不稳定状态,需要通过控制策略来实现其稳定控制。
因此,我们可以使用单摆系统来研究直线一级倒立摆系统的控制策略。
4. 实验步骤:(1)搭建实验平台:搭建直线一级倒立摆系统实验平台,包括直线导轨、摆杆、质点、力传感器、位移传感器和控制电路等。
将质点放置在导轨上,并用摆杆将其固定在弹簧上。
使用力传感器和位移传感器来测量系统的状态变量。
(2)设置系统模型:对实验平台的动力学模型进行建模,将系统的状态变量与控制策略联系起来。
(3)设计控制策略:根据系统的特性设计相应的控制策略,使系统保持稳定状态。
常用的控制策略包括模型预测控制、PID控制、滑模控制等。
(4)记录实验数据:实验过程中需要记录系统的状态变量和控制参数,并进行数据处理和分析,得到实验结论。
5. 实验结果分析:通过对直线一级倒立摆系统的实验研究,我们发现系统的稳定控制需要根据其特性和实际情况来确定相应的控制策略。
在实验中,我们采用了模型预测控制策略,通过对系统的状态变量进行预测和调节,成功实现了系统的稳定控制。
一级倒立摆控制系统设计
基于双闭环PID控制的一阶倒立摆控制系统设计一、设计目的倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。
设计一个倒立摆的控制系统,使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
、设计要求倒立摆的设计要求是使摆杆尽快地达到一个平衡位置,并且使之没有大的振荡和过大的角度和速度。
当摆杆到达期望的位置后,系统能克服随机扰动而保持稳定的位置。
实验参数自己选定,但要合理符合实际情况,控制方式为双PID控制,并利用MATLAB进行仿真,并用simulink对相应的模块进行仿真。
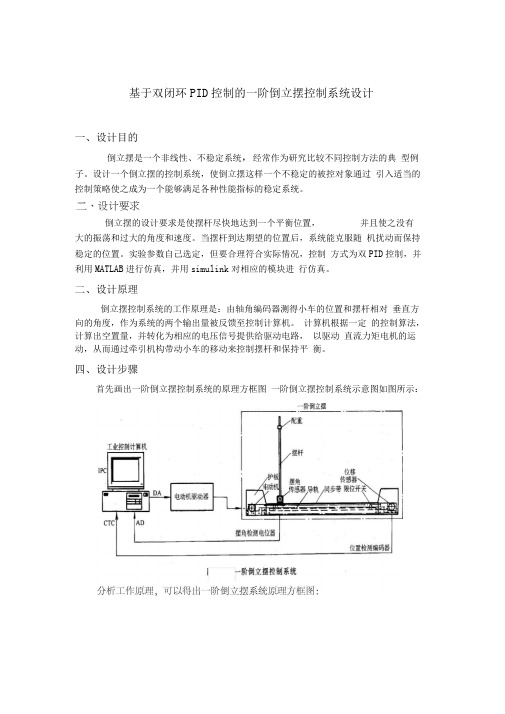
二、设计原理倒立摆控制系统的工作原理是:由轴角编码器测得小车的位置和摆杆相对垂直方向的角度,作为系统的两个输出量被反馈至控制计算机。
计算机根据一定的控制算法,计算出空置量,并转化为相应的电压信号提供给驱动电路,以驱动直流力矩电机的运动,从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
四、设计步骤首先画出一阶倒立摆控制系统的原理方框图一阶倒立摆控制系统示意图如图所示:工业控制计算机电动机驱动器一阶倒立摆一阶倒立摆控制系统动态结构图F面的工作是根据结构框图,分析和解决各个环节的传递函数!1. 一阶倒立摆建模在忽略了空气流动阻力,以及各种摩擦之后,可将倒立摆系统抽象成小车和匀质杆组成的系统,如下图所示,其中:M小车质量m为摆杆质量J :为摆杆惯量F:加在小车上的力x :小车位置摆杆与垂直向上方向的夹角l :摆杆转动轴心到杆质心的长度根据牛顿运动定律以及刚体运动规律,可知:(1) 摆杆绕其重心的转动方程为J鎳F y lsin 二- F x l cos: (1)(2) 摆杆重心的运动方程为F x d2(x l sin r)彳『=mg-m d2 d2t(3) 小车水平方向上的运动为-1-L+10-0一4即 G 1(s)=' ; G 2(s)='-一阶倒立摆环节问题解决!2. 电动机驱动器选用日本松下电工MSMA02型小惯量交流伺服电动机,其有关参数如下:F — F x 二 M d 2x联列上述4个方程,可以得出一阶倒立精确气模型:J ml 2F ml J ml 2sin u 2-m 2l 2gsin r COST2 2 2 2J ml j[ M m :-m l cos )mlcos v.F m 2l 2sin vcos m 2-<; M m mlg sin vm 2l 2cos 20—(M + m )(J +ml 2)式中J 为摆杆的转动惯量:J 』3若只考虑B 在其工作点附近B 0=0附近(-10 —”:10 )的细微变化,则可 以近似认为: 石2“* sin^比日 cos 日“若取小车质量M=2kg,摆杆质量 m=1kg,摆杆长度2 l =1m,重力加速度取g=10m/s 2,则可以得阶倒立摆简化模型:x =0.44F -3.33^ v - -0.4 F 12^拉氏变换=^>日(s)』F(s) x(s) ?(s)-0.42s-122 -1.1s 102 s2(J ml 2)F -m 2l 2g J J(M m) Mml (M m)mlg mlF J(M m) Mml电磁时间常数:Tl=0.001s电机时间常数:TM=0.003s经传动机构变速后输出的拖动力为: F=0~16N 与其配套的驱动器为:MSDA021A1A S 制电压:UDA=0± 10V 。
单级旋转倒立摆系统

《现代控制理论》课程综合设计单级旋转倒立摆系统1引言单级旋转倒立摆系统一种广泛应用的物理模型,其物理模型如下:图示为单级旋转倒立摆系统原理图。
其中摆的长度∕1=lm,质量∏71 =Olkg ,横杆的长度厶 =1 m f 质量nt2 =Olkg1重力加速度g =0.98∕π/52O以在水平方向对横杆施加的力矩M 为输入,横杆相对参考系产生的角位移q为输出。
控制的目的是当横杆在水平方向上旋转时,将倒立摆保持在垂直位置上。
图1单级旋转倒立摆系统模型单级旋转倒立摆可以在平行于纸面360°的范围内自由摆动。
倒立摆控制系统的目的是使倒立摆在外力的推动下,摆杆仍然保持竖直向上状态。
在横杆静止的状态下,由于受到重力的作用,倒立摆的稳定性在摆杆微小的扰动下,就会使倒立摆的平衡无法复位,这时必须使横杆在平行于纸面的方向通过位移产生相应的加速度。
作用力与物体位移对时间的二阶导数存在线性关系,故单级倒立摆系统是一个非线性系统。
本文综合设计以以在水平方向对横杆施加的力矩M为输入,横杆相对参考系产生的角位移q为输出,建立状态空间模型,在原有系统上中综合带状态观测器状态反馈系统,从而实现当横杆在旋转运动时,将倒立摆保持在垂直位置上。
2模型建立本文将横杆和摆杆分别进行受力分析,定义以下物理量:本文将横杆和摆杆M-NI 2=J 2d~θx分别进行受力分析,定义以下物理量:M 为加在横杆上的力矩;〃勺为摆杆质量; 厶为摆杆长度;人为摆杆的转动惯量;“为横杆的质量;厶为横杆的长度;厶为 横杆的转动惯量;q 为横杆在力矩作用下转动的角度;g 为摆杆与垂直方向的夹 角;N 和H 分别为摆杆与横杆之间相互作用力的水平和垂直方向的分量。
倒立 摆模型受力分析如图2所示。
图2倒立摆模型受力分析 摆杆水平方向受力平衡方程:NM I 牛甸/+O + ? Sina) (∕2-横杆的转动弧长即位移)摆杆垂直方向受力平衡方程:〃2 I I卑g=卑 2叶一寸COSq)Ur 2 2摆杆转矩平衡方程:横杆转矩平衡方程:XX考虑到摆杆在设定点q,Q=o 附近做微小振动,对上式进行线性化,即• ml JSi 吨≈q, cos^2 ≈1 ‘心0,其中八〒,近似线性化得到,JlN = OΛ-(Θ +OM (IV ・//-0.98 = 0 1 /1If)——= H ∙0.5IN ∙0.5∙l 30 dfM-N = -^∙30 dr整理上式可得倒立摆的状态方程:1 ∙∙ ∙∙—q —0 + 14.70—15M<4 ∙∙ 1 ∙∙-<91 + -6>2-10M =O l3 2本文参数代入计算可得:& =-4.642Q+11.05 3M Q= 12.3790—9.474M■x=q=[ι 0 0 0]■■ ■X =■ qO I■O^Λ ^^0χ2OO -¾.OO"P ■O 尤2 + 11.053 1O O9.474取状态变量如下:故1 OO -4.642 O O O 12.3793稳定性和能控性分析3.1稳定性分析判断一个系统是否稳定,只需判断该系统传递函数的极点是否都在左半平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单级倒立摆经典控制系统摘要:倒立摆控制系统虽然作为热门研究课题之一,但见于资料上的大多采用现代控制方法,本课题的目的就是要用经典的方法对单级倒立摆设计控制器进行探索。
本文以经典控制理论为基础,建立小车倒立摆系统的数学模型,使用PID控制法设计出确定参数(摆长和摆杆质量)下的控制器使系统稳定,并利用MATLAB软件进行仿真。
关键词:单级倒立摆;经典控制;数学模型;PID控制器;MATLAB 1绪论自动控制理论是研究自动控制共同规律的技术科学。
它的发展初期,是以反馈理论为基础的自动调节原理,并主要用于工业控制。
控制理论在几十年中,迅速经历了从经典理论到现代理论再到智能控制理论的阶段,并有众多的分支和研究发展方向。
1.1经典控制理论控制理论的发展,起于“经典控制理论”。
早期最有代表性的自动控制系统是18世纪的蒸汽机调速器。
20世纪前,主要集中在温度、压力、液位、转速等控制。
20世纪起,应用范围扩大到电压、电流的反馈控制,频率调节,锅炉控制,电机转速控制等。
二战期间,为设计和制造飞机及船用自动驾驶仪、火炮定位系统、雷达跟踪系统及其他基于反馈原理的军用装备,促进了自动控制理论的发展。
至二战结束时,经典控制理论形成以传递函数为基础的理论体系,主要研究单输入-单输出、线性定常系统的分析问题。
经典控制理论的研究对象是线性单输入单输出系统,用常系数微分方程来描述。
它包含利用各种曲线图的频率响应法和利用拉普拉斯变换求解微分方程的时域分析法。
这些方法现在仍是人们学习控制理论的入门之道。
1.2倒立摆1.2.1倒立摆的概念图1 一级倒立摆装置倒立摆是处于倒置不稳定状态,人为控制使其处于动态平衡的一种摆。
如杂技演员顶杆的物理机制可简化为一级倒立摆系统,是一个复杂、多变量、存在严重非线性、非自治不稳定系统。
常见的倒立摆系统一般由小车和摆杆两部分构成,其中摆杆可能是一级、两级甚至多级。
在复杂的倒立摆系统中,摆杆长度和质量均可变化。
据研究的目的和方法不同,又有悬挂式倒立摆、球平衡系统和平行式倒立摆等。
1.2.2研究倒立摆稳定性的意义倒立摆的研究具有重要的工程背景。
机器人行走就类似倒立摆系统。
从日常生活中所见到的任何重心在上、也是支点在下的控制问题,到空间飞行器和各类伺服云台的稳定,都和倒立摆系统的稳定控制有很大相似性,故对其稳定控制在实际中有很多用场,如海上钻井平台的稳定控制、卫星发射架的稳定控制、火箭姿态控制、飞机安全着陆、化工过程控制等。
2单级倒立摆的数学模型2.1模型的推导原理建立控制系统的数学模型有两种基本方法。
其一,对系统各部分的运动机理进行分析,根据它们所依据的物理规律或化学规律分别列写相应的运动方程,合在一起便成为描述整个系统的方程。
其二,人为地给系统施加某种测试信号,记录其输出响应,并用适当的数学模型去逼近。
主要用于系统运动机理复杂因而不便分析或不可能分析的情况。
系统的建模原则:1、建模之前,要全面了解系统的自然特征和运动机理,明确研究目的和准确性要求,选择合适的分析方法。
2、按照所选分析法,确定相应的数学模型的形式;3、根据允许的误差范围,进行准确性考虑,然后建立尽量简化的合理的数学模型。
倒立摆的形状较为规则,而且是一个绝对不稳定系统,无法通过测量频率特性方法获取其数学模型。
故适合用数学工具进行理论推倒。
2.2单级倒立摆系统描述小车—倒立摆系统是各种控制理论的研究对象。
只要一提小车—倒立摆系统,一般均认为其数学模型也已经定型。
事实上,小车—倒立摆的数学模型与驱动系统有关,常见到的模型只是对应于直流电机的情况,如果执行机构是交流伺服电机,就不是这个模型了。
本文主要分析由直流电机驱动的小车—倒立摆系统。
小车倒立摆系统是检验控制方式好坏的一个典型对象,其特点是高阶次、不稳定、非线性、强耦合,只有采取有效的控制方式才能稳定控制。
图2 单级倒立摆系统的原理图图中u是施加于小车的水平方向的作用力,x是小车的位移,θ是摆的倾斜角。
若不给小车施加控制力,倒摆会向左或向右倾斜,控制的目的是当倒摆出现偏角时,在水平方向上给小车以作用力,通过小车的水平运动,使倒摆保持在垂直的位置。
即控制系统的状态参数,以保持摆的倒立稳定。
2.3单级倒立摆系统数学建模为了建立倒立摆系统的数学模型,先作如下假设:①倒立摆与摆杆均为匀质刚体。
②可忽略摆与载体,载体与外界的摩擦,即忽略摆轴、轮轴、轮与接触面之间的摩擦力等。
2.3.1结构参数倒立摆是不稳定的,如果没有适当的控制力作用在它的上面,它将随时可能向任何方向倾倒。
这里只考虑二维问题,即认为倒立摆只在图2所示平面内运动。
控制力u作用于小车上。
摆杆长度为2L,质量为m,小车的质量为M,小车瞬时位移为x,摆杆瞬时位置为(x+2L*sinθ),在外力的作用下,系统产生运动。
假设摆杆的重心位于其几何中心。
设输入为作用力u,输出为摆角θ。
2.3.2系统的运动方程图3 小车沿x轴的受力分析图4 摆的受力分析小车沿x轴方向的受力分析如图4所示,根据牛顿第二定律得方程⑴⑵⑶⑷为车载倒立摆系统运动方程组。
因为含有项,所以为非线性微分方程组。
中间变量不易相消。
2.4单级倒立摆系统模型的线性化处理及传递函数3单级倒立摆控制系统原理3.1线性系经统的校正方法所谓校正,就是在系统中加入一些其参数可以根据需要而改变的机构或装置,使系统整个特性发生变化,从而满足给定的各项性能指标。
按照校正装置在系统中的连接方式,控制系统校正方式可分为串联校正、反馈校正和复合校正四种。
根据被控对象及技术指标要求这里采用串联校正。
3.2基本控制定律确定校正装置的具体形式时,应先了解校正装置所提供的控制规律,以便选择相应的元件。
包含校正装置在内的控制器,常常采用比例、微分、积分等基本控制规律,或者采用这些基本控制规律的某种组合,如比例-微分、比例-积分、比例-积分-微分等组合控制规律,以实现对被控对象的有效控制。
比例--微分—微分(P ID)控制定律具有比例—积分—微分控制规律的控制器,称PID控制器。
这种组合具有三种基本控制规律各自的特点,其运动方程为当利用PID控制器进行串联校正时,除可使系统的型别提高一级外,还将提供两个负实零点。
与PI控制器相比,除了同样具有提高系统的稳态性能的优点外,还多提供了一个负实零点,从而在提高系统动态性能方面,具有更大的优越性。
因此,在工业过程控制系统中,广泛使用PID控制器。
PID控制器各部分参数的选择,在系统现场调试中最后确定。
通常,应使I部分发生在系统频率特性的低频段,以提高系统的稳态性能;而使D部分发生在系统频率特性的中频段,以改善系统的动态性能。
本系统采用即为PID控制器。
3.3PID控制3.3.1.1PID控制器的结构所有的PID控制器都有可以分解成给定值控制单元,PID作用单元及手动/自动转换单元等三个主要单元,如图6所示。
图中,给定值单元①接收工业控制过程的测量量c,以及控制装置的给定值。
PID作用单元②接受给定值控制单元产生的误差信号e,并按给定控制律算出闭环控制信号。
手动/自动单元③在“自动A位置时,将PID单元的输出信号送入工业过程,此时工业过程在闭环中受到控制;而在“手动M位置时,把用户直接在控制器上调整手动输出信号送至工业过程,于是系统采用开环控制方式。
图5 PID控制器原理性结构3.3.1.2PID控制器的使用实用PID控制器的传递函数可以表示为PID单元的原理电路如图7所示。
图6 PID单元原理电路4单级倒立摆的系统控制器设计4.1系统的控制校正设计控制系统的目的是使系统动态稳定,即保持倒立摆在垂直的位置,使小车在外力作用下其位移以较小的误差跟随输入的变化。
由于系统的动态响应主要是由它的极点位置决定的,而假如系统是状态完全能控的,即可使系统得到良好的动态性能。
我们在第2.4节中对单级倒立摆系统模型的进行了线性化并推导出了其传递函数。
本课题将采用PID控制法为系统设计控制器。
设原系统小车的质量M=2.00kg,摆的质量m=0.20kg,摆长2L=0.80m,重力加速度4.2利用MATLAB的系统仿真进入MATLAB的工作环境之后,通过键盘输入MATLAB命令,便可以执行相应的操作了,这与DOS的操作十分接近。
如,通过下面的MATLAB程序即可获得G (s)的单位阶跃响应及极零点分布。
(见图7)图7 G (s)的单位阶跃响应及极零点分布>> s=tf('s') Transfer function:s>> sys=tf(-1,[1 0 29.6964])Transfer function:-1----------s^2 + 29.7>>step(sys)>>pzmap(sys)4.3仿真结果的修正与分析本实验采用MATLAB软件进行仿真实验,进一步验证了PID控制器中各个参数对系统的稳定性和动态性能的影响,在大量的仿真结果中进行比较和挑选,同时根据调节时间<3s的设计要求,最后确定PID 控制器的各参数分别为:微分时间系数=1,积分时间系数T =1,比例系数K =20。
则系统的闭环传递函数为(系统的闭环传递函数的单位阶跃响应为图8):20 s^2 + 20 s + 20------------------------s^3 + 23 s^2 + 25 s + 20图8 的单位阶跃响应结论倒立摆系统的控制研究长期以来被认为是控制理论极其应用领域里引起人们极大兴趣的问题。
它是检验各种控制理论和方法的有效性的著名实验装置,作为一个高阶、非线性、不稳定系统,倒立摆的稳定控制相当困难,对该领域的学者来说是一个极具挑战性的难题。
本文以经典控制理论为基础,建立了小车倒立摆系统的数学模型,使用PID控制法设计出确定参数下的控制器使系统稳定。
本实验采用MATLAB软件进行仿真实验,进一步验证了PID控制器中各个参数对系统的稳定性和动态性能的影响,在大量的仿真结果中进行比较和挑选,同时根据调节时间<3s的设计要求,最后确定PID控制器的各参数值,通过MATLAB软件的仿真可知,单级倒立摆的经典控制可以实现。
