吉林省东北师范大学附属中学2015届高三一轮复习阶段测试卷(第5周)数学文 Word版含答案
吉林省东北师范大学附属中学高三数学总复习阶段测试卷6 理

吉林省东北师范大学附属中学2015届高三数学总复习阶段测试卷6理选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合212 {|10},{|log} A x x B x y x =-<==,则A∩B等于()A.{|1}x x>B.{|01}x x<<C.{|1}x x<D.{|01}x x<≤2.已知α∈(π2,π),tanα=-34,则sin(α-π)=()A.35B.-35 C.45D.-453.在△ABC中,“3sin A>”是“3πA>”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.若cos22π2sin4αα=-⎛⎫-⎪⎝⎭,则cos sinαα+的值为()A.72-B.12C.12-725.在△ABC中,若tanA+tanB=1- tanAtanB,则cosC的值是()A.-22 B.22 C.12D.-126.函数2sin2xy x=-的图象大致是()7.若角α的终边在直线y=2x上,则ααααcos2sincossin2+-的值为()A.0 B.34C.1 D.548.ABC∆的内角A B C、、的对边分别是a b c、、,若2B A=,1a=,3b=,则c=( )A..2CD .19.已知3()f x x ax =-在[)1,+∞上是单调增函数,则a 的取值范围是( ) A .]3,(-∞ B .)3,1( C .)3,(-∞ D .),3[+∞10.函数()()x x x f 21ln -+=的零点所在的大致区间是( )A.(0,1)B.(1,2)C.(2,3)D.(3,4)11.)0)(sin(3)(>+=ωϕωx x f 部分图象如图,若2||AB BC AB =⋅,ω等于( )12πB .4πC .3πD .6π12.函数()x f 是R 上的偶函数,在区间[)+∞,0上是增函数.令⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=75tan ,75cos ,72sin πππf c f b f a ,则( ) A .c b a << B .a b c << C .a c b << D .c a b <<源:学科网] 二、填空题:本大题共4小题,每小题5分,共20分.13.设1232,2()log (1),2x e x f x x x -⎧<⎪=⎨-≥⎪⎩,则((2))f f 的值为 .14.若sin cos θθ+=,则tan 3πθ⎛⎫+ ⎪⎝⎭的值是 ___________. 15.已知213sin =⎪⎭⎫ ⎝⎛+πα,则⎪⎭⎫ ⎝⎛+6cos πα的值等于 . 16.已知函数)(x f y =()x ∈R 满足1(1)()f x f x +=-,且[1,1]x ∈-时,2)(x x f =,则)(x f y =与x x g 5log )(=的图象的交点个数为____________.三、解答题: 解答应写出文字说明,证明过程或演算步骤. 17、(本小题12分)已知函数f(x)=4cos ωx ·sin ⎪⎭⎫ ⎝⎛+4πωx (ω>0)的最小正周期为2π. (1)求ω的值; (2)讨论f (x )在区间⎥⎦⎤⎢⎣⎡20π,上的单调性.18.(本小题12分)已知()⎪⎭⎫⎝⎛∈=-2,0,54sin πααπ求2cos 2sin 2αα+的值求函数x x x f 2cos 212sin cos 65)(-=α的单调递增区间。
吉林省东北师范大学附属中学高考数学一轮复习阶段测试卷(第15周)文(无答案)

吉林省东北师范大学附属中学2015届高考数学一轮复习阶段测试卷(第15周)文(无答案)10.[2014·江西卷]11.若曲线y =xln x 上点P 处的切线平行于直线2x -y +1=0,则点P 的坐标是________.11.[2014·江西卷] 21.将连续正整数1,2,…,n(n ∈N*)从小到大排列构成一个数123…n ,F(n)为这个数的位数(如n =12时,此数为123456789101112,共有15个数字,F(12)=15),现从这个数中随机取一个数字,p(n)为恰好取到0的概率.(1)求p(100);(2)当n≤2014时,求F(n)的表达式;(3)令g(n)为这个数中数字0的个数,f(n)为这个数中数字9的个数,h(n)=f(n)-g(n),S ={n|h(n)=1,n ≤100,n ∈N*},求当n ∈S 时p(n)的最大值.12.[2014·辽宁卷] 12.当x ∈[-2,1]时,不等式ax3-x2+4x +3≥0恒成立,则实数a 的取值范围是( )A .[-5,-3] B.⎣⎢⎡⎦⎥⎤-6,-98 C .[-6,-2] D .[-4,-3]13.[2014·新课标全国卷Ⅱ] 11. 若函数f(x)=kx -ln x 在区间(1,+∞)单调递增,则k 的取值范围是( )A .(-∞,-2]B .(-∞,-1]C .[2,+∞)D .[1,+∞)14.[2014·新课标全国卷Ⅱ] 21. 已知函数f(x)=x3-3x2+ax +2,曲线y =f(x)在点(0,2)处的切线与x 轴交点的横坐标为-2.(1)求a ;(2)证明:当k <1时,曲线y =f(x)与直线y =kx -2只有一个交点.15. [2014·全国新课标卷Ⅰ] 12.已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a 的取值范围是( )A .(2,+∞)B .(1,+∞)C .(-∞,-2)D .(-∞,-1)16. [2014·全国新课标卷Ⅰ] 21. 设函数f(x)=aln x +1-a 2x2-bx(a≠1),曲线y =f(x)在点(1,f(1))处的切线斜率为0.(1)求b ;(2)若存在x0≥1,使得f(x0)<a a -1,求a 的取值范围.17.[2014·山东卷] 20.设函数f(x)=aln x +x -1x +1,其中a 为常数. (1)若a =0,求曲线y =f(x)在点(1,f(1))处的切线方程;(2)讨论函数f(x)的单调性.18.[2014·陕西卷] 21. 设函数f(x)=ln x +m x,m ∈R. (1)当m =e(e 为自然对数的底数)时,求f(x)的极小值;(2)讨论函数g(x)=f ′(x)-x 3零点的个数; (3)若对任意b >a >0,f (b )-f (a )b -a<1恒成立,求m 的取值范围.19. [2014·天津卷] 19.已知函数f(x)=x2-23ax3(a >0),x ∈R. (1)求f(x)的单调区间和极值;(2)若对于任意的x1∈(2,+∞),都存在x2∈(1,+∞),使得f(x1)·f(x 2)=1,求a 的取值范围.20.[2014·浙江卷] 21. 已知函数f(x)=x3+3|x -a|(a >0).若f(x)在[-1,1]上的最小值记为g(a).(1)求g(a);(2)证明:当x ∈[-1,1]时,恒有f(x)≤g(a)+4.21.[2014·重庆卷]19. 已知函数f(x)=x 4+a x -ln x -32,其中a∈R,且曲线y =f(x)在点(1,f(1))处的切线垂直于直线y =12x. (1)求a 的值;(2)求函数f(x)的单调区间与极值.(十四)单元综合1. [2014·江苏卷] 19. 已知函数f(x)=ex +e -x ,其中e 是自然对数的底数.(1)证明:f(x)是R 上的偶函数.(2)若关于x 的不等式mf(x)≤e -x +m -1在(0,+∞)上恒成立,求实数m 的取值范围.(3)已知正数a 满足:存在x0∈[1,+∞),使得f(x0)<a(-x30+3x0)成立.试比较ea -1与ae -1的大小,并证明你的结论.3[2014·辽宁卷] .21. 已知函数f(x)=π(x -cos x)-2sin x -2,g(x)=(x -π)1-sin x 1+sin x+2x π-1.证明: (1)存在唯一x0∈⎝⎛⎭⎪⎫0,π2,使f(x0)=0; (2)存在唯一x1∈⎝ ⎛⎭⎪⎫π2,π,使g(x1)=0,且对(1)中的x0,有x0+x1>π.4.[2014·山东卷] 9.对于函数f(x),若存在常数a≠0,使得x 取定义域内的每一个值,都有f(x)=f(2a -x),则称f(x)为准偶函数,下列函数中是准偶函数的是( )A .f(x)=xB .f(x)=x2C .f(x)=tan xD .f(x)=cos(x +1)5.[2014·四川卷] 15.以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M ,使得函数φ(x)的值域包含于区间[-M ,M].例如,当φ1(x)=x3,φ2(x)=sin x 时,φ1(x )∈A,φ2(x)∈B.现有如下命题:①设函数f(x)的定义域为D ,则“f(x)∈A”的充要条件是“∀b ∈R ,∃a ∈D ,f(a)=b”; ②若函数f(x)∈B,则f(x)有最大值和最小值;③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B ,则f(x)+g(x)∈/B; ④若函数f(x)=aln(x +2)+x x2+1(x >-2,a∈R)有最大值,则f(x)∈B. 其中的真命题有________.(写出所有真命题的序号)。
吉林省东北师范大学附属中学2015届高三上学期第一次摸底考试数学(理)试题及答案

(2)命题“对任意的,都有”的否定是(A)对任意的,都有(B)存在,使(C)不存在,使(D)存在,使(3)曲线在点处的切线与坐标轴所围成的三角形的面积为(4)下列函数中是偶函数且在上单调递增的是(A)(B)(C)(D)(5)“”是“”的(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件(6)若,则下列不等式成立的是(A)(B)(C)(D)(7)如图,已知直线和圆,当从开始在平面上绕点按逆时针方向匀速转动(转动角度不超过)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是(A)(B)(C)(D)(8)定积分的值为(A)(B)(C)(D)(9)偶函数的定义域为,,是奇函数,且,则(A)0 (B)1 (C)(D)2014(10)函数在处有极值10,则点的坐标为(A)(B)(C)或(D)不存在(11)若,则实数的取值范围是(A)(B)(C)(D)(12)表示不超过的最大整数,函数.①是周期为1 的周期函数;②的定义域为;③的值域为;④是偶函数;⑤的单调递增区间为.上面结论中正确的个数是(A) 2 (B)3 (C)4 (D)5第Ⅱ卷请将答案写在答题卡上,写在试卷上无效.本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答。
二、填空题:本大题共4小题,每小题5分.(13)设,若,则的值为;(14)函数恰好有两个零点,则的值为_________;(15)函数是定义在上的减函数,且,则的取值范围是__________;(16)已知是定义在上的奇函数,当时,. 若对任意的,不等式恒成立,则实数的取值范围是.三、解答题:解答应写出文字说明,演算步骤或证明过程。
(17)(本小题满分12分)已知二次函数,不等式的解集为. (Ⅰ)若方程有两个相等的正根,求的解析式;(Ⅱ)若的最大值为正数,求的取值范围.(18)(本小题满分12分)根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01.该地区某工地上有一台大型设备,遇到大洪水时损失60000元,遇到小洪水时损失10000元.为保护设备,有以下3种方案:方案1:运走设备,搬运费为3800元.方案2:建保护围墙,建设费为2000元,但围墙只能防小洪水.方案3:不采取任何措施。
吉林省东北师范大学附属中学2015届高三文科高考总复习阶段测试卷(20141125)

一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.已知集合}111|{≥-+=x x x M ,集合}032|{>+=x x N ,则=⋂N M C R )(( ) A .(-1,23) B .(-1,23] C . 2.已知α是第二象限角,且sin(53)-=+απ,则tan2α的值为( ) A .54 B .723- C .724- D .924- 3.下列函数中,在其定义域是减函数的是( )A. 12)(2++-=x x x f B. xx f 1)(=C. ||)41()(x x f = D. )2ln()(x x f -= 4. 下列函数中,最小正周期为π,且图象关于直线x=3π对称的函数是( ) A .y=2sin(2x+3π) B .y=2sin(2x-6π)C .y=2sin(32π+x ) D .y=2sin(2x-3π) 5. 函数xx x f 2)1ln()(-+=的零点所在的大致区间是( ) A .(3,4) B .(2,e ) C .(1,2) D .(0,1) 6.已知二次函数4)(2+-=ax x x f ,若)1(+x f 是偶函数,则实数的值为( ) A. -1B. 1C. -2D. 27. 2||,0)(sin(πϕωϕω<>+=x y )的图象的一部分图形如图所示,则函数的解析式为( ) A .y=sin(x+3π) B .y=sin(x-3π) C .y=sin(2x+3πD .y=sin(2x-3π)8. 设a 为实数,函数f (x )=x 3+ax 2+(a -2)x 的导数是)('x f ,且)('x f 是偶函数,则曲线y =f (x )在原点处的切线方程为( )A .y =-2xB .y =3xC .y =-3xD .y =4x9. 将函数y=sin(2x+4π)的图象向左平移4π个单位,再向上平移2个单位,则所得图象的函数解析式是( )A .y=2cos 2(x+8π) B .y=2sin 2(x+8π)C .y=2-sin(2x-4π) D .y=cos2x10.已知函数⎩⎨⎧≤<+-<≤---=)10(1)01(1)(x x x x x f ,则1)()(->--x f x f 的解集为( )A .(-∞,-1)∪(1,+∞) B. C .(-∞,0)∪(1,+∞) D. ∪(0,1)11.对于任意的实数a 、b ,记max{a,b}=⎩⎨⎧<≥)()(b a b b a a .若F(x)=max{f(x),g(x)}(x ∈R),其中函数y=f(x)(x ∈R)是奇函数,且在x=1处取得极小值-2,函数y=g(x) (x ∈R)是正比例函数,其图象与x ≥0时的函数y=f(x)的图象如图所示,则下列关于函数y=F(x)的说法中,正确的是( ) A .y=F(x)为奇函数 B .y=F(x)有极大值F(-1)C .y=F(x)的最小值为-2,最大值为2D .y=F(x)在(-3,0)上为增函数12.设函数⎪⎩⎪⎨⎧<-≥-=)2(1)21()2()2()(x x x a x f x 是R 上的单调递减函数,则实数a 的取值范围为( )A .(-∞,2)B .(-∞,813]C .(0,2)D .[813,2)二.填空题:(本大题共4小题,每小题5分。
吉林省东北师范大学附属中学2015届高三数学(文科)第一轮高考总复习阶段测试卷(第27周)(含答案)
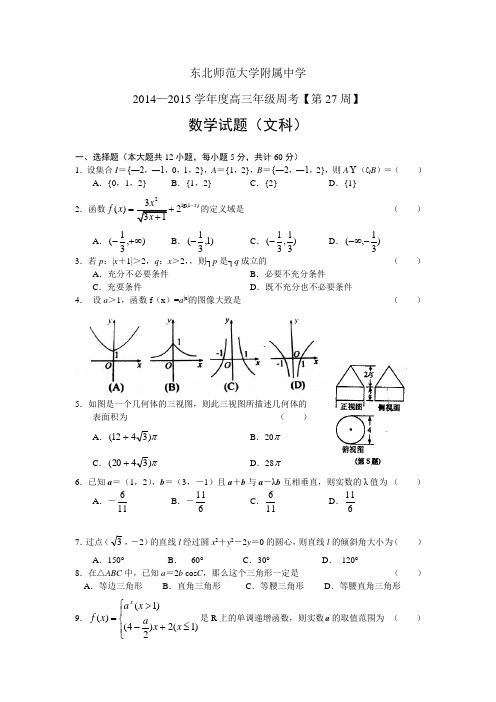
东北师范大学附属中学2014—2015学年度高三年级周考【第27周】数学试题(文科)一、选择题(本大题共12小题,每小题5分,共计60分)1.设集合I ={―2,―1,0,1,2},A ={1,2},B ={―2,―1,2},则A (C I B )=( )A .{0,1,2}B .{1,2}C .{2}D .{1}2.函数2lg(1)()2x f x -=+的定义域是 ( )A .),31(+∞-B .)1,31(-C .)31,31(-D .)31,(--∞3.若p :|x +1|>2,q :x >2,,则┐p 是┐q 成立的 ( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4. 设a >1,函数f (x )=a |x|的图像大致是 ( )5.如图是一个几何体的三视图,则此三视图所描述几何体的表面积为 ( ) A .π)3412(+ B .20π C .π)3420(+D .28π6.已知a =(1,2),b =(3,-1)且a +b 与a -λb 互相垂直,则实数的λ值为 ( ) A .-116B .-611 C .116 D .6117.过点(3,-2)的直线l 经过圆x 2+y 2-2y =0的圆心,则直线l 的倾斜角大小为( ) A .150° B . 60° C .30° D . 120°8.在△ABC 中,已知a =2b cos C ,那么这个三角形一定是 ( ) A .等边三角形 B .直角三角形 C .等腰三角形 D .等腰直角三角形9.⎪⎩⎪⎨⎧≤+->=)1(2)24()1()(x x ax a x f x 是R 上的单调递增函数,则实数a 的取值范围为 ( )A .(1,+∞)B .[4,8]C .(4,8)D .(1,8)10.2008年3月份开始实施的《个人所得税法》规定:全月总收入不超过2000元的免征个人工资、薪金所得税,超过2000元的部分需征税,设全月总收入金额为x 元,前三级税率如下表:当全月总收入不超过4000元时,计算个人所得税的一个算法框图如上所示,则输出①,输出②分别为 ( ) A .0.05x,0.1x B .0.05x, 0.1x -225C .0.05x -100, 0.1xD .0.05x -100, 0.1x -22511.若不等式组5003x y y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的平面区域是一个三角形,则a 的取值范围是( )A .5a <B .8a ≥C .5a <或8a ≥D .58a ≤<12.对于任意实数x ,符号[x ]表示x 的整数部分,即[x ]是不超过x 的最大整数,例如[2]=2;[1.2]=2;[2.2-]=3-, 这个函数[x ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
吉林省东北师范大学附属中学高三数学总复习阶段测试卷

吉林省东北师范大学附属中学2015届高三数学总复习阶段测试卷1文本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟,考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U R =,集合{}|2A x x =≥,{|05}B x x =≤<,则集合)U C A B ⋂=(( )A .{|02}x x <<B .{|02}x x <≤C .{|02}x x ≤<D .{|02}x x ≤≤2.命题“若1,x >则0x >”的否命题是 ( )A .若1x >,则0x ≤B .若1x ≤,则0x >C .若1x ≤,则0x ≤D .若1x <,则0x <3.在复平面内复数-31+z i =的对应点在( )A .第一象限B .第二象限C .第三象限D .第四象限4.函数1()(0,1)x f x a a a -=>≠的图象恒过点A ,下列函数中图象不经过点A 的是( ) A 、yB 、y =|x -2|C 、y =2x -1D 、y =2log (2)x5.与椭圆:C 2211612y x +=共焦点且过点的双曲线的标准方程为( ) A .2213y x -= B .2221y x -=C .22122y x -= D .2213y x -=6.已知向量a b r r 、是夹角为60°的两个单位向量,向量λa b r r +(λ∈R )与向量2-a b r r垂直,则实数λ的值为( )A 、1B 、-1C 、2D 、07按如图所示的程序框图运行后,若输出的结果是63,则判断框的整数M 的值是( ) A .5B .6C .7D .88、已知函数sin()y x ωϕ=+的最小正周期为2π,直线3x π=是其图像的一条对称轴,则下面各式中符合条件的解析式为( )A .sin(4)6y x π=+ B .sin(2)3y x π=+ C .sin(4-)3y x π= D .15sin()412y x π=+ 9.点A B C D 、、、在同一个球的球面上,AB BC ==,2AC =,若四面体ABCD 体积的最大值为23,则这个球的表面积为 ( ) A .1256π3 B .8π C .254π D .2516π10、已知函数()1,()ln f x g x a x =+=,若在14x =处函数f (x )与g (x )的图象的切线平行,则实数a的值为( )A、14B、12C、1D、411若点P在抛物线24y x=上,则点P到点(2,3)A的距离与点P到抛物线焦点的距离之差()A.有最小值,但无最大值B有最大值但无最小值C.既无最小值,又无最大值D.既有最小值,又有最大值12.已知函数132,0()log,0xa xf x x x⎧⨯≤⎪=⎨>⎪⎩,若关于x的方程f(f(x))=0有且仅有一个实数解,则实数a的取值范围是()A、(-∞,0)B、(-∞,0)∪(0,1)C、(0,1)D、(0,1)∪(1,+∞)第II卷(非选择题,共90分)本卷包括必考题和选考题两部分,第13题~ 第21题为必考题,每个试题要求考生必须作答,第22题~ 第24题为选考题,考生根据要求作答。
吉林省东北师范大学附属中学2015届高三一轮复习阶段测试卷(第2周)数学文 Word版含答案

高三文科数学阶段质量检查试题(第2周) (考试时间:120分钟 满分100分) 拟题人:冯维丽 审题人:杨艳昌 2014.8.8一、选择题(本大题共10小题,每小题5分,共50分.每小题中只有一项符合题目要求)1、下列函数为偶函数的是( )A .sin y x =B .3y x =C .x y e = D.y =2、幂函数()f x x α=的图像经过点)21,4(,则1()4f 的值为( )A .4B .3C .2D .13、函数1()ln(1)f x x =++ ( )A .[2,0)(0,2]-B .(1,0)(0,2]-C .[2,2]-D .(1,2]-4、已知函数3log ,0()2,0xx x f x x >⎧=⎨≤⎩,则1(())9f f =( ) A.4 B.14 C.4- D.14- 5、函数()2xf x e x =+-的零点所在的一个区间是( )A .(2,1)--B .(1,0)-C .(0,1)D .(1,2)6、函数⎪⎩⎪⎨⎧≥-<=)0(12)0(2x x x y x 的图象大致是( )7、设2131og a =,3.02)21(3log ==c b ,,则( ) A. a<b<c B. a<c<b C. b<c<a D. b<a<c8、利用计算器,列出自变量和函数值的对应值如下表:那么方程的一个根位于下列区间的( ).A.(0.6,1.0)B.(1.4,1.8)C.(1.8,2.2)D.(2.6,3.0) 9、已知函数()f x 是(,)-∞+∞上的偶函数,若对于0x ≥,都有(2()f x f x +=),且当[0,2)x ∈时,2()log (1f x x =+),则(2011)(2012)f f -+的值为( ) A .2- B .1- C .1 D .210、设0x 是方程3log 3x x =-的根,且0(,1)x k k ∈+,则k =( )A .(0,1)B .(1,3)C .(3,4)D .(4,+∞)二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)11、已知函数3,1,(),1,x x f x x x ⎧≤=⎨->⎩若()2f x =,则x = .12、若函数()()2ln 1f x x ax =++是偶函数,则实数a 的值为 .13、若函数()() y f x x R =∈满足()()2f x f x +=且[]1,1x ∈-时,()21f x x =-;函数()lg g x x = ,则函数()()()h x f x g x =-在区间[]5,5-内的零点的个数为____14、已知()f x 为偶函数,且(1)(3),20,()3x f x f x x f x +=--≤≤=当时,则=)2011(f三、解答题(本大题共4小题,共50分,解答应写出文字说明、证明过程或演算步骤)15、(10分)计算: (1)0021)51(1212)4(2---+-+-(2)91log 161log 25log 532∙∙16、(13分)已知定义域为R 的函数ab x f x x+-=22)(是奇函数。
吉林省东北师范大学附属中学2015届高三数学总复习阶段测试卷4 文

吉林省东北师范大学附属中学2015届高三数学总复习阶段测试卷4 文第Ⅰ卷一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合M ={-1,0,1},N ={x|x2≤x},则M ∩N =( ) A .{0} B .{0,1} C .{-1,1} D .{-1,0,1} 2.命题p :0∀>x ,都有sinx ≥-1,则( )A .p ⌝:0∃>x ,使得sin 1x <- B. p ⌝:0∀>x ,都有sinx<-1 C. p ⌝:0∃>x ,使得sin 1x >- D. p ⌝:0x ∀>,都有sinx ≥-1 3.已知向量)0,3(),1,2(-=-=b a ,则a 在b 方向上的投影为( )A .5-B .5C .-2D .24.在等差数列{an}中,已知a4+a8=16,则a2+a10=( ) A.12 B.16 C.20 D.245. 设a ∈R ,则“a =1”是“直线l1:ax +2y -1=0与直线l2:x +(a +1)y +4=0平行”的( ) A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件 6.同时具有性质:①最小正周期是π;②图像关于直线3π=x 对称;③在]3,6[ππ-上是增函数的一个函数是( )A .)62sin(π+=x y B .)32cos(π+=x y C .)62sin(π-=x y D .cos()26x y π=- 7.双曲线)0(122≠=-mn n y m x 的离心率为2,有一个焦点与抛物线x y 42=的焦点重合,则mn 的值为( )A .38B .83C .316D .1638.已知函数32()22f x x x =-+有唯一零点,则下列区间必存在零点的是( )A .3(2,)2-- B .3(,1)2--C .1(1,)2-- D .1(,0)2-9. 与直线04=--y x 和圆02222=-++y x y x 都相切的半径最小的圆的方程是( )A.22(1)(1)2x y B. 22(1)(1)4x yC. 2)1()1(22=++-y xD.4)1()1(22=++-y x 10. 已知)(x f ,)(x g 都是定义在R 上的函数,且满足以下条件:①)(x f =x a ·)(x g (1,0≠>a a );②)(x g 0≠; ③)()()()(x g x f x g x f ⋅'>'⋅;若25)1()1()1()1(=--+g f g f ,则a 等于( )A .21B .2C .45D .2或2111.已知()2sin(+)f x x ωϕ= , (ω>0 ,22πϕπ<<-) , A 、B 为图象上两点,B 是图象的最高点,C 为B 在x 轴上射影,且点C 的坐标为),0,12(π则AB ·BC =( ).A. 4π4+B. 4π4-C. 4D. 4- 12.已知定义在R 上的奇函数()f x 满足()()4f x f x -=-,且[]0,2x ∈时,()()2log 1f x x =+,甲,乙,丙,丁四位同学有下列结论:甲:()31f =;乙:函数()f x 在[]6,2--上是增函数;丙:函数()f x 关于直线4x =对称;丁:若()0,1m ∈,则关于x 的方程()0f x m -=在[]8,8-上所有根之和为-8,其中正确的是( )A.甲,乙,丁B.乙,丙C.甲,乙,丙D.甲,丁第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.)13.已知圆x2+y2-6x -7=0与抛物线y2=2px (p>0)的准线相切,则此抛物线的焦点坐标是___________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三文科数学阶段质量检查试题
(第5周) (考试时间:120分钟 满分150分) 拟题人:冯维丽 审题人:杨艳昌 2014.8.30 选题范围:【全国各地高三模拟优秀试题选练】(2)
一、选择题:(10×5=50分)
1.设复数z 满足(1)1,||i z i z -=+则=
A .0
B .1
C
D .2
2.已知2{|2,},{|log 1},M x x x N N x x M N =>-∈=<则=
A .{|21}x x -<<
B .{|22}x x -<<
C .{0,1}
D .{1}
3.已知()()1,513,517x
f x x f x x ⎧-≥⎪
=⎨⨯<⎪⎩
,则()3log 255f = A .
3log 255
17
B .85
C . 5
D .15
4.22
"
2""00"a b a b ab
+≤-><是且的
A .必要不充分条件
B .充要条件
C .充分不必要条件
D .既不充分也不必要条件
5.函数()lg(||1)f x x =-的大致图象是
6.设{}n a 是等差数列,246a a +=,则这个数列的前5项和等于 A .12 B .13 C .15
D .18
7.下列命题正确的是 A .在(
,2ππ)内,存在x ,使5sin cos 4
x x += B .函数2sin()5y x π=+的图像的一条对称轴是4
5
x π=
C .函数21
1tan y x
=
+的周期为2π
D .函数2sin y x =的图像可以由函数2sin(2)4
y x π
=-
的图像向左平移
8
π
个单位得到 8.向量),(),0,2(y x b a ==
,若b 与a b -的夹角等于6
π,则b 的最大值为
A .4
B .
C .2
D
9.已知,x y 满足约束条件02,
02,32,
x y z ax y y x ≤≤⎧⎪
≤≤=-⎨⎪-≥⎩
如果的最大值的最优解为4(2,)3,则a 的取
值范围是
A .1[,1]3
B .1(,1)3
C .1[,)3
+∞
D .1(,)3
+∞
10.已知函数()f x 和()g x 的图象关于y 轴对称,且()21
2
f x x x =+
.则不等式()()4g x f x x ≥--的解集为
A .(,0]-∞
B .[]0,2
C .(,2]-∞
D .[2,)+∞
二、填空题:(5×5=25分)
11.2(lg 2)2
+lg 2·lg5+12lg )2(lg 2
+--
3
3
9·-a
a ÷
3
7
13a a =
12.对于向量c b a
,,,下列给出的条件中,能使c b a c b a ⋅⋅=⋅⋅)()(成立的序号是
①0 =b ②b a // ③c a
// ④c b //
13.已知3211,11==;332129,(12)9+=+=;333212336,(123)36++=++=;
333321234100,(1234)100+++=+++=;……;则3333
31234n ++++
+=
14.若函数2
()2ln f x x x =-在其定义域内的一个子区间(1,1)k k -+内不是单调函数,则实数k 的
取值范围是
15.若函数2()(*)f x x n N =∈图像在点(1,1)处的切线为12,l l 在x 轴,y 轴上的截距分别为
,n n a b ,则数列{25}n n a b +的最大项为
三、解答题:(10+12+13=35分)
16、(本小题满分10分)递增的等比数列{n a }的前n 项和为Sn ,且30,642==S S (1)求数列{n a }的通项公式。
(2)若n b =n a 12
log n a ,求数列{n b }的前n 项和为n T 。
17.(本小题满分12分)在ABC △中,角,,A B C 的对边分别为,,a b c ,且满足(2)cos cos ,a c B b C -= 222sin sin 1cos cos cos B C A B C λ-=--. (1)求角B 的大小;(2)若ABC △为直角三角形,求实数λ的取值集合.
18.(本小题满分13分)已知函数()1x
f x e ax =+- (,)a R a ∈且为常数. (1)求函数()f x 的单调区间;
(2)当0a <时,若方程()0f x =只有一解,求a 的值; (3)若对所有0x ≥都有()()f x f x ≥-,求a 的取值范围.
参考答案
一、选择题:(12×5=60分)
二、填空题:(5×5=25分)
11. 0 ;12.① ③ ;13.2(1234)n +++++ ;14. 3
[1,
)2
;15.16。
三、解答题:(10+12+13=35分)
16、解析:(1)30,642==S S 2±=⇒q ,∵数列{}n a 递增,∴2=q 21=⇒a ,∴n n a 2=, (2)n
n
n
n n b 22log 22
1⋅-==,)2232221(321n n n T ⋅++⋅+⋅+⋅-=
设n n n H 223222321⋅++⋅+⋅+= …………..①
14322232222+⋅++⋅+⋅+=n n n H ………..②
①
-②
得:
1
2
3
1
22222
n
n n H n +-=+++
+⋅-⋅1+112(12)2222=12
n n n n n n n T ++-=-⋅=-⋅+--,
17.解析:(1)因为(2)cos cos ,a c B b C -= 由正弦定理得:
(2sin sin )cos sin cos ,A C B B C -=
所以
2
s
i n
c o
s
s i A B C B B
C
C
B
A
=+=+= 因为sin 0A ≠,所以1
cos 2
B = 因为(0,)B π∈,所以3
B π
=
(2)由已知条件222sin sin 1cos cos cos B C A B C λ-=--可得,222sin sin sin sin sin A B C B C λ=+-, 根据正弦定理知:222a b c bc λ=+-,所以22222
b c a bc λ+-= 再由余弦定理可得cos 2A λ
=
因为3
B π=
,且三角形为直角三角形,所以6
A π=
或2
A π=
,所以cos A =
或cos 0A =,
所以λ的取值集合为}
18.解析:(1)由已知得()x f x e a '=+,
当0a ≥时,()0f x '>,()f x 在(,)-∞+∞上是单调增函数.
当0a <时,由()0f x '>,得ln()x a >-,()f x 在(ln(),)a -+∞上是单调增函数; 由()0f x '<,得ln()x a <-,()f x 在(,ln())a -∞-上是单调减函数. 综上可得:当0a ≥时,()f x 的单调增区间是(,)-∞+∞;
当0a <时,()f x 的单调增区间是(ln(),)a -+∞,单调减区间是(,ln())a -∞-. (2)由(1)知,当0a <,ln()x a =-时,()f x 最小,即min ()(ln())f x f a =-, 由方程()0f x =只有一解,得
(ln())0f a -=,又注意到(0)0f =,所以ln()0
a -=,解得1a =-.
(3)当0x ≥时,()()f x f x -
≥恒成立,即得x x
e ax e ax -+-≥恒成立,即得20x x e e ax --+≥恒成立.令1
()2x x
h x e ax e
=-
+(0x ≥),即当0x ≥时,()0h x ≥恒成立.又()2x x h x e e a -'=++,且
()2
222h x a a '=+≥,当0x =时等号成立.
①当1a >-时,()0h x '>,所以()h x 在[0,)+∞上是增函数,故()(0)0h x h =≥恒成立. ②当1a =-时,若0x =,()0h x '=,若0x >,()0h x '>, 所以()h x 在[0,)+∞上是增函数,故()(0)0h x h =≥恒成立.
③当1a <-时,方程()0h x '=的正根为1ln(x a =-, 此时,若1(0)x x ∈,,则()0h x '<,故()h x 在该区间为减函数. 所以,1(0)x x ∈,时,()(0)0h x h <=,与0x ≥时,()0h x ≥恒成立矛盾. 综上,满足条件的a 的取值范围是[1,)-+∞.。
