全维、降维观测器
江苏大学线性系统理论(现代控制理论)考试必备--第6章.答案

=
C R
P1
CP1
RP
1
I qq 0
0 I ( n q )( n q )
再来讨论(n-q)维状态观测器的构建,用线性变换 x = Px,
将方程(1)变换成
x = PAP-1x + PBu y = CP-1x = CP-1x = Iqq 0 x
记 : A=PAP-1 B=PB
C CP1
以足够快的速度趋近于零,也就是说,不管状态观测器的
初始状态如何,状态观测器所重构的状态变量 xˆ 终将逐渐
趋近于实际状态 x ,所以,这样的状态观测器也称之为渐 进状态观测器。该性质也使其在实际使用中毋需设置初始 状态。
第6章 状态观测器
江苏大学电气学院
值得一提的是,虽然 (A-MC) 特征值的负实部离虚
i (A C M ) i , i =1,2, , n
求出M后,即可构成闭环状态观测器:
xˆ = (A - MC)xˆ + My + Bu
(8)
第6章 状态观测器
江苏大学电气学院
全维状态观测器的另一种设计方法是,先对被观测系
统进行非奇异变换 z=T,x 再从形式上列出类似于式(8)
的观测器方程。
B
x
x C
y
A
xˆ 0
B
xˆ
xˆ C
yˆ
A
第6章 状态观测器
江苏大学电气学院
这样的观测器称为开环状态观测器,从开环状态观测
器中取出 xˆ 可作为 x 的估计值近似替代,当然希望 xˆ 与x 是相等的。用 x 来表示 x 和 xˆ 的偏差,即 x x xˆ , 下面来简单分析估计偏差 x的特性。式(1)和式(2)相减得
一类线性时变系统的状态观测器设计方法

摘要该论文主要研究控制领域中的线性时变系统的状态观测器设计问题,其目获得的问题。
区别于在状态观测器理论方面已经趋于成熟的线性定常系统,线性时变系统的研究相对困难并且具有挑战性,所发表出的理论成果较少,并且容。
该论文的设计思路是对于原有的线性时变系统,首先对其进行线性非奇异变换以使得变换后的系统具有某种特殊形式,而后对变换后的系统进行状态观测器设计,并最终达到重构原有系统状态的设计要求。
针对此思路能够得知设计工作主要划分为两个部分,即线性非奇异变换以及状态观测器设计。
首先,该论文提出线性时变系统基于方块展开的状态观测器设计。
线性非奇异变换后的系统中系数矩阵皆为分块形式,并且其中包含较多的零阵以及单位阵。
而后对变换后的系统进行全维,降维以及Luenberger状态函数观测器设计,给出各自的动态方程,系数矩阵求解方法以及算法步骤等。
其次,该论文提出线性时变系统基于行展开的状态观测器设计。
线性非奇异变换矩阵由原有系统能观测性矩阵中线性无关的行经过运算得到。
变换后的系统仍为分块形式,不同点在于其各个子块中均包含较多的零元。
而后对变换后的系统进行全维状态观测器设计。
上述基于一种设计思路,两种设计方法得到的各个状态观测器均由仿真验证其可行性以及有效性。
并且针对两种设计方法该论文给出对比,从而在具体最后,该论文还对线性时变系统中闭环系统的分离原理问题进行了初步研究,得到该论文所设计出的状态观测器均符合分离原理的结论。
该论文主要研究成果是对线性时变系统的状态观测器设计此研究课题在理论层面上的推进与添补。
所设计出的状态观测器其优点在于可以避免求解复杂的矩阵微分方程,并且将部分运算转化到线性定常系统中。
这样极大地降低与关键词:线性时变系统;状态观测器设计;线性非奇异变换;分离原理AbstractIn this paper, linear state observer design of linear time-varying systems has been researched to solve the state reconstruction problem that states cannot be acquired compeletely or partialy due to various reasons in actual engineering. Different from the mature theory of state observer for linear time-invariant systems, research on linear time-varying systems is ralatively more difficult and challenging, less amount of theoretical achievements and closer to the actual project. So it is the research focus in recent years. The main contents of this paper are described below.Design ideas of this paper is to transform the original linear time-varying systems into some special form with linear non-singular transformations initially. Then the state observer design based on the linear time-varying systems transformed can achieve the reconstructed state of original linear time-varying systems. For this idea, we can know that the design work is divided into two parts, namely, linear nonsingular transformation and state observer design.Firstly, the state observer design of linear time-varying systems based on the square matrices is presented. The coefficient matrices of systems transformed are all partitioned including much zero and unit submatrices. Then the full, reduced and Luenberger state observer design of transformed systems are illustrated detailed including some aspects such as the solutions of dynamis equations and coefficient matrices, as well as the algorithms and their steps.Secondly, we propose the state observer design for linear time-varying systems based on row expansion. The linear nonsingular transformation matrix is obtained by computing the linearly independent rows of observation matrix. The coefficient matrices of transformed system are still partitioned, and the difference between two linear nonsingular metiods is that each of its sub-blocks contains much zero elements. The the full state observer is designed.Based on a design idea, all the state observers obtained by the two design methods are proved to be feasible and effective by simulation. Moreover, the contrast of two methods is proposed in this paper in order to select in actual engineering.Finally, the paper studies the separation principle of closed loop system in linear time-varying system, and obtains the conclusion that the state observer designed in this paper meets the separation principle.The main research results of the paper is to promote and increase theoritical achienements of the state observer design for linear time-varying systems. The pivotal merit is that it can avoid solving complex differential equations by transforming them into constant partially. These reduces and simplifies the computational complexity aswell as the amount of computation greatly. Therefore, they also have practical engineering significance.Keywords: Linear time-varying systems; state observer design; Linear nonsingular transformation; Separation principle目录摘要 (I)ABSTRACT (II)第1章绪论 (1)1.1论文课题来源及研究背景和意义 (1)1.1.1 课题来源 (1)1.1.2 课题的背景及意义 (1)1.1.3 时变系统分类 (2)1.1.4 观测器分类 (3)1.2国内外研究现状 (3)1.3论文主要研究内容及安排 (5)第2章基础内容介绍 (6)2.1线性时变系统概述 (6)2.1.1 线性时变系统模型及相关定义 (6)2.1.2 线性时变系统稳定性 (7)2.2线性时变系统的线性非奇异变换 (8)2.3线性定常系统状态观测器设计基本介绍 (10)2.3.1 全维状态观测器 (10)2.3.2 降维状态观测器 (11)2.3.3 LUENBERGER状态函数观测器 (12)2.4函数矩阵运算介绍 (12)2.5本章小节 (13)第3章基于方块展开的状态观测器设计 (14)3.1基于方块展开的线性非奇异变换 (14)3.2全维状态观测器设计 (17)3.3降维状态观测器设计 (21)3.4LUENBERGER状态函数观测器设计 (23)3.5状态观测器的分离原理研究 (27)3.6仿真验证 (32)3.7本章小结 (37)第4章基于行展开的状态观测器设计 (38)4.1相关理论基础 (38)4.2基于行展开的线性非奇异变换 (41)4.3全维状态观测器设计 (44)4.4两种状态观测器设计方法对比 (46)4.5仿真验证 (46)4.6本章小结 (48)结论 (50)参考文献 (51)攻读硕士学位期间发表的论文及其它成果 (56) (57)致谢 (59)第1章绪论1.1 论文课题来源及研究背景和意义1.1.1 课题来源本课题来源于国家自然科学基金重大项目-空间翻滚目标的捕获策略及组合体的快速稳定控制以及国家自然科学基金创新研究群体项目-航天飞行器的鲁棒控制理论及应用。
现代控制理论基础_周军_第五章状态反馈与状态观测器
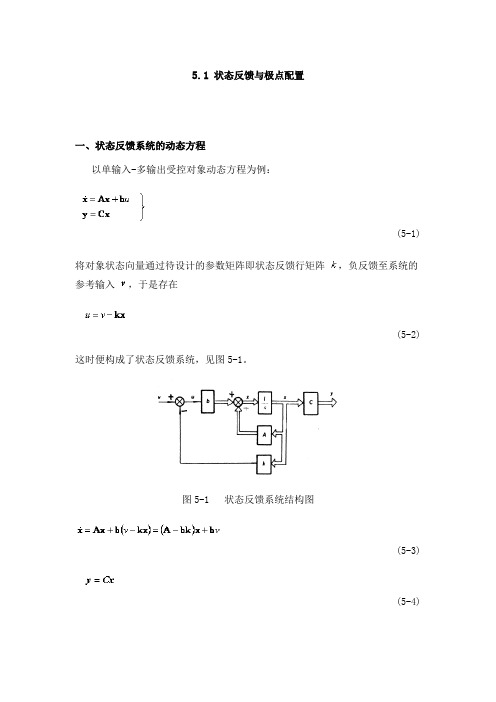
5.1状态反馈与极点配置一、状态反馈系统的动态方程以单输入-多输出受控对象动态方程为例:(5-1)将对象状态向量通过待设计的参数矩阵即状态反馈行矩阵,负反馈至系统的参考输入,于是存在(5-2)这时便构成了状态反馈系统,见图5-1。
图5-1 状态反馈系统结构图(5-3)(5-4)式中v为纯量,为维向量,为维矩阵,为维向量,为维行矩阵,为维向量,为维矩阵。
为闭环状态阵,为闭环特征多项式。
二、用状态反馈使闭环极点配置在任意位置上的充要条件是:受控对象能控证明若式(5-1)所示对象可控,定可通过变换化为能控标准形,有若在变换后的状态空间内引维状态反馈矩阵:(5-5)其中分别为由状态变量引出的反馈系数,则变换后的状态反馈系统动态方程为:(5-6)(5-7)式中(5-8)该式与仍为能控标准形,故引入状态反馈后,系统能控性不变。
特征方程为:(5-9)显见,任意选择阵的个元素,可使特征方程的个系数满足规定要求,能保证特征值(即闭环极点)任意配置。
将逆变换代入式(5-6),可求出原状态空间内的状态反馈系统状态方程:(5-10)与式(5-3)相比,式(5-10)所示对象应引入状态反馈阵为:(5-11)需指出,当受控对象可控时,若不具有能控标准形形式,并不必象如上证明那样去化为能控标准形,只要直接计算状态反馈系统闭环特征多项式,这时,其系数为的函数,与给定极点的特征多项式系数相比较,便可确定。
能控的多输入-多输出系统,经如上类似分析可知,实现闭环极点任意配置的状态反馈阵K为维。
若受控对象不稳定,只要有能控性,完全可由状态反馈配置极点使系统稳定。
状态变量受控情况下,引入状态反馈表示增加一条反馈通路,它能改变反馈所包围环节的传递特性,即通过改变局部回路的极点来改变闭环极点配置。
不能控状态变量与控制量无关,即使引入状态反馈,对闭环极点位置也不会产生任何影响,这是因为传递函数只与系统能控、能观测部分有关的缘故。
若不能控状态变量是稳定的状态变量,那么系统还是能稳定的,否则,系统不稳定。
现代控制理论习题之状态观测设计

对应于原系统的观测器矩阵: ⎡0 ⎤ ⎡0 ⎤ P1 = V0 −1 ⎢ ⎥ = ⎢ ⎥, Po = [ p1 ⎣1 ⎦ ⎣1 ⎦
u
∑ ( A, B, C )
y
6.5
2
1 x
x1
15.3 x
x3
题 6-2 图 1
(2) 确定降维观测器的维数:m=1,n=3,则 n-m= 2。 分解输出系数矩阵 c,获得线性变换矩阵 T,对原状态空间表达式进行线性变换,使 各输出变量 y 变成各状态变量的单值函数:
f *(s) = (s + 3)(s + 4) = s2 + 7s +12 ⎡s 0⎤ ⎡−1 −1⎤ ⎡l1⎤ f (s) = sI − (A22 − LA 12) = ⎢ ⎥ −⎢ ⎥ + ⎢ ⎥[− 2 − 4] ⎣0 s⎦ ⎣−1 −1⎦ ⎢ ⎣l2⎥ ⎦ = s2 + (−4l2 − 2l1 + 2)s + (2l1 − 2l2) ⎡l ⎤ ⎡ 3.1667⎤ f *(s) = f (s) ⇒ L = ⎢ 1⎥ = ⎢ ⎥ ⎢l2⎦ ⎥ ⎣− 2.8333 ⎦ ⎣
系统能观,可设计观测器。 求希望特征多项式:
f * ( s ) = ( s + 3)( s + 4)( s + 5) = s 3 + 12 s 2 + 47 s + 60
求观测器特征多项式:
f ( s ) = sI − A + LC
5.5状态观测器设计

N =B, K =E
于是得到一特定的n 维KX 观测器。
⎧ z& = ( A − LC )z + Bu + Ly
⎨ ⎩W
=
Kz
(5-35)
称此为∑ 的一个全维KX观测器;K=I为 ∑ 的一个全维状态观测
器.
因为满足结构条件的L 不唯一,全维观测器也不唯一。全6 维
观测器设计较简单。
5.5.2 全维状态观测器设计
⎨ ⎩
W = Ez
(5-34)
称为全维观测器。
若 r < n ,M ≠ 0 ,相应观测器称为降维观测器。
对 r = n 全维观测器,参数除按通常步骤外,有特定取法:
F = A − LC ,
G=L
则 PA− FP = PA− (A − LC)P = PA− AP + LCP = LC
有 P = In 从而
y = [1 1 0 ] x
设计特征值为-3,-3和-4的全维状态观测器.
解:
⎡c⎤
⎡1 1 0⎤
rank
⎢ ⎢
cA
⎥ ⎥
=
rank
⎢ ⎢
−1
−3
−1⎥⎥ = 3 = n
8
⎢⎣cA2 ⎥⎦
⎢⎣ 0 5 0 ⎥⎦
可知系统完全观测.
⎡−1 0 1 ⎤
⎡1⎤
A
=
AT
=
⎢ ⎢
−
2
−1
0
⎥ ⎥
,
b
= cT
=
完全能控
⎡ 1 0 0⎤ ⎡0 −1 1⎤ ⎡1 0 0⎤ ⎡ 2 2 1⎤
P = ⎡⎣ A2b Ab b ⎤⎦ ⎢⎢α 2
1
降维状态观测器课件

闭环传递函数不变性:观测器不改变直接状态反馈系统的
传递函数矩阵 C(sI A BK )1 B C (sI A)1 B
鲁棒性:一般地,鲁棒性变差。
总结
总结
总结
ROB
dim ROB n q # 降维状态观测器在工程实现上比全维状态观测器简便;
# 降维状态观测器在抗噪声方面不及全维状态观测器。
降维状态观测器:综合方案 I
方法1
降维状态观测器:综合方案 I
降维状态观测器:综合方案 I
方案1的降维状态观测器结构图
降维状态观测器:综合方案 I I
方法2(思路类似于全维状态观测器方案2)
降维状态观测器:综合方案 I I
降维状态观测器:综合方案 I I
方案2的降维状态观测器结构图
6.14 Kx―函数观测器
Kx―函数观测器
基本思想
有时重构状态的最终目的是为了获得状态的某种组合如 Kx 的估计。 直接重构 Kx可能使观测器的维数较降维状态观测器的维数更低。
问题描述
给定线性系统
x :n 维 u :p 维 y :q维
Kx―函数观测器的综合算法
Kx―函数观测器组成结构图
Kx―函数观测器组成结构图
6.15 基于观测器的状态反馈控制系统的特性
6.15 基于观测器的状态反馈控制系统的特性
6.15 基于观测器的状态反馈控制系统的特性
基于观测器的状态反馈控制系统的特性
6.15 具有观测器状态反馈控制系统和具有补偿器输出反馈系统的等价性
6.13 降维状态观测器
降维观测器
全维观测器的原理

全维观测器的原理
全维观测器(全局观测器)是一种系统控制理论中常用的观测器设计方法,它用于估计一个系统的未测量状态变量。
全维观测器的原理基于系统状态方程和输出方程,通过在系统中引入一个观测器来估计系统的状态变量。
观测器的结构与实际系统的结构相似,由一个状态方程、一个输出方程和一个观测误差方程组成。
全维观测器的状态方程是由实际系统的状态方程推导得到的,但是观测器的参数是通过一定的设计方法确定的。
观测器的输出方程与实际系统的输出方程相同,即观测器可以输出与实际系统完全相同的测量结果。
观测器的原理是基于对实际系统的估计误差进行反馈修正的原理。
通过观测器的输出与实际系统的输出之间的误差,可以得到对实际系统状态变量估计的误差。
利用这个误差,可以通过一定的修正算法来更新观测器的参数,使得观测器的估计结果逐渐接近实际系统的状态变量。
全维观测器的设计方法有很多,常见的方法包括最小二乘法、Kalmman滤波器等。
其中,最小二乘法是利用观测器的输出与实际系统的输出之间的误差最小化来确定观测器的参数。
Kalmman滤波器则是一种利用贝叶斯定理来估计系统状态的方法,它通过观测器的输出与实际系统的输出之间的协方差矩阵来确定观测器的参数。
总之,全维观测器通过利用系统的状态方程、输出方程和观测误差方程来估计系统的状态变量。
利用观测器的输出与实际系统的输出之间的误差,可以对观测器的参数进行修正,从而逐渐接近实际系统的状态变量。
全维状态观测器的设计

全维状态观测器的设计全维状态观测器(Full State Observer)是一种常用于控制系统中的重要部件,用于获取系统的全部状态信息。
它通常是通过对系统的输入输出进行观测,并通过数学模型来估算系统的状态。
全维状态观测器的设计可以通过以下步骤来完成。
第一步是系统建模。
将所要观测的系统建立数学模型,可以采用物理方程或者数学模型的方式。
常见的数学模型包括状态方程和输出方程。
状态方程描述了系统状态的时间演变规律,输出方程则描述了系统输出与状态之间的关系。
这些方程可以通过系统的运动方程,控制方程和物理特性等来建立。
第二步是选择观测器类型。
全维状态观测器有多种类型,包括基本观测器、极点配置观测器和最优观测器等。
基本观测器是使用系统的状态方程和输出方程来估算系统状态的观测器,而极点配置观测器和最优观测器则是通过最小化误差来估算系统状态,从而提高观测器的精度。
合适的观测器类型应该根据控制系统的需求来选择。
第三步是计算观测器矩阵。
观测器矩阵是观测器中用来计算系统状态的矩阵。
它可以使用系统的状态方程和输出方程来计算。
观测器矩阵需要满足一些性质,例如它需要是可观测的,并且需要保证系统状态与观测器状态的误差最小。
第五步是实现观测器。
实现观测器需要将观测器矩阵和观测器增益输入到观测器中,并对观测器的输入输出进行校验。
一旦观测器被设计并实现,它就可以用于控制系统中,并用来估算系统的全部状态信息。
总之,全维状态观测器的设计是控制系统中的重要部件,可以极大地提高控制系统的精度和稳定性。
设计一个好的全维状态观测器需要仔细分析系统模型和观测器类型,计算观测器矩阵和观测器增益,并进行实现和调试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本文通过具体的例子阐明如何在 MATLAB 系统中进行全维状态观测器和降维状态观测器的设计。
MATLAB 为状态空间设计提供了很多有用的函数,方便了矩阵方程的求解,其中的MATLAB 里面提供的库函数对全维状态观测器和降维状态观测器的设计也显得非常地方便。
现通过例子说明如何用 MATLAB 设计状态观测器。
为了评价 MATLAB 所设计的状态观测器的性能,本文通过在 SIMULINK 环境下来仿真一个三阶状态观测器,来说明用 MATLAB 设计状态观测器的准确性。
1、全维观测器的设计
已知三阶系统的状态空间方程为:
u x X ⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡
---=102201210112 []
x y 012=
首先检验系统的是否完全能观
A=[2 -1 1;0 -1 2;1 0 -2];
C=[2 1 0];
N=[C;C*A;C*A*A]
rank(N)
⎥⎥
⎥⎦
⎤
⎢⎢⎢⎣⎡--=10112434012N
rank(N)
ans = 3 ,说明系统是完全能观的。
下面选择观测器需要配置的期望极点为:s 1 =-12 s
2,3 =-3±0.88i
由此求出观测器增益矩阵G :
A=[2 -1 1;0 -1 2;1 0 -2];
C=[2 1 0];
P =[-12;-3+0.88*i;-3-0.88*i];
G = acker(A',C',P);
求得G = [11.6527 -6.3054 1.0619]
可得全维观测器的方程为:
y u x Gy Bu x GC A x ⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=++-=0619.13054.66527.11102~0000.20619.11238.10000.23054.56108.120000.16527.123054.21~)(~ 下面可依据上式构建simulink 图,据此观察观测器的跟踪能力
:
跟踪效果图如下: X1
X2
X3
从图中可以看出状态观测器的状态X1,X2,X3 能够完全估计原三阶系统的状态。
如果原三阶系统和其状态观测器的初始状态不同,状态观测器的状态
X1,X2,X3 不能同原三阶系统状态完全一致,但能很快跟踪原三阶系统状态(主要取决于状态观测器的响应速度,即状态观测器的极点配置。
)
2、降维观测器设计
从上面的全维观测器输出方程可以看出,此系统输出就等于第一个状态,因此该状态可以有输出求得,即变换矩阵P 为单位阵,而降维观测器的阶次为2。
d d c c
b b
a a
====
降维观测器的期望特征根选为-3±0.88i
⎥⎦⎤⎢⎣⎡=-=1021111a a []⎥⎦⎤⎢⎣⎡--=--=1011222212a a ⎥⎦⎤⎢⎣⎡==1022
1b b ]00[211==c c y l u b l b y a l a x a l a x q n q n +-+-+-=--)12()1121()
1222(~ 据此求观测器增益
a22=[-1 1;0 -1];
a12=[-2 -2];
pe=[-3+1i*2*7^(1/2)/3;-3-1i*2*7^(1/2)/3];
lt=acker(a22',a12',pe);
l=lt'
求得⎥⎦
⎤⎢⎣⎡-=5556.35556.1l ,得到
y u y x x q n q n ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=--5556.35556.11112.81112.35556.25556.1~1112.81112.71112.41112
.2~引入中间变量
y x ly x q n q n ⎥⎦
⎤⎢⎣⎡--=-=--5556.35556.1~~η 得降维观测器的状态方程为
u y ⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡-+⎥⎦⎤⎢⎣⎡--=1112.81112.32224.15778.91112.81112.71112.41112.2ηη ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=y y y x 42~21ηη 下面可依据上式构建simulink 图,据此观察观测器的跟踪能力
X2
X3
从降维观测器仿真的输出图形中可以看出,系统状态变量X2、X3的跟踪能力比较理想。
3、结论
本文提供了一种利用 MATLAB 软件,方便、快捷地设计全维状态观测器的方法。
通过本方法很容易设计出不同参数下性能良好的状态观测器,从而容易仿真出状态观测器参数变化对状态跟踪性能的影响。
进一步可以对具有状态观测器的反馈控制系统进行设计和仿真,能够迅速地对系统在不同参数下进行性能仿真。
参考文献
〔1〕薛定宇.科学运算语言 MATLAB5.3 程序设计与应用〔M〕.北京:清华大学出版社,2000.
〔2〕魏克新. MATLAB 语言与自动控制系统设计[M].北京:机械工业出版社,1999.。
