三角形中的三角函数PPT
合集下载
2024年度高中数学必修四三角函数PPT课件

建筑设计
在建筑设计中,利用三角函数计算建筑物的角度、高度和距离等 参数,确保设计的准确性和美观性。
机械设计
在机械设计中,三角函数用于计算齿轮、轴承等机械元件的尺寸和 角度,保证机械传动的精确性和稳定性。
航空航天工程
在航空航天工程中,利用三角函数分析飞行器的姿态、航向和速度 等参数,确保飞行安全。
21
2024/3/24
32
THANKS
感谢观看
2024/3/24
33
周期性、奇偶性、单调性等
解三角形
正弦定理、余弦定理及应用
29
常见题型解析及技巧点拨
01
三角函数求值问题:利 用同角关系式、诱导公 式等求解
2024/3/24
02
三角函数的图像与性质 应用:判断单调性、周 期性等
03
04
三角恒等变换的应用: 证明等式、化简表达式 等
30
解三角形问题:利用正 弦定理、余弦定理求解 边或角
易错知识点剖析及防范措施
混淆三角函数定义域和值域
注意定义域和值域的区别,避免混淆
忽视三角函数的周期性
在解题时要考虑周期性,避免漏解或 多解
2024/3/24
错误使用三角恒等变换公式
注意公式的适用条件和变形方式,避 免误用
忽视解三角形的限制条件
在解三角形时要注意边和角的限制条 件,避免得出不符合题意的解
第三象限
正弦、余弦均为负、正切为正 。
第四象限
正弦为负、余弦为正、正切为 负。
2024/3/24
7
02 三角函数诱导公 式与变换
2024/3/24
8
诱导公式及其应用
2024/3/24
诱导公式的基本形式
《三角函数的有关计算》直角三角形的边角关系PPT课件4教学课件

用科学计算器求锐角的三角函数值,要用到三个键:
sin cos tan 例如,求sin16°,cos42°, tan85°和sin72° 38′25″ 的按键盘顺序如下:
按键的顺序
显示结果
Sin160 sin 1 6
=
0.275635355
Cos420 cos 4 2
=
0.743144825
tan850 tan 8 5
解:如图,根据题意,可知 BC=300 m,BA=100 m, ∠C=40°,∠ABF=30°.
在Rt△CBD中,BD=BCsin40°≈300×0.6428 =192.8(m)
在Rt△ABF中,AF=ABsin30° =100× 1 =50(m).
2
所以山高AE=AF+BD=192.8+50=242.8(m).
好不能直射室内,求挡板AC的宽度.(结果精确到0.01 m)
解:因为tan80°= AB
AC
所以AC=
AB tan 80
≈ 1 .8 5 . 671
=0.317≈0.32(m).
所以水平挡板AC的宽度应为0.32米.
中考 试题
1.用计算器计算cos 44°的结果(精确到0.01)是( )
A 0.90 B 0.72 C 0.69 D 0.66
∴tanB= AC 6.3 ≈0.642 9
BC 9.8
∴∠B≈ 32 4413 因此,射线与皮肤的夹角约为 3 24413 。
北京师范大学出版社 九年级 | 下册
3、如图,工件上有一V形槽,测得它的上口宽20mm,深19.2mm, 求V形角( ∠ACB)的大小。(结果精确到1°)
解:∵tan∠ACD = AD 10 ≈0.520 8
三角形的诱导公式及图像PPT幻灯片

三角形的诱导公式
角的始边与终边
终边 正角
象限角:将角的顶点与坐标原点重合
,始边与x轴正半轴重合,角的终边落 在第几象限,就称之为第几象限角。
O
零角(始边)
负角
终边
弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
用符号rad表示,读作弧度。
l ,l r
同角三角函数的关系
特殊角的三角函数值
α
0
sinα
0
cosα
1
tanα
0
1
2
1
0
-1
0
0
-1
0
1
不存在 0 不存在 0
三角函数的诱导公式
(公式三)
三角函数的诱导公式
(公式四)
y 1
P′(y,x)
-1
1P(x,y)
0
x
-1
公 式六:
s
i
定义域问题
求y= sin x 的定义域
值域问题
(1)函数 y 2 cos(x )( ≤ x ≤ 2 ) 的最小值是
36
3
(2)求值域 y 2 cos x 2 cos x
正弦
周期性
奇偶性
奇函数, 图象关于原点对称
对称轴
x k , (k Z)
对称中心 2
练一练
1.4
三角函数的图像与性质
五点法作图
作正弦函数yy=sinx , x∈[0,2 π]的图象
1
(
2
,1)
( 2 ,1)
五点法
( ,0)
角的始边与终边
终边 正角
象限角:将角的顶点与坐标原点重合
,始边与x轴正半轴重合,角的终边落 在第几象限,就称之为第几象限角。
O
零角(始边)
负角
终边
弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
用符号rad表示,读作弧度。
l ,l r
同角三角函数的关系
特殊角的三角函数值
α
0
sinα
0
cosα
1
tanα
0
1
2
1
0
-1
0
0
-1
0
1
不存在 0 不存在 0
三角函数的诱导公式
(公式三)
三角函数的诱导公式
(公式四)
y 1
P′(y,x)
-1
1P(x,y)
0
x
-1
公 式六:
s
i
定义域问题
求y= sin x 的定义域
值域问题
(1)函数 y 2 cos(x )( ≤ x ≤ 2 ) 的最小值是
36
3
(2)求值域 y 2 cos x 2 cos x
正弦
周期性
奇偶性
奇函数, 图象关于原点对称
对称轴
x k , (k Z)
对称中心 2
练一练
1.4
三角函数的图像与性质
五点法作图
作正弦函数yy=sinx , x∈[0,2 π]的图象
1
(
2
,1)
( 2 ,1)
五点法
( ,0)
《30°、45°、60°角的三角函数值》直角三角形的边角关系PPT课件教学课件

B 如图所示 在 Rt△ABC中,∠C=90°。
(1)a、b、c三者之间的关系是
,
c
∠A+∠B=
。
a (2)sinA=
,
cosA=
,
A
b
C
tanA= sinB= cosB=
。 , ,
tanB=
。
(3)若A=30°,则=
。
为了测量一棵大树的高度,准备了如下测量工具: ①含30°和60°两个锐角的三角尺; ②皮尺.
2
4 2 sin 2 300 cos2 600 2 cos2 450.
2
直击中考
(1+ 2 )0-|1-sin30°|+ ( 1 ) -1;
2
知识应用
1.某商场有一自动扶梯,其倾斜 角为30°,高为7m.扶梯的长度 是多少?
2.如图,身高1.5m的小丽用一个两锐 角分别是300和600 的三角尺测量一棵 树的高度.已知她与树之间的距离为5m, 那么这棵树大约有多高?
拓展思维
某市在“旧城改造”中计划内一块如 图所示的三角形空地上种植某种草皮
以美化环境,已知这种草皮每平方米a
元,则购买这种草皮至少要多少元.
20米
30米
150
知识应用
3.一个小孩荡秋千,秋千链子的长度为 2.5m,当秋千向两边摆动时,摆角恰为60°, 且两边的摆动角度 相同,求它摆至最高 位置时与其摆至最 低位置时的高度之差
解: (1)sin300+cos450
1 2 1 2 . 22 2
(2) sin2600+cos2600-tan450
3 2
2
1 2
2
1
3 1 1
新北师大版九年级数学下册《三角函数的计算》优质ppt教学课件
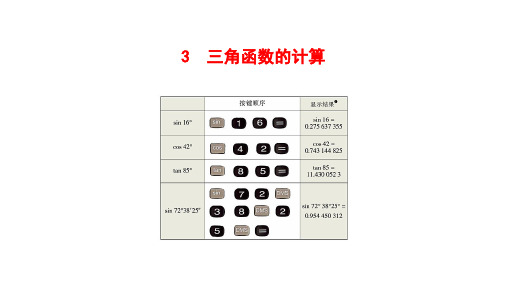
上表的显示结果是以“度”为单位的,再按 ˚ ′ ″ 键即可显示 以“度、分、秒”为单位的结果.
根据上述方法你能求出问题1中∠A的大小吗?
sin A = 1 = 0.25. 按键顺序和显示结果为
4
SHIFT sin 0 · 2 5 = 14.477 512 19°
再按 ° ′ ″ 键可显示14˚28′39″,所以∠A=14˚28′39″.
正弦值随着角度的增大(或减小)而增大(或减小); 余弦值随着角度的增大(或减小)而减小(或增大); 正切值随着角度的增大(或减小)而增大(或减小).
知识点1 利用计算器求锐角三角函数值
1.如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器 求边AC的长,则下列按键顺序正确的是( D )
D 39°
E
45°
C
A
【解析】(1)由题意,AC=AB=610 米.
(2)DE=AC=610米,
在Rt△BDE中,tan∠BDE= BE ,
DE
故BE=DEtan39°. 因为CD=AE,
所以CD=AB-DE·tan 39°
=610-610×tan 39°≈116(米). 答:大楼的高度CD约为116 米.
B.sin65°54′-sin35°54′=sin30°
C.2sin15°30′=sin31°
D.sin72°18′-sin12°18′=sin47°42′
•2. 已知sin α=1 ,求α,若用科学计算器计算且结果以“度、分、秒
2
”为单位,最后按键(D )
•A.AC/ON
B. SHIFT
C.MODE
(4)sin18°+cos55°-tan59°≈-0.7817.
30度45度60度角的三角函数值ppt课件

三角函数 锐角α
正弦sinα
余弦cosα
正切tanα
余切cotα
要能记 住有多 好
30o
1
2
3
3
3
2
3
45o
2 2
2 2
1
1
60o
3 2
1 2
3
3
3
这张表还可以看出许多 知识之间的内在联系?
5
例题欣赏 5
行家看“门道”
驶向胜利 的彼岸
例1 计算: (1)sin30o+cos45o;(2) sin260o+cos260o-tan45o.
解: (1)sin30o+cos45o
1 2 1 2 .
22 2
?怎样
解答
(2) sin260o+cos260o-tan45o
3 2
2 Leabharlann 1 22 1
3 1 1
44
0.
老师提示:
Sin260o表示 (sin60o)2, cos260o表示 (cos60o)2,其余 类推.
6
随堂练习 6
直角三角形中的边角关系
驶向胜利 的彼岸
B
看图说话: 直角三角形三边的关系. 直角三角形两锐角的关系. 直角三角形边与角之间的关系. A
c
a
┌
b
C
特殊角30o,45o,60o角的三角函数
值. 互余两角之间的三角函数关系.
30o
同角之间的三角函数关系
45o
45o ┌ 60o ┌
10
独立
扶梯的长度是多少?
B
3.如图,在Rt△ABC中,∠C=90°,
∠A,∠B ,∠C的对边分别是a,b,c.
高三文科数学总复习课件:三角形中的三角函数

6
2 为 3 ,则 a 的值为=
.
2
sin A
第八页,编辑于星期日:二十二点 四十九分。
例5
在 ABC中,角A、B、C所对的边分别为a、b、c,
若A= ,(1+ 3)c=2b.
6 (1)求C的大小; (2)若CB CA=1+ 3,求a,b,c.
第九页,编辑于星期日:二十二点 四十九分。
例6
在 ABC中,角A、B、C所对的边分别为a、b、c, 若 2sinA= 3cosA. (1)若a2 -c2 =b2 -mbc,求实数m的值; (2)若a 3,求 ABC面积的最大值.
2.解决三角形中的问题,要从统一着手, 或统一成角的关系,或统一成边的关系,
要视情况灵活处理.
第十二页,编辑于星期日:二十二点 四十九分。
《单元滚动卷检测一》
第十三页,编辑于星期日:二十二点 四十九分。
第三页,编辑于星期日:二十二点 四十九分。
(2) 余弦定理:
a2 b2 c2 2bc cos A
b2 a2 c2理可变形为:
cos A b2 c2 a2 cos B a2 c2 b2
2bc
2ac
a2 b2 c2 cosC
第十页,编辑于星期日:二十二点 四十九分。
在 ABC中,角A、B、C所对的边分别为a、b、c, 若a2 -c2 =2b,且sinAcosC=3cosAsinC,求b.
第十一页,编辑于星期日:二十二点 四十九分。
1.利用正弦定理、余弦定理将三角形 的边角转化、三角形形状的判断、进行 三角形内三角函数的求值及三角恒等式 的证明.
湖南师大附中 刘东红
第一页,编辑于星期日:二十二点 四十九分。
1.掌握正弦定理、余弦定理,并能解决 一些简单的三角度量问题。
2 为 3 ,则 a 的值为=
.
2
sin A
第八页,编辑于星期日:二十二点 四十九分。
例5
在 ABC中,角A、B、C所对的边分别为a、b、c,
若A= ,(1+ 3)c=2b.
6 (1)求C的大小; (2)若CB CA=1+ 3,求a,b,c.
第九页,编辑于星期日:二十二点 四十九分。
例6
在 ABC中,角A、B、C所对的边分别为a、b、c, 若 2sinA= 3cosA. (1)若a2 -c2 =b2 -mbc,求实数m的值; (2)若a 3,求 ABC面积的最大值.
2.解决三角形中的问题,要从统一着手, 或统一成角的关系,或统一成边的关系,
要视情况灵活处理.
第十二页,编辑于星期日:二十二点 四十九分。
《单元滚动卷检测一》
第十三页,编辑于星期日:二十二点 四十九分。
第三页,编辑于星期日:二十二点 四十九分。
(2) 余弦定理:
a2 b2 c2 2bc cos A
b2 a2 c2理可变形为:
cos A b2 c2 a2 cos B a2 c2 b2
2bc
2ac
a2 b2 c2 cosC
第十页,编辑于星期日:二十二点 四十九分。
在 ABC中,角A、B、C所对的边分别为a、b、c, 若a2 -c2 =2b,且sinAcosC=3cosAsinC,求b.
第十一页,编辑于星期日:二十二点 四十九分。
1.利用正弦定理、余弦定理将三角形 的边角转化、三角形形状的判断、进行 三角形内三角函数的求值及三角恒等式 的证明.
湖南师大附中 刘东红
第一页,编辑于星期日:二十二点 四十九分。
1.掌握正弦定理、余弦定理,并能解决 一些简单的三角度量问题。
三角函数解三角形正弦定理和余弦定理课件理新ppt

正弦定理的应用
01
正弦定理可以应用于求解三角形中的边、角、面积等问题,其中最常用的应用 是求解三角形的三边关系和三角形的面积公式。
02
在求解三角形的三边关系时,可以使用正弦定理得到两边之比的表达式,再结 合余弦定理得到第三边的表达式,从而得到三边之间的关系。
03
在求解三角形的面积公式时,可以使用正弦定理得到三角形的底和高,从而得 到三角形的面积公式。
三角函数解三角形正弦定理和余弦 定理课件理新ppt
xx年xx月xx日
contents
目录
• 引言 • 正弦定理 • 余弦定理 • 案例分析 • 结论与展望 • 参考文献
01
引言
课程背景
1
三角函数是数学中的基础内容之一,具有广泛 的应用价值。
2
解三角形是三角函数应用的重要方面之一,涉 及到很多实际问题。
《三角函数解题方 法与技巧》
《高中数学竞赛教 程》
《三角函数图像与 性质》
THANKS
利用正弦定理和余弦定理解三角形
如何根据三角形的已知信息求解三边长
利用正弦定理求解三角形边长
利用余弦定理求解三角形边长
通过具体案例展示,进行计算
三角形的判定方法
如何判断一个三角形是否为直 角三角形
利用正弦定理和余弦定理进行 三角形判定
通过具体案例展示,进行计算
05
结论与展望
总结正余弦定理在解三角形中的应用
正弦定理:对于任意三角形,已知一边和它的对角 ,无法确定三角形的大小和形状,需要再知道其他
一些信息才能确定三角形的大小和形状.
余弦定理:对于任意三角形,已知三边,可确定这 个三角形的形状和大小;已知两边和其中一边的对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2+b2-c2 a 5.在 △ABC 中, 若其面积 S= , 则 C=____. 30 4 3
6.在 △ABC 中, a=60, b=1, 其面积为 3 , 则 △ABC 外接圆的 2 39 直径是_______. 3
7.在 △ABC 中, a, b, c 是角 A, B, C 的对边, a= 3 , cosA= 1 , 3 1 , b2+c2 的最大值为 9 . 则 cos2 B+C = 2 3 2 ] (0, 8.在 △ABC 中, AB=1, BC=2, 则角 C 的取值范围是______. 6 9.设 O 是锐角三角形 ABC 的外心, 若 C=75, 且 △AOB, △BOC, △COA 的面积满足关系式 S△AOB+S△BOC= 3 S△COA, 求 A. 45 5 , 求 cosC 的值. 10.在 △ABC 中, 已知 sinA= 3 , cosB= 5 13 5 < 1, 解: ∵在 △ABC 中, cosB= 13 2 2B = 12 . 且 sinB= 1 cos ∴60º <B<90º , 13 2 又sinA= 3 < , ∴0º <A<45º 或 135º <A<180º . 2 5 4 ∵A+B<180º , ∴0º <A<45º . ∴cosA= 1-sin2A = 5 . ∴cosC=-cos(A+B)=sinAsinB-cosAcosB 3 12 4 5 = 16 . = 5 × 13 - 5 × 13 65
应用二: 判断三角形的形状
例1 △ABC 中, 若 sin2Acos2B-cos2Asin2B=sin2C, 判断 △ABC 的形状. 直角三角形 sin2A+sin2B-sin2C 1+cos2C 例2 在 △ABC 中, 已知 2 = , 试判 2 2 sin A-sin B+sin C 1+cos2B 断三角形的形状. 直角三角形或等腰三角形 例3 在 △ABC 中, 已知 (a+b+c)(a+b-c)=3ab, sinA+sinB= 3 , 试判断三角形的形状. 正三角形 例4 在 △ABC 中, 已知 (a2+b2)sin(A-B)=(a2-b2)sinC, 试判断 三角形的形状. 直角三角形或等腰三角形 例5 在△ABC中, 若 a2sin2B+b2sin2A=2abcosAcosB, (1)试判 断三角形的形状; (2)若 cosB=4(1-cosA), 求 △ABC 三边 a, b, c 的比. 直角三角形; 8:15:17
b a c (2)sinA= 2R , sinB= 2R , sinC= 2R ; (3)a=2RsinA, b=2RsinB, c=2RsinC. 已知三角形两边一对角运用正弦定理求解时, 务必注意可 能有两解. 2+c2-a2 b 2 2 2 3.余弦定理: a =b +c -2bccosA, cosA= 2bc 等, 常选用余 弦定理鉴定三角形的形状. 4.射影定理: a=bcosC+ccosB. 1absinC= 1r(a+b+c)(其中 r 为三角形内 5.面积公式: S= 1 ah = 2 a 2 2 切圆半径). 特别提醒: (1)求解三角形中的问题时, 一定要注意 A+B+C= 这一特性: A+B=-C, sin(A+B)=sinC, sin A+B =cos C ; (2)求解 2 2 三角形中含有边角混合关系的问题时, 常运用正弦定理、余弦 定理实现边角互化.
应用三: 三角形的证明
例1 在 △ABC 中, 求证: (1) a-ccosB = sinB ; b-ccosA sinA (2)a2-2abcos(60+C)=c2-2bccos(60+A); (3)a2+b2+c2≥4 3 S(S 为 △ABC 的面积). 提示: (1)法一: 边换角 (2)法一: 边换角 法三: 构造图形 (3)作差换 c2 即可. 差为: 2(a2+b2)-4absin(C+30) ≥2(a2+b2)-4ab=2(a-b)2≥0. (正三角形时取等号). 法二: 角换边 A c a b b D b C
应用举例
应用一: 解三角形
例1 设△ABC也成等差数列, 求三内角. A=B=C=60 提示: 令 A-C=2, 可得: 4cos2-3cos-1=0 得: cos=1 得: A=C. 例2 在△ABC 中, 已知 b= 3 , c=2 3 , 角 A 的平分线 AD=2, 求三角形的三内角的度数. A=60, B=30, C=90 例3 在△ABC 中, 若面积为 S, 且 2S=(a+b)2-c2, 求 tanC 的值. 4 3
三角形中的有关公式
设 △ABC 中, 角 A、B、C 的对边为 a、b、c,
1.内角和定理: 三角形三内角之和为, 即 A+B+C=. 注 任意两角和与第三个角总互补; 任意两半角和与第三个角的半角总互余; 锐角三角形三内角都是锐角 三内角的余弦值为正值 任两角和都是钝角 任意两边的平方和大于第三边的平方. c a b 2.正弦定理: sinA = sinB = sinC =2R(R 为三角形外接圆的半 径) . 注 正弦定理的一些变式: (1)a:b:c=sinA:sinB:sinC;
课后练习
1. △ABC 中, A, B 的对边分别为a, b, 且 A=60, a= 6, b=4, 那 么满足条件的 △ABC ( C ) A.有一个解 B.有两个解 C.无解 D.不能确定 充要 条件. 2.在 △ABC 中, A>B 是sinA>sinB 成立的_____ 3.在 △ABC 中, (1+tanA)(1+tanB)=2, 则 log2sinC= - 1 2 . 4. △ABC 中, a, b, c 分别是角 A, B, C 所对的边, 若 (a+b+c) (sinA+sinB-sinC)=3asinB, 则 C= 60 .
法二: 角换边
B
例2 已知 △ABC 的三边均为有理数, A=3, B=2, 试证 cos5 与 cos 均为有理数.
证: 由余弦定理知, cosA, cosB, cosC 为有理数,
∴cos5 即 -cosC 为有理数, 而cos=cos(A-B)=cosAcosB+sinAsinB, 证明 sinAsinB 为有理数即可(由正弦定理可证). 或由 coscos5=cos(3-2)cos(3+2) =cos23cos22-sin23sin22 =cos23cos22-(1-cos23)(1-cos22) =cos2Acos2B-(1-cos2A)(1-cos2B) 为有理数, 且 cos0, cos5 为有理数知: cos 为有理数.
6.在 △ABC 中, a=60, b=1, 其面积为 3 , 则 △ABC 外接圆的 2 39 直径是_______. 3
7.在 △ABC 中, a, b, c 是角 A, B, C 的对边, a= 3 , cosA= 1 , 3 1 , b2+c2 的最大值为 9 . 则 cos2 B+C = 2 3 2 ] (0, 8.在 △ABC 中, AB=1, BC=2, 则角 C 的取值范围是______. 6 9.设 O 是锐角三角形 ABC 的外心, 若 C=75, 且 △AOB, △BOC, △COA 的面积满足关系式 S△AOB+S△BOC= 3 S△COA, 求 A. 45 5 , 求 cosC 的值. 10.在 △ABC 中, 已知 sinA= 3 , cosB= 5 13 5 < 1, 解: ∵在 △ABC 中, cosB= 13 2 2B = 12 . 且 sinB= 1 cos ∴60º <B<90º , 13 2 又sinA= 3 < , ∴0º <A<45º 或 135º <A<180º . 2 5 4 ∵A+B<180º , ∴0º <A<45º . ∴cosA= 1-sin2A = 5 . ∴cosC=-cos(A+B)=sinAsinB-cosAcosB 3 12 4 5 = 16 . = 5 × 13 - 5 × 13 65
应用二: 判断三角形的形状
例1 △ABC 中, 若 sin2Acos2B-cos2Asin2B=sin2C, 判断 △ABC 的形状. 直角三角形 sin2A+sin2B-sin2C 1+cos2C 例2 在 △ABC 中, 已知 2 = , 试判 2 2 sin A-sin B+sin C 1+cos2B 断三角形的形状. 直角三角形或等腰三角形 例3 在 △ABC 中, 已知 (a+b+c)(a+b-c)=3ab, sinA+sinB= 3 , 试判断三角形的形状. 正三角形 例4 在 △ABC 中, 已知 (a2+b2)sin(A-B)=(a2-b2)sinC, 试判断 三角形的形状. 直角三角形或等腰三角形 例5 在△ABC中, 若 a2sin2B+b2sin2A=2abcosAcosB, (1)试判 断三角形的形状; (2)若 cosB=4(1-cosA), 求 △ABC 三边 a, b, c 的比. 直角三角形; 8:15:17
b a c (2)sinA= 2R , sinB= 2R , sinC= 2R ; (3)a=2RsinA, b=2RsinB, c=2RsinC. 已知三角形两边一对角运用正弦定理求解时, 务必注意可 能有两解. 2+c2-a2 b 2 2 2 3.余弦定理: a =b +c -2bccosA, cosA= 2bc 等, 常选用余 弦定理鉴定三角形的形状. 4.射影定理: a=bcosC+ccosB. 1absinC= 1r(a+b+c)(其中 r 为三角形内 5.面积公式: S= 1 ah = 2 a 2 2 切圆半径). 特别提醒: (1)求解三角形中的问题时, 一定要注意 A+B+C= 这一特性: A+B=-C, sin(A+B)=sinC, sin A+B =cos C ; (2)求解 2 2 三角形中含有边角混合关系的问题时, 常运用正弦定理、余弦 定理实现边角互化.
应用三: 三角形的证明
例1 在 △ABC 中, 求证: (1) a-ccosB = sinB ; b-ccosA sinA (2)a2-2abcos(60+C)=c2-2bccos(60+A); (3)a2+b2+c2≥4 3 S(S 为 △ABC 的面积). 提示: (1)法一: 边换角 (2)法一: 边换角 法三: 构造图形 (3)作差换 c2 即可. 差为: 2(a2+b2)-4absin(C+30) ≥2(a2+b2)-4ab=2(a-b)2≥0. (正三角形时取等号). 法二: 角换边 A c a b b D b C
应用举例
应用一: 解三角形
例1 设△ABC也成等差数列, 求三内角. A=B=C=60 提示: 令 A-C=2, 可得: 4cos2-3cos-1=0 得: cos=1 得: A=C. 例2 在△ABC 中, 已知 b= 3 , c=2 3 , 角 A 的平分线 AD=2, 求三角形的三内角的度数. A=60, B=30, C=90 例3 在△ABC 中, 若面积为 S, 且 2S=(a+b)2-c2, 求 tanC 的值. 4 3
三角形中的有关公式
设 △ABC 中, 角 A、B、C 的对边为 a、b、c,
1.内角和定理: 三角形三内角之和为, 即 A+B+C=. 注 任意两角和与第三个角总互补; 任意两半角和与第三个角的半角总互余; 锐角三角形三内角都是锐角 三内角的余弦值为正值 任两角和都是钝角 任意两边的平方和大于第三边的平方. c a b 2.正弦定理: sinA = sinB = sinC =2R(R 为三角形外接圆的半 径) . 注 正弦定理的一些变式: (1)a:b:c=sinA:sinB:sinC;
课后练习
1. △ABC 中, A, B 的对边分别为a, b, 且 A=60, a= 6, b=4, 那 么满足条件的 △ABC ( C ) A.有一个解 B.有两个解 C.无解 D.不能确定 充要 条件. 2.在 △ABC 中, A>B 是sinA>sinB 成立的_____ 3.在 △ABC 中, (1+tanA)(1+tanB)=2, 则 log2sinC= - 1 2 . 4. △ABC 中, a, b, c 分别是角 A, B, C 所对的边, 若 (a+b+c) (sinA+sinB-sinC)=3asinB, 则 C= 60 .
法二: 角换边
B
例2 已知 △ABC 的三边均为有理数, A=3, B=2, 试证 cos5 与 cos 均为有理数.
证: 由余弦定理知, cosA, cosB, cosC 为有理数,
∴cos5 即 -cosC 为有理数, 而cos=cos(A-B)=cosAcosB+sinAsinB, 证明 sinAsinB 为有理数即可(由正弦定理可证). 或由 coscos5=cos(3-2)cos(3+2) =cos23cos22-sin23sin22 =cos23cos22-(1-cos23)(1-cos22) =cos2Acos2B-(1-cos2A)(1-cos2B) 为有理数, 且 cos0, cos5 为有理数知: cos 为有理数.
