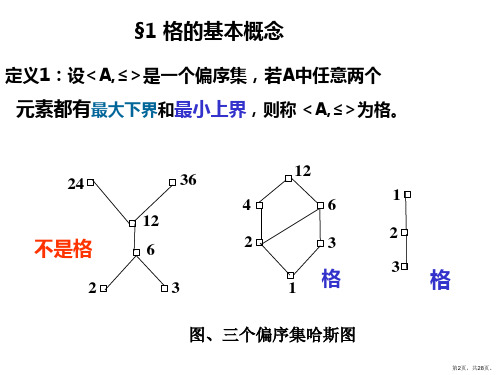
离散数学结构 第十三章 格与布尔代数
代数结构-布尔代数与格
布尔代数举例
({0, 1}, +, ⋅ , , 0, 1)为布尔代数 n度布尔函数全体也构成一个布尔代数
布尔和 布尔积 补函数 全取0的函数、全取1的函数
A的幂集也构成一个布尔代数(ρ(A), ⋂, ⋃, ∼, ∅, A）
布尔代数举例
Bn={(x1, …, xn)| xi∈B, i =1, …, n}构成布尔代数 x= (a1 , …, an), y=(b1 , …, bn), ai∈B, bi∈B
111 110
Bn as Product of n B’s
B1, ({0,1}, ∧, ∨, 1, 0, ’), is denoted as B. For any n≥1, Bn is the product B×B×...×B of B, n factors, where B×B×...×B is given the product partial order.
格中的原子
a
a a b c d (1) e (2) b c d b
c 原子 d e (3)
有限布尔代数的表示定理
任一有限布尔代数B 同构于 B中所有的原子构成的 集合A的幂集代数系统P(A)。 即(B, ∧, ∨, ', 0, 1) ≅ (P(A), ⋂, ⋃, ∼, ∅, A)
备注（关于无限布尔代数）
若 x∧y =x，则 x∨y = (x∧y) ∨ y = y //吸收律
若 x∨y =y，则 x∧ y = x∧ (x∨y) = x //吸收律
证明这个关系满足自反性、反对称性、传递性。 这个偏序构成一个格。
lub{x,y} 即为 x∨y。 glb{x,y} 即为 x∧y。
格与布尔代数
对P(S)中任一元素A,S与A的差集S-A是其唯一补元
因为:
(S-A)∪A=S和(S-A)∩A=Φ.
36
7.5 几种特殊的格
定义4(分配格) 格<L, ,*>称作一个分配格,如果对L中 任意元素a,b,c都有: (1) a*(bc)=(a*b)(a*c); (2) a(b*c)=(ab)*(ac). 例：幂集格<P(S),∩,∪>都是分配格. 格<P(S),∩,∪> 的两个二元运算分别是S幂集合上的交和并运算,交 对并和并对交都具有分配律;
M={c,d}
无上确界，下确界为e 上确界为a，下确界为b
12
7.1 偏序集
M={{a},{b}}
上确界{{a,b}}，下确界为
M={{a},{a,b}}
上确界{{a,b}}，下确界为{a}
M={{a},{b,c}}或 M={{a},{b},{c}}或
上确界{{a,b,c}}，下确界为
M={{a,b},{b,c}}
31
7.5 几种特殊的格
定义1 (有界格) 若格<L,≤>存在最大元和最小元，则称该格为有界格。
记最大元为1，最小元为0。记有界格为<L,≤,0,1>。
例： <P(S), , ,S>有界格。
32
7.5 几种特殊的格
定义2 (补元) 有界格<L,≤,0,1>中，如果a*b=0且ab=1. 则称元素b为a的补元。
18
7.2 格的定义
例. 设S是任意集合, 则< P(s), >为偏序格。
|S|=1
|S|=2
|S|=3 两个集合A，B的上确界是A∪B，下确界是A∩B
离散数学代数结构部分-PPT
例5、2 设Q就是有理数集合,*就是Q上得 二元运算,对任意得a,b∈Q,a*b＝a+ba· b,问运算*就是否可交换。
例5、3 设A=Z,“+”就是整数中得加法: 则
“+”在Z中适合结合律。 “。”就是整数中得减法:则特取
而 运算“。”不满足结合律
➢定义5、4 设*就是定义在集合A上得 一个二元运算,如果对于任意得x∈A, 都有x*x＝x,则称运算*就是等幂得。
例5、4 设P(S)就是集合S得幂集,在P(S) 上定义得两个二元运算,集合得“并”运 算∪和集合得“交”运算∩,验证∪,∩ 就是等幂得。
➢ 定理6、19 设
例6、16 例6、17 设
➢ 定义6、18 设 例6、18 设
➢ 定义6、19 设 例6、19 4元置换
➢ 定义6、20设
➢ 定理6、20
➢ 定义6、21
例6、20 如图 进行旋转,也可以围绕她得对称轴进行翻转,但 经过旋转或翻转后仍要与原来得方格重合(方格 中得数字可以改变)。如果把每种旋转或翻转看 作就是作用在
➢定理5、2 设*就是S上得二元运算,
如果S中既存在关于运算*得左幺元 el ,
又存在关于运算得右幺元 er
则S中必存在关于运算*得幺元e并且
2、 零元 ➢定义5、8 设*就是S上得二元运算,
在自然数集N上普通乘法得零元就是0, 而加法没有零元。
➢ 定理5、3 设 *就是S上得二元运算,如果S 中存在(关于运算*得)零元,则必就是唯一得。 所以零元就是唯一得。
证明: 略。 推论6、1
格与布尔代数课件2
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f，使得对 x1,x2 A， 有f(x1∨1x2)=f(x1)∨2f(x2)，f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律：a∨(a∧b) = a、a∧(a∨b) = a
证明：幂等律 ∵ a≤a，∴ a是a的上界，而a∨a是a的最小上界， ∴a∨a≤a ，又 ∵ a≤a ∨a，
由反对称性得：a∨a = a 由对偶原理得，a∧a = a
第15页，共28页。
证明：吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a， a∨(a ∧ b)≤a
解：< I+ , D>是格 ∵整除关系是偏序关系，对a,bI， a、b的最小上界等于a、b的最小公倍数， a、b的最大上界等于a、b的最大公约数。
第3页，共28页。
< P(S) , > 是格
∵子集关系是偏序关系，对a,b P(S)，
a、b的最小上界等于a∪b，
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2，>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1：,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}
离散数学课件13.4布尔代数
有限布尔代数的表示定理
定理13.11 若B是有限布尔代数,则 B含有2n个元(n∈N), 并且B与<P(S),∩,∪,~,,S>同构, 其中S是一个n元集合.
举例
格S12,gcd.lcm是布尔代数吗? 解: S12={1,2,3,4,6,12}的元素个数6, 不是2的整数幂, 故不是布尔代数. 不难看出2没有补元,因为 2∨x=lcm(2,x)=12当且仅当 x=12, 而12的补元是1而不是2.
例
集合代数<P(S),∩,∪,~,,S>是 布尔代数.
开关代数<{0,1},∧,∨,￢,0,1>是 布尔代数,其中∧为与运算,∨为或 运算, ￢为非运算.
布尔代数有以下性质.
定埋13.10 设<B,∧,∨,',0,1>是布尔代数, 则有:
a∈B,(a’)’＝a(双重否定律), a,b∈B, (a∨b)'=a'∧b'
布尔格、布尔代数
定义13.12 如果格<L,∧,∨,0,1>是有 补分配格,则称L为布尔格,也叫做布 尔代数. 由于布尔代数L中的每个元都有唯一 的补元,求补运算也可以看成是L中的 一元运算. 因此,布尔代数L可记为<L,∧,∨,',0,1>, 其中'表示求补运算.
布尔代数的等价定义
定义13.13(公理化定义): 有两个二元运算的代 数B,*, 称为布尔代数,如果对任意元素 a,b,cB,成立
•此类布尔表达式可用带3个基本元件的电路来实 现.3个基本元件是:
①反相器
x
x’
②与门
x xy
y
③或门
x xy
y
实例之一
•实例1: 三人委员会表决某个提案,如有两张赞 成票即获通过,实现上述过程的表决机器的控制 电路如下图所示:
离散数学 格与布尔代数共89页
66、节制使快乐增加并使享受加强。 ——德 谟克利 特 67、今天应做的事没有做，明天再早也 是耽误 了。——裴斯 泰洛齐 68、决定一个人的一生，以及整个命运 的，只 是一瞬 之间。 ——歌 德 69、懒人无法享受休息之乐。——拉布 克 70、浪费时间是一桩大罪过。——卢梭
离散数学 格与布尔代数
21、没有人陪你走一辈子，所以你要 适应孤 独，没 有人会 帮你一 辈子， 所以你 要奋斗 一生。 22、当眼泪流尽的时候，留下的应该 是坚强 。 23、要改变命运，首先改变自己。
24、勇气很有理由被当作人类德性之 首，因 为这种 德性保 证了所 有其余 的德性 。--温 斯顿． 丘吉尔 。 25、梯子的梯阶从来不是用来搁脚的 ，它只 是让人 们的脚 放上一 段时间 ，以便 让别一 只脚能 够再往 上登。
离散数学格与布尔代数
§7.1 格
例 < P(S) ， >是格 表示为<P(S), , * > 又可表示为< P(S) ,∪,∩>
例 <Z+,≤>,或 <Z+,|> <Z+, , * > <Z+, LCM,GCD>
§7.2 格——代数系统
格〈L，≤〉中自然存在两个运算 和 * ，从而 派生出一个代数系统〈L，，*〉
6
<S15,|>,
2
2019/10/5
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/5
§7.1 格
例 设Z+为正整数集合，对于a,b Z+，关系“≤”定义为： a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格，
并、交 运算的性质
定理１ 设〈L，≤〉是一个格，并运算与交运算 * 满足 如下性质：
L1 a a ＝ a
a*a＝a
（幂等律）
L2 a b ＝ b a a * b ＝ b * a （交换律）
L3 （a b） c ＝ a （b c）
13格与分配格
证明思路： 因为a和b的并是a的一个上界，所以 a ≤ a∨b 同理 b ≤ a∨b 由对偶原理，即得 a∧b ≤ a a∧b ≤ b
定理6-1.2 在一个格<A, ≤>中，对于任意元素a,b,c,dA, 如果 则 a≤b 和 c≤d a∨c ≤ b∨d a∧c ≤ b∧d
证明 因为b ≤ b∨d，d ≤ b∨d，所以，由传递性可得 a ≤ b∨d和 c ≤ b∨d 这就表明b∨d是a和c的一个上界，而a∨c是a和c的最小上界， 所以，必有a∨c ≤ b∨d 类似地可以证明 a∧c ≤ b∧d
例3 给定S={a，b}，(S)={,{a},{b},{a,b}}，那么，格
<(S)，>如图6-1.3所示。
二、由格<A, ≤>所诱导的代数系统
定义6-1.2 设<A, ≤>是一个格,如果在上定义两个二元运 算∨和∧ ,使得对于任意的a,b A ， a∨b等于 a和b的最小 上界, a∧b等于a和b的最大下界,那么,就称<A,∨,∧>为由格 <A, ≤>所诱导的代数系统。二元运算∨和∧分别称为并运算和 交运算。 通常用a∨b 表示{a,b}的上确界,用a∧b 表示{a，b}的下 确界,∨和∧分别称为保联(join)和保交(meet)运算。由于对任 何a，b，因为在格中，a∨b及a∧b都是A 中确定的成员，因 此 ∨,∧均为A上的运算。 设S={a,b} ， (S) ={, {a},{b},{a,b}}由格<(S), > 诱导的代数系统为<(S),∨,∧> 。其中∨为集合的并运算和 ∧为集合的交运算。如表6-1.1所示。
定理6-1.4 设<A,∨,∧>是一个代数系统,其中 ∨,∧都是二元运算且满足交换律、结合律和吸收律，
离散数学-格和布尔代数
的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集，则对于任意元素 l1, l2, l3 L，有以 下六个关系式成立： l1 l1 若 l1 l2，l2 l1，则 l1 = l2 若 l1 l2，l2 l3，则 l1 l3 l1 l1 若 l1 l2，l2 l1，则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的，格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的，是他在研究命题演算中发现的，通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集，也可以看作是有两个二元运算的代数系统， 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中，都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集，如果 L 中任意两个元素都 存在着最大下界和最小上界，则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一，故引入记号： l1 l2 = glb(l1, l2)，l1 l2 = lub(l1, l2)， 其中 和 均可看作是集合 L 上的二元运算，分别称为交和并。 注：若 < L; > 是一个格，则意味着 < L; > 也是一个形为 < L; , > 的代数系统，其中 和 是 L 上的两个二元运算， 对于任意 l1, l2 L，l1 l2 表示在偏序 “ ” 意义下，l1 和 l2 的最小上界，l1 l2 表示 l1 和 l2 的最大下界。
离散数学格与布尔代数
6
<S15,|>,
2
2019/10/12
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)
e d
c b
a (b)
f
d
e
d
e
c
b
c
a (c)
a
b
(d)
e
c
d
a
b
(e)
2019/10/12
§7.1 格
例 设Z+为正整数集合，对于a,b Z+，关系“≤”定义为： a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格，
Input A B Cin
00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1
Output S Cout
00 10 10 01 10 01 01 11
S A BCin A BCin A BCin A BCin
Cout A B Cin A B Cin A B Cin A B Cin
§7.2 格——代数系统
证〈L，≤〉为要求的格
a，b∈L，（a * b）* a ＝ a*（a * b）＝（a * a）*b＝a*b，
故a*b≤a，
L3
L1
同理a*b≤b，因此a*b是｛a，b｝的下界，
又设c是｛a，b｝的任一下界，即c≤a，c≤b，则a * c＝c，b * c＝c，于是（a * b）* c＝a *（b * c）＝a * c＝c，即c≤a * b， 所以a * b是｛a，b｝的最大下界，即a * b＝inf｛a，b｝，
离散数学格的概念
∵整除关系是偏序关系，对a,bI， a、b的最小上界等于a、b的最小公倍数， a、b的最大下界等于a、b的最大公约数。
❖ 基本概念
< B2 , D >是否 < S30 , D >的子格?
30
6
30
10
6 15
2
3
10
15
1 ∨1 2 3 6 11236 22266
2
53
5
∧1 2 3 6
1
11111
21212
说明：
33636 66666
31133 61236
(1) 子格必是格。
运算∨和∧在B1上封闭，B1 S30 且B1 ≠Ø, ∴ < B1, D >是 < S30 , D >的子格； 同理可证< B2 , D >是 < S30 , D >的子格
例：A={a, b, c }, < P(A) , > 所诱导的代数系统为？
< P(A),∪,∩>
❖ 基本概念
定义3:设<A,≤ >是一个格，由其所诱导的代数系统为 <A,∨,∧>。设BA且B ≠Ø ，如果运算∨和∧在B上封闭， 则称<B,≤ > 是<A,≤ >的子格。
❖ 基本概念
例2：B1 = {1,2,3,6} ， B2 = {5,10,15,30} ，< B1, D >和
离散数学
❖ 格与布尔代数 1 格的概念
离散数学格与布尔代数
证明：⑴ 因 a≤a∨b，a≤a∨c 所以 a ≤(a∨b)∧(a∨c)
又因 b∧c≤b≤ a∨b，b∧c≤c≤ a∨c
所以 b∧c ≤(a∨b)∧(a∨c)
于是有 a∨(b∧c) ≤(a∨b)∧(a∨c) 。
由对偶原理得 a∧(b∨c)≥ (a∧b)∨(a∧c) 。
即 (a∧b)∨(a∧c)≤ a∧(b∨c) 。
第二页，共87页
7-1 格 (Lattice)
一 . 基本概念
1. 格的定义
<A,≤>是偏序集，如果任何a,b∈A,使得{a,b}都有最大
下界和最小上界，则称<A,≤>是格。
右图的三个偏 序集， <A,≤>不是格， 因为{24,36} 无最小上界。
<B,≤><C,≤>
。 。 24
36
。 30
2。
。 12 6。
离散数学格与布尔代数
第一页，共87页
2.B的最小元与最大元 y是B的最小元y∈B∧x(x∈By≤x) y是B的最大元y∈B∧x(x∈Bx≤y) {2,3,6}的最小元:无 最大元: 6 B如果有最小元(最大元), 则是唯一的。 3.B的下界与上界
。 。 24
36
。 12
６。 ２。 ３。
１。
y是B的下界y∈A∧x(x∈By≤x)
a∧1b=a f(a∧1b)=f(a) 即 f(a)∧2f(b)=f(a) 而 f(a)∧2f(b) ≤2f(b) 所以 f(a)≤2f(b). 3. 格同构的保序性 定理：设两个格为<A1,≤1>和<A2, ≤2> ，f是A1到A2的双射，则f是
<A1,≤1> 到<A2, ≤2>的格同构，当且仅当 对任意a,b∈A1，a≤1b f (a)≤2f(b) 证明：令<A1,∨1,∧1>和 <A2,∨2,∧2>是格<A1,≤1> 和 <A2, ≤2>诱导的代数系统，
格与布尔代数
格与布尔代数后述，一部分关于格与一部分关于布尔代数。
关于格格是数学中的一种代数结构，它被广泛用于数学、计算机科学和逻辑学等领域。
在数学中，格是一种偏序集合，它具有两个基本运算：上下拟合和交并运算。
其中，上下拟合是指存在最小上估和最大下估，而交并运算则是指对于任意两个元素都可以求出它们的最大公共上界和最小公共下界。
尽管最初格是在点集拓扑学中发现的，但它们的概念在其他领域中也扮演着重要角色，例如，它们在科学中被用来定义空间，它们被用来解决许多计算机科学问题，例如，程序正确性证明，它们与数据结构有关，在逻辑学中，格被用来理解一些推理系统。
关于布尔代数布尔代数是一种代数结构，它被广泛用于逻辑学、电子工程和计算机科学中。
布尔代数是邓纳-Bier恩论文提出的一种基于命题逻辑的代数系统，其中对于两个命题P和Q，存在两个二元运算，即并（∨）和交（∧）。
这种代数系统可以用0和1表示，其中0表示假，1表示真。
布尔代数中的一些重要性质是：交换律、结合律、分配律等。
尽管在布尔代数中并和交这两个朴素的逻辑运算都不是独立产生的概念，但该理论在数学和计算机科学中有着重要应用。
布尔代数不仅用于设计电路和硬件，还用于在计算机程序和算法中描述逻辑条件，可编程逻辑和任意逻辑等方面。
格与布尔代数的关系虽然格和布尔代数看起来似乎是两种完全不同类型的代数结构，但它们之间有着密切的联系。
一些格配合着一些次区域可以构成布尔代数；同样，对于一个布尔代数而言，它也可以被看作是某个格所描述的偏序集合。
在交集上平凡地定义结构子格也叫布尔子格。
一个布尔代数的子集都可以看做是一种决策支持系统（Decision Support System，DSS）或决策信息系统（Decision Information System，DIS）。
由此可见，布尔代数是格论的一种特例，而格论是布尔代数的一种扩展。
总体而言，格与布尔代数的关系很紧密。
事实上，这种关系已经在数学和计算机科学的广泛应用中得到了充分的体现。
离散数学布尔代数与逻辑
离散数学布尔代数与逻辑离散数学是数学的一个分支，研究离散的、离散的结构和离散的现象。
而布尔代数是离散数学的重要组成部分，是代数学中关于二元关系的理论。
同时，与布尔代数密切相关的是逻辑学，研究命题的真值、论证的正确性以及推理的方法。
一、布尔代数基础布尔代数是一种逻辑代数，它使用逻辑运算符号和变量，描述和分析命题逻辑关系。
在布尔代数中，变量只有两个取值，即真（用1表示）和假（用0表示）。
布尔代数的基本运算包括逻辑与、逻辑或和逻辑非。
逻辑与表示当且仅当两个变量都为真时，结果为真；逻辑或表示当至少有一个变量为真时，结果为真；逻辑非表示当某个变量为真时，结果为假，反之亦然。
在布尔代数中，可以使用真值表来描述和分析布尔函数的取值情况。
布尔函数是指由布尔代数运算符组成的表达式，它接受一个或多个输入变量，并产生一个输出变量。
布尔函数在逻辑电路设计、计算机科学、编程等领域中有广泛的应用。
通过真值表分析布尔函数的取值规律，可以优化逻辑电路的设计和布尔函数的运算。
二、逻辑学与命题逻辑逻辑学是研究推理和论证的科学，其中命题逻辑是逻辑学的一个重要分支。
命题逻辑的基本概念是命题，它是陈述句，可以被判断为真或假。
命题逻辑使用逻辑连接词和命题变量来组成复合命题，并通过逻辑运算符来描述复合命题之间的关系。
逻辑连接词包括逻辑与、逻辑或、逻辑非、蕴涵和等价。
逻辑与表示两个命题同时为真时，复合命题为真；逻辑或表示两个命题至少有一个为真时，复合命题为真；逻辑非表示命题的否定，即真变为假，假变为真；蕴涵表示如果第一个命题为真，则第二个命题为真，否则为假；等价表示两个命题具有相同的真值。
逻辑学通过推理规则和推理方法来分析和判断复合命题的真假。
其中包括代入规则、假言推理、拒取否定、双重否定等推理规则。
通过应用这些推理规则，可以推导出逻辑上正确的结论，并解决实际问题中的逻辑推理和决策问题。
三、离散数学中的应用离散数学是计算机科学和信息技术的基础学科，广泛应用于计算机算法、数据结构、数据库、图论等领域。
布尔代数
任何有限布尔代数的基数为2n, n是自然数。
设B是有限代数系统，A是B中所有原子的集合。 则：B≅P(A), ∴|B|=|P(A)|=2|A|
等势的布尔代数系统均同构
设B1和B2是有限布尔代数，且|B1|=|B2|；A1,A2分别是相应 的原子的集合。由同构关系的传递性，只需证明： P(A1)≅P(A2)。
则称ϕ是B1到B2的同态映射。(若ϕ是双射，则是同构)
其实，上述3个等式不是独立的。
(2)+(3)⇒(1): ϕ(a∨b)=ϕ(((a∨b)')')= -ϕ((a∨b)')= -ϕ(a'∧ b')= -(ϕ(a')⋂ϕ(b'))= -(-ϕ(a)⋂-ϕ(b))=ϕ(a)⋃ϕ(b) 同理：(1)+(3)⇒(2)
有限布尔代数的表示定理的证明
ϕ: B → P(A), ∀x∈B, ϕ(x)=T(x)是同态映射。
ϕ(x∧y) = T(x∧y) = {b|b∈A, b≼x∧y} = {b|(b∈A, b≼x)且 (b∈A, b≼y)} = {b|b∈A,b≼x}⋂{b|b∈A,b≼y} = T(x)⋂T(y) = ϕ(x)⋂ϕ(y) 令x=a1 ∨ a2 ∨ … ∨ an , y=b1 ∨ b2 ∨ … ∨ bm 。 则x ∨ y= a1 ∨ … ∨ an ∨ b1 ∨ … ∨ bm , 显然：ϕ(x∨y) = T(x∨y) = T(x)⋃T(y) = ϕ(x) ⋃ ϕ(y) 设x'是x在B中的补元。注意： ϕ(x)⋃ϕ(x')=ϕ(x ∨ x')=ϕ(1)=A 且 ϕ(x)⋂ϕ(x')=ϕ(x ∧ x')=ϕ(0)=∅ ∴ϕ(x') = ∼ϕ(x)
Chapt22 格与布尔代数.
同理可证(a×b)(a×c) ≤ a×(bc)。
2019/5/12
离散数学
23
模不等式
定理22.2.4：设L, ≤是格， a, b, c∈L。于是， a≤b当且仅当a(b×c) ≤b×(ac)。
证明：若a≤b，则由定理22.2.1知， ab=b。又 由定理22.2.3知， a(b×c) ≤ (ab)×(ac) = b×(ac)。
≤的子格。
a1
例但如是，右若图S,所≤示是的L格, ≤，的其子中格L=，{而a1,S, a×2,,a3,a不4,一a5}定。是取LS,=×{a,1,a2的, a子3, a格5}。。
a2
a4
a3
显这然说明S,，≤偏是序L格, ≤的的子子格格和，代则数格的S,
×子,格的却定不义是是L有, 区×别, 的的。子格。因 为a2×a3= a4S。
因为aa××b(a=ibn)f{=a,inbf}{，a, asupb{=a,sbu}p}{a，, b所}。以 a×这(a两种b)运≤a算，满即足in如f{a下, s的up性{a质, b：}} ≤a (1又)交因换为律，：a≤aa×且ba=≤sbu×p{aa，, ba}，b所= 以baa是；
2019/5/12
离散数学
13
从代数系统来定义格
定义22.1.3：设L是一个集合，×和是L上的 两个二元封闭运算，若×和对a, b, c∈L， 满足：
(1)交换律： a×b= b×a， ab= ba； (2)结合律： a×(b×c) = (a×b) ×c,
a(bc) = (ab)c (3)吸收律： a×(ab) = a, a(a×b) = a。 则称代数系统L, ×, 是一个格。 L, ≤ 称为偏序格，L, ×, 称为代数格。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十三章格与布尔代数13.1 格的定义与性质一、格作为偏序集的定义1．格的定义定义13.1设<S,>是偏序集,如果x,y S,{x,y}都有最小上界和最大下界,则称S 关于偏序作成一个格。
由于最小上界和最大下界的唯一性,可以把求{x,y}的最小上界和最大下界看成x与y的二元运算∨和∧,即求x∨y和x∧y分别表示x与y的最小上界和最大下界。
这里要说明一点，本章中出现的∨和∧符号只代表格中的运算，而不再有其它的含义。
2．格的实例例13.1设n是正整数,S n是n的正因子的集合。
D为整除关系,则偏序集<S n,D>构成格。
x,y∈S n,x∨y是lcm(x,y),即x与y的最小公倍数。
x∧y是gcd(x,y),即x与y的最大公约数。
图13.1给出了格<S8,D>，<S6,D>和<S30,D>.图13.1例13.2 判断下列偏序集是否构成格,并说明理由。
(1) <P(B),>,其中P(B)是集合B的幂集。
(2) <Z,≤>,其中Z是整数集,≤为小于或等于关系。
(3) 偏序集的哈斯图分别在图13.2中给出。
二．格的性质1．对偶原理定义13.2设f是含有格中元素以及符号=,,,∨和∧的命题。
令f*是将f中的替换成,替换成,∨替换成∧,∧替换成∨所得到的命题。
称f*为f的对偶命题。
例如,在格中令f是(a∨b)∧c c, 则f*是(a∧b)∨c c .格的对偶原理设f是含有格中元素以及符号=,,,∨和∧等的命题。
若f对一切格为真,则f的对偶命题f*也对一切格为真。
例如,对一切格L都有a,b∈L,a∧b a那么对一切格L都有a,b∈L,a∨b a许多格的性质都是互为对偶命题的。
有了格的对偶原理,在证明格的性质时,只须证明其中的一个命题就可以了。
2. 运算性质定理13.1设<L,>是格,则运算∨和∧适合交换律、结合律、幂等律和吸收律,即(1) a,b ∈L 有a∨b=b∨a, a∧b=b∧a(2) a,b,c∈L 有(a∨b)∨c=a∨(b∨c), (a∧b)∧c=a∧(b∧c)(3) a∈L 有a∨a=a, a∧a=a(4) a,b∈L 有a∨(a∧b)=a, a∧(a∨b)=a证(1)a∨b和b∨a分别是{a,b}和{b,a}的最小上界。
由于{a,b}={b,a},所以a∨b=b∨a.由对偶原理,a∧b=b∧a得证。
(2) 由最小上界的定义有(a∨b)∨c a∨b a (13.1)(a∨b)∨c a∨b b (13.2)(a∨b)∨c c (13.3)由式13.2和13.3有(a∨b)∨c b∨c (13.4)再由式13.1和13.4有(a∨b)∨c a∨(b∨c)同理可证(a∨b)∨c a∨(b∨c)根据偏序关系的反对称性有(a∨b)∨c=a∨(b∨c)由对偶原理,(a∧b)∧c=a∧(b∧c)得证。
(3)显然a a∨a,又由a a可得a∨a a。
根据反对称性有a∨a=a，由对偶原理,a∧a=a得证。
(4)显然a∨(a∧b) a (13.5)又由a a,a∧b a可得a∨(a∧b) a (13.6)由式13.5和13.6可得a∨(a∧b)=a，根据对偶原理,a∧(a∨b)=a得证。
3. 关于序的性质定理13.2设L是格,则a,b ∈L有a b a∧b=a a∨b=b证先证a b a∧b=a.由a a和a b可知a是{a,b}的下界,故a a∧b.显然有a∧b a.由反对称性得a∧b=a.再证a∧b=a a∨b=b.根据吸收律有b=b∨(b∧a)由a∧b=a和上面的等式得b=b∨a, 即a∨b=b.最后证a∨b=b a b.由a a∨b得a a∨b=b.定理13.3设L是格,a,b,c,d∈L.若a b且c d,则a∧c b∧d, a∨c b∨d.证a∧c a ba∧c c d因此a∧c b∧d. 同理可证a∨c b∨d.例13.4设L是格,证明a,b,c∈L有a∨(b∧c)(a∨b)∧(a∨c).证由a a, b∧c b 得a∨(b∧c)a∨b由a a, b∧c c 得a∨(b∧c)a∨c从而得到a∨(b∧c)(a∨b)∧(a∨c)例13.4说明在格中分配不等式成立。
一般说来,格中的∨和∧运算并不是满足分配律的。
三．格作为代数系统的定义定理13.4设<S,*,>是具有两个二元运算的代数系统,若对于*和运算适合交换律、结合律、吸收律,则可以适当定义S中的偏序,使得<S,>构成一个格,且a,b∈S 有a∧b=a*b, a∨b=a b.证明省略.根据定理13.4,可以给出格的另一个等价定义。
定义13.3 设<S,*,>是代数系统,*和是二元运算,如果*和满足交换律,结合律和吸收律,则<S,*,>构成一个格。
读者可能会注意到,格中运算满足四条算律,还有一条幂等律(见定理13.1),但幂等律可以由吸收律推出,所以定义13.3中只须满足三条算律即可。
以后我们不再区别是偏序集定义的格,还是代数系统定义的格,而统称为格L.主要内容1． 偏序集构成格的条件：任意二元子集都有最大下界和最小上界。
2. 格的实例：正整数的因子格，幂集格，子群格。
3. 格的性质：对偶原理，格中算律（交换、结合、幂等、吸收），保序性，分配不等式。
4. 格作为代数系统的定义。
学习要求1. 能够判断给定偏序集是否构成格。
2. 能够确定一个命题的对偶命题。
3. 能够证明格中的等式和不等式。
4. 了解格作为代数系统的等价定义。
1. 判断下述偏序集是否构成格？如果不是说明理由。
（1） 可以构成格 不能构成格（2） 可以构成格 不能构成格（3） 可以构成格 不能构成格提示 参看定义13.1和例13.1，13.2。
答案只有第一个图不是格，因为最下面的两个元素没有最大下界。
2.求下述命题的对偶命题。
（1）(a∧b)∨b = b（2）b∨(c∧a)(b∨c)∧a提示参看定义13.2。
答案(1) (a∨b)∧b = b(2) b∧(c∨a) (b∧c)∨a3.证明题（1）证明题2（1）中的命题，即(a∧b)∨b=b（2）证明(a∧b)∨(c∧d)(a∨c)∧(b∨d)提示利用定理13.1，定理13.2，定理13.3。
答案证明：（1）(a∧b)∨b是a∧b与b的最小上界，根据最小上界的定义有(a∧b)∨b b。
又b是a∧b与b的上界，故有(a∧b)∨b b，由于偏序的反对称性，等式得证。
（2）a∧b a a∨c，a∧b b b∨d，所以(a∧b)(a∨c)∧(b∨d)，同理(c∧d)(a∨c)∧(b∨d)从而得到(a∧b)∨(c∧d)(a∨c)∧(b∨d)13.2 子格与格同态一、子格定义及其判别方法定义13.4设<L,∧,∨>是格,S是L的非空子集,若S关于L中的运算∧和∨仍构成格,则称S是L的子格。
例13.5设格L如图13.3所示。
令S1={a,e,f,g}，S2={a,b,e,g}则S1不是L的子格,S2是L的子格。
因为对于e和f,有e∧f=c,但c S1.图13.3二．格同态的定义及其性质1．格同态的定义定义13.5设L1和L2是格,f: L1→L2,若a,b∈L1有f(a∧b)=f(a)∧f(b), f(a∨b)=f(a)∨f(b)成立，则称f为格L1到L2的同态映射,简称格同态。
例13.6 (1)设L1={2n|n∈Z+}，L2={2n+1|n∈Z+}则L1和L2关于通常数的小于或等于关系构成格。
令f: L1→L2,f(x)=x-1不难验证f是L1到L2的同态映射,因为对任意的x,y∈L1有f(x∨y)=f(max(x,y))=max(x,y)-1f(x)∨f(y)=(x-1)∨(y-1)=max(x-1,y-1)=max(x,y)-1f(x∧y)=f(min(x,y))=min(x,y)-1f(x)∧f(y)=(x-1)∧(y-1)=min(x-1,y-1)=min(x,y)-1即f(x∨y)=f(x)∨f(y), f(x∧y)=f(x)∧f(y)成立。
(2) 如图13.4中的格L1,L2和L3，若定义图13.4f1: L1→L2f1(a)=f1(b)=f1(c)=a1,f1(d)=d1f2: L1→L3f2(a)=a2,f2(b)=b2,f2(c)=c2,f2(d)=d2则f1和f2都不是格同态，因为f1(b∨c)=f1(d)=d1f1(b)∨f1(c)=a1∨a1=a1f2(b∨c)=f2(d)=d2f2(b)∨f2(c)=b2∨c2=c2从而f1(b∨c)≠f1(b)∨f1(c)f2(b∨c)≠f2(b)∨f2(c)2. 格同态的性质定理13.5设f是格L1到L2的映射,(1)若f是格同态映射,则f是保序映射,即x,y∈L1,有x y f(x)f(y)(2)若f是双射,则f是格同态映射当且仅当x,y∈L1,有x y f(x)f(y)证(1)任取x,y∈L1,x y 由格的性质知x∨y=y.又由于f是格同态映射,必有f(y)=f(x∨y)=f(x)∨f(y)从而得到f(x)f(y).(2)充分性.只须证明f是L1到L2的同态映射即可。
任取x,y∈L1,令x∨y=z,由x z和y z知f(x)f(z), f(y)f(z)从而有f(x)∨f(y)f(z)=f(x∨y)另一方面,由f(x)∨f(y)∈L2和f的满射性可知,必存在u∈L1使得f(u)=f(x)∨f(y)因此有f(x)f(u), f(y)f(u). 由已知条件可得x u,y u. 从而推出x∨y u.再次使用已知条件得f(x∨y)f(u)=f(x)∨f(y).综合上述有f(x∨y)=f(x)∨f(y). 同理可证f(x∧y)=f(x)∧f(y).必要性.由(1)的结论必有x y f(x)f(y)反之,若f(x)f(y),由于f是同构映射,则f(x∨y)=f(x)∨f(y)=f(y)又由于f 是双射,必有x∨y=y.从而证明了x y.例13.7设L1=<S12,D>, L2=<S12,≤>是格,其中S12是12的所有正因子构成的集合,D 为整除关系,≤为通常数的小于或等于关系.令f:S12→S12,f(x)= x则f是双射,但f不是格L1到L2的同构映射.因为f(2)≤f(3),但2不整除3.根据定理13.5可知f不是同构映射。
三．格的直积类似于半群,群和环,也可以定义格的直积。
定义13.6设L1和L2是格,定义L1×L2上的运算∩,∪:<a1,b1>,<a2,b2>∈L1×L2<a1,b1>∩<a2,b2>=<a1∧a2,b1∧b2><a1,b1>∪<a2,b2>=<a1∨a2,b1∨b2>称<L1×L2,∩,∪>为格L1和L2的直积。