您的位置：360文档中心› (完整版)最短路径习题

(完整版)最短路径习题

合集下载

初中数学八年级上册课题学习_最短路径问题练习题含答案

初中数学八年级上册课题学习_最短路径问题练习题含答案

初中数学八年级上册课题学习最短路径问题练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________1. 如图，已知Rt△ABC中，∠B=90∘，AB=3，BC=4，D，E，F分别是边AB，BC，AC上的动点，则DE+EF+FD的最小值为（）A.4.8B.6C.10D.无法确定2. 如图，在矩形ABCD中，AB=6，AD=8，点P在矩形内部，且满足S PCD=1 4S长方形ABCD，则点P到A,B两点的距离之和PA+PB的最小值为( )A.8B.10C.14D.2√133. 如图，直线l表示石家庄的太平河，点P表示朱河村，点Q表示黄庄村，欲在太平河l 上修建一个水泵站（记为点M），分别向两村供水，现有如下四种修建水泵站供水管道的方案，图中实线表示修建的管道，则修建的管道最短的方案是（）A. B. C. D.4. 如图，直线l是一条河，P，Q是两个村庄．欲在l上的某处修建一个水泵站，向P，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是( )A. B.C. D.5. 如图①，在边长为4cm的正方形ABCD中，点P从点A出发，沿AB→BC的路径匀速运动，当点C停止，过点P作PQ//BD，PQ与边AD(或边CD)交于点Q，PQ的长度y(cm)与点P的运动时间x(s)的函数关系图象如图②所示，当点P运动2.5s时，PQ的长是（）cm．A.5√2B.√2C.4√2D.3√26. 如图，已知△ABC为等腰直角三角形，AC=BC=4，∠BCD=15∘，P为CD上的动点，则|PA−PB|的最大值是（）A.4B.5C.6D.87. 如图，一个实心圆柱高8cm，底面周长为30cm，一只蚂蚁在圆柱表面爬行，从点A爬到点B的最短路程是（）)cm C.√161cm D.2√241cmA.17cmB.(8+30π8. 已知：如图，四边形ABCD中，∠ABC=60∘，AB=BC=2，对角线BD平分∠ABC，E是BC的中点，P是对角线BD上的一个动点，则PE+PC的最小值为（）A.√3B.3C.2D.√229. 如图，在长方体中，AB=5，BC=4，CC1=3，动点从A1出发沿长方体的表面运动到达C点，则动点的最短距离是()A.√90B.√80C.√78D.√7410. 如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM周长的最小值为( )A.6B.8C.10D.1211. 一个圆桶儿，底面直径为16cm，高为18cm，有一只小虫从底部点A处爬到上底B 处，则小虫所爬的最短路径长是(π取3)________．AC，AB=8，E是AB上12. 如图，在Rt△ABC中，∠CAB=30∘，∠C=90∘．AD=14任意一点，F是AC上任意一点，则折线DEFB的最短长度为________．13. 小明在广场上散步，先向东走12m后，再向北又走了9m，现要以最短距离________m回到原地．14. 如图，菱形ABCD中，∠BAD=45∘，E，F，P分别是AB，BC，AC上的动点，PE+PF的最小值等于2，则AB=________．15. 对于平面直角坐标系中的线段MN及点Q，给出如下定义：若点Q满足QM=QN，则称点Q为线段MN的“对称点”；当QM=QN=MN时，称点Q为线段MN的“完美对称点”．（1）如图1，点A坐标为(4,0)，有点Q1(0,4),Q2(2,−4)，Q3(1,√3)，则线段OA的“对称点”是________．（填“Q1”"Q2"或 "Q3"）(2)如图2，已知Q(2,2√3)为线段OA的“完美对称点”，D为线段OQ的中点，B为线段OA 的一个“对称点”，则BO+BD的最小值为________．16. 如图，在△ABC中，AB=3，AC=4，EF垂直平分BC，点P为直线EF上一动点，则△ABP周长的最小值是________.17. 圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程（π取3）是________．18. 如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF 交AC于点F，若D为BC边上的动点，M为线段EF上一动点，则BM+DM最小值为________．19. 如图，已知蚂蚁沿着长为2的正方体表面从点A出发，经过3个侧面爬到点B，如果它运动的路径是最短的，则此经过3个侧面的最短路径长为________．20. 如图，在平面直角坐标系xOy中，A(1,0),B(3,0)，点P为y轴正半轴上的一个动点，以线段PA为边在PA的右上方作等边△APQ，连接QB，在点P运动的过程中，线段QB长度的最小值为________.21. 如图，若∠AOB=30∘，点P在∠AOB内，且OP=2cm，分别在OA、OB上找一点E，F使△PEF的周长最小，并求△PEF的周长最小值．22. 如图，有一个圆柱高为6cm，底面半径为2cm，圆柱下底面的A点有一只蚂蚁，它想吃到上底边与点A相对B处的食物，需要爬行的最短路程是多少(π取3)？23. 在直线m上找一点C，使CA+CB的值最小．24. 如图，一只小蚂蚁要从A点沿长方体木块表面爬到B点处吃蜜糖．已知长方体木块的长、宽、高分别为10cm、8cm、6cm，试计算小蚂蚁爬行的最短距离．25. 有一圆柱体高为8cm，底面圆的半径为2cm，如图所示，在AA1上的点Q处有一只蜘蛛，QA1=3cm，在BB1上的点P处有一只苍蝇，PB=2cm．（1）蜘蛛要从点Q处沿圆柱体表面去吃点P处的苍蝇，请在图中大致画出蜘蛛爬行的最短路径；（2）求蜘蛛爬行的最短路径长．(π取3)26. 如图，一正方形的棱长为2，一只蚂蚁在顶点A处，在顶点G处有一米粒．（1）问蚂蚁吃到这粒米需要爬行的最短距离是多少？（2）在蚂蚁刚要出发时，突然一阵大风将米粒吹到了GF的中点M处，问蚂蚁要吃到这粒米的最短距离又是多少？x2+1具有如下性质：该抛物线上任意一点到定点F(0, 2)的距离27. 已知抛物线y=14x2+1上一个与到x轴的距离始终相等，如图，点M的坐标为(√3,3)，P是抛物线y=14动点．(1)若PF=5，求点P的坐标；(2)求△PMF周长的最小值.28. 同学们在灯管上缠绕5cm彩带．已知灯管长100cm，灯管截面圆的周长是15cm，彩带至少应剪多长？29. 如图所示，P、Q是△ABC中AB、AC边上的点，你能在BC边上确定一点R，使△PQR的周长最小吗？30. 如图，Q为马厩甲，AB为草地边缘（下方为草地），CD为一河流，放牧人欲从马厩甲牵马先去草地M处让马吃草，然后到河边N处饮水，最后回到马厩乙P．请你帮他确定一条最佳行走路线QM→MN→NP，使其所走路程最短.31. 判断说理：元旦联欢会上，八年级(1)班的同学们在礼堂四周摆了一圈长条桌子，其中北边条桌上摆满了苹果，东边条桌上摆满了香蕉，礼堂中间B处放了一把椅子，游戏规则是这样的：甲、乙二人从A处（如图）同时出发，先去拿苹果再去拿香蕉，然后回到B处，谁先坐到椅子上谁赢．张晓和李岚比赛，比赛一开始，只见张晓直奔东北两张条桌的交点处，左手抓苹果，右手拿香蕉，回头直奔B处，可是还未跑到B处，只见李岚已经手捧苹果和香蕉稳稳地坐在B处的椅子上了．如果李岚不比张晓跑得快，张晓若想获胜有没有其他的捷径？若有，请说明你的捷径，若没有，请说明理由．32. 如图，矩形ABCD，AB=6cm，AD=12cm，P是AB上的动点，Q是AD上的动点．P以1cm/s的速度从B到A，Q以2cm/s的速度从A到D，P到A（或Q到D）时停止运动．求PQ+QC最小值．33. 如图，A，B两村在一条小河的同一侧，要在河边建一水厂向两村供水．(1)若要使自来水厂到两村的距离相等，厂址应选在哪个位置？(2)若要使自来水厂到两村的输水管用料最省，厂址应选在哪个位置？请将上述两种情况下的自来水厂厂址标出，并保留作图痕迹．34. 如图，在四边形ABCD中，P为BC的中点，试在CD边上找一点Q，使△APQ的周长最小．35.作图题：现要在形如△ABC的地面范围内建一中心医院，使医院到A，B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．（要求：保留作图痕迹，并用适当的文字说明作图方法）36. 如图，有一只蚂蚁从一个圆柱体的A点沿着侧面绕圆柱至少一圈爬到B点，已知圆柱的底面半径为1.5cm，高为12cm，则蚂蚁所走过的最短路径是多少？(π取3)37. 在一条笔直公路上分布A，B，C，D，E五个工厂（各相邻工厂之间的距离均不相等），为方便这些工厂的员工，现要在公路上设一个汽车站，使各工厂到汽车站的距离之和最小．【简化分析】(1)假若由三个工厂A，B，C时，汽车站的位置有五种情形：①A厂门口，②AB之间，③B厂门口，④BC之间，⑤C厂门口.【分类讨论】①当车站设在A工厂门口时，则A厂到汽车站的距离为0，B厂到汽车站的距离为AB，C厂到汽车站的距离为AB＋BC，所以各工厂到车站的距离之和为________②当车站设在A，B两工厂之间的P点时，则A厂到汽车站的距离为AP，B厂到汽车站的距离为BP，C厂到汽车站的距离为BP+BC，所以各工厂到车站的距离之和为_________③当车站设在B工厂门口，则各工厂到汽车站的距离之和为_________④当车站设在B，C两工厂之间的Q点时，则各工厂到汽车站的距离之和为_________⑤当车站设在C工厂门口，则各工厂到汽车站的距离之和为________【总结归纳】综上可知：汽车站设在________时，各工厂到汽车站的距离之和最小.【问题解决】 (2)当有A，B，C，D，E五个工厂时，汽车站设在哪里，才能使各工厂到汽车站的距离之和最小？请说明理由.38. 如图，A,B,C,D为四家超市，其中超市D距A,B,C三家超市的路程分别为25km，10km，5km.现计划在A,D之间的道路上建一个配货中心P，为避免交通拥堵，配货中心与超市之间的距离不少于2km.假设一辆货车每天从P出发为这四家超市送货各次，由于货车每次仅能给一家超市送货，因此每次送货后均要返回配货中心P，重新装货后再前往其他超市.设P到A的路程为xkm，这辆货车每天行驶的路程为ykm.(1)求y与x之间的函数关系式，并写出自变量x的取值范围；(2)直接写出配货中心P建在什么位置，这辆货车每天行驶的路程最短？最短路程是多少?39. 如图，一块砖宽AN=5cm，长ND=10cm，CD上的点B距地面的高BD=8cm，地面上A处的一只蚂蚁到B处吃食，要爬行的最短路线是多少？40. 下图，要在燃气管道L上修建一个泵站，分别向A、B两镇供气．泵站修在管道的什么地方，可使所用的输气管线最短？（不写做法，保留作图痕迹）参考答案与试题解析初中数学八年级上册课题学习最短路径问题练习题含答案一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】A【考点】轴对称——最短路线问题【解析】此题暂无解析【解答】解：如图作F关于直线AB的对称点M，作F关于直线BC的对称点N，连接BM，BN，BF，EF，EN，DE，DM．∵∠MBA=∠FBA，∠CBN=∠CBF，∠ABF+∠CBF=90∘，∴∠MBF+∠FBN=180∘，∴M、B、N共线，∵DF+DE+EF=DM+DE+EN，∵DM+DE+EN≥MN，∴当D、E、M、N共线时，且BF⊥AC时，DE+EF+FD的值最小，最小值=2BF，∵BF⊥AC，∴12⋅AC⋅BF=12⋅AB⋅AC，∴BF=AB⋅BCAC =125=2.4，∴DE+EF+FD的最小值为4.8．故选A．2.【答案】B【考点】路径最短问题【解析】此题暂无解析【解答】解：∵S PCD=14S长方形ABCD，设△PCD的CD边上的高为ℎ∴12CD⋅ℎ=14CD⋅AD，又AD=8，∴ℎ=4,∴动点P在与CD平行且与CD的距离为4的直线l上，如图，作D关于直线l的对称点A，连接AC，则AC的长就是所求的最短距离.在Rt△ADC中，CD=AB=6，AD=8∴AC=√AD2+CD2解得AC=10.故选B.3.【答案】B【考点】轴对称——最短路线问题【解析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．【解答】解：作点P关于直线l的对称点P′，连结QP′交直线l于M，根据两点之间，线段最短，可知选项B修建的管道，则所需管道最短．故选B.4.【答案】D【考点】轴对称——最短路线问题【解析】利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．【解答】解：作点P关于直线l的对称点P′，连结QP′交直线l于M．根据两点之间，线段最短，可知选项D铺设的管道，所需管道最短．故选D．5.【答案】A【考点】路径最短问题【解析】此题暂无解析【解答】此题暂无解答6.【答案】A【考点】轴对称——最短路线问题【解析】作A关于CD的对称点A′，连接A′B交CD于P，则点P就是使|PA−PB|的值最大的点，|PA−PB|=A′B，连接A′C，根据等腰直角三角形的性质得到∠CAB=∠ABC=45∘，∠ACB=90∘，根据三角形的内角和得到∠ACD=75∘，于是得到∠CAA′=15∘，根据轴对称的性质得到A′C=BC，∠CA′A=∠CAA′=15∘，推出△A′BC是腰三角形，根据等边三角形的性质即可得到结论．【解答】解：作A关于CD的对称点A′，连接A′B交CD于P，则点P就是使|PA−PB|的值最大的点，|PA−PB|=A′B，连接A′C，∵△ABC为等腰直角三角形，AC=BC=4，∴∠CAB=∠ABC=45∘，∠ACB=90∘，∵∠BCD=15∘，∴∠ACD=75∘，∴∠CAA′=15∘，∵AC=A′C，∴A′C=BC，∠CA′A=∠CAA′=15∘，∴∠ACA′=150∘，∵∠ACB=90∘，∴∠A′CB=60∘，∴△A′BC是等腰三角形，∴A′B=BC=4．故选A．7.【答案】A【考点】平面展开-最短路径问题【解析】沿过A点和过B点的母线剪开，展成平面，连接AB，则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程，求出AC和BC的长，根据勾股定理求出斜边AB即可．【解答】如图所示：沿过A点和过B点的母线剪开，展成平面，连接AB，则AB的长是蚂蚁在圆柱表面从A点爬到B点的最短路程．×30＝15(cm)，∠C＝90∘，BC＝8cm，在Rt△ABC中，∵AC=12∴AB=√AC2+BC2=17(cm)．故选：A．8.【答案】A【考点】轴对称——最短路线问题【解析】根据菱形的判定，得出平行四边形ABCD为菱形，作出E关于BD的对称点E′，转化为线段长度的问题，再根据等边三角形的性质判断出△BCE′为直角三角形，利用勾股定理即可求出CE′的长．【解答】解：∵BA=BC=2，∴平行四边形ABCD为菱形．∴∠ABD=∠CBD，∴BD是∠ABC的平分线．作E关BD的对称点E′，连接CE′，PE，则PE=PE′，此时，PE+PC=PE′+PC=CE′，CE′即为PE+PC的最小值．∵∠ABC=60∘，又∵BE′=BE，∴△E′BE为正三角形，EE′=1，∠ABE=60∘，故EE′=EC，∠EE′C=∠ECE′=30∘，∴∠BE′C=60∘+30∘=90∘，在Rt△BCE′中，CE′=√22−12=√3．故选：A．9.【答案】D【考点】平面展开-最短路径问题【解析】连接AC1，求出AC1的长即可，分为三种情况：画出图形，根据勾股定理求出每种情况时AC1的长，再找出最短的即可．【解答】解：展开成平面后，连接AC1，则AC1的长就是绳子最短时的长度，分为三种情况：如图1，AB=5，BC=4，CC1=BB1=3，在Rt△ABC′中，由勾股定理得：AC1=√AB2+(BB1+B1C1)2=√25+49=√74；如图2，AC=5+4=9，CC1=3，在Rt△ACC1中，由勾股定理得：AC1=√AC2+CC12=√81+9=√90>√74，如图3，同法可求AC1=√(3+5)2+42=√80>√74，即绳子最短时的长度是√74，故选D．10.【答案】C【考点】轴对称——最短路线问题【解析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再再根据EF是线段AC的垂直平分线可知，点C关于直线EF 的对称点为点A，故AD的长为CM+MD的最小值，由此即可得出结论．【解答】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC=12BC⋅AD=12×4×AD＝16，解得AD=8，∵EF是线段AC的垂直平分线，∴点C关于直线EF的对称点为点A，∴AD的长为CM+MD的最小值，∴△CDM的周长最短=(CM+MD)+CD=AD+1BC=8+1×4=8+2=10．故选C.二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】30cm【考点】平面展开-最短路径问题【解析】先将圆柱的侧面展开为一矩形，而矩形的长就是地面周长的一半，高就是圆柱的高，再根据勾股定理就可以求出其值．【解答】解：展开圆柱的侧面如图，根据两点之间线段最短就可以得知AB最短．由题意，得AC =3×16÷2=24，在Rt △ABC 中，由勾股定理，得AB =√AC 2+BC 2=√242+182=30cm ．故答案为：30cm ．12.【答案】 √67【考点】轴对称——最短路线问题【解析】利用轴对称求最短路径的方法，重新构造直角三角形，进而利用勾股定理求出即可．【解答】解：作D 点关于AB 的对称点D′，B 点关于AC 的对称点B′，连接D′B′分别交AB 于点E ，AC 于点F ，作B′R ⊥AB ，过点D′作D′W ⊥B′R 于点W ，∵ ∠CAB =30∘，∠C =90∘．AD =14AC ，AB =8， ∴ BC =4，AC =4√3，则AD =√3，BB′=8，B′R =4√3，∴ DT =12AD =√32，AT =√AD 2−DT 2=32，BR =4， ∴ RW =√32，D′W =8−32−4=52， ∴ B′W =9√32，B′D′=√D′W 2+B′W 2=(52)(9√32)=√67．故答案为：√67．13.【答案】15【考点】勾股定理路径最短问题【解析】此题暂无解析【解答】解：设小明散步原地为O，则先向东走12m到达A点后，再向北又走了9m到达B点，则要回到原地，最短行走距离为OB的距离，根据勾股定理可得OB=√122+92=15m.故答案为：15.14.【答案】2√2【考点】轴对称——最短路线问题【解析】先找出点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，根据轴对称确定最短路线问题以及垂线段最短可知E′F为PE+PF的最小值的最小值，过点B作BG⊥AD 于G，解直角三角形求出AB即可．【解答】解：如图，点E关于AC的对称点E′，过点E′作E′F⊥BC于F，交AC于P，即E′F为PE+PF的最小值.过点B作BG⊥AD于G，易知BG=FE′=2，在Rt△ABG中，∠BAG=45∘，∴AB=BG÷sin45∘=2√2.故答案为：2√2.15.【答案】Q22．【考点】图形间的距离定义新图形路径最短问题坐标与图形性质【解析】（1）找到OA的垂直平分线即可找到对应的点．（2）利用“完美对称点”的特征，作出图象，从而确定最小值．【解答】解：(1)当点Q满足QO=QA时，Q为OA的“对称点”，∴ Q在线段OA的垂直平分线上，∵ A(4,0)，∴ 线段OA的垂直平分线是直线x=2，∵Q2(2,−4)，∴ 线段OA的“对称点”是Q2.故答案为：Q2．∵ Q(2,2√3)为线段OA的“完美对称点”，∴ QO=OA=QA，∴ △QOA是等边三角形，过点Q作QH⊥OA于H，则直线QH为线段AO的垂直平分线，如图：∵ B为线段OA的一个“对称点”，∴ BO=BA，∴ B是直线QH上的一点，显然，当Q、B重合时，BQ+BD有最小值，此时BQ+BD=BD，∵ Q(2,2√3)，∴ OQ=√22+(2√3)2=4，∵ D为线段OQ的中点，∴ DQ=12OQ=12×4=2，∴ BD=2，∴ BQ+BD的最小值为2. 故答案为：2.16.【答案】7【考点】轴对称——最短路线问题根据题意知点B关于直线EF的对称点为点C，故当点P与点D重合时，AP+BP的最小值，求出AC长度即可得到结论．【解答】解：∵EF垂直平分BC，∴B，C关于EF对称.设AC交EF于点D，∴当P和D重合时，AP+BP的值最小，最小值等于AC的长，∴△ABP周长的最小值是4+3=7.故答案为：7.17.【答案】【考点】路径最短问题【解析】此题暂无解析【解答】此题暂无解答18.【答案】6cm【考点】轴对称——最短路线问题【解析】连接AD，由于△ABC是等腰三角形，点D是BC边的中点，故AD⊥BC，再根据三角形的面积公式求出AD的长，再根据EF是线段AB的垂直平分线可知，点B关于直线EF的对称点为点A，故AD的长为BM+MD的最小值，由此即可得出结论．【解答】解：连接AD，∵△ABC是等腰三角形，点D是BC边的中点，∴AD⊥BC，∴S△ABC=12BC⋅AD=12×4×AD=12，解得AD=6cm，∵EF是线段AB的垂直平分线，∴点B关于直线EF的对称点为点A，∴AD的长为BM+MD的最小值，∴BM+DM最小值为6cm.故答案为：6cm．19.2√17【考点】平面展开-最短路径问题【解析】将正方体展开，根据两点之间线段最短，构造出直角三角形，进而求出最短路径的长．【解答】解：将正方体展开，右边与后面的正方形与前面正方形放在一个面上，展开图如图所示，此时AB最短，AB=√82+22=2√17，故答案为：2√17．20.【答案】2【考点】勾股定理路径最短问题【解析】【解答】解：当PQ//x轴时QB长度最小，设Q(m，n)，P(0，n)，△APQ为等边三角形，∴1+n2=(m−1)2+n2，解得m=2或m=0（舍），∴PQ=PA=m=2，∴1+n2=4，解得n=√3，故BQ=√3+1=2.故答案为：2.三、解答题（本题共计 20 小题，每题 10 分，共计200分）21.【答案】解：作点P关于OA对称的点P1，作点P关于OB对称的点P2，连接P1P2，与OA交于点E，与OB交于点F，此时△PEF的周长最小．从图上可看出△PEF的周长就是P1P2的长，∵∠AOB=30∘，∴∠P1OP2=60∘．∵OP1=OP2，∴△OP1P2是等边三角形．∴P1P2=OP1=OP=2cm．∴△PEF周长的最小值是2cm．【考点】轴对称——最短路线问题【解析】作点P关于OA对称的点P1，作点P关于OB对称的点P2，连接P1P2，与OA交于点E，与OB交于点F，此时△PEF的周长最小，然后根据∠AOB=30∘，点P在∠AOB内，点E、F分别在边OA、OB上移动，如果OP=2cm，可求出值．【解答】解：作点P关于OA对称的点P1，作点P关于OB对称的点P2，连接P1P2，与OA交于点E，与OB交于点F，此时△PEF的周长最小．从图上可看出△PEF的周长就是P1P2的长，∵∠AOB=30∘，∴∠P1OP2=60∘．∵OP1=OP2，∴△OP1P2是等边三角形．∴P1P2=OP1=OP=2cm．∴△PEF周长的最小值是2cm．22.【答案】需要爬行的最短路程是6√2cm．【考点】平面展开-最短路径问题【解析】要想求得最短路程，首先利用BC长等于底面圆的一半，即可求出BC的长．根据两点之间，线段最短求出蚂蚁爬行的最短路程．【解答】解：利用展开图，根据题意可得：BC=2π≈6cm，AC=6cm，AB=√BC2+AC2=6√2(cm)，23.【答案】解：如图，点C即为所求．【考点】轴对称——最短路线问题【解析】作点A关于直线m的对称点A′，连接A′B交直线m于点C，则CA+CB的值最小．【解答】解：如图，点C即为所求．24.【答案】解：展开后有三种不同的情况如图，如图1，AB=√(10+8)2+62=√360，如图2，AB=√102+(6+8)2=√296，如图3，AB=√82+(10+6)2=√320，∵√296<√320<√360，∴小蚂蚁爬行的最短路线为√296cm．【考点】平面展开-最短路径问题【解析】根据题意画出不同数值的三种情况，根据勾股定理求出每种情况的AB，再比较即可．【解答】解：展开后有三种不同的情况如图，如图1，AB=√(10+8)2+62=√360，如图2，AB=√102+(6+8)2=√296，如图3，AB=√82+(10+6)2=√320，∵√296<√320<√360，∴小蚂蚁爬行的最短路线为√296cm．25.【答案】蜘蛛爬行的最短路径长是3√5cm．【考点】平面展开-最短路径问题【解析】（1）划出符合条件的QP即可；（2）展开后构造直角三角形，根据勾股定理求出线段QP的长即可．【解答】解：（1）如图：（2）如图，沿AA1剪开，过Q作QM⊥BB1于M，连接QP，则PM=8−3−2=3(cm)，QM=A1B1=1×2×π×2=6(cm)，2在Rt△QMP中，由勾股定理得：PQ=√QM2+PM2=√32+62=3√5(cm)，答：蜘蛛爬行的最短路径长是3√5cm．26.【答案】解：（1）如图所示：∵正方形的棱长为2，∴AC=2AB=4，CG=2，AG=√AC2+CG2=√16+4=√20=2√5，∴蚂蚁吃到这粒米需要爬行的最短距离是2√5；（2）如图所示：由题意可知：AN=AB+BN=3，MN=2，∴AM=√AN2+MN2=√32+22=√13，∴蚂蚁要吃到这粒米的最短距离是√13．【考点】平面展开-最短路径问题【解析】（1）根据图形是立方体得出最短路径只有一种情况，利用勾股定理求出即可．（2）把此正方体的点M所在的面展开，然后在平面内，利用勾股定理求点A和点M间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于2长，另一条直角边长等于3，利用勾股定理可求得．【解答】解：（1）如图所示：∵正方形的棱长为2，∴AC=2AB=4，CG=2，AG=√AC2+CG2=√16+4=√20=2√5，∴蚂蚁吃到这粒米需要爬行的最短距离是2√5；（2）如图所示：由题意可知：AN=AB+BN=3，MN=2，∴AM=√AN2+MN2=√32+22=√13，∴蚂蚁要吃到这粒米的最短距离是√13．27.【答案】解：(1)由题意可知，当PF=5时，P到x轴的距离为5，∴P(x,5)，将P(x,5)代入y=14x2+1，得5=14x2+1，解得，x=±4，∴点P的坐标为(4,5)或(−4,5).(2)过点M作ME⊥x轴于点E，ME与抛物线交于点P′，如图所示：∵点P′在抛物线上，∴P′F=P′E．又∵点到直线之间垂线段最短，MF=√(√3−0)2+(3−2)2=2，∴当点P运动到点P′时，△PMF周长取最小值，最小值为ME+MF=3+2=5．【考点】路径最短问题二次函数的性质二次函数图象上点的坐标特征点到直线的距离垂线段最短【解析】过点M作ME⊥x轴于点E，ME与抛物线交于点P′，由点P′在抛物线上可得出P′F＝P′E，结合点到直线之间垂线段最短及MF为定值，即可得出当点P运动到点P′时，△PMF周长取最小值，【解答】解：(1)由题意可知，当PF=5时，P到x轴的距离为5，∴P(x,5)，将P(x,5)代入y=14x2+1，得5=14x2+1，解得，x=±4，∴点P的坐标为(4,5)或(−4,5).(2)过点M作ME⊥x轴于点E，ME与抛物线交于点P′，如图所示：∵点P′在抛物线上，∴P′F=P′E．又∵点到直线之间垂线段最短，MF=√(√3−0)2+(3−2)2=2，∴当点P运动到点P′时，△PMF周长取最小值，最小值为ME+MF=3+2=5．28.【答案】彩带至少应剪125cm．【考点】平面展开-最短路径问题【解析】将灯管上缠的彩带展开，得到直角三角形，用勾股定理解答即可．【解答】解：如图，展开后可得AB=15×5=75cm，BC=100cm，AC=√AB2+BC2=√752+1002=125cm．29.【答案】解：如图所示：作P点关于BC的对称点P′，连接P′Q，与BC交于点R，R点即为所求．【考点】轴对称——最短路线问题【解析】作P点关于BC的对称点P′，连接P′Q，与BC交于点R，由两点之间线段最短可知△PQR 周长最小即为所求点．【解答】解：如图所示：作P点关于BC的对称点P′，连接P′Q，与BC交于点R，R点即为所求．30.【答案】解：使其所走路程最短的最佳行走路线QM→MN→NP如图：【考点】路径最短问题【解析】此题暂无解析【解答】解：使其所走路程最短的最佳行走路线QM→MN→NP如图：31.【答案】解：如图，假设北边和东边条桌各为一个平面镜，光线经过两次反射到达B点．因此，分别以北条桌和东条桌为对称轴，找到A，B的对称点A′，B′，连接A′B′，交两长条桌于C，D两点，则折线ACDB就是捷径．【考点】轴对称——最短路线问题【解析】利用轴对称得出找到A，B的对称点A′，B′，连接A′B′，交两长条桌于C，D两点，则折线ACDB就是捷径．【解答】解：如图，假设北边和东边条桌各为一个平面镜，光线经过两次反射到达B点．因此，分别以北条桌和东条桌为对称轴，找到A，B的对称点A′，B′，连接A′B′，交两长条桌于C，D两点，则折线ACDB就是捷径．32.【答案】解：设t秒后PQ+QC最小，取点P关于AD的对称点P′，连接CP′与AD相交，由轴对称确定最短路线问题，交点即为所求的使PQ+QC最小的点Q的位置，∵AB=6cm，AD=12cm，∴AP=AP′=6−t，AQ=2t，QD=12−2t，∵AB // CD，∴△AP′Q∽△DCQ，∴AP′CD =AQQD，即6−t6=2t12−2t，整理得，t2−18t+36=0，解得t1=9−3√5，t2=9+3√5（舍去），所以，BP′=AB+AP′=6+(6−9+3√5)=3+3√5，所以，P′C=√BP′2+BC2=√(3+3√5)2+122=3√22+2√5，即PQ+QC最小值是3√22+2√5．【考点】轴对称——最短路线问题【解析】设t秒后PQ+QC最小，取点P关于AD的对称点P′，连接CP′与AD相交，根据轴对称确定最短路线问题，交点即为所求的使PQ+QC最小的点Q的位置，表示AP′、AQ、QD，然后根据△AP′Q和△DCQ相似，利用相似三角形对应边成比例列式求出t，再表示出BP′，然后利用勾股定理列式计算即可得解．【解答】解：设t秒后PQ+QC最小，取点P关于AD的对称点P′，连接CP′与AD相交，由轴对称确定最短路线问题，交点即为所求的使PQ+QC最小的点Q的位置，∵AB=6cm，AD=12cm，∴AP=AP′=6−t，AQ=2t，QD=12−2t，∵AB // CD，∴△AP′Q∽△DCQ，∴AP′CD =AQQD，即6−t6=2t12−2t，整理得，t2−18t+36=0，解得t1=9−3√5，t2=9+3√5（舍去），所以，BP′=AB+AP′=6+(6−9+3√5)=3+3√5，所以，P′C=√BP′2+BC2=√(3+3√5)2+122=3√22+2√5，即PQ+QC最小值是3√22+2√5．33.【答案】解：(1)根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，作出AB的中垂线与河岸交于点P，则点P满足到AB的距离相等．(2)作出点A关于河岸的对称点C，连接CB，交于河岸于点P，连接AP，则点P能满足AP+PB最小，理由：AP=PC，三角形的任意两边之和大于第三边，当点P在CB的连线上时，CP+ BP是最小的．路径最短问题作图—应用与设计作图线段垂直平分线的性质【解析】根据中垂线和轴对称及三角形的三边关系求解．【解答】解：(1)根据中垂线的性质：中垂线上的点到线段两个端点的距离相等，作出AB的中垂线与河岸交于点P，则点P满足到AB的距离相等．(2)作出点A关于河岸的对称点C，连接CB，交于河岸于点P，连接AP，则点P能满足AP+PB最小，理由：AP=PC，三角形的任意两边之和大于第三边，当点P在CB的连线上时，CP+ BP是最小的．34.【答案】解：如图所示，点Q即为所求点．【考点】轴对称——最短路线问题作PH⊥CD于点H，延长PH到点P′，使P′H=PH，连接AP′交CD于点Q，连接PQ，则D点Q就是△APQ的周长最小的点．【解答】解：如图所示，点Q即为所求点．35.【答案】【考点】路径最短问题【解析】此题暂无解析【解答】此题暂无解答36.【答案】解：如图所示，∵圆柱的底面半径为1.5cm，高为12cm，∴AC=2π×1.5≈9cm，∴AB=√AC2+BC2=√92+122=15(cm)．答：蚂蚁所走过的最短路径是15cm．【考点】平面展开-最短路径问题【解析】根据题意画出圆柱的侧面展开图，再利用勾股定理求解即可．【解答】解：如图所示，。

最短路径问题练习题【优质】

最短路径问题练习题【优质】

最短路径问题Description:平面上有n个点（n＜＝100），每个点的坐标均在-10000到10000之间．其中的一些点之间有连线．若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离．现在的任务是找出从一点到另一点之间的最短路径．Input：共n+m+3行第一行为整数n．第２行到第n＋行，每行两个整数x和y，描述了一个点的坐标（以一个空格分开）第n＋２行为一个整数m，表示图中连线的个数．以后的m行，每行描述一条连线，由两个整数i和j组成，表示第i个点和第j个点之间有连线．最后一行；两个整数s和t，分别表示源点和目标点．Output:仅一行，一个实数（保留两位小数），表示从s到t的最短路径长度Sample Input50 02 02 20 23 151 21 31 42 53 51 5Sample Output:3.41最小花费【问题描述】:在n个人中，某些人的银行账号之间可以互相转账。

这些人之间转账的手续费各不相同。

给定这些人之间转账时需要从转账金额里扣除百分之几的手续费，请问A 最少需要多少钱使得转账后B收到100元。

【输入数据】:第一行输入两个正整数n,m，分别表示总人数和可以互相转账的人的对数。

以下m行每行输入三个正整数x,y,z，表示标号为x的人和标号为y的人之间互相转账需要扣除z%的手续费 (z<100)。

最后一行输入两个正整数A,B。

数据保证A与B之间可以直接或间接地转账。

【输出数据】:输出A使得B到账100元最少需要的总费用。

精确到小数点后8位。

【输入样例】:3 31 2 12 3 21 3 31 3【输出样例】:103.07153164【数据规模】: 1<=n<=2000公园漫步(park.pas)【问题描述】小M 和小Z 饭后在公园散步，走着走着小Z 忽然想起来家中的水龙头没有关，于是他们要在最快的时间内走出公园赶到家中。

最短路径经典练习题

最短路径经典练习题

最短路径经典练习题一、基础理论题1. 请简述迪杰斯特拉（Dijkstra）算法的基本原理。

2. 什么是贝尔曼福特（BellmanFord）算法？它适用于哪些类型的图？3. 请解释A搜索算法中启发式函数的作用。

4. 如何判断一个图中是否存在负权环？5. 简述弗洛伊德（Floyd）算法的基本步骤。

二、单选题A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 弗洛伊德算法D. A搜索算法A. 初始化距离表B. 选择当前距离最小的顶点C. 更新相邻顶点的距离D. 重复步骤B和C，直到所有顶点都被访问A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 弗洛伊德算法D. A搜索算法A. 启发式函数B. 起始节点C. 目标节点D. 图的规模三、多选题A. 迪杰斯特拉算法B. 贝尔曼福特算法C. 深度优先搜索算法D. 广度优先搜索算法A. 初始化距离矩阵B. 更新距离矩阵C. 查找负权环D. 输出最短路径A. 图的存储结构B. 顶点的数量C. 边的数量D. 起始顶点四、计算题A (3)>B (2)> D\ | ^ \ | | \(2)\ | (1)/C \|(4)A (1)>B (2)> D\ ^ |\(2)\ | (3)/C \ |(1)A (2)>B (3)> D\ | ^\(3)\ | (1)/C \ |(2)五、应用题1. 假设你是一名地图软件的开发者，请简述如何利用最短路径算法为用户提供导航服务。

2. 在一个网络游戏中，玩家需要从起点到达终点，途中会遇到各种障碍。

请设计一种算法，帮助玩家找到最佳路径。

六、判断题1. 迪杰斯特拉算法只能用于无向图的最短路径问题。

（）2. 贝尔曼福特算法可以检测图中是否存在负权环。

（）3. 在A搜索算法中，如果启发式函数h(n)始终为0，则算法退化为Dijkstra算法。

（）4. 弗洛伊德算法的时间复杂度与图中顶点的数量无关。

（）七、填空题1. 迪杰斯特拉算法中，用来存储顶点到源点最短距离的数组称为______。

(word完整版)初二数学最短路径问题知识归纳+练习,推荐文档

(word完整版)初二数学最短路径问题知识归纳+练习,推荐文档

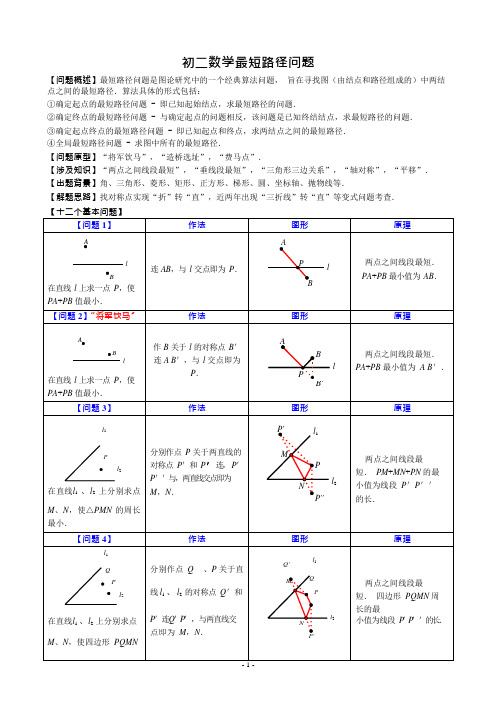
初二数学最短路径问题【问题概述】最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径．算法具体的形式包括：①确定起点的最短路径问题 - 即已知起始结点，求最短路径的问题．②确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题．③确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径．④全局最短路径问题 - 求图中所有的最短路径．【问题原型】“将军饮马”，“造桥选址”，“费马点”．【涉及知识】“两点之间线段最短”，“垂线段最短”，“三角形三边关系”，“轴对称”，“平移”．【出题背景】角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等．【解题思路】找对称点实现“折”转“直”，近两年出现“三折线”转“直”等变式问题考查．【问题1】作法图形原理AlB在直线l 上求一点P，使PA+PB 值最小．连AB，与l 交点即为P．AP lB两点之间线段最短．PA+PB 最小值为AB．【问题2】“将军饮马”作法图形原理ABl在直线l 上求一点P，使PA+PB 值最小．作B 关于l 的对称点B＇连A B＇，与l 交点即为P．ABlP两点之间线段最短．PA+PB 最小值为A B＇．B'【问题3】作法图形原理l1Pl2在直线l1、l2上分别求点M、N，使△PMN 的周长最小．分别作点P 关于两直线的对称点P＇和P＇连，P＇P＇＇与，两直线交点即为M，N．P' l1MPNl2P''两点之间线段最短．PM+MN+PN 的最小值为线段P＇P＇＇的长．【问题4】作法图形原理l1QPl2在直线l1、l2上分别求点M、N，使四边形PQMN 分别作点Q 、P 关于直线l1、l2的对称点Q＇和Q'l1M QP两点之间线段最短．四边形PQMN 周长的最P＇连Q＇P＇，与两直线交l2N 小值为线段P＇P＇＇的长．点即为M，N．P'PE3在直线 l 上求一点 P ，使 直线 l 的交点即为 P ．端点的距离相等．PA - PB ＝0．PA - PB 的值最小．【问题 10】作法图形原理ABl在直线 l 上求一点 P ，使PA - PB 的值最大．作直线 AB ，与直线 l 的交点即为 P ．ABPl三角形任意两边之差小于第三边． PA - PB ≤AB ．PA - PB 的最大值＝AB ．【问题 11】作法图形原理AlB在直线 l 上求一点 P ，使PA - PB 的值最大．三角形任意两边之差小于A第三作 B 关于 l 的对称点 B ＇ 作直线 A B ＇，与 l 交点B'Pl边． PA - PB ≤AB ＇．即为 P ．BPA - PB 最大值＝AB ＇．【问题 12】“费马点”作法 图形原理A所求点为“费马点”，即满足DBC∠APB ＝∠BPC ＝∠APC＝120°．以 AB 、AC 为APE两点之间线段最短． PA +PB +PC 最小值△ABC 中每一内角都小于 边向外作等边△ABD 、△ BC＝CD ．120°，在△ABC 内求一 ACE ，连 CD 、BE 相交于 点 P ，使 PA +PB +PC 值最 P ，点 P 即为所求．小．【精品练习】1. 如图所示，正方形 ABCD 的面积为 12，△ABE 是等边三角形，点 E 在正方形 ABCD 内，在对角线 AC 上有一点 P ，使 PD +PE 的和最小，则这个最小值为（ ）A. 2B. 2 ADC ．3D ．BC2. 如图，在边长为 2 的菱形 ABCD 中，∠ABC ＝60°，若将△ACD 绕点 A 旋转，当 AC ′、AD ′分别与 BC 、CD- 3 -662 EDM3交于点 E 、F ，则△CEF 的周长的最小值为（）A ．2B ． 2C ． 2 +D ．43. 四边形 ABCD 中，∠B ＝∠D ＝90°，∠C ＝70°，在 BC 、CD 上分别找一点 M 、N ，使△AMN 的周长最小时，∠AMN +∠ANM 的度数为（）A ．120°B ．130°C ．110°D ．140°A DBNC4. 如图，在锐角△ABC 中，AB ＝4 ，∠BAC ＝45°，∠BAC 的平分线交 BC 于点 D ，M 、N 分别是 AD 和AB 上的动点，则 BM +MN 的最小值是 ．A5. 如图，Rt △ABC 中，∠C ＝90°，∠B ＝30°，AB ＝6，点 E 在 AB 边上，点 D 在 BC 边上（不与点 B 、C 重合），且 ED ＝AE ，则线段 AE 的取值范围是 ．ACB6. 如图，∠AOB ＝30°，点 M 、N 分别在边 OA 、OB 上，且 OM ＝1，ON ＝3，点 P 、Q 分别在边 OB 、OA 上，则 MP ＋PQ ＋QN 的最小值是 ．（注“勾股定理”：直角三角形中两直角边的平方和等于斜边的平方，即 Rt △ABC 中，∠C ＝90°，则有 AC 2 + BC 2 = AB 2 ）- 4 -D M33 yABOxyBA OCDx7. 如图，三角形△ABC 中，∠OAB ＝∠AOB ＝15°，点 B 在 x 轴的正半轴，坐标为 B ( 6 ，0)．OC 平分∠AOB ，点 M 在 OC 的延长线上，点 N 为边 OA 上的点，则 MA ＋MN 的最小值是．8. 已知 A （2，4）、B （4，2）．C 在 y 轴上，D 在 x 轴上，则四边形 ABCD 的周长最小值为，此时 C 、D 两点的坐标分别为．9．已知 A （1，1）、B （4，2）．（1）P 为 x 轴上一动点，求 PA +PB 的最小值和此时 P 点的坐标；（2）P 为 x 轴上一动点，求 PA PB 的值最大时 P 点的坐标；（3）CD 为 x 轴上一条动线段，D 在 C 点右边且 CD ＝1，求当 AC +CD +DB 的最小值和此时 C 点的坐标；10. 点 C 为∠AOB 内一点．（1） 在 OA 求作点 D ，OB 上求作点 E ，使△CDE 的周长最小，请画出图形；（2） 在（1）的条件下，若∠AOB ＝30°，OC ＝10，求△CDE 周长的最小值和此时∠DCE 的度数．A- 5 -yBA OxyBA OxCO BAF11．（1）如图①，△ABD 和△ACE 均为等边三角形，BE 、CE 交于 F ，连 AF ，求证：AF +BF +CF ＝CD ；（2）在△ABC 中，∠ABC ＝30°，AB ＝6，BC ＝8，∠A ，∠C 均小于 120°，求作一点 P ，使 PA +PB +PC 的值最小，试求出最小值并说明理由．DEBC① ①① ①12．荆州护城河在 CC ＇处直角转弯，河宽相等，从 A 处到达 B 处，需经过两座桥 DD ＇、EE ＇，护城河及两桥都是东西、南北方向，桥与河岸垂直．如何确定两座桥的位置，可使 A 到 B 点路径最短？- 6 -- 7 -“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

最短路径练习题

最短路径练习题

最短路径练习题一、基础理论题1. 请简述迪杰斯特拉（Dijkstra）算法的基本原理。

2. 什么是贝尔曼福特（BellmanFord）算法？它与迪杰斯特拉算法有什么区别？3. 请解释弗洛伊德（Floyd）算法的核心思想。

4. A算法是如何工作的？它相较于其他最短路径算法有什么优势？5. 请列举几种常见的最短路径问题应用场景。

二、单项选择题A. 初始化距离表，将起点到其他点的距离设置为无穷大B. 每次从距离表中找出未确定最短路径的点中距离最小的点C. 更新距离表时，可以出现负权边D. 确定起点到所有点的最短路径后，算法结束A. 图中存在负权边B. 图中存在负权环C. 图中不存在负权环D. 图中存在多条边3. 在弗洛伊德算法中，path[i][j]表示的是？A. 从点i到点j的最短路径长度B. 从点i到点j的最短路径C. 从点j到点i的最短路径长度D. 从点j到点i的最短路径A. 当前点到终点的直线距离B. 当前点到终点的实际路径长度C. 当前点的邻接点数量D. 当前点的父节点三、填空题1. 在迪杰斯特拉算法中，用来存储起点到各点最短距离的数据结构是______。

2. 贝尔曼福特算法的时间复杂度为______。

3. 弗洛伊德算法的核心三重循环分别对应三个变量：______、______和______。

4. A算法的启发式函数f(n) = g(n) + h(n)，其中g(n)表示______，h(n)表示______。

四、应用题A 6 B| \ |1 2 3| \ |D 4 CA >B (2)^ || vC <D (1)A >B (4)^ || vC >D (2)4. 请简述如何使用A算法解决迷宫问题，并给出一个示例。

五、编程题1. 编写一个迪杰斯特拉算法的实现，输入为一个带权无向图和起点，输出为起点到其他各顶点的最短路径长度。

2. 编写一个贝尔曼福特算法的实现，输入为一个带权有向图和起点，输出为起点到其他各顶点的最短路径长度及是否存在负权环。

中考专题复习——最短路径问题

中考专题复习——最短路径问题

word专业资料-可复制编辑-欢迎下载A B C DABABL A BCDDO CP中考专题复习——路径最短问题一、具体内容包括：蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题；线段（之和）最短问题；二、原理：两点之间，线段最短；垂线段最短。

（构建“对称模型”实现转化）三、例题：例1、①如右图是一个棱长为4的正方体木块，一只蚂蚁要从木块的点A沿木块侧面爬到点B处，则它爬行的最短路径是。

②如右图是一个长方体木块，已知AB=3,BC=4,CD=2，假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

例2、①如图，要在河边修建一个水泵站，分别向张村、李庄送水，水泵站修在河边什么地方可使所用的水管最短。

②如图，直线L同侧有两点A、B，已知A、B到直线L的垂直距离分别为1和3，两点的水平距离为3，要在直线L上找一个点P，使PA+PB的和最小。

请在图中找出点P的位置，并计算PA+PB的最小值。

③要在河边修建一个水泵站，向张村、李庄铺设管道送水，若张村、李庄到河边的垂直距离分别为1Km和3Km，张村与李庄的水平距离为3Km，则所用水管最短长度为。

四、练习题（巩固提高）（一）1、如图是一个长方体木块，已知AB=5,BC=3,CD=4，假设一只蚂蚁在点A 处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

2、现要在如图所示的圆柱体侧面A点与B点之间缠一条金丝带（金丝带的宽度忽略不计），圆柱体高为6cm，底面圆周长为16cm，则所缠金丝带长度的最小值为。

3、如图是一个圆柱体木块，一只蚂蚁要沿圆柱体的表面从A点爬到点B处吃到食物，知圆柱体的高为5 cm，底面圆的周长为24cm，则蚂蚁爬行的最短路径为。

4、正方形ABCD的边长为8，M在DC上，且DM＝2，N是AC上的一动点，DN第2题张村李庄张村李庄AABB第1题第3题图(2)EBDACP＋MN 的最小值为 。

第4题 第5题 第6题 第7题 5、在菱形ABCD 中，AB=2， ∠BAD=60°，点E 是AB 的中点，P 是对角线AC 上的一个动点，则PE+PB 的最小值为 。

初中数学八年级上册最短路径问题同步专项练习题含答案

初中数学八年级上册最短路径问题同步专项练习题含答案

初中数学八年级上册最短路径问题同步专项练习题含答案学校：__________ 班级：__________ 姓名：__________ 考号：__________一、选择题（本题共计 10 小题，每题 3 分，共计30分，）1. 如图，在Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值是（）A.2√5+2B.2√3C.2√5D.2√3+22. 如图，圆柱形纸杯高8cm，底面周长为l2cm，在纸杯内壁离杯底2cm的点C处有一滴蜂蜜，一只蚂蚁正好在纸杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为（）A.2√3B.6√2C.10D.以上答案都不对3. 如图，在矩形ABCD中，AB=6，AD=8，点P在矩形内部，且满足S PCD=1 4S长方形ABCD，则点P到A,B两点的距离之和PA+PB的最小值为( )A.8B.10C.14D.2√134. 如图，直线l是一条河，P，Q是两个村庄．欲在l上的某处修建一个水泵站，向P，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是( )A. B.C. D.5. 如图，直线l是一条河，A、B两地相距10km，A、B两地到l的距离分别为8km、14km，欲在l上的某点M处修建一个水泵站，向A、B两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是（）A. B.C. D.6. 如图所示，矩形ABCD中，BC=6,AB=4，点P是平面内的一个动点，点P运动过程中始终满足∠BPC=90∘，线段AP的最小值是( )A.1B.2C.3D.47. 如图，一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点，那么它所爬行的最短路线的长是( )A.√2B.√3C.√5D.28. 如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+ MN的最小值为( )A.6B.8C.12D.109. 已知∠MON=40∘，P为∠MON内一定点，OM上有一点A，ON上有一点B，当△PAB的周长取最小值时，∠APB的度数是（）A.40∘B.100∘C.140∘D.50∘10. 如图，△ABC中，AC＝BC＝3，AB＝2，将它沿AB翻折得到△ABD，点P、E、F 分别为线段AB、AD、DB上的动点，则PE+PF的最小值是（）A. B. C. D.二、填空题（本题共计 10 小题，每题 3 分，共计30分，）11. 对于平面直角坐标系中的线段MN及点Q，给出如下定义：若点Q满足QM=QN，则称点Q为线段MN的“对称点”；当QM=QN=MN时，称点Q为线段MN的“完美对称点”．（1）如图1，点A坐标为(4,0)，有点Q1(0,4),Q2(2,−4)，Q3(1,√3)，则线段OA的“对称点”是________．（填“Q1”"Q2"或 "Q3"）(2)如图2，已知Q(2,2√3)为线段OA的“完美对称点”，D为线段OQ的中点，B为线段OA 的一个“对称点”，则BO+BD的最小值为________．12. 在矩形ABCD中，AB=20cm，BC=10cm，若在AC，AB上各取点M，N，使BM+NM最小，则BM+NM的最小值是________．AC，AB=8，E是AB上13. 如图，在Rt△ABC中，∠CAB=30∘，∠C=90∘．AD=14任意一点，F是AC上任意一点，则折线DEFB的最短长度为________．14. 小明在广场上散步，先向东走12m后，再向北又走了9m，现要以最短距离________m回到原地．15. 如图，一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点，那么它所爬行的最短路线的长是________.16. 如图，矩形ABCD中，AB=3，BC=6，点E，F将对角线AC三等分，点P是矩形的边上的动点．则△PEF周长的最小值为________.17. 如图，△ABC中，∠ACB=45∘，边AB上一定点P，M、N分别是AC和BC边上的动点，当△PMN的周长最短时，∠MPN的度数是________．18. 一只蚂蚁从长为4cm、宽为3cm，高是12cm的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是________．19. 如图，在△ABC中，AC=4，AB=5，BC=6，⊙A的半径为2，点P是BC边上的动点，过点P作⊙A的一条切线PQ(其中点Q为切点)，则线段PQ长度的最小值为________．20. 如图，∠AOB＝45∘，点C在∠AOB内部，CD⊥OB于点D，CD＝5，OD＝13，点E、点F分别是射线OA、射线OB上的动点，那么FE+FC的最小值是________．三、解答题（本题共计 20 小题，每题 10 分，共计200分，）21. 如图所示，在△ABC中，∠ACB=90∘，AC=BC=2，D是BC的中点，E是AB上的一动点，且不与A，B重合，是否存在一个位置，使DE+CE的值最小？若不存在，说明理由；若存在，试求出最小值．22. 如图，要在河岸l修建一个水泵站P，分别向张庄、李庄送水，修在河岸l的什么地方：(1)使到张庄、李庄的距离相等．(2)使所用的水管最短？（请通过你所学的知识画出这个地点的位置，不必说明理由.请保留作图痕迹）.23. 已知：如图所示（每个小正方形的边长为1），（1）求△ABC的面积，并求出它的AC边上高的长度；（2）在x轴上画出点P，使PA+PC最小，并求出该最小值．24. 一只蚂蚁从长为4cm，高时5cm的长方体纸箱的A点沿纸箱跑到B点，有不同的爬行路线．画出平面图示（相同类型画一个），并通过计算说明哪条线路最短，最短路线长多少？，高BC=12cm，P为BC的中点，求蚂25. 如图：有一个圆柱，底面圆的直径AB=16π蚁从A点爬到P点的最短距离．26. 如图，一圆柱高8cm，底面半径为2cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是多少厘米？注：π取3．27. 如图，圆柱的高为12cm，底面半径为3cm，在圆柱下底面A处有一只蚂蚁，它想得到上底面B处的食物，则蚂蚁经过的最短距离是多少cm？(π取3)．28. 如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=5，DE=1，BD=8，设CD=x．（1）用含x的代数式表示AC+CE的长；并求AC+CE的最小值；（2）若x+y=12，x>0，y>0请仿照（1）中的规律，运用构图法求出代数式√x2+4+√y2+9的最小值．29. 如图，已知∠MON=30∘，在OM上有两点A、B分别到ON的距离为2cm和1cm，若在ON上找一点P使|PA−PB|的值最大，求P点到O点的距离．30. 从A村到B村要修一条路，中间隔着两条河，在河上需要架2座桥，桥与两岸垂直，桥架在什么地方，使A村到B村总路程最短？31. 如图，已知∠AOB=30∘，P为其内部一点，OP=3，M，N分别为OA，OB边上的一点，要使△PMN的周长最小，请给出确定点M，N位置的方法，并求出最小周长．32. 一只螳螂在松树树干的A点处，发现它的正上方B点处有一只小虫子，螳螂想捕到这只虫子，但又怕被发现，于是按如图所示的路线，绕到虫子后面吃掉它．已知树干的半径为10cm，A、B两点的距离为40cm．（其中π取3）（1）若螳螂想吃掉在B点的小虫子，求螳螂绕行的最短距离．（要求画图）（2）螳螂得知又有一只虫子在点C处被松树油粘住不能动弹，这时螳螂还在A点，螳螂想吃掉虫子，求螳螂爬行的最短距离．（要求画图）（3）如果螳螂在点A处时，虫子在点E处不动，其中点E是CD的中点那么螳螂吃掉虫子的最短距离是多少cm？（要求画图）33.作图题：现要在形如△ABC的地面范围内建一中心医院，使医院到A，B两个居民小区的距离相等，并且到公路AB和AC的距离也相等，请确定这个中心医院的位置．（要求：保留作图痕迹，并用适当的文字说明作图方法）34. 在一条笔直公路上分布A，B，C，D，E五个工厂（各相邻工厂之间的距离均不相等），为方便这些工厂的员工，现要在公路上设一个汽车站，使各工厂到汽车站的距离之和最小．【简化分析】(1)假若由三个工厂A，B，C时，汽车站的位置有五种情形：①A厂门口，②AB之间，③B厂门口，④BC之间，⑤C厂门口.【分类讨论】①当车站设在A工厂门口时，则A厂到汽车站的距离为0，B厂到汽车站的距离为AB，C厂到汽车站的距离为AB＋BC，所以各工厂到车站的距离之和为________②当车站设在A，B两工厂之间的P点时，则A厂到汽车站的距离为AP，B厂到汽车站的距离为BP，C厂到汽车站的距离为BP+BC，所以各工厂到车站的距离之和为_________③当车站设在B工厂门口，则各工厂到汽车站的距离之和为_________④当车站设在B，C两工厂之间的Q点时，则各工厂到汽车站的距离之和为_________⑤当车站设在C工厂门口，则各工厂到汽车站的距离之和为________【总结归纳】综上可知：汽车站设在________时，各工厂到汽车站的距离之和最小.【问题解决】 (2)当有A，B，C，D，E五个工厂时，汽车站设在哪里，才能使各工厂到汽车站的距离之和最小？请说明理由.35. 如图是平放在桌面上的长方体木块，其长为14cm，宽为10cm，高为20cm，点B是高CD的中点，一只蜘蛛要沿长方体木块的表面从A点爬到B点，请你求出蜘蛛爬行的最短路程是多少？36. （1）如图，已知：线段r和∠ACB=60∘，求作一⊙O，使它与∠ACB的两边相切，且圆的半径等于r；（不写作法，要求用直尺和圆规作图，保留作图痕迹）36.（2）如图，已知点A是锐角∠MON内的一点，试分别在OM，ON上确定点B，点C，使△ABC的周长最小．（不写作法，要求用直尺和圆规作图，保留作图痕迹）37. 如图，要在河边修建一个水泵站，分别向张村A和李村B送水，已知张村A、李村B 到河边的距离分别为2km和7km，且张、李二村庄相距13km．(1)水泵应建在什么地方，可使所用的水管最短？请在图中设计出水泵站的位置；（用尺规作图，保留作图痕迹，不写作法，不要求证明）(2)如果铺设水管的工程费用为每千米3000元，为使铺设水管费用最节省，请求出最节省的铺设水管的费用为多少元？38. 如图所示，一只昆虫要从正方体的一个顶点A爬到相距它最远的另一个顶点B，哪条路径最短？说明理由．39. 如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC、EC．已知AB＝5，DE＝1，BD＝8，设CD＝x（1）用含x的代数式表示AC+CE的长；（2）试求AC+CE的最小值．40. 李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题，请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长．（1）如图1，正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处；（2）如图2，正四棱柱的底面边长为5cm，侧棱长为6cm，一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处；（3）如图3，圆锥的母线长为4cm，圆锥的侧面展开图如图4所示，且∠AOA1=120∘，一只蚂蚁欲从圆锥的底面上的点A出发，沿圆锥侧面爬行一周回到点A．参考答案与试题解析初中数学八年级上册最短路径问题同步专项练习题含答案一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】A【考点】轴对称——最短路线问题【解析】求△BDE周长的最小值，就是要求DE+BE的最小值，根据勾股定理即可求得．【解答】解：过点B做BO⊥AC于点O，延长BO到B′，使OB′=OB，连接DB′，交AC于E，此时DB′=DE+EB′=DE+BE的值最小，连接CB′易证CB′⊥BC在RT△DCB′中，根据勾股定理可得DB′=√B′C2+CD2=√42+22=√20=2√5．故△BDE周长的最小值为2√5+2．故选：A．2.【答案】C【考点】平面展开-最短路径问题【解析】将杯子侧面展开，建立A关于EF的对称点A′，根据两点之间线段最短可知A′C的长度即为所求．【解答】解：如图：将杯子侧面展开，作A关于EF的对称点A′，连接A′C，则A′C即为最短距离，由题意可得出：A′D=6cm，CD=8cm，A′C=√A′D2+CD2=10(cm)，故选：C．3.【答案】B【考点】路径最短问题【解析】此题暂无解析【解答】解：∵S PCD=14S长方形ABCD，设△PCD的CD边上的高为ℎ∴12CD⋅ℎ=14CD⋅AD，又AD=8，∴ℎ=4,∴动点P在与CD平行且与CD的距离为4的直线l上，如图，作D关于直线l的对称点A，连接AC，则AC的长就是所求的最短距离.在Rt△ADC中，CD=AB=6，AD=8∴AC=√AD2+CD2解得AC=10.故选B.4.【答案】D【考点】轴对称——最短路线问题利用对称的性质，通过等线段代换，将所求路线长转化为两定点之间的距离．【解答】解：作点P关于直线l的对称点P′，连结QP′交直线l于M．根据两点之间，线段最短，可知选项D铺设的管道，所需管道最短．故选D．5.【答案】B【考点】轴对称——最短路线问题【解析】作点A关于直线l的对称点，再把对称点与点B连接，根据轴对称确定最短路线问题，交点即为所求点M．【解答】解：根据轴对称确定最短路线问题，B选项图形方案符合．故选B．6.【答案】B【考点】路径最短问题【解析】要想求得点P的个数，由∠BPC=90∘可判断以BC为直径的圆与AD的交点个数即可．【解答】解：∵ 点P运动过程中始终满足∠BPC=90∘,∴ 点P在以BC为直径的半圆上，圆心为O，如下图所示，连接AO，AO与半圆的交点为P，此时AP距离最短.由题意知，AO=√AB2+OB2=√42+32=5，∴ AP=AO−OP=5−3=2，∴ 线段AP的最小值是2.7.【答案】C【考点】平面展开-最短路径问题【解析】本题考查了平面展开-最短路径问题，“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．【解答】解：将纸箱展开，如图所示，由勾股定理得：AB2=12+(1+1)2=5，∴ AB=√5．故选C.8.【答案】D【考点】轴对称——最短路线问题【解析】要使DN+MN最小，首先应分析点N的位置．根据正方形的性质：正方形的对角线互相垂直平分．知点D的对称点是点B，连接MB交AC于点N，此时DN+MN最小值即是BM的长．【解答】解：根据题意，连接BD，BM，则BM就是所求DN+MN的最小值，在Rt△BCM中，BC=8，CM=6根据勾股定理得：BM=√62+82=10，即DN+MN的最小值是10.故选D．9.【答案】B【考点】轴对称——最短路线问题【解析】AB+BP=P′P″，此时周长最小．根据轴对称的性质，可求出∠APB的度数．【解答】解：分别作点P关于OM、ON的对称点P′、P″，连接OP′、OP″、P′P″，P′P″交OM、ON 于点A、B，连接PA、PB，此时△PAB周长的最小值等于P′P″．由轴对称性质可得，OP′=OP″=OP，∠P′OA=∠POA，∠P″OB=∠POB，∴∠P′OP″=2∠MON=2×40∘=80∘，∴∠OP′P″=∠OP″P′=(180∘−80∘)÷2=50∘，又∵∠BPO=∠OP″B=50∘，∠APO=∠AP′O=50∘，∴∠APB=∠APO+∠BPO=100∘．故选B．10.【答案】C【考点】平面展开-最短路径问题【解析】首先证明四边四边形ABCD是菱形，得AD//BC，作出F关于AB的对称点M，再过M作ME′⊥AD，交AB于点P，此时PE′+PF最小，求出ME即可．【解答】解：作出F关于AB的对称点M，再过M作iM′⊥AD，交AB于点P，此时FE′+PF最小，此时PE′+PF=ME，过点A作AN⊥BC&nbspCH⊥AB于H，________△ABC沿AB翻折得到△ABDAC=AD&nbspBC=BD．AC=BCAC=AD=BC=BD四边形ADBC是菱形，．AD//BC∵AC=BCAE=1AB=1由勾股定理可得，CH=√32−12=2√2．12×AB×CH=12×BC×AN可得AN=4√23ME′=AN=4√2 3PE+PF最小为4√23故选：C．二、填空题（本题共计 10 小题，每题 3 分，共计30分）11.【答案】Q22．【考点】图形间的距离定义新图形路径最短问题坐标与图形性质【解析】（1）找到OA的垂直平分线即可找到对应的点．（2）利用“完美对称点”的特征，作出图象，从而确定最小值．【解答】解：(1)当点Q满足QO=QA时，Q为OA的“对称点”，∴ Q在线段OA的垂直平分线上，∵ A(4,0)，∴ 线段OA的垂直平分线是直线x=2，∵Q2(2,−4)，∴ 线段OA的“对称点”是Q2.故答案为：Q2．∵ Q(2,2√3)为线段OA的“完美对称点”，∴ QO=OA=QA，∴ △QOA是等边三角形，过点Q作QH⊥OA于H，则直线QH为线段AO的垂直平分线，如图：∵ B为线段OA的一个“对称点”，∴ BO=BA，∴ B是直线QH上的一点，显然，当Q、B重合时，BQ+BD有最小值，此时BQ+BD=BD，∵ Q(2,2√3)，∴ OQ=√22+(2√3)2=4，∵ D为线段OQ的中点，∴ DQ=12OQ=12×4=2，∴ BD=2，∴ BQ+BD的最小值为2. 故答案为：2.12.【答案】16cm【考点】轴对称——最短路线问题【解析】过B点作BE⊥AC于O，使OE=OB，过E作EN⊥AB交AB于N点，交AC于M，此时BM+NM有最小值，EN就是所求的线段．【解答】解：过B点作BE⊥AC于O，使OE=OB，过E作EN⊥AB交AB于N点，交AC于M，此时BM+NM有最小值，EN就是所求的线段．∵AB=20cm，BC=10cm，∴AC=√AB2+BC2=10√5cm，∵12AB⋅BC=12AC⋅OB，∴OB=4√5cm，∴BE=8√5cm．∵△ABC∽△BEN，∴ENAB =BEAC，∴EN=AB⋅BEAC =√510√5=16cm．∴BM+NM的最小值为16cm，故答案为16cm．13.【答案】√67【考点】【解析】利用轴对称求最短路径的方法，重新构造直角三角形，进而利用勾股定理求出即可．【解答】解：作D 点关于AB 的对称点D′，B 点关于AC 的对称点B′，连接D′B′分别交AB 于点E ，AC 于点F ，作B′R ⊥AB ，过点D′作D′W ⊥B′R 于点W ，∵ ∠CAB =30∘，∠C =90∘．AD =14AC ，AB =8， ∴ BC =4，AC =4√3，则AD =√3，BB′=8，B′R =4√3，∴ DT =12AD =√32，AT =√AD 2−DT 2=32，BR =4， ∴ RW =√32，D′W =8−32−4=52， ∴ B′W =9√32，B′D′=√D′W 2+B′W 2=(52)+(9√32)=√67．故答案为：√67．14.【答案】15【考点】勾股定理路径最短问题 【解析】此题暂无解析【解答】解：设小明散步原地为O ，则先向东走12m 到达A 点后，再向北又走了9m 到达B 点，则要回到原地，最短行走距离为OB 的距离，根据勾股定理可得OB =√122+92=15m .15.【答案】√5【考点】平面展开-最短路径问题【解析】把此正方体的一面展开，然后在平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于棱长，另一条直角边长等于两条棱长，利用勾股定理可求得．【解答】解:∵展开后由勾股定理得：AB2=12+(1+1)2=5，∴AB=√5．故答案为：√5.16.【答案】√5+√13【考点】轴对称——最短路线问题【解析】此题暂无解析【解答】解: ①P在AD上，如图所示:则作E点关于AD的对称点G，连接EG，FG交AD于点P′，则对AD上点P，PG=PE，则△PEF周长=PE+PF+EF=PG+PF+EF≥GF+EF，故当C△PEF最小时，PG+PF=GF，即P与P′重合，记GE交AD于点M，由AB=3，BC=6，四边形ABCD为矩形知：AC=√32+62=3√5，∵EF为三等分点，知AE=EF=13AC=√5，GM=ME=13CD=1，作FN⊥GE于N，则EN=1，FN=2，GF=√22+32=√13，C△PEF=GF+EF=√13+√5；②P在CD上，如图所示，则同理QF=FR=RH=2,EQ=1，当P与P′重合时，C△PEF最小，最小值为EF+EH=√5+√62+12=√5+√37>√13+√5，所以C△DEF最小值为√5+√13.故答案为：√5+√13.17.【答案】90∘【考点】轴对称——最短路线问题【解析】根据对称的性质，易求得∠C+∠EPF=180∘，由∠ACB=45∘，易求得∠D+∠G=45∘，继而求得答案．【解答】解：∵PD⊥AC，PG⊥BC，∴∠PEC=∠PFC=90∘，∴∠C+∠EPF=180∘，∵∠C=45∘，∴∠EPF=135∘，∵∠D+∠G+∠EPF=180∘，∴∠D+∠G=45∘，由对称可知：∠G=∠GPN，∠D=∠DPM，∴∠GPN+∠DPM=45∘，∴∠MPN=135∘−45∘=90∘，故答案为：90∘18.【答案】√193【考点】平面展开-最短路径问题【解析】先将图形展开，再根据两点之间线段最短，再由勾股定理求解即可．【解答】解：如图1：AB=√162+32=√265(cm)，如图2：AB=√152+42=√241(cm)，如图3：AB=√122+72=√193(cm)，∴√265>√241>√193，∴它所行的最短路线的长是√193cm．故答案为：√193cm．19.【答案】√1114【考点】切线的性质勾股定理路径最短问题【解析】连接PA，AQ，由切线的性质得到∠AQP=90∘，由AQ=2是定值，要使PQ的长度最小，只有PA的值最小时才成立，进而确定出△PCA和△PBA是直角三角形，由勾股定理求出PC的长度，进而求出PA2，最后求勾股定理求解.【解答】解：连接PA，AQ，如下图.∵ PQ是⊙A的切线，∴ AQ⊥PQ，∴ ∠AQP=90∘.∵ AQ=2是定值，要使PQ的长度最小，∴ PA ⊥BC ，即PA 的值最小时才成立，∴ PQ 2=PA 2−AQ 2.由PA ⊥BC 可知，△PCA 和△PBA 是直角三角形，∵ AC =4，AB =5，BC =PC +PB =6，∴ PA 2=AC 2−PC 2，PA 2=AB 2−PB 2，∴ AC 2−PC 2=AB 2−PB 2，即42−PC 2=52−(6−PC )2，解得PC =94，∴ PA 2=42−(94)2， ∴ PQ =√PA 2−AQ 2=√16−8116−4=√11116=√1114， 即线段PQ 的最小值是√1114. 故答案为：√1114. 20.【答案】 9√2【考点】轴对称——最短路线问题【解析】如图，作点E 关于OD 的对称点E′，作射线OE′，作CE ″⊥OE′交OD 于F′，延长DC 交OA 于H ，作CM ⊥OA 于M ．因为EF +CF ＝E′F +CF ，所以根据垂线段最短可知，当CE ″⊥OE′时，EF +CF 的值最小，最小值为CE ″，求出CE ″即可解决问题．【解答】如图，作点E 关于OD 的对称点E′，作射线OE′，作CE ″⊥OE′交OD 于F′，延长DC 交OA 于H ，作CM ⊥OA 于M ．∵ EF +CF ＝E′F +CF ，∴ 根据垂线段最短可知，当CE ″⊥OE′时，EF +CF 的值最小，最小值为CE ″， ∵ ∠AOD ＝45∘，∠ADO ＝90∘，∴ ∠DOH ＝∠DHO ＝45∘，∴ OD ＝DH ＝13，∵ CD ＝5，∴ CH ＝8，∵ CM ⊥OA ，∴ ∠CMH ＝90∘，∠MCH ＝∠MHC ＝45∘，∴ CM ＝MH ＝4√2，∵ ∠AOE′＝2∠AOD ＝90∘＝∠OE ″C ＝∠CMO ，∴四边形CMOE″是矩形，∴OE″＝CM＝4√2，在Rt△OCD中，OC2＝OD2+CD2＝132+52＝194，在Rt△OCE″中，CE″$= \sqrt{OC^{2} - OE"^{2}} = \sqrt{194 - 32} = 9\sqrt{2}$，∴EF+CF的值最小为9√2．三、解答题（本题共计 20 小题，每题 10 分，共计200分）21.【答案】解：如图所示：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC；连接DC′，交AB于E，连接CE，此时DE+CE=DE+EC′=DC′的值最小；连接BC′，由轴对称的性质得：∠C′BE=∠CBE=45∘，∴∠CBC′=90∘，∴BC′⊥BC，∠BCC′=∠BC′C=45∘，∴BC=BC′=2，∵D是BC边的中点，∴BD=1，根据勾股定理得：DC′=√BC′2+BD2=√22+12=√5；∴DE+CE的最小值为√5．【考点】轴对称——最短路线问题【解析】过点C作CO⊥AB于O，延长CO到C′，使OC′=OC；连接DC′，交AB于E，连接CE，此时DE+CE=DE+EC′=DC′的值最小；再根据勾股定理求出DC′即可．【解答】解：如图所示：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC；连接DC′，交AB于E，连接CE，此时DE+CE=DE+EC′=DC′的值最小；连接BC′，由轴对称的性质得：∠C′BE=∠CBE=45∘，∴∠CBC′=90∘，∴BC′⊥BC，∠BCC′=∠BC′C=45∘，∴BC=BC′=2，∵D是BC边的中点，∴BD=1，根据勾股定理得：DC′=√BC′2+BD2=√22+12=√5；∴DE+CE的最小值为√5．22.【答案】解：(1)如图1，设河边为直线CD，∵到A，B两点的距离相等，∴可以作线段AB的垂直平分线，交河边CD于点P，则PA=PB，∴P点位置即为到张庄、李庄距离相等的点；(2)如图2，设河边为直线CD，点A关于直线CD的对称点为A′，连接A′B，交CD于点Q，则AQ=A′Q，∴A′B=AQ+BQ，∴此时到A、B两地的距离最短，∴Q点即为所求的位置．【考点】路径最短问题作图—应用与设计作图轴对称——最短路线问题线段垂直平分线的性质【解析】（1）可作线段AB的垂直平分线，与河边的交点即为所求的点；（2）找出A点关于河边的对称点A′，连接A′B交河边于点Q，则Q即为所求的点．【解答】解：(1)如图1，设河边为直线CD，∵到A，B两点的距离相等，∴可以作线段AB的垂直平分线，交河边CD于点P，则PA=PB，∴P点位置即为到张庄、李庄距离相等的点；(2)如图2，设河边为直线CD，点A关于直线CD的对称点为A′，连接A′B，交CD于点Q，则AQ=A′Q，∴A′B=AQ+BQ，∴此时到A、B两地的距离最短，∴Q点即为所求的位置．23.【答案】解：(1)△ABC的面积=3×4−12×1×2−12×2×3−12×2×4，=12−1−3−4，=12−8，=4，由勾股定理得，AC=√22+42=2√5，设AC边上高的长度为ℎ，则12×2√5ℎ=4，解得ℎ=4√55．所以，AC边上高的长度为4√55；（2）点P如图所示，由勾股定理得，PA+PC最小值=√62+42=2√15．【考点】轴对称——最短路线问题【解析】（1）利用三角形所在的矩形的面积减去四周三个直角三角形的面积列式求出△ABC的面积，再利用勾股定理列式求出AC，然后根据三角形的面积公式列式计算即可得解；（2）找出点A关于直线l的对称点A′，连接A′C，根据轴对称确定最短路线问题，A′C与直线l的交点即为所求的点P，最短距离为A′C的长度，再利用勾股定理列式计算即可得解．【解答】解：(1)△ABC的面积=3×4−12×1×2−12×2×3−12×2×4，=12−1−3−4，=12−8，=4，由勾股定理得，AC=√22+42=2√5，设AC边上高的长度为ℎ，则12×2√5ℎ=4，解得ℎ=4√55．所以，AC边上高的长度为4√55；（2）点P如图所示，由勾股定理得，PA+PC最小值=√62+42=2√15．24.【答案】解：如图1所示：AB=√(4+3)2+52=√74(cm)，如图2所示：AB=√(5+3)2+42=√80(cm)，∵√74<√80，∴蚂蚁按照图1这条路线爬行，路线最短，最短路线长为：√74cm．【考点】平面展开-最短路径问题【解析】利用展开图不同，分别结合勾股定理得出AB的长，进而求出答案．【解答】解：如图1所示：AB=√(4+3)2+52=√74(cm)，如图2所示：AB=√(5+3)2+42=√80(cm)，∵√74<√80，∴蚂蚁按照图1这条路线爬行，路线最短，最短路线长为：√74cm．25.【答案】解：已知如图：∵圆柱底面直径AB=16πcm、母线BC=12cm，P为BC的中点，∴圆柱底面圆的半径是8πcm，BP=6cm，∴AB=12×2×8π=8cm，在Rt△ABP中，AP=√AB2+BP2=10cm，∴蚂蚁从A点爬到P点的最短距离为10cm．【考点】平面展开-最短路径问题【解析】把圆柱的侧面展开，连接AP，利用勾股定理即可得出AP的长，即蚂蚁从A点爬到P点的最短距离．【解答】解：已知如图：∵圆柱底面直径AB=16πcm、母线BC=12cm，P为BC的中点，∴圆柱底面圆的半径是8πcm，BP=6cm，∴AB=12×2×8π=8cm，在Rt△ABP中，AP=√AB2+BP2=10cm，∴蚂蚁从A点爬到P点的最短距离为10cm．26.【答案】解：B为CE的中点．AB就是蚂蚁爬的最短路径．∵CE=2π⋅r=2×3×2=12厘米，∴CB=12÷2=6厘米．∵AC=8厘米，∴AB=√62+82=10厘米．蚂蚁要爬行的最短距离是10厘米．【考点】平面展开-最短路径问题【解析】圆柱展开为长方形，根据题意可知道点A和B在平面上的位置，根据两点之间线段最短可求出解．【解答】解：B为CE的中点．AB就是蚂蚁爬的最短路径．∵CE=2π⋅r=2×3×2=12厘米，∴CB=12÷2=6厘米．∴AB=√62+82=10厘米．蚂蚁要爬行的最短距离是10厘米．27.【答案】解：如图，将圆柱的侧面沿过A点的一条母线剪开，得到长方形ADFE，连接AB，则线段AB的长就是蚂蚁爬行的最短距离，其中C，B分别是AE，DF的中点．∵AD=12cm，DB=πr=3π=9cm(π取3)，∴AB=√AD2+DB2=√122+92=15cm．故蚂蚁经过的最短距离为15cm．【考点】平面展开-最短路径问题【解析】先把圆柱的侧面展开得其侧面展开图，则A，B所在的长方形的长为圆柱的高12cm，宽为底面圆周长的一半为πr，蚂蚁经过的最短距离为连接A，B的线段长，由勾股定理求得AB的长．【解答】解：如图，将圆柱的侧面沿过A点的一条母线剪开，得到长方形ADFE，连接AB，则线段AB的长就是蚂蚁爬行的最短距离，其中C，B分别是AE，DF的中点．∵AD=12cm，DB=πr=3π=9cm(π取3)，∴AB=√AD2+DB2=√122+92=15cm．故蚂蚁经过的最短距离为15cm．28.【答案】解：（1）∵CD=x，BD=8，∴CB=8−x，AC+CE=√52+(8−x)2+√x2+1，当A、C、E在同一直线上，AC+CE最小；当A、C、E在同一直线上时，延长AB，作EF⊥AB于点F，∵AB=5，DE=1，∴AF=6，∵∠ABD=90∘，∵∠BDE=∠BFE=90∘，∴四边形BFED是矩形，∴BD=EF=8，∴AE=√AF2+EF2=√62+82=10，；（2）如下图所示：作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，当BC=x，∵x+y=12，∴y=12−x，AE的长即为代数式√x2+4+√(12−x)2+9的最小值，过点A作AF // BD交ED的延长线于点F，得矩形ABDF，则AB=DF=2，AF=BD=12，所以AE=√AF2+EF2=√122+(3+2)2=13，即代数式√x2+4+√y2+9的最小值为13．【考点】轴对称——最短路线问题【解析】（1）根据勾股定理得出AC，CE的长进而得出用含x的代数式表示AC+CE的长；由于△ABC和△CDE都是直角三角形，故AC，CE可由勾股定理求得；若点C不在AE的连线上，根据三角形中任意两边之和>第三边知，AC+CE>AE，故当A、C、E三点共线时，AC+CE的值最小，利用勾股定理求出即可；（2）由（1）的结果可作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，则AE的长即为代数式√x2+4+√y2+9的最小值，然后构造矩形AFDB，Rt△AFE，利用矩形的直角三角形的性质可求得AE的值．【解答】解：（1）∵CD=x，BD=8，∴CB=8−x，AC+CE=√52+(8−x)2+√x2+1，当A、C、E在同一直线上，AC+CE最小；当A、C、E在同一直线上时，延长AB，作EF⊥AB于点F，∵AB=5，DE=1，∴AF=6，∵∠ABD=90∘，∴∠FBD=90∘，∵∠BDE=∠BFE=90∘，∴四边形BFED是矩形，∴BD=EF=8，∴AE=√AF2+EF2=√62+82=10，；（2）如下图所示：作BD=12，过点B作AB⊥BD，过点D作ED⊥BD，使AB=2，ED=3，连接AE交BD于点C，当BC=x，∵x+y=12，∴y=12−x，AE的长即为代数式√x2+4+√(12−x)2+9的最小值，过点A作AF // BD交ED的延长线于点F，得矩形ABDF，则AB=DF=2，AF=BD=12，所以AE=√AF2+EF2=√122+(3+2)2=13，即代数式√x2+4+√y2+9的最小值为13．29.【答案】解：因为A、B在OM上，要使|PA−PB|的值最大，P应在OM上，如果P不在OM上，则P、A、B构成三角形，根据三角形的三边关系，|PA−PB|<AB，所以，P是OM和ON的交点，即O点，所以P到O的距离为0．【考点】轴对称——最短路线问题【解析】根据三角形的三边关系，两边的差小于第三边，可以判定当P点在OM和ON的交点处|PA−PB|的值最大，从而求得P点到O点的距离．【解答】解：因为A、B在OM上，要使|PA−PB|的值最大，P应在OM上，如果P不在OM上，则P、A、B构成三角形，根据三角形的三边关系，|PA−PB|<AB，所以，P是OM和ON的交点，即O点，所以P到O的距离为0．30.【答案】解：把点A向下平移河②的宽度后得到A″，平移两条河的宽度后到点A′，连接A′B交于b于点P，作PQ⊥b，连接A″Q，交c于M，作MN⊥d于N，由于A″A′平行且等于PQ，AA′平行且等于MN，则四边形A″A′PQ是平行四边形，四边形AA′MN是平行四边形，有A′P=QA″，AN=A″M，由于A′B是点A′到点B的最短距离，所以在PQ、MN处建桥就是使得A村到B村总路程最短的桥的位置．【考点】轴对称——最短路线问题【解析】把点A向下平移河②的宽度后得到A″，平移两条河的宽度后到点A′，连接A′B交于b于点P，连接A″Q，交c于M，则点P、M就是所求的建桥的位置．【解答】解：把点A向下平移河②的宽度后得到A″，平移两条河的宽度后到点A′，连接A′B交于b于点P，作PQ⊥b，连接A″Q，交c于M，作MN⊥d于N，由于A″A′平行且等于PQ，AA′平行且等于MN，则四边形A″A′PQ是平行四边形，四边形AA′MN是平行四边形，有A′P=QA″，AN=A″M，由于A′B是点A′到点B的最短距离，所以在PQ、MN处建桥就是使得A村到B村总路程最短的桥的位置．31.【答案】解：作点P关于OA的对称点P1，点P关于OB的对称点P2，连结P1P2，与OA的交点即为点M，与OB的交点即为点N，△PMN的最小周长为：PM+MN+PN=P1M+MN+P2N=P1P2，。

最短路径问题专项练习题

最短路径问题专项练习题

AB最短路径问题专项练习共13页，全面复习与联系最短路径问题一、具体内容包括：蚂蚁沿正方体、长方体、圆柱、圆锥外侧面吃食问题；线段（之和）最短问题；二、原理：两点之间，线段最短；垂线段最短。

（构建“对称模型”实现转化）1．最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题，只要连接这两点，与直线的交点即为所求．如图所示，点A，B分别是直线l异侧的两个点，在l上找一个点C，使CA＋CB最短，这时点C是直线l与AB的交点．(2)求直线同侧的两点与直线上一点所连线段的和最小的问题，只要找到其中一个点关于这条直线的对称点，连接对称点与另一个点，则与该直线的交点即为所求．如图所示，点A，B分别是直线l同侧的两个点，在l上找一个点C，使CA＋CB最短，这时先作点B关于直线l的对称点B′，则点C是直线l与AB′的交点．为了证明点C的位置即为所求，我们不妨在直线上另外任取一点C′，连接AC′，BC′，B′C′，证明AC＋CB＜AC′＋C′B.如下：证明：由作图可知，点B和B′关于直线l对称，所以直线l是线段BB′的垂直平分线．因为点C与C′在直线l上，所以BC＝B′C，BC′＝B′C′.在△AB′C′中，AB′＜AC′＋B′C′，所以AC＋B′C＜AC′＋B′C′，所以AC＋BC＜AC′＋C′B.【例1】在图中直线l上找到一点M，使它到A，B两点的距离和最小．分析：先确定其中一个点关于直线l的对称点，然后连接对称点和另一个点，与直线l的交点M即为所求的点．解：如图所示：(1)作点B关于直线l的对称点B′；(2)连接AB′交直线l于点M.(3)则点M即为所求的点．点拨：运用轴对称变换及性质将不在一条直线上的两条线段转化到一条直线上，然后用“两点之间线段最短”解决问题.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质，将所求线段之和转化为一条线段的长，是解决距离之和最小问题的基本思路，不论题目如何变化，运用时要抓住直线同旁有两点，这两点到直线上某点的距离和最小这个核心，所有作法都相同．警误区 利用轴对称解决最值问题应注意题目要求 根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种方法．解决这类最值问题时，要认真审题，不要只注意图形而忽略题意要求，审题不清导致答非所问．3．利用平移确定最短路径选址选址问题的关键是把各条线段转化到一条线段上．如果两点在一条直线的同侧时，过两点的直线与原直线的交点处构成线段的差最大，如果两点在一条直线的异侧时，过两点的直线与原直线的交点处构成的线段的和最小，都可以用三角形三边关系来推理说明，通常根据最大值或最小值的情况取其中一个点的对称点来解决．解决连接河两岸的两个点的最短路径问题时，可以通过平移河岸的方法使河的宽度变为零，转化为求直线异侧的两点到直线上一点所连线段的和最小的问题．在解决最短路径问题时，我们通常利用轴对称、平移等变换把不在一条直线上的两条线段转化到一条直线上，从而作出最短路径的方法来解决问题．【例2】 如图，小河边有两个村庄A ，B ，要在河边建一自来水厂向A 村与B 村供水．(1)若要使厂部到A ，B 村的距离相等，则应选择在哪建厂？ (2)若要使厂部到A ，B 两村的水管最短，应建在什么地方？分析：(1)到A ，B 两点距离相等，可联想到“线段垂直平分线上的点到线段两端点的距离相等”，又要在河边，所以作AB 的垂直平分线，与EF 的交点即为符合条件的点．(2)要使厂部到A 村、B 村的距离之和最短，可联想到“两点之间线段最短”，作A (或B )点关于EF 的对称点，连接对称点与B 点，与EF 的交点即为所求．解：(1)如图1，取线段AB 的中点G ，过中点G 画AB 的垂线，交EF 于P ，则P 到A ，B 的距离相等．也可分别以A 、B 为圆心，以大于12AB 为半径画弧，两弧交于两点，过这两点作直线，与EF 的交点P 即为所求．(2)如图2，画出点A 关于河岸EF 的对称点A ′，连接A ′B 交EF 于P ，则P 到A ，B 的距离和最短．【例3】 如图，从A 地到B 地经过一条小河(河岸平行)，今欲在河上建一座与两岸垂直的桥，应如何选择桥的位置才能使从A 地到B 地的路程最短？思路导引：从A 到B 要走的路线是A →M →N →B ，如图所示，而MN 是定值，于是要使路程最短，只要AM ＋BN 最短即可．此时两线段应在同一平行方向上，平移MN 到AC ，从C 到B 应是余下的路程，连接BC的线段即为最短的，此时不难说明点N即为建桥位置，MN即为所建的桥．解：(1)如图2，过点A作AC垂直于河岸，且使AC等于河宽．(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置．4．生活中的距离最短问题由两点之间线段最短(或三角形两边之和大于第三边)可知，求距离之和最小问题，就是运用等量代换的方式，把几条线段的和想办法转化在一条线段上，从而解决这个问题，运用轴对称性质，能将两条线段通过类似于镜面反射的方式转化成一条线段，如图，AO＋BO＝AC的长．所以作已知点关于某直线的对称点是解决这类问题的基本方法．【例4】(实际应用题)茅坪民族中学八(2)班举行文艺晚会，桌子摆成如图a所示两直排(图中的AO，BO)，AO桌面上摆满了橘子，OB桌面上摆满了糖果，站在C处的学生小明先拿橘子再拿糖果，然后到D处座位上，请你帮助他设计一条行走路线，使其所走的总路程最短？图a 图b解：如图b.(1)作C点关于OA的对称点C1，作D点关于OB的对称点D1，(2)连接C1D1，分别交OA，OB于P，Q，那么小明沿C→P→Q→D的路线行走，所走的总路程最短．5.运用轴对称解决距离之差最大问题利用轴对称和三角形的三边关系是解决几何中的最大值问题的关键．先做出其中一点关于对称轴的对称点，然后连接对称点和另一个点，所得直线与对称轴的交点，即为所求．根据垂直平分线的性质和三角形中两边之差小于第三边易证明这就是最大值．破疑点解决距离的最值问题的关键运用轴对称变换及三角形三边关系是解决一些距离的最值问题的有效方法．【例5】如图所示，A，B两点在直线l的两侧，在l上找一点C，使点C到点A、B的距离之差最大．分析：此题的突破点是作点A(或B)关于直线l的对称点A′(或B′)，作直线A′B(AB′)与直线l交于点C，把问题转化为三角形任意两边之差小于第三边来解决．解：如图所示，以直线l为对称轴，作点A关于直线l的对称点A′，A′B的连线交l于点C，则点C即为所求．理由：在直线l上任找一点C′(异于点C)，连接CA，C′A，C′A′，C′B.因为点A，A′关于直线l对称，所以l为线段AA′的垂直平分线，则有CA＝CA′，所以CA－CB＝CA′－CB＝A′B.又因为点C′在l上，所以C′A＝C′A′.在△A′BC′中，C′A－C′B ＝C′A′－C′B＜A′B，所以C′A′－C′B＜CA－C B.点拨：根据轴对称的性质、利用三角形的三边关系，通过比较来说明最值问题是常用的一种BC ABLCD方法．三、例题：例1、①如右图是一个棱长为4的正方体木块，一只蚂蚁要从木块的点A沿木块侧面爬到点B处，则它爬行的最短路径是。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

13.4课题学习最短路径问题
1、①如右图是一个棱长为4的正方体木块，一只蚂蚁要从木块的点A沿木块侧面爬到点B 处，则它爬行的最短路径是。

B
A
②如右图是一个长方体木块，已知AB=3，BC=4，CD=2，假设一只蚂蚁在点A处，它要沿着木块侧面爬到点D处，则蚂蚁爬行的最短路径是。

D
C
A B
2．①如图，要在河边修建一个水泵站，分别向张村、李庄送水，水泵站修在河边什么地方可使所用的水管最短。

李庄
张村
②如图，直线L同侧有两点A、B，已知A、B到直线L的垂直距离分别为1和3，两点的水平距离为3，要在直线L上找一个点P，使PA+PB的和最小。

请在图中找出点P的位置，并计算PA+PB的最小值。

B
A
L
③要在河边修建一个水泵站，向张村、李庄铺设管道送水，若张村、李庄到河边的垂直距离分别为1Km和3Km，张村与李庄的水平距离为3Km，则所用水管最短长度
为。

3．如图是一个长方体木块，已知AB=5，BC=3，CD=4，假设一只蚂蚁在点A 处，它要沿着木块侧面爬到点D
处，则蚂蚁爬行的最短路径是 。

4．现要在如图所示的圆柱体侧面A 点与B 点之间缠一条金丝带（金丝带的宽度忽略不计），圆柱体高为6cm ，底面圆周长为16cm ，则所缠金丝带长度的最小值为 。

5．如图是一个圆柱体木块，一只蚂蚁要沿圆柱体的表面从A 点爬到点B 处吃到食物，知圆柱体的高为5 cm ，底面圆的周长为24cm ，则蚂蚁爬行的最短路径为 。

6．正方形ABCD 的边长为8，M 在DC 上，且DM ＝2，N 是AC 上的一动点，DN ＋MN 的最小值为 。

7．在菱形ABCD 中，AB=2，∠BAD=60°，点E 是AB 的中点，P 是对角线AC 上的一个动点，则PE+PB 的最小值为 。

张村
李庄
A
B
C
D
A
B
A
B
图(2)
8．如图，在△ABC中，AC＝BC＝2，∠ACB＝90°，D是BC边的中点，E是AB边上一动点，则EC＋ED的最小值为____ ___。

9．如图，点P关于OA、OB的对称点分别为C、D，连接CD，交OA于M，交OB 于N，若CD＝18cm，则△PMN的周长为________。

10．已知，如图DE是△ABC的边AB的垂直平分线，D为垂足，DE交BC于E，且AC＝5，BC＝8，则△AEC的周长为__________。

11．已知，如图，在△ABC中，AB＜AC，BC边上的垂直平分线DE交BC于点D，交AC于点E，AC＝8，△ABE的周长为14，则AB的长。

12．如图，在锐角△ABC中，AB＝42，∠BAC＝45°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是____．
13．△ABC中，∠C = 90°，AB = 10，AC=6，BC=8，过AB边上一点P作PE⊥AC 于E，PF⊥BC于F，E、F是垂足，则EF的最小值等于．
14．如图，菱形ABCD中，AB=2，∠BAD=60°，点E、F、P分别是AB、BC、AC 上的动点，则PE+PF的最小值为___________.
15．如图，村庄A、B位于一条小河的两侧，若河岸a、b彼此平行，现在要建设一座与河岸垂直的桥CD，问桥址应如何选择，才能使A村到B村的路程最近．
16．一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．
（1）求该函数的解析式；
（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC＋PD的最小值，并求取得最小值时P点坐标．
17．如图，已知∠AOB内有一点P，试分别在边OA和OB上各找一点E、F，使得△PEF的周长最小。

试画出图形，并说明理由。

18．如图，直线l是第一、三象限的角平分线．
实验与探究：
（1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（－2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′、C′；
归纳与发现：
（2）结合以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为；
运用与拓广：
（3）已知两点D （1，－3）、E （－1，－4），试在直线l 上确定一点Q ，使点Q 到D 、E 两点的距离之和最小，并求出Q 点坐标．
19．几何模型：
条件：如图，A 、B 是直线L 同旁的两个定点．问题：在直线L 上确定一点P ，使PA+PB 的值最小．
方法：作点关于直线的对称点，连结交于点，则的值
最小（不必证明）．
模型应用：
（1）如图1，正方形的边长为2，为的中点，是上一动点．连结，由正方形对称性可知，
与关于直线对称．连结交于，则
的最小值是___________；
（2）如图2，的半径为2，点在上，，
，是上一动点，求的最小值；
（3）如图3，∠AOB=45°，P 是∠AOB 内一点，PO=10，Q 、R 分别是OA 、OB 上的动点，求△PQR 周长的最小值．
20．问题探究
（1）如图①，四边形是正方形，
，为边的中点，为
上的一个动点，求的最小值；
A l A 'A
B 'l P ABCD E AB P A
C B
D D AC ED AC P PB P
E +O ⊙A B C 、、O ⊙OA OB ⊥60AOC ∠=°P OB PA PC +ABCD E BC P BD PC PE + A
B
P
l
A B E C
B
D
图1
O
A
B C 图2
P O
A B P
R
Q 图3
（2）如图②，若四边形是菱形， ，，为边上的一个动点，为上的一个动点，求的最小值；
问题解决（3）如图③，若四边形ABCD 是矩形，
，，为
边上的一个动点，为上的一个动点，求的最小值；
ABCD 45ABC ∠=°E BC
P BD PC PE +20BC cm =E BC P BD PC PE +A D
B
C
A
D
B C
E P
A
C
D
B。

相关文档
最新文档