河南省正阳县第二高级中学2019届高三上学期9月月考试题 数学(理) Word版含答案
河南省正阳县第二高级中学2019届高三数学上学期周练(六)理

河南省正阳县第二高级中学2018-2019学年上期高三理科数学周练六一、选择题:1.已知集合{}2|20A x x x =->,集合{}b x a x B <<=且B A ⊆,则a b -的取值范围是( )A.(2,)-+∞B.[2,)-+∞C.(,2)-∞-D.(,2]-∞-2.下列命题中,真命题是( )A .00,0x x R e ∃∈≤使得B .2,2x x R x ∀∈>C .a>1,b>1是ab>1的充分条件D .22sin 3(,)sin x x k k Z x π+≥≠∈ 3.已知命题:[0,],cos 2cos 02p x x x m π∃∈+-=为真命题,则实数m 的取值范围是( )A. 9[,1]8--B. 9[,2]8- C. [1,2]- D. 9[,)8-+∞4. 执行右图的程序框图,若输出的5n =,则输入整数p 的最大值是( )A .15B .14C .7D .65.已知直线0=++c by ax 与圆1:22=+y x O 相交于,,A B 两点,且,3=AB 则OB OA ⋅ 的值是( )A .0B .12C .34- D .12- 6. 设221(32)=⎰-a x x dx ,则二项式261()-ax x 展开式中的第4项为( ) A .31280-x B .1280- C .240 D .240-7. 已知函数()()()210(2)0x ax x f x a e x ⎧+≥⎪=⎨-<⎪⎩为R 上的单调函数,则实数a 的取值范围是( ) A. (2,3] B.(2,)+∞ C.(,3]-∞ D.(2,3)8.在三角形ABC 中,已知060B ∠=,最大边与最小边的比为312,则三角形的最大角是( )A 060 B 075 C 090 D 0115 9.二次函数222y x x =-+与()20,0y x ax b a b =-++>>在它们的一个交点处的切线互相垂直,则14a b+的最小值是( )A165B 4 C185D24510.过双曲线M:x2-y2b2=1的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且|AB|=|BC|,则双曲线M的离心率是( )11.已知函数21(0)()(1)1(0)x xf xf x x⎧-≤=⎨-->⎩,把函数g(x)=f(x)-x+1的零点按从小到大的顺序排列成一个数列,则该数列的前n项的和nS,则10S=()A.15 B.22 C.45 D. 5012.抛物线22(0)y px p=>的焦点为F,点,A B在此抛物线上,且90AFB∠=,弦AB的中点M在该抛物线准线上的射影为'M,则|'|||MMAB的最大值为( )A3B.32C.1 D.22二.填空题13.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,则该三棱锥的外接球的体积为_______________.(第13题)(第4题)14.已知复数z1=a+b i,z2=1+a i(a,b∈R),若|z1|<z2,则b的取值范围是________.15.不等式组140xx ykx y≥⎧⎪+-≤⎨⎪≤⎩表示面积为1的直角三角形区域,则k的值为_______________.16.在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,三边a、b、c成等差数列,且B=4π,则|cosA一cosC|的值为____三、解答题:(解答应写出文字说明,证明过程或演算步骤。
河南省正阳县第二高级中学2019届高三数学上学期周练(四)文
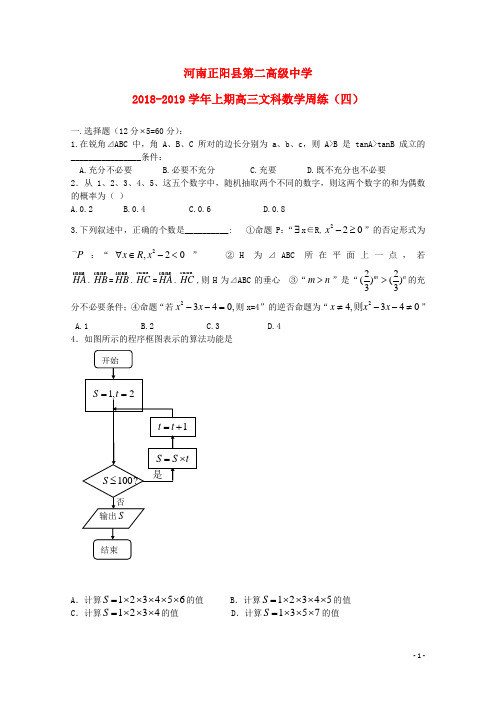
河南正阳县第二高级中学2018-2019学年上期高三文科数学周练(四)一.选择题(12分⨯5=60分):1.在锐角⊿ABC 中,角A 、B 、C 所对的边长分别为a 、b 、c ,则A>B 是tanA>tanB 成立的________________条件:A.充分不必要B.必要不充分C.充要D.既不充分也不必要2.从1、2、3、4、5、这五个数字中,随机抽取两个不同的数字,则这两个数字的和为偶数的概率为( )A.0.2B.0.4C.0.6D.0.83.下列叙述中,正确的个数是__________: ①命题P :“∃x ∈R,220x -≥”的否定形式为P ⌝:“2,20x R x ∀∈-<” ②H 为⊿ABC 所在平面上一点,若HA .HB =HB .HC =HA .HC ,则H 为⊿ABC 的垂心 ③“m n >”是“22()()33m n >的充分不必要条件;④命题“若2340,x x --=则x=4”的逆否命题为“24,340x x x ≠--≠则”A.1B.2C.3D.44.如图所示的程序框图表示的算法功能是A .计算123456S =⨯⨯⨯⨯⨯的值B .计算12345S =⨯⨯⨯⨯的值C .计算1234S =⨯⨯⨯的值D .计算1357S =⨯⨯⨯的值5.设{}n a 是公比为q 的等比数列,令1()n n b a n N +=+∈,若数列{}n b 的连续四项均在集合{53,23,19,37,82}--中,则q=_________ A.43- B.32- C.3223--或 D.3443-或- 6. 复数ii z +=1(其中i 为虚数单位)的虚部是 ( ) A.21- B.i 21 C.21 D.i 21- 7. 在⊿ABC 中, 角A 、B 、C 所对的边长分别为a 、b 、c ,3C π=,若,O D a O E b O F =+且D 、E 、F 三点共线(该直线不经过O 点),则⊿ABC 周长的最小值是____________ A.12 B.54 C.32 D.948.已知1122log (4)log (32)x y x y ++<+-,若x y λ-<恒成立,则λ的取值范围是_______ A.(,10]-∞ B.(,10)-∞ C.[10,)+∞ D.(10,)+∞9.已知函数2,0()2,0x x x x f x x ⎧-≤⎪=⎨->⎪⎩,则"()0"0"f x x ≤=是"的_______条件 A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要10.将函数sin y x x =+的图像向左平移m (m>0)个单位后得到一个偶函数的图像,则实数m 的最小值是____________ A.12π B. 6π C. 3π D.56π 11.从2013年1月1号开始,铁道部对火车票大面积降价,但降价幅度引发了争议。
河南省正阳县第二高级中学2019届高三数学上学期周测(一)理

河南省正阳县第二高级中学2018-2019学年上期高三理科数学周测一一.选择题:1.已知集合A={1,2},B=2{|280}x Z x x ∈--<,则A B =( )A.{1}B.{1,2}C.{0,1,2}D.{0,1,3}2.已知平面向量(1,2),(2,3)a b x ==-,若()a a b ⊥+,则x=_________A.6.5B.5.5C.4.5D.3.5 3.实数x,y 满足不等式组2421x y x y x +≤⎧⎪-≤⎨⎪≥⎩,则目标函数z=3x+2y 的最大值是____________A.2B.6C.7D.54.现有A ,B ,C ,D ,E 五人站成一排,其中A 与B 必须相邻,C 与D 不等相邻,则不同的排列方法有________种:A.12B.18C.24D.365.已知2()ln f x x x =+,则不等式(21)()f x f x -≥的解集是( ) A.1(,][1,)3-∞+∞ B.1(,0)(0,][1,)3-∞+∞ C.1[,1]3 D.(0,1]6.当a=_____时,直线340x y a ++=将圆2244x y x y +=+分成1:3两部分A.-4B.-24C.-16D.-4或-247.在△ABC 中,A ,B ,C 的对边分别为a,b,c,若A 、B 、C 依次成等差数列,a,c 分别为方程213400x x -+=的二根,则b=_______A.7B.5C.8D.68.若实数a,b,c 满足2520a b c ==,则211a b c+-的值为_________ A.1 B.0 C.2 D.49.若{}n a 为等差数列,,p q a q a p ==,则p q a +=( )A.1B.0C.2D.-110.已知椭圆22221(0)x y a b a b +=>>的左焦点为F ,点P(-3,1)在直线2x =上,经过点P 且方向向量为(2,5)-的直线,经过直线y=-2反射后通过椭圆的左焦点,则此椭圆的离心率为( )13 C.2 D. 12 11.三棱锥A-BCD 的所有棱长均为1,AB ∥平面α,则三棱锥A-BCD 上的所有点在平面α内的射影构成的图形面积的取值范围是( )A.11[,]42 B.1]42 C. 1,]42D. 4412.已知函数32(),()f x x ax g x bx c =+=+,它们的图像有一个公共点P(t,0)(t>0),且这两个函数的图像在点P 处有相同的切线,则a c b a+的值为( ) A.1 B.-1 C.2 D.0二.填空题:13.已知二次函数2()(21)1f x ax a x =+-+在区间3[,2]2-上的最大值为3,则正实数a 的值为( )14.在直棱柱111ABC A B C -中,∠ACB=90°,AC=6,1BC CC ==,P 为1BC 上一动点,则1CP PA +的最小值为( )15.圆O 的半径为1,PA 、PB 为该圆的两条切线,A ,B 为切点则.PA PB 的最小值为( )16.已知周期为4的函数(1,1]()12,(1,3]x f x x x ⎧∈-⎪=⎨--∈⎪⎩,若3f(x)=x 恰好有5个实数解,则正实数m 的取值范围是三.解答题:17.在△ABC 中,a,b,c 分别是A ,B ,C 的对边,已知△ABC 的面积为23sin a A(1)求sinB.sinC (2)若6cosBcosC=1,a=3,求△ABC 的周长18. 已知命题P:直线x+3=2y 与抛物线2(0)y mx m =≠没有交点;已知命题q:方程22152x y m m+=-表示双曲线;若p q ∨为真,p q ∧为假,试求实数m 的取值范围.19.如图,三棱柱111C B A ABC -中,CB AC =,1AA AB =,0160=∠BAA(1)证明:C A AB 1⊥;(2)若平面⊥ABC 平面B B AA 11,CB AB =,求直线C A 1与平面C C BB 11所成角的正弦值.20. 已知12,F F 是椭圆22221(0)x y a b a b+=>>的左右焦点,O 为原点,(2,5P -在椭圆上,线段1PF 与y 轴的交点N 满足12OP OF ON +=.(1)求椭圆的标准方程;(2)过椭圆右焦点2F 作直线l 交椭圆于A,B 两点,交y 轴于M 点,若1222,MA AF MB BF λλ==,求12λλ+.21. 已知函数()x x f ln =,()xg x e =. (1)求函数()x x f y -=的单调区间与极值;(2)求证:在函数()f x 和()g x 的公共定义域内,()()2g x f x ->恒成立.22. 在直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系。
河南省正阳县第二高级中学2019届高三数学上学期周练(十三)理

河南省正阳县第二高级中学2017-2018学年上期高三理科数学周练十三一.选择题:1.已知全集{}1,2,3,4,5,6U =,集合{}1,2,4A =,{}2,4,6B =,则()UA B =A .{}1B .{}2C . {}4D .{}1,22.已知复数z =103i+2i -(其中i 是虚数单位),则z =( ) 2 3 2 3 3.已知),0(πα∈,且,21cos sin =+αα则α2cos 的值为( ) A. 47± B.47- C.47 D. 43-4.设,a b 为向量, 则“..a b a b =”是“a b 分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5. 已知实数,x y 满足约束条件332434120y x y x x y ≥-⎧⎪≤+⎨⎪++≥⎩,则2z x y =-的最大值为( )A .2B .3C . 4D .56.一直线l 与平行四边形ABCD 中的两边,AB AD 分别交于点,E F ,且交其对角线AC 于点M ,若2AB AE =,3AD AF =,(,)AM AB AC R λμλμ=-∈,则52μλ-=( )A .12-B . 1C . 32D .3-7.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )cm 3. A .4+23π B .4+ 32π C .6+23π D .6+32π8. 已知P 是双曲线22221x y a b-= (a >0,b >0)上的点,F 1,F 2是其焦点,双曲线的离心率是54,且12.0PF PF =,若△PF 1F 2的面积为9,则a +b 的值为( ) A .5 B .6 C .7 D .89. 设抛物线y 2=8x 的焦点为F ,准线为l ,P 为抛物线上一点,PA⊥l ,A 为垂足.如果直线AF 的斜率为-3,那么|PF|等于( ) A .4 3 B .8 C .8 3D .1610.定义12...nnp p p +++为n 个正数12,,...,n p p p 的“均倒数”.若已知数列{}n a 的前n 项的“均倒数”为121n +,又14n n a b +=,则122320152016111...b b b b b b +++ = A.20132014 B. 20142015 C. 20152016 D. 1201511、在△ABC 中,BC=7 ,AC=6 ,26cos C =.若动点P 满足2(1)3AP AB AC λλ=-+,λ为实数,则点P 的轨迹与直线BC ,AC 所围成的封闭区域的面积为( )C.6D. 612、设函数f(x)满足223/2()(),(2)8xe xf x x f x e f +==,则2x ≥时,f(x)的最小值为( )A. 22eB. 232e C. 24e D. 28e二.填空题: 13.2321(44)x x ++展开式的常数项为 14. 已知抛物线的方程为22(0)y px p =>, O 为坐标原点, A , B 为抛物线上的点,若OAB 为等边三角形,且面积为483p 的值为__________.15. 已知O 为△ABC 的外接圆的圆心,||16,||102AB AC ==若AO x AB y AC =+, 且322525x y +=,则||AO = 16. 已知函数()f x 满足(1)(ln )1()=(ln )e f x f x f x -+,当(0,1]x ∈时,()xf x e =,设()()g x f x kx =-,若方程()g x e =在(0,]e 上有且仅有3个实数解,则实数k 的取值范围是 .三.解答题:17. 已知ABC 的内角,,A B C 的对边分别为,,a b c 且有2224ABCa b c S+-=.(Ⅰ)求角C 的大小;(Ⅱ)若2c =2a -的取值范围. 18. 在四棱锥P —ABCD 中,AD ∥BC ,∠ABC=∠APB=90°,点M 是线段AB 上的一点,且PM ⊥CD ,AB=BC=2PB=2AD=4BM .(1)证明:面PAB ⊥面ABCD ; (2)求直线CM 与平面PCD 所成角的正弦值.19. 某科技公司生产一种手机加密芯片,其质量按测试指标划分为:指标大于或等于70为合格品,小于70为次品.现随机抽取这种芯片共120件进行检测,检测结果统计如表:测试指标 [)50,60[)60,70[)70,80[)80,90[]90,100芯片数量(件) 82245378已知生产一件芯片,若是合格品可盈利400元,若是次品则亏损50元.(1)试估计生产一件芯片为合格品的概率;并求生产3件芯片所获得的利润不少于700元的概率.(2)记X 为生产4件芯片所得的总利润,求随机变量X 的分布列和数学期望PABMCD20. 已知一动点M 到直线4-=x 的距离是它到()0,1-F 距离的2倍.(1)求动点M 的轨迹方程C ;(2)若直线l 经过点F ,交曲线C 于B A ,两点,直线AO 交曲线C 于D .求ABD ∆面积的最大值及此时直线BD 的斜率.21. 已知函数()2()3,xmf x e x a a R =--+∈(1)若m=1时,函数f(x)存在两个零点,求a 的取值范围(2)若m=2时,不等式()0f x ≥在[0,)+∞上恒成立,求a 的取值范围四.选做题:22. 已知曲线1C 的参数方程为()为参数θθθ⎩⎨⎧==sin 3cos 2y x ,以原点O 为极点,以x 轴的非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为ρθθ1cos sin =-m .(1)求1C ,2C 的直角坐标方程;若曲线2C 与1C 交于N M ,两点,与x 轴交于P 点,若,2PN MP = 的值求m23. 已知函数f (x )=|x ﹣a|+12a(a≠0). (1)若a=1,解关于x 的不等式f (x )≥|x﹣2|;(2)若不等式f (x )﹣f (x+m )≤1恒成立,求正数m 的最大值.7-12. DCBCAD 16. 211(,]4e e --17.(1)45°(2)(2)- 18.(1)略(2)75113619.(1)2732(2) X 1600 1150 700 250 -200 P81:25627:6427:1283:641:256E (X )=115020.(1)22143x y +=(2)3 21.(1)5a >-(2)[ln 35]-22.(1)22143x y +=,x-my+1=0 (2)2523.(1)5[,)4+∞ (2) 1。
河南省正阳县第二高级中学2019高三上学期10月月考(理科)科数学试卷含答案

河南省正阳县第二高级中学2018-2019学年上期高三10月月考理科数学一.选择题:1.已知集合2{|20}M x x x =--<,2{|1,}N y y x x R ==-+∈,则MN =____A.{|21}x x -≤<B.{|12}x x <<C. {|11}x x -<≤D. {|12}x x ≤<2.函数sin()23x y π=-+在[2,2]x ππ∈-上的单调递减区间是( ) A.5[,]33ππ- B. 5[2,]3ππ- C. [,2]3ππ D. 5[2,]3ππ-和[,2]3ππ3.已知2222()123...(2)f n n =++++,则f(k+1)与f(k)的关系式( ) A.22(1)()(21)(22)f k f k k k +=++++ B.2(1)()(1)f k f k k +=++ C. 2(1)()(22)f k f k k +=++ D. 2(1)()(21)f k f k k +=++ 4.设n S 为等比数列{}n a 的前n 项和且13n n S A +=-,则A=_________ A.13- B.13C.-3D.3 5.已知点P(x,y)在不等式组20020x y x y y -≥⎧⎪-≤⎨⎪-≤⎩表示的平面区域上运动,则z=x+y 的最大值时( )A.4B.3C.2D.16.高三在新的学期里,刚刚搬入新教室,随着楼层的升高,上下楼耗费的精力增多,因此不满意度升高,当教室在第n 层楼时,上下楼造成的不满意度为n,但高处空气清新,嘈杂音较小,环境较为安静,因此随教室所在楼层升高,环境不满意度降低,设教室在第n 层楼时,环境满意度为8n,则同学们认为最适宜的教室应在( )楼 A.2 B.3 C.4 D.87.执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )A.k<32B.k<33C.k<64D.k<658.已知函数y=f(2x-1)的定义域是[0,1],则2(21)log (1)f x x ++的定义域是( )A.[1,2]B.(1,1]- D.1[,0]2- D.(-1,0)9.在△ABC 中,a,b,c 分别是角A ,B ,C 的对边,且2222sin )ab C b c a =+-,若则△ABC 的面积是( )A.3B.C.10.某几何体的三视图如图所示,则该集合体中,面积最大的侧面的面积是( )B.C. D.311.已知双曲线22142x y -=的右焦点为F ,P 为左支上的一点,点A ,则△ABF 的周长的最小值为( )A.4(1+B. 4C.12.若对,x y R ∀∈,有f(x+y)=f(x)+f(y)-2,则函数22()()1xg x f x x =++的最大值和最小值之和为( )A.4 B.6 C.9 D.12二.填空题:13.已知函数2()422f x x ax a =+++的值域是[0,)+∞,则a 的取值集合为__________14.已知20sin()x dx πϕ-=⎰,则sin 2ϕ=____________ 15.设1e ,2e 是夹角为60°的单位向量,1223OP e e =+,则OP =( )16.已知12,F F 是双曲线22221(0,0)x y a b a b-=>>的左右焦点,以12F F 为直径的圆与双曲线的一条渐近线交于点M ,与双曲线交于点N ,且M,N 均在第一象限,当1MF ∥ON 时,双曲线的离心率为e,若函数22()2f x x x x=+-,则f(e)=__________三.解答题:17.记n S 为等差数列{}n a 的前n 项和,已知113926,81a a S +== (1)求数列{}n a 的通项公式(2)令12121,...n n n n n b T b b b a a ++==+++,若300n T m -≤对一切正整数n 成立,求实数m 的取值范围18.某超市计划订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格每天全部处理完。
河南省正阳县第二高级中学2019-2020学年高二上学期9月月考数学试卷 Word版含答案

河南省正阳县第二高级中学 2019-2020学年上期九月月考数学试卷一.选择题(60分)1.在△ABC 中,角A 、B 、C 对应的边分别是a 、b 、c ,已知60,A a ︒==b=4,则B=A.300B.450C.600D.9002.在等差数列{a }n 中,已知12a =,2316a a +=,则456a a a ++等于 A.50 B.52 C.54 D.563.在△ABC 中,角A B C 、、对应的边分别是a ,b ,c ,已知A =60°,b =1,△ABC,则△ABC 外接圆的直径为A.81B.C.3D.34. 在等差数列{}n a 中,若12344,12a a a a +=+=,则56a a +=( ) A.8 B.16 C.20 D.285. 在△ABC 中,角A 、B 、C 的对边为a,b,c ,且a cosA=b cosB,则此三角形为( )三角形A.等腰B.直角C.等腰三或直角D.等腰直角 6. 若数列{}n a 满足111n nd a a +-=(d 为常数),则称数列{}n a 为“调和数列”.已知数列1{}nx 为调和数列,且12320...200x x x x ++++=,则318x x +=( ) A.50 B.100 C.150 D.20 7. 一船向正北方向航行,看见正西方向有两个相距10海里的灯塔恰好与它在一条直线上,继续航行半小时后, 看见一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是 ( ) A. 5海里/时 B.海里/时 C. 10海里/时 D. /时 8.若数列{}n a 满足1119,3()n n a a a n N ++==-∈,而数列{}n a 的前n 项和最大时,n 值为( ) A. 6 B. 7C. 8D. 99.在△ABC 中,a,b,c 分别为角A,B,C 所对的边,若a=2b cosC,则此三角形一定是( )三角形A.等腰B.直角C.等腰三或直角D.等腰直角 10.在等差数列{}n a 中,n S 为其前n 项之和,若1020100,400S S ==,则30S =( )A.300 B.900 C.1600 D.600 11. 在△ABC 中,a,b,c 分别为角A,B,C 所对的边,S 为△ABC 的面积,23sin b S B=,若tanA.tanC=4,则∠B=( ) A.60° B.30° C.120° D.150°12.设n S 为{}n a 的前n 项之和,若不等式22212nnS a a nλ+≥对任意首项非零的等差数列{}n a 以及任意正整数n 恒成立,则实数λ的最大值为( ) A.15B.14 C. 45D.4 二.填空题(20分):13.若n S 为正项等差数列{}n a 的前n 项之和,且221n n S a -=,则20S =( ) 14. 在△ABC 中,a,b,c 分别为角A,B,C 所对的边,若a sin2B=bsinA,则B=( )15. 在△ABC 中,a=16,B=30°,使△ABC 有两解的b 的取值范围是( ) 16.在△ABC 中,a,b,c 分别为角A,B,C 所对的边,n S 为等差数列{}n a 的前n 项之和,若函数2()(58)(sin )f x a b x B x =-+为一个奇函数,22375n S n n b c =-+-,则cosB=( )三.解答题:17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin()B A B ac =+==(10分) (1)求sinA 的值; (2)求b 和c 的值。
河南省正阳县第二高级中学2019届高三上学期理科数学周练(五) Word版含答案
河南省正阳县第二高级中学 2018-2019学年高三上期理科数学周练五一.选择题(12X5=60分):1.已知命题p :x a x f =)((a >0且a ≠1)是单调增函数:命题)45,4(:ππ∈∀x q ,x x cos sin >则下列命题为真命题的是( )A.q p ∧B.q p ⌝∨C.q p ⌝∧⌝D.q p ∧⌝ 2. 已知复数z 满足(z+2i)(3+i)=7-i ,则复数z 在复平面内对应的点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.的球的体积与一个长、宽分别为6、4的长方体的体积相等,则长方体的表面积为( )A .44 B .54 C .88 D .1084. 如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A.263π+B.83π+ C.243π+ D.43π+5. .以(,1)a 为圆心,且与两条直线240x y -+=与260x y --=同时相切的圆的标准方程为( )A.()()22115x y -+-=B.()()22115x y +++= C.()2215x y -+= D.()2215x y +-= 6. 函数1ln --=x ey x的图像大致是( )7. 在ABC ∆中,已知cos cos )4cos cos B B C C B C --=,且AB+AC=4,则BC 长度的取值范围为( )A .(]0,2B . [)2,4C . [)2,+∞ D . ()2,+∞ 8. 如图所示,程序框图的功能是( ) A .求{n 1}前10项和 B .求{n 21}前10项和 C .求{n 1}前11项和 D .求{n21}前11项和 9. 已知y x ,满足约束条件⎪⎩⎪⎨⎧≤≥-+≥+-301205x y x y x ,则22(1)z x y =++的最小值是 .A.15 B.25 C.45 D. 3510. 已知抛物线28,y x P =为其上一点,点N(5,0),点M 满足||1,.0MN MN MP == ,则||MP 的最小值为( )B.4D.11. 定义一种运算(,)a b ※(c,d)=ad-bc ,若函数3()(1,log )f x x =※131(tan,)45x π,0x 是方程f(x)=0的解,且010x x <<,则1()f x 的值( )A .恒为负值B .等于0C .恒为正值D .不大于012.已知正实数是自然对数的底数其中满足、、e c c a b c ace c b a ,ln ln ,21+=≤≤,则abln 的取值范围是( ) A. [)∞+,1 B. ⎥⎦⎤⎢⎣⎡+2ln 21,1 C. (]1,-∞-e D. []11-e , 二.填空题(4X5=20分):13. 已知函数1)(-=x x f ,关于x 的方程0)()(2=+-k x f x f ,若方程恰有8个不同的实根,则实数k 的取值范围是 .14. 曲线y =e x 在点(0,1)处的切线与曲线y =1x (x >0)上点P 处的切线垂直,则P 的坐标为_____ 15. 在ABC 中,边AB 的垂直平分线交边AC 于D ,若,8,73C BC BD π===,则ABC 的面积为 .16. 已知椭圆C :22221(0)x y a b a b+=>>的上顶点为A ,右焦点为F ,椭圆C 上存在点P 使线段OP 被直线AF 平分,其中O 为原点,则椭圆C 的离心率的取值范围是______.第5题图三.解答题:17. (本小题满分12分)已知向量a =(sinx,-cosx),b =(3cosx,cosx),设函数f(x)=.a b.(1)求函数f(x)在(0,π)上的单调增区间;(2)在△ABC 中,已知a,b,c 分别为角A,B,C 的对边,A 为锐角,若f(A)=0,sin(A+C)=3sinC,C =3,求边a 的长18.假设{}n a 时递增的等比数列,已知131235,3,3,4a a a a a +=++成等差数列 (1)求数列{}n a 的通项(2)令31ln n n b a +=,求数列{}n b 的前n 项和n T19. (本小题满分12分)如图,已知等边ABC ∆中,,E F 分别为,AB AC 边的中点,M 为EF 的中点,N 为BC 边上一点,且14CN BC =,将AEF ∆沿EF 折到A EF '∆的位置,使平面A EF '⊥平面EF CB -.(I)求证:平面A MN '⊥平面A BF ';(II)求二面角E A F B '--的余弦值.20.已知椭圆)0(12222>>=+b a b y a x 的中心为O ,它的一个顶点为()1,0,离心率为22,过其右焦点的直线交该椭圆于B A ,两点. (1)求这个椭圆的方程; (2)若OB OA ⊥,求OAB ∆的面积.21. 在区间D 上,如果函数f (x )为增函数,而函数()f x x为减函数,则称函数f (x )为“弱增函数”.已知函数f (x )=1(1)判断函数f (x )在区间(0,1]上是否为“弱增函数”; (2)设x 1,x 2∈[0,+∞),且x 1≠x 2,证明:|f (x 2)﹣f (x 1)|<1212x x -; (3)当x ∈[0,1]时,不等式1﹣ax1﹣bx 恒成立,求实数a ,b 的取值范围.选做题:22.(本小题满分10分)选修4-4:坐标系与参数方程已知圆C 在极坐标方程为4cos 2sin ρθθ=-,直线l 的参数方程为5cos ,sin x t y t αα=+⎧⎨=⎩(t 为参数).若直线l 与圆C 相交于不同的两点,P Q .(Ⅰ)写出圆C 的直角坐标方程,并求圆心的坐标与半径;(Ⅱ)若弦长4PQ =,求直线l 的斜率.23.设()10f x x x =++.(Ⅰ)求()15f x x ≤+的解集M ;(Ⅱ)当,a b M ∈时,求证:525a b ab +≤+.参考答案:1-6.DBCCAD 7-12.ABBCAD13.1(0,)4 14.(1,1) 15. 16.17.(1)[,],63k k k Z ππππ-+∈(218.(1)12n n a -=(2)3(1)ln 22n T n n =+19.(1)略(220.(1)2212x y +=(221.(1)略(2)略(3)12a ≥或1b ≤- 22.(1)22(2)(1)5x y -++=(2)0或0.75 23.(1)[-5,5](2)略。
河南省正阳县第二高级中学2019届高三上学期理科数学周练(十二)(精校Word版含答案)
河南省正阳县第二高级中学2018-2019学年上期高三理科数学周练十二一.选做题:1.集合M={y|y=lg (x 2+1)},N={x|4x <4},则M ∩N 等于( ) A .[0,+∞) B .[0,1) C .(1,+∞)D .[0,1)2.设复数z 1,z 2在复平面内的对应点关于虚轴对称,z 1=2+i ,则z 1z 2=( ) A .﹣5 B .5 C .﹣4+i D .﹣4﹣i3.角θ的终边与单位圆的交点的横坐标为-0.5,则tanθ的值为( )A .B .±1C .D .4. 下列命题中,真命题是A .00,0x x R e ∃∈≤B .2,2x x R x ∀∈>C .a+b=0的充要条件是1ab=- D .a>1,b>1是ab>1的充分条件 5. 在如图所示的正方形中随机投掷1000个点,则落入阴影部分(曲线C 为正态分布N (-1,1)的密度曲线)的点的个数的估计值为A . 1193B .1359C .2718D .3413附:若2(,)XN μσ,则()0.6826P X μσμσ-<<+=(22)0.9544P X μσμσ-<<+=6. 设P 是双曲线22221(0,0)x y a b a b-=>>上除顶点外的任意一点,12,F F 分别是双曲线的左、右焦点,△12PF F 的内切圆与边12F F 相切于点M ,则12.FM MF = A .2a B .2b C .2a + 2b D .0.52b7.已知函数y=f(x)是周期为2的周期函数,并且当[1,1]x ∈-时,()21xf x =-,则函数()()lg F x f x x =-的零点个数是A .9B .10C .11D .128. △ABC 中,内角A 、B 、C 对边分别为a 、b 、c ,c 2=(a -b)2+6,C =π3,则△ABC 的面积为( )A.332B.932 C .3 D . 3 39. 已知三棱锥P -ABC 的各顶点都在以O 为球心的球面上,且PA 、PB 、PC 两两垂直,若PA =PB =PC =2,则球心O 到平面ABC 的距离为( )A.233B. 3 C .1 D.3310.定义:分子为1且分母为正整数的分数称为单位分数.我们可以把1分拆为若干个不同的单位分数之和.如:1111236=++,1111124612=+++,1111112561220=++++, 依此类推可得:1111111111111126123042567290110132156m n =++++++++++++,其中n m ≤,*,m n ∈N .设n y m x ≤≤≤≤1,1,则12+++x y x 的最小值为( )A.223B. 25C.78D.33411. 已知圆C :22210x y x +--=,直线:34120l x y -+=,圆C 上任意一点P 到直线l 的距离小于2的概率为( ) A .16 B .13 C .12 D .1412. 已知函数11,2()2ln ,2x x f x x x ⎧+≤⎪=⎨⎪>⎩,方程()0f x ax -=恰有3个不同实根,则实数a 的取值范围是( )A .ln 21(,)2e B .1(0,)2 C .1(0,)e D .11(,)2e 二.填空题:13.等腰直角三角形ABC 的斜边BC =().AB AC BC BA BC ++-= . 14.将3名支教教师安排到2所学校任教,每校至多2人的分配方法总数为a,则二项式53(x a 的展开式中含x 项的系数为 (用数字作答). 15. 若一元二次不等式2(2)20mx m x +-->恰有3个整数解,则实数m 的取值范围是 16. 在△ABC 中,已知AB=8,BC=7,cos (C ﹣A )=1314,则△ABC 的面积为 .解答题:17. 设数列{a n }的前n 项和S n =2n+1,数列{b n }满足b n =21(1)log nn n a -+.(1)求数列{a n }的通项公式;(2)求数列{b n }的前n 项和T n .18. 在2016年,我国诸多省市将使用新课标全国卷作为高考用卷.(以下简称A 校)为了调查该校师生对这一举措看法,随机抽取了30名教师,70名学生进行调查,得到以下22⨯列联表:”与“师生身份”有关?(2)现将这100名师生按教师、学生身份进行分层抽样,从中抽取10人,试求恰好抽取到持“反对使用新课标全国卷”态度的教师2人的概率;(3)将上述调查所得到的频率视为概率,从A 校所有师生中,采用随机抽样的方法抽取4位师生进行深入调查,记被抽取的4位师生中持“支持新课标全国卷”态度的人数为X. ①求X 的分布列;②求X 的数学期望E(X)和方差D(X).参考公式:22()()()()()n ad bc K a b c d a c bd -=++++,其中n=a+b+c+d.19. 已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c 3cos()2aA π=+. (I )求C 的值;(II )若c=2a ,b=△ABC 的面积. 20. 已知直棱柱ABC ﹣A 1B 1C 1中,AC=BC=CC 1=2AB ,E 是线段CC 1的中点,连接AE ,B 1E ,AB 1,B 1C ,BC 1,得到的图形如图所示. (I )证明BC 1⊥平面AB 1C ;(II )求二面角E ﹣AB 1﹣C 的大小.21. 已知椭圆22221(0)x y a b a b+=>>的右焦点F ,过点F 作平行于y 轴的直线截椭圆C(1)求椭圆的标准方程 (2)过点(1,0)的直线m 交椭圆C 于P 、Q 两点,N 点在直线x=-1上,若△NPQ 是等边三角形,求直线m 的方程。
河南省正阳县第二高级中学2019届高三上学期理科数学周练(八) Word版含答案
河南省正阳县第二高级中学2018-2019学年上期高三理科数学周练八一、选择题:本大题共12个小题,每题5分,共60分。
每小题所给四个选项中,只有一个选项符合题目要求。
1.若集合{|23},M x x =-<<2{|1,}N y y x x R ==+∈,则集合MN =( )A. (2,)-+∞B. (2,3)-C. [1,3)D. R 2. 关于x 的二次方程)(,01)2(2R a ai x i x ∈=+++-有实根,则复数ia aiz +-=2对应的点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.阅读右面程序框图,如果输出的函数值在区间11[,]42内,则输入的实数x 的取值范围是( )A.(,2]-∞-B.[-2,-1]C.[-1,2]D.[2,)+∞ 4.直线l 与函数sin ,[0,]y x x π=∈的图像相切于点A ,且l ∥OP ,O 为坐标原点,P 为图像的一个最高点,与x 轴交于点B ,过切点A 作x 轴的垂线,垂足为C ,则BA BC ⋅=( )A. 2B. 2πC. 24πD. 244π-5.已知 a b ,为非零向量,则“函数2()()f x ax b =+为偶函数”是“a b ⊥”的 ( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件6、等差数列{}n a 的前n 项和为n S ,且3456,8,20S S S ≤≥≤当4a 取得最大值时,数列{}n a 的公差为( ) A. 1 B. 4C. 2D. 37.若圆C: 222430x y x y ++-+=关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )A. 2B. 3C. 4D. 68.平面四边形ABCD 中,1===CD AD AB ,CD BD BD ⊥=,2,将其沿对角线BD 折成四面体BCD A -',使平面⊥BD A '平面BCD ,若四面体BCD A -'顶点在同一个球面上,则该球的体积为( )A. π23B. π3C. π32D. π2 9、已知函数①y=sinx+cosx,②cos y x x =,则下列结论正确的是( )正视图 侧视图 俯视图 A.两个函数的图象均关于点(,0)4π-成中心对称.B.①的纵坐标不变,横坐标扩大为原来的2倍,再向右平移4π个单位即得②. C.两个函数在区间(,)44ππ-上都是单调递增函数. D.两个函数的最小正周期相同.10.设F 1, F 2分别为双曲线2221x a b2y (a >0,b>0)的左、右焦点,P 为双曲线右支上任一点。
精品2019届高三数学上学期第二次月考试题 理(无答案)新 人教版新版
2019学年度上学期高三年级第二次月考数学试卷(理)满分:150分 时间:120分钟一、选择题(每小题5分,共60分)1.设向量()()1,2,,1a b m =-=,若向量2a b +与2a b -平行,则 m =( ) A .B .C.D .2.下列命题错误的是( )A .命题“若0m >,则方程20x x m +-=有实数根”的逆否命题为:“若方程20x x m +-=无实数根,则0m ≤”B .若p q ∨为真命题,则p ,q 至少有一个为真命题C .“1x =”是“2320x x +=-”的充分不必要条件D .若p q ∧为假命题,则p ,q 均为假命题3.已知 1.30.72,4,ln6a b c ===,则,,a b c 的大小关系为( ) A. a b c <<B. b c a <<C. c a b <<D. c b a <<4.已知,()0 x π∈,,则 tan x =( )A.B.D. 5.已知函数()()()()3512log 1a a x x f x a xx -+≤⎧⎪=⎨->⎪⎩对于任意21x x ≠都有()()02121<--x x x f x f 成立,则实数a 的取值范围是( ) A .(]1,3B. ()1,3C. (]1,2D. ()1,26.已知命题()():0,32:,0,32xxp x q x x x ∀∈+∞>∃∈-∞>,;命题,则下列命题为真命题的是( ) A .P ∧qB .()p q ∧⌝C .()p q ⌝∧D .()()p q ⌝∧⌝7.定义行列式运算=a 1a 4﹣a 2a 3.将函数f (x )=的图象向左平移n (n >0)个单位,所得图象对应的函数为偶函数,则n 的最小值为(). A .6πB .56π C .3π D .23π 8.定义在R 上的函数()y f x =满足()555,'0f x f x x f x ⎛⎫⎛⎫⎛⎫+=-->⎪ ⎪ ⎪,则对任意的()()1212,x x f x f x <>,是125x x +<的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件9.已知非零向量 a ,b 的夹角为 60︒,且满足 |2|2a b -=,则 a b ⋅的最大值为( ) A .12B .1C .2D .310.已知0a >,0b >,'()f x 为()f x 的导函数,若()ln 2x f x =,且31112'()12b b dx f a b x =+-⎰,则a b +的最小值为( ) A.B.C .92D.92+ 11.已知()()23,x f x x g x me =-=,若方程()()f x g x =有三个不同的实根, 则m 的取值范围是( )A .360,e ⎛⎫ ⎪⎝⎭B .363,e ⎛⎫- ⎪⎝⎭C .362,e e ⎛⎫- ⎪⎝⎭D .()0,2e 12.已知0,2x π⎛⎫∈ ⎪⎝⎭,则函数()sin tan cos cot f x x x x x =+的值域为( ) A .[)12, B.)∞ C.(1 D .[)1+∞,二、填空题(每小题5分,共20分)13.如右图,正方形ABCD 中,M ,N 分别是BC ,CD 的中点,若 AC AM BN λμ=+,则 λμ+= . 14. 已知函数sin 4y x πω⎛⎫=+⎪⎝⎭( 0ω>)的周期为π,求f (x )在区间34ππ⎡⎤⎢⎥⎣⎦,上的值域为 .15.在△ABC 中,边AB 的垂直平分线交边AC 于D ,若C=BC=8BD=73π,,,,则 ABC ∆的面积为 . 16. 已知关于 x 的函数()222sin 42cos tx x xf x x xπ⎛⎫+++ ⎪⎝⎭=+的最大值为a ,最小值为b ,若2a b +=,则实数 t 的值为_________. 三、解答题(共70分)17.(10分)设()()21;:lg -2+1l :2-g 03++1x q x t x t t P ≤≤.(1)若q 是所表示不等式的解集为{}=10100A x x ≤≤,求实数t 的值.(2)若¬¬p q 是的必要不充分条件,求实数t 的取值范围.18.(12分)已知锐角三角形ABC 中,.51)sin(,53)sin(=-=+B A B A (1)求tan tan AB; (2)设AB=3,求AB 边上的高.19.(12分)已知函数1tan x 2x )x (f 2-θ⋅+=,x∈[3-,3],θ∈(2π-,2π). (1)当θ=6π-时,求函数f (x)的最大值与最小值;(2)求θ的取值范围,使y= f (x)在区间[-1]上是单调函数.20.(12分)在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos 2cos 2cos A C c aB b--=. (I )求sin Csin A的值; (II )若cosB=14,b=2,△ABC 的面积S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省正阳县第二高级中学
2018—2019学年上期高三9月考试数学(理)
一.选择题:
1.已知:如图,集合U 为全集,则图中阴影部分表示的集合是 A .C U (A∩B )∩C B .C
U (B∩C )∩A C .A∩C U (B ∪C ) D .C U (A ∪B )∩C
2.已知x ∈C ,若关于x 实系数一元二次方程2ax +bx +c =0 (a ,b ,c ∈R ,a≠0)有一根为1+i .则该方程的另一根为 A .-1+i B .1-i C .-1-i D .1
3.已知函数f (x )=x e 1++x e 1-,则满足f (x -2)<e 2+1的x 的取值范围是 A .x <3 B .0<x <3 C .1<x <e D .1<x <3 4.己知数列{n a }为正项等比数列,且a 1a 3+2a 3a 5+a 5a 7=4,则a 2+a 6= A .1 B .2 C .3 D .4 5.市场调查发现,大约
4
5
的人喜欢在网上购买家用小电器,其余的人则喜欢在实
体店购买家用小电器。
经工商局抽样调查发现网上购买的家用小电器合格率约为
1720,而实体店里的家用小电器的合格率约为910。
现工商局12315电话接到一个关于家用小电器不合格的投诉,则这台被投诉的家用小电器是在网上购买的可能性是
A .
67 B .56 C .45 D .25
6.已知:sinα+cosβ=3
2
,则cos2α+cos2β的取值范围是
A .[-2,2]
B .[-3
2
,2]
C .[-2,32]
D .[-32,3
2
]
7.某篮球运动员6场比赛得分如下表:(注:第n 场比赛得分为n a )
在对上面数据分析时,一部分计算如右算法流程图(其中a 是
这6个数据的平均数),则输出的s 的值是 A .
73 B .2 C .53 D .4
3
8.已知:8
(2)x x -=a 0+a 1(x -1)+a 2(x -1)2+…+a 9(x -1)9,则a 6= A .-28 B .-448
C .112
D .448
9.某多面体的三视图如图所示,每一小格单位长度为l ,则
该多面体的外接球的表面积是
A .27π
B .
27
2π C .9π D .27
4
π
10.已知抛物线C :2
y =4x ,过抛物线C 焦点F 的直线l 交抛物线C 于A 、B 两点(点A
在第一象限),且交抛物线C 的准线于点E .若AE uu u r =2BE uur
,则直线l 的斜率为
A .3
B .
C
D .1
11.设r 是方程f (x )=0的根,选取x 0作为r 的初始近似值,过点(x 0,f (x 0))做曲线y
=f (x )的切线l ,l 的方程为y =f (x 0)+0()f x '(x -x 0),求出l 与x 轴交点的横坐 标x 1=x 0-
00()
()
f x f x ',称x 1为r 的一次近似值。
过点(x 1,f (x 1))做曲线y =f (x )的 切线,并求该切线与x 轴交点的横坐标x 2=x 1-
11()
()
f x f x ',称x 2为r 的二次近似值。
重复 以上过程,得r 的近似值序列,其中,1n x +=n x -
()
()
n n f x f x ',称为r 的n +1次近似值,
是方程2x -6=0的一个根,若取x 0=2作为r 的初始
≈
A .2.4494
B .2.4495
C .2.4496
D .2.4497
12.己知函数f (x )=21
2ln ,1x e ax x a x x ⎧⎨⎩
-,≤+>在定义域(-∞,+∞)上是单调增函数,则实数a 的
取值范围是 A .(-∞,
2e ] B .[3e ,+∞) C .[3e ,2e ] D .(3e ,2
e )
第Ⅱ卷 非选择题(共90分)
二、填空题(每小题5分,共20分)
13.已知P 是边长为2的正△ABC 边BC 上的动点,则AP uu u r · (AB uu u r +AC uuu r
)=_________.
14.某学生计划用不超过50元钱购买单价分别为6元、7元的软皮和硬皮两种笔记本,根据
需要软皮笔记本至少买3本,硬皮笔记本至少买2本,则不同的选购方式共有__________种.
15.已知双曲线C :22
221x y a b
-=(a >0,b >0),其右焦点为F (c ,0),O 为坐标原点,以
OF 为直径的圆交曲线C 于A 、B 两点,若S 四边形OAFB
,则双曲线C 的离心率e =___________. 16.己知:f (x )=
x x e ,若方程[f (x )]2-23
f (x )+a =0有四个不等的实根,则a 的取值范围是____________.
三、解答题:(17~21题每题12分;22、23题二选一 10分) 17.(本小题满分12分)
△ABC 的内角A ,B ,C 对应的边分别为a ,b ,c .已知:(1-tanA )(1-tanB )=2. (1)求角C ;
(2)若b =,c =4,求△ABC 的面积S
△ABC .
18.(本小题满分12分)
如图,在四棱锥P -ABCD 中,底面ABCD 是平 行四边形,且平面PAD ⊥平面ABCD ,PA ⊥AB . (1)求证:四边形ABCD 是矩形;
(2)若PA =PD =AD =DC ,求二面角A -PB -C
的余弦值.
19.(本小题满分12分)
在某校举行的一次数学竞赛中,全体参赛学生的竞赛成绩X 近似服从正态分布N (70, 100).已知成绩在90分以上(含90分)的学生有16名. (1)试问此次参赛的学生总数约为多少人?
(2)若该校计划奖励竞赛成绩在80分以上(含80分)的学生,试问此次竞赛获奖励的
学生约为多少人?
附:P (|X -μ|<σ)=0.683,P (|X -μ|<2σ)=0.954,P (|X -μ|<3σ)=0.997
20.(本小题满分12分)
如图,设M(x,y)与定点F(1,0)的距离和它到直线l1:x=3
的距离的比是常数
3
,
(1)求点M的轨迹曲线C的方程:
(2)过定点F的直线l2交曲线C于A、B两点,以O、A、B三点(O为坐标原点)为顶点作平行四边形OAPB,若点P刚好在曲线C上,求直线l2的方程.
21.(本小题满分12分)
己知:f(x)=(2-x)x e+a(x-1)2 (a∈R)
(1)讨论函数f(x)的单调区间:
(2)若对任意的x∈R,都有f(x)≤2x e,求a的取值范围.
请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.
22.(本小题满分10分)【选修4-4:坐标系与参数方程】
在直角坐标系中,直线l的参数方程为
1
2
1
2
x at
t
⎧
⎪⎪
⎨
⎪
⎪⎩
=-
y=+
(t为参数).以坐标原点为极点,x
轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sinθ.
(1)在直角坐标系中,若以过原点的直线的倾斜角α为参数,求出曲线C的参数方程.(2)求直线l与曲线C相交弦的最小值.
23.(本小题满分10分)【选修4-5:不等式选讲】
已知:f(x)=|x+a|+|x-1|
(1)当a=1时,求不等式f(x)<3的解集;
(2)若对任意的x∈R,f(x)≥3恒成立,求a的取值范围.
CBDBAD CAABBC 13.6 14.7
16.2
23
(0,
)3e e
- 17.(1)45°(2
)2+ 18.(1)略(2
)7
-
19.(1)696 (2)110 20.(1)22
132
x y +=
(2)y =± 21.(1)当0a ≤时,函数在(,1)-∞上递增,在(1,)+∞上递减;当02
e
a <<
时,函数在 (,ln 2)a -∞,(1,)+∞上递减,在(ln 2,1)a 上递增;当2
e
a >
时,函数在(,1)-∞,(ln 2,)a +∞上递减在(1,ln 2)a 上递增;当2
e
a =
时,函数在R 上递减 (2)孤立
a,1a ≤
22.2
2sin cos 2sin x y ααα
=⎧⎨=⎩(α为参数)
23.(1)(-1.5,1.5)(2)2a ≥或4a ≤-。
