热力学与统计物理范德瓦尔斯方程的讨论2
对范德瓦尔斯方程和内能公式的探讨

对范德瓦尔斯方程和内能公式的探讨
范德瓦尔斯方程和内能公式是化学及分子物理学中常见的两个概念,它们都有着十分重要的科学意义,在认识宇宙的形成和演变过程中具有重要作用。
范德瓦尔斯方程是18世纪瑞士物理学家范德瓦尔发明的,它是用来解决物理
演化问题的重要数学方程,其本质是它结合了力学和热力学描述的两个方面,并使物质系统的变化成为一个可能的过程。
内能、或称内能原理,是由19世纪德国物理学家利奥波德·弗里德曼提出的,它指在物理学中,物质系统释放潜在能源时所发生的能量变化。
与物理变化相同,内能的变化是无可争议的,能量守恒原理仍然成立。
比较而言,了解范德瓦尔斯方程和内能公式是理解新的体系,了解宏观统一的
过程,以及宇宙的构造、特性和运行非常重要的。
此外,范德瓦尔斯方程和内能公式还为探索物理未知和物质的不同特性提供了理论框架,其在化学、热力学及宇宙演变等研究中产生巨大影响。
因此,范德瓦尔斯方程和内能公式有着深远的科学意义,它们已经成为物理、
化学以及相关领域的基础理论和重要发展方向,对我们认识物质的结构、性质和演化起着不可多得的作用。
范德瓦尔斯方程中有关分子吸引力引起的修正问题

范德瓦尔斯方程中有关分子吸引力引起的修正问题专业:电子信息与物理系姓名:郑凯学号:08405142指导教师:张栓柱摘要:本文用统计的方法导出范德瓦尔斯方程及修正值的具体表达式, 并讨论修正量与状态量的关系,对范德瓦尔斯方程的提出背景及其内涵作一系统介绍关键词:范德瓦尔斯方程统计解释历史分子力1873年以前, 人们一直沿用理想气体的状态方程PV=νRT, 此方程适用于低压、高温的条件下; 可是由实际气体的等温线可知, 在低温高压下, 实际气体与理想气体有很大不同。
因此, 需要对理想气体的状态方程作一定的修正, 1873年范德瓦尔斯对理想气体的两条假设作改进, 得出了能描述真实气体行为的范德瓦尔斯方程。
这一方程的建立, 对气体动理论与实际气体的状态更加的接近了, 范德瓦尔斯的贡献及历史沿革可以由以下几个方面论述。
1、气体动理论的发展范德瓦尔斯方程是1873年提出的,它是分气体动理论中最重要的一叶。
在此之前,气体动理论经历了大致三个阶段。
第一阶段是在17世纪。
意大利托里拆利研究大气压强,获得了托里拆利真空。
法国的帕斯卡研究了流体压强,建立了液体压强的有关定律。
在这基础上形成了朴素的热动力学概念。
1658年,波意耳通过实验,取得空气体积和压强成反比的定量关系。
波意耳认为:空气是由大量的小颗粒组成的,浮游在涡旋运动的宇宙物质中,所以这些粒子不停地杂乱无章地云顶。
这是最初的气体动理论,用它能解释压强是如何形成的。
第二阶段是187世纪到19世纪上半叶。
1738年,伯努利提出“弹子球”模型:把空气看成是“弹性流体”,一颗颗的“弹子球”与器壁碰撞, 由此可导出气体定律。
这个观点是气体动理论的基础, 也正是后来被称之为“理想气体”的模型。
第三阶段是在19世纪中叶后。
焦耳热功当量实验和空气自由膨胀实验, 推动了热动力学的发展, 使气体动理论的研究进入了一个新阶段。
作为热动力学奠基人之一的德国物理学家克劳休修, 第一个发表论文, 阐述了分子运动理论, 他还提出了气体分子平均自由程的概念, 创立了作为后来导出气体状态方程基础的“维里理论”。
热力学与统计物理第二章知识总结

§2.1内能、焓、自由能和吉布斯函数的全微分热力学函数中的物态方程、内能和熵是基本热力学函数,不仅因为它们对应热力学状态描述第零定律、第一定律和第二定律,而且其它热力学函数也可以由这三个基本热力学函数导出。
焓:自由能:吉布斯函数:下面我们由热力学的基本方程(1)即内能的全微分表达式推导焓、自由能和吉布斯函数的全微分•焓、自由能和吉布斯函数的全微分o焓的全微分由焓的定义式,求微分,得,将(1)式代入上式得(2)o自由能的全微分由得(3)o吉布斯函数的全微分(4)从方程(1)(2)(3)(4)我们容易写出内能、焓、自由能和吉布斯函数的全微分dU,dH,dF,和dG独立变量分别是S,V;S,P;T,V和T,P所以函数U(S,V),H(S,P),F(T,V),G(T,P)就是我们在§2.5将要讲到的特性函数。
下面从这几个函数和它们的全微分方程来推出麦氏关系。
二、热力学(Maxwell)关系(麦克斯韦或麦氏)(1)U(S,V)利用全微分性质(5)用(1)式相比得(6)再利用求偏导数的次序可以交换的性质,即(6)式得(7)(2) H(S,P)同(2)式相比有由得(8)(3) F(T,V)同(3)式相比(9)(4) G(T,P)同(4)式相比有(10)(7),(8),(9),(10)式给出了热力学量的偏导数之间的关系,称为麦克斯韦(J.C.Maxwell)关系,简称麦氏关系。
它是热力学参量偏导数之间的关系,利用麦氏关系,可以从以知的热力学量推导出系统的全部热力学量,可以将不能直接测量的物理量表示出来。
例如,只要知道物态方程,就可以利用(9),(10)式求出熵的变化,即可求出熵函数。
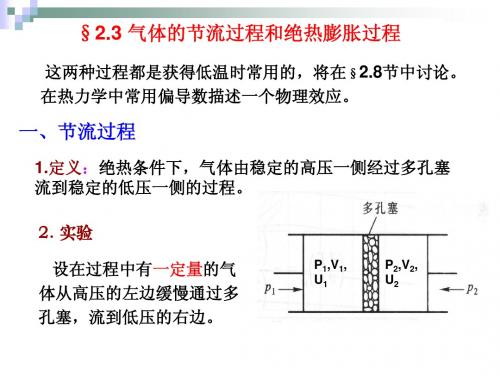
§2.2麦氏关系的简单应用证明1. 求选T,V为独立变量,则内能U(T,V)的全微分为(1)熵函数S(T,V)的全微分为( 2)又有热力学基本方程(3)由(2)代入(3)式得(4)•(4)相比可得(5)(6)由定容热容量的定义得(7)2. 求选T 、P为独立参量,焓的全微分为(8)焓的全微分方程为(9)以T、P为自变量时熵S(T、P)的全微分表达式为(10)将(10)代入(9)得(11)(8)式和(11)式相比较得(12)(13)(14)3求由(7) (14)式得(15) 把熵S看作T,V的函数,再把V看成T,P的函数,即对上式求全微分得∴代入(15)式得由麦氏关系得(16)即得证4、P,V,T三个变量之间存在偏导数关系而可证(17)§2.3气体的节流过程和绝热膨胀过程气体的节流过程(节流膨胀)和绝热膨胀是获得低温的两种常用方法,我们利用热力学函数来分析这两种过程的性质一,气体的节流(焦耳---汤姆逊效应)1、定义:如图所示有一由绝热材料制成的管子,中间用一多孔塞(节流阀)隔开,塞子一边维持较高的压强P,另一边维持较低的压强P,在压力的作用下,气体由高压的一边经过多孔塞流向低压的一边。
对范德瓦耳斯气体的热力学函数及热容量的研究

对范德瓦耳斯气体的热力学函数及热容量的研究范德瓦耳斯气体是一种理想气体的延伸,它在描述实际气体的热力学性质方面更准确。
本文将对范德瓦耳斯气体的热力学函数及热容量进行研究,并探讨范德瓦耳斯方程的应用。
1.范德瓦耳斯气体的热力学函数:范德瓦耳斯气体可以用以下方程描述:P(V-b)=nRT其中,P为气体的压强,V为气体的体积,n为气体的物质的量,R为气体常数,T为气体的温度,b为修正系数。
从这个方程中可以得到范德瓦耳斯气体的热力学函数。
首先,我们可以计算出范德瓦耳斯方程的状态方程:PV=nRT/(V-b)然后,根据理想气体的状态方程,可以知道热力学函数U与范德瓦耳斯方程的关系:dU = C_vdT = TdS - PdV其中,C_v为定容热容量,T为温度,S为熵,dU表示内能的微分。
将前面推导的范德瓦耳斯方程代入上述等式,可以得到范德瓦耳斯气体的热力学函数:dU = C_vdT = TdS - (nRT)/(V - b)dV2.范德瓦耳斯气体的热容量:根据上一节的推导,范德瓦耳斯气体的定容热容量C_v可以表示为:C_v=T(∂S/∂T)V现在来计算这个偏导数。
假设范德瓦耳斯气体满足简单的状态方程:P = nkT其中,k为玻尔兹曼常数。
由于S与V无关,我们可以得到:dS=(∂S/∂T)VdT将以上两式代入定容热容量的表达式中:C_v = T(dS/dT)V = T(1/T)kndT从而可以化简为:C_v = kn即范德瓦耳斯气体的定容热容量与物质的量成正比。
3.范德瓦耳斯方程的应用:范德瓦耳斯方程可以广泛应用于研究气体的行为和性质,特别是高压下的气体。
它可以用于计算气体的物质的量、压强、温度和体积之间的关系。
通过范德瓦耳斯方程,我们可以定量地描述气体的压力、体积和温度之间的关系。
例如,在常温常压下,我们可以计算气体的物质的量。
另外,范德瓦耳斯方程还可以用于计算气体的体积在不同压力和温度下的变化。
总结:本文对范德瓦耳斯气体的热力学函数及热容量进行了研究。
关于范德瓦尔斯方程的讨论

范德瓦尔斯方程(又译范德华方程),简称范氏方程,是荷兰物理学家范德瓦尔斯于1873年提出的一种实际气体状态方程。
范氏方程是对理想气体状态方程的一种改进,特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来,以便更好地描述气体的宏观物理性质。
范德瓦尔斯方程式中p 为气体的压强a 为度量分子间引力的参数b 为每个分子平均占有的空间大小(即气体的体积除以总分子数量)范德瓦尔斯方程T 为热力学温度范德瓦尔斯常量下表列出了部分气体的a,b 的值[1]适用范围范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。
对温度稍低于临界温度的液体和低压气体也有较合理的描述。
但是,当描述对象处于状态参量空间(P,V,T)中气液相变区(即正在发生气液转变)时,对于固定的温度,气相的压强恒为所在温度下的饱和蒸气压,即不再随体积V(严格地说应该是单位质量气体占用的体积,即比容)变化而变化,所以这种情况下范氏方程不再适用。
方程提出水分子之间的范氏引力(中国大陆的中学教科书称为“范德瓦尔斯力”或“范德华力”)一个双原子分子的排斥体积(黑色的部分)下面以理想气体状态方程为基础,推导范氏方程。
若把气体视为由体积无限小、相互之间无作用力的分子组成,这种模型便是理想气体模型,与其相对应的状态方程是:若抛弃前一个的假设,把组成气体的分子视为有一定大小的刚性球(其半径称为范德瓦尔斯半径),用b 表示这些“球”的体积,上面的方程便改写为:在这里,每个分子的“占有体积”v 被所谓“排斥体积”v - b 代替,反映了分子在空间中不能重叠。
若气体被压缩至体积接近分子体积之和(即分子间空隙v - b 趋向于0),那么其压强将趋于无穷大。
下一步,我们考虑原子对之间的引力。
引力的存在会使分子的平均亥姆霍兹自由能下降,减少量正比于流体的密度。
但压强的大小满足热力学关系式中A* 为每个分子的亥姆霍兹自由能。
由此得到,引力使压强减小的量正比于1/v²。
对范德瓦耳斯气体的热力学函数及热容量的研究

目 录摘 要 ................................................................................................... 1 Abstract ................................................................................................. 1 1 引 言 ................................................................................................. 1 2 范德瓦耳斯气体的热力学函数 (2)2.1范德瓦耳斯气体的熵(S ) (3)2.2 范德瓦耳斯气体的内能(U ) (4)2.3 范德瓦耳斯气体的焓(H ) (4)2.4 范德瓦耳斯气体的自由能(F ) ......................................................... 5 3范德瓦耳斯气体的摩尔容量 (5)3.1 范德瓦耳斯气体的P C 与V C 之差 (5)3.2 范德瓦耳斯气体的V C 与V 的关系 (7)3.3 范德瓦耳斯气体的P C 与P 的关系 ...................................................... 7 4结束语 ................................................................................................. 8 参考文献 (8)对范德瓦耳斯气体的热力学函数及热容量的研究摘 要:范德瓦耳斯方程是描述真实气体行为的基础。
本文从热力学函数的定义出发,结合范德瓦耳斯方程,推导出范德瓦耳斯气体的几个基本热力学函数,分析了其特性并研究了范德瓦耳斯气体的定容摩尔热容量和定压摩尔热容量的性质,指出了其同理想气体的区别。
范德瓦耳斯和他的状态方程

范德瓦耳斯和他的状态方程顾韶晖宁波工程学院化学工程与工艺精化071班摘要:在物理学发展史上,范德瓦耳斯对气一液流体系统做了开创性的研究工作,建立了人类历史上第一个既能反映气、液各相性质,又能描述相变和临界现象的状态方程。
范德瓦耳斯的理论成就和研究方法对热力学、统计力学和低温物理学的发展产生了重要而深远的影响。
关键词:范德瓦耳斯,状态方程前言状态方程是描述热力学系统平衡态的独立参量与温度之间的函数关系式,是物理学的一个重要研究内容。
人类对状态方程的研究可以追溯到很早的年代。
早在1662年和1679年,英国化学家玻意耳(Boyle R)和法国物理学家马略特(Mariotte)就分别提出了描述理想气体性质的状态方程。
两个世纪后,范德瓦耳斯在克劳修斯热力学理论的启发下,通过考虑分子体积和分子间引力的影响,导出了描述实际气体性质的状态方程,即著名的范德瓦耳斯方程。
范德瓦耳斯方程在历史上具有莫大的重要性,它是人类历史上第一个既能描述气、液各相性质,又能显示出相变的状态方程。
由于它形式简单,物理意义清楚,成为热力学和统计物理学的重要应用对象。
范德瓦耳斯也是第一个定量研究分子间相互作用的物理学家,他所使用的研究方法实际上就是后来所说的平均场方法,这一方法对铁磁、超导、超流等众多物理系统相变和临界现象的研究,对热力学和统计物理论的发展产生了重大影响[1]。
1 范德瓦耳斯的生平及科学成就范德瓦耳斯(Johannes Diderik van der Waals),荷兰人,1837年1月23日生于荷兰莱顿一个普通工人家庭。
范德瓦耳斯早年家境不甚宽裕,在出生地完成了他的初等教育后,便做了一名小学教师。
按照荷兰当时的法律,要进一步接受他所喜爱的自然科学的教育,就必须首先通过希腊文和拉丁文的考试。
范德瓦耳斯在这方面的基础不够好,未能获得参加考试的资格。
尽管如此,范德瓦耳斯并未放弃自己的努力。
在1862-1865年期间,他利用业余时间在莱顿大学继续学业,并获得了数学和物理的教学资格。
热力学与统计物理 汪志城 第四版 2章3-4节讲义
若热容看作常数 Gm = C pmT − C pmT ln T + RT ln p + H m 0 − TS m 0 利用分部积分, 利用分部积分,令 得
1 , dx = − 1 dT T T2
y =
∫
xdy
= xy −
∫
∫C ydx
pm
dT , dy = C pm dT
1 − dT G m = ∫ C pm dT − T [ ∫ C pm dT − ∫ 2 ∫ C pm dT ] + RT ln p + H m 0 − TS m 0 T T =0 dT G m = −T ∫ 2 ∫ C pm dT + RT ln p + H m 0 − TS m 0 T dT RT ϕ = H m 0 − T ∫ 2 ∫ C pm dT − TS m 0 常写成 Gm = RT (ϕ + ln p )
7.实际气体的焦汤效应分析
昂尼斯气体: 昂尼斯气体: 气体
p=
n p = V RT
nRT n nRT p [1 + B(T )] ≈ [1 + B(T )] V V V RT
又可写成 V = n[
B H2 Ne He 700K N2
R dB ∂V = n + p dT ∂T p 1 ∂V 焦汤系数 µ = T −V C p ∂T p
T
H m0 Sm 0 dT ϕ (T ) = −∫ C pm dT − 2∫ RT RT R
若将热容量看作常数
H m0 Sm 0 dT ϕ (T ) = −∫ C pm dT − 2∫ RT RT R
H m0 Sm 0 dT = −∫ C T− 2 pm RT RT R
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于范氏方程、伯赛洛特方程、狄特里奇方程气体的若干讨论姓名:樊聪年级:2011级学号:20110515623专业:物理学(师范)学院:物理与电子工程学院目录1引言 (2)2 范德瓦尔斯气体的讨论 (2)2.1范德瓦耳斯气体的内能 (2)2.2 范德瓦尔斯气体的熵 (3)2.3范德瓦尔斯方气体的准静态绝热过程方程 (4)3 伯赛洛特气体的讨论 (4)3.1伯赛洛特气体的内能 (4)3.2伯赛洛特气体的熵 (5)3.3伯赛洛特气体的准静态绝热过程方程 (5)4 狄特里奇气体的讨论 (6)4.1狄特里奇气体的内能 (6)4.2狄特里奇气体的熵 (7)4.3狄特里奇气体的准静态绝热过程方程 (7)5 结论 (8)6 参考文献 (9)关于范氏方程、伯赛洛特方程、狄特里奇方程气体的若干讨论摘要:讨论了范德瓦尔斯气体、伯赛洛特气体及狄特里奇气体的内能和熵,给出了相应的数学表达式;推导了范德瓦尔斯气体伯赛洛特气体和狄特里奇气体在相应准静态的绝热过程中的过程方程.关键字:范德瓦尔斯,伯赛洛特,狄特里奇,气体,内能,熵,绝热过程1. 引言一般的教材[1~3]对理想气体的内能、熵及过程方程讨论都比较详细,而对理想气体只是热力学理论中的理想化模型,其基本特点是:(1)分子本身的线度与分子之间的距离相比可忽略不计;(2) 除碰撞的瞬间外分子之间及分子与器壁之间没有相互作用力;(3) 分子之问及分子与器壁之间作完全弹性碰撞.即只有当温度不太低、压强不太高时才能把真实气体当作理想气体看待,对真实气体的内能、熵及过程的方程却很少涉及,范德瓦耳斯气体(包括范德瓦尔斯方程、伯赛洛特方程和狄特里奇方程)的模型既考虑了气体分子本身的大小,也考虑了气体分子之间的相互作用,比理想气体更接近于真实气体.而多数教材及期刊论文中都只对范氏气体—即范氏方程做了较为详细的讨论,我认为我们有必要将伯赛洛特方程、狄特里奇方程所对应的内能、熵、准静态过程进行讨论,以增强我们对于以上三种实际气体的认识和理解.为此,本文对范德瓦耳斯气体及伯赛洛特方程、狄特里奇方程对应的内能、熵和准静态的绝热过程中的过程方程进行讨论.2.范德瓦尔斯气体的讨论2.1范德瓦耳斯气体的内能范德瓦尔斯1873年在他的博士论文《论液态与气态的连续性》[4]中,通过简单的物理分析得到下述方程,即范德瓦耳斯气体的状态方程(p+n 2aV2)(V−nb)=nRT (1)式中,“n 2aV2” 代表分子间引力引起的修正(其中a和b分别是对压强和体积修正的常量,称为范德瓦耳斯常数,该常量可由实验求得[4])称为内压强,用P i表示;而nb是分子之间的排斥力引起的修正—即体积修正.可以看出,若气体的密度足够低,使“n 2aV2”和nb可以忽略时,范德瓦尔斯气体方程就还原为理想气体方程.对于范德瓦耳斯气体内能不仅包括各个分子热运动动能之和E K,而且还应包括各对分子间相互作用的位能总和EP.即U=E K+E P.对Ek来讲,其值和理想气体一样,仅由气体的温度而定,当温度变化dT时,气体的动能增量为dE k=nC V dT, (2)式中C V为气体的定容摩尔热容,而对E P来说,当容器的体积改变时,分子间平均距离的改变必然引起各对分子间位能的改变.设想范德瓦耳斯气体在等温下膨胀,气体不仅要反抗外力做功,而且还要反抗各对分子问的相互作用力做功.显然,反抗内力所做的功就等于气体分子引力位能E P的增量,因此当体积的微小增量dV时,n摩尔范德瓦耳斯气体反抗内压强所做的功为:dA=P i dV,即位能的增量为:dE P=P i dV=n2a V2⁄ .dV . 由式 ( 2 )和上式得范德瓦耳斯气体内能的增量为dU=nC V dT+n2aV2.dV (3)在温度变化范围不大时,气体的定容摩尔热容C V可以看作常数,积分(3 )式得到范德瓦耳斯气体的内能表达式为U=−n 2Va+nC V T+U02.2范德瓦尔斯气体的熵对于气体系统通常选取T,V或T,P作状态参量,若以T,V为状态参量,则由热力学第一定律d Q =dU −d A =dU +PdV ,而dU=(ðU ðT )|V dT +(ðU ðV )|T dV ,于是气体状态1,2之间的熵差为∆S =S 2−S 1=∫d ̅Q T 21=∫1T T 2T 1 .(ðU ðT )V dT +∫1T V 2V 1 .[(ðU ðV )T +P]dV (4) 又由(3)式得:[∂U ∂T ]V =nC V , [ðU ðV ]T=n 2a V 2 .再由(1)式得:P =nRT (V−nb )−n 2a V 2⁄,将以上三个式子代入(4)式并积分整理得: ∆S =n ∫C V T ⁄ T 2T 1 .dT +nR ln [(V 2−nb )(V 1−nb )⁄] .2.3范德瓦尔斯方气体的准静态绝热过程方程根据热力学第一定律:dU =d Q +d A ,在准静态的绝热过程中,气体与外界没有热量交换,即d Q =0,外界对气体做的功为:d A =−PdV ,将式(3)和以上两式代入dU =d Q +d A 得:[P +n 2a V 2⁄]dV +nC V dT =0.再将(1)式代入上式得:nRT (V −nb )⁄ .dV +nC V dT =0 ,积分上式并令γ=(C V +R )C v⁄得:T (V −nb )γ−1=常量 .同理,如果以T,P 或P,V 作状态参量,则可得绝热过程的另外两个方程 :(P +n 2a V 2⁄)γ−1T γ⁄ =常量 , (P +n 2a V 2⁄)(V −nb )γ=常量 .3 伯赛洛特气体的讨论3.1伯赛洛特气体的内能伯赛洛特气体的状态方程为(p +n 2aTv 2)(v −nb )=nRT (1)可以看出与范氏气体方程相比,式中除了含有与范氏气体相同的“n 2a v 2”项,还含有“1T ”项,即伯赛洛特方程中还考虑了温度“T ”对分子引力的影响,由分子间引力和温度引起的修正项“n 2a Tv 2”同样称为内压强,用P i 表示;“nb ”是分子本身的体积引起的修正.对于伯赛洛特气体的内能同样包括各个分子热运动动能之和E K 和各对分子间相互作用的位能总和E P .即U =E K +E P .对Ek 来讲, 其值和理想气体一样,仅由气体的温度而定,当温度变化dT 时,气体的动能增量为dE k =nC V dT, (2)式中C V 为气体的定容摩尔热容,而对E P 来说,当容器的体积改变时,分子间平均距离的改变必然引起各对分子间位能的改变.设想伯赛洛特气体在等温下膨胀,气体不仅要反抗外力做功,而且还要反抗各对分子问的相互作用力做功.显然,反抗内力所做的功就等于气体分子引力位能E P 的增量,因此当体积的微小增量dV 时,n 摩尔伯赛洛特气体反抗内压强所做的功为:dA =P i dV , 即位能的增量为:dE P =P i dV =n 2a (TV 2)⁄ .dV . 由式 ( 2 )和上式得伯赛洛特气体内能的增量为dU =nC V dT +n 2aTv 2 .dV (3)在温度变化范围不大时,气体的定容摩尔热容C V 可以看作常数,积分(3 )式得到伯赛洛特气体的内能表达式为 U =−n 2TV a +nC V T +U 0 3.2伯赛洛特气体的熵对于气体系统通常选取T,V 或T,P 作状态参量,若选前者,则由热力学第一定律d Q =dU −d A =dU +PdV ,而dU=(ðU ðT )|V dT +(ðU ðV )|T dV ,于是气体状态1,2之间的熵差为∆S =S 2−S 1=∫d ̅Q T 21=∫1T T 2T 1 .(ðU ðT )V dT +∫(1T V 2V 1 .[(ðU ðV )T +P)]dV (4) 又由(3)式得:[∂U ∂T ]V =nC V , [ðU ðV ]T =n 2a TV 2 .再由(1)得:P =nRT(V−nb )−n 2a (TV 2⁄),将以上三个式子代入(4)式并积分整理得:∆S =n ∫C V T ⁄ T 2T 1 .dT +nR ln [(V 2−nb )(V 1−nb )⁄] .3.3伯赛洛特气体的准静态绝热过程方程根据热力学第一定律:dU =d Q +d A ,在准静态的绝热过程中,气体与外界没有热量交换,即d Q =0,外界对气体做的功为:d A =−PdV ,将式(3)和以上两式代入dU =d Q +d A 得:[P +n 2a (TV 2)⁄]dV +nC V dT =0.再将(1)式代入上式得:nRT (V −nb )⁄ .dV +nC V dT =0 ,积分上式并令γ=(C V+R )C V⁄得:T (V −nb )γ−1=常量 .同理,如果以T,P 或P,V 作状态参量,则可得绝热过程的另外两个方程 :(P +n 2a (TV 2)⁄)γ−1T γ⁄ =常量 , (P +n 2a (TV 2)⁄)(V −nb )γ=常量 .4 狄特里奇气体的讨论4.1狄特里奇气体的内能狄特里奇气体的状态方程为Pe na VRT (V −nb )=nRT (1)式中,"e na VRT " 是由分子间引力引起的修正(a 与分子间的相互作用有关,压强这一项考虑温度以后P i +P =Pe na VRT ,由此可以得到系统内压强P i =P(e na VRT −1) ;nb 是分子本身的体积引起的修正).对于狄特里奇气体的内能不仅包括各个分子热运动动能之和E K ,而且还应包括各对分子间相互作用的位能总和E P .即U =E K +E P .对Ek 来讲, 其值和理想气体一样,仅由气体的温度而定,当温度变化dT 时,气体的动能增量为dE k =nC V dT, (2)式中C V 为气体的定容摩尔热容,而对E P 来说,当容器的体积改变时,分子间平均距离的改变必然引起各对分子间位能的改变.设想狄特里奇气体在等温下膨胀,气体不仅要反抗外力做功,而且还要反抗各对分子问的相互作用力做功.显然,反抗内力所做的功就等于气体分子引力位能E P 的增量,因此当体积的微小增量dV 时,n 摩尔狄特里奇气体反抗内压强所做的功为:dA =P i dV , 即位能的增量为:dE P =P i dV =P(ena VRT −1).dV . 由式 ( 2 )和上式得狄特里奇气体内能的增量为dU =nC V dT +P(e na VRT −1) .dV (3)在温度变化范围不大时,气体的定容摩尔热容C V 可以看作常数,积分(3 )式得到范德瓦耳斯气体的内能表达式为U =∫P(e na VRT −1).dV V 2V 1+nC V T +U 04.2狄特里奇气体的熵对于气体系统通常选取T,V 或T,P 作状态参量,以T,V 为状态参量,则由热力学第一定律d Q =dU −d A =dU +P i dV ,而dU=(ðU ðT )|V dT +(ðU ðV )|T dV ,于是气体状态1,2之间的熵差为∆S =S 2−S 1=∫d ̅Q T 21=∫1T T 2T 1 .(ðU ðT )V dT +∫1T V 2V 1 .[(ðU ðV )T+P]dV (4) 又由(3)式得:[∂U ∂T ]V =nC V , [ðU ðV ]T=P(e na VRT −1) .再由(1)得:P =nRT(V−nb )×e −na VRT ,将以上三个式子代入(4)式并积分整理得:∆S =n ∫C V T ⁄ T 2T 1 .dT +∫1T V 2V 1 .(nRT (V−nb )×e −na VRT .(e na VRT −1)+nRT (V−nb )×e −na VRT ).dV .=nC V ln T 2T 1+∫(1T V 2V 1 .nRT (V−nb)×1)dV = nC V ln T 2T 1+nRln (V 2−nb)(V 1−nb)4.3狄特里奇气体的准静态绝热过程方程根据热力学第一定律:dU =d Q +d A ,在准静态的绝热过程中,气体与外界没有热量交换,即d Q =0,外界对气体做的功为:d A =−PdV ,将式(3)和以上两式代入dU =d Q +d A 得:P dV +nC V dT =0.再将(1)式代入上式得:(nRT (V−nb )×e −na VRT ) .dV +nC V dT =0积分上式并令γ=(C V +R )C v⁄得: nRT ∫(1(V−nb )×e −na VRT ) .dV +n ∫C V dT T2T 1V 2V 1=0 .即: ∫(1(V −nb )×e −na VRT ).dV =−C V RV 2V 1 T (V −nb )γ−1=常量同理,如果以T,P 或P,V 作状态参量,则可得绝热过程的另外两个方程 :(P .e na VRT )γ−1T γ⁄ =常量(Pe na VRT )(V −nb )γ=常量5 结论本文讨论了范德瓦尔斯气体、伯赛洛特气体及狄特里奇气体的内能、熵、和绝热过程.经过计算,发现以上三种气体的内能、熵和绝热过程都有着相同的形式,如果忽略修正项的影响,即得:以 T,V 为状态参量的内能形式都为U =∫Pe na VRT . dV V 2V 1+nC V T +U 0 熵的形式为∆S =n ∫C V T ⁄ T 2T 1 .dT +nR ln [(V 2)(V 1)⁄]以T,V 为参量的准静态绝热方程形式为T (V )γ−1=常量 以T,P 为参量的准静态绝热方程形式为(P )γ−1T γ⁄ =常量以P,V 为参量的准静态绝热方程形式为P (V )γ=常量事实上,对以上三种形式的气体的讨论,当忽略气体分子的引力修正和由于排斥力引起的体积修正时,所得气体热力学方程即为理想气体物态方程所对应的内能、熵和绝热过程的多方过程方程。
