第二章(3)传递函数
合集下载
传递函数

在控制工程中,一般并不需要精确地求出系统微分方程式的 解,作出它的输出响应曲线,而是希望用简单的方法了解系统 是否稳定及其在动态过程中的主要特征,能判别某些参数的改 变或校正装置的加入对系统性能的影响。
实用文档
因为控制理论着重分析系统的结构、参数与系统的动 态性能之间的关系,所以为简化分析,设系统的初始条 件为零。
例: 试求 RLC无源网络的传递函数
R
L
解: 该网络微分方程已求出,如式
ui(t)
i(t)
C uo(t) Ld C 2d uo2(tt)RdC d o(ut)tuo(t)ui(t)
实用文档
在零初始条件下,对上式进行拉氏变换,令 U0(s)=L[U0(t)], U i(s)=L[Ui(t)] 得: (L2 C Rs C 1 )U o ( s s) U i(s)
实用文档
于是,由定义得系统的传递函数为
G ( s ) C R ( ( s s ) ) b a 0 0 s s m n b a 1 1 s s m n 1 1 b a m n 1 1 s s b a m n M N ( ( s s ) )
式中
M ( s ) b 0 s m b 1 s m 1 b m 1 s b m N ( s ) a 0 s n a 1 s n 1 a n 1 s a n
R(s)
C(s)
G(s)
传递函数的图示
实用文档
说明:
传递函数是物理系统的数学模型,但不能 反应系统的物理性质,不同的物理系统可 以有相同的传递函数; 传递函数只适用于线性定常系统;
实用文档
⑶ 物理意义
传递函数是在零初始条件下定义的,控制系统的零初始 条件有两方面的含义:
一是指输入量是在t≥0时才作用于系统,因此在t=0-时 输入量及其各阶导数均为零;
实用文档
因为控制理论着重分析系统的结构、参数与系统的动 态性能之间的关系,所以为简化分析,设系统的初始条 件为零。
例: 试求 RLC无源网络的传递函数
R
L
解: 该网络微分方程已求出,如式
ui(t)
i(t)
C uo(t) Ld C 2d uo2(tt)RdC d o(ut)tuo(t)ui(t)
实用文档
在零初始条件下,对上式进行拉氏变换,令 U0(s)=L[U0(t)], U i(s)=L[Ui(t)] 得: (L2 C Rs C 1 )U o ( s s) U i(s)
实用文档
于是,由定义得系统的传递函数为
G ( s ) C R ( ( s s ) ) b a 0 0 s s m n b a 1 1 s s m n 1 1 b a m n 1 1 s s b a m n M N ( ( s s ) )
式中
M ( s ) b 0 s m b 1 s m 1 b m 1 s b m N ( s ) a 0 s n a 1 s n 1 a n 1 s a n
R(s)
C(s)
G(s)
传递函数的图示
实用文档
说明:
传递函数是物理系统的数学模型,但不能 反应系统的物理性质,不同的物理系统可 以有相同的传递函数; 传递函数只适用于线性定常系统;
实用文档
⑶ 物理意义
传递函数是在零初始条件下定义的,控制系统的零初始 条件有两方面的含义:
一是指输入量是在t≥0时才作用于系统,因此在t=0-时 输入量及其各阶导数均为零;
传递函数的定义

2 2s 1)L 2 T2s 1)L
( i s 1)
(Tjs 1)
2 62
其分子、分母各因式中常数项均为1(若不是零), 式中i, Ti称为各环节的时间常数,因此又称时间 常数表达式。包括以下几种典型的基本环节。
1 放大环节 2 纯微分 3 一阶微分环节 4 二阶微 分环节 5 积分环节 6 惯性环节 7 振荡环节 8 延迟环节
2.3.2 传递函数的性质和含义
1. 传递函数是线性定常系统数学模型的另一种表达形式。 传递函数的形式完全取决于系统本身的结构和参数, 与输入信号的形式无关。它与系统微分方程是一一对 应的,即与微分方程中各导数项的系数相对应,所以 传递函数也是系统的动态数学模型。 对同一系统, 若谈到传递函数,必须首先指明输入量和输出量。否 则,得到的传递函数形式可能不同。
下午4时15分
5. 传递函数可表示成有理分式的形式, 又可写成零、极点表示的形式。
m
G(s)
C(s) R( s )
K
g
s zi
i 1 n
s pj
j 1
2 59
6. 传递函数还可用时间常数的形式来表示。
m1
m2
K
i s 1
(
2 k
s2
2
k
k
s
1)
G(s)
i 1 n1
k 1 n2
若相加点由方框之后移到方框之前,应在移动之路上串入 具有相同传递函数倒数的方框。 若相加点由方框之前移到方框之后,应在移动之路上串入 具有相同传递函数的方框。
(2)分支点的移动和互换
若分支点由方框之后移到方框之前,应在移动之路上串入 具有相同传递函数的方框。 若分支点由方框之前移到方框之后,应在移动之路上串入 具有传递函数倒数的方框。
第二章 控制系统的传递函数

第二章
控制系统的传递函数
2.1 微分方程模型(时间域模型)
一、控制系统微分方程的分类
线性系统:可由线性微分方程描述的系统。线性微分方程是指微分方程 是定常和线性的。线性系统可应用叠加原理,将多输入及多输出的 系统转化为单输入和单输出的系统进行处理分析,最后进行叠加。 另外线性系统还有一个重要的性质,就是齐次性,即当输入量的数 值成比例增加时,输出量的数值也成比例增加,而且输出量的变化 规律只与系统的结构、参数及输入量的变化规律有关,与输入量数 值的大小是无关的。 非线性系统:研究非线性系统的运动规律和分析方法的一个分支学科。 非线性系统最重要的问题之一就是确定模型的结构,如果对系统的 运动有足够的知识,则可以按照系统运动规律给出它的数据模型。 一般来说,这样的模型是由非线性微分方程和非线性差分方程给出 的,对这类模型的辨别可以采用线性化,展开成特殊函数等方法。 非线性系统理论的研究对象是非线性现象,它反映出非线性系统运 动本质的一类现象,不能采用线性系统的理论来解释,主要原因是 非线性现象有频率对振幅的依赖性、多值响应和跳跃谐振、分谐波 振荡、自激振荡、频率插足、异步抑制、分岔和混沌等。
控制系统的传递函数
例 2:RLC 电路(L-R-C 无源四端网络)如图,建立输入输出间的微分方程关
由基尔霍夫定律,回路的压降为 0,即输入电压由电感、电阻、电容上的电压 平衡。 Ur=UL+UR+UC 电流 与 有 即 的关系
第二章
控制系统的传递函数
与 在数值上具有一 ~
注意:该系统也是一个二阶系统 与例 1 相比,它们具有相同的模型形式。当
线性系统满足叠加原理,而非线性系统不满足叠加原理。
第二章
控制系统的传递函数
二、微分方程模型的建立 根据系统物理机理建立系统微分方程模型的基本步骤: (1)确定系统中各元件的输入、输出物理量; (2)根据物理定律或化学定律(机理),列出元件的原始方程,在条 件允许的情况下忽略次要因素,适当简化; (3)列出原始方程中中间变量与其他因素的关系; (4)消去中间变量,按模型要求整理出最后形式。
自动控制原理-第二章-控制系统的数学模型—结构图-信号流图-传递函数

(1)单位脉冲 (2)单位阶跃 (3)单位斜坡 (4)单位加速度 (5)指数函数 (6)正弦函数 (7)余弦函数
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
f (t)
(t)
1(t )
t t2 2
e at
sin t cos t
F (s)
1
1s 1 s2 1 s3
1 (s a)
(s2 2) s (s2 2)
2.2 线性定常微分方程的求解 拉普拉斯反变换:部分分式展开法
时域 差分方程
解析式模型
状态方程
复域
传递函数 结构图-信号流图
图模型
频域 频率特性
数学模型是一个反应变量之间关系的表达式,在不同的域中有不同的表现形式!
1.引言
解析法:依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表 达式,并实验验证。
实验法:对系统或元件输入一定形式的信号(例如阶跃信号、单位脉冲信号、正弦信 号等),根据系统或元件的输出响应,经过数据处理而辨识出系统的数学模型。
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s2
2Tj
s
1)
i 1
j 1
适用于 频域分
析
3.2 传递函数的基本概念 传递函数的标准形式
K:增益
K*=根轨迹增益
K与K*的关系:
两者关系
m
zj
K K*
j 1 n
pi
i 1
3.3 典型环节及其传递函数
一个传递函数可以分解为若干个基本因子的乘积,每个基本因子就称为典型环节。常见 的几种形式有:
Y (s)
R(s)
Y (s)
第二章 传递函数-梅逊公式
第二章 自动控制系统的数学模型
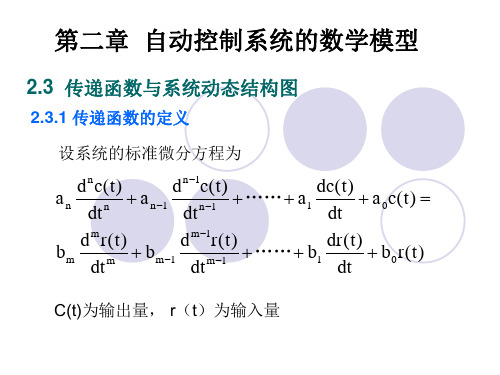
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
第二章-系统的传递函数方框图及其简化.

系统闭环传递函数
GB (s)
X o (s) Xi (s)
由图可知
X i (s) E(s) G(s)
B(s)
H (s)
X o (s)
E(s) Xi (s) B(s) Xi (s) Xo(s)H (s) Xo(s) G(s)E(s) G(s)[Xi (s) Xo(s)H (s)]
G(s)Xi (s) G(s)Xo(s)H (s) 由此可得:
GK (s) G(s)H (s) E(s)
无量纲.
系统闭环传递函数
GB (s)
X o (s) Xi (s)
注意:我们所指的前向通道的传递函数、反馈回路的
传递函数和开环传递函数都是针对一个闭环系统而
言的。它们都是闭环系统的一部分。系统闭环传递
函数是闭环系统的传递函数。看一个传递函数是什
么具体类型,要从定义出发,而不能只看其符号。
8.分支点和相加点之间等效规则
X1(s)
X1(s) X2(s)
X 2 (s)
X1(s) X2(s)
X1(s)
X 2 (s)
X1(s) X2(s)
X1(s) X2(s)
X 2 (s)
一般应避免分支点和相加点之间的相互移动
三、方框图简化的一般方法 (法1)
1.确定系统的输入量和输出量.若作用在系统上的输 入量或输出量有多个,则必须分别对每一输入量,逐个 进行方框图的简化,以求得各自的传递函数. 2.若方框图中有交叉连接,则利用分支点或相加点的 移动规则,将交叉消除,简化成无交叉的多回路方框图 的形式.(大回路套小回路) 3.对多回路方框图,按照先里后外的顺序依次对各个 回路进行简化. 4.写出系统的传递函数.
Ua (s) 0
自动控制原理2.3 传递函数1.3 传递函数

U a (s) TaTm s 2 Tm K 0 s 1
1 K0
1 K0
(s) Mc (s)
Km 1 K0
(Ta
s
1)
TaTm s 2 Tm K 0 s 1
1 K0
1 K0
2.性质与说明:
(1)传递函数是复变量s的有理真分式,具有复变
函数的所有性质,且所有系数均为实数。
a1
d n1c(t) dt n1
an1
dc(t ) dt
a n c(t )
b0
d mr(t) dt m
b1
d m1r(t) dt m1
bm1
dr (t ) dt
bm r(t)
当初始条件为零时有:
[a0 s n a1s n1 an1s an ]C(s)
一、基本概念:
第二章 数学模型
以 RC 网络为例。
R
RC
duc dt
uc
ur,设
uc (0)
0
C
则有 RCsUc (s) Uc (s) Ur (s)
ur i
uc
即(RCs 1)Uc (s) Ur (s)
Uc (s)
1 RCs
1
U
r
(
s)。
其中 Ur (s)随
ur (t) 形式而变,
号的性质和能力,故称它为RC网络的传函。
1、定义:对于线性定常系统来说,当初始条件为零 时,输入量拉氏变换与输出量拉氏变换之 比叫做系统的传递函数 。
G(s) C(s) . R(s) R(s)
机械工程控制基础-第二章-传递函数

华中科技大学材料学院
典型环节
比例环节 惯性环节 微分环节 积分环节 振荡环节 延时节例
华中科技大学材料学院
比例环节
1、传递函数函:G(s) K (放大环节)
2、特性:输入输出成正比,无惯性,不失真, 无延迟 X(s) Y(s) K 3、参数:K 4、单位阶跃响应:输出按比值复现输入, 无过渡过程。
华中科技大学材料学院
4)方框图不唯一。由于研究角度不一样,传递函数 列写出来就不一样,方框图也就不一样。 5) 研究方便。对于一个复杂的系统可以画出它的方 框图,通过方框图简化,不难求得系统的输入、输出 关系,在此基础上,无论是研究整个系统的性能,还 是评价每一个环节的作用都是很方便的。
华中科技大学材料学院
n 2
2
p1 p2 n , p1 p2 2n 2 1
n e p t e p t y (t ) 1 ( ) 2 p1 p2 2 1
1 2
华中科技大学材料学院
p1 p2 ,当 1时, p1 p2
则
n e p t y (t ) 1 2 2 1 p2
华中科技大学材料学院
延迟环节
1. 传函
W ( s) e
s
x
y
1
t
1
(t ) 2.单位阶跃响应 y(t ) L1[es 1 s ] 1 3.参数 延迟时间 4.特性:能充分复现输入,只是相差 ,该环节
t
是线性的,他对系统稳定性不利。然而过程控制中,
系统多数都存在延迟环节,常用带延迟环节的一阶
x(t )
1
y(t )
K
t
t
比例环节实例
1)分压器
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特点:改善系统的动态性能; 增加系统的阻尼,提高系统的稳定性 常被作为校正装置
例 如图所示永磁式直流测速机, 已知 u (t) k di (t) 0 dt U 0 (s ) G ( s ) ks 进行拉氏变换后得 i (s ) d i 则
U 0 (s) k dt (t )
U0(t)
式中,T—振荡环节的时间常数 ζ—阻尼比,对于振荡环节,0<ζ<1 K—比例系数
特点:在一定条件下,具有振荡可能,取决于系统本身的固有特性, 这是因为有两个储能元件,有能量交换,这种能量交换在一定条件下 以振荡方式存在。
只有当|Ts|<<1时,才近似为微分环节。
(4)积分环节
如果输出变量正比于输入变量的积分,即 进行拉氏变换得 X 0 (s) k
x 0 ( t ) k x i ( t )dt
G (s) X 0 (s ) k X i (s ) s
则
X i (s) s
特点:系统的输出和输入之间没有唯一对应的关系, 有记忆功能,能提高系统的稳态精度, 系统中的积分环节不能大于2个,否则系统不稳定。
例
如图所示弹簧-阻尼系统。
Xi(t)
kx i (t ) x 0 (t ) D
dx0 (t ) dt
Xo(t)
kX i (s) X o (s) DsXo (s)
D s 1X o (s) X i (s) k
X (s) 1 G (s) 0 X i (s) D s 1 k
i (t)
对于相同量纲的理想微分环节物理上是难以实现的, 电路中常遇到下述的近似微分环节。
i (t ) ——输入转角; 其中, u0(t) ——输出电压。
图 永磁式直流测速机
kTs G ( s ) 2 近似微分环节 Ts 1
例7 图2-14所示的无源微分电路
u i (t)
1 u ( t ) i(t )dt i(t )R 已知 i C u 0 (t ) i(t )R
设线性定常系统的微分方程为
a x (t ) a x
(n) 0 o
n 1 1 o
o (t ) a n x0 (t ) (t ) a n1 x
m 1 1 i
b x
( m) 0 i
(t ) b x
i (t ) a m xi (t ) (t ) bm1 x
C
i( t )
图 无源微分网络
1 U i (s) I(s) RI(s) 拉氏变换得 Cs u 0 (t) U 0 (s) RI(s) 其中, RCs 1 ui(t) ——输入电压 化简得 U i (s) R U 0 (s) u0(t) ——输出电压 RCs RC=T U ( s ) RCs R——电阻; G (s) 0 K=1 则 C——电容。 U i (s) RCs 1
u i (t )
i1 (t )
+
K
0
u o (t )
R1
U o (s) K U i (s)
z1 ni(t) z2
z1 z2
n 0 (t ) z 2 n i (t ) z1
N 0 (s) z 2 N i (s) z 1 G (s) N 0 (s) z 1 , N i (s) z2
X i ( s)
输出的拉氏变换 X o ( s) G( s) X i ( s)
时域中的输出 xo (t ) L [G( s) X i ( s)]
单位脉冲响应:
G ( s)
X 0 ( s)
1
g (t ) L1[G(s)]
传递函数具有以下特点:
(1) 传递函数的分母是系统的特征多项式,代表系统的 固有特性;分子代表输入与系统的关系,而与输入
式中,K—环节增益(放大系数); T—时间常数,表征环节的惯性,和 环节结构参数有关
特点:有一个阻尼元件存在,当有一个输入信号时,不会 马上达到一定值,而是需要一个缓慢上升的过程。
xi (t )
x0 (t )
忽略质量,由达朗贝尔 原理可知 o 0 数学模型 ( xi xo )k cx o kxo kxi csX o ( s ) kX o ( s ) kX i ( s ) cx X o (s) k 1 传递函数 G ( s ) X i ( s ) cs k Ts 1
M k
D
f i (t) ——输入外力; 其中, y 0 ( t ) ——输出位移; M——质量; k——弹簧刚度; D——拈行阻尼系数。 图 质量-弹簧-阻尼系统
返回
5 二阶振荡环节
含有两个独立的储能元件,且所存储的能量能够相互 转换,从而导致输出带有振荡的性质,运动方程为:
2 d d T 2 2 xo (t ) 2 T xo (t ) xo (t ) Kxi (t ), 0 1 dt dt X o ( s) K G ( s ) 传递函数: X i ( s) T 2 s 2 2 Ts 1
示系统Байду номын сангаас输出函数。因而,也可以把传递函数看成
单位脉冲响应的像函数; (5)分母s的阶次n大于等于分子中s的阶次m (6)传递函数可以是有量纲的,也可以是无量纲的。 自变量s的量纲为1/秒 (7) 如果将传递函数进行代换s=jω,可以直接得到系统 的频率特性函数(详见第3章)。
需要特别指出的是:
由于传递函数是经过拉氏变换导出的,而拉氏变换是一种 线性积分运算,因此传递函数的概念仅适用于线性定常系 统; 传递函数是在零初始条件下定义的,因此,传递函数原则
数学模型 o (t ) ui (t ) RCu
uo(t)
RCsUo (s) U i (s)
U o ( s) 1 K G( s) U i ( s) RCs s
5
二阶振荡环节
G (s)
1 T s 2Ts 1
2 2
, 0 1
0 (t ) 2Tx 0 (t ) x 0 (t ) x i (t ) 如果输入,输出函数可表达为如下二阶微分方程: T 2 x 经拉氏变换得 T 2 s 2 X 0 (s) 2TsX 0 (s) X 0 (s) X i (s)
特点:输出量与输入量成正比,输出不失真也不延迟,而是按比例反映输入, 即线性变化。
由运算放大器构成的比例环节
R2 uo (t ) ui (t ) Kui (t ) R1 拉氏变换 U o ( s ) KU i ( s ) G ( s )
如图所示齿轮传动副,
R2
i2 (t )
U i (s) (RCs 1)U o (s)
则
G (s )
U 0 (s ) 1 , 图 无源滤波电路 U i (s) RCs 1
其中,ui(t) ——输入电压; uo(t) ——输出电压; R为电阻;C为电容。
R
求低通滤波器的传递函数
u i (t )
i (t )
C
u o (t )
量无关,因此传递函数表达了系统本身的固有特性。 (2) 传递函数不说明被描述系统的具体物理结构,不同
的物理系统可能具有相同的传递函数。 (3) 传递函数比微分方程简单,通过拉氏变换将时域内 复杂的微积分运算转化为简单的代数运算;
(4) 当系统输入典型信号时,输出与输入有对应关系。 特别地,当输入是单位脉冲信号时,传递函数就表
其中,xi(t) ——输入位移; x0(t) ——输出位移 K——弹簧刚度; D——粘性阻尼系统。
图 弹簧-阻尼系统
(3)微分环节
输出量正比于输入量的微分。
i (t ) 微分环节的数学模型 xo (t ) T x X o ( s) X o ( s) TsX i ( s) 传递函数 G( s) Ts X i ( s)
(t )
r
x(t )
数学模型 x(t ) r (t )dt
0
t
X (s)
r X (s) r ( s) G ( s) s ( s) s
齿轮——齿条传动
积分环节传递函数的一般形式 : K G ( s) s
i2(t) ui(t)
i1(t)
R a +
C
k
n0(t)
其中,ni(t) ——输入轴转速; n0(t) ——输出轴速; Z1,Z2——齿轮齿数。
(2)一阶惯性环节
凡运动方程为下面一阶微分方程
T d xo (t ) xo (t ) Kxi (t ) dt
形式的环节称为一阶惯性环节。其传递函数为:
G( s) X o ( s) K X i ( s ) Ts 1
例 如图所示无源滤波电路,
1 u ( t ) i ( t ) R i( t )dt i C u ( t ) 1 i( t )dt 0 C
k
m
c
略去质量的阻尼—弹簧系统
Ui(t)
R
i(t)
Uo(t) C
已知
拉氏变换后得 消去I(s),得
1 U ( s ) I ( s ) R I(s) i Cs U (s) 1 I(s) 0 Cs
2.4 传递函数
2.4.1 传递函数的定义
传递函数的概念和定义
X o ( s) 传递函数 G ( s) ˆ X i ( s)
在零初始条件下,线性定常系统输出量的拉氏 变换与引起该输出的输入量的拉氏变换之比。 零初始条件: t<0时,输入量及其各阶导数均为0;
输入量施加于系统之前,系统处于稳定 的工作状态,即t < 0 时,输出量及其各阶 导数也均为0;
例 如图所示永磁式直流测速机, 已知 u (t) k di (t) 0 dt U 0 (s ) G ( s ) ks 进行拉氏变换后得 i (s ) d i 则
U 0 (s) k dt (t )
U0(t)
式中,T—振荡环节的时间常数 ζ—阻尼比,对于振荡环节,0<ζ<1 K—比例系数
特点:在一定条件下,具有振荡可能,取决于系统本身的固有特性, 这是因为有两个储能元件,有能量交换,这种能量交换在一定条件下 以振荡方式存在。
只有当|Ts|<<1时,才近似为微分环节。
(4)积分环节
如果输出变量正比于输入变量的积分,即 进行拉氏变换得 X 0 (s) k
x 0 ( t ) k x i ( t )dt
G (s) X 0 (s ) k X i (s ) s
则
X i (s) s
特点:系统的输出和输入之间没有唯一对应的关系, 有记忆功能,能提高系统的稳态精度, 系统中的积分环节不能大于2个,否则系统不稳定。
例
如图所示弹簧-阻尼系统。
Xi(t)
kx i (t ) x 0 (t ) D
dx0 (t ) dt
Xo(t)
kX i (s) X o (s) DsXo (s)
D s 1X o (s) X i (s) k
X (s) 1 G (s) 0 X i (s) D s 1 k
i (t)
对于相同量纲的理想微分环节物理上是难以实现的, 电路中常遇到下述的近似微分环节。
i (t ) ——输入转角; 其中, u0(t) ——输出电压。
图 永磁式直流测速机
kTs G ( s ) 2 近似微分环节 Ts 1
例7 图2-14所示的无源微分电路
u i (t)
1 u ( t ) i(t )dt i(t )R 已知 i C u 0 (t ) i(t )R
设线性定常系统的微分方程为
a x (t ) a x
(n) 0 o
n 1 1 o
o (t ) a n x0 (t ) (t ) a n1 x
m 1 1 i
b x
( m) 0 i
(t ) b x
i (t ) a m xi (t ) (t ) bm1 x
C
i( t )
图 无源微分网络
1 U i (s) I(s) RI(s) 拉氏变换得 Cs u 0 (t) U 0 (s) RI(s) 其中, RCs 1 ui(t) ——输入电压 化简得 U i (s) R U 0 (s) u0(t) ——输出电压 RCs RC=T U ( s ) RCs R——电阻; G (s) 0 K=1 则 C——电容。 U i (s) RCs 1
u i (t )
i1 (t )
+
K
0
u o (t )
R1
U o (s) K U i (s)
z1 ni(t) z2
z1 z2
n 0 (t ) z 2 n i (t ) z1
N 0 (s) z 2 N i (s) z 1 G (s) N 0 (s) z 1 , N i (s) z2
X i ( s)
输出的拉氏变换 X o ( s) G( s) X i ( s)
时域中的输出 xo (t ) L [G( s) X i ( s)]
单位脉冲响应:
G ( s)
X 0 ( s)
1
g (t ) L1[G(s)]
传递函数具有以下特点:
(1) 传递函数的分母是系统的特征多项式,代表系统的 固有特性;分子代表输入与系统的关系,而与输入
式中,K—环节增益(放大系数); T—时间常数,表征环节的惯性,和 环节结构参数有关
特点:有一个阻尼元件存在,当有一个输入信号时,不会 马上达到一定值,而是需要一个缓慢上升的过程。
xi (t )
x0 (t )
忽略质量,由达朗贝尔 原理可知 o 0 数学模型 ( xi xo )k cx o kxo kxi csX o ( s ) kX o ( s ) kX i ( s ) cx X o (s) k 1 传递函数 G ( s ) X i ( s ) cs k Ts 1
M k
D
f i (t) ——输入外力; 其中, y 0 ( t ) ——输出位移; M——质量; k——弹簧刚度; D——拈行阻尼系数。 图 质量-弹簧-阻尼系统
返回
5 二阶振荡环节
含有两个独立的储能元件,且所存储的能量能够相互 转换,从而导致输出带有振荡的性质,运动方程为:
2 d d T 2 2 xo (t ) 2 T xo (t ) xo (t ) Kxi (t ), 0 1 dt dt X o ( s) K G ( s ) 传递函数: X i ( s) T 2 s 2 2 Ts 1
示系统Байду номын сангаас输出函数。因而,也可以把传递函数看成
单位脉冲响应的像函数; (5)分母s的阶次n大于等于分子中s的阶次m (6)传递函数可以是有量纲的,也可以是无量纲的。 自变量s的量纲为1/秒 (7) 如果将传递函数进行代换s=jω,可以直接得到系统 的频率特性函数(详见第3章)。
需要特别指出的是:
由于传递函数是经过拉氏变换导出的,而拉氏变换是一种 线性积分运算,因此传递函数的概念仅适用于线性定常系 统; 传递函数是在零初始条件下定义的,因此,传递函数原则
数学模型 o (t ) ui (t ) RCu
uo(t)
RCsUo (s) U i (s)
U o ( s) 1 K G( s) U i ( s) RCs s
5
二阶振荡环节
G (s)
1 T s 2Ts 1
2 2
, 0 1
0 (t ) 2Tx 0 (t ) x 0 (t ) x i (t ) 如果输入,输出函数可表达为如下二阶微分方程: T 2 x 经拉氏变换得 T 2 s 2 X 0 (s) 2TsX 0 (s) X 0 (s) X i (s)
特点:输出量与输入量成正比,输出不失真也不延迟,而是按比例反映输入, 即线性变化。
由运算放大器构成的比例环节
R2 uo (t ) ui (t ) Kui (t ) R1 拉氏变换 U o ( s ) KU i ( s ) G ( s )
如图所示齿轮传动副,
R2
i2 (t )
U i (s) (RCs 1)U o (s)
则
G (s )
U 0 (s ) 1 , 图 无源滤波电路 U i (s) RCs 1
其中,ui(t) ——输入电压; uo(t) ——输出电压; R为电阻;C为电容。
R
求低通滤波器的传递函数
u i (t )
i (t )
C
u o (t )
量无关,因此传递函数表达了系统本身的固有特性。 (2) 传递函数不说明被描述系统的具体物理结构,不同
的物理系统可能具有相同的传递函数。 (3) 传递函数比微分方程简单,通过拉氏变换将时域内 复杂的微积分运算转化为简单的代数运算;
(4) 当系统输入典型信号时,输出与输入有对应关系。 特别地,当输入是单位脉冲信号时,传递函数就表
其中,xi(t) ——输入位移; x0(t) ——输出位移 K——弹簧刚度; D——粘性阻尼系统。
图 弹簧-阻尼系统
(3)微分环节
输出量正比于输入量的微分。
i (t ) 微分环节的数学模型 xo (t ) T x X o ( s) X o ( s) TsX i ( s) 传递函数 G( s) Ts X i ( s)
(t )
r
x(t )
数学模型 x(t ) r (t )dt
0
t
X (s)
r X (s) r ( s) G ( s) s ( s) s
齿轮——齿条传动
积分环节传递函数的一般形式 : K G ( s) s
i2(t) ui(t)
i1(t)
R a +
C
k
n0(t)
其中,ni(t) ——输入轴转速; n0(t) ——输出轴速; Z1,Z2——齿轮齿数。
(2)一阶惯性环节
凡运动方程为下面一阶微分方程
T d xo (t ) xo (t ) Kxi (t ) dt
形式的环节称为一阶惯性环节。其传递函数为:
G( s) X o ( s) K X i ( s ) Ts 1
例 如图所示无源滤波电路,
1 u ( t ) i ( t ) R i( t )dt i C u ( t ) 1 i( t )dt 0 C
k
m
c
略去质量的阻尼—弹簧系统
Ui(t)
R
i(t)
Uo(t) C
已知
拉氏变换后得 消去I(s),得
1 U ( s ) I ( s ) R I(s) i Cs U (s) 1 I(s) 0 Cs
2.4 传递函数
2.4.1 传递函数的定义
传递函数的概念和定义
X o ( s) 传递函数 G ( s) ˆ X i ( s)
在零初始条件下,线性定常系统输出量的拉氏 变换与引起该输出的输入量的拉氏变换之比。 零初始条件: t<0时,输入量及其各阶导数均为0;
输入量施加于系统之前,系统处于稳定 的工作状态,即t < 0 时,输出量及其各阶 导数也均为0;
