电工学-第2章电路的瞬态分析(生物10)
合集下载
第2章电路的瞬态分析_02

R0 2Ω + US - 48 V a S b R1 6Ω + uC - i1 i2 R2 1.6 Ω C 25 µF R3 i3 4Ω
27
第2章 电路的瞬态分析
R0
a S b
R1 6Ω
i1 i2 R2 1.6 Ω + uC - C 25 µF R3 i3 4Ω
ቤተ መጻሕፍቲ ባይዱ
[解]
+
2Ω US - 48 V
(1)初始值 ) 由换路前电路
τ
t
+IS ( 1-e -
τ
t
τ
t
)
= I S + ( I 0- I S ) e uL =-RI0 e -
τ
t
+RIS e
τ
t
τ
t
t
= R ( IS - I0 ) e
20
= ( US-U0 ) e
τ
第2章 电路的瞬态分析
i L = I S + ( I 0- I S ) e 当 I0 > IS
iL I0
τ
t
a + U0 -
S + b
R + uC - iC C
US -
换路瞬间的电容电流为 US-U0 15-10 - = mA = 0.5 mA iC = R 10
10
第2章 电路的瞬态分析
a
S + b
R + uC - iC C
该电路的时间常数
τ = RC
= 10 × 103 × 20 × 10 = 0.2 s 根据
换路前, 断开, 换路前,开关 S 断开,且 电路已稳定。 电路已稳定。
I0 S R iL + uL -
iL ( 0 ) = I 0
换路后, 闭合。 换路后,开关 S 闭合。
27
第2章 电路的瞬态分析
R0
a S b
R1 6Ω
i1 i2 R2 1.6 Ω + uC - C 25 µF R3 i3 4Ω
ቤተ መጻሕፍቲ ባይዱ
[解]
+
2Ω US - 48 V
(1)初始值 ) 由换路前电路
τ
t
+IS ( 1-e -
τ
t
τ
t
)
= I S + ( I 0- I S ) e uL =-RI0 e -
τ
t
+RIS e
τ
t
τ
t
t
= R ( IS - I0 ) e
20
= ( US-U0 ) e
τ
第2章 电路的瞬态分析
i L = I S + ( I 0- I S ) e 当 I0 > IS
iL I0
τ
t
a + U0 -
S + b
R + uC - iC C
US -
换路瞬间的电容电流为 US-U0 15-10 - = mA = 0.5 mA iC = R 10
10
第2章 电路的瞬态分析
a
S + b
R + uC - iC C
该电路的时间常数
τ = RC
= 10 × 103 × 20 × 10 = 0.2 s 根据
换路前, 断开, 换路前,开关 S 断开,且 电路已稳定。 电路已稳定。
I0 S R iL + uL -
iL ( 0 ) = I 0
换路后, 闭合。 换路后,开关 S 闭合。
电工学第2章电路的瞬态分析2

二、RL 电路的零状态响应
换路前,开关 S 闭合, 电路已稳定。 iL ( 0 ) = 0 换路后,开关 S 断开。 iL ( ∞) = IS 阶跃零状态响
iL + uL -
IS S R
L
换路时电感中无储能,在外部输入的阶跃电流的作用下, 电感电流将从零逐渐增长到稳态值 IS 。
二、RL 电路的零状态响应
0.15 0.2 0.15 0.1
) A=5.28 A ) A=7.77 A
2.6 一阶电路瞬态分析的三要素法
凡是含有一个储能元件或经等效简化后含有 一个储能元件的线性电路,在进行瞬态分析 时所列出的微分方程式都是一阶微分方程 式。这种电路称为一阶电路。
S R1
+ U0 − +
S
iC
C
uC − + U −
τ
t
a + U0 -
S + b
R + uC - iC C
US -
换路瞬间的电容电流为 US-U0 15-10 = mA = 0.5 mA iC = R 10
例题
该电路的时间常数
a + U0 10-6 s - S + US - b R + uC - iC C
τ = RC
= 10 × 103 × 20 × = 0.2 s 根据
τ
t
τ
t
)
τ
t
diL uL = L = RIS e dt L τ= R
RL电路的 时间常数
= US e
uL iL IS US
电压发生突变
iL uL
工程上,只要 t≥3τ ,即可认 为瞬态过程基本结束。
O
t
三、RL 电路的全响应
如果 RL 电路在换路后 iL ( 0 ) = I 0 iL ( ∞) = IS
电工与电子技术基础:第二章 动态电路的瞬态分析

1)稳态:电路长期所处的工作状态或者不随时间发生变化; 或者周期性地变化。 这一状态称为电路的稳定工作状态, 简称稳态。
2)暂态过程:介于两个稳态之间的过渡状态。
如图(a) ,当K合上之前,i 0,uR 0 在某一时刻t,合上K,则由KVL有:
R
+
+ uR - +
uS
uL L
- - uC + -
零输入响应的特点
电压uC衰减的快慢是由电路的时间常数 τ决定的。 τ越小,电压、电流衰减越快。
对RC电路: 1)一个RC电路,仅有一个对应的τ ;
1
2)
uC(t)、 i(t)的形式为
t
Ae RC
τ如何求呢?τ=RC,故关键是求R 。
例:求图(a)电路中i(t) 、 u0(t) 。
S从1打到2后,欲使uC=0 ,需要一定
R
时间,这个过程就称为过渡过程或
S(t 0)
暂态过程。
1
特点:当动态电路的结构或元件参数
E
2
uC C
发生改变时,电路将从一个稳定状态
逐步过渡到另一个稳定状态,这中间的过程即是过渡过程。
暂态过程产生的原因:是由于物质所具有的能量不能突变所 造成的,当条件改变时,能量随着改变,但是能量的积累或 衰减是需要一定的时间的,不能跃变。 电路的接通、切断、短路、电压改变或电路参数的改变称电 路发生了换路。
【答】 可用二只 50 V,10 μF 的电容并联或用二只 30 V,20 μF 的电容串联。这样,不仅总电容值满足要求,而且 每个电容的实际工作电压亦满足其各自额定工作电压的要求。
练习:P.55 2.2.1
返 回分析与思考题集
上一题
电工学课件-第2章电路的瞬态分析

高等教育出版社
第
2
章 根据 KVL ,由换路后
电 路 的 瞬
的电路列出回路方程式 RiC+uC = 0
+ U0
-
态
分 析
而
iC
=
C
duC dt
aS b
得 RC ddutC+uC = 0
uC的通解为
t
uC = Ae RC
24
R
+ iC uC C -
将 t=0,uC= U0 代入,得
A = U0
高等教育出版社
分 作用下产生的电压和电流统称为响应。响应有 析 时又称输入。
按照产生响应原因的不同,响应可分为:
(1) 零输入响应 电路在无外部激励的情况下,仅由内部储能 元件中所储存的能量引起的响应。
高等教育出版社
5
第
2
章 (2) 零状态响应
电 路
在换路时储能元件未储存能量的情况下,由
的
激励所引起的响应。
瞬 态
L iL
+
+ uL - +
iC
US
uC C
IS S
瞬 后的电路求得:
-
-
+ -
态
uR
分 析
iR ( 0 ) = iL ( 0 ) = 1 A
R iR
uR ( 0 ) = RiR ( 0 ) = ( 5 1) V = 5 V
iC ( 0 ) = IS + iL ( 0 ) = ( 5 + 1) A = 6 A
U0
瞬 态
= 10 103 20 10-6 s-
分
= 0.2 s
析
根据
t
uC = US+ ( U0- US ) e
电工C第2章电路的瞬态分析

所以电容是一种储能元件,能量的转换是可 逆的,它不消耗能量。
3、电容器中储存的电场能
当t = 0 ξ时,u 由0 U,则输入电能
pdt
uidt
uC
du
dt
U
Cudu
1 CU 2
0
0
0 dt
0
2
则C储存的电场能为:
We =
1 CU 2 2C
单位:焦 [耳] (J)
5V
uC(0)
5V
u(L 0) US u(R 0) uC(0)
iL(0 ) iL(0 ) 1A
5- 5- 0 0V
u(C 0) u(C 0) 0
2、求稳态值即t=∞时的值 t=∞时的等效电路
iL () iR () IS 5A
uR () iR ()R 5 5 25V
电容的单位 1F 106 F 109 nF 1012 pF
1、电容上电压与电流的关系
若电压uc与电流ic取关联参考方向 (电容充电)
ic (t)
dq dt
dCuc dt
C
duc dt
当u U时, i 0
所以在直流电路中电容相当于开路
当电压变化时,电容电流才有值
故电容具有隔直流、通交流的作用
电感中的电流不能突变。
t 0 --- 换路前瞬间
t 0 --- 换路后瞬间
f(t)
则: uC (0 ) uC (0 )
t
0- 0 0+
iL (0 ) iL (0 )
注意:换路瞬间,uC、iL 不能突变。其它电量均可能突变,
第2章电路瞬态分析

U
τ RC
0.368U
12 3
0 1 2 3
t
越大,曲线变化越慢,u C 达到稳态所需要的
时间越长。
(3) 暂态时间
理论上认为 t、uC 0电路达稳态
工程上认为 t(3~ 5)、uC 0电容放电基本结束。
e
t
随时间而衰减
t
2 3 4 5 6
t
e
微分方程式:
RC
d uC dt
uC
0
通解:
uC Aest
U0
特征方程式:RC 1s0
aS
b
R
iC
uC
特征根:
s 1 RC
初始条件: t0 uC(0)U0
积分常数: A U0
令: RC
最后求得: uCU0eRt CU0et
iCCddutC
U0 et R
2.4 RC 电路的暂态分析
(一) RC 电路的零输入响应
t = 0 时换路
换路前,S 合在 a 端 U 0
uC(0-) = U0
aS
b
R
iC
uC
C
换路后,S 合在 b 端
图 2.3.1 RC 电路的零输入响应
uC(∞) = 0 研究 uC 和 iC
放电过程
返回
上一节
下一节
上一页
下一页
回路方程式: RC iuC0
返回
下一节
下一页
电路暂态分析的内容
(1) 暂态过程中电压、电流随时间变化的规律。 (2) 影响暂态过程快慢的电路的时间常数。 研究暂态过程的实际意义
1. 利用电路暂态过程产生特定波形的电信号 如锯齿波、三角波、尖脉冲等,应用于电子电路。
τ RC
0.368U
12 3
0 1 2 3
t
越大,曲线变化越慢,u C 达到稳态所需要的
时间越长。
(3) 暂态时间
理论上认为 t、uC 0电路达稳态
工程上认为 t(3~ 5)、uC 0电容放电基本结束。
e
t
随时间而衰减
t
2 3 4 5 6
t
e
微分方程式:
RC
d uC dt
uC
0
通解:
uC Aest
U0
特征方程式:RC 1s0
aS
b
R
iC
uC
特征根:
s 1 RC
初始条件: t0 uC(0)U0
积分常数: A U0
令: RC
最后求得: uCU0eRt CU0et
iCCddutC
U0 et R
2.4 RC 电路的暂态分析
(一) RC 电路的零输入响应
t = 0 时换路
换路前,S 合在 a 端 U 0
uC(0-) = U0
aS
b
R
iC
uC
C
换路后,S 合在 b 端
图 2.3.1 RC 电路的零输入响应
uC(∞) = 0 研究 uC 和 iC
放电过程
返回
上一节
下一节
上一页
下一页
回路方程式: RC iuC0
返回
下一节
下一页
电路暂态分析的内容
(1) 暂态过程中电压、电流随时间变化的规律。 (2) 影响暂态过程快慢的电路的时间常数。 研究暂态过程的实际意义
1. 利用电路暂态过程产生特定波形的电信号 如锯齿波、三角波、尖脉冲等,应用于电子电路。
电工学第2章

uC C S
uR -
R iR
L
iL
uL
iC C
uC
uR -
R iR
返回
上一节
下一节
上一页
IS
IS
下一页
第2章 电路的暂态分析
2.3 RC 电路旳暂态分析
(一) RC 电路旳零输入响应
t = 0 时换路
aS
R
b
iC
换路前,S 合在 a 端 U0
uC
C
uC(0) = U0
换路后,S 合在 b 端
L2
L L1 L2
电感并联:
i
u
L1 L2
11 1
L L1 L2
返回
上一节
下一节
上一页
下一页
第2章 电路的暂态分析
(三)换路定理
电容电压、电感电流在换路瞬间不能突变。
设:t =0 时换路 t 0 --- 换路前瞬间
t 0 --- 换路后瞬间
则:
uC (0 ) uC (0 )
注意:
iL (0 ) iL (0 )
[解] (1) 求初始值
根据换路定律,由换路
前( S 闭合时)旳电路求
得
uC (0)
iL (0)
US R
0
5 5
A
US
1A
返回
上一节
L iL
uL iC
IS
uC C
S
uR -
R iR
图 2.2.4 例2.2.1 旳电路
L
iL
uL
iC C
IS
uC
S
uR -
R
下一节
iR
上一页
电工学课后答案-第2章-电路的瞬态分析习题及答案
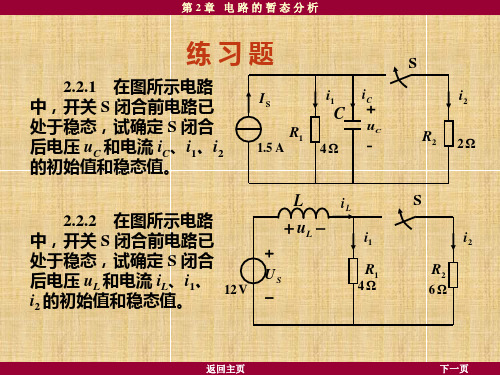
u L (0) US R1 12 4 A 3 A
然后,根据,由换路后 (S 闭合时) 的电路求得
i1 ( 0 ) i2 (0 ) R2 R 1 R2 R1 R1 R 2 iL (0) iL (0) 6 46 4 46 3 A 1 .8 A 3 A 1 .2 A
iL
R2
6Ω
L
1H
返 回
第2章 电路的暂态分析
2.4.2图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL,并画出 其变化曲线。
i1
IS
S
i2
R3
7Ω
R1
24 A
R2
3Ω
uL
iL
1 .5 Ω
L
0 .4 H
a
S
b
R1
3Ω
2.4.3图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL,并说明是什么 响应。
uC U 0 e iC C
30 e U0 R
10
4
C
t
V 3e
10
4
R
t
uC
d uC dt
t
e
A
上一题 下一题
返 回练习题题集
上一页
第2章 电路的暂态分析
2.3.2在图所示电路原已处于稳态,在 t = 0 时,将开 关 S 闭合,试求响应 uC 和 iC,并说明是什么响应?
100 t
)V
e
15 e
mA
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析
然后,根据,由换路后 (S 闭合时) 的电路求得
i1 ( 0 ) i2 (0 ) R2 R 1 R2 R1 R1 R 2 iL (0) iL (0) 6 46 4 46 3 A 1 .8 A 3 A 1 .2 A
iL
R2
6Ω
L
1H
返 回
第2章 电路的暂态分析
2.4.2图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL,并画出 其变化曲线。
i1
IS
S
i2
R3
7Ω
R1
24 A
R2
3Ω
uL
iL
1 .5 Ω
L
0 .4 H
a
S
b
R1
3Ω
2.4.3图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL,并说明是什么 响应。
uC U 0 e iC C
30 e U0 R
10
4
C
t
V 3e
10
4
R
t
uC
d uC dt
t
e
A
上一题 下一题
返 回练习题题集
上一页
第2章 电路的暂态分析
2.3.2在图所示电路原已处于稳态,在 t = 0 时,将开 关 S 闭合,试求响应 uC 和 iC,并说明是什么响应?
100 t
)V
e
15 e
mA
返 回练习题题集
上一页
上一题
下一题
第2章 电路的暂态分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电 a 端,电路已稳定。换路后将 S 合到 b 端。试求响
路 的
应 i1 、i2 和 i3 。
瞬
态
分
R0 a S R1 i1
析
2
6
i2
i3
b
+
R2 1.6
US 48 V -
+ uC -
R3 4 C 25 F
大连理工大学电气工程系
第2章 电路的瞬态分析
14
第2章 电路的瞬态分析
15
第
2
R0 a S
t
= [ 0 + ( 4-0 ) e ] 10-4 A = 4 e-10 4t A
章
电 (2)稳态值
路
2 b
+
的 瞬
由于换路后电
US -
48 V
பைடு நூலகம்
态 路无外部激励
分
析 i1 ( ) = i2 ( ) = i3 ( ) = 0
16
R1 i1
6
i2
i3
R2 1.6
+ uC -
R3 4 C 25 F
(3)时间常数
( ) = RC =
R2+
R1R3 R1+R3
C
( ) =
6 4 1.6 + 6+4
电容电压和电感电流在换路后的初始值应等于
换路前的终了值。换路前的终了时刻表示为 t = 0-
uC ( 0+ ) = uC ( 0-) iL ( 0+ ) = iL ( 0-)
大连理工大学电气工程系
5
第
2
章 换路定律仅适用于换路瞬间。
电
路
的
换路定律 初始值用 u (0) 和 i (0) 表示
瞬
态 分 析
电工技术
第 2 章 电路的瞬态分析
2.1 换路定则和初始值的确定 2.2 一阶电路暂态过程分析方法
返回主页 上一章1 下一章
2
第
2
章
2.1 瞬态分析的基本概念
电
路
的 瞬
一、稳态和瞬态
态 电路的结构和元件的参数一定时,电路的工作
分 析
状态一定,电压和电流不改变。这时电路所处
的状态称为稳定状态,简称稳态。
+ uL - +
iC
US
uC C
IS S
瞬 后的电路求得:
-
-
+ -
态
uR
分 析
iR ( 0 ) = iL ( 0 ) = 1 A
R iR
uR ( 0 ) = RiR ( 0 ) = ( 5 1) V = 5 V
iC ( 0 ) = IS + iL ( 0 ) = ( 5 + 1) A = 6 A
大连理工大学电气工程系
10
第
2
章 电
t
uC = US+ ( U0- US ) e
路
t
的 瞬
iL = IS + ( I0- IS ) e
态 分 析
由于零输入响应和零状态响应可看成全响应在 初始值为零或稳态值为零时的特例
因此,任何形式的一阶电路的零输入响应、阶 跃零状态响应和阶跃全响应可归纳为
t
f ( t ) = f ( ) +[ f ( 0 ) - f ( ) ] e
25 10-6 s = 10-4 s
大连理工大学电气工程系
17
第
2 章
(4)求出待求响应
电 路
t
i1 = i1 ( ) +[ i1 ( 0 ) - i1 ( ) ] e
的
t
瞬
= [ 0 + ( 1.6-0 ) e 10-4 ] A = 1.6 e-10 4t A
态
分
t
析
i2 = i2 ( ) +[ i2 ( 0 ) - i2 ( ) ] e
-
uR
+ -
R iR
uL ( ) = 0
由换路后的电路再求得:
iL ( ) = iR ( ) = iC ( ) -IS = ( 0-5 ) A = -5 A
uR ( ) = RiR ( ) = [ 5 (-5 ) ] V = -25 V
uC ( ) = US-uL ( ) -uR ( ) = [ 5-0-(-25 ) ] V = 30 V
换路
当电路在接通、断开、改接以及参数和电源发 生突变时,都会引起电路工作状态的变化。
大连理工大学电气工程系
3
第
2
章 电
换路后,旧的工作状态被破坏、新的工作状态
路 在建立,电路将从一个稳态变化到另一个稳态,
的 瞬 态
这种变化往往不能瞬间完成,而是有一个瞬态 过程。
分 析
电路在瞬态过程中所处的状态称为瞬态状态,
三要素法
大连理工大学电气工程系
第
2
章 电
f ( 0 ) 、 f ( ) 的求法见 2.3 节
路
的
瞬 态
的求法
分
析
用除源等效法 将换路后电路 中的电源除去
求出从储能元 件( C 或 L) 两端看进去的 等效电阻 R
12
= RC
或 L
= R
大连理工大学电气工程系
13
第
2
章 [例2.6.1]在图示电路中,换路前开关 S 闭合在
uL ( 0 ) = US-uR ( 0 ) -uC ( 0 ) = ( 5 -5 -0 ) V = 0 V
大连理工大学电气工程系
8
第
2
章 (2) 求稳态值
电 路
在稳态直流电
的
路中,C 相当
瞬 态
于开路, L 相
分
当于短路。
析
iC ( ) = 0
L iL
+
+ uL - +
iC
IS
US
uC C
S
-
大连理工大学电气工程系
11
第
2 章 电
t
f ( t ) = f ( ) +[ f ( 0 ) - ff (( )) ] e
路
的
瞬 待求响应
态 分
待求响应 的初始值
待求响应 的稳态值
电路的 时间常数
析
f ( 0 ) 、 f ( ) 和 是确定任何一个一阶电路
阶跃响应的三要素。
t
f ( t ) = f ( ) +[ f ( 0 ) - f ( ) ] e
换路 前的 电路
换初和路始i后L的值uC
换路后其他 电流和电压 的初始值
换路 后的 电路
稳态值用 u () 和 i () 表示 电路达到新稳态 时电流和电压
的稳态值
大连理工大学电气工程系
第2章 电路的瞬态分析
6
7
第
2 章 电 路 的
根据 uC ( 0 ) 和 iL ( 0 ) ,由换路
L iL
+
简称瞬态。
换路后为什么会有瞬态过程? 换路是引起瞬态过程的外因。
电容中的电场能和电感中的磁场能的不能突变 是引起瞬态过程的内因。
大连理工大学电气工程系
4
第
2
章 电
二、
换路定律
路
的 由于电容中的电场能和电感中的磁场能不能突变,所以换
瞬 态
路瞬间,电容上的电压和电感中的电流不可能突变。
分
析 换路定律
换路后的初始时刻表示为 t = 0+
大连理工大学电气工程系
9
第
2
章 2.2 一阶电路瞬态分析的三要素法
电
路
的 凡是含有一个储能元件或经等效简化后含有
瞬 态
一个储能元件的线性电路,在进行瞬态分析
分 时所列出的微分方程式都是一阶微分方程
析 式。这种电路称为一阶电路。
任何形式的一阶电路只要将储能元件从电路 中提出,使剩下的电路成为有源二端网络, 都可以利用等效电源定理将该电路简化成上 两节介绍的最简单的一阶电路。
