中考数学 二次函数综合试题含答案
2023安徽中考数学专题《二次函数综合》含答案解析
热点05 二次函数综合安徽中考数学中二次函数部分主要考向分为三类：一、二次函数的图象与性质；二、二次函数中求动点坐标（与图形面积相关）；三、二次函数的实际运用（近几年主要考察利润相关为题）；需要注意的是综合运用的题型，难度系数较大，考察的内容较多，特别是动点，还是计算利润时由于数值比较大需细心。
考点一：利用对称轴解决问题抛物线的开口向下，对称轴x = −b2a =−2A，当x1 +x2 >2时，x1< x2，点A离对称轴的距离比点B，当x1+x2< 2时，x1< x2，点A离对称轴的距离比点确，考点二：最值问题【答案】 8 43a2），则点B坐标为【分析】设点A（a，18由AC2＝（xc﹣xA）2+（yC﹣yA）2可得求解．a2），则点B 【详解】解：设点A（a，18∴OB＝|a|，AB＝1a2，想解答即可．【详解】解：二次函数y=2(x−1)2+1的图像如图：所以函数有最小值1，当x=0时，y=3，当x=3时，y=9，当0≤x≤3时，x=1在范围内，故函数值能取到最小值，故1≤y≤9．故选：B．【点睛】本题考查了抛物线的顶点坐标，最值，增减性，数形结合思想，熟练掌握抛物线的性质和数形结合思想是解题的关键．考点三：二次函数与不等式【例6】．（2022秋·安徽淮南）二次函数y＝x2，当1 ≤y ≤ 9时，自变量x的取值范围是（）A．1≤x≤3B．-3≤x≤3C．-3≤x≤-1或1≤x≤3D．-3≤x≤1或1≤x≤3【答案】C【分析】根据题目中的函数解析式和二次函数的性质，可以计算出当1≤y ≤9时，自变量x 的取值范围．【详解】解：∵y＝x2，∴该函数图像开口向上，对称轴为直线x＝0，当x＞0时，y随x的增大而增大，当x＜0时，y随x的增大而减小，∵当y＝1时，x＝±1；当y＝9时，x＝±3，∴ 当1≤y ≤9时，自变量x 的取值范围是-3≤x ≤-1或1≤x ≤3，故选：C ．【点睛】本题考查二次函数的性质及二次函数图像上点的坐标特征，解答本题的关键是明确题意，利用二次函数的性质解答．【例7】． （2022秋·安徽合肥）在平面直角坐标系中，已知点A (4,2)，B (4,4)，抛物线L ：()()20y x t t t =--+≥，当L 与线段AB 有公共点时，t 的取值范围是（ ）A ．3≤t ≤4B ．5≤t ≤6C ．3≤t ≤4，t =6D ．3≤t ≤4或5≤t ≤6【答案】D【分析】根据题意知线段AB 平行于y 轴，故根据二次函数与线段交点的情况列式()2244t t --+≤≤求解即可．【详解】根据题意知：∵点A (4,2)，B (4,4)，故对于二次函数()()20y x t t t =--+≥与线段AB 有公共点时，即当x=4时，2≤y ≤4，即()2244t t --+≤≤，解得：3≤t ≤4或5≤t ≤6；故选：D ．【点睛】此题考查二次函数与线段交点问题，主要理解函数图像与线段有交点的真实含义，难度一般，主要是计算．【例8】． （2022秋·安徽合肥）如图是二次函数y 1=ax 2+bx +c (a ≠0)和一次函数y 2=mx +n (m ≠0)的图象，当y 2>y 1，x 的取值范围是________．【答案】−2<x <1【分析】关键是从图像上找出两函数图像交点坐标，再根据两函数图像的上下位置关系，判断y 2＞y 1时，x 的取值范围．【详解】从图像上看出，两个交点坐标分别为(−2,0)，(1,3)【例10】． （2022秋·安徽芜湖·）如图，抛物线23y ax bx =++与x 轴交于A ，B 两点，且点B 的坐标为(2，0)，与y 轴交于点C ，抛物线对称轴为直线x =−1．连接AC ，BC ，点P 是抛物线上在第二象限内的一个动点．过点P 作x 轴的垂线PH ，垂足为点H ，交AC 于点Q ．过点P 作PG ⊥AC 于点G ．。
中考数学 二次函数综合试题附详细答案
中考数学 二次函数综合试题附详细答案一、二次函数1．如图，已知抛物线y =x 2＋bx ＋c 与x 轴交于A 、B 两点（A 点在B 点左侧），与y 轴交于点C （0，－3），对称轴是直线x =1，直线BC 与抛物线的对称轴交于点D ．（1）求抛物线的函数表达式；（2）求直线BC 的函数表达式；（3）点E 为y 轴上一动点，CE 的垂直平分线交CE 于点F ，交抛物线于P 、Q 两点，且点P 在第三象限．①当线段PQ =34AB 时，求tan ∠CED 的值； ②当以点C 、D 、E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标．【答案】（1）抛物线的函数表达式为y =x 2－2x －3．（2）直线BC 的函数表达式为y =x －3．（3）①23．①P 1（122），P 2（16，74）． 【解析】【分析】已知C 点的坐标，即知道OC 的长，可在直角三角形BOC 中根据∠BCO 的正切值求出OB 的长，即可得出B 点的坐标．已知了△AOC 和△BOC 的面积比，由于两三角形的高相等，因此面积比就是AO 与OB 的比．由此可求出OA 的长，也就求出了A 点的坐标，然后根据A 、B 、C 三点的坐标即可用待定系数法求出抛物线的解析式．【详解】（1）∵抛物线的对称轴为直线x=1， ∴− 221bb a-⨯＝＝1 ∴b=-2 ∵抛物线与y 轴交于点C （0，-3），∴c=-3，∴抛物线的函数表达式为y=x 2-2x-3；（2）∵抛物线与x 轴交于A 、B 两点，当y=0时，x 2-2x-3=0．∴x1=-1，x2=3．∵A点在B点左侧，∴A（-1，0），B（3，0）设过点B（3，0）、C（0，-3）的直线的函数表达式为y=kx+m，则033k mm＝＝+⎧⎨-⎩，∴13 km⎧⎨-⎩＝＝∴直线BC的函数表达式为y=x-3；（3）①∵AB=4，PQ=34 AB，∴PQ=3∵PQ⊥y轴∴PQ∥x轴，则由抛物线的对称性可得PM=32，∵对称轴是直线x=1，∴P到y轴的距离是12，∴点P的横坐标为−12，∴P（−12，−74）∴F（0，−74），∴FC=3-OF=3-74=54∵PQ垂直平分CE于点F，∴CE=2FC=5 2∵点D在直线BC上，∴当x=1时，y=-2，则D（1，-2），过点D作DG⊥CE于点G，∴DG=1，CG=1，∴GE=CE-CG=52-1=32．在Rt△EGD中，tan∠CED=23 GDEG＝．②P1（2，-2），P2（6-52）．设OE=a，则GE=2-a，当CE为斜边时，则DG2=CG•GE，即1=（OC-OG）•（2-a），∴1=1×（2-a），∴a=1，∴CE=2，∴OF=OE+EF=2∴F、P的纵坐标为-2，把y=-2，代入抛物线的函数表达式为y=x2-2x-3得：2或2∵点P在第三象限．∴P1（2-2），当CD为斜边时，DE⊥CE，∴OE=2，CE=1，∴OF=2.5，∴P和F的纵坐标为：-52，把y=-52，代入抛物线的函数表达式为y=x2-2x-3得：x=1-621+62∵点P在第三象限．∴P2（6-52）．综上所述：满足条件为P1（2-2），P2（6-52）．【点睛】本题是二次函数的综合题型，其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法．在求有关动点问题时要注意分析题意分情况讨论结果．2．某市实施产业精准扶贫，帮助贫困户承包荒山种植某品种蜜柚．已知该蜜柚的成本价为6元/千克，到了收获季节投入市场销售时，调查市场行情后，发现该蜜柚不会亏本，且每天的销售量y （千克）与销售单价x （元）之间的函数关系如图所示．（1）求y 与x 的函数关系式，并写出x 的取值范围；（2）当该品种蜜柚定价为多少时，每天销售获得的利润最大？最大利润是多少？（3）某村农户今年共采摘蜜柚12000千克，若该品种蜜柚的保质期为50天，按照（2）的销售方式，能否在保质期内全部销售完这批蜜柚？若能，请说明理由；若不能，应定销售价为多少元时，既能销售完又能获得最大利润？【答案】（1）y ＝﹣20x +500，（x ≥6）；（2）当x ＝15.5时，w 的最大值为1805元；（3）当x ＝13时，w ＝1680，此时，既能销售完又能获得最大利润．【解析】【分析】（1）将点（15，200）、（10，300）代入一次函数表达式：y ＝kx +b 即可求解；（2）由题意得：w ＝y （x ﹣6）＝﹣20（x ﹣25）（x ﹣6），∵﹣20＜0，故w 有最大值，即可求解；（3）当x ＝15.5时，y ＝190，50×190＜12000，故：按照（2）的销售方式，不能在保质期内全部销售完；由50（500﹣20x ）≥12000，解得：x ≤13，当x ＝13时，既能销售完又能获得最大利润．【详解】解：（1）将点（15，200）、（10，300）代入一次函数表达式：y ＝kx +b 得：2001530010k b k b =+⎧⎨=+⎩， 解得：20500k b =-⎧⎨=⎩， 即：函数的表达式为：y ＝﹣20x +500，（x ≥6）；（2）设：该品种蜜柚定价为x 元时，每天销售获得的利润w 最大，则：w ＝y （x ﹣6）＝﹣20（x ﹣25）（x ﹣6），∵﹣20＜0，故w 有最大值，当x ＝﹣2b a ＝312＝15.5时，w 的最大值为1805元；（3）当x＝15.5时，y＝190，50×190＜12000，故：按照（2）的销售方式，不能在保质期内全部销售完；设：应定销售价为x元时，既能销售完又能获得最大利润w，由题意得：50（500﹣20x）≥12000，解得：x≤13，w＝﹣20（x﹣25）（x﹣6），当x＝13时，w＝1680，此时，既能销售完又能获得最大利润．【点睛】本题考查了二次函数的性质在实际生活中的应用．最大销售利润的问题常利函数的增减性来解答，我们首先要吃透题意，确定变量，建立函数模型，然后结合实际选择最优方案．其中要注意应该在自变量的取值范围内求最大值（或最小值）.3．抛物线y＝ax2+bx﹣3（a≠0）与直线y＝kx+c（k≠0）相交于A（﹣1，0）、B（2，﹣3）两点，且抛物线与y轴交于点C．（1）求抛物线的解析式；（2）求出C、D两点的坐标（3）在第四象限抛物线上有一点P，若△PCD是以CD为底边的等腰三角形，求出点P的坐标．【答案】（1）y＝x2﹣2x﹣3;（2）C（0，﹣3）,D（0，﹣1）;（3）P（2，﹣2）.【解析】【分析】（1）把A（﹣1，0）、B（2，﹣3）两点坐标代入y＝ax2+bx﹣3可得抛物线解析式．（2）当x＝0时可求C点坐标，求出直线AB解析式，当x＝0可求D点坐标．（3）由题意可知P点纵坐标为﹣2，代入抛物线解析式可求P点横坐标．【详解】解：（1）把A（﹣1，0）、B（2，﹣3）两点坐标代入y＝ax2+bx﹣3可得30 4233 a ba b--=⎧⎨+-=-⎩解得12 ab=⎧⎨=-⎩∴y＝x2﹣2x﹣3（2）把x＝0代入y＝x2﹣2x﹣3中可得y＝﹣3∴C（0，﹣3）设y＝kx+b，把A（﹣1，0）、B（2，﹣3）两点坐标代入023k b k b -+=⎧⎨+=-⎩解得11k b =-⎧⎨=-⎩∴y ＝﹣x ﹣1∴D （0，﹣1）（3）由C （0，﹣3），D （0，﹣1）可知CD 的垂直平分线经过（0，﹣2）∴P 点纵坐标为﹣2，∴x 2﹣2x ﹣3＝﹣2解得：x ＝1±2，∵x ＞0∴x ＝1+2．∴P （1+2，﹣2）【点睛】本题是二次函数综合题，用待定系数法求二次函数的解析式，把x ＝0代入二次函数解析式和一次函数解析式可求图象与y 轴交点坐标，知道点P 纵坐标带入抛物线解析式可求点P 的横坐标．4．（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m ，宽是4 m ．按照图中所示的直角坐标系，抛物线可以用y=16-x 2+bx+c 表示，且抛物线上的点C 到OB 的水平距离为3 m ，到地面OA 的距离为172m. （1）求抛物线的函数关系式，并计算出拱顶D 到地面OA 的距离；（2）一辆货运汽车载一长方体集装箱后高为6m ，宽为4m ，如果隧道内设双向车道，那么这辆货车能否安全通过？（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m ，那么两排灯的水平距离最小是多少米？【答案】（1）抛物线的函数关系式为y=16-x 2+2x+4，拱顶D 到地面OA 的距离为10 m ；(2)两排灯的水平距离最小是3．【解析】【详解】试题分析：根据点B和点C在函数图象上，利用待定系数法求出b和c的值，从而得出函数解析式，根据解析式求出顶点坐标，得出最大值；根据题意得出车最外侧与地面OA的交点为（2,0）（或（10,0）），然后求出当x=2或x=10时y的值，与6进行比较大小，比6大就可以通过，比6小就不能通过；将y=8代入函数，得出x的值，然后进行做差得出最小值．试题解析：（1）由题知点17(0,4),3,2B C⎛⎫⎪⎝⎭在抛物线上所以41719326cb c=⎧⎪⎨=-⨯++⎪⎩，解得24bc=⎧⎨=⎩，所以21246y x x=-++所以，当62bxa=-=时，10ty=≦答：21246y x x=-++，拱顶D到地面OA的距离为10米（2）由题知车最外侧与地面OA的交点为（2,0）（或（10,0））当x=2或x=10时，2263y=>，所以可以通过（3）令8y=，即212486x x-++=，可得212240x x-+=，解得12623,623x x=+=-1243x x-=答：两排灯的水平距离最小是43考点：二次函数的实际应用．5．如图，抛物线212222y x x=-++与x轴相交于A B，两点，（点A在B点左侧）与y轴交于点C.（Ⅰ）求A B，两点坐标.（Ⅱ）连结AC，若点P在第一象限的抛物线上，P的横坐标为t，四边形ABPC的面积为S.试用含t的式子表示S，并求t为何值时，S最大.（Ⅲ）在（Ⅱ）的基础上，若点,G H 分别为抛物线及其对称轴上的点，点G 的横坐标为m ，点H 的纵坐标为n ，且使得以,,,A G H P 四点构成的四边形为平行四边形，求满足条件的,m n 的值.【答案】（Ⅰ）(A B ；（Ⅱ）2(2S t t =--+<<,当t =时，S =最大；（Ⅲ）满足条件的点m n 、的值为：34m n ==，或154m n ==-，或14m n == 【解析】【分析】（Ⅰ）令y=0，建立方程求解即可得出结论；（Ⅱ）设出点P 的坐标，利用S=S △AOC +S 梯形OCPQ +S △PQB ，即可得出结论；（Ⅲ）分三种情况，利用平行四边形的性质对角线互相平分和中点坐标公式建立方程组即可得出结论．【详解】解：（Ⅰ）抛物线21222y x x =-++，令0y =，则212022x x -++=，解得：x =x =∴((,A B（Ⅱ）由抛物线21222y x x =-++，令0x =，∴2y =，∴()0,2C ， 如图1，点P 作PQ x ⊥轴于Q ，∵P 的横坐标为t ，∴设(),P t p ，∴212,,22p t PQ p BQ t OQ t =-++===，∴()()11122222AOC PQB OCPQ S S S S p t t p =++=++⨯+⨯⨯V V 梯形 1122t pt pt t =++-=++21222t t ⎫=-+++⎪⎪⎭2t t =+<<，∴当2t =时，42S =最大；（Ⅲ）由（Ⅱ）知，2t =， ∴)2,2P ，∵抛物线212222y x x =-++的对称轴为22x =， ∴设2122,2,222G m m m H n ⎛⎫⎛⎫-++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭以,,,A G H P 四点构成的四边形为平行四边形，()2,0A ，①当AP 和HG 为对角线时， ∴()2112111222,20222222m m n ⎛⎛⎫=++=-+++ ⎪ ⎪⎝⎭⎝⎭， ∴234m n ==， ②当AG 和PH 是对角线时， ∴(()2112112122,20222222m m n ⎛⎫=-++=+ ⎪ ⎪⎭⎝⎭， ∴215,24m n ==-， ③AH 和PG 为对角线时， ∴(()2121112122,22022222m m n ⎛⎛⎫-=+-+++=+ ⎪ ⎪⎝⎭⎝⎭， ∴3214m n ==， 即：满足条件的点m n 、的值为： 2324m n =-=，或5215,24m n ==-，或32124m n =-= 【点睛】此题是二次函数综合题，主要考查了坐标轴上点的特点，三角形的面积公式，梯形的面积公式，平行四边形的性质，中点坐标公式，用方程的思想解决问题是解本题的关键．6．如图，抛物线y=﹣（x ﹣1）2+c 与x 轴交于A ，B （A ，B 分别在y 轴的左右两侧）两点，与y 轴的正半轴交于点C ，顶点为D ，已知A （﹣1，0）．（1）求点B ，C 的坐标；（2）判断△CDB 的形状并说明理由；（3）将△COB 沿x 轴向右平移t 个单位长度（0＜t ＜3）得到△QPE ．△QPE 与△CDB 重叠部分（如图中阴影部分）面积为S ，求S 与t 的函数关系式，并写出自变量t 的取值范围．【答案】(Ⅰ)B(3，0)；C(0，3)；(Ⅱ)CDB ∆为直角三角形；(Ⅲ)22333(0)221933(3)222t t t S t t t ⎧-+<≤⎪⎪=⎨⎪=-+<<⎪⎩. 【解析】【分析】（1）首先用待定系数法求出抛物线的解析式，然后进一步确定点B ，C 的坐标．（2）分别求出△CDB 三边的长度，利用勾股定理的逆定理判定△CDB 为直角三角形． （3）△COB 沿x 轴向右平移过程中，分两个阶段：①当0＜t≤32时，如答图2所示，此时重叠部分为一个四边形； ②当32＜t ＜3时，如答图3所示，此时重叠部分为一个三角形． 【详解】解：(Ⅰ)∵点()1,0A -在抛物线()21y x c =--+上， ∴()2011c =---+，得4c = ∴抛物线解析式为：()214y x =--+， 令0x =，得3y =，∴()0,3C ；令0y =，得1x =-或3x =，∴()3,0B . (Ⅱ)CDB ∆为直角三角形.理由如下： 由抛物线解析式，得顶点D 的坐标为()1,4. 如答图1所示，过点D 作DM x ⊥轴于点M ， 则1OM =，4DM =，2BM OB OM =-=.过点C 作CN DM ⊥于点N ，则1CN =，1DN DM MN DM OC =-=-=. 在Rt OBC ∆中，由勾股定理得：22223332BC OB OC =+=+=； 在Rt CND ∆中，由勾股定理得：2222112CD CN DN =+=+=； 在Rt BMD ∆中，由勾股定理得：22222425BD BM DM =+=+=.∵222BC CD BD +=， ∴CDB ∆为直角三角形.(Ⅲ)设直线BC 的解析式为y kx b =+， ∵()()3,0,0,3B C ，∴303k b b +=⎧⎨=⎩，解得1,3k b =-=，∴3y x =-+，直线QE 是直线BC 向右平移t 个单位得到，∴直线QE 的解析式为：()33y x t x t =--+=-++； 设直线BD 的解析式为y mx n =+， ∵()()3,0,1,4B D ， ∴304m n m n +=⎧⎨+=⎩，解得：2,6m n =-=，∴26y x =-+.连续CQ 并延长，射线CQ 交BD 交于G ，则3,32G ⎛⎫ ⎪⎝⎭. 在COB ∆向右平移的过程中： (1)当302t <≤时，如答图2所示：设PQ 与BC 交于点K ，可得QK CQ t ==，3PB PK t ==-.设QE 与BD 的交点为F ，则：263y x y x t =-+⎧⎨=-++⎩. 解得32x t y t =-⎧⎨=⎩，∴()3,2F t t -.111222QPE PBK FBE F S S S S PE PQ PB PK BE y ∆∆∆=--=⋅-⋅-⋅ ()221113333232222t t t t t =⨯⨯---⋅=-+. (2)当332t <<时，如答图3所示：设PQ 分别与BC BD 、交于点K 、点J . ∵CQ t =，∴KQ t =，3PK PB t ==-.直线BD 解析式为26y x =-+，令x t =，得62y t =-， ∴(),62J t t -.1122PBJ PBK S S S PBPJ PB PK ∆∆=-=⋅-⋅ ()()()211362322t t t =---- 219322t t =-+. 综上所述，S 与t 的函数关系式为：2233302219333222t t t S t t t ⎧⎛⎫-+<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪=-+<< ⎪⎪⎝⎭⎩.7．如图，直线l ：y ＝﹣3x +3与x 轴、y 轴分别相交于A 、B 两点，抛物线y ＝ax 2﹣2ax +a +4（a ＜0）经过点B ，交x 轴正半轴于点C ． （1）求该抛物线的函数表达式；（2）已知点M 是抛物线上的一个动点，并且点M 在第一象限内，连接AM 、BM ，设点M 的横坐标为m ，△ABM 的面积为S ，求S 与m 的函数表达式，并求出S 的最大值及此时动点M 的坐标；（3）将点A 绕原点旋转得点A ′，连接CA ′、BA ′，在旋转过程中，一动点M 从点B 出发，沿线段BA ′以每秒3个单位的速度运动到A ′，再沿线段A ′C 以每秒1个单位长度的速度运动到C 后停止，求点M 在整个运动过程中用时最少是多少？【答案】（1）y ＝﹣x 2+2x +3；（2）S 与m 的函数表达式是S ＝252m m--，S 的最大值是258，此时动点M 的坐标是（52，74）；（3）点M 82秒． 【解析】 【分析】（1）首先求出B 点的坐标，根据B 点的坐标即可计算出二次函数的a 值，进而即可计算出二次函数的解析式;（2）计算出C 点的坐标，设出M 点的坐标，再根据△ABM 的面积为S ＝S 四边形OAMB ﹣S △AOB ＝S △BOM +S △OAM ﹣S △AOB ，化简成二次函数，再根据二次函数求解最大值即可. （3）首先证明△OHA ′∽△OA ′B ，再结合A ′H +A ′C ≥HC 即可计算出t 的最小值. 【详解】（1）将x ＝0代入y ＝﹣3x +3，得y ＝3， ∴点B 的坐标为（0，3），∵抛物线y ＝ax 2﹣2ax +a +4（a ＜0）经过点B ， ∴3＝a +4，得a ＝﹣1，∴抛物线的解析式为：y ＝﹣x 2+2x +3；（2）将y ＝0代入y ＝﹣x 2+2x +3，得x 1＝﹣1，x 2＝3， ∴点C 的坐标为（3，0），∵点M 是抛物线上的一个动点，并且点M 在第一象限内，点M 的横坐标为m ， ∴0＜m ＜3，点M 的坐标为（m ，﹣m 2+2m +3）， 将y ＝0代入y ＝﹣3x +3，得x ＝1， ∴点A 的坐标（1，0）， ∵△ABM 的面积为S ，∴S ＝S 四边形OAMB ﹣S △AOB ＝S △BOM +S △OAM ﹣S △AOB ＝()2123313222m m m ⨯-++⨯⨯+-， 化简，得S ＝252m m --＝21525228m ⎛⎫--+ ⎪⎝⎭，∴当m ＝52时，S 取得最大值，此时S ＝258，此时点M 的坐标为（52，74）， 即S 与m 的函数表达式是S ＝252m m--，S 的最大值是258，此时动点M 的坐标是（52，74）； （3）如右图所示，取点H 的坐标为（0，13），连接HA ′、OA ′， ∵∠HOA ′＝∠A ′OB ，13OH OA '=，13OA OB '=， ∴△OHA ′∽△OA ′B ，∴3BA A H''=， 即3BA A H ''=，∵A′H+A′C≥HC＝2218233⎛⎫+=⎪⎝⎭，∴t≥82，即点M在整个运动过程中用时最少是82秒．【点睛】本题主要考查抛物线的性质，关键在于设元，还有就是（3）中利用代替法计算t的取值范围，难度系数较大，是中考的压轴题.8．如图，已知抛物线的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）。
(新)中考数学二次函数与几何综合典型试题(附答案解析)
解：（1）当x=0时，y=3，即A（0，3），
设抛物线的解析式为：y=a（x+3）（x-1），
把A（0，3）入得：3=-3a，
a=-1，
∴y=-（x+3）（x-1）=-x2-2x+3，
1．（1）m2；（2）m1=-3，m2=1；（3） 或 ；（4）-3＜m≤-1或m＞1
【分析】
（1）根据平行线的性质知，点B与点A的横坐标相同，所以把x=m代入抛物线解析式，即可求得点B的纵坐标；
（2）把点A代入二次函数解析式，列出方程，然后解方程即可；
（3）根据等量关系AB=2和两点间的距离公式列出方程，解方程即可求得m的值；
∴线段AB的长度随m的增大而增大时，-3＜m≤-1．
当m＞1时，根据题意知，线段AB的长度随m的增大而增大时，m＞1．
综上所述，m的取值范围是-3＜m≤-1或m＞1．
【点睛】
本题主要考查了二次函数综合题，注重培养二次函数的解析式的求法和与几何图形结合的综合能力．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．
所以方程组的解为： 或 ，
∴
【点睛】
本题考查的是全等三角形的判定与性质，利用待定系数法求解二次函数的解析式，旋转的性质，求解一次函数与二次函数的交点坐标，作出适当的辅助线构建全等三角形，再利用全等三角形的性质证明相等的线段，再得到点的坐标是解本题的关键.
4．（1） （2）P（4，5）（3）（-2，5）或（4，5）．
【详解】
解：（1）将A（－1，0），B（3，0）代入抛物线解析式得
解得
∴抛物线的解析式为
（2）∵抛物线的解析式为 ，A（－1，0），B（3，0）
2023年九年级中考数学专题复习：二次函数综合题(特殊三角形问题)含答案
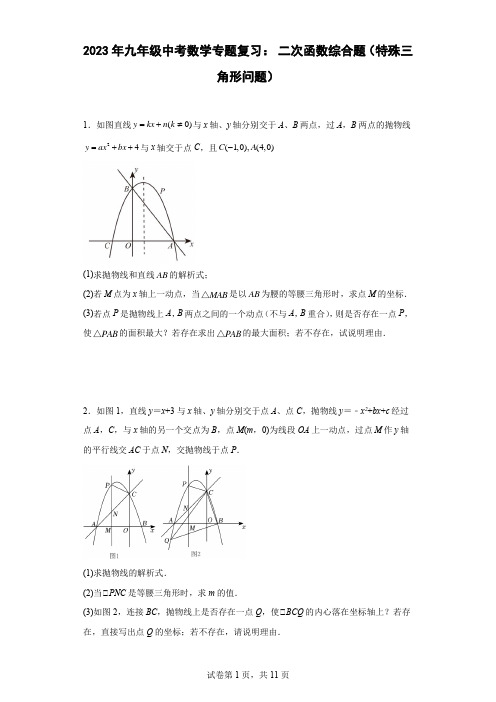
20．如图，抛物线y＝ x2﹣ x﹣ 与x轴交于点A和点B，与y轴交于点C，经过点C的直线l与抛物线交于另一点E（4，a），抛物线的顶点为点Q，抛物线的对称轴与x轴交于点D．
13．如图，抛物线 经过点A（0，3），B（－1，0）．
(1)求抛物线的解析式；
(2)抛物线的顶点为D，对称轴与x轴交于点E，连接BD，求BD的长．
(3)在抛物线上是否存在点P，使△PBD是以BD为直角边的直角三角形，若存在请直接写出点P的坐标，若不存在，请说明理由．
14．如图，抛物线 过点 ， ， ．
(3)如图2，在（2）的条件下，点D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，使得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．
7．如图，抛物线y＝ x2＋bx＋c与x轴交于A(3，0)、B(－1，0)两点，过点B作直线BC⊥x轴，交直线y＝－2x于点C．
(1)求a、b满足的关系式及c的值；
(2)如果 ，点P是直线AB下方抛物线上的一点，过点P作PD垂直于x轴，垂足为点D，交直线AB于点E，使 ．
①求点P的坐标；
②若直线PD上是否存在点Q，使 为直角三角形？若存在，求出符合条件的所有点Q的坐标；若不存在，请说明理由．
16．如图，抛物线y＝﹣x2+bx+c经过A(4，0)，C(﹣1，0)两点，与y轴交于点B，P为第一象限抛物线上的动点，连接AB，BC，PA，PC，PC与AB相交于点Q．
(1)点E的坐标为；
2023年九年级数学中考专题：二次函数综合压轴题(角度问题)(含简单答案)
2023年九年级数学中考专题：二次函数综合压轴题（角度问题）1．如图，抛物线2y ax2x c=++（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．(1)求该抛物线的函数解析式；(2)如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD，OD交BC于点F，当:COD COBS S＝1：3时，求点F的坐标；(3)如图2，点E的坐标为（0，﹣32），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请求出点P的坐标；若不存在，请说明理由．2．如图，在二次函数2221y x mx m=-+++（m是常数，且0m>）的图像与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．其对称轴与线段BC交于点E，与x轴交于点F．连接AC，BD．(1)求A，B，C三点的坐标（用数字或含m的式子表示），并求OBC∠的度数；(2)若ACO CBD∠=∠，求m的值；(3)若在第四象限内二次函数2221y x mx m=-+++（m是常数，且0m>）的图像上，始终存在一点P ，使得75ACP ∠=︒，请结合函数的图像，直接写出m 的取值范围． 3．如图1，直线y ＝2x ＋2交x 轴于点A ，交y 轴于点C ，过A 、C 两点的抛物线232y ax x c =++与x 轴的另一交点为B ．(1)求该抛物线的函数表达式；(2)如图2，点D 是抛物线在第一象限内的一点，连接OD ，将线段OD 绕O 逆时针旋转90°得到线段OM ，过点M 作MN ∠x 轴交直线AC 于点N ．求线段MN 的最大值及此时点D 的坐标；(3)在（2）的条件下，若点E 是点A 关于y 轴的对称点，连接DE ，试探究在抛物线上是否存在点P ，使得∠PED ＝45°？若存在，求出点P 的坐标；若不存在，请说明理由． 4．如图，抛物线22y ax bx =++与x 轴相交于A 、B 两点，与y 轴相交于点C ，已知B 点的坐标为()4,0，抛物线的对称轴为直线32x =，点D 是BC 上方抛物线上的一个动点．(1)求抛物线的函数表达式；(2)当BCD △的面积为74时，求点D 的坐标； (3)过点D 作DE BC ⊥，垂足为点E ，是否存在点D ，使得CDE 中的某个角等于ABC ∠的2倍？若存在，请直接写出点D 的横坐标．．．；若不存在，请说明理由． 5．如图，在平面直角坐标系中，抛物线211322y x x =-++与x 轴交于A 、B 两点（点B 在点A 的右侧），与y 轴交于点C ，D 为线段AB 上一点．(1)求A ，B ，C 三点的坐标；(2)过点D 作x 轴的垂线与抛物线交于点E ，与直线BC 相交于点F ，求出点E 到直线BC 距离d 的最大值；(3)连接CD ，作点B 关于CD 的对称点B '，连接AB '，B D '．在点D 的运动过程中，ADB ∠'能否等于45°？若能，请直接写出此时点B '的坐标，若不存在请说明理由．6．如图1，二次函数2y x bx c =++的图像与x 轴交于点A (﹣2，0)，B (4，0)，抛物线的顶点为C ，作射线AC ，BC ．动点P 从点A 出发，以每秒1个单位长度的速度沿射线AC 做匀速运动，动点Q 从B 出发，以每秒2个单位长度的速度沿射线BC 运动．(1)填空：b ＝_____，c ＝_____，C 的坐标为_____．(2)点P ，Q 运动过程中，∠CPQ 可能为等腰三角形吗？说明理由．(3)如图2，连接PO ，QO ，当∠POQ ＝30°时，直接写出t 的值．7．如图，抛物线2y ax bx c =++经过()1,0A -，()3,0B 且与y 轴交于点()0,3C -．(1)求抛物线的函数表达式；(2)若点P 是x 轴的正半轴上一点，1tan 3APC ∠=，求点P 的坐标； (3)当点P 是抛物线上第一象限上的点，1tan 3APC ∠=，直接写出点P 的坐标为______． 8．如图，抛物线24y ax bx =+-与x 轴交于点A （-2，0）、B （4，0），与y 轴交于点C ，过点C 作x 轴的平行线交抛物线于点D ，连接AC ，作直线BC ．(1)求抛物线24y ax bx =+-的表达式； (2)如图2，点E （x ，0）是线段OB 上的点，过点E 作与x 轴垂直的直线与直线BC 交于点F ，与抛物线交于点G ．∠线段FG 的长是否存在最大值？若存在，求出这个最大值：若不存在，说明理由； ∠连接CG ，当∠DCG =∠ACO 时，求点G 的坐标；(3)若点P 是直线BC 下方的抛物线上的一点，点Q 在y 轴上，点M 在线段BC 上，当以C ，P ，Q ，M 为顶点的四边形是菱形时，直接写出菱形的边长．9．如图1，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴交于A （1，0），与y 轴交于C （0，－3）．(1)求抛物线的解析式；(2)在抛物线上是否存在这样的点P ，使得∠ACP=∠ABC ，若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图2，点D 为线段BC 上一点，过点D 作y 轴的平行线交抛物线于点E ，连结BE ．当∠DBE =90°时，求BEC S ∆．10．如图，在平面直角坐标系xOy 中，抛物线y =ax 2-2x +c 与x 轴交于点A 和点B （1，0），与y 轴相交于点C （0，3）．(1)求抛物线的解析式和顶点D 的坐标；(2)找出图中与∠DAB 相等的一个角，并证明；(3)若点P 是第二象限内抛物线上的一点，当点P 到直线AC 的距离最大时，求点P 的坐标．11．如图所示：二次函数26y ax bx =+-的图象与x 轴交于()2,0A -，()3,0B 两点，与y 轴交于点C ，连接AC ，BC ．(1)求二次函数表达式及直线BC 的函数表达式；(2)如图1，若点M 为抛物线上线段BC 右侧的一动点，连接CM ，BM ．求四边形ACMB 面积最大时点M 的坐标；(3)如图2，该抛物线上是否存在点P ，使得ACO BCP ∠=∠？若存在，请求出所有点P 的坐标；若不存在，请说明理由．12．已知如图，二次函数23y x bx =++的图像与x 轴相交于点A 、B 两点，与y 轴相交于点C ，连接AC 、BC ，tan 1ABC ∠=，抛物线的顶点为D ．(1)求抛物线的解析式；(2)抛物线的对称轴上有一动点E ，当AE CE +取得最小值时，E 点坐标为________；此时AE 与BC 的位置关系是________，tan ACE ∠=________；(3)抛物线对称轴右侧的函数图像上是否存在点M ，满足ACB BAM ∠=∠，若存在求M 点的横坐标；若不存在，请说明理由；(4)若抛物线上一动点Q ，当BAQ ACO ∠=∠时，直接写出Q 点坐标________． 13．如图，在平面直角坐标系中，抛物线212y x bx c =++与x 轴交于B ，C 两点（C 在B的左侧），与y 轴交于点A ，已知()0,4A -，2OA OB =．(1)求抛物线的表达式；(2)若点Q 是线段AC 下方抛物线上一点，过点Q 作QD 垂直AC 交AC 于点D ，求DQ 的最大值及此时点Q 的坐标；(3)点E 是线段AB 上一点，且14AOE AOC S S =△△；将抛物线212y x bx c =++沿射线AB 的方向平移，当抛物线恰好经过点E 时，停止运动，已知点M 是平移后抛物线对称轴上的动点，N 是平面直角坐标系中一点，直接写出所有使得以点A ，B ，M ，N 为顶点的四边形是菱形的点N 的坐标，并把求其中一个点N 的坐标的过程写出来．14．如图，抛物线()()22369=++-+y mx m x m 与x 轴交于点A 、B ，与y 轴交于点C ，已知()3,0B ．(1)m 的值是________；(2)P （异于点A ）为抛物线上一点，若PBC ABC S S =△△，求点P 的坐标：(3)Q 为抛物线上一点，若45ACQ ∠=︒，请直接写出点Q 的坐标．15．如图，在平面直角坐标系中，抛物线22y ax bx =++与x 轴交于1,0A ，()4,0B 两点，与y 轴交于点C ．直线l ：2y kx =+过点C ．（1）求抛物线的解析式；（2）当直线l 经过点B 时，取线段BC 的中点M ，作直线l 的平行线，恰好与抛物线有一个交点P 时，判断以点P ，O ，M ，B 为顶点的四边形是什么特殊的平行四边形，并说明理由；（3）在直线l 上是否存在唯一一点Q ，使得90AQB ∠=︒？若存在，请求出此时l 的解析式；若不存在，请说明理由．16．我们不妨约定，过坐标平面内任意两点（例如A ，B 两点）作x 轴的垂线，两个垂足之间的距离叫做这两点在x 轴上的“足距”，记作AB ．根据该约定，完成下列各题：（1）若点1(,6)A x ，2(,4)B x -．当点A 、B 在函数2y x =的图象上时，AB =______；当点A ，B 在函数24y x=-的图像上时，AB =______； （2）若反比例函数()11k y k x -=≠的图象上有两点()1,A x k ，()22,B x k k -，当AB k =时，求正整数k 的值． （3）在（2）条件下抛物线223y kx x =+-与x 轴交于1A ，1B 两点，与y 轴交于点C ．如图，点D 是该抛物线的顶点，点(,)P m n 是第一象限内该抛物线上的一个点，分别连接1A D 、1A C 、1A P ，当1112PA B CA D ∠=∠时，求m 的值．17．在平面直角坐标系xOy 中，二次函数y ＝ax 2+bx 的图象与x 轴交于O 、A 两点，其顶点B 的坐标为（2，﹣6）．（1）求a 、b 的值；（2）如图1，点C 是该二次函数图象的对称轴上的一个动点，连接BO 、CO ，当∠OBC 是以BC 为腰的等腰三角形时，求点C 的坐标；（3）如图2，P 是该二次函数图象上的位于第一象限内的一个动点，连接OP ，与对称轴交于点M ，点Q 在OP 上，满足OQ PQ ＝21，设点P 的横坐标为n ； ∠请用含n 的代数式表示点Q 的坐标（，）；∠连接BQ ，OB ，当∠OBQ 的面积为15时，求点P 的坐标；∠当∠POA ＝2∠OBM 时，直接写出点P 的横坐标．18．如图1，直线4y x =-+与x 轴、y 轴分别交于点A 与点B ，抛物线212y x bx c =-++经过点A 、B ，在线段OA 上有一动点(),0D m ，点D 不与O 、A 重合，过点D 作x 轴的垂线交直线AB 于点C ，交抛物线于点E ．（1）求抛物线的函数表达式；（2）当点C 是DE 的中点时，求m 的值；（3）在（2）的条件下，将线段OD 绕点O 逆时针旋转得到OD '，旋转角为()090αα︒<<︒，连接'D A 、'D B ，直接写出''12D A D B +的最小值．参考答案：1．(1)223y x x =-++；(2)F （35，125）； (3)存在，P （13，329）或（﹣73，﹣649）．2．(1)A （-1，0）；B （2m +1，0）；C （0，2m +1）；45OBC ∠=︒(2)1m =(3)0m <<3．(1)213222y x x =-++ (2)最大值为3；()2,3D(3)存在，11P ⎛ ⎝⎭，()20,2P4．(1)213 2.22y x x (2)79,28D 或121,.28(3)点D 的横坐标为2或2911．5．(1)A （-2，0），B （3，0），C （0，3）；(2)点E 到直线BC 的距离d ；(3)在点D 的运动过程中，∠ADB '能等于45°，此时点B ′的坐标为（0，-或（-，3）．6．；(1， (2)不可能，理由见解析(3)t 的值为：17．(1)2=23y x x --(2)点P 的坐标为()9,0(3)点P 的坐标为()4,58．(1)2142y x x =-- (2)∠当2x =时，FG 有最大值，FG 的最大值=2；∠G （3，－52）或（1，－4.5）． (3)2或49．(1)2=+43y x x --(2)存在点P ，使得∠ACP=∠ABC ，点P 的坐标为7524,⎛⎫- ⎪⎝⎭(3)3△BEC S =10．(1)y ＝﹣x 2﹣2x +3，顶点D 的坐标为（﹣1，4）(2)∠ACB ，证明见解析(3)点P 坐标为（32-，154）11．(1)26y x x =--，26y x =-(2)点M 的坐标为321,24⎛⎫- ⎪⎝⎭ (3)存在，（2，-4）或（8，50）12．(1)y =x 2-4x +3；(2)（2，1）；AE ∠BC ，12； (3)存在，M 点的横坐标为52或72； (4)Q 点的坐标为(103，79)或(83，59-) ．13．(1)2142y x x =+-(2)DQ ()2,4Q -(3)N 点坐标为(2,或(2,-或()2,0-或52,2⎛⎫- ⎪⎝⎭，见解析14．(1)1-(2)()2,1P ，⎝⎭P ，⎝⎭P (3)75,24⎛⎫- ⎪⎝⎭Q15．（1）215222y x x =-+；（2）菱形；（3）存在，122y x =-+或2y x =+或2y x =+． 16．（1）5；10；（2）1；（3）74m =17．（1）a ＝32，b ＝﹣6；（2）点C 的坐标为（2，6--2，6-+2，83-）；（3）∠23n ，n 2﹣4n ；∠P （5，152）；∠点P 的横坐标为92．18．（1）2142y x x =-++；（2）2；（3。
中考数学总复习《二次函数的最值》练习题及答案
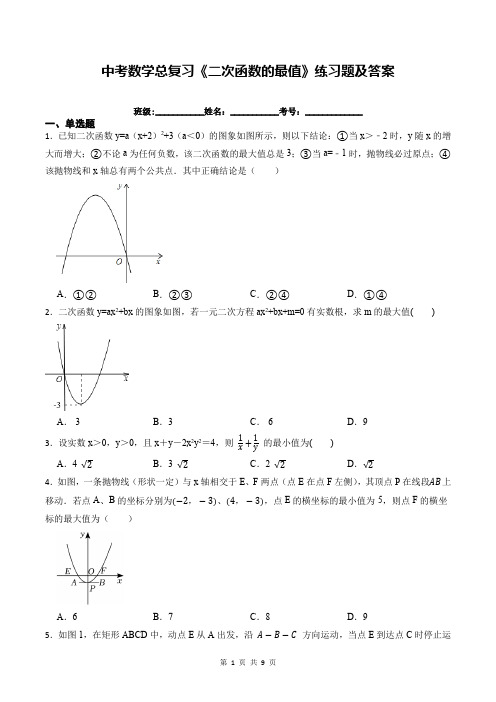
中考数学总复习《二次函数的最值》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．已知二次函数y=a（x+2）2+3（a＜0）的图象如图所示，则以下结论：①当x＞﹣2时，y随x的增大而增大；②不论a为任何负数，该二次函数的最大值总是3；③当a=﹣1时，抛物线必过原点；④该抛物线和x轴总有两个公共点．其中正确结论是（）A．①②B．②③C．②④D．①④2．二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，求m的最大值() A．-3B．3C．-6D．93．设实数x＞0，y＞0，且x＋y－2x2y2＝4，则1x+1y的最小值为()A．4 √2B．3 √2C．2 √2D．√24．如图，一条抛物线（形状一定）与x轴相交于E、F两点（点E在点F左侧），其顶点P在线段AB上移动．若点A、B的坐标分别为(−2，−3)、(4，−3)，点E的横坐标的最小值为-5，则点F的横坐标的最大值为（）A．6B．7C．8D．95．如图1，在矩形ABCD中，动点E从A出发，沿A−B−C方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是25，则矩形ABCD的面积是()A．235B．254C．6D．56．已知0≤x≤32，则函数y=x2+x+1（）A．有最小值34，但无最大值B．有最小值34，有最大值1C．有最小值1，有最大值194D．无最小值，也无最大值7．已知二次函数y＝ax2＋bx＋c（a，b，c是常数，a≠0）的y与x的部分对应值如表：x﹣5﹣4﹣202y60﹣6﹣46；③若点（﹣8，y1），点（8，y2）在二次函数图象上，则y1＜y2；④方程ax2＋bx＋c＝﹣5有两个不相等的实数根．其中，正确结论的是（）A．①②③B．①③④C．①②④D．②③④8．已知二次函数y=ax2−2ax+a+2(a≠0)，若−1≤x≤2时，函数的最大值与最小值的差为4，则a的值为（）A．1B．-1C．±1D．无法确定9．如图，已知二次函数的图象（0≤x≤1+2 √2）.关于该函数在所给自变量取值范围内，下列说法正确的是（）A．有最小值﹣2，无最大值B．有最小值﹣2，有最大值﹣1.5C．有最小值﹣2，有最大值2D．有最小值﹣1.5，有最大值210．如图，Rt△ABC中，∠ACB=90°，AC=12BC=2点D是AB上一动点，连接CD，将线段CD绕点C逆时针旋转90°得到线段CE，连接DE，BE，当△BED面积最大时，AD的长为（）A．2B．√5C．25√5D．4√5511．若二次函数y＝﹣x2+mx在﹣1≤x≤2时的最大值为3，那么m的值是（）A．﹣4或72B．﹣2 √3或72C．﹣4 或2 √3D．﹣2 √3或2 √3 12．若二次函数y＝ax2＋4x＋a－1的最小值是2，则a的值为（）A．4B．－1C．3D．4或－1二、填空题13．二次函数y=x2−2x+3的最小值是．14．当实数a满足2≤a≤5时，且代数式−a2+2ab−b2取最大值－1时，则b的值为．15．抛物线y=ax2+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：x-2-1012y04664从上表可知，下列说法中正确的是．)①抛物线与x轴的一个交点为(3，0)；②函数y=ax2+bx+c的最大值为6；②抛物线的对称轴是直线x=12；④在对称轴左侧，y随x增大而增大．16．二次函数y=﹣x2﹣4x+k的最大值是9，则k=．17．已知关于x的函数y=−x2−ax+1，当0≤x≤3时函数有最大值5，则a=．18．已知关于x的二次函数y＝x2－2ax＋3，当1≤x≤3时，函数有最小值2a，则a的值为.三、综合题19．已知抛物线y=ax2+bx+c与y轴交于点(0，3a)，对称轴为x=1.（1）试用含a的代数式表示b、c.（2）当抛物线过点(2，3)时，求此抛物线的解析式.（3）求当b(c+6)取得最大值时的抛物线的顶点坐标.20．如图，正方形ABCD的边长为4，点G，H分别是BC、CD边上的点，直线GH与AB、AD的延长线相交于点E，F，连接AG、AH．（1）当BG=2，DH=3时，则GH：HF=，∠AGH=°；（2）若BG=3，DH=1，求DF、EG的长；（3）设BG=x，DH=y，若∠ABG∠∠FDH，求y与x之间的函数关系式，并求出y的取值范围．21．如图，抛物线y=12x2−32x−2与x轴交于A，B两点，与y轴交于点C，连接AC，BC，点M是线段BC下方抛物线上的任意一点，点M的横坐标为m，过点M画MN∠x轴于点N，交BC于点P.（1）填空：A（，），C（，）；（2）探究∠ABC的外接圆圆心的位置，并求出圆心的坐标；（3）探究当m取何值时线段PM的长度取得最大值，最大值为多少？22．某商品现在的售价为每件50元，每天可卖出200件．市场调查反映：如调整价格，每涨价1元，每天要少卖出10件，已知商品的进价为每件40元，请你帮助分析，当每件商品涨价多少元时，可使每天的销售利润最大，最大利润是多少？设每件商品涨价x元，每天售出商品的利润为y元．（1）根据题意，填写下表：每件售价（元）505152……50+x每天售出商品的数量（件）200190……每天售出商品的利润（元）20002090……23．已知，一个铝合金窗框如图所示，所使用的铝合金材料长度为18m．设AB长为xm，窗户的总面积为Sm2．（1）求S关于x的函数表达式．（2）若AB的长不能低于2m，且AB＜BC，求此时窗户总面积S的最大值和最小值．24．已知关于x的一元二次方程x2﹣（m+1）x+ 12（m2+1）=0有实数根．（1）求m的值；（2）先作y=x2﹣（m+1）x+ 12（m2+1）的图象关于x轴的对称图形，然后将所作图形向左平移3个单位长度，再向上平移2个单位长度，写出变化后图象的解析式；（3）在（2）的条件下，当直线y=2x+n（n≥m）与变化后的图象有公共点时，求n2﹣4n的最大值和最小值．参考答案1．【答案】C2．【答案】B3．【答案】A4．【答案】B5．【答案】B6．【答案】C7．【答案】B8．【答案】C9．【答案】C10．【答案】C11．【答案】C12．【答案】A13．【答案】214．【答案】1或615．【答案】①③④16．【答案】517．【答案】-418．【答案】119．【答案】（1）解：∵抛物线与y轴交于点(0，3a)∴c=3a∵对称轴为x=1∴x=−b2a=1∴b=−2a（2）解：∵抛物线过点(2，3)∴3=a×22+2(−2a)+3a∴a=1∴b=−2a=−2，c=3a=3∴抛物线为y=x2−2x+3（3）解：∵b(c+6)=−2a(3a+6)=−6a2−12a=−6(a+1)2+6∴当a=−1时，b(c+6)的最大值为6；∴抛物线y=−x2+2x−3=−(x−1)2−2故抛物线的顶点坐标为(1，−2)20．【答案】（1）1：3；90（2）解：∵正方形ABCD的边长为4，BG=3，DH=1∴CG=1，CH=3∵CG∠DF，CH∠BE∴∠CGH∠∠BGE∠∠DFH∴GCHC=BGBE=DFDH，即13=3BE=DF1解得BE=9，DF= 1 3∴Rt∠BEG中，EG= √BG2+BE2= √32+92=3 √10（3）解：∵正方形ABCD的边长为4，BG=x，DH=y ∴CG=4﹣x，CH=4﹣y由（1）可得，∠FDH∠∠GCH，而∠ABG∠∠FDH∴∠ABG∠∠GCH∴ABGC=BGCH，即44−x=x4−y∴y与x之间的函数关系式为：y= 14x2﹣x+4∵44−x=x4−y∴4﹣y= x(4−x)4=﹣14x2+x∴当x=﹣12×(−14)=2时，4﹣y有最大值，且最大值为﹣14×4+2=1∴0＜4﹣y≤1解得3≤y＜4．21．【答案】（1）-1；0；0；-2（2）解：|OA|=1，|OC|=2，|OB|=4∠AOC=∠COB=90°∴OAOC=OCOB=12∴∠AOC∠∠COB∴∠ACO=∠OBC∠ACO+∠OCB=90°∠OBC+∠OCB=90°=∠ACB∴Rt∠ACB的外接圆圆心为AB的中点∵A（-1，0）B（4，0）∴圆心的坐标（ 32，0 ）.（3）解：C （0，-2），B （4，0） 又∵直线BC 解析式y =12x −2 p(m ，12m −2) ，M （m ， 12m 2−32m −2 ）PM=（ 12m −2 ）-（ 12m 2−32m −2 ）PM =−12m 2+2m =−12(m −2)2+2 当m=2时，PM 最大值=2.22．【答案】（1）180；200﹣10x ；2160；（200﹣10x ）（10+x ）（2）解：y ＝（200﹣10x ）（10+x ）＝﹣10x 2+100x+2000＝﹣10（x ﹣5）2+2250 ∴当x ＝5时，y 取得最大值，此时y ＝2250即y ＝﹣10x 2+100x+2000，当每件商品涨价5元时，可使每天的销售利润最大，最大利润是2250元23．【答案】（1）解：∵AB=xm ，铝合金材料长为18m∴AD=BC=18−3x 2∴S ＝x·18−3x2＝−32x 2+9x即S 与x 的函数表达式为：S ＝−32x 2+9x.（2）解：由题意得：2≤x ＜18−3x 2解得：2≤x ＜3.6∵S ＝−32x 2+9x ＝−32（x -3）2+272∵−32＜0，对称轴是直线x ＝3，且2≤x ＜3.6∴当x ＝3时，S 取得最大值，此时S ＝272当x ＝2时，S 取得最小值，此时S ＝−32（2-3）2+272＝12答：窗户总面积S 的最大值272m 2，最小值是12m 2．24．【答案】（1）解：对于一元二次方程x 2﹣（m+1）x+ 12（m 2+1）=0∠=（m+1）2﹣2（m 2+1）=﹣m 2+2m ﹣1=﹣（m ﹣1）2 ∵方程有实数根∴﹣（m﹣1）2≥0∴m=1．（2）解：由（1）可知y=x2﹣2x+1=（x﹣1）2图象如图所示：平移后的解析式为y=﹣（x+2）2+2=﹣x2﹣4x﹣2．（3）解：由{y=2x+ny=−x2−4x−2消去y得到x2+6x+n+2=0由题意∠≥0∴36﹣4n﹣8≥0∴n≤7∵n≤m，m=1∴1≤n≤7令y′=n2﹣4n=（n﹣2）2﹣4∴n=2时，y′的值最小，最小值为﹣4n=7时，y′的值最大，最大值为21∴n2﹣4n的最大值为21，最小值为﹣4．。
2023年九年级中考数学：二次函数综合题压轴题(特殊四边形问题)(含答案)
(1)求该抛物线的解析式和顶点 的坐标；
(2)设点 的横坐标是 ，问当 取何值时，四边形 的面积最大；
(3)如图，若直线 的解析式是 ，点 和点 分别在抛物线上和直线 上，问：是否存在以点 为顶点的四边形是平行四边形？若存在，请直接写出符合题意的点 的坐标
3．综合与探究
如图，在平面直角坐标系中，抛物线 与 轴交于 、 两点，与 轴交于点 ，点 为抛物线顶点．
(1)求抛物线解析式；
(2)点 在此抛物线的对称轴上，当 最大时，点 的坐标为_____，此时 的面积为_____；
(3)点 在抛物线上，平面内存在点 使四边形 为菱形时，请直接写出点 的坐标．
4．如图，在平面直角坐标系中，抛物线 和直线 交于 、 两点，直线 交 轴于点 ．
20．如图，在平面直角坐标系中，矩形OABC的两边OA，OC分别在x轴和y轴上， ， ，抛物线 经过点B，且与x轴交于点 和点E．
(1)求抛物线的表达式：
(2)若P是第一象限抛物线上的一个动点，连接CP，PE，当四边形OCPE的面积最大时，求点P的坐标，此时四边形OCPE的最大面积是多少；
(3)若N是抛物线对称轴上一点，在平面内是否存在一点M，使以点C，D，M，N为顶点的四边形是矩形？若存在，请直接写出点M的坐标；若不存在，说明理由．
(1)求点 的坐标与 的值；
(2)当点 恰好是 的中点时，求点 的坐标；
(3)连结 ，作点 关于直线 的对称点 ，当点 落在线段 上时，则点 的坐标为______ 直接写出答案
6．已知抛物线 与x轴有公共点．
中考数学 二次函数综合试题及详细答案
中考数学 二次函数综合试题及详细答案一、二次函数1．已知二次函数223y ax ax =-+的最大值为4，且该抛物线与y 轴的交点为C ，顶点为D .（1）求该二次函数的解析式及点C ，D 的坐标；（2）点(,0)P t 是x 轴上的动点，①求PC PD -的最大值及对应的点P 的坐标；②设(0,2)Q t 是y 轴上的动点，若线段PQ 与函数2||23y a x a x =-+的图像只有一个公共点，求t 的取值范围.【答案】（1）2y x 2x 3=-++，C 点坐标为(0,3)，顶点D 的坐标为(1,4)；（2）①最，P 的坐标为(3,0)-，②t 的取值范围为3t ≤-或332t ≤<或72t =. 【解析】【分析】（1）先利用对称轴公式x=2a 12a--=，计算对称轴，即顶点坐标为（1，4），再将两点代入列二元一次方程组求出解析式；（2）根据三角形的三边关系：可知P 、C 、D 三点共线时|PC-PD|取得最大值，求出直线CD 与x 轴的交点坐标，就是此时点P 的坐标；（3）先把函数中的绝对值化去，可知22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩，此函数是两个二次函数的一部分，分三种情况进行计算：①当线段PQ 过点（0，3），即点Q 与点C 重合时，两图象有一个公共点，当线段PQ 过点（3，0），即点P 与点（3，0）重合时，两函数有两个公共点，写出t 的取值；②线段PQ 与当函数y=a|x|2-2a|x|+c （x≥0）时有一个公共点时，求t 的值；③当线段PQ 过点（-3，0），即点P 与点（-3，0）重合时，线段PQ 与当函数y=a|x|2-2a|x|+c （x ＜0）时也有一个公共点，则当t≤-3时，都满足条件；综合以上结论，得出t 的取值．【详解】解：（1）∵2a x 12a-=-=， ∴2y ax ax 3=-+的对称轴为x 1=.∵2y ax ax 3=-+人最大值为4，∴抛物线过点()1,4.得a 2a 34-+=，解得a 1=-.∴该二次函数的解析式为2y x 2x 3=-++.C 点坐标为()0,3，顶点D 的坐标为()1,4.（2）①∵PC PD CD -≤，∴当P,C,D 三点在一条直线上时，PC PD -取得最大值.连接DC 并延长交y 轴于点P ，PC PD CD -===∴PC PD -.易得直线CD 的方程为y x 3=+.把()P t,0代入，得t 3=-.∴此时对应的点P 的坐标为()3,0-.②2y a |x |2a x 3=-+的解析式可化为22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩ 设线段PQ 所在直线的方程为y kx b =+，将()P t,0，()Q 0,2t 的坐标代入，可得线段PQ 所在直线的方程为y 2x 2t =-+.（1）当线段PQ 过点()3,0-，即点P 与点()3,0-重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时t 3=-. ∴当t 3≤-时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （2）当线段PQ 过点()0,3，即点Q 与点C 重合时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点，此时3t 2=. 当线段PQ 过点()3,0，即点P 与点()3,0重合时，t 3=，此时线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像有两个公共点. 所以当3t 32≤<时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点. （3）将y 2x 2t =-+带入()2y x 2x 3x 0=-++≥，并整理，得2x 4x 2t 30-+-=. ()Δ1642t 3288t =--=-.令288t 0-=，解得7t 2=. ∴当7t 2=时，线段PQ 与函数22x 23,0,y x 23,0.x x x x ⎧-++≥=⎨--+<⎩的图像只有一个公共点.综上所述，t 的取值范围为t 3≤-或3t 32≤<或7t 2=. 【点睛】 本题考查了二次函数的综合应用，先利用待定系数法求解析式，同时把最大值与三角形的三边关系联系在一起；同时对于二次函数利用动点求取值问题，从特殊点入手，把函数分成几部分考虑，按自变量从大到小的顺序或从小到大的顺序求解．2．如图：在平面直角坐标系中，直线l ：y=13x ﹣43与x 轴交于点A ，经过点A 的抛物线y=ax 2﹣3x+c 的对称轴是x=32． （1）求抛物线的解析式；（2）平移直线l 经过原点O ，得到直线m ，点P 是直线m 上任意一点，PB ⊥x 轴于点B ，PC ⊥y 轴于点C ，若点E 在线段OB 上，点F 在线段OC 的延长线上，连接PE ，PF ，且PE=3PF ．求证：PE ⊥PF ；（3）若（2）中的点P 坐标为（6，2），点E 是x 轴上的点，点F 是y 轴上的点，当PE ⊥PF 时，抛物线上是否存在点Q ，使四边形PEQF 是矩形？如果存在，请求出点Q 的坐标，如果不存在，请说明理由．【答案】（1）抛物线的解析式为y=x 2﹣3x ﹣4；（2）证明见解析；（3）点Q 的坐标为（﹣2，6）或（2，﹣6）．【解析】【分析】（1）先求得点A 的坐标，然后依据抛物线过点A ，对称轴是x=32列出关于a 、c 的方程组求解即可；（2）设P （3a ，a ），则PC=3a ，PB=a ，然后再证明∠FPC=∠EPB ，最后通过等量代换进行证明即可；（3）设E （a ，0），然后用含a 的式子表示BE 的长，从而可得到CF 的长，于是可得到点F 的坐标，然后依据中点坐标公式可得到22x x x x Q P F E ++=，22y y y y Q P F E ++=，从而可求得点Q 的坐标（用含a 的式子表示），最后，将点Q 的坐标代入抛物线的解析式求得a 的值即可．【详解】（1）当y=0时，14033x -=，解得x=4，即A （4，0），抛物线过点A ，对称轴是x=32，得161203322a c a -+=⎧⎪-⎨-=⎪⎩， 解得14a c =⎧⎨=-⎩，抛物线的解析式为y=x 2﹣3x ﹣4； （2）∵平移直线l 经过原点O ，得到直线m ，∴直线m 的解析式为y=13x ． ∵点P 是直线1上任意一点， ∴设P （3a ，a ），则PC=3a ，PB=a ．又∵PE=3PF ，∴PC PB PF PE=． ∴∠FPC=∠EPB ．∵∠CPE+∠EPB=90°，∴∠FPC+∠CPE=90°，∴FP ⊥PE ．（3）如图所示，点E 在点B 的左侧时，设E （a ，0），则BE=6﹣a ．∵CF=3BE=18﹣3a ，∴OF=20﹣3a ．∴F （0，20﹣3a ）．∵PEQF 为矩形，∴22x x x x Q P F E ++=，22y y y y Q P F E ++=， ∴Q x +6=0+a ，Q y +2=20﹣3a+0，∴Q x =a ﹣6，Q y =18﹣3a ．将点Q 的坐标代入抛物线的解析式得：18﹣3a=（a ﹣6）2﹣3（a ﹣6）﹣4，解得：a=4或a=8（舍去）．∴Q （﹣2，6）．如下图所示：当点E 在点B 的右侧时，设E （a ，0），则BE=a ﹣6．∵CF=3BE=3a ﹣18，∴OF=3a ﹣20．∴F （0，20﹣3a ）．∵PEQF 为矩形， ∴22x x x x Q P F E ++=，22y y y y Q P F E ++=， ∴Q x +6=0+a ，Q y +2=20﹣3a+0，∴Q x =a ﹣6，Q y =18﹣3a ． 将点Q 的坐标代入抛物线的解析式得：18﹣3a=（a ﹣6）2﹣3（a ﹣6）﹣4，解得：a=8或a=4（舍去）．∴Q （2，﹣6）．综上所述，点Q 的坐标为（﹣2，6）或（2，﹣6）．【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式，用含a 的式子表示点Q 的坐标是解题的关键．3．如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上。
九年级中考数学专题复习：二次函数综合题(面积问题)含答案
中考数学专题复习：二次函数综合题（面积问题）1．如图，一次函数y ＝kx +b 的图象与二次函数y ＝ax 2的图象交于点A （1，m ）和B （﹣2，4），与y 轴交于点C ．(1)求k ，b ，a 的值； (2)求△AOB 的面积．2． 如图，已知二次函数212y x bx c =-++的图象经过点A (2，0)，B (0，-6)两点．(1)求这个二次函数的解析式；(2)设该二次函数的对称轴与x 轴交于点C ，连接BA 、BC ，求△ABC 的面积．3．如图，在平面直角坐标系中，一次函数y ＝kx +b 的图象经过点A （0，﹣4）、B （2，0），交反比例函数y 6x=（x ＞0）的图象于点C ，点P 在反比例函数的图象上，横坐标为n （0＜n ＜3），PQ y ∥轴交直线AB 于点Q ，D 是y 轴上任意一点，连接PD 、QD ．(1)求一次函数的表达式和C点坐标；(2)求△DPQ面积的最大值．4．如图，抛物线2y x bx c=-++交x轴于A，B两点，交y轴于点C直线122y x=-+经过点B，C．(1)求抛物线的解析式；(2)点P是直线BC上方抛物线上一动点，设点P的横坐标为m．△求△PBC面积最大值和此时m的值；△Q是直线BC上一动点，是否存在点P，使以A、B、P、Q为顶点的四边形是平行四边形，若存在，直接写出点P的坐标．5．图1，抛物线2y x 2x 3=-++与x 轴交于A ，B 两点，与y 轴交于点C ．(1)求点A ，B ，C 的坐标．(2)P 为直线BC 上方抛物线上的一个动点，当PBC 的面积最大时，求点P 的坐标； (3)设M 为该抛物线的顶点，D 为抛物线的对称轴与x 轴的交点，如图2所示，在直线MD 上是否存在点N ，使点N 到直线MC 的距离等于点N 到点A 的距离？若存在，直接写出点N 的坐标；若不存在，请说明理由．6．如图，已知二次函数2y x bx c =-++的图像交x 轴于点()1,0A -，()5,0B ，交y 轴于点C ．(1)求这个二次函数的表达式；(2)如图1，点M 从点B 出发，BC 向点C 运动，点N 从点O 出发，以每秒1个单位长度的速度沿线段OB 向点B 运动，点M ，N 同时出发．设运动时间为t 秒（05t <<）．当t 为何值时，BMN △的面积最大？最大面积是多少？ (3)已知P 是抛物线上一点，在直线BC 上是否存在点Q ，使以A ，C ，P ，Q 为顶点的四边形是平行四边形？若存在，直接写出点Q 坐标；若不存在，请说明理由．7．如图，已知抛物线2342y ax x =++的对称轴是直线x =3，且与x 轴相交于A 、B 两点（B 点在A 点的右侧），与y 轴交于C 点．(1)A 点的坐标是_____________；B 点坐标是________________； (2)求直线BC 的解析式；(3)点P 是直线BC 上方的抛物线上的一动点（不与B 、C 重合），是否存在点P ，使△PBC 的面积最大．若存在，请求出△PBC 的最大面积，若不存在，试说明理由；(4)若点M 在x 轴上，点N 在抛物线上，以A 、C 、M 、N 为顶点的四边形是平行四边形时，请直接写出点M 点坐标．8．如图，抛物线()20y ax bx c a =++≠与y 轴交于点C （0，4），与x 轴交于点A 和点B ，其中点A 的坐标为（﹣2，0），抛物线的对称轴x ＝1与抛物线交于点D ，与直线BC 交于点E ．(1)求抛物线的解析式；(2)若点F 是直线BC 上方的抛物线上的一个动点，是否存在点F 使四边形ABFC 的面积最大，若存在，求出点F 的坐标和最大值；若不存在，请说明理由；(3)平行于DE 的一条动直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求P 点的坐标．(4)探究对称轴上是否存在一点P ，使得以点P ，C ，A 为顶点的三角形是等腰三角形？若存在，请求出所有符合条件的P 点的坐标，若不存在，请说明理由．9．如图，在平面直角坐标系中，直线334y x =-+与x 轴交于点A ，与y 轴交于点C ．抛物线214y x bx c =-++经过点A 、C ．(1)求抛物线解析式及顶点M 坐标；(2)P 为抛物线第一象限内一点，使得PAC △面积最大，求PAC △面积的最大值及此时点P 的坐标；(3)当1m x m +≤≤时，（1）中二次函数有最大值为2-，求m 的值．10．如图，在平面直角坐标系中，二次函数2y ax x c =-+的图像与x 轴交于点A (2-，0)、B (4，0)，与y 轴交于点C ．(1)求a 和c 的值；(2)若点D （不与点C 重合）在该二次函数的图像上，且ABD ABC S S =△△，求点D 的坐标；(3)若点P 是该二次函数图像上位于x 轴上方的一点，且BPABPCS S=，直接写出点P 的坐标．11．如图，抛物线()214y x =--的图像与x 轴交于的A 、B 两点，与y 轴交于点D ，抛物线的顶点为C ．(1)求点A 、B 、C 坐标； (2)求ABC 的面积；(3)点P 是抛物线上一动点，当ABP △的面积为6时，求所有符合条件的点P 的坐标；12．如图，抛物线()20y ax bx c a =++≠经过点A (2，0)，B (-2，4)，(-4，0)，直线AB 与抛物线的对称轴交于点E ．(1)求抛物线的表达式；(2)点M 在直线AB 上方的抛物线上运动，当ΔABM 的面积最大时，求点M 的坐标； (3)若点F 为平面内的一点，且以点,,,B E C F 为顶点的四边形是平行四边形，请写出符合条件的点F 的坐标．13．如图，直线y=-x+4与x轴交于点C，与y轴交于点B，抛物线y=23x2+bx+c经过B、C两点．(1)求抛物线的解析式；(2)如图，点E是抛物线上的一动点（不与B，C两点重合），当S△BEC=14S△BOC时，求点E的坐标；(3)若点F是抛物线上的一动点，当S△BFC取值在什么范围时，对应的点F有且只有两个？14．如图，已知抛物线y＝ax2＋bx－8的图像与x轴交于A（2，0），B（﹣8，0）两点，与y轴交于点C（0，﹣8）．(1)求抛物线的解析式；(2)点F是直线BC下方抛物线上的一点，当△BCF的面积最大时，求出点F的坐标；(3)在（2）的条件下，是否存在这样的点Q（0，m），使得△BFQ为等腰三角形？如果有，请直接写出点Q 的坐标；如果没有，请说明理由．15．如图，已知抛物线2y ax bx c ++＝交x 轴于点A 、B ，交y 轴于点C （0，6），且顶点坐标为（4，﹣2）．直线x ＝m 分别交直线BC 和抛物线于点E 、P ．(1)求该抛物线的解析式及A 、B 两点坐标； (2)当0＜m ＜6时，求△BCP 面积的最大值； (3)当△BPE 是等腰三角形时，直接写出m 的值．16．已知二次函数242y ax x =++的图象经过点()3,4A -．(1)求a 的值；(2)直接写出函数y 随自变量的增大而减小的x 的取值范围．(3)设242y ax x =++的顶点为M ，与y 轴相交于C ，连结MC 、MA 、AC ，求AMC S △．17．如图，抛物线23y ax bx =++与x 轴交于点()3,0A ，与y 轴交于点B ，点C 在直线AB 上，过点C 作CD x ⊥轴于点()1,0D ，将ACD △沿CD 所在直线翻折，使点A 恰好落在抛物线上的点E 处．(1)求抛物线解析式；(2)连接BE ，求BCE 的面积；(3)拋物线上是否存在一点P ，使PEA BAE ∠=∠？若存在，求出P 点坐标；若不存在，请说明理由．18．在平面直角坐标系中，点O 为坐标原点，抛物线y =ax 2+bx +3交x 轴负半轴于点A ，交x 轴正半轴于点B ，交y 轴于点C ，且OA =OC =3OB ．(1)求这个抛物线的解析式；(2)如图1，点P 为第三象限抛物线上的点，设点P 的横坐标为t ，△P AC 面积S ，求S 与t 的函数解析式（直接写出自变量t 的取值范围）；(3)如图2，在（2）的条件下，Q 为CA 延长线上的一点，若P 到x 轴的距离为d ，△PQB 的面积为2d ，且△P AQ =△AQB ，求点P 的坐标．19．如图，已知抛物线2y x bx c =++经过点()30A -,和点()0,3C -．解答下列问题．(1)求抛物线的解析式；(2)抛物线的顶点为D ，对称轴与x 轴的交点为E ，求线段BD 的长；(3)点F 在抛物线上运动，是否存在点F 使FAB 的面积等于6？如果存在，求出点F 的坐标；如果不存在，说明理由．20．如图，抛物线23y ax bx =++经过点A （2，3），与x 轴负半轴交于点B ，与y 轴交于点C ，且3OC OB =．(1)求该抛物线的解析式；(2)点D 在y 轴上，且BDO BAC ∠=∠，求点D 的坐标；(3)点P 在直线AB 上方的抛物线上，当△P AB 的面积最大时，直接写出点P 的坐标．参考答案：1．(1)k =−1，a =1，b =2(2)S △AOB =32．(1)21462y x x =-+- (2)63．(1)一次函数的表达式：y =2x -4，点C （3，2）；(2)DPQ 面积的最大值是4．4．(1)2722y x x =-++(2)△最大值为8，m ＝2；△存在，⎝⎭或⎝⎭5．(1)A (﹣1，0)，B (3，0)，C (0，3) (2)31524P ⎛⎫ ⎪⎝⎭，(3)存在，(14N -+，或(14--，6．(1)245y x x =-++(2)当52t =时，BMN △的面积最大，最大面积是258(3)存在，Q 的坐标为()7,12-或()7,2-或()1,4或()2,37．(1)()-2,0，()8,0(2)直线BC 的解析式为142y x =-+ (3)存在点P ，使PBC ∆的面积最大，最大面积是16，理由见详解(4)满足条件的点M 的坐标为(8,0)-，(4,0)，(50)，(5，0)8．(1)y ＝﹣12x 2+x +4(2)存在，四边形ABFC 的面积最大为16，F （2，4）(3)P 点坐标为（3，1）或（，2）或（2(4)存在，P 点坐标为（1或（1，或（1，1）或（1，或（1，49．(1)211344y x x =-++，顶点M 的坐标为149,216⎛⎫ ⎪⎝⎭ (2)最大值为2，此时P 点坐标为52,2⎛⎫ ⎪⎝⎭(3)5-或510．(1)142a c ==-，4)或(14)或(2，-4)(3)(-6，20)11．(1)()1,0A -，()3,0B ，()1,4C -(2)8(3)()0,3-或()2,3-或()1或()112．(1)2142y x x =--+(2)（0，4）(3)（-5，1）或（1，7）或（-3，-1）13．(1)y ＝23-x 2+53x +4(2)E 1)，E 2)，E 34222，，E 44222， (3)当S △BFC ＞163时，对应的点F 有且只有两个．14．(1)抛物线解析式为y ＝122x +3x ﹣8；(2)点F 的坐标是F （﹣4，﹣12）；(3)存在，点Q 有坐标为（0，0，﹣0，﹣4）或（0，0）．15．(1)21462y x x =-+，点A （2，0），点B （6，0） (2)S △BCP 的最大值为272(3)当△BPE 是等腰三角形时，m 的值为2或416．(1)2242y x x =-++(2)1x >(3)617．(1)2y x 2x 3=-++(2)2(3)存在，()2,3或()4,5-18．(1)y =－x 2－2x +3(2)S =23922t t +(t <－3) (3)P 的坐标为（－4，－5）19．(1)223y x x =+-(2)(3)存在，点F 的坐标为：()1-或()1-或()0,3-或()2,3-- 20．(1)2y x 2x 3=-++(2)点D 的坐标为（0，1）或（0，－1）(3)P （12，154）。
2023年九年级数学中考专题：二次函数综合压轴题附答案附答案
2023年九年级数学中考专题：二次函数综合压轴题附答案1．如图，已知抛物线2y x bx c =++（b ，c 是常数）与x 轴交于()1,0A ，()3,0B -两点，顶点为C ，点P 为线段AB 上的动点（不与A 、B 重合），过P 作PQ BC ∥交抛物线于点Q ，交AC 于点D ．(1)求该抛物线的表达式；(2)求CPD △面积的最大值；(3)连接CQ ，当CQ PQ ⊥时，求点Q 的坐标；(4)点P 在运动过程中，是否存在以A 、O 、D 为顶点的三角形是等腰三角形？若存在，求出所有点P 的坐标；若不存在，请说明理由2．在平面直角坐标系中，抛物线24y x x c =--+与x 轴交于点A ，B （点A 在点B 的左侧），与y 轴交于点C ，且点A 的坐标为()5,0-．(1)求点C 的坐标；(2)如图1，若点P 是第二象限内抛物线上一动点，求点P 到直线AC 距离的最大值，并求出此时点P 的坐标；(3)如图2，若点M 是抛物线上一点，点N 是抛物线对称轴上一点，是否存在点M 使以A ，C ，M ，N 为顶点的四边形是平行四边形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．3．已知：如图，抛物线()2430y mx mx m =++>交x 轴于E 、F 两点，交y 轴于A 点，直线AE ：y x b =+交x 轴于E 点，交y 轴于A 点．(1)求抛物线的解析式；(2)若Q 为抛物线上一点，连接,QE QA ，设点Q 的横坐标为()3t t <-，QAE 的面积为S ，求S 与t 函数关系式；（不要求写出自变量t 的取值范围）(3)在（2）的条件下，点M 在线段QA 上，点N 是位于Q 、E 两点之间的抛物线上一点，15S =，QMN AEM ∠=∠，且MN EM =，求点N 的坐标．4．如图，抛物线22y ax ax c =++经过()()1003B C ，，，两点，与x 轴交于另一点A ，点D 是抛物线的顶点．(1)求抛物线的解析式及点D 的坐标；(2)如图1，连接AC ，点E 在直线AC 上方的抛物线上，连接EA EC ，，当EAC 面积最大时，求点E 坐标；(3)如图2，连接AC BC 、，在抛物线上是否存在点M ，使ACM BCO ∠=∠，若存在，求出M 点的坐标；若不存在，请说明理由．5．抛物线21164y ax x =+-与x 轴交于(,0),(8,0)A t B 两点，与y 轴交于点C ，直线6y kx =-经过点B ．点P 在抛物线上，设点P 的横坐标为m ．(1)求二次函数与一次函数的解析式；(2)如图1，连接AC ，AP ，PC ，若APC △是以CP 为斜边的直角三角形，求点P 的坐标；(3)如图2，若点P 在直线BC 上方的抛物线上，过点P 作PQ BC ⊥，垂足为Q ，求12CQ PQ +的最大值．6．在平面直角坐标系中，抛物线223y x x =-++与x 轴交于点A 、B （A 在B 左侧），与y 轴交于点C ，顶点为D ，对称轴为直线l ，点P 是抛物线上位于点B 、C 之间的动点．(1)求ABC ∠的度数；(2)若PBC ACO ∠=∠，求点P 的坐标；(3)已知点(),P p n ，若点(),Q q n 在抛物线上，且p q >；①仅用无刻度的直尺在图2中画出点Q ；②若2PQ t =，求232022p tq t +-+的值．7．如图，在平面直角坐标系中，抛物线2y x bx c =-++经过()0,1A ，()4,1B -．直线AB 交x 轴于点C ，P 是直线AB 上方且在对称轴右侧的一个动点，过P 作PD AB ⊥，垂足为D ，E 为点P 关于抛物线的对称轴的对应点．(1)求抛物线的函数表达式；(2)PE +的最大值时，求此时点P PE +的最大值；(3)将抛物线y 关于直线3x =作对称后得新抛物线y '，新抛物线与原抛物线相交于点F ，M 是新抛物线对称轴上一点，N 是平面中任意一点，是否存在点N ，使得以C ，F ，M ，N 为顶点的四边形是菱形，写出所有符合条件的点N 的坐标，并写出求解点N 的坐标的其中一种情况的过程．8．如图所示，在平面直角坐标系中，直线3y x =-+交坐标轴于B 、C 两点，抛物线23y ax bx =++经过B 、C 两点，且交x 轴于另一点()1,0A -．点D 为抛物线在第一象限内的一点，过点D 作DQ CO ∥，DQ 交BC 于点P ，交x 轴于点Q ．(1)求抛物线的解析式；(2)设点P 的横坐标为m ，在点D 的移动过程中，存在DCP DPC ∠=∠，求出m 值；(3)在抛物线上取点E ，在平面直角坐标系内取点F ，问是否存在以C 、B 、E 、F 为顶点且以CB 为边的矩形？如果存在，请求出点F 的坐标；如果不存在，请说明理由．9．在平面直角坐标系中，抛物线2y ax bx c =++与x 轴交于点()1,0A -和点B ，与y 轴交于点C ，顶点D 的坐标为()1,4-．(1)求出抛物线的解析式；(2)如图1，若点P 在抛物线上且满足PCB CBD ∠=∠，求点P 的坐标；(3)如图2，M 是线段CB 上一个动点，过点M 作MN x ⊥轴交抛物线于点N ，Q 是直线AC 上一个动点，当QMN 为等腰直角三角形时，直接写出此时点M 的坐标．10．二次函数2y ax bx c =++交x 轴于点()10A -，和点()30B -，，交y 轴于点()03C -，．(1)求二次函数的解析式；(2)如图1，点E 为抛物线的顶点，点()0T t ，为y 轴负半轴上的一点，将抛物线绕点T 旋转180︒，得到新的抛物线，其中B ，E 旋转后的对应点分别记为B E ''，，当四边形BEB E ''的面积为12时，求t 的值；(3)如图2，过点C 作CD x ∥轴，交抛物线于另一点D ．点M 是直线CD 上的一个动点，过点M 作x 轴的垂线，交抛物线于点P ．是否存在点M 使PBC 为直角三角形，若存在，请直接写出点M 的坐标，若不存在，请说明理由．11．如图，已知抛物线2y ax 2x c =++交x 轴于点()10A -，和点()30B ，，交y 轴于点C ，点D 与点C 关于抛物线的对称轴对称．(1)求该抛物线的表达式，并求出点D 的坐标；(2)若点E 为该抛物线上的点，点F 为直线AD 上的点，若EF x ∥轴，且1EF =（点E 在点F 左侧），求点E 的坐标；(3)若点P 是该抛物线对称轴上的一个动点，是否存在点P ，使得APD △为直角三角形？若不存在，请说明理由；若存在，直接写出点P 坐标．12．在平面直角坐标系中，O 为坐标原点，直线3y x =-+与x 轴、y 轴分别交于B 、C 两点，抛物线2y x bx c =-++经过B 、C 两点，与x 轴的另一个交点为A ．(1)如图1，求b 、c 的值；(2)如图2，点P 是第一象限抛物线2y x bx c =-++上一点，直线AP 交y 轴于点D ，设点P 的横坐标为t ，ADC △的面积为S ，求S 与t 的函数关系式；(3)如图3，在（2）的条件下，E 是直线BC 上一点，45EPD ∠=︒，ADC △的面积S 为54，求E 点坐标．13．抛物线24y ax =-经过A 、B 两点，且OA OB =，直线EC 过点()41E -，，()03C -，，点D 是线段OA （不含端点）上的动点，过D 作PD x ⊥轴交抛物线于点P ，连接PC 、PE ．(1)求抛物线与直线CE 的解析式；(2)求证：PC PD +为定值；(3)在第四象限内是否存在一点Q ，使得以C 、P 、E 、Q 为顶点的平行四边形面积最大，若存在，求出Q 点坐标；若不存在，请说明理由．14．如图，已知抛物线()230y ax bx a =++≠与x 轴交于()1,0A 、()4,0B 两点，与y 轴交于点C ，点D 为抛物线的顶点．(1)求抛物线的函数表达式及点D 的坐标；(2)若四边形BCEF 为矩形，3CE =．点M 以每秒1个单位的速度从点C 沿CE 向点E 运动，同时点N 以每秒2个单位的速度从点E 沿EF 向点F 运动，一点到达终点，另一点随之停止．当以M 、E 、N 为顶点的三角形与BOC 相似时，求运动时间t 的值；(3)抛物线的对称轴与x 轴交于点P ，点G 是点P 关于点D 的对称点，点Q 是x 轴下方抛物线上的动点．若过点Q 的直线l ：94y kx m k ⎛⎫=+< ⎪⎝⎭与抛物线只有一个公共点，且分别与线段GA 、GB 相交于点H 、K ，求证：GH GK +为定值．15．在平面直角坐标系中，已知抛物线2y ax bx =+经过(40)(13)A B ，，，两点．P 是抛物线上一点，且在直线AB的上方．(1)求抛物线的表达式；(2)若OAB 面积是PAB 面积的2倍，求点P 的坐标；(3)如图，OP 交AB 于点C ，PD BO ∥交AB 于点D ．记CPB △，BCO 的面积分别为12S S ，，判断12S S 是否存在最大值．若存在，求出最大值；若不存在，请说明理由．16．已知抛物线212y x bx c =-++（b 、c 是常数）的顶点B 坐标为()1,2-，抛物线的对称轴为直线l ，点A 为抛物线与x 轴的右交点，作直线AB ．点P 是抛物线上的任意一点，其横坐标为m ，过点P 作x 轴的垂线交直线AB 于点Q ，过点P 作PN l ⊥于点N ，以PQ PN 、为边作矩形PQMN ．(1)b =___________，c =___________．(2)当点Q 在线段AB 上（点Q 不与A 、B 重合）时，求PQ 的长度d 与m 的函数关系式，并直接写出d 的最大值．(3)当抛物线被矩形PQMN 截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时，求点P 的坐标．(4)矩形PQMN 的任意两个顶点到直线AB 的距离相等时，直接写出m 的值．17．如图1．在平面直角坐标系中，抛物线2(0)y ax bx c a =++≠与x 轴交于点()2,0A -，点()4,0B ，与y 轴交于点()0,2C ．(2)点P 是第一象限内的抛物线上一点．过点P 作PH x ⊥轴于点H ，交直线BC 于点Q ，求PQ 的最大值，并求出此时点P 的坐标；(3)如图2．将地物线沿射线BC()2111110y a x b x c a =++≠，新抛物线与原抛物线交于点G ，点M 是x 轴上一点，点N 是新抛物线上一点，若以点C 、G 、M 、N 为顶点的四边形是平行四边形时，请直接写出点N 的坐标．18．如图，抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点，与y 轴交于点()0,6C ，顶点为D ，且()1,8D ．(1)求抛物线的解析式；(2)若在线段BC 上存在一点M ，过点O 作OH OM ⊥交BC 的延长线于H ，且MO HO =，求点M 的坐标；(3)点P 是y 轴上一动点，点Q 是在对称轴上一动点，是否存在点P ，Q ，使得以点P ，Q ，C ，D 为顶点的四边形是菱形？若存在，求出点Q 的坐标；若不存在，请说明理由．参考答案：1．(1)223y x x =+-(2)2(3)11524Q ⎛⎫-- ⎪⎝⎭(4)1,05⎛⎫- ⎪ ⎪⎝⎭或()0,0或1,05⎛⎫ ⎪⎝⎭2．(1)()0,5(2)点P 到直线AC 距离为8，此时535,24P ⎛⎫- ⎪⎝⎭(3)点M 的坐标为()3,8-或()7,16--或()3,16-3．(1)243y x x =++(2)23922S t t =+(3)()2N -4．(1)223y x x =--+，()14D -，(2)E 的坐标为31524⎛⎫- ⎪⎝⎭，(3)存在，()45M --，或5724⎛⎫- ⎪⎝⎭，5．(1)2111644y x x =-+-；364y x =-(2)710,2P ⎛⎫- ⎪⎝⎭(3)169166．(1)45︒(2)(1,4)P(3)①见解析；②20237．(1)2712y x x =-++PE +的最大值为1，此时点P 的坐标为961,416⎛⎫ ⎪⎝⎭(3)存在点N ，使以C ，F ，M ，N 为顶点的四边形是菱形，此时点N 的坐标为215,424N ⎛+ ⎝⎭或215,424⎛- ⎝⎭或13,544N ⎛⎫+ ⎪ ⎪⎝⎭或13,544N ⎛- ⎝⎭或299,204N ⎛⎫ ⎪⎝⎭8．(1)223y x x =-++(2)2m =(3)存在，此时点F 的坐标为()4,1或()5,2--9．(1)2=23y x x --(2)满足PCB CBD ∠=∠，点P 的坐标为(4,5)或(2,2)-(3)M 点的坐标为(1,2)-或(2,5)--或924,55⎛⎫-- ⎪⎝⎭10．(1)243y x x =---(2)3t =-(3)存在，532⎛⎫-- ⎪ ⎪⎝⎭或532⎛⎫-- ⎪ ⎪⎝⎭或(23)--，或(53)--，11．(1)223y x x =-++，()23D ，(2)11024E ++⎝⎭，或1124E --+⎝⎭，(3)存在点P ，使得APD △为直角三角形，此时点P 的坐标为312⎛⎫+ ⎪⎝⎭，或312⎛ ⎝⎭，或()12-，或()14，12．(1)2b =，3c =(2)12S t =(3)3513,1616⎛⎫ ⎪⎝⎭13．(1)2144y x =-；132y x =-(2)见解析(3)存在，754Q ⎛⎫- ⎪⎝⎭，14．(1)2315344y x x =-+，527,216D ⎛⎫- ⎪⎝⎭(2)当911t =或65t =时(3)见解析15．(1)24y x x=-+(2)(24)P ，或(3,3)(3)见解析16．(1)1-，32(2)21122d m =-+()11m -<<，d 最大值为12(3)()3,0-或1--(4)3-或0或317．(1)211242y x x =-++；(2)5PQ +最大值为94，此时点5(3,4P ；(3)(1-，14-或(1-，1)4-或(1-+1)4或(1--1)4．18．(1)2246y x x =-++(2)129,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭。
中考数学总复习《二次函数的最值》练习题附带答案
中考数学总复习《二次函数的最值》练习题附带答案一、单选题(共12题；共24分)1．二次函数y=−(x−1)2+5，当m≤x≤n且mn<0时，y的最小值为2m，最大值为2n，则m+ n的值为（）A．52B．2C．12D．322．已知二次函数y=（x-1）2-3，则此二次函数（）A．有最大值1B．有最小值1C．有最大值-3D．有最小值-33．二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：x﹣3﹣2﹣1012345y1250﹣3﹣4﹣30512⑴二次函数y=ax2+bx+c有最小值，最小值为﹣3；⑴当−12<x<2时，y＜0；⑴二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是（）A．3B．2C．1D．04．对于代数式x2－10x＋24，下列说法：①它是二次三项式；②该代数式的值可能等于2017；③分解因式的结果是(x－4)(x－6)；④该代数式的值可能小于－1．其中正确的有（）A．1个B．2个C．3 个D．4个5．已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2=0无实数根；③a﹣b+c≥0；④a+b+cb−a的最小值为3．其中，正确结论的个数为（）A．1个B．2个C．3个D．4个6．已知非负数a，b，c满足a+b＝3且c﹣3a＝﹣6，设y＝a2+b+c的最大值为m，最小值为n，则m ﹣n的值是（）A．16B．15C．9D．77．由二次函数y=（x﹣1）2﹣3可知（）A．图象开口向下B．对称轴是直线x=﹣1C．函数最小值是3D．顶点是（1，﹣3）8．抛物线y=x2，当﹣1≤x≤3时，y的取值范围是（）A．﹣1≤y≤9B．0≤y≤9C．1≤y≤9D．﹣1≤y≤39．已知二次函数的图象（-0.7≤x≤2）如图所示。
2023年九年级中考数学：二次函数综合题压轴题(特殊三角形问题)(含答案)
(2)求该二次函数的表达式；
(3)如果点p在坐标轴上，且 是等腰三角形，直接写出p点坐标．
14．如图，在平面直角坐标系中，抛物线 与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接 ．
(1)求线段AC的长；
(2)若点Р为该抛物线对称轴上的一个动点，当 时，求点P的坐标；
(2)点F的坐标为：F1（2 ，3 ）或F2（﹣1，4）；
(3)
20．(1) ；
(3)
(2)
(3)点P的坐标为 或 或 或
5．(1)抛物线解析式为 ；
(2)点 运动到 时，四边形CDBF的面积最大，最大面积为
(3)存在，点P 或 或 或
6．(1)
(2)
(3) 或 或 或
7．(1)
(2)点E的坐标为 或 或（
8．(1) ；
(2)存在，点P的坐标为（ ，0）或（4+2 ，0）或（4﹣2 ，0）或（﹣4，0）；
(1)求该抛物线对应的函数表达式；
(2)x轴上是否存在一点P，使△PBC为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由；
(3)当点P在线段OB上运动时，试探究：当m为何值时，四边形CQMD是平行四边形？请说明理由．
9．如图，在平面直角坐标系中，二次函数 的图象与 轴交于 、 两点，与 轴交于 ， 点在原点的左侧， 点的坐标为 ．点 是抛物线上一个动点，且在直线 的上方．
(2)点E是第一象限内抛物线的一个动点，其横坐标为m，直线 交y轴于点F．
①用m的代数式表示直线 的截距；
②在 的面积与 的面积相等的条件下探究：在y轴右侧存在这样一条直线，满足：以该直线上的任意一点及点C、F三点为顶点的三角形的面积都等于 面积，试用规范、准确的数学语言表达符合条件的直线．
2024成都中考数学第一轮专题复习之第三章 微专题 二次函数综合题 知识精练(含答案)
2024成都中考数学第一轮专题复习之第三章微专题二次函数综合题知识精练类型一线段问题1.(2023重庆A卷节选)如图，在平面直角坐标系中，抛物线y＝ax2＋bx＋2过点(1，3)，且交x轴于点A(－1，0)，B两点，交y轴于点C.(1)求抛物线的表达式；(2)点P是直线BC上方抛物线上的一动点，过点P作PD⊥BC于点D，过点P作y轴的平行线交直线BC于点E，求△PDE周长的最大值及此时点P的坐标．第1题图2.(2023济宁节选)如图，直线y＝－x＋4交x轴于点B，交y轴于点C，对称轴为x＝32的抛物线经过B，C两点，交x轴负半轴于点A.P为抛物线上一动点，点P的横坐标为m，过点P作x轴的平行线交抛物线于另一点M，作x轴的垂线PN，垂足为N，直线MN交y轴于点D.(1)求抛物线的解析式；(2)若m<32，设直线MN交直线BC于点E，是否存在这样的m值，使MN＝2ME？若存在，求出此时m的值；若不存在，请说明理由．第2题图类型二面积问题3.(2023安徽)在平面直角坐标系中，点O是坐标原点，抛物线y＝ax2＋bx(a≠0)经过点A(3，3)，对称轴为直线x＝2.(1)求a，b的值；(2)已知点B，C在抛物线上，点B的横坐标为t，点C的横坐标为t＋1.过点B作x轴的垂线交直线OA于点D，过点C作x轴的垂线交直线OA于点E.(ⅰ)当0<t<2时，求△OBD与△ACE的面积之和；(ⅱ)在抛物线对称轴右侧，是否存在点B，使得以B，C，D，E为顶点的四边形的面积为32若存在，请求出点B的横坐标t的值；若不存在，请说明理由．类型三等腰三角形存在性问题4.(2023青海省卷节选)如图，二次函数y＝－x2＋bx＋c的图象与x轴相交于点A和点C(1，0)，交y轴于点B(0，3)．(1)求此二次函数的解析式；(2)二次函数图象的对称轴上是否存在点M，使得△AMB是以AB为底边的等腰三角形？若存在，请求出满足条件的点M的坐标；若不存在，请说明理由．第4题图类型四直角三角形存在性问题5.如图，在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋c(a≠0)与x轴，y轴分别交于点A(4，0)，B(0，－4)，对称轴是直线x＝1，点P为平面内一点．(1)求抛物线的函数表达式；(2)若点P为y轴右侧抛物线上一点，其横坐标为t，过点P分别作AB和y轴的垂线，垂足分别为点E，F，PF交AB于点G，当△PEG≌△BFG时，求t的值；(3)若P是抛物线对称轴上的点，将抛物线y＝ax2＋bx＋c先向左平移4个单位，再向上平移3个单位，得到新的抛物线y1，抛物线y1与y轴交于点M，点N为抛物线y1的顶点，当△PMN 为直角三角形时，直接写出所有符合条件的点P的纵坐标．第5题图备用图类型五特殊四边形存在性问题6.(2023邵阳节选)如图，在平面直角坐标系中，抛物线y＝ax2＋x＋c经过点A(－2，0)和点B(4，0)，且与直线l：y＝－x－1交于D，E两点(点D在点E的右侧)，点M为直线l上的一动点，设点M的横坐标为t.(1)求抛物线的解析式；(2)抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B，C，M，R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．第6题图类型六相似三角形问题7.(2023随州节选)如图，平面直角坐标系xOy中，抛物线y＝ax2＋bx＋c过点A(－1，0)，B(2，0)和C(0，2)，连接BC，点P(m，n)(m>0)为抛物线上一动点，过点P作PN⊥x轴交直线BC于点M，交x轴于点N.(1)直接写出．．．．抛物线和直线BC的解析式；(2)当P点在运动过程中，在y轴上是否存在点Q，使得以O，P，Q为顶点的三角形与以B，C，N为顶点的三角形相似(其中点P与点C相对应)，若存在，直接写出．．．．点P和点Q的坐标；若不存在，请说明理由．第7题图类型七角度问题x2＋bx＋c经过点A(－4，0)，B(2，0)，与y轴8.如图，在平面直角坐标系中，抛物线y＝12交于点C，作直线A C.(1)求抛物线的函数表达式；(2)点M是直线AC下方抛物线上的一个动点，连接MA，MC，BC，求四边形ABCM面积的最大值及此时点M的坐标；(3)若点D是抛物线的顶点，点P是抛物线上的一个动点，是否存在点P，使得∠ACP＝∠CAD，若存在，请直接写出点P的坐标；若不存在，请说明理由．第8题图参考答案与解析1.解：(1)将点(1，3)，(－1，0)代入抛物线y＝ax2＋bx＋2，＋b＋2＝3，－b＋2＝0，＝－12，＝32，∴该抛物线的表达式为y＝－12x2＋32x＋2；(2)∵当x＝0时，y＝2，∴C(0，2).∵当y＝0时，x＝－1或x＝4，∴B(4，0)，∴OC＝2，OB＝4，BC＝25.∵直线BC过点B(4，0)，C(0，2)，∴直线BC的函数表达式为y＝－12x＋2.∵PD⊥BC，PE∥y轴，∴∠PDE＝∠BOC＝90°，∠PED＝∠BCO，∴△PDE∽△BOC，∴DEOC＝PEBC＝PDBO，∴DE2＝PE25＝PD4，∴DE＝55PE，PD＝255PE.设P(m，－12m2＋32m＋2)，则E(m，－12m＋2)(0<m<4).∴PE＝－12m2＋32m＋2－(－12m＋2)＝－12(m－2)2＋2.∵－12<0，∴当m＝2时，PE有最大值，最大值为2，∴△PDE 周长的最大值为DE ＋PD ＋PE ＝55PE ＋255PE ＋PE ＝655＋2.此时点P 的坐标为(2，3).2.解：(1)在直线y ＝－x ＋4中，当x ＝0时，y ＝4，当y ＝0时，x ＝4，∴B (4，0)，C (0，4).由题可设抛物线的解析式为y ＝a (x －32)2＋k (a ≠0)，把B (4，0)，C (0，4)（4－32）2＋k ＝0，（0－32）2＋k ＝4，＝－1，＝254，∴抛物线的解析式为y ＝－(x －32)2＋254＝－x 2＋3x ＋4；(2)存在，理由如下：∵点A 是抛物线y ＝－x 2＋3x ＋4与x 轴的另一个交点，∴点A (－1，0).①当－1＜m ＜32时，点P 在x 轴的上方，∵MN ＝2ME ，∴点E 为线段MN 的中点，∴点E 的横坐标为x E ＝3－m ＋m 2＝32，纵坐标y E ＝y M ＋y N 2＝－m 2＋3m ＋42∴点E 的坐标为(32，－m 2＋3m ＋42).又∵点E 在直线BC ：y ＝－x ＋4上，代入得m 2－3m ＋1＝0，解得m 1＝3＋52(舍去)，m 2＝3－52.②当m ＝－1时，P 点即A 点，此时点E 与点M 重合，不合题意．③当m ＜－1时，点P 在x 轴下方，点E 在射线NM 上．设线段MN 的中点是点F (32，－m 2＋3m ＋42).∵MN ＝2ME ，∴M 为EF 的中点，∴点M 的横坐标为x m ＝3－m ＝x E ＋x F 2＝x E ＋322.纵坐标为y m ＝－m 2＋3m ＋4＝y E ＋y F 2＝y E ＋－m 2＋3m ＋422.∴点E 的坐标为(92－2m ，－3m 2＋9m ＋122).又∵点E 在y ＝－x ＋4上，∴代入得－3m 2＋9m ＋122＝2m －12，即3m 2－5m －13＝0，解得m 1＝5＋1816(舍去)，m 2＝5－1816.综上，存在m 使MN ＝2ME ，m ＝3－52或m ＝5－1816. 3.解：(1)－b 2a＝2，a ＋3b ＝3，＝－1＝4；(2)(i)如解图①，延长BD 与x 轴交于点M ，延长CE 与x 轴交于点N ，过点A 作AF ⊥CE 于点F ，第3题解图①由(1)知抛物线的解析式为y ＝－x 2＋4x ，由题意知直线OA 的解析式为y ＝x ，∴B (t ，－t 2＋4t )，C (t ＋1，－(t ＋1)2＋4(t ＋1))，D (t ，t )，E (t ＋1，t ＋1)，∴OM ＝t ，BD ＝－t 2＋3t ，CE ＝－(t ＋1)2＋3(t ＋1)，AF ＝－t ＋2，∵0<t <2，∴1<t ＋1<3，∴S △OBD ＋S △ACE＝12OM ·BD ＋12CE ·AF＝12t ·(－t 2＋3t )＋12[－(t ＋1)2＋3(t ＋1)]·(－t ＋2)＝2.(ii)存在．如解图②，当点B 在点D 上方，即2<t <3时，过点D 作DQ ⊥EC 于点Q ，第3题解图②∵BD ∥EC ，∴四边形DBEC 为梯形，则S 四边形DBEC ＝12(BD ＋EC )·DQ ＝12(－t 2＋3t ＋t 2－t －2)·1＝t －1，当S 四边形DBEC ＝32时，可得t －1＝32，解得t ＝52；当点D 在点B 上方，即t >3时，如解图③，过点D 作DQ ⊥EC 于点Q ，第3题解图③此时S 四边形DBCE ＝12(BD ＋EC )·DQ ＝12(t 2－3t ＋t 2－t －2)·1＝t 2－2t －1，令t 2－2t －1＝32，解得t 1＝142＋1<3，t 2＝－142＋1<3，均舍去．综上所述，t 的值为52.4.解：(1)∵点C (1，0)和点B (0，3)是二次函数y ＝－x 2＋bx ＋c 图象上的两点，把点C (1，0)和点B (0，3)1＋b ＋c ＝0，＝3，＝－2，＝3，∴二次函数的解析式为y ＝－x 2－2x ＋3；(2)存在．如解图，连接AB ，作线段AB 的垂直平分线交对称轴于点M ，连接AM ，BM ，过点M 作MG ⊥y 轴于点G .设点M (－1，y )，对称轴与x 轴交于点Q ，则QM ＝y ，BG ＝3－y .∵△AMB 是等腰三角形，∴AM ＝BM ，则AM 2＝BM 2，∴在Rt △AQM 中，AM 2＝AQ 2＋MQ 2＝22＋y 2.在Rt △BMG 中，BM 2＝MG 2＋BG 2＝12＋(3－y )2∴22＋y 2＝12＋(3－y )2，解得y ＝1，∴点M 的坐标为(－1，1).第4题解图5.解：(1)∵抛物线过点B (0，－4)，∴c ＝－4，即抛物线的函数表达式为y ＝ax 2＋bx －4.将点A (4，0)代入y ＝ax 2＋bx －4中，得16a ＋4b －4＝0.∵抛物线的对称轴是直线x ＝1，∴－b 2a＝1，a ＋4b －4＝0，－b 2a＝1，＝12，＝－1，∴抛物线的函数表达式为y ＝12x 2－x －4；(2)∵PE ⊥AB ，PF ⊥y 轴，∴∠PEG ＝∠BFG ＝90°.∵∠PGE ＝∠BGF ，∴△PEG ∽△BFG .∵A (4，0)，B (0，－4)，∴OA ＝OB ＝4，∴△OAB 是等腰直角三角形，∴∠OBA ＝45°.∵PF ⊥y 轴，∴△BFG 是等腰直角三角形，∴∠BGF ＝45°，∴∠PGE ＝45°∵PE ⊥AB ，∴△PEG 是等腰直角三角形，∴PG ＝2EG .当△PEG ≌△BFG 时，∴EG ＝FG ，∴PG ＝2FG .由A (4，0)，B (0，－4)可知直线AB 的函数表达式为y ＝x －4，∴P (t ，12t 2－t －4)，G (12t 2－t ，12t 2－t －4)，∴PG ＝t －(12t 2－t )＝－12t 2＋2t ，FG ＝12t 2－t ，∴－12t 2＋2t ＝2(12t 2－t )，解得t ＝0(舍去)或t ＝22；第5题解图(3)当△PMN 为直角三角形时，所有符合条件的点P 的纵坐标为－256或73或3＋174或3－174.【解法提示】∵y ＝12x 2－x －4＝12(x －1)2－92，∴y 1＝12(x －1＋4)2－92＋3＝12(x ＋3)2－32＝12x 2＋3x ＋3，∴N (－3，－32).令x ＝0，则y 1＝3，∴M (0，3).∵抛物线y 的对称轴为直线x ＝1，点P 在抛物线对称轴上，∴设P (1，m )，∴PN 2＝(1＋3)2＋(m ＋32)2，MN 2＝1174，PM 2＝12＋(m －3)2.∵△PMN 为直角三角形，∴需要分以下三种情况：①当∠MNP ＝90°时，MN 2＋PN 2＝PM 2，1174＋(1＋3)2＋(m ＋32)2＝12＋(m －3)2，解得m ＝－256；②当∠PMN ＝90°时，PM 2＋MN 2＝PN 2，12＋(m －3)2＋1174＝(1＋3)2＋(m ＋32)2，解得m ＝73；③当∠MPN ＝90°时，PM 2＋PN 2＝MN 2，12＋(m －3)2＋(1＋3)2＋(m ＋32)2＝1174，解得m ＝3＋174或m ＝3－174.综上所述，当△PMN 为直角三角形时，所有符合条件的点P 的纵坐标为－256或73或3＋174或3－174.6.解：(1)∵抛物线y ＝ax 2＋x ＋c 经过A ，B 两点，a －2＋c ＝0a ＋4＋c ＝0，＝－12，＝4，∴抛物线的解析式为y ＝－12x 2＋x ＋4；(2)∵抛物线与y 轴交于点C ，∴当x ＝0时，y ＝4，即C (0，4).∵B (4，0)，M (t ，－t －1)，∴BC ＝42＋42＝42，BM 2＝(t －4)2＋(－t －1)2＝2t 2－6t ＋17，CM 2＝t 2＋(t ＋5)2＝2t 2＋10t ＋25，①如解图①，当BC 为对角线时，MB ＝CM ，∴2t 2－6t ＋17＝2t 2＋10t ＋25，解得t ＝－12，∴M (－12，－12).R －12＝4＋0，R －12＝4＋0，R ＝92，R ＝92，∴R (92，92)；②当CM 为对角线时，如解图②，∵四边形BMRC 为菱形，∴BM ＝BC ，∴2t 2－6t ＋17＝(42)2，解得t ＝3－392或t ＝3＋392，∴－t －1＝－3－392－1＝－5＋392或－t －1＝－3＋392－1＝－5－392，∴M (3－392，－5＋392)或M (3＋392，－39－52).由菱形的性质可得，R ＋4＝3－392＋0，R ＋0＝－5＋392＋4，或R ＋4＝3＋392＋0，R ＋0＝－5－392＋4，解得R ＝－5－392，R ＝3＋392，或R ＝－5＋392，R ＝3－392，∴R (－5－392，3＋392)或R (－5＋392，3－392)；③当BM 为对角线时，如解图③，即四边形CMRB 是菱形，点R 的坐标即为四边形BMRC 为菱形时，点M 的坐标，∴R (3－392，－5＋392)或R (3＋392，－39－52).综上所述，点R 的坐标为(3－392，－5＋392)或(3＋392，－39－52)或(－5－392，3＋392)或(－5＋392，3－392)或(92，92).图①图②图③第6题解图7.解：(1)抛物线的解析式为y ＝－x 2＋x ＋2，直线BC 的解析式为y ＝－x ＋2；【解法提示】(1)∵抛物线过点A (－1，0)，B (2，0)，∴抛物线的解析式为y ＝a (x ＋1)·(x －2)，将点C (0，2)的坐标代入上式，得2＝－2a ，∴a ＝－1.∴抛物线的解析式为y ＝－(x ＋1)(x －2)，即y ＝－x 2＋x ＋2.设直线BC 的解析式为y ＝kx ＋t ，将点B (2，0)，C (0，2)的坐标代入上0＝2k ＋t2＝t k ＝－1t 2.∴直线BC 的解析式为y ＝－x ＋2；(2)存在．P (2，2)，Q (0，2－1)或P (13＋13，7＋139)，Q (0，4－2139)或P (1＋3，－1－3)，Q (0，1)或P (1＋5，－3－5)，Q (0，－2).【解法提示】∵点P 与点C 相对应，∴△POQ ∽△CBN 或△POQ ∽△CNB .①若点P 在点B 左侧，则∠CBN ＝45°，BN ＝2－m ，CB ＝22.当△POQ ∽△CBN ，即∠POQ ＝45°时，直线OP 的解析式为y ＝x ，∴－m 2＋m ＋2＝m ，解得m ＝2或m ＝－2(舍去).∴OP 2＝(2)2＋(2)2＝4，即OP ＝2.∴OP BC ＝OQ BN ，即222＝OQ 2－2，解得OQ ＝2－1.∴P (2，2)，Q (0，2－1).当△POQ ∽△CNB ，即∠PQO ＝45°时，当点Q 在点P 上方时，PQ ＝2m ，OQ ＝－m 2＋m ＋2＋m ＝－m 2＋2m ＋2，∴PQ CB ＝OQ NB ，即2m 22＝－m 2＋2m ＋22－m，解得m ＝1＋5(舍去)或m ＝1－5(舍去).当点Q 在点P 下方时，PQ ＝2m ，直线QP 的解析式为y ＝x －m 2＋2.∴OQ ＝m 2－2，∴PQ CB ＝OQ NB，即2m 22＝m 2－22－m，解得m ＝13＋13或m ＝1－133(舍去)，∴OQ ＝－4＋2139，∴P (13＋13，7＋139)，Q (0，4－2139).②若点P 在点B 右侧，则∠CBN ＝135°，BN ＝m －2.当△POQ ∽△CBN ，即∠POQ ＝135°时，直线OP 的解析式为y ＝－x ，∴－m 2＋m ＋2＝－m ，解得m ＝1＋3或m ＝1－3(舍去)，∴OP ＝2m ＝2＋6，∴OP BC ＝OQ BN ，即2＋622＝OQ 3－1，解得OQ ＝1.∴P (1＋3，－1－3)，Q (0，1).当△POQ ∽△CNB ，即∠PQO ＝135°时，PQ ＝2m ，OQ ＝|－m 2＋m ＋2＋m |＝m 2－2m －2.∴PQ CB ＝OQ NB ，即2m 22＝m 2－2m －2m －2，解得m ＝1＋5或m ＝1－5(舍去).∴P (1＋5，－3－5)，Q (0，－2).综上所述，P (2，2)，Q (0，2－1)或P (13＋13，7＋139)，Q (0，4－2139)或P (1＋3，－1－3)，Q(0，1)或P(1＋5，－3－5)，Q(0，－2).8.解：(1)∵抛物线y＝12x2＋bx＋c经过点A(－4，0)，B(2，0)，－4b＋c＝0，2b＋c＝0，＝1，＝－4，∴抛物线的函数表达式为y＝12x2＋x－4；(2)在y＝12x2＋x－4中，令x＝0，得y＝－4，∴点C(0，－4).设直线AC的函数表达式为y＝kx＋c，将A(－4，0)，C(0，－4)代入，＝－4k＋c，4＝c，＝－1，＝－4，∴直线AC的函数表达式为y＝－x－4.如解图①，过点M作ME⊥x轴于点E，交AC于点F，设点M的坐标为(d，12d2＋d－4)，则点F的坐标为(d，－d－4)，∴MF＝(－d－4)－(12d2＋d－4)＝－12d2－2d.∵A(－4，0)，B(2，0)，C(0，－4)，∴OA＝4，AB＝6，OC＝4，∴S△ABC＝12AB·OC＝12×6×4＝12，S△ACM＝12MF·OA＝12×(－12d2－2d)×4＝－d2－4d＝－(d＋2)2＋4.当d＝－2时，S△ACM取得最大值，为4.∴四边形ABCM面积的最大值＝12＋4＝16，此时点M的坐标为(－2，－4)；第8题解图①(3)存在点P，点P的坐标为(－5，72)或(－103，－169).【解法提示】如解图②，过点D 作DG ⊥x 轴于点G ，过点P 作PH ⊥y 轴于点H ，则∠DGA ＝∠CHP ＝90°.由题意得点D (－1，－92)，设P (m ，12m 2＋m －4)，∴DG ＝92，AG ＝3，CH ＝12m 2＋m －4－(－4)＝12m 2＋m ，PH ＝－m ，分两种情况讨论：①当点P 在直线AC 上方时，记为P 1，设过点P 1作P 1H ⊥y 轴的点H 为H 1，∵∠ACP 1＝∠CAD ，∴P 1C ∥AD ，易得∠DAG ＝∠CP 1H 1.又∵∠DGA ＝∠CH 1P 1＝90°，∴△DAG ∽△CP 1H 1，∴DG CH 1＝AG P 1H 1，即9212m 2＋m ＝3－m ，解得m ＝0(舍去)或m ＝－5，∴点P 1(－5，72)；②当点P 在直线AC 下方时，记为P 2，设过点P 2作P 2H ⊥y 轴的点H 为H 2，∵OA ＝OC ＝4，∴∠OAC ＝∠OCA .∵∠ACP 2＝∠CAD ，∴∠OAC ＋∠CAD ＝∠OCA ＋∠ACP 2，即∠DAG ＝∠P 2CH 2.又∵∠DGA ＝∠P 2H 2C ＝90°，∴△DAG ∽△P 2CH 2，∴DG P 2H 2＝AG CH 2，即92－m ＝312m 2＋m ，解得m ＝0(舍去)或m ＝－103，∴点P 2(－103，－169).综上所述，存在点P，点P的坐标为(－5，72)或(－103，－169).第8题解图②。
中考数学二次函数专题训练50题(含参考答案)
中考数学二次函数专题训练50题含答案一、单选题1．二次函数y ＝﹣2x 2﹣1图象的顶点坐标为（ ） A ．（0，0）B ．（0，﹣1）C ．（﹣2，﹣1）D ．（﹣2，1）2．下列函数图象不属于中心对称图形的是（ ） A ．20222023yxB ．220222023yx x C ．2023y =- D ．2022xy =-3．下列关系式中，属于二次函数的是（ ）A ．22y x =-B ．y =C ．31y x =-D ．1y x=4．若抛物线2(2)(2)=-≠y a x a 开口向上，则a 的取值范围是（ ） A ．2a <B ．2a >C ．a<0D ．0a >5．已知点1(4)y -，、2(1)y -，、353y ⎛⎫⎪⎝⎭，都在函数245y x x =--+的图象上，则123y y y 、、的大小关系为( )A ．123y y y >>B ．321y y y >>C ．213y y y >>D ．312y y y >> 6．在平面直角坐标系中，将抛物线221y x x =+-，绕原点旋转180°，所得到的抛物线的函数关系式是（ ） A ．221y x x =-+ B ．221y x x =--- C ．221y x x =-+-D ．221y x x =-++7．已知二次函数2y ax bx c =++的图象经过原点和第一、二、三象限，则（ ） A ．0,0,0a b c >>> B ．0,0,0a b c <<= C ．0,0,0a b c <D ．0,0,0a b c >>=8．二次函数241y mx x =-+有最小值3-，则m 等于（ ） A ．1B ．1-C ．1±D ．12±9．已知点 A （−1，a ），B （1，b ），C （2，c ）是抛物线 y = -2x + 2x 上的三点，则 a ，b ，c 的大小关系为（ ） A ．a>c>bB ．b>a>cC ．b>c>aD ．c>a>b10．如图1，在矩形ABCD 中，动点E 从A 出发，沿AB →BC 方向运动，当点E 到达点C时停止运动，过点E作FE⊥AE，交CD于F点，设点E运动路程为x，FC＝y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是25，则矩形ABCD的面积是（）A．235B．5C．6D．25411．如图，已知直线x=﹣1是抛物线y=ax2+bx+c（a≠0）的对称轴，则①abc、①a﹣b+c、①a+b+c、①2a﹣b、①3a﹣b，其中是负数的有（）A．1个B．2个C．3个D．4个12．用配方法将二次函数y=x2﹣8x﹣9化为y=a（x﹣h）2+k的形式为（）A．y=（x﹣4）2+7B．y=（x+4）2+7C．y=（x﹣4）2﹣25D．y=（x+4）2﹣2513．若二次函数y=（x﹣k）2+m，当x≤2时，y随x的增大而减小，则k的取值范围是（）A．k=2B．k＞2C．k≥2D．k≤214．已知二次函数y＝ax2＋bx＋c（a≠0）图象上部分点的坐标（x，y）的对应值如下表所示：则方程ax2＋bx＋3＝0的根是（）A．0或4B．1或3C．-1或1D．无实根15．二次函数图像如图所示，下列结论：①0abc >，①20a b +=，①，①方程20ax bx c ++=的解是-2和4，①不等式20ax bx c ++>的解集是24-<<x ，其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个16．二次函数y ＝ax 2＋bx ＋c （a ≠0）的图像如图所示，有下列5个结论：①abc ＜0，①3a ﹣b ＝0，①a ＋b ＋c ＝0，①9a ﹣3b ＋c ＜0，①b 2﹣4ac ＞0.其中正确的有（ ）A ．①①①B ．①①①C ．①①①D ．①①17．将抛物线y=2x2向右平移1个单位后，得到的抛物线的表达式是（ ） A ．y=2（x+1）2B ．y=2（x ﹣1）2C ．y=2x2﹣1D ．y=2x2+118．如图为二次函数y=ax 2+bx+c 的图象，在下列说法中：①ac <0；①2a ﹣b=0；①当x ＞1时，y 随x 的增大而增大；①方程ax 2+bx+c=0的根是x 1=﹣1，x 2=3；①30a c +=；①对于任意实数m ，2am bm a b +≥+总是成立的．正确的说法有（ ）A ．2B ．3C ．4D ．519．如图是二次函数21y ax bx c =++，反比例函数2my x=在同一直角坐标系的图象，若y 1与y 2交于点A (4，yA )，则下列命题中，假命题是( )A ．当x ＞4时，12y y ＞B ．当1x <-时，12y y ＞C ．当12y y ＜时，0＜x ＜4D ．当12y y ＞时，x ＜020．如图是二次函数y =ax 2+bx +c （a ≠0）图象的一部分，对称轴为x =12， 且经过点（2，0），下列结论正确的是（ ）A ．abc ＞0B ．2-4ac<0bC ．a+b=1D ．当x ＞2或x ＜-1时，y ＜0二、填空题21．写出一个函数的表达式，使它满足：①图象经过点(1，1)；①在第一象限内函数y 随自变量x 的增大而减少，则这个函数的表达式为__________． 22．抛物线()269y x =-++的顶点坐标是______． 23．抛物线244y x x =+-的对称轴是直线______． 24．抛物线y ＝－（x －1）2－2的顶点坐标是________．25．二次函数210y ax bx a =+≠-（）的图象经过点（1，1），则代数式1a b --的值为______． 26．将抛物线2yx 向左平移2个单位后，得到的抛物线的解析式是______；27．若抛物线2y ax bx c =++与直线4y =的公共点的坐标是（1，4），（5，4），则这条抛物线的对称轴是直线____________．28．抛物线 245y x x =-+，当34x -≤≤时，y 的取值范围是___________ 29．已知二次函数21y mx x =+-的图象与x 轴有两个交点，则m 的取值范围是______．30．如图，抛物线2=23y x x --与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C ，过点B ，C 作一条直线l ． （1）ABC ∠的度数是______；（2）点P 在线段OB 上，且点P 的坐标为()2,0，过点P 作PM x ⊥轴，交直线l 于点N ，交抛物线于点M ，则线段MN 的长为______．31．如图，一段抛物线：y ＝﹣x （x ﹣3）（0≤x≤3），记为C 1，它与x 轴交于点O ，A 1；将C 1绕点A 1旋转180°得C 2，交x 轴于点A 2；如此进行下去，直至得C 13．若P （37，m ）在第13段抛物线C 13上，则m ＝_____．32．二次函数y ＝2x 2的图象向左平移2个单位长度，再向下平移5个单位长度后得到的图象的解析式为_____．33．如图，直角梯形OABC 的直角顶点是坐标原点，边OA ，OC 分别在x 轴，y 轴的正半轴上．OA ①BC ，D 是BC 上一点，BD =14OA AB =3，①OAB =45°，E ，F 分别是线段OA ，AB 上的两个动点，且始终保持①DEF =45°．设OE =x ，AF =y ，则y 与x 的函数关系式为_____．34．已知某抛物线上部分点的横坐标x ，纵坐标y 的对应值如下表：那么该抛物线的顶点坐标是_____．35．已知点A(－3，m)在抛物线y ＝x 2＋4x ＋10上，则点A 关于抛物线对称轴的对称点的坐标为________．36．若二次函数()22212y x m x m m =-+-+-的图象关于y 轴对称，则m 的值为：________．此函数图象的顶点和它与x 轴的两个交点所确定的三角形的面积为：________.37．二次函数y=ax 2+bx+c （a ，b ，c 为常数，且a≠0）中的x 与y 的部分对应值如表下列结论：①ac ＜0； ①当x ＞1时，y 的值随x 值的增大而减小； ①当2x =时，5y =； ①3是方程ax 2+（b ﹣1）x+c=0的一个根. 其中正确的结论是_________（填正确结论的序号）.38．如图所示，已知二次函数()20y ax bx c a =++≠的部分图象，下列结论中：0abc >①； 40a c +>②；③若t 为任意实数，则有2a bt at b -≥+； ④若函数图象经过点()2,1，则311222a b c ++=；⑤当函数图象经过()2,1时，方程210ax bx c ++-=的两根为1x ，212()x x x <，则1228x x -=-．其中正确的结论有______．39．如图，正方形ABCD 的边长为4，E 、F 、G 、H 分别是边AB 、BC 、CD 、DA 上的动点，且AE ＝BF ＝CG ＝DH ．则四边形EFGH 面积的最小值为___．40．如图，已知二次函数2y x 2x 3=-++的图象与y 轴交于点A ，MN 是该抛物线的对称轴，点P 在射线MN 上，连结PA ，过点A 作AB AP ⊥交x 轴于点B ，过A 作AC MN ⊥于点C ，连结PB ，在点P 的运动过程中，抛物线上存在点Q ，使QAC PBA ∠∠=，则点Q 的横坐标为______．三、解答题41．已知抛物线y =x 2+（b -2）x +c 经过点M （-1，-2b ）． （1）求b +c 的值．（2）若b =4，求这条抛物线的顶点坐标．42．某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同． （1）求该种水果每次降价的百分率；（2）从第一次降价的第1天算起，第x 天（x 为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤，设销售该水果第x （天）的利润为y （元），求y 与x （1≤x ≤14）之间的函数关系式，并求出第几天时销售利润最大？43．我们不妨约定：若某函数图象上至少存在不同的两点关于原点对称，则把该函数称之为“D 函数”，其图象上关于原点对称的两点叫做一对“D 点”根据该约定，完成下列各题．(1)在下列关于x 的函数中，是“D 函数”的，请在相应题目后面的括号中打“√”，不是“D 函数”的打“×”，my x=（0m ≠）（_______）；31y x =-（_______）；2y x =（_______）．(2)若点A （1，m ）与点B （n ，4-）是关于x 的“D 函数”2y ax bx c =++（0a ≠）的一对“D 点”，且该函数的对称轴始终位于直线1x =的右侧，求a ，b ，c 的值或取值范围；(3)若关于x 的“D 函数”223y ax bx c =++（a ，b ，c 是常数）同时满足下列两个条件：①0a b c ++=；①()()2230c b a c b a +-++<；求该“D 函数”截x 轴得到的线段长度的取值范围．44．（1）近年来，我市大力发展城市快速交通，小王开车从家到单位有两条路线可选择，路线A 为全程25km 的普通道路，路线B 包含快速通道，全程30km ，走路线B 比走路线A 平均速度提高50%，时间节省6min ，求走路线B 的平均速度；（2）如图，在距某居民楼AB 楼底B 点左侧水平距离60m 的C 点处有一个山坡，山坡CD 的坡度（或坡比）i ＝1：0.75，山坡坡底C 点到坡顶D 点的距离CD ＝50m ，在坡顶D 点处测得居民楼楼顶A 点的仰角为28°，居民楼AB 与山坡CD 的剖面在同一平面内，求居民楼AB 的高度．（参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）（3）已知飞机着陆后滑行的距离y（单位：m）关于滑行时间t（单位：s）的函数解析式是y＝60t﹣32t2，求在飞机着陆滑行中最后4s滑行的距离．45．已知二次函数222y x x k=-+++与x轴的公共点有两个．求：()1求k的取值范围；()2当1k=时，求抛物线与x轴的公共点A和B的坐标及顶点C的坐标；()3观察图象，当x取何值时0y>？46．如图，抛物线245y x x=-++与x轴交于点A和点B，与y轴交于点C．(1)求出A、B、C三点的坐标；(2)将抛物线245y x x=-++图像x轴上方部分沿x轴向下翻折，保留抛物线与x轴的交点和x轴下方图像，得到的新图像记作M，图像M与直线y t=恒有四个交点，从左到右四个交点依次记为D，E，F，G．若以EF为直径作圆，该圆记作图像N．①在图像M上找一点P，使得PAB的面积为3，求出点P的坐标；①当图像N与x轴相离时，直接写出t的取值范围．47．如图，在△ABC 中，AB=4，D 是AB 上的一点（不与点A、B 重合），DE①BC，交AC 于点E.设△ABC 的面积为S，△DEC 的面积为S'.（1）当D是AB中点时，求SS'的值；（2）设AD=x，SS'=y，求y与x的函数表达式，并写出自变量x的取值范围；（3）根据y的范围，求S-4S′的最小值．48．如图1，在平面直角坐标系中，抛物线y＝﹣38x2+34x+3与x轴交于点A和点B，A在B的左侧，与y轴交于点C，点P为直线BC上方抛物线上一动点．（1）求直线BC的解析式；（2）过P作PM①x轴，交BC于M，当PM﹣CM的值最大时，求P的坐标和PM﹣CM的最大值；（3）如图2，将该抛物线向右平移1个单位，得到新的抛物线y1，过点P作直线BC 的垂线，垂足为E，作y1对称轴的垂线，垂足为F，连接EF，请直接写出当PEF是以PF为腰的等腰三角形时，点P的横坐标．49．如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，抛物线y=a（x﹣2）2+k经过点A、B．求：（1）点A 、B 的坐标；（2）抛物线的函数表达式；（3）若点M 是该抛物线对称轴上的一点，求AM+BM 的最小值及点M 的坐标； （4）在抛物线对称轴上是否存在点P ，使得以A 、B 、P 为顶点的三角形为等腰三角形？若存在，求点P 的坐标；若不存在，请说明理由．50．如图所示，抛物线2y ax bx c =++的图象过(03)A ，，()10B -，，0(3)C ，三点，顶点为P ．(1)求抛物线的解析式；(2)设点G 在y 轴上，且OGB OAB ACB ∠+∠=∠，求AG 的长；(3)若//AD x 轴且D 在抛物线上，过D 作DE BC ⊥于E ，M 在直线DE 上运动，点N 在x 轴上运动，是否存在这样的点M 、N 使以A 、M 、N 为顶点的三角形与APD △相似若存在，请求出点M 、N 的坐标．参考答案：1．B【分析】根据二次函数的解析式特点可知其图象关于y 轴对称，可得出其顶点坐标．【详解】解：①221y x =-- ,①其图象关于y 轴对称，①其顶点在y 轴上，当0x =时，1y =-，所以顶点坐标为（0，﹣1），故选择：B.【点睛】本题主要考查二次函数的顶点坐标，掌握二次函数y=ax 2+c 的图象关于y 轴对称是解题的关键．2．B【分析】分别根据一次函数图象，二次函数图象，常数函数的图象的对称性分析判断即可得解．【详解】解：A ．直线20222023y x 是轴对称图形，也是中心对称图形，故本选项不符合题意；B ．抛物线220222023y x x 是轴对称图形，不是中心对称图形，故本选项符合题意；C ．直线2023y =-是轴对称图形，也是中心对称图形，故本选项不符合题意；D ．直线2022x y =-是轴对称图形，也是中心对称图形，故本选项不符合题意． 故选：B ．【点睛】本题考查了二次函数图象，一次函数图象，常数函数的图象，熟记各图形以及其对称性是解题的关键．3．A【分析】根据二次函数的定义进行解答即可．【详解】22y x =-符合二次函数的定义，故A 符合题意；y B 不符合题意； 31y x =-是一次函数，故C 不符合题意；1y x=中含自变量的代数式不是整式，不符合二次函数的定义，故D 不符合题意；故选A【点睛】本题考查了二次函数的定义，掌握二次函数的一般形式()20y ax bx c a =++≠是解题的关键．4．B【分析】根据抛物线的开口向上，可得20a ->，进而即可求得a 的取值范围．【详解】解：①抛物线2(2)(2)=-≠y a x a 开口向上，①20a ->即2a >故选B【点睛】本题考查了二次函数2y ax =图象的性质，掌握0a >时，抛物线的开口向上是解题的关键．5．C【分析】根据函数解析式求出对称轴，在根据函数的性质求解即可；【详解】解：①245y x x =--+，①函数图像的对称轴是直线422x -=-=--，图象的开口向下， ①当<2x -时，y 随x 的增大而增大， 点353y ⎛⎫ ⎪⎝⎭，关于对称轴的对称点是⎛⎫- ⎪⎝⎭317,3y ， ①17413-<-<-， ①213y y y >>；故选：C ．【点睛】本题主要考查了二次函数图象上点的坐标特征，掌握二次函数图象的性质是解题的关键．6．D【分析】先求出抛物线的顶点坐标，再根据旋转求出旋转后的抛物线顶点坐标，然后根据顶点式写出抛物线的解析式即可．【详解】解：①()222112y x x x =+-=+-，①抛物线的顶点坐标为()1,2--，①将抛物线221y x x =+-，绕原点旋转180︒后顶点坐标变为()1,2，1a =-，①旋转后的函数关系式为()221221y x x x =--+=-++．故选：D ．【点睛】本题主要考查了求抛物线的解析式，关于原点对称的两个点的坐标特点，解题的关键是求出旋转后抛物线的顶点坐标和a 的值．7．D【详解】试题分析：由题意得，二次函数经过原点可知，,又只经过第一，二，三象限，画图可知抛物线开口向上，对称轴在轴的负半轴，综合可知，故选D.考点：二次函数的对称轴及开口方向综合问题.8．A【分析】根据二次函数的最值公式列式计算即可得解．【详解】①二次函数241y mx x =-+有最小值3-， ①41634m m-=-， 解得1m =．故选A ．9．C【分析】根据二次函数的性质得到抛物线y =-x 2+2x 的开口向下，对称轴为直线x =1，然后根据三个点离对称轴的远近判断函数值的大小．【详解】解：①抛物线y =-x 2+2x =-（x -1）2+1，①抛物线y =-x 2+2x 的开口向下，对称轴为直线x =1，而A （-1，a ）离直线x =1的距离最远，B （1，b ）在直线x =1上，①b ＞c ＞a ，故选：C ．【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了二次函数的性质．10．B【分析】易证△CFE ∽△BEA ，可得CF CE BE AB=，根据二次函数图象对称性可得E 在BC 中点时，CF 有最大值，列出方程式即可解题．【详解】若点E 在BC 上时，如图∵∠EFC +∠AEB ＝90°，∠FEC +∠EFC ＝90°，∴∠CFE ＝∠AEB ，∵在△CFE 和△BEA 中，90CFE AEB C B ︒∠=∠⎧⎨∠=∠=⎩， ∴△CFE ∽△BEA ，由二次函数图象对称性可得E 在BC 中点时，CF 有最大值，此时CF CE BE AB=，BE ＝CE ＝x ﹣52，即525522x y x -=-， ∴225()52y x =-， 当y ＝25时，代入方程式解得：x 1＝32（舍去），x 2＝72， ∴BE ＝CE ＝1，∴BC ＝2，AB ＝52， ∴矩形ABCD 的面积为2×52＝5； 故选B ． 【点睛】本题考查了二次函数顶点问题，考查了相似三角形的判定和性质，考查了矩形面积的计算，本题中由图象得出E 为BC 中点是解题的关键．11．B【分析】根据抛物线的开口方向，对称轴，与y 轴的交点判定系数符号,及运用一些特殊点解答问题.【详解】由抛物线的开口向下可得:a ＜0,根据抛物线的对称轴在y 轴左边可得:a ,b 同号，所以b ＜0,根据抛物线与y轴的交点在正半轴可得:c ＞ 0,直线x ＝－1是抛物线y ＝ ax 2＋bx ＋c (a ≠0)的对称轴，所以－b 2a＝－1,可得b ＝2a ,由图知，当x ＝－3时y ＜0,即9a －3b ＋c ＜ 0,所以9a －6a ＋c ＝3a ＋c ＜0,因此①abc ＞0;①a －b ＋c ＝a －2a ＋c ＝c －a ＞ 0;①a ＋b ＋c ＝ a ＋2a ＋c ＝3a ＋c ＜ 0;①2a －b ＝2a － 2a ＝ 0;①3a －b ＝3a － 2a ＝ a ＜0所以①①小于0,故负数有2个，故答案选B.【点睛】本题主要考查了结合图形判断抛物线方程的系数，解本题的要点在于熟知抛物线的基本性质.12．C【分析】直接利用配方法进而将原式变形得出答案．【详解】y =x 2-8x -9=x 2-8x +16-25=（x -4）2-25．故选C ．【点睛】此题主要考查了二次函数的三种形式，正确配方是解题关键．13．C【详解】试题分析：根据二次函数的增减性可得：当x≤k 时，y 随x 的增大而减小，则k≥2．考点：二次函数的性质14．B【分析】将（0，2）（3，-1）（4，2）代入到二次函数y ＝ax 2＋bx ＋c 中，分别求出a 、b 的值，即可求出方程的解.【详解】由题意得：29311642c a b c a b c =⎧⎪++=-⎨⎪++=⎩解得：142a b c =⎧⎪=-⎨⎪=⎩①方程230ax bx ++=为2430x x -+=(1)(3)0x x --=解得：121,3x x ==故选B【点睛】本题考查二次函数抛物线与坐标轴的交点以及待定系数法函数解析式和一元二次方程求解，熟练掌握相关知识点是解题关键.15．C【详解】试题分析： ①抛物线开口向上，①0a >，①抛物线对称轴为直线2b x a =-=1，①0b <，①抛物线与y 轴交点在x 轴下方，①0c <，①0abc >，所以①正确； ①2b x a=-=1，即2b a =-，①20a b +=，所以①正确； ①抛物线与x 轴的一个交点为（﹣2，0），而抛物线对称轴为直线x=1，①抛物线与x 轴的另一个交点为（4，0），①当3x =时，0y <，①，所以①错误． ①抛物线与x 轴的两个交点为（﹣2，0），（4，0），①方程20ax bx c ++=的解是-2和4，①①正确；由图像可知：不等式20ax bx c ++>的解集是24-<<x ，①①正确．①正确的答案为：①①①①．故选C ．考点：二次函数图象与系数的关系．16．B【分析】根据二次函数的图像和性质逐一进行判断即可【详解】解：①抛物线开口朝下，①a ＜0，①对称轴x =3-22b a=- ①b =3a ＜0，①3a ﹣b ＝0，故①正确；①抛物线与y 轴的交点在x 轴的上方，①c ＞0，①abc ＞0，故①错误；①抛物线的对称轴x =3-2，与x 轴的一个交点为（-4，0）， ①抛物线与x 轴的一个交点为（1，0），①a +b +c =0，故①正确；根据图象知道当x =-3时，y =9a -3b +c ＞0，故①错误；根据图象知道抛物线与x 轴有两个交点，①b 2-4ac ＞0，故①正确．①正确答案为：①①①．故选：B【点睛】此题主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a 与b 的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．17．B【分析】可根据二次函数图象左加右减，上加下减的平移规律进行解答．【详解】二次函数y=2x 2的图象向右平移1个单位，得：y=2（x-1）2，故选B ．【点睛】本题考查了函数图象的平移，用平移规律“左加右减，上加下减”直接代入函数解析式求得平移后的函数解析式．18．D【分析】根据二次函数系数与图像性质，二次函数与方程，二次函数与不等式之间的关系判断每一个结论，从而得出答案．【详解】①由图像可知，抛物线的开口向上，①a ＞0，①抛物线与y 轴的交点为在y 轴的负半轴上，①c ＜0，①ac ＜0，故此选项正确；①由图像可知，对称轴为x=1， ①12b x a=-=， ①-b=2a ，①2a+b=0，故此选项错误；①当x ＞1时，y 随x 的增大而增大，故此选项正确；①由图像可知，方程ax 2+bx+c=0的根是x 1=﹣1，且对称轴为x=1， ①1212x x +=， ①2122(1)3x x =-=--=，故此选项正确；①由①可知，12133c x x a==-⨯=-， 3c a ∴=-，30a c ∴+=，故此选项正确；①由图像可知，抛物线的顶点坐标为(1,)a b c ++，∴当x=1时，二次函数y=ax 2+bx+c 有最小值a+b+c ，∴2ax bx c a b c ++≥++，当x=m 时，则有2am bm c a b c ++≥++，∴2am bm a b +≥+，故此选项正确；①正确的说法有①①①①①共5个．故选：D ．【点睛】本题考查了二次函数的图像与性质、方程、不等式之间的知识点，要掌握如何利用图像上的信息确定字母系数的范围，并记住特殊值的特殊用法，如x=1，x=-1时对应的y 值是解题的关键．19．D【分析】结合图形、利用数形结合思想解答．【详解】由函数图象可知，当x ＞4时，y 1＞y 2，A 是真命题；当x ＜-1时，y 1＞y 2，C 是真命题；当y 1＜y 2时，0＜x ＜4，C 是真命题；y 1＞y 2时，x ＜0或x ＞4，D 是假命题；故选D ．【点睛】本题考查的是命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．20．D【分析】根据抛物线开口方向、对称轴位置、抛物线与y 轴交点位置求得a 、b 、c 的符号；根据对称轴求出b=-a ；把x=2代入函数关系式，结合图象判断函数值与0的大小关. ．【详解】：①二次函数的图象开口向下，①a<0，①二次函数的图象交y 轴的正半轴于一点，①c>0，①对称轴是直线x=12，①−2b a =12， ①b=−a>0，①abc<0.故A 错误；①抛物线与x 轴有两个交点，①b 2-4ac>0, 故B 错误①b=−a ，①a+b=0，故C 错误；故答案选D【点睛】本题考查的知识点是二次函数图像与系数的关系，解题的关键是熟练的掌握二次函数图像与系数的关系.21．1y x= 【分析】根据反比例函数、一次函数以及二次函数的性质作答． 【详解】解：该题答案不唯一，可以为1y x=等． 故答案为：1y x =． 【点睛】本题考查的是反比例函数、一次函数以及二次函数的性质，熟知函数的增减性是解答此题的关键．22．()6,9-【分析】直接根据顶点式解析式写出顶点坐标即可．【详解】解：()269y x =-++的顶点为()6,9-， 故答案为：()6,9-．【点睛】本题考查了抛物线顶点式解析式的顶点坐标，解题关键是理解抛物线()()20y a x h k a =-+≠的顶点坐标为()h k ，． 23．2x =-【分析】将题目的解析式化为顶点式，即可得到该抛物线的对称轴，本题得以解决．【详解】解：①抛物线2244(2)8y x x x =+-=+-，①该抛物线的对称轴是直线2x =-，故答案为：2x =-．【点睛】本题考查二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．24．(1，－2)【分析】对于二次函数的顶点式()2y a x h k =-+,顶点坐标为()h k ，． 【详解】由y ＝－（x －1）2－2，根据顶点式的坐标特点可知，顶点坐标为()12-，故答案为：()12-，． 【点睛】本题考查了抛物线的顶点式及顶点坐标；对于二次函数的顶点式()2y a x h k =-+,顶点坐标为()h k ，，掌握顶点式是解题的关键．25．-1【详解】①二次函数y=ax2+bx−1(a≠0)的图象经过点(1，1)，①a+b−1=1，①a+b=2，①1−a−b=1−(a+b)=1−2=−1.故答案为-1.26．()22y x =+或244y x x =++【分析】根据函数的平移规律：左加右减；上加下减即可求解．【详解】解：①抛物线2y x 向左平移2个单位，①平移后抛物线的解析式为()22y x =+故答案为：()22y x =+【点睛】本题考查了抛物线的平移变换，熟练掌握抛物线的平移规律是解题的关键． 27．x =3【分析】因为点（1，4），（5，4）的纵坐标都为4，所以可判定是一对对称点，把两点的横坐标代入公式x =122x x +求解即可．【详解】解：抛物线2y ax bx c =++与直线4y =的公共点的坐标是（1，4），（5，4）， ①两交点关于抛物线的对称轴对称，则此抛物线的对称轴是直线x =1532+=，即x =3． 故答案为：3．【点睛】本题考查抛物线与x 轴的平行线交点问题．掌握抛物线的性质，会利用关于对称轴对称的两点坐标求对称轴是解题关键．28．126y ≤≤【分析】先化为顶点式，然后根据二次函数的性质求解即可．【详解】解：①2245(2)1y x x x =-+=-+，①抛物线开口向上，对称轴为直线=2x ，函数有最小值1，当3x =-时，26y =，当=4x 时， 5.y =，①当34x -≤≤时，y 的取值范围是126y ≤≤；故答案为：126y ≤≤．【点睛】本题考查了二次函数的性质，二次函数图象上点的坐标特征，熟知二次函数的性质是解题的关键．29．14m >-且0m ≠ 【分析】根据题意可得0m ≠，且判别式0∆>，求解不等式即可．【详解】解：①二次函数21y mx x =+-的图象与x 轴有两个交点①0m ≠，且判别式240b ac ∆=->①14(1)0m ∆=-⨯⨯->，0m ≠ 解得14m >-且0m ≠ 故答案为：14m >-且0m ≠ 【点睛】此题考查了二次函数的定义以及二次函数与x 轴交点问题，掌握二次函数的定义以及性质是解题的关键．30． 45°； 2【分析】（1）分别求出A,B,C 的坐标，得到OB OC =，故可求解；（2）先求出直线l 的解析式，再得到M,N 的坐标即可求解．【详解】（1）当0y =时，2230x x --=，解得11x =-，23x =，①点A 在点B 的左侧， ①点A 坐标为()1,0-，点B 坐标为()3,0．当0x =时，=3y -，①点C 坐标为()0,3-，①OB OC =，①=45ABC ∠︒．（2）设直线l 的函数表达式为y kx b =+，根据题意得303k b b +=⎧⎨=-⎩，解得13k b =⎧⎨=-⎩， ①直线l 的函数表达式为3y x =-；当2x =时，31=-=-y x ，①点N 的坐标为2,1；当2x =时，22232433=--=--=-y x x ，①点M 的坐标为()2,3-；①()132=---=MN ．故答案为：45°；2．【点睛】此题主要考查二次函数与一次函数综合，解题的关键是求出各点坐标． 31．m=2【分析】根据图像的旋转变化规律及二次函数的平移规律得出平移后的解析式，进而即可求值．【详解】①一段抛物线：y ＝﹣x （x ﹣3）（0≤x≤3），①点O （0,0），A 1（3,0）①将C 1绕点A 1旋转180°得C 2，交x 轴于点A 2；如此进行下去，直至得C 13．①C 13的解析式与x 轴的坐标为（36,0）、（39,0）①C 13的解析式为：y ＝﹣（x －36）（x －39）当x ＝37时，m=y ＝﹣1×（﹣2）＝2故答案为：2【点睛】本题主要考查二次函数的平移规律，解题的关键是得出二次函数平移后的解析式．32．y ＝2（x+2）2﹣5【分析】直接根据“上加下减，左加右减”的原则进行解答．【详解】由“左加右减”的原则可知，将二次函数y ＝2x 2的图象向左平移2个单位长度所得抛物线的解析式为：y ＝2（x+2）2，即y ＝2（x+1）2；由“上加下减”的原则可知，将抛物线y ＝2（x+2）2向下平移5个单位长度所得抛物线的解析式为：y ＝2（x+2）2﹣5，即y ＝2（x+2）2﹣5．故答案为：y ＝2（x+2）2﹣5．【点睛】本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．33．213y x x =【分析】首先过B 作x 轴的垂线，设垂足为M ，由已知易求得OA Rt①ABM 中，已知①OAB 的度数及AB 的长，即可求出AM 、BM 的长，进而可得到BC 、CD 的长，再连接OD ，证①ODE ①①AEF ，通过得到的比例线段，即可得出y 与x 的函数关系式．【详解】解：过B 作BM ①x 轴于M ．在Rt①ABM 中，①AB =3，①BAM =45°，①AM =BM =2， ①BD =14OA ，OA ∴=，①BC =OA﹣AM =，CD =BC ﹣BD ，①D ，3OD ∴== ． 连接OD ，则点D 在①COA 的平分线上，所以①DOE =①COD =45°．又①在梯形DOAB 中，①BAO =45°，①由三角形外角定理得：①ODE =①DEA ﹣45°，又①AEF =①DEA ﹣45°，①①ODE=①AEF ，①①ODE ①①AEF ，OE OD AF AE∴= 即x y =①y 与x 的解析式为：213y x =-．故答案为：213y x =-．【点睛】本题主要考查二次函数的应用，掌握相似三角形的判定及性质是解题的关键．34．（1，﹣4）【分析】根据二次函数的对称性求得对称轴，进而根据表格的数据即可得到抛物线的顶点坐标．【详解】①抛物线过点（0，﹣3）和（2，﹣3），①抛物线的对称轴方程为直线x＝022+＝1，①当x＝1时，y＝﹣4，①抛物线的顶点坐标为（1，﹣4）；故答案为（1，﹣4）．【点睛】本题考查了二次函数的性质，掌握二次函数的对称性是解题的关键．35．(－1，7)【详解】先根据抛物线上点的特点求出点A的坐标，再利用抛物线的对称性即可得出答案.解：把点A(－3，m)代y＝x2＋4x＋10得，m＝(-3)2＋4×(-3)＋10=7,①点A(－3，7),①对称轴42 22ba-=-=-，①点A(－3，7)关于对称轴x＝2的对称点坐标为（－1，7）.故答案为（－1，7）.36．11【分析】由图象关于y轴对称可知对称轴为x=0，由此可求解m的值；代入m值后，分别求解抛物线与x 轴的两个交点以及与y 轴的交点，利用三角形面积公式计算三角形面积.【详解】①图象关于y 轴对称，①对称轴为x=0， ①()211022m b m a --=-=-=- 解得m=1，代入原方程得：21y x =-+当y=0时，210x -+=，x=±1，当x=0时，y=1，则S △=2112⨯=. 【点睛】本题考查了二次函数对称轴及其与x 、y 轴的交点.37．①①①．【详解】试题解析：①x =-1时y =-1，x =0时，y =3，x =1时，y =5，①1{35a b c c a b c -+-++＝＝＝，解得1{33a b c -＝＝＝，①y =-x 2+3x +3，①ac =-1×3=-3＜0，故①正确；对称轴为直线x =-33212=⨯-（）， 所以，当x ＞32时，y 的值随x 值的增大而减小，故①错误； 当x =2时，y =-4+4+3=3；故①正确.方程为-x 2+2x +3=0，整理得，x 2-2x -3=0，解得x 1=-1，x 2=3，所以，3是方程ax 2+（b -1）x +c =0的一个根，正确，故①正确.综上所述，结论正确的是①①①．【点睛】本题考查了二次函数的性质，主要利用了待定系数法求二次函数解析式，二次函数的增减性，二次函数与不等式，根据表中数据求出二次函数解析式是解题的关键．38．①①①【分析】根据二次函数的开口方向、对称轴、顶点坐标以及二次函数与一元二次方程的关系综合进行判断即可．【详解】解：由抛物线开口向上，因此0a >， 对称轴是直线12b x a=-=-，因此a 、b 同号，所以0b >， 抛物线与y 轴的交点在负半轴，因此0c <． ，所以0abc <，故①不正确； 由对称轴12b x a=-=-可得2b a =， 由图象可知，当1x =时，0y a b c =++>，即20a a c ++>，30a c ∴+>，又0a >，40a c ∴+>，因此①正确；当=1x -时，y a b c =-+最小值，∴当()1x t t =≠-时，2a b c at bt c -+<++，即2a bt at b -<+，x t ∴=（t 为任意实数）时，有2a bt at b -≤+，因此①不正确；函数图象经过点()2,1，即421a b c ++=，而2b a =，231a b c ∴++=，311222a b c ∴++=， 因此①正确；当函数图象经过()2,1时，方程21ax bx c ++=的两根为1x ，212()x x x <，而对称轴为=1x -， 14x ∴=-，22x =，122448x x ∴-=--=-，因此①正确；综上所述，正确的结论有：①①①，故答案为：①①①．【点睛】本查二次函数的图象和性质，掌握二次函数图象的开口方向、对称轴、顶点坐标与系数a 、b 、c 的关系以及二次函数与一元二次方程的根的关系是正确判断的前提． 39．8【分析】由已知可证明①AHE ①①BEF ①①CFG ①①DGH （SAS ），再证明四边形EFGH 是正方形，设AE ＝x ，则AH ＝DG ＝BE ＝CF ＝4﹣x ，在Rt①EAH 中，由勾股定理得EH 2＝x 2+（4﹣x ）2，所以S 四边形EFGH ＝EH 2＝2（x ﹣2）2+8，可知当x ＝2时，S 四边形EFGH 有最小值8，【详解】解：设AE ＝x ，则AE ＝BF ＝CG ＝DH ＝x ，①正方形ABCD ，边长为4，①AH ＝DG ＝BE ＝CF ＝4﹣x ，①A =①B =①C =①D =90°①①AHE ①①BEF ①①CFG ①①DGH （SAS ），①①AEH +①BEF ＝90°，①EFB +①GFC ＝90°，①FGC +①HGD ＝90°，①①HEF ＝①EFG ＝①FGH ＝90°，①EF ＝EH ＝HG ＝FG ，①四边形EFGH 是正方形，在Rt ①EAH 中，EH 2＝AE 2+AH 2，即EH 2＝x 2+（4﹣x ）2，①S 四边形EFGH ＝EH 2＝2x 2﹣8x +16＝2（x ﹣2）2+8，当x ＝2时，S 四边形EFGH 有最小值8，故答案为：8．【点睛】本题主要考查了全等三角形的性质与判定，正方形的性质和二次函数的实际应用，解题的关键在于能够熟练掌握相关知识进行求解.40．53【分析】通过作辅助线，连接CO ，过点Q 作AC 的垂线交AC 延长线于点D ，先证明AOB 与ACP 相似，得到ABP AOC ∠∠=，再证QDA 与CAO 相似，设出点Q 的坐标，通过相似比即可求出点Q 坐标．【详解】如图，连接CO ，过点Q 作AC 的垂线交AC 延长线于点D ，。
中考数学总复习《二次函数综合题》专项提升练习题(附答案)
中考数学总复习《二次函数综合题》专项提升练习题(附答案)学校：___________班级：___________姓名：___________考号：___________类型一 线段问题1. 如图，抛物线y ＝14 x 2＋bx ＋c 过点A (4，0)，B (－4，4)，与y 轴交于点C ，连接AB .(1)求抛物线的表达式；(2)若E 是线段AB 上的一个动点(不与点A ，B 重合)，过点E 作y 轴的平行线，分别交抛物线，x 轴于F ，D 两点，若DE ＝2DF ，请求出点E 的坐标．第1题图2. 平面直角坐标系中已知抛物线y ＝ax 2＋83 x ＋c (a ≠0)与x 轴交于点A (1，0)和点B ，与y轴交于点C (0，－4).(1)求这条抛物线的函数解析式；(2)P 是抛物线上一动点(不与点A ，B ，C 重合)，作 PD ⊥x 轴，垂足为D ，连接PC . ①如图，若点P 在第三象限，且tan ∠CPD ＝2，求点P 的坐标；②直线PD 交直线BC 于点E ，当点E 关于直线PC 的对称点E ′落在y 轴上时，请直接写出四边形 PECE ′的周长．第2题图 备用图类型二 面积问题1. 如图，抛物线y ＝ax 2＋bx ＋5(a ≠0)交x 轴于A (－1，0)，B (5，0)两点，交y 轴于点C ，连接AC ，BC ，点G 为线段BC 上方的抛物线上一点，过点G 作GH ∥AC 交BC 于点H . (1)求抛物线的解析式；(2)连接AG ，AH ，BG ，设h ＝S △AGB －S △AHB ，点G 的横坐标为t ，求h 关于t 的函数解析式，并求出h 的最大值．第1题图2. 在平面直角坐标系中点O 是坐标原点，抛物线y ＝ax 2＋bx (a ≠0)经过点A (3，3)，对称轴为直线x ＝2. (1)求a ，b 的值；(2)已知点B ，C 在抛物线上，点B 的横坐标为t ，点C 的横坐标为t ＋1.过点B 作x 轴的垂线交直线OA 于点D ，过点C 作x 轴的垂线交直线OA 于点E . (ⅰ)当0＜t ＜2时，求△OBD 与△ACE 的面积之和；(ⅱ)在抛物线对称轴右侧，是否存在点B ，使得以B ，C ，D ，E 为顶点的四边形的面积为32 ？若存在，请求出点B 的横坐标t 的值；若不存在，请说明理由．类型三存在性问题典例精析例如图，在平面直角坐标系xOy中抛物线y＝－x2＋2x＋3与x轴交于点A(－1，0)，B(3，0)，与y轴交于点C，连接BC，点D为抛物线的顶点．(1)若点M为抛物线对称轴上一点，是否存在点M，使得△BCM为等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由；例题图①【思路点拨】判断等腰三角形存在性问题，一般要进行分类讨论．①BC为腰时：分别以点B，C为圆心，BC长为半径画圆，与直线x＝1的交点即为所求作的点；②BC为底时：作线段BC的垂直平分线，与直线x＝1的交点即为所求作的点．(2)在抛物线上是否存在一点N，使得△BCN是以BC为直角边的直角三角形？若存在，求出点N的坐标；若不存在，请说明理由；例题图②【思路点拨】判断直角三角形存在性问题，一般要进行分类讨论．①BC 为直角边时：分别过点B ，C 作BC 的垂线，与抛物线的交点即为所求作的N 点； ②BC 为斜边，点N 为直角顶点时：以BC 的中点为圆心，12 BC 的长为半径作圆，所作的圆与抛物线的交点即为所求作的N 点．(3)若点Q 为第一象限内抛物线上一点，过点Q 作QG ⊥x 轴，垂足为G ，连接AC ，OQ .是否存在点Q ，使得△QGO ∽△AOC ？若存在，求出点Q 的坐标；若不存在，请说明理由； 【思路点拨】判断相似三角形存在性问题，通常利用相似三角形的性质，列出线段比例关系，求解即可．例题图③(4)若点E 在抛物线上，点F 在x 轴上，是否存在点E ，使得以D ，C ，E ，F 为顶点的四边形是平行四边形？若存在，求出点E 的坐标；若不存在，请说明理由； 【思路点拨】判断平行四边形存在性问题，一般要进行分类讨论． ①当DE ，FC 是平行四边形对角线时； ②当DF ，EC 是平行四边形对角线时； ③当DC ，EF 是平行四边形对角线时．再利用平行四边形对角线的性质结合中点坐标公式求点坐标即可．例题图④(5)若点H是x轴上一点，点K是平面任意一点，是否存在点H，使得以点A，C，H，K为顶点的四边形是矩形？若存在，求出点H的坐标；若不存在，请说明理由；【思路点拨】判断矩形存在性问题，一般要进行分类讨论．①当AC为矩形的边时，∠ACH＝90°；②当AC为矩形的对角线时，∠AHC＝90°.再利用勾股定理求解即可．例题图⑤(6)若点S是第一象限抛物线上一点，过点S作ST⊥BC于点T，连接AC，CS，是否存在点S使得△CST中有一个角与∠CAO相等，若存在，求出S点坐标；若不存在，请说明理由．【思路点拨】判断角度存在性问题，一般要进行分类讨论．①若∠SCT＝∠CAO；②若∠CST＝∠CAO.再构造直角三角形，利用三角函数求解即可．例题图⑥对接中考1. 如图，抛物线y＝x2＋bx＋c过点A(－1，0)，点B(5，0)，交y轴于点C.(1)求b，c的值；(2)点P(x0，y0)(0＜x0＜5)是抛物线上的动点．①当x0取何值时，△PBC的面积最大？并求出△PBC面积的最大值；②过点P作PE⊥x轴，交BC于点E，再过点P作PF∥x轴，交抛物线于点F，连接EF，问：是否存在点P，使△PEF为等腰直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．第1题图2. 如图，将一块自制的直角三角板放置在平面直角坐标系中顶点为坐标原点，A(0，－3)，B(6，0)，将此三角板绕原点O顺时针旋转90°，得到△A′B′O，抛物线L经过点A′，B′，B.(1)求抛物线L的解析式；(2)点Q为平面内一点，在直线AB上是否存在点P，使得以点A，B′，P，Q为顶点的四边形是菱形？若存在，求出点P的坐标；若不存在，请说明理由．第2题图拓展类型二次函数性质综合题1. 在二次函数y＝x2－2tx＋3(t＞0)中(1)若它的图象过点(2，1)，则t的值为多少？(2)当0≤x≤3时，y的最小值为－2，求出t的值；(3)如果A(m－2，a)，B(4，b)，C(m，a)都在这个二次函数的图象上，且a＜b＜3，求m的取值范围．2. 已知抛物线y＝ax2＋bx＋3(a，b均为常数，且a≠0)的对称轴为直线x＝2.(1)求抛物线顶点M的坐标和b的值(用含a的代数式表示)；(2)已知点A(x1，y1)，B(x2，y2)都在此抛物线上，且x1＜2＜x2，x1＋x2＜4，若a＞0，试比较y1与y2的大小，并说明理由；(3)若自变量x的值满足－1≤x≤1，与其对应的函数的最大值为18，请直接写出b的值．3. 在平面直角坐标系中抛物线y＝ax2－4ax＋c(a＜0)与x轴交于A(1，0)，B两点，与y轴交于点C.(1)若OC＝2OB，求抛物线的解析式；(2)若抛物线的最大值为6，求a 的值；(3)若点P (x 0，m )，Q (52，n )在抛物线上，且m ＜n ，求x 0的取值范围．参考答案类型一 线段问题1. 解：(1)∵抛物线y ＝14 x 2＋bx ＋c 过点A (4，0)，B (－4，4)∴将A (4，0)，B (－4，4)分别代入y ＝14x 2＋bx ＋c 中得⎩⎪⎨⎪⎧4＋4b ＋c ＝04－4b ＋c ＝4 解得⎩⎪⎨⎪⎧b ＝－12c ＝－2∴抛物线的表达式为y ＝14 x 2－12x －2；(2)由点A (4，0)，B (－4，4)可得直线AB 的表达式为y ＝－12 x ＋2设点E (x ，－12 x ＋2)，其中－4<x <4，则F (x ，14 x 2－12 x －2)∴DE ＝2－12 x ，DF ＝|14 x 2－12 x －2|分两种情况讨论：①当点F 在x 轴上方时，即2－12 x ＝2×(14 x 2－12 x －2)解得x 1＝－3，x 2＝4(舍去) 将x ＝－3代入y ＝－12 x ＋2中得y ＝72∴E (－3，72)；②当点F 在x 轴下方时，即2－12 x ＝2×(－14 x 2＋12 x ＋2)解得x 1＝－1，x 2＝4(舍去)将x ＝－1代入y ＝－12 x ＋2得y ＝52 ，∴E (－1，52)；综上所述，当DE ＝2DF 时，点E 的坐标为(－3，72 )或(－1，52).2. 解：(1)∵抛物线y ＝ax 2＋83 x ＋c (a ≠0)与x 轴交于点A (1，0)，与y 轴交于点C (0，－4)∴⎩⎪⎨⎪⎧a ＋83＋c ＝0c ＝－4 ，解得⎩⎪⎨⎪⎧a ＝43c ＝－4∴抛物线的函数解析式为y ＝43 x 2＋83x －4；(2)①如解图①，过点C 作CE ⊥PD 于点E第2题解图①则∠PEC ＝∠CED ＝90° ∵C (0，－4) ∴OC ＝4∵PD ⊥x 轴，垂足为D ∴∠PDO ＝90°，∠DOC ＝90° ∴四边形DOCE 是矩形 ∴DE ＝OC ＝4 设P (x ，43 x 2＋83 x －4)∴CE ＝－x∴PE ＝PD －DE ＝－(43 x 2＋83 x －4)－4＝－43 x 2－83 x∵tan ∠CPD ＝CEPE ＝2∴－x －43x 2－83x ＝2解得x 1＝－138 ，x 2＝0(不合题意，舍去)当x ＝－138 时，43 x 2＋83 x －4＝－7716∴P (－138 ，－7716)；②四边形PECE ′的周长为353 或853.【解法提示】设P (m ，43 m 2＋83 m －4)，对于y ＝43 x 2＋83 x －4，当y ＝0时，43 x 2＋83 x －4＝0，解得x 1＝1，x 2＝－3，∴B (－3，0)，∴OB ＝3，在Rt △BOC 中由勾股定理得BC ＝OB 2＋OC 2 ＝5.当点P 在第三象限时，如解图②，过点E 作EF ⊥y 轴于点F第2题解图②则四边形DEFO 是矩形，∴EF ＝DO ＝－m ，∵点E 与点E ′关于PC 对称，∴∠ECP ＝∠E ′CP ，CE ＝CE ′，PE ＝PE ′，∵PE ∥y 轴，∴∠EPC ＝∠PCE ′，∴∠EPC ＝∠ECP ，∴PE ＝CE ，∴PE ＝CE ＝CE ′＝PE ′，∴四边形PECE ′是菱形，∵EF ∥OA ，∴△CEF ∽△CBO ，∴CE CB ＝EFBO，∴CE 5 ＝－m 3 ，∴CE ＝－53m ，设直线BC 的解析式为y ＝kx ＋b (k ≠0)，把B (－3，0)，C (0，－4)代入得，⎩⎪⎨⎪⎧－3k ＋b ＝0b ＝－4 ，解得⎩⎪⎨⎪⎧k ＝－43b ＝－4，∴直线BC 的解析式为y ＝－43 x －4，∴E (m ，－43 m －4)，∴PE ＝－43 m 2－4m ，∵PE ＝CE ，∴－43 m 2－4m ＝－53 m ，解得m 1＝－74 ，m 2＝0(舍去)，∴CE ＝－53 ×(－74 )＝3512 ，∴四边形PECE ′的周长为4CE ＝4×3512 ＝353；当点P 在第二象限时，如解图③第2题解图③同理可得43 m 2＋4m ＝－53 m ，解得m 1＝－174 ，m 2＝0(舍去)，∴CE ＝－53 ×(－174 )＝8512 ，∴四边形PECE ′的周长为4CE ＝4×8512 ＝853 ；综上所述，四边形PECE ′的周长为353 或853.类型二 面积问题1. 解：(1)∵抛物线y ＝ax 2＋bx ＋5(a ≠0)交x 轴于A (－1，0)，B (5，0)两点∴⎩⎪⎨⎪⎧a －b ＋5＝025a ＋5b ＋5＝0 ，解得⎩⎪⎨⎪⎧a ＝－1b ＝4 ∴抛物线的解析式为y ＝－x 2＋4x ＋5；(2)如解图，过点G 作GD ∥y 轴交BC 于点D ，连接CG ∵当x ＝0时，y ＝－x 2＋4x ＋5＝5 ∴C (0，5) ∵GH ∥AC ∴S △AGH ＝S △CGH∴h ＝S △AGB －S △AHB ＝S △AGH ＋S △BGH ＝S △CGH ＋S △BGH ＝S △BGC . 设直线BC 的解析式为y ＝kx ＋b 1(k ≠0) 将B (5，0)，C (0，5)代入y ＝kx ＋b 1中∴⎩⎪⎨⎪⎧5k ＋b 1＝0b 1＝5 ，解得⎩⎪⎨⎪⎧k ＝－1b 1＝5 ∴直线BC 的解析式为y ＝－x ＋5∵点G 的横坐标为t (0＜t ＜5)，∴G (t ，－t 2＋4t ＋5)，D (t ，－t ＋5) ∴GD ＝－t 2＋4t ＋5－(－t ＋5)＝－t 2＋5t ∴h ＝S △BGC ＝S △CGD ＋S △BGD ＝12 GD ·t ＋12 GD ·(5－t ) ＝－52 (t －52 )2＋1258∵－52＜0，0＜t ＜5∴当t ＝52 时，h 取最大值，最大值为1258.第1题解图2. 解：(1)由题意得⎩⎪⎨⎪⎧－b 2a ＝2，9a ＋3b ＝3，解得⎩⎪⎨⎪⎧a ＝－1，b ＝4；(2)(i)如解图①，延长BD 与x 轴交于点M ，延长CE 与x 轴交于点N ，过点A 作AF ⊥CE 于点F ，连接OB ，AC第2题解图①由(1)知抛物线的解析式为y ＝－x 2＋4x ，易知直线OA 的解析式为y ＝x ∵点B ，C 在抛物线上，点B 横坐标为t ，点C 的横坐标为t ＋1 ∴B (t ，－t 2＋4t )，C (t ＋1，－(t ＋1)2＋4(t ＋1))，D (t ，t )，E (t ＋1，t ＋1) ∴OM ＝t ，BD ＝－t 2＋3t ，CE ＝－(t ＋1)2＋3(t ＋1)，AF ＝－t ＋2 ∵0<t <2 ∴1<t ＋1<3∴S △OBD ＋S △ACE ＝12 OM ·BD ＋12 CE ·AF ＝12 t ·(－t 2＋3t )＋12 [－(t ＋1)2＋3(t ＋1)]·(－t ＋2)＝2；(ii)存在．如解图②，当点B 在点D 上方，即2<t <3时，过点D 作DQ ⊥EC 于点Q ，连接BE ，CD第2题解图②∵BD ∥EC∴四边形DBEC 为梯形此时，BD ＝－t 2＋3t ，CE ＝－(t ＋1)2＋3(t ＋1) ∵DQ ＝1∴S 四边形DBEC ＝12 (BD ＋EC )·DQ ＝12 [－t 2＋3t －(t ＋1)2＋3(t ＋1)]·1＝t －1当S 四边形DBEC ＝32 时，可得t －1＝32 ，解得t ＝52；当点D 在点B 上方，即t >3时，如解图③，过点D 作DQ ⊥EC 于点Q ，连接BC第2题解图③此时BD ＝t 2－3t ，CE ＝(t ＋1)2－3(t ＋1)∴S 四边形DBCE ＝12 (BD ＋EC )·DQ ＝12 [t 2－3t ＋(t ＋1)2－3(t －1)]·1＝t 2－2t －1令t 2－2t －1＝32 ，解得t 1＝142 ＋1<3，t 2＝－142 ＋1<3，均舍去；综上所述，t 的值为52.类型三 存在性问题典例精析例 解：(1)存在 设点M (1，m )由题意得BC ＝32 ，BM ＝4＋m 2 ，CM ＝1＋（m －3）2①当BC 为腰时 a ．若BC ＝BM ，如解图①例题解图①即32＝4＋m2解得m＝±14则M1(1，14)，M2(1，－14)；b．若BC＝CM，如解图②即32＝1＋（m－3）2，解得m＝3±17，则M3(1，3＋17)，M4(1，3－17)；②当BC为底边时，则CM＝BM，如解图②，即1＋（m－3）2＝4＋m2解得m＝1，则M5(1，1)；∴综上所述，满足条件的点M的坐标为(1，14)或(1，－14)或(1，3＋17)或(1，3－17)或(1，1)；例题解图②(2)存在设点N(x，－x2＋2x＋3).①当点C为直角顶点时，如解图③，则∠N1CB＝90°，过点N1作N1H⊥y轴于点H∵△BOC是等腰直角三角形∴∠BCO＝45°∴∠N1CH＝180°－90°－45°＝45°∴△N1CH是等腰直角三角形∴N1H＝HC，即x＝－x2＋2x＋3－3解得x1＝0(舍去)，x2＝1∴N1(1，4)；例题解图③②当点B 为直角顶点时，如解图③，则∠CBN 2＝90°，过点N 2作N 2G ⊥y 轴，过点B 作BG ⊥x 轴交N 2G 于点G∴同理可得∠BN 2G ＝45°，△BN 2G 是等腰直角三角形 ∴N 2G ＝BG ，即3－x ＝－(－x 2＋2x ＋3) 解得x 1＝－2，x 2＝3(舍去) ∴N 2(－2，－5).综上所述，满足条件的点N 的坐标为 (1，4)或(－2，－5)； (3)存在∵点Q 在第一象限内抛物线上 ∴设Q (m ，－m 2＋2m ＋3)，0＜m ＜3 ∵QG ⊥x 轴∴G (m ，0)，OG ＝m ，QG ＝－m 2＋2m ＋3 ∵△AOC ∽△QGO ∴AO QG ＝CO OG ，即1－m 2＋2m ＋3 ＝3m解得m 1＝5＋1336 或m 2＝5－1336 (舍去)此时点Q 的坐标为(5＋1336 ，5＋13318 )；(4)存在设E (m ，－m 2＋2m ＋3)，F (n ，0)，易得抛物线顶点D 的坐标为(1，4)，点C 的坐标为(0，3)①如解图④，当DE ，FC 是平行四边形对角线时 ∵平行四边形对角线互相平分 ∴DE ，FC 的中点重合∴⎩⎪⎨⎪⎧1＋m ＝n ＋04－m 2＋2m ＋3＝0＋3 解得m ＝1＋5 或m ＝1－5∴E 1(1＋5 ，－1)或E 2(1－5 ，－1)；例题解图④②如解图⑤，当DF ，EC 是平行四边形对角线时，同理DF ，EC 的中点重合∴⎩⎪⎨⎪⎧1＋n ＝m ＋04＋0＝－m 2＋2m ＋3＋3 解得m ＝1＋3 或m ＝1－3 ∴E 3(1＋3 ，1)或E 4(1－3 ，1)；例题解图⑤③当DC ，EF 是平行四边形对角线时，DC ，EF 的中点重合∴⎩⎪⎨⎪⎧1＋0＝m ＋n 4＋3＝－m 2＋2m ＋3＋0方程组无实数解．综上所述，满足条件的点E 的坐标为(1＋5 ，－1)或(1－5 ，－1)或(1＋3 ，1)或(1－3 ，1)； (5)存在如解图⑥，由题意知，A (－1，0)，C (0，3)，设点H 的坐标为(p ，0) ∴AH 2＝(p ＋1)2，CH 2＝p 2＋32，AC 2＝12＋32＝10 当AC 为矩形的边时，∠ACH ＝90° ∴AH 2＝CH 2＋AC 2即(p ＋1)2＝p 2＋32＋10，解得p ＝9 ∴点H 的坐标为(9，0)；当AC 为矩形的对角线时，∠AHC ＝90° ∴此时点H 与原点重合，点H 的坐标为(0，0). 综上所述，满足条件的点H 的坐标为(9，0)或(0，0)；例题解图⑥(6)存在如解图⑦，过点S 作SZ ⊥x 轴于点Z ，交BC 于点X ∵A (－1，0)，B (3，0)，C (0，3)∴OA ＝1，OC ＝OB ＝3，易得直线BC 的函数解析式为y ＝－x ＋3 ∴∠OBC ＝∠OCB ＝45° ∵SZ ⊥x 轴∴∠BXZ ＝∠SXT ＝45° ∵ST ⊥BC ∴XT ＝ST设S (m ，－m 2＋2m ＋3)，且0＜m ＜3，则X (m ，－m ＋3) ∴CX ＝m 2＋（－m ＋3－3）2 ＝2 m ，SX ＝－m 2＋3m ∴ST ＝TX ＝22 SX ＝－22 m 2＋322m ∴CT ＝CX －TX ＝2 m －(－22 m 2＋322 m )＝22 m 2－22m ①若∠SCT ＝∠CAO∴tan ∠SCT ＝tan ∠CAO ＝OCOA ＝3∵tan ∠SCT ＝STCT ＝3∴ST ＝3CT ∴－22 m 2＋322 m ＝3×(22 m 2－22m )解得m ＝32 或m ＝0(舍去)∴点S 的坐标为(32 ，154 )；②若∠CST ＝∠CAO 则tan ∠CST ＝tan ∠CAO ＝3 ∵tan ∠CST ＝CTST ＝3∴3ST ＝CT ∴3×(－22 m 2＋322 m )＝22 m 2－22m 解得m ＝52 或m ＝0(舍去)∴点S 的坐标为(52 ，74)；综上所述，存在点S ，使得△CST 中有一个角与∠CAO 相等，点S 的坐标为(32 ，154 )或(52 ，74).例题解图⑦对接中考1. 解：(1)由题意可知，抛物线y ＝x 2＋bx ＋c 过点A (－1，0)，点B (5，0)∴⎩⎪⎨⎪⎧1－b ＋c ＝025＋5b ＋c ＝0 ，解得⎩⎪⎨⎪⎧b ＝－4c ＝－5； (2)①如解图，过点P 作y 轴的平行线交BC 于点D ∴S △PBC ＝S △CPD ＋S △PDB由(1)可知，c ＝－5，故点C 的坐标为(0，－5) 易知BC 的表达式为y ＝x －5∵点P 的坐标为(x 0，y 0)(0<x 0<5)，点P 在抛物线上 ∴y 0＝x 20 －4x 0－5设点D 的坐标为(x 0，x 0－5)∴|PD |＝x 0－5－x 20 ＋4x 0＋5＝－x 20 ＋5x 0∴S △PBC ＝12 ×|PD |×5＝12 ×(－x 20 ＋5x 0)×5 ＝－52 (x 0－52 )2＋1258∴当x 0＝52 时，△PBC 面积最大，最大值为1258；第1题解图②存在．由题意可知，∠EPF ＝90°，△PEF 为等腰直角三角形 ∴PE ＝PF∵PE ⊥x 轴，PF ∥x 轴，且点E 在线段BC 上，点F 在抛物线上 由(2)可知PE ＝－x 20 ＋5x 0 易知PF ＝|4－2x 0|∴|PF |＝|PE |，即|4－2x 0|＝|－x 20 ＋5x 0|解得x 0＝4或x 0＝7－332 或x 0＝－1(舍去)或x 0＝7＋332 (舍去)当x 0＝4时，解得y ＝－5当x 0＝7－332 时，解得y 0＝3－3332∴综上所述，当△PEF 为等腰直角三角形时，点P 的坐标为(4，－5)或(7－332 ，3－332 ).2. 解：(1)由题意得A ′(－3，0)，B ′(0，－6)，B (6，0)已知抛物线L 经过点A ′，B ′，B ，设抛物线L 的解析式为y ＝a (x ＋3)(x －6)(a ≠0) 将点B ′(0，－6)代入抛物线解析式中得－6＝a (0＋3)(0－6)，解得a ＝13∴抛物线L 的解析式为y ＝13 (x ＋3)(x －6)＝13 x 2－x －6；(2)存在．∵A (0，－3)，B ′(0，－6) ∴AB ′＝3设直线AB 的解析式为y ＝kx ＋b (k ≠0) 将A (0，－3)，B (6，0)代入直线AB 的解析式得⎩⎪⎨⎪⎧b ＝－36k ＋b ＝0 ，解得⎩⎪⎨⎪⎧b ＝－3k ＝12∴直线AB 的解析式为y ＝12 x －3∵点P 在直线AB 上∴设点P (m ，12m －3)，分情况讨论：①当以AB ′为边且AP 2＝AB ′2时，即m 2＋(12 m )2＝9解得m 1＝655 ，m 2＝－655∴点P 的坐标为(655 ，355 －3)或(－655 ，－355 －3)；②当以AB ′为边且B ′P 2＝AB ′2时，即m 2＋(12 m ＋3)2＝9解得m 1＝0(舍去)，m 2＝－125∴P (－125 ，－215 )；③当以AB ′为对角线时 ∵AB ′＝3∴AB ′的中点坐标为(0，－92 )由菱形的性质可得y P ＝－92即12 m －3＝－92 ，解得m ＝－3 ∴P (－3，－92)；综上所述，点P 的坐标为(655 ，355 －3)或(－655 ，－355 －3)或(－125 ，－215 )或(－3，－92). 拓展类型 二次函数性质综合题1. 解：(1)把点(2，1)代入y ＝x 2－2tx ＋3中 得4－4t ＋3＝1解得t ＝32； (2)∵抛物线对称轴为直线x ＝t①若0<t ≤3∵a ＝1>0∴当x ＝t 时，函数y 取得最小值∵y 的最小值为－2∴t 2－2t 2＋3＝－2解得t ＝±5 .∵0＜t ≤3∴t ＝5 ；②若t >3，∵a ＝1>0∴当0≤x ≤3时，y 随x 的增大而减小∴当x ＝3时，函数y 取得最小值∵y 的最小值为－2∴9－6t ＋3＝－2解得t ＝73(不符合题意，舍去). 综上所述，t 的值为5 ；(3)∵A (m －2，a )，C (m ，a )关于对称轴直线x ＝t 对称∴m －2＋m 2＝t ，即m －1＝t ，且点A 在对称轴左侧，点C 在对称轴右侧． 在y ＝x 2－2tx ＋3中令x ＝0，则y ＝3∴抛物线与y 轴交点为(0，3)∴此交点关于对称轴直线x ＝t 的对称点为(2m －2，3).∵a <3，b <3且t >0∴4<2m －2，解得m >3.当点A ，B 都在对称轴左边时∵a <b∴4<m －2，解得m >6∴m >6；当点A ，B 分别在对称轴两侧时∴B 到对称轴的距离大于A 到对称轴的距离∴4－(m －1)>m －1－(m －2)，解得m <4∴3<m <4.综上所述，m 的取值范围为3<m <4或m >6.2. 解：(1)由题意得，－b 2a＝2 解得b ＝－4a∴4ac －b 24a ＝12a －（－4a ）24a＝3－4a ∴抛物线顶点M 的坐标为(2，3－4a )；(2)y 2＜y 1，理由如下：由题可知，抛物线的对称轴为直线x ＝2∴A (x 1，y 1)关于直线x ＝2的对称点为(4－x 1，y 1)∵x 1＜2＜x 2，x 1＋x 2＜4∴2＜x 2＜4－x 1∵a ＞0∴抛物线开口向上∴在对称轴右侧y 随x 的增大而增大∴y 2＜y 1；(3)b 的值为－12或20.【解法提示】由(1)知，b ＝－4a ，∴抛物线的解析式为y ＝ax 2－4ax ＋3，当a ＞0时，抛物线开口向上，此时在对称轴左侧，y 随x 的增大而减小，∴当x ＝－1时，函数值y 最大，最大值为a ＋4a ＋3，∴a ＋4a ＋3＝18，解得a ＝3，∴b ＝－4a ＝－12；当a ＜0时，抛物线开口向下，此时在对称轴左侧，y 随x 的增大而增大，∴当x ＝1时，函数值y 最大，最大值为a －4a ＋3，∴a －4a ＋3＝18，解得a ＝－5，∴b ＝－4a ＝20.综上所述，b 的值为－12或20.3. 解：(1)∵抛物线的对称轴为直线x ＝－－4a 2a＝2，抛物线与x 轴的交点为A (1，0)，B ∴B (3，0)∴OB ＝3.∵OC ＝2OB∴OC ＝6.∴抛物线开口向下∴C (0，－6).把A (1，0)，C (0，－6)代入y ＝ax 2－4ax ＋c 中得⎩⎪⎨⎪⎧a －4a ＋c ＝0，c ＝－6， 解得⎩⎪⎨⎪⎧a ＝－2，c ＝－6， ∴抛物线的解析式为y ＝－2x 2＋8x －6；(2)由解析式可知抛物线的最大值为4ac －（－4a ）24a ＝4ac －16a 24a＝c －4a . ∵抛物线的最大值为6∴c －4a ＝6.∵抛物线过点A (1，0)∴a －4a ＋c ＝0，即c －4a ＝－a∴－a ＝6，即a ＝－6；(3)已知抛物线的对称轴为直线x ＝2，a ＜0∴(52 ，n )与(32，n )关于对称轴对称 当点P 在对称轴的左侧(含顶点)时，y 随x 的增大而增大，由m ＜n ，得x 0＜32； 当点P 在对称轴的右侧时，y 随x 的增大而减小，由m ＜n ，得x 0＞52. 综上所述，x 0的取值范围为x 0＜32 或x 0＞52.。
最新九年级中考数学专题： 二次函数综合题(特殊三角形问题)含答案
2023年九年级中考数学专题：二次函数综合题（特殊三角形问题）1．如图，抛物线y＝ax2+bx+2经过A（﹣1，0），B（4，0）两点，与y轴交于点C．(1)求该抛物线的解析式；(2)在y轴上是否存在点P使得∠OBP+∠OBC＝45°，若存在，求出点P的坐标，若不存在，请说明理由；(3)点M是BC为直径的圆上的动点，将点M绕原点O顺时针旋转90°得点N，连接NA，求NA的取值范围．2．已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB上方抛物线上的一个动点，过点P作x轴的垂线，交线段AB于点D，再过点P作PE∥x轴交抛物线于点E．(1)求抛物线解析式；(2)当点P运动到什么位置时，DP的长最大？(3)是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．3．如图，抛物线y＝ax2＋bx﹣3经过A、B、C三点，点A（﹣3，0）、C（1，0），点B在y轴上．点P是直线AB下方的抛物线上一动点（不与A、B重合）．(1)求此抛物线的解析式；(2)过点P作x轴的垂线，垂足为D，交直线AB于点E，动点P在什么位置时，PE最大，求出此时P点的坐标；(3)点Q是抛物线对称轴上一动点，是否存在点Q，使以点A、B、Q为顶点的三角形为直角三角形？若存在，请求出点Q坐标；若不存在，请说明理由．4．如图，在平面直角坐标系xOy中，△ABC是等腰直角三角形，△BAC＝90°，A（1，0），B（0，2），二次函数y＝x2+bx﹣2的图象经过C点．（1）求二次函数的解析式；（2）若点P是抛物线的一个动点且在x轴的下方，则当点P运动至何处时，恰好使△PBC的面积等于△ABC的面积的两倍．（3）若点Q是抛物线上的一个动点，则当点Q运动至何处时，恰好使△QAC＝45°？请你求出此时的Q点坐标．5．如图，抛物线y＝ax2+bx+2交x轴于点A（﹣3，0）和点B（1，0），交y轴于点C．（1）求该抛物线的解析式；（2）点D的坐标为（﹣1，0），点P为第二象限内抛物线上的一个动点，求四边形ADCP面积的最大值；（3）抛物线对称轴上是否存在点M，使△MAB是以AB为斜边的直角三角形，若存在，请直接写出点M 的坐标；若不存在，并说明理由；（4）在对称轴上是否存在点N，使△BCN为直角三角形，若存在，直接写出N点坐标，若不存在，说明理由．6．抛物线2y x bx c=++经过A、B(1，0)、C(0，-3)三点．点D为抛物线的顶点，连接AD、AC、BC、DC．（1）求抛物线的解析式；（2）在抛物线的对称轴上找一点P，使PB+PC最小，求出P点坐标；（3）在线段AC上找一点M，使AOM△ABC，请你直接写出点M的坐标；（4）在y轴上是否存在一点E，使ADE为直角三角形？若存在，请你直接写出点E的坐标；若不存在，请说明理由．7．如图，在平面直角坐标系中，已知抛物线y＝x2＋bx＋c与直线AB相交于A，B两点，其中A（﹣3，﹣4），B（0，﹣1）．（1）求该抛物线的函数表达式．（2）点P为直线AB下方抛物线上的任意一点，连接P A，PB，求△P AB面积的最大值．（3）在二次函数的对称轴上找一点C，使得△ABC是等腰三角形，求满足条件的点C的坐标．8．如图，二次函数y＝ax2＋bx＋c（a≠0）的图象交x轴于A，B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．（1）求二次函数的解析式和直线BD的解析式；（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；（3）在抛物线上是否存在点Q，且点Q在第一象限，使△BDQ中BD Q 的坐标；若不存在，请说明理由．9．如图，已知点A的坐标为（－2，0），直线y＝－34x＋3与x轴，y轴分别交于点B和点C，连接AC，顶点为D的抛物线y＝ax2＋bx＋c，过A，B，C三点．（1）求抛物线的解析式及顶点D的坐标；（2）设抛物线的对称轴DE交线段BC于点E，P为第一象限内抛物线上一点，过点P作x轴的垂线，交线段BC于点F，若四边形DEFP为平行四边形，求点P的坐标；（3）设点M是线段BC上的一动点，过点M作MN△AB，交AC于点N．点Q从点B出发，以每秒1个单位长度的速度沿线段BA向点A运动，运动时间为t（秒）．当以MN为直角边的△QMN是等腰直角三角形时，直接写出此时t的取值．10．如图，在平面直角坐标系中，抛物线2=++与x轴交于A，B两点，与y轴交于点C，已知y x bx cB(3，0)，C(0，3-)，连接BC，点P是抛物线上的一个动点，点N是对称轴上的一个动点．（1）求该抛物线的解析式；（2）抛物线的对称轴上是否存在点M，使得MBC为等腰三角形，若存在，求M的坐标；（3）若点P在直线BC的下方，当点P到直线BC的距离最大时，在抛物线上是否存在点Q，使得以点P，C，N，Q为顶点的四边形是平行四边形？若存在，求出点Q的坐标；若不存在，请说明理由．11．如图，抛物线2y x bx c=++经过A（－1，0）、B（5，6）两点，点E是线段AB上一动点，过点E作x轴的垂线，交抛物线于点F．（1）求抛物线的解析式；（2）求线段EF的最大值；（3）在抛物线的对称轴上是否存在一个动点P，使得ABP∆是直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．x+2与x轴交于点B，与y轴交于点C，已知二次函数的图象经过点B、C和点12．如图，直线y＝﹣12A(﹣1，0)．（1）求B、C两点的坐标；（2）求该二次函数的解析式；（3）若抛物线的对称轴与x轴交于点D，则在抛物线的对称轴上是否存在一点N，使NCD为等腰三角形？若存在，求点N的坐标；若不存在，请说明理由．13．如图，直线y ＝﹣x +3与x 轴、y 轴分别交于B 、C 两点，抛物线y ＝﹣x 2+bx +c 经过B 、C 两点，与x 轴另一交点为A ，顶点为D ．（1）求抛物线的解析式．（2）如果一个圆经过点O 、点B 、点C 三点，并交于抛物线AC 段于点E ，求△OEB 的度数．（3）在抛物线的对称轴上是否存在点P ，使△PCD 为等腰三角形，如果存在，求出点P 的坐标，如果不存在，请说明理由．14．如图，抛物线2y ax bx =+过(4,0)A ，()1,3B 两点，点C 、B 关于抛物线的对称轴对称，过点B 作直线BH x ⊥轴，交x 轴于点H ．（1）求抛物线的表达式；（2）直接写出点C 的坐标，并求出ABC ∆的面积；（3）若点M 在直线BH 上运动，点N 在x 轴上运动，是否存在以点C 、M 、N 为顶点的三角形为等腰直角三角形？若存在，求出其值；若不存在，请说明理由．15．如图，已知抛物线224233y x x =-++的图象与x 轴交于A ，B 两点，与y 轴交于点C ，抛物线的对称轴与x 轴交于点D ．点M 从O 点出发，以每秒1个单位长度的速度向B 运动，过M 作x 轴的垂线，交抛物线于点P ，交BC 于Q ．（1）求点B 和点C 的坐标；（2）设当点M 运动了x （秒)时，四边形OBPC 的面积为S ，求S 与x 的函数关系式，并指出自变量x 的取值范围；（3）在线段BC 上是否存在点Q ，使得DBQ ∆成为以BQ 为一腰的等腰三角形？若存在，求出点Q 的坐标，若不存在，说明理由．16．如图，已知一条直线过点（0，4）且与抛物线y ＝14x 2交于A ，B 两点，其中点B 的横坐标是8． （1）求这条直线AB 的函数关系式及点A 的坐标；（2）在x 轴上是否存在点C ，使得△ABC 是直角三角形？若存在，写出点C 的坐标，若不存在，请说明理由．（3）过线段AB 上一点P ，作PM △x 轴，交抛物线于点M ，点M 在第一象限，点N （0，1），当点M 的横坐标为何值时，MN +3MP 的长度最大？最大值是多少？17．如图，已知抛物线()()62y a x x =+-过点()0,2C ，交x 轴于点A 和点B （点A 在点B 的左侧），抛物线的顶点为D ，对称轴DE 交x 轴于点E ，连接EC ．（1）直接写出a 的值，点A 的坐标和抛物线对称轴的表达式．（2）若点M 是抛物线对称轴DE 上的点，当MCE 是等腰三角形时，求点M 的坐标．（3）点P 是抛物线上的动点，连接PC ，PE ，将PCE 沿CE 所在的直线对折，点P 落在坐标平面内的点P '处．求当点P '恰好落在直线AD 上时点P 的横坐标．18．如图，直线y x n =-+与x 轴交于点()3,0A ，与y 轴交于点B ，抛物线2y x bx c =-++经过点A ，B ．（1）求抛物线的解析式；（2）(),0E m 为x 轴上一动点，过点E 作ED x ⊥轴，交直线AB 于点D ，交抛物线于点P ，连接BP ． △点E 在线段OA 上运动，若BPD △直角三角形，求点E 的坐标；△点E 在x 轴的正半轴上运动，若45PBD ABO ∠+∠=︒，请直接写出m 的值．19．如图，抛物线2y x bx c =-++的图象交x 轴于,A B 两点，交y 轴于点C ，直线3y x =-+经过,B C 两点．（1）求抛物线的解析式；PC PB，求PBC面积的最大值，并求出此时点P的坐（2）点P为抛物线第一象限上的一动点，连接,标；（3）在抛物线的对称轴上是否存在点M，使得BCM为直角三角形?若存在，请直接写出点M的坐标；若不存在，请说明理由．20．如图，抛物线y＝ax2+bx+6（a≠0）与x轴交于点A（2，0）和点B（﹣6，0），与y轴交于点C．(1)求抛物线的解析式；(2)在抛物线上是否存在一点P，使△P AB的面积与△ABC的面积相等，若存在，求出点P的坐标；若不存在，请说明理由．(3)设抛物线的对称轴与x轴交于点M，在对称轴上存在点Q，使△CMQ是以MC为腰的等腰三角形，请直接写出所有符合条件的点Q的坐标．答案1．(1)y ＝﹣12x 2+32x +2 (2)存在，（0，﹣43）或（0，43）NA ≤2．(1)y ＝﹣x 2﹣2x +3(2)点P 的坐标为315,24⎛⎫- ⎪⎝⎭(3)存在，点P 坐标为（﹣2，33．(1)y ＝x 2+2x ﹣3； (2)（﹣32，154-）(3)（-1，2）或（-1，﹣4）或（-1-14．（1）222y x x -=-；（2）当点P 运动至坐标为()2,2-时，恰好使△PBC 的面积等于△ABC 的面积的两倍； （3）Q ⎝⎭或.Q ⎝⎭ 5．（1）y ＝﹣23x 2﹣43x +2；（2）174；（3）存在，M 点坐标为（﹣1，﹣2）或（﹣1，2）；（4）存在，N 的坐标为（﹣1，32）或（﹣1，﹣1） 6．（1）223y x x =+-；（2）P (－1，－2)；（3）(34-，94-)；（4）存在，E 1(0，－3)或E 2(0，－1)或E 3(0，72-)或E 4(0，32)7．（1）y ＝x 2+4x ﹣1；（2）278；（3）C 点坐标为1(2,1C --，2(2,1C --，3(2,4C --，4(2,4C --，57(2,)3C -- 8．（1）抛物线解析式为y ＝﹣x 2+2x +3，直线BD 解析式为y ＝﹣x +3；（2）94；（3）存在，（1，4）或（2，3）9．（1）y =-38x 2+34x +3；D （1，278）；（2）P （3，158）；（3）83或14310．（1）223y x x =--；（2）存在，M 的坐标为(1，1-)或(1或(1，或(1，3-+或(1，3-；（3）存在，Q 的坐标为(52，74-)或(12-，74-)或(12，154-)11．（1）y =x 2-3x -4；（2）9；（3）存在，点P 的坐标为3(2，3(2 ，35(,)22-，319(,)22 12．（1）B (4，0)，C (0，2)；（2）213222y x x =-++；（3）存在，123435353325(,),(,),(,4),(,),22222216N N N N - 13．（1）抛物线解析式y ＝﹣x 2+2x +3；（2）△OEB ＝45°；（3）存在，点P （1，2）、（1，3）、（1，4）、（1，、（1，4△PCD 为等腰三角形14．（1）24y x x =-+；（2）3(3)C ，，3；（3）N 点坐标为(2,0)或(4,0)-或(2,0)-或(4,0)，15．（1）(3,0)B ，(0,2)C ；（2）2321()(03)24S x x =--+；（3）存在，Q 的坐标为2(2)3，或(3， 16．（1）y ＝32x +4，A 点的坐标为（﹣2，1）；（2）存在，点C 的坐标为（﹣12，0），（0，0），（6，0），（32，0）；（3）当M 的横坐标为6时，MN +3PM 的长度的最大值是1817．（1）a ＝−16；对称轴为直线x ＝−2；A （−6，0）；（2）（−2，2）或（−2，4）或（−2，）或（−2，；（3 18．（1）2y x 2x 3=-++；（2）△E (1，0)或(2，0)；△5m =或73．19．（1）2y x 2x 3=-++；（2）315(,)24P ；（3）1234,,(1,2),(1,4)M M M M ⎛⎛- ⎝⎭⎝⎭． 20．(1)y ＝26122x x -+﹣(2)存在，点P 的坐标为：（﹣6）或（﹣2，﹣6）或（﹣4，6）(3)点Q 的坐标为1Q （﹣2，）或2Q （﹣2，﹣3Q （﹣2，12）。
最新九年级数学中考复习：二次函数综合压轴题题(相似三角形问题)含答案
(1)求抛物线的函数表达式；
(2)当 PDE的周长取得最大值时，求点P的坐标和 PDE周长的最大值；
(3)把抛物线 平移，使得新抛物线的顶点为（2）中求得的点P．M是新抛物线上一点，N是新抛物线对称轴上一点，直接写出所有使得以点A，B，M，N为顶点的四边形是平行四边形的点M的坐标，并把求其中一个点M的坐标的过程写出来．
3．如图，抛物线 交 轴于 ， 两点，与 轴交于点 连接 ， ．
(1)求抛物线的解析式；
(2)如图 ，点 为抛物线在第三象限的一个动点， 轴于点 ，交 于点 ， 于点 ，当 的面积为 时，求点 的坐标；
(3)如图 ，若 为抛物线上一点，直线 与线段 交于点 ，是否存在这样的点 ，使得以 ， ， 为顶点的三角形与 相似．若存在，请求出此时点 的坐标；若不存在，请说明理由．
18．如图，在平面直角坐标系中，抛物线 与x轴交于点A，B，与y轴交于点C，点A和点C的坐标分别为 和
(1)求抛物线 的函数表达式；
(2)将线段CB绕点C顺时针旋转90°，得到线段CD，连接AD，求线段AD的长；
(3)点M是抛物线上位于第一象限图象上的一动点，连接AM交BC于点N，连接BM，当 时，请直接写出点M的横坐标的值．
15．在平面直角坐标系中，二次函数 的图像与x轴交于 ， 两点，与y轴交于点C．
(1)求a，b的值；
(2)点P是直线 上方的抛物线上一动点，是否存在点P，使 的面积最大？若存在，求出点P的坐标；若不存在，说明理由；
(3)点Q是直线 上方抛物线上一动点，过点 作 轴于点E， 是否存在点Q．使以点B、Q、E为顶点的三角形与 相似？若存在，求出Q点的坐标；若不存在，说明理由．
人教全国中考数学二次函数的综合中考真题汇总含答案解析
一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图：在平面直角坐标系中，直线l ：y=13x ﹣43与x 轴交于点A ，经过点A 的抛物线y=ax 2﹣3x+c 的对称轴是x=32． （1）求抛物线的解析式；（2）平移直线l 经过原点O ，得到直线m ，点P 是直线m 上任意一点，PB ⊥x 轴于点B ，PC ⊥y 轴于点C ，若点E 在线段OB 上，点F 在线段OC 的延长线上，连接PE ，PF ，且PE=3PF ．求证：PE ⊥PF ；（3）若（2）中的点P 坐标为（6，2），点E 是x 轴上的点，点F 是y 轴上的点，当PE ⊥PF 时，抛物线上是否存在点Q ，使四边形PEQF 是矩形？如果存在，请求出点Q 的坐标，如果不存在，请说明理由．【答案】（1）抛物线的解析式为y=x 2﹣3x ﹣4；（2）证明见解析；（3）点Q 的坐标为（﹣2，6）或（2，﹣6）． 【解析】 【分析】（1）先求得点A 的坐标，然后依据抛物线过点A ，对称轴是x=32列出关于a 、c 的方程组求解即可；（2）设P （3a ，a ），则PC=3a ，PB=a ，然后再证明∠FPC=∠EPB ，最后通过等量代换进行证明即可；（3）设E （a ，0），然后用含a 的式子表示BE 的长，从而可得到CF 的长，于是可得到点F 的坐标，然后依据中点坐标公式可得到22x x x x Q P F E ++=，22y y y yQ P F E ++=，从而可求得点Q 的坐标（用含a 的式子表示），最后，将点Q 的坐标代入抛物线的解析式求得a 的值即可． 【详解】（1）当y=0时，140 33x-=，解得x=4，即A（4，0），抛物线过点A，对称轴是x=32，得161203322a ca-+=⎧⎪-⎨-=⎪⎩，解得14ac=⎧⎨=-⎩，抛物线的解析式为y=x2﹣3x﹣4；（2）∵平移直线l经过原点O，得到直线m，∴直线m的解析式为y=13x．∵点P是直线1上任意一点，∴设P（3a，a），则PC=3a，PB=a．又∵PE=3PF，∴PC PBPF PE=．∴∠FPC=∠EPB．∵∠CPE+∠EPB=90°，∴∠FPC+∠CPE=90°，∴FP⊥PE．（3）如图所示，点E在点B的左侧时，设E（a，0），则BE=6﹣a．∵CF=3BE=18﹣3a，∴OF=20﹣3a．∴F（0，20﹣3a）．∵PEQF为矩形，∴22x x x xQ P F E++=，22y y y yQ P F E++=，∴Q x+6=0+a，Q y+2=20﹣3a+0，∴Q x=a﹣6，Q y=18﹣3a．将点Q的坐标代入抛物线的解析式得：18﹣3a=（a﹣6）2﹣3（a﹣6）﹣4，解得：a=4或a=8（舍去）．∴Q（﹣2，6）．如下图所示：当点E 在点B 的右侧时，设E （a ，0），则BE=a ﹣6．∵CF=3BE=3a ﹣18， ∴OF=3a ﹣20． ∴F （0，20﹣3a ）． ∵PEQF 为矩形，∴22x x x x Q P F E ++=，22y y y yQ P F E ++=， ∴Q x +6=0+a ，Q y +2=20﹣3a+0， ∴Q x =a ﹣6，Q y =18﹣3a ．将点Q 的坐标代入抛物线的解析式得：18﹣3a=（a ﹣6）2﹣3（a ﹣6）﹣4，解得：a=8或a=4（舍去）． ∴Q （2，﹣6）．综上所述，点Q 的坐标为（﹣2，6）或（2，﹣6）． 【点睛】本题主要考查的是二次函数的综合应用，解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式，用含a 的式子表示点Q 的坐标是解题的关键．2．（2017南宁，第26题，10分）如图，已知抛物线2239y ax ax a =--与坐标轴交于A ，B ，C 三点，其中C （0，3），∠BAC 的平分线AE 交y 轴于点D ，交BC 于点E ，过点D 的直线l 与射线AC ，AB 分别交于点M ，N ．（1）直接写出a 的值、点A 的坐标及抛物线的对称轴；（2）点P 为抛物线的对称轴上一动点，若△PAD 为等腰三角形，求出点P 的坐标； （3）证明：当直线l 绕点D 旋转时，11AM AN+均为定值，并求出该定值．【答案】（1）a =13-，A 0），抛物线的对称轴为x 2）点P 的坐标为04）；（3）2． 【解析】试题分析：（1）由点C 的坐标为（0，3），可知﹣9a =3，故此可求得a 的值，然后令y =0得到关于x 的方程，解关于x 的方程可得到点A 和点B 的坐标，最后利用抛物线的对称性可确定出抛物线的对称轴；（2）利用特殊锐角三角函数值可求得∠CAO =60°，依据AE 为∠BAC 的角平分线可求得∠DAO =30°，然后利用特殊锐角三角函数值可求得OD =1，则可得到点D 的坐标．设点P 的，a ）．依据两点的距离公式可求得AD 、AP 、DP 的长，然后分为AD =PA 、AD =DP 、AP =DP 三种情况列方程求解即可；（3）设直线MN 的解析式为y =kx +1，接下来求得点M 和点N 的横坐标，于是可得到AN 的长，然后利用特殊锐角三角函数值可求得AM 的长，最后将AM 和AN 的长代入化简即可．试题解析：（1）∵C （0，3），∴﹣9a =3，解得：a =13-．令y =0得：290ax a --=，∵a ≠0，∴290x --=，解得：x =x =∴点A 0），B （0），∴抛物线的对称轴为x（2）∵OA OC =3，∴tan ∠CAO ∴∠CAO =60°．∵AE 为∠BAC 的平分线，∴∠DAO =30°，∴DO =1，∴点D 的坐标为（0，1）．设点P a ）．依据两点间的距离公式可知：AD 2=4，AP 2=12+a 2，DP 2=3+（a ﹣1）2． 当AD =PA 时，4=12+a 2，方程无解．当AD =DP 时，4=3+（a ﹣1）2，解得a =0或a =2（舍去），∴点P 0）．当AP =DP 时，12+a 2=3+（a ﹣1）2，解得a =﹣4，∴点P ，﹣4）．综上所述，点P 04）．（3）设直线AC 的解析式为y =mx +3，将点A 的坐标代入得：30+=，解得：m ∴直线AC 的解析式为3y =+． 设直线MN 的解析式为y =kx +1．把y =0代入y =kx +1得：kx +1=0，解得：x =1k -，∴点N 的坐标为（1k-，0），∴AN =1k-．将3y =+与y =kx +1联立解得：x，∴点M ．过点M 作MG ⊥x 轴，垂足为G ．则AG =33k +-．∵∠MAG =60°，∠AGM =90°，∴AM =2AG 33k +-2323k k --，∴11AM AN +323231k k --3232k -3(32(31)k k - =32． 点睛：本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求一次函数、二次函数的解析式，分类讨论是解答问题（2）的关键，求得点M 的坐标和点N 的坐标是解答问题（3）的关键．3．抛物线2y x bx c =-++（b ，c 为常数）与x 轴交于点()1,0x 和()2,0x ，与y 轴交于点A ，点E 为抛物线顶点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，在平面直角坐标系中有抛物线y ＝a （x ﹣2）2﹣2和y ＝a （x ﹣h ）2，抛物线y ＝a （x ﹣2）2﹣2经过原点，与x 轴正半轴交于点A ，与其对称轴交于点B ；点P 是抛物线y ＝a （x ﹣2）2﹣2上一动点，且点P 在x 轴下方，过点P 作x 轴的垂线交抛物线y ＝a （x ﹣h ）2于点D ，过点D 作PD 的垂线交抛物线y ＝a （x ﹣h ）2于点D ′（不与点D 重合），连接PD ′，设点P 的横坐标为m ：（1）①直接写出a 的值；②直接写出抛物线y ＝a （x ﹣2）2﹣2的函数表达式的一般式；（2）当抛物线y ＝a （x ﹣h ）2经过原点时，设△PDD ′与△OAB 重叠部分图形周长为L ： ①求PD DD'的值； ②直接写出L 与m 之间的函数关系式；（3）当h 为何值时，存在点P ，使以点O 、A 、D 、D ′为顶点的四边形是菱形？直接写出h 的值．【答案】（1）①12；②y ＝212x ﹣2x ； （2）①1； ②L ＝2(22)(02)21(221)4(24)2m m m m π⎧+<⎪⎨-++<<⎪⎩； （3）h ＝±3 【解析】【分析】（1）①将x ＝0，y ＝0代入y ＝a （x ﹣2）2﹣2中计算即可；②y ＝212x ﹣2x ； （2）将（0，0）代入y ＝a （x ﹣h ）2中，可求得a ＝12，y ＝12x 2，待定系数法求OB 、AB 的解析式，由点P 的横坐标为m ，即可表示出相应线段求解；（3）以点O 、A 、D 、D ′为顶点的四边形是菱形，DD ′＝OA ，可知点D 的纵坐标为2，再由AD ＝OA ＝4即可求出h 的值．【详解】解：（1）①将x ＝0，y ＝0代入y ＝a （x ﹣2）2﹣2中，得：0＝a （0﹣2）2﹣2，解得：a ＝12； ②y ＝212x ﹣2x ；． （2）∵抛物线y ＝a （x ﹣h ）2经过原点，a ＝12； ∴y ＝12x 2， ∴A （4，0），B （2，﹣2），易得：直线OB 解析式为：y ＝﹣x ，直线AB 解析式为：y ＝x ﹣4如图1，222111,2,,,(,0),(,),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ①221122,222PD m m m m DD m '⎛⎫=--== ⎪⎝⎭PD 2m 1DD 2m'∴== ②如图1，当0＜m ≤2时，L ＝OE +EF +OF ＝2(22)m m m m ++=+，当2＜m ＜4时，如图2，设PD ′交x 轴于G ，交AB 于H ，PD 交x 轴于E ，交AB 于F ，则222111,2,,,(,0),(,4),,222P m m m D m m E m F m m D m m '⎛⎫⎛⎫⎛⎫--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，2211(4)23422PF m m m m m ⎛⎫=---=-+- ⎪⎝⎭， 2222322m m 22,PG m 22m FH PH PF ===-+-=-+ ∵DD ′∥EG EG PE DD PD '∴=，即：EG •PD ＝PE •DD ′，得：EG •（2m ）＝（2m ﹣12m 2）•2m ∴EG ＝2m ﹣12m 2，EF ＝4﹣m ∴L ＝EG +EF +FH +GH ＝EG +EF +PG221224222m m m m m ⎛⎫=-+-+-+ ⎪ ⎪⎝⎭221m (221)m 42+=-+++ 2(22)m(0m 2)21m (221)m 4(2m 4)2L ⎧+<⎪∴=⎨+-+++<<⎪⎩； （3）如图3，∵OADD ′为菱形∴AD ＝AO ＝DD ′＝4，∴PD ＝2，23PA =23h ∴=±【点睛】本题是二次函数综合题，考查了待定系数法求函数解析式，菱形的性质，抛物线的平移等，解题时要注意考虑分段函数表示方法．2．如图，在平面直角坐标系中，二次函数2y ax bx c =++交x 轴于点()4,0A -、()2,0B ，交y 轴于点()0,6C ，在y 轴上有一点()0,2E -，连接AE .（1）求二次函数的表达式；（2）若点D 为抛物线在x 轴负半轴上方的一个动点，求ADE ∆面积的最大值； （3）抛物线对称轴上是否存在点P ，使AEP ∆为等腰三角形，若存在，请直接写出所有P 点的坐标，若不存在请说明理由.【答案】（1）二次函数的解析式为233642y x x =--+；（2）当23x =-时，ADE ∆的面积取得最大值503；（3）P 点的坐标为()1,1-，(1,11-，(1,219--. 【解析】分析：（1）把已知点坐标代入函数解析式，得出方程组求解即可；（2）根据函数解析式设出点D 坐标，过点D 作DG ⊥x 轴，交AE 于点F ，表示△ADE 的面积，运用二次函数分析最值即可；（3）设出点P 坐标，分PA =PE ，PA =AE ，PE =AE 三种情况讨论分析即可．详解：（1）∵二次函数y =ax 2+bx +c 经过点A （﹣4，0）、B （2，0），C （0，6）， ∴16404206a b c a b c c -+=⎧⎪++=⎨⎪=⎩， 解得：34326a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩， 所以二次函数的解析式为：y =233642x x --+； （2）由A （﹣4，0），E （0，﹣2），可求AE 所在直线解析式为y =122x --，过点D 作DN ⊥x 轴，交AE 于点F ，交x 轴于点G ，过点E 作EH ⊥DF ，垂足为H ，如图，设D （m ，233642m m --+），则点F （m ，122m --）， ∴DF =233642m m --+﹣（122m --）=2384m m --+， ∴S △ADE =S △ADF +S △EDF =12×DF ×AG +12DF ×EH =12×DF ×AG +12×DF ×EH =12×4×DF =2×（2384m m --+） =23250233m -++（）， ∴当m =23-时，△ADE 的面积取得最大值为503． （3）y =233642x x --+的对称轴为x =﹣1，设P （﹣1，n ），又E （0，﹣2），A （﹣4，0），可求PA 29n +PE 212n ++（）AE 16425+=，分三种情况讨论： 当PA =PE 29n +212n ++（）n =1，此时P （﹣1，1）； 当PA =AE 29n +16425+=n =11，此时点P 坐标为（﹣1，11）；当PE =AE 212n ++（）16425+=n =﹣219P 坐标为：（﹣1，﹣219）．综上所述：P 点的坐标为：（﹣1，1），（﹣1，111，﹣219）． 点睛：本题主要考查二次函数的综合问题，会求抛物线解析式，会运用二次函数分析三角形面积的最大值，会分类讨论解决等腰三角形的顶点的存在问题时解决此题的关键．3．（10分）（2015•佛山）如图，一小球从斜坡O点处抛出，球的抛出路线可以用二次函数y=﹣x2+4x刻画，斜坡可以用一次函数y=x刻画．（1）请用配方法求二次函数图象的最高点P的坐标；（2）小球的落点是A，求点A的坐标；（3）连接抛物线的最高点P与点O、A得△POA，求△POA的面积；（4）在OA上方的抛物线上存在一点M（M与P不重合），△MOA的面积等于△POA的面积．请直接写出点M的坐标．【答案】（1）（2，4）；（2）（，）；（3）；（4）（，）．【解析】试题分析：（1）利用配方法抛物线的一般式化为顶点式，即可求出二次函数图象的最高点P的坐标；（2）联立两解析式，可求出交点A的坐标；（3）作PQ⊥x轴于点Q，AB⊥x轴于点B．根据S△POA=S△POQ+S△梯形PQBA﹣S△BOA，代入数值计算即可求解；（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，由于两平行线之间的距离相等，根据同底等高的两个三角形面积相等，可得△MOA的面积等于△POA的面积．设直线PM的解析式为y=x+b，将P（2，4）代入，求出直线PM的解析式为y=x+3．再与抛物线的解析式联立，得到方程组，解方程组即可求出点M的坐标．试题解析：（1）由题意得，y=﹣x2+4x=﹣（x﹣2）2+4，故二次函数图象的最高点P的坐标为（2，4）；（2）联立两解析式可得：，解得：，或．故可得点A的坐标为（，）；（3）如图，作PQ⊥x轴于点Q，AB⊥x轴于点B．S△POA=S△POQ+S△梯形PQBA﹣S△BOA=×2×4+×（+4）×（﹣2）﹣××=4+﹣=；（4）过P作OA的平行线，交抛物线于点M，连结OM、AM，则△MOA的面积等于△POA的面积．设直线PM的解析式为y=x+b，∵P的坐标为（2，4），∴4=×2+b，解得b=3，∴直线PM的解析式为y=x+3．由，解得，，∴点M的坐标为（，）．考点：二次函数的综合题4．如图，二次函数245y x x =-++图象的顶点为D ，对称轴是直线l ，一次函数215y x =+的图象与x 轴交于点A ，且与直线DA 关于l 的对称直线交于点B ．（1）点D 的坐标是 ______；（2）直线l 与直线AB 交于点C ，N 是线段DC 上一点（不与点D 、C 重合），点N 的纵坐标为n ．过点N 作直线与线段DA 、DB 分别交于点P ，Q ，使得DPQ ∆与DAB ∆相似．①当275n =时，求DP 的长； ②若对于每一个确定的n 的值，有且只有一个DPQ ∆与DAB ∆相似，请直接写出n 的取值范围 ______．【答案】（1）()2,9；（2）①95DP =②92155n <<. 【解析】【分析】（1）直接用顶点坐标公式求即可；（2）由对称轴可知点C （2，95），A （-52，0），点A 关于对称轴对称的点（132，0），借助AD 的直线解析式求得B （5，3）；①当n=275时，N （2，275），可求95，DN=185，CD=365，当PQ ∥AB 时，△DPQ ∽△DAB ，5；当PQ 与AB 不平行时，5②当PQ ∥AB ，DB=DP 时，5DN=245，所以N （2，215），则有且只有一个△DPQ 与△DAB 相似时，95＜n ＜215. 【详解】（1）顶点为()2,9D ；故答案为()2,9；（2）对称轴2x =，9(2,)5C ∴， 由已知可求5(,0)2A -， 点A 关于2x =对称点为13(,0)2， 则AD 关于2x =对称的直线为213y x =-+， (5,3)B ∴，①当275n =时，27(2,)5N ，DA ∴=，182DN =，365CD = 当PQ AB ∥时，PDQ DAB ∆∆，DAC DPN ∆∆，DP DN DA DC∴=，DP ∴=当PQ 与AB 不平行时，DPQ DBA ∆∆，DNQ DCA ∴∆∆，DP DN DB DC∴=，DP ∴=综上所述DP =②当PQ AB ∥，DB DP =时，DB =DP DN DA DC∴=， 245DN ∴=， 21(2,)5N ∴， ∴有且只有一个DPQ ∆与DAB ∆相似时，92155n <<； 故答案为92155n <<； 【点睛】 本题考查二次函数的图象及性质，三角形的相似；熟练掌握二次函数的性质，三角形相似的判定与性质是解题的关键．5．在平面直角坐标系xOy 中(如图)，已知抛物线y ＝x 2－2x ，其顶点为A ．(1)写出这条抛物线的开口方向、顶点A 的坐标，并说明它的变化情况；(2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点” ①试求抛物线y ＝x 2－2x 的“不动点”的坐标；②平移抛物线y ＝x 2－2x ，使所得新抛物线的顶点B 是该抛物线的“不动点”，其对称轴与x 轴交于点C ，且四边形OABC 是梯形，求新抛物线的表达式.【答案】(l)抛物线y ＝x 2－2x 的开口向上，顶点A 的坐标是(1，－1)，抛物线的变化情况是：抛物线在对称轴左侧的部分是下降的，右侧的部分是上升的；(2)①(0，0)、(3，3)； ②新抛物线的表达式是y ＝(x ＋1)2－1.【解析】【分析】（1）10a =>，故该抛物线开口向上，顶点A 的坐标为()1,1-；（2）①设抛物线“不动点”坐标为(),t t ，则22t t t =-，即可求解；②新抛物线顶点B 为“不动点”，则设点(),B m m ，则新抛物线的对称轴为：x m =，与x 轴的交点(),0C m ，四边形OABC 是梯形，则直线x m =在y 轴左侧，而点()1,1A -，点(),B m m ，则1m =-，即可求解.【详解】 (l)10a =>，抛物线y ＝x 2－2x 的开口向上，顶点A 的坐标是(1，－1)，抛物线的变化情况是：抛物线在对称轴左侧的部分是下降的，右侧的部分是上升的.(2)①设抛物线y ＝x 2－2x 的“不动点”坐标为(t ，t).则t ＝t 2－2t ，解得t 1＝0，t 2＝3.所以，抛物线y ＝x 2－2x 的“不动点”的坐标是(0，0)、(3，3).②∵新抛物线的顶点B 是其“不动点”，∴设点B 的坐标为(m ，m)∴新抛物线的对称轴为直线x ＝m ，与x 轴的交点为C(m ，0)∵四边形OABC 是梯形，∴直线x ＝m 在y 轴左侧.∵BC 与OA 不平行∴OC ∥AB.又∵点A 的坐标为(1，一1)，点B 的坐标为(m ，m)，∴m ＝－1.∴新抛物线是由抛物线y ＝x 2－2x 向左平移2个单位得到的，∴新抛物线的表达式是y ＝(x ＋1)2－1.【点睛】本题为二次函数综合运用题，涉及到二次函数基本知识、梯形基本性质，此类新定义题目，通常按照题设顺序，逐次求解即可.6．如图，在平面直角坐标系中，已知点B 的坐标为()1,0-，且4OA OC OB ==，抛物线()20y ax bx c a =++≠图象经过,,A B C 三点．（1）求,A C 两点的坐标；（2）求抛物线的解析式；（3）若点P 是直线AC 下方的抛物线上的一个动点，作PD AC ⊥于点D ，当PD 的值最大时，求此时点P 的坐标及PD 的最大值．【答案】解：（1）点A 、C 的坐标分别为（4，0）、（0，﹣4）；；（2）抛物线的表达式为：234y x x ＝﹣﹣ ； （3）PD 有最大值，当x ＝2时，其最大值为2，此时点P （2，﹣6）．【解析】【分析】（1）OA ＝OC ＝4OB ＝4，即可求解；（2）抛物线的表达式为：234y x x ＝a （x+1）(x-4)=a(﹣﹣) ，即可求解； （3）224342--++＝（）PD x x x ，即可求解． 【详解】 解：（1）OA ＝OC ＝4OB ＝4，故点A 、C 的坐标分别为（4，0）、（0，﹣4）；（2）抛物线的表达式为：234y x x ＝a （x+1）(x-4)=a(﹣﹣)，即﹣4a ＝﹣4，解得：a ＝1，故抛物线的表达式为：234y x x --＝ ；（3）直线CA 过点C ，设其函数表达式为：4y kx -＝，将点A 坐标代入上式并解得：k ＝1，故直线CA 的表达式为：y ＝x ﹣4，过点P 作y 轴的平行线交AC 于点H ，∵OA ＝OC ＝4，45OAC OCA ∴∠∠︒＝＝ ，∵//PH y 轴，45PHD OCA ∴∠∠︒＝＝，设点234P x x x --（，），则点H （x ，x ﹣4）， 22243422222--+++＝（）=-PD x x x x x ∵22- ＜0，∴PD 有最大值，当x ＝2时，其最大值为22 此时点P （2，﹣6）．【点睛】本题考查的是二次函数综合运用，涉及到一次函数、解直角三角形、图象的面积计算等，其中（3），用函数关系表示PD ，是本题解题的关键7．如图甲，直线y=﹣x+3与x 轴、y 轴分别交于点B 、点C ，经过B 、C 两点的抛物线y=x 2+bx+c 与x 轴的另一个交点为A ，顶点为P ．（1）求该抛物线的解析式；（2）在该抛物线的对称轴上是否存在点M ，使以C ，P ，M 为顶点的三角形为等腰三角形？若存在，请直接写出所符合条件的点M 的坐标；若不存在，请说明理由；（3）当0＜x＜3时，在抛物线上求一点E，使△CBE的面积有最大值（图乙、丙供画图探究）．【答案】（1）y=x2﹣4x+3；（2）（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）E点坐标为（，）时，△CBE的面积最大．【解析】试题分析：（1）由直线解析式可求得B、C坐标，利用待定系数法可求得抛物线解析式；（2）由抛物线解析式可求得P点坐标及对称轴，可设出M点坐标，表示出MC、MP和PC 的长，分MC=MP、MC=PC和MP=PC三种情况，可分别得到关于M点坐标的方程，可求得M点的坐标；（3）过E作EF⊥x轴，交直线BC于点F，交x轴于点D，可设出E点坐标，表示出F点的坐标，表示出EF的长，进一步可表示出△CBE的面积，利用二次函数的性质可求得其取得最大值时E点的坐标．试题解析：（1）∵直线y=﹣x+3与x轴、y轴分别交于点B、点C，∴B（3，0），C（0，3），把B、C坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=x2﹣4x+3；（2）∵y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线对称轴为x=2，P（2，﹣1），设M（2，t），且C（0，3），∴MC=，MP=|t+1|，PC=，∵△CPM为等腰三角形，∴有MC=MP、MC=PC和MP=PC三种情况，①当MC=MP时，则有=|t+1|，解得t=，此时M（2，）；②当MC=PC时，则有=2，解得t=﹣1（与P点重合，舍去）或t=7，此时M（2，7）；③当MP=PC时，则有|t+1|=2，解得t=﹣1+2或t=﹣1﹣2，此时M（2，﹣1+2）或（2，﹣1﹣2）；综上可知存在满足条件的点M，其坐标为（2，）或（2，7）或（2，﹣1+2）或（2，﹣1﹣2）；（3）如图，过E作EF⊥x轴，交BC于点F，交x轴于点D，设E（x，x2﹣4x+3），则F（x，﹣x+3），∵0＜x＜3，∴EF=﹣x+3﹣（x2﹣4x+3）=﹣x2+3x，∴S△CBE=S△EFC+S△EFB=EF•OD+EF•BD=EF•OB=×3（﹣x2+3x）=﹣（x﹣）2+，∴当x=时，△CBE的面积最大，此时E点坐标为（，），即当E点坐标为（，）时，△CBE的面积最大．考点：二次函数综合题．8．如图，已知抛物线y=ax2+bx﹣2（a≠0）与x轴交于A、B两点，与y轴交于C点，直线BD交抛物线于点D，并且D（2，3），tan∠DBA=12．（1）求抛物线的解析式；（2）已知点M为抛物线上一动点，且在第三象限，顺次连接点B、M、C、A，求四边形BMCA面积的最大值；（3）在（2）中四边形BMCA面积最大的条件下，过点M作直线平行于y轴，在这条直线上是否存在一个以Q点为圆心，OQ为半径且与直线AC相切的圆？若存在，求出圆心Q 的坐标；若不存在，请说明理由．【答案】（1）y=12x2+32x﹣2；（2）9；（3）点Q的坐标为（﹣2，4）或（﹣2，﹣1）．【解析】（1）如答图1所示，利用已知条件求出点B的坐标，然后用待定系数法求出抛物线的解析式．（2）如答图1所示，首先求出四边形BMCA面积的表达式，然后利用二次函数的性质求出其最大值．（3）如答图2所示，首先求出直线AC与直线x=2的交点F的坐标，从而确定了Rt△AGF 的各个边长；然后证明Rt△AGF∽Rt△QEF，利用相似线段比例关系列出方程，求出点Q的坐标．考点：二次函数综合题，曲线上点的坐标与方程的关系，锐角三角函数定义，由实际问题列函数关系式，二次函数最值，勾股定理，相似三角形的判定和性质，圆的切线性质．9．如图，在平面直角坐标系中，已知抛物线y=12x2+32x﹣2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，直线l经过A，C两点，连接BC．（1）求直线l的解析式；（2）若直线x=m（m＜0）与该抛物线在第三象限内交于点E，与直线l交于点D，连接OD．当OD⊥AC时，求线段DE的长；（3）取点G（0，﹣1），连接AG，在第一象限内的抛物线上，是否存在点P，使∠BAP=∠BCO﹣∠BAG？若存在，求出点P的坐标；若不存在，请说明理由．【答案】（1）y=122x--；（2）DE=3225；（3）存在点P（139，9881），使∠BAP=∠BCO﹣∠BAG，理由见解析.【解析】【分析】（1）根据题目中的函数解析式可以求得点A和点C的坐标，从而可以求得直线l的函数解析式；（2）根据题意作出合适的辅助线，利用三角形相似和勾股定理可以解答本题；（3）根据题意画出相应的图形，然后根据锐角三角函数可以求得∠OAC=∠OCB，然后根据题目中的条件和图形，利用锐角三角函数和勾股定理即可解答本题．【详解】（1）∵抛物线y=12x2+32x-2，∴当y=0时，得x1=1，x2=-4，当x=0时，y=-2，∵抛物线y=12x2+32x-2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，∴点A的坐标为（-4，0），点B（1，0），点C（0，-2），∵直线l经过A，C两点，设直线l的函数解析式为y=kx+b，402k bb-+⎧⎨-⎩＝＝，得122kb⎧-⎪⎨⎪-⎩＝＝，即直线l的函数解析式为y=−12x−2；（2）直线ED与x轴交于点F，如图1所示，由（1）可得，AO=4，OC=2，∠AOC=90°，∴5∴45525=，∵OD⊥AC，OA⊥OC，∠OAD=∠CAO，∴△AOD ∽△ACO ， ∴AD AO AO AC ＝， 即425AD ＝，得AD=85， ∵EF ⊥x 轴，∠ADC=90°，∴EF ∥OC ，∴△ADF ∽△ACO ， ∴AF DF AD AO OC AC＝＝， 解得，AF=165，DF=85， ∴OF=4-165=45， ∴m=-45， 当m=-45时，y=12×（−45）2+32×（-45）-2=-7225， ∴EF=7225， ∴DE=EF-FD=7225−85＝3225； （3）存在点P ，使∠BAP=∠BCO-∠BAG ，理由：作GM ⊥AC 于点M ，作PN ⊥x 轴于点N ，如图2所示，∵点A （-4，0），点B （1，0），点C （0，-2），∴OA=4，OB=1，OC=2，∴tan ∠OAC=2142OC OA ＝＝，tan ∠OCB=12OB OC ＝，5， ∴∠OAC=∠OCB ，∵∠BAP=∠BCO-∠BAG ，∠GAM=∠OAC-∠BAG ，∴∠BAP=∠GAM ，∵点G（0，-1），OA=4，∴OG=1，GC=1，∴，••22AC GM CG OA＝142⨯，解得，，∴5 =，∴tan∠GAM=29GMAM=，∴tan∠PAN=29，设点P的坐标为（n，12n2+32n-2），∴AN=4+n，PN=12n2+32n-2，∴21322 2249n nn+-+＝，解得，n1=139，n2=-4（舍去），当n=139时，12n2+32n-2=9881，∴点P的坐标为（139，9881），即存在点P（139，9881），使∠BAP=∠BCO-∠BAG．【点睛】本题是一道二次函数综合题，解答本题的关键是明确题意，作出合适的辅助线，找出所求问题需要的条件，利用三角形相似、锐角三角函数和二次函数的性质解答．10．如图，抛物线y=ax2+bx经过△OAB的三个顶点，其中点A（1），点B（3，﹣），O为坐标原点．（1）求这条抛物线所对应的函数表达式；（2）若P（4，m），Q（t，n）为该抛物线上的两点，且n＜m，求t的取值范围；（3）若C为线段AB上的一个动点，当点A，点B到直线OC的距离之和最大时，求∠BOC 的大小及点C的坐标．【答案】（1）2235333y x x =-+；（2）t＞4；（3）∠BOC =60°，C （32，3） 【解析】 分析：（1）将已知点坐标代入y=ax 2+bx ，求出a 、b 的值即可；（2）利用抛物线增减性可解问题；（3）观察图形，点A ，点B 到直线OC 的距离之和小于等于AB ；同时用点A （1，3），点B （3，﹣3）求出相关角度．详解：（1）把点A （1，3），点B （3，﹣3）分别代入y=ax 2+bx 得3=393a b a b ⎧+⎪⎨-=+⎪⎩ ，解得2353a b ⎧=-⎪⎪⎨⎪=⎪⎩∴y=﹣22353x x + （2）由（1）抛物线开口向下，对称轴为直线x=54， 当x ＞54时，y 随x 的增大而减小， ∴当t ＞4时，n ＜m ． （3）如图，设抛物线交x 轴于点F ，分别过点A 、B 作AD ⊥OC 于点D ，BE ⊥OC 于点E∵AC≥AD ，BC≥BE ，∴AD+BE≤AC+BE=AB ，∴当OC ⊥AB 时，点A ，点B 到直线OC 的距离之和最大．∵A（1B （3∴∠AOF=60°，∠BOF=30°，∴∠AOB=90°，∴∠ABO=30°．当OC ⊥AB 时，∠BOC=60°，点C 坐标为（32 点睛：本题考查综合考查用待定系数法求二次函数解析式，抛物线的增减性．解答问题时注意线段最值问题的转化方法．。