3.10晶格的状态方程和热膨胀

合集下载

固体物理-热膨胀

0
T A , r r0
两原子间距不变，无热膨胀现象
U(r)
R
0 r
（2）非简谐效应（保留到第三项）
1 2U 2 1 3U 3 U ( R0 ) U ( R0 ) 2 3 2 ! R R 3 ! R R
B

e u kBT d

e
u kBT
d
e

( c 2 g 3 ) kBT
d
g kBT kBT c
5/ 2
3 π 4 Biblioteka 12e
( c g ) kBT
2 3
d
πk BT c
与温度有相似的规律
V

KVm
CV ,m
（书中公式7.2-17）
γ,格临爱森常数，1~3; K,体积模量，N/m2
（4）热膨胀与其他物理性能的关系
膨胀系数越大，德拜温度越__. 膨胀系数越大，硬度越__. 碱金属与过渡族金属相比，谁的膨胀系数更大？
下节课内容
•简要介绍热传导 •习题课
补充：晶体的状态方程推导热膨胀
3 g 2 kBT 4c
在非简谐效应下，有热膨胀现象。

e
u kBT
d
e

( c 2 g 3 ) kBT
d
e

c 2 / kBT
e
g 3 / kBT
d
e

c
2
g 3 k BT 1 d k T B
热膨胀和其他物理性能的联系势能曲线的不对称程度越高，热膨胀越----，而不对称程度随偏离简谐振动程度的增加而增加。（1）化学键型化学键的键强越大，膨胀系数越小。

第3章晶格振动与晶体的热学性质

温度较低: 热运动较弱——在平衡位置附近微振动,平衡位
置是晶格格点,所以称为晶格振动；晶格振动是原子的热运动，对晶体的热学性能起主要贡献。
温度较高:
热运动较强——少数原子脱离格点－热缺陷；热运动很强——整个晶体瓦解，溶解。
温度很高:
晶格振动的研究 —— 晶体的热学性质
固体热容量 ——是晶体热运动宏观性质的表现
系统有N个原胞
第2n+1个M原子的方程
第2n个m原子的方程 —— N个原胞，有2N个独立的方程
方程解的形式
—— 两种原子振动的振幅A和B一般来说是不同的
第2n+1个M原子
第2n个m原子
方程的解
—— A、B有非零的解，系数行列式为零
—— 一维复式晶格中存在两种独立的格波
—— 声学波
—— 光学波
第n个原子和第n＋1个原子间的距离
平衡位置时，两个原子间的互作用势能发生相对位移后，相互作用势能
—— 常数
—— 平衡条件
简谐近似 —— 振动很微弱，势能展式中只保留到二阶项
相邻原子间的作用力
dU f d
—— 恢复力常数
原子的运动方程:
—— 只考虑相邻原子的作用，第n个原子受到的作用力
1
声子:晶格振动中格波的能量量子声子这个名词是模仿光子而来（因为电磁波也是一种简谐振动）。声子与光子都代表简谐振动能量的量子。所不同的是光子可存在于介质或真空中，而声子只能存在于晶体之中，只有当晶体中的点阵由于热激发而振动时才会有声子，在绝对零度下，即在OK时，所有的简正模式都没有被激发，这时晶体中没有声子，称之为声子真空。声子与光子存在的范围不同，即寄居区不同。

3.3状态方程、热膨胀、热传导

nj 1 2 j Z j exp kBT n j 0

j exp 2k BT j 1 exp k T B
j exp 2k BT 系统的总配分函数： Z Z j j j j 1 exp k T B
d ln j dU 1 Ej dV V j d ln V
其中
1 Ej j 2
d ln j d ln V
exp 1 kBT
j j
是表征频率随体积变化的量，设与j无关。
dU E 晶格状态方程： p dV V d ln —— Grü neisen const. d ln V
d j dU F p dV j dV V T j 2 exp 1 k BT dU 1 1 V dj j j dV V j 2 j j dV exp 1 k BT
u(r)
du f dr
较大
0
r0
r
du 向左运动： dr
du 向右运动： dr
较小
以双原子链为例：
双原子链的振动频率,设相邻原子间的距离为a
mM 只有β依赖于链的长度2Na（链的长度相当于三维晶格的体积V），所以，上式两边求对数，并对ln(2Na)求微商得到
d ln 1 d ln 1 d ln [ ] , d ln(2 Na ) 2 d ln(2 Na ) 2 d lna d 2V (r ) (a) β实际是相邻原子势能的二次微商系数 ( ) V dr 2 (a) aV β代入γ得到 2V (a)

晶格振动与晶体的热学性质

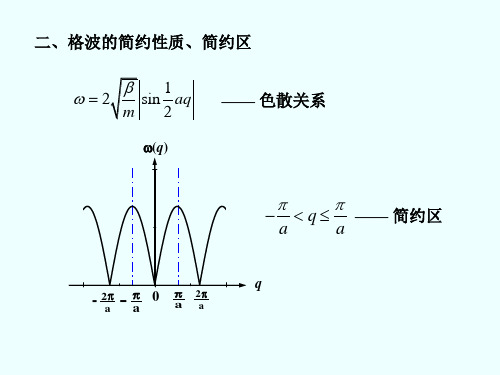
q1
2 1
2a
q2
2 2
5
2a
q2
q1
2
a

三、周期性边界条件（Born－Karman边界条件）
N+1
12
n
N N+2 N+n
N n
n
Aeit N naq Aeitnaq
eiNaq 1 ei2h 1
q 2 h
Na
h =整数
在q轴上，每一个q的取值所占的空间为 2
Na
q的分布密度：
q Na L
q0时
2
M
Mm
m
1
1
4
M
Mm m
2
sin
2
1 2
aq
M
m
1
Mm
1
4Mm
M m2
1 2
aq2
2
M
Mm
m
2Mm
M m2
1 2
aq
2
2
M m
1 2
aq
2
1 2
a
2 q q
M m
这与连续介质的弹性波＝vq 一致
当q0时
n n
q0
1
在长波极限下，原胞内两种原子的运动完全一致，振
M 2 m2 2Mm cosaq
i 1 aq
M
2
2m
cos
1 2
aq
e
2
m2 2Mm cosaq
M
m
Rei
1 aq
2
即：
2 2
－在Ⅰ、Ⅳ象限，属于同位相型
物理图象：原胞中的两种原子的振动位相基本相同，原胞基本上是作为一个整体振动，而原胞中两种原子基本上无相对振动。

晶格状态方程和热膨胀

由热力学知，压强P、熵S、定容比热CV和自由能F之间的关系为：
F U TS
dF PdV SdT
P F V T
S F T V
CV
T
S T
V
自由能F(T，V)是最基本的物理量,求出F(T，V)，其他热力
学量或性质就可以由热力学关系导出。
T=0时晶格的结合能
由晶格振动决定
相同。
表示频率为i的格波在温度T时的平均能量，而
d lni ,
d lnV
由于一般情况下， V ,
所以 0
是与晶格的非线性振动有关与i无关的常数，称为格林艾森数。
P dU 1
dV T V
i
Ei
dU dV T
E V
,
§8 晶格状态方程和热膨胀
P dU E ,
dV T V
U(R0 ) c 2 g 3
eu kBT d
e d u kBT
eu kBTd
e d
( c 2 g 3 ) kBT
g kBT 5 / 2 3 π kBT c 4
e d (c 2 g 3 ) kBT
πkBT 1 2 c
3g 4 c2
kBT
在非简谐效应下，有热膨胀现象。
K
1
dV
V dE E dV
dT dT
CV
E
dV
V0 dT
V2
V V 2 dT
上式等号右边第二项是非常小的量可略去，所以
K CV ,其中 1 dV 是膨胀系数。
V
V0 dT
VK
CV
格律乃森定律
用简谐近似理论不能解释晶体的热膨胀现象。
§8 晶格状态方程和热膨胀

计算晶格能的公式

计算晶格能的公式全文共四篇示例，供读者参考第一篇示例：晶格能是固体材料中一种非常重要的物理量，它是描述固体内部晶格结构稳定性的一个重要参数。

在固体物理学中，晶格能通常用于描述晶体中原子或离子之间的相互作用力强度，是一个评价固体结构稳定性和形变行为的重要指标。

晶格能的计算方法有多种，其中一种常用的方法是利用电子结构理论和分子动力学模拟来计算固体的晶格能。

在电子结构理论中，晶格能可以通过计算晶体中原子或离子之间相互吸引或排斥的相互作用力来获取。

具体而言，电子结构理论将固体中的原子或离子看作是受到外部势场影响的粒子，通过计算这些粒子之间相互作用的库伦势和交换-相关能来得到晶格能。

晶格能的计算公式通常可以表示为以下形式：\[E_{\text{总}} = E_{\text{能带}} + E_{\text{核}} + E_{\text{排斥}}\]\(E_{\text{总}}\)表示晶格的总能量，\(E_{\text{能带}}\)表示晶格中电子的能带结构对晶格能的贡献，\(E_{\text{核}}\)表示核之间的库伦势能和交换-相关能对晶格能的贡献，\(E_{\text{排斥}}\)表示晶格中原子或离子之间的排斥力对晶格能的影响。

在实际计算中，通常会采用密度泛函理论（DFT）来计算固体的晶格能。

密度泛函理论是一种基于量子力学原理的电子结构计算方法，通过求解固体中电子的薛定谔方程来得到晶格的总能量。

在密度泛函理论中，采用交换-相关泛函来描述电子之间的交换和相关作用，从而得到晶体的总能量。

分子动力学模拟也是一种常用的计算晶格能的方法。

通过分子动力学模拟，可以模拟固体中原子或离子的运动行为，通过计算原子或离子之间的相互作用力和位移来得到晶格的总能量。

分子动力学模拟可以更直观地模拟固体内部的结构和性质，对于探索固体的晶格能具有重要意义。

计算晶格能是一个复杂而重要的问题，涉及到多种物理量和计算方法。

通过电子结构理论、密度泛函理论和分子动力学模拟等方法，我们可以得到固体的晶格能，从而进一步了解固体结构的稳定性和性质。

晶格振动 (5.热膨胀)

r r0

e
e
f 2 k BT
d

f 2 k BT

d
g k BT

e
e
f 2 k BT 4 f 2 k BT
d

d
• 于是得 • 其中
3 g 1 r r0 k T r0 kT 2 B 2 B 4 f 2
i B
ln i ln V • Grueneisen假定这是一个对所有的振动都相同的与温度无关的常数(Grueneisen常数) • 于是压强为
U (V ) p V V i 1 2 i ei / kBT 1 i
• 即得Grueneisen状态方程

r0

• 简谐近似下，平均间距不随温度变化
• 如果用非简谐近似
U (r ) f g
2
3
1 d 2U f; 2 2 dr 0
U ( ) / k BT 0
1 d 3U g 3 6 dr 0
r e r e

d
U ( ) / k BT
非谐
简谐
r0
r
E (T )
非谐平均位置
热膨胀定量计算
• 考虑一维原子链。如果两个原子的间距为r，根据玻尔兹曼统计，温度T时原子的能量分布为
e
U ( r ) / k BT
• 那么两个原子之间的平均间距为
r

re U ( r ) / k T dr
B

e U ( r ) / k T dr
1 p 1 E B T V B T V CV cV BV B

第9讲晶格的热膨胀和热传导2

1 2
d
d ln β
ln
(
2 Na )
=
−
1 2
d ln β d ln a
(3-164)
格临爱森常数为
β
=
d 2V (r )
dr 2 a
= V(a)
2
γ
=
aV( a ) − V(a)
(3-165)
考虑到晶格势能的展开式
V (r ) = V (a + δ ) = V (a) + 1 V(a)δ 2 + 1 V(a)δ 3 + ⋅⋅⋅
∑j
n
j
+
1 2
=ω
j
j 标志各不同格波，nj 为相应的量子数。配分函数 Z 包括系统的所有量子态，因此应分别对
每个 nj ＝1, 2, …相加，从而得到
∏ ∑ ∏ Z = e−U kBT
e e =e ( ) −
1 2
=ω j
kBT
∞ −n j =ω j kBT
−U kBT
j
nj =0
j
e (−
p
=
−
∂F ∂V
T
写出晶格的状态方程，温度 T 不变
格临爱森假设
∑ p = − dU − dV
j
1 2
=
+
e=ω j
=
kBT
dωj −1 dV
上式包含了各振动频率对体积 V 的复杂的依赖关系，格临爱森针对这种情况，提出了一个
有用的近似，首先将上式写成
∑ p = − dU − dV
j
1 2
第九讲：晶格的热膨胀和热传导
如果已知晶体的自由能函数 F(T,V), V 为晶体体积，就可以根据

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

E Ei 为晶格振动总能量。
i
2.由状态方程讨论晶体的热膨胀
dU 对于大多数固体，体积的变化不大，因此可将 dV 在晶
体的平衡体积V0附近展开:
d 2U d U dU V V0 2 dV dV V0 dV V0
dU 0, dV V0
能量交换
系统达到热平衡
两个声子通过非简谐项的作用，而产生第三个声子。这可以看成是两个声子的相互碰撞，最后产生第三个声子。
声子间的相互作用遵循能量守恒和准动量守恒
1 2 3 q1 q2 q3 G h
(1) G h
qy
q1
q3 q2
5/ 2
3 g k BT 1 k T d B
c 令x k T B
1/ 2

xe
4 x2
dx
g kBT 2 kBT c
5/ 2

0
xe
4 x2
dx
g kBT 2 kBT c
0 0
T A ,r R
0
两原子间距增大，有热膨胀现象。 2.理论计算
斜率=原子间的相互作用力F
r
由玻尔兹曼 e

u k BT
d
r0处斜率相等，所以F=0 简谐近似：
u k BT
d
2
R0 处陡，F大,排斥力非简谐近似：r< r>R处平缓，吸引力小
1/ 2
0
e
a 2 x 2
1 π kBT 2 2 c
c a k T B
线膨胀系数
1 d 3 g kB 2 R0 dT 4 c R0
3 g 2 kBT 4c
显然，在简谐近似下，g=0，=0。当势能只保留到3次方项时，线膨胀系数与温度无关。若保留更高次项，则线膨胀系数与温度有关。
若只取一次方项，则
V V0 dU V V0 d 2U K V0 2 dV V0 V0 dV V
0
E dU V V0 E P K V dV T V0 V
其中K是体积弹性模量。
dp 0 )，体积随温度热膨胀是在不施加压力的情况下( dV
0
U ( r)
R0
A
T A ,r R
r
0
两原子间距不变，无热膨胀现象
（2）非简谐效应
1 2U 2 1 3U 3 U ( R0 ) U ( R0 ) 2 3 2 ! R R 3 ! R R
d
e

( c 2 g 3 ) k BT
d
g kBT kBT c
5/ 2
3 π 4
12

e
( c g ) kBT
2
3
d
πk BT c
3 g 2 kBT 4c
在非简谐效应下，有热膨胀现象。推导在后
0
1 2U 2 1 3U 3 U ( R0 ) U ( R0 ) 2 3 2 ! R R 3 ! R R
0 0
（1）简谐近似
1 2U 2 U ( R0 ) U ( R0 ) 2 2! R R
F P V T
F P V T
i k BT d i d U 1 e i k BT 1e dV T i 2 dV
i 1 d ln i dU i i kBT dV 2 e 1 dV T i d ln i dU Ei dV dV T i 1 dU dV T V d ln i Ei , d ln V i
k BT
1 i i F2 k BT ln 1 e i 2 kBT

1 i F U V i kBTln( 1 e i 2
k BT
)
由于非线性振动，格波频率i也是宏观量V的函数，所以
0
U f ( R R0 ) R (1)在简谐近似的情况下，晶格原子振动可描述为3N个线性
独立的谐振子的叠加，各振子间不发生作用，也不交换能量；
(2)晶体中某种声子一旦产生，其数目就一直保持不变，既不能把能量传递给其他声子，也不能使自己处于热平衡状态。用简谐近似理论不能解释晶体的热膨胀和热传导现象。晶体的非简谐效应：
§3－10 晶格的状态方程和热膨胀
§ 3－11 晶格的热传导
一、晶体的热膨胀和非简谐效应
简谐近似：
1 2U 2 U U ( R0 ) U ( R0 ) 2 2! R R R R0 0 1 2U 2 U ( R0 ) ( R R ) 0 2 2! R R
位置附近展开：
1.物理图象
0
R
1 2U 2 1 3U 3 U U ( R0 ) U ( R0 ) 2 3 2! R R 3! R R R R0 0 0
1 2U 2 1 3U 3 U U ( R0 ) U ( R0 ) 2 3 2! R R 3! R R R R0 0 0
微扰项
微扰项
声子间有相互作用
qx
0 ---正常过程(
N过程)；
qy
Gh
q1
碰撞前后系统准动量不变，对热流无影响。
(2)
G h 0 ---反常过程(
q3
q1 q 2
U过程)。
q2
qx
碰撞前后系统准动量变化，对热流有影响。
二、热膨胀
热膨胀：在不施加压力的情况下，晶体体积随温度变化的现象称为热膨胀。
R0 假设有两个原子，一个在原点固定不动，另一个在平衡位置R0附近作振动，离开平衡位置的位移用表示，势能在平衡
推导

e
u kBT
d
e

( c 2 g 3 ) kBT
d
e

c 2 / kBT g 3 / kBT
e
d
e

c
2
g 4 c 2 kBT e d k T B
g kBT kBT c
自由能F(T，V)是最基本的物理量,求出F(T，V)，其他热力学量或性质就可以由热力学关系导出。
晶格自由能
F1=U(V)
F2
T=0时晶格的结合能由晶格振动决定
由统计物理知道：
F2 kBT ln Z
Z是晶格振动的配分函数。
若能求出晶格振动的配分函数，即可求得热振动自由能。频率为i的格波，配分函数为：
Zi
ni 0
e

1 ( ni ) i k BT 2
e i 1e
i 2 k BT k BT
忽略晶格之间的相互作用能，总配分函数为：
e i 2 kBT Z Zi i kBT 1 e i i
F2 kBT ln Z
三、晶体的状态方程和热膨胀
1.晶体的状态方程由热力学知，压强P、熵S、定容比热CV和自由能F之间的关系为：
F U TS dF PdV SdT
F P V T F S T V S CV T T V
0
1 3U g 3 3! R R
0
U ( R0 ) c 2 g 3 (c、g均为正常数。)
(1)简谐近似：
U ( R0 ) c 2

e u k T d
B

e u k B T d

g kBT kBT c
5/ 2
5/ 2

0
xe
4 x2
dx
3 π 4

e

0
x e
2 n ax 2
1 3 5 (2n 1) π dx 2 n 1 a n a
( n 2, a 1)
c 2 / k T g 3 / k T B B

( c 2 g 3 ) k T B

e
d
e
d d
π dx 2a
1/ 2
e

c
2
3 g k BT (1 )d kBT
e

c 2 k T B

2 e
0
c 2 k T B
d
1/ 2

π kBT c
的变化。上式两边对温度T求导得：
1 dV K V0 dT V dE dV E dT dT CV E dV V2 V V 2 dT
上式等号右边第二项是非常小的量可略去，所以
CV 1 dV K , 其中是膨胀系数 V V0 dT

VK CV
格林艾森定律
C 1 dV K 。 V dT V

e
u kBT
d
e