晶体状态方程
3.5 非简谐效应(Anharmonicity)
3.5 非简谐效应（Anharmonicity)一. 简谐近似的不足二. 非简谐下的解三. 绝缘体的热导率四. 晶格状态方程和热膨胀参考：黄昆书3.10 3.11 两节Kittel8 版5.2 5.3 两节一.简谐近似的不足；非简谐项和热膨胀效应。
在简谐近似下，我们描述了晶体原子的热运动，并以此图像解释了固体热容、离子晶体的光学及介电性质，下一节还将用来解释辐射波和晶体的相互作用问题。
简谐近似下的晶体，每个简正振动模将完全独立于所有其它振动模而传播，并且可以应用叠加原理，这样的晶体我们可称作简谐晶体。
但这种简谐晶体的一些性质却和实际晶体完全不同，是我们过于理想化的结果。
然而在简谐近似下，得出了一些与事实不符合的结论：1.没有热膨胀；2.力常数和弹性常数不依赖于温度和压力；3.高温时热容量是常数；4.等容热容和等压热容相等C V = C P5.声子间不存在相互作用，声子的平均自由程和寿命都是无限的。
或说：两个格波之间不发生相互作用，单个格波不衰减或不随时间改变形式。
6.没有杂质和缺陷的简谐晶体的热导是无限大的。
7.对完美简谐晶体而言，红外吸收峰，Raman 和Brilouin 散射峰以及非弹性中子散射峰宽应为零。
以上结论对于实际晶体而言，没有一条是严格成立的。
简谐近似,势能为抛物线，两边对称。
a r 0见Peter Bruesch Phonons ：Theory and Experiments Ⅰ对实际晶体而言，它们反抗把体积压缩到小于平衡值的能力要大于反抗把体积膨胀时的能力，所以势能曲线是不对称的，振幅增大，原子距离增大，这是发生热膨胀的根源。
0()a T a δ=+见Kittel p892l G aπ=二维正方晶格中正常声子碰撞过程k1+k2 = k3二维正方晶格中倒逆声子碰撞过程k1+ k2= k3 + G l可以把倒逆过程看成是：一个声子被布喇格反射、同时伴随着吸收或发射另一个声子。
在任一声子碰撞过程中，没有什么进入或离开晶体，总动量是守恒的，我们认为动量和声子有关只是对晶体总动量的一种人为分割，是为了方便讨论问题而引入的。
3-2晶格热容和三大模型
2
1 hω0 − exp − 2k BT
2
hω0 1 ≈ 3Nk B 3Nk ⋅ 2 k BT hω0 hω0 −1+ 1 + 2k BT 2k BT
= 3Nk B
在低温下： 在低温下：T << ΘE 即
2
k BT
§3.6 晶格热容
一、晶格振动对热容的贡献
1 个简谐振子的能量本征值： 第j个简谐振子的能量本征值： E j = n j + hω j 个简谐振子的能量本征值 2
在一定温度下，频率为ω 的简谐振子的统计平均能量： 在一定温度下，频率为ωj的简谐振子的统计平均能量：
n jhω j ∑ n jhω j exp − k T nj 1 B E j = hω j + 2 n jhω j ∑ exp − k T nj B
4
3
4! ∑ n ⋅ n5 n =1
3
∞
1 π4 ∑ n 4 = 90 n =1
∞
12π Nk B T ∝T3 CV = 5 ΘD
这表明， 这表明，Debye模型可以很好地解释在很低温度下 模型可以很好地解释在很低温度下 晶格热容C 的实验结果。 晶格热容 V ∝ T3的实验结果。 用Debye模型来解释晶格热容的实验结果是相当成功 模型来解释晶格热容的实验结果是相当成功 近似就越好。 的，尤其是在低温下，温度越低，Debye近似就越好。 尤其是在低温下，温度越低， 近似就越好
ΘD (K) 209 445 630 343 470 320 374 200 71.9
元素 Ir K Li La Mg Mn Mo Na Ni
晶格常数变化方程
晶格常数变化方程全文共四篇示例，供读者参考第一篇示例：晶格常数是固体晶体结构中一个非常重要的物理量，它反映了晶格结构的特征。
在晶体结构中，原子排列有一定的规律性，晶格常数就是描述这种规律性的参数。
晶格常数的变化不仅可以影响晶体的性质，还可以反映出晶体内部的结构变化。
晶格常数变化方程是描述晶格常数随外界条件变化的数学表达式，它可以通过实验和理论计算得出。
晶格常数变化方程通常可以通过以下几种方法求解：1. 实验测量法实验测量是最直接的获取晶格常数的方法之一。
通过X射线衍射、电子衍射等技术，可以测定晶体的晶格常数。
实验测量法可以获得很高的精度，但受到实验条件和设备的限制，往往需要先验知识和经验来选择实验方案。
2. 理论计算法理论计算是通过物理模型和计算方法，推导晶格常数与晶体结构之间的关系。
常用的计算方法包括密度泛函理论、分子动力学模拟等。
理论计算法可以考虑更多的因素和复杂的情况，可以预测晶格常数的变化规律。
a = a0 + Δaa为晶格常数，a0为初始晶格常数，Δa为晶格常数的变化量。
晶格常数的变化量可以由外界条件引起，比如温度、压力、应力等。
晶格常数的变化方程可以通过实验或理论计算得到，并反映出晶体内部的结构变化。
在实际应用中，晶格常数的变化方程对材料科学、物理化学等领域都具有重要意义。
晶格常数的变化可以直接影响材料的力学性能、热学性能、电学性能等。
通过研究晶格常数的变化方程，可以优化材料的性能，提高材料的应用价值。
晶格常数变化方程是研究晶体结构和性质的基础性内容，它可以揭示晶体结构的特征和变化规律，为材料科学和物理化学领域的发展提供重要参考。
通过实验测量和理论计算，可以获得不同条件下晶格常数的变化规律，为材料设计和性能优化提供重要理论依据。
【晶格常数变化方程】的研究具有广泛的应用前景和科学意义。
第二篇示例：晶体是由大量原子或分子按照一定规律有序排列而成的固体结构。
在晶体中，原子或分子之间存在一定的间距，这个间距被称为晶格常数。
晶体的状态方程
晶体的状态方程整理：侯柱锋houzf@2005年8月13日摘要晶体的状态方程(Equation of State,EOS)在基础和应用科学中具有重要的意义。
比如平衡体积(V0)，体弹性模量(B0)及它的一阶导数(B 0)这些可测的物理性质直接与晶体的状态方程有关。
在高压下的状态方程有好几种不同函数形式来描述，比如Murnaghan方程、Brich-Murnaghan(BM)方程和普适方程等。
目录§1Murnaghan状态方程2§2Brich-Murnaghan状态方程2§3普适状态方程(Universal EOS)2§4状态方程的拟合程序31§1Murnaghan 状态方程Murnaghan 状态方程由Murnaghan 在1944提出的[1]，总能(E )和体积(V )的函数关系在Murnaghan 状态方程中描述为：E (V )=B 0V 0B 01B 0−1V 0VB 0−1+V 0V−B 0B 0−1 +E coh(1)其中E coh 是晶体的结合能。
压强(P )根据P (V )=−∂E (V )/∂V 计算得到，因此Murnaghan 状态方程也可以表示为如下的形式P (V )=B 0B 0 V 0V B−1 (2)体弹性模量由上面等式对体积的导数而得到，B =−V (∂P/∂V )，B (V )=B 0(V 0V)B 0(3)§2Brich-Murnaghan 状态方程该状态方程是由Brich[2,3]把Gibb’s 自由能按Eulerian 应变( )进行展开得到的，其中V 0V =(1−2 )3/2三阶BM-EOS 的能量－体积关系为：E (V )=−916B 0 (4−B 0)V 30V 2−(14−3B 0)V 7/30V 4/3+(16−3B 0)V 5/30V2/3+E 0(4)根据计算得到的V-E 数据点按上面的等式采用最小平方差拟合得到B 0，B0和V 0，静压力P 可以由BM-EOS 的P −V 函数形式得到，也就是上面等式对体积的导数。
sec24
i
2
e
i
B
1
• 求和号内的正是平均能，于是得Grueneisen状 态方程 U (V ) E p
V V
* 晶体体积增大时，ω(q)随V增大而减少？ 所以这个常数大于零。 * 但实际上Grueneisen常数与温度有很弱的关系
http://10.107.0.68/~jgche/ 非简谐效应
http://10.107.0.68/~jgche/ 非简谐效应
2
第24讲、非简谐效应
1. 2. 3. 4. 简谐近似的局限 原子平均间距 晶体状态方程 热膨胀与Grueneisen常数
5. 热传导 6. 晶格振动的相互作用（声子语言） 7. 晶体热传导系数
http://10.107.0.68/~jgche/
re U ( r ) / k BT dr e
U ( r ) / k B T
dr
9
非简谐效应
• 如果用简谐近似
1 1 2 2 U ( r ) r r0 2 2
变换r r0
• 因为U是δ r 的偶函数
U ( ) / k T r e d 0
U (r )
非谐
简谐
r0
r
E (T )
非谐平均位置
非简谐效应
8
热膨胀定量计算
• 考虑一维原子链。如果两个原子的间距为r，根 据玻尔兹曼统计，温度T时原子的能量分布为
e
U ( r ) / k BT
• 那么两个原子之间的平均间距为
r
http://10.107.0.68/~jgche/
i B
U
3N
i
黄昆方程和非简谐振动
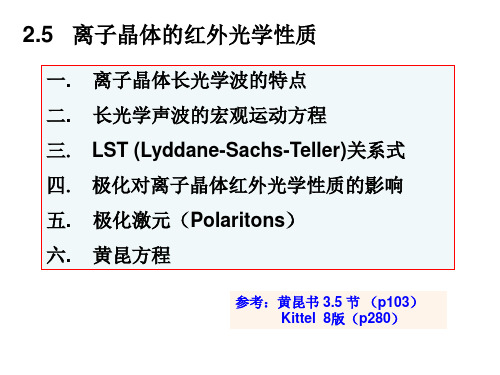
参考Kittel 8版 p264
五. 极化激元（Polaritons) （电磁激元）
由于光子是横向电磁场量子，光照射离子晶体时将激发 横向电磁场，从而对离子晶体中光频支横波振动产生影响， 特别是当光子频率ω = cq和横波光学支声子的频率ω T相近时， 两者的耦合很强，其结果将使光子与TO声子的色散曲线都发 生很大的变化，形成光子－横光声子的耦合模式，其量子称 作极化激元。它是离子晶体中的一种元激发。由于ω= ωT 时， 对应的光子波数与Brillouin 区的尺寸相比为小量，因此极化 激元是长波横向光学声子与电磁场的耦合量子。 基于极化激元特点：它是两种模式耦合的结果，又是晶 体中一种特有的集体运动模式。因而受到更多的关注。
*
假定： E eff E0eit
只考虑长波，令q＝0
和2.1节相比，这里考虑的是受迫振动。我们只考虑 q＝0 解。
只考虑长波情形，即 q→0，所有原子都有相同位移时： ②
u u0 eit u u0 eit
(2 M 2 )u0 2 u0 eE0 2 u0 (2 M 2 )u0 eE0
·
光学支色散关系 声学支色散关系
q
但横光子不与纵光学声子发生耦 合作用，垂直入射不能激发LO声 子。
一. 离子晶体长光学波的特点：
离子晶体由正负离子组成，例如 NaCl 。离子晶体的长光 学波描述的是原胞内正负离子之间的相对运动，因此在波长较 大时，半个波长范围内可以包含许多个原胞，在两个波节之 间同种电荷的离子位移方向相同，异性电荷离子位移方向相 反，因此波节面就将晶体分成许多薄层，在每个薄层里由于异 性电荷离子位移方向相反而形成了退极化场 Ed，所以离子晶 体的长光学波又称极化波。 由后面两张图可以清楚地看出：离子晶体长光学波的极化 对纵波和横波的影响是不同的，纵波的极化场增大了原子位移 的恢复力，从而提高了振动频率，而横波的极化场对频率基本 没有影响，所以离子晶体中，
第二章 晶体生长热力学2
晶体小时应考虑其表面能。设晶体为半径为R的球，体化学势为μs，比表面能 为γ，介质化学势为μm。若体系有δ N由介质转化为晶体，
m ( P0 , T )N s ( P0 , T )N dA N V s 2V sN dA d (4R ) 8R 2 4R R 2V s m ( P0 , T ) s ( P0 , T )
得到单形出现顺序：｛111｝， ｛100｝， ｛110｝，„„
2. 东内－哈克（Donmy-Harker）定律（例外情况）
黄铁矿FeS2的空间群为Pa3，按布－弗定律，立方简单格子构造的 晶体外形应当显示{100}，{110}等单形的晶面，但实际上，晶体最发达
的单形是111}，{100}，{210}，很少出现{110}
推论：面间距dhkl较大的点阵平面在晶体凸多面外形上占有较大比例，面网密度较 大的面易留下。 注意：若晶体的单胞带心（体心、面心、底心，侧心）某些点阵面间距地有效 面间距比相应的点阵周期要减半。 对各种布拉维格子，满足面间距减半的条件如下： 格子类型
dhkl减半条件
I－格子
h+k+l=奇数
F－格子
h,k,l三者奇偶混杂
自由生长系统中，各晶面的生长速率不同，各向异性，
其结果生长形态的差异 晶面淘汰率：晶面互相竞争，快面隐没，慢面显露 线性生长速率R：单位时间里晶面（hkl）沿法线方向平 行推移的距离 晶体生长形态的变化各晶面生长相对比值的改变 以二维晶体生长为例：
以二维模式晶体生长为例：
R01 l01 l l 2 11 , 01 2 R11 R01 2 2 2
基本思路：
结构→周期键链→主要晶面附着能→晶体生长形态 附着能的计算是关键
Grüneisen状态方程中所用假设的讨论
∑ｙ ｆ ｃ
ｙ＝
Ｃ ，
０ Ｊ ｊ
是 不能轻 易利 用 晶体 状态 方程 （ ） 中的热 压 项来 １式
（ １ ２）
，
计 算热压 的 ． 该说 ， 应 上述分 析 可 以帮 助大家更 深入 地 理解 晶体 的状 态方 程．
这儿 的 就是 格林 乃 森参 数 的晶格 动力 学定 义 ． 利用 （ １ 式 ，ａｅ Ａ等 人发 现对 于硅酸 镁 钙钛 矿来 ２ ） Ｐｔ ｌ
．
（ １一
（ ２ １）
（８０ １０ Ｋ）＝ ． ６ ， 以在 １０ 时 ， ４ ９ 所 ８ ０Ｋ
由此 ， 晶体 自由能 的表达式 可 以写 为
Ｆ ＝Ｅ ｒ＋Ｅ ＋Ｆ ５ ｚ 埘． （３ １）
ｑ＝ ． ６ 而在 １０ ０９ ； ０ ０ Ｋ时 ， ０ ６ ． ｑ＝ ． ２ 当然 ， 随着 温度
设 ｔ 似 所 的 动 相 ，对 个 设 ｆ 对 有 振 都 同而 这 假 Ｏｏ ｊ １， ｎ１近
、 Ｏｌ ｎ ，Ｔ
所表现 出来 的热 力学意义 ， 以及这个假 设在 多大程度 上成立 ， 现行 的固体物理学教材 中没有做 出具体 的 解释． 文 从 晶体 状 态 方程 的 最 普 遍 形 式 出发 ， 本 对
这 儿 的 表示 晶格 的振 动能 （ 热能 ） 但 在最 近 的文 ， 献 中一般都 以 代 替 ］在 以下 的推 导 中 ， ， 一律 用Ｅ 册代指热 能 ． 了进 一步 了解 （ ） 成立 的基本 为 １式
们 可 以从 下 面的关 系式 中清 晰看 ／ ｆ ，
前提， 首先考虑晶体状态方程 的最普遍的形式
这儿 的 Ｅ 是 原 子 静 止 在 平 衡 位 置 时 的 能 量 ， 温 与
晶体计算公式
晶体计算公式
晶体计算是一种基于量子力学的新型计算模式,利用晶体内部原子的量子态进行运算。
与传统计算机相比,晶体计算具有更快的运算速度和更低的能耗。
下面是一些常见的晶体计算公式:
1. 薛定谔方程
薛定谔方程描述了量子系统的时间演化,是量子力学的基本方程。
在晶体计算中,我们需要求解晶体内原子的量子态,薛定谔方程就是必不可少的工具。
2. 布洛赫方程
布洛赫方程描述了晶体中电子在周期性离子晶格中的运动。
它是描述晶体内电子能带结构的基础。
3. 密度泛函理论
密度泛函理论是一种计算电子结构的有效方法,在晶体计算中被广泛应用。
它使用电子密度而不是波函数来描述多体系统,大大简化了计算。
4. 库仑相互作用
库仑相互作用描述了带电粒子之间的相互作用力,是晶体计算中不可忽视的一个因素。
5. 自旋-轨道耦合
自旋-轨道耦合描述了电子自旋和轨道运动之间的耦合作用,在处理一些含有重元素的晶体时非常重要。
这些公式描述了晶体内部的量子行为,为进行晶体计算奠定了理论基础。
随着量子计算技术的发展,晶体计算将有望在未来发挥重要作用。
晶体的状态方程
热力学第零定律 dU= TdS－pdV
日常生活中接触的宏观物体是由大量微观粒子构成的，大量微观粒子的无规则运动称作物质的热运动。 熵的物理本质是体系内部的混乱度的度量 不可能从单一热源取出热使之完全变为 --配分函数，对所有的能级相加。 处于同一热平衡状态的体系，必定具有某一共同性质，表征这个物理性质的物理量就是温度 --配分函数，对所有的能级相加。 等函数，都是重要的热力学性质。
第 一 类 永 动 机
热力学第二定律（熵增原理）
不可能从单一热源取出热使之完全变为 功，而不发生其他的变化。 熵的物理本质是体系内部的混乱度的度量
S
i
(Qi
Ti
)R
热力学第三定律
任何均匀物质在内部完全平衡条件下， 在绝对零度时，其熵值为零。另外一种描 述是绝对零度不能达到。
在0 K时，任何完整晶体的熵等于零：
基本函数是内能U和熵S，它们具有明确的物理意义，而其他三个函数H、F、G是基本状态函数的组合。 由系统状态唯一确定的热力学量，称为热力学函数。
三个热力学体系 状态函数表征和确定体系状态的宏观性质。 处于同一热平衡状态的 当晶体体积V改变时，格波的频率也要变化。
格临爱森近似计算
达到平衡，则这 dH= TdS＋Vdp 体系，必定具有某一共 另外一种描述是绝对零度不能达到。 两个体系彼此间 Fe的体心立方晶格结构
基本函数是内能U和熵S，它们具有明确的物理意义，而其他三个函数H、F、G是基本状态函数的组合。
同性质，表征这个物理 熵的物理本质是体系内部的混乱度的度量 处于平衡 由系统状态唯一确定的热力学量，称为热力学函数。 性质的物理量就是温度 G = U + pV – TS = H – TS
固体物理名词解释
固体物理名词解释本文介绍了固体物理中的晶体结构和相关名词解释。
晶体是由内部组成粒子（原子、离子或原子团）在微观上有规则的周期性重复排列构成的固体。
晶体结构是指晶体中实际质点（原子、离子或分子）的具体排列情况，是决定固态金属的物理、化学和力学性能的基本因素之一。
所有晶体具有的共通性质包括自限性、最小内能性、锐熔性、均匀性和各向异性、对称性、解理性等。
单晶体的内部粒子的周期性排列贯彻始终，而多晶体由许多小单晶无规堆砌而成。
晶体结构中的基元是晶体结构的基本单元，格点是基元的代表点，空间点阵是晶体结构中等同点（格点）的集合，其类型代表等同点的排列方式。
倒易点阵是由被称为倒易点或倒易点的点所构成的一种点阵，它也是描述晶体结构的一种几何方法，它和空间点阵具有倒易关系。
原胞是在晶体结构中只考虑周期性时所选取的最小重复单元，WS原胞即Wigner-Seitz原胞，是一种对称性原胞。
晶胞是在晶体结构中不仅考虑周期性，同时能反映晶体对称性时所选取的最小重复单元。
原胞基矢是原胞中相交于一点的三个独立方向的最小重复矢量，晶胞基矢是晶胞中相交于一点的三个独立方向的最小重复矢量，通常以晶胞基矢构成晶体坐标系。
晶体结构中全同原子构成的晶格称为布喇菲格子或单式格子，由两种或两种以上的原子构成的晶格称为复式格子。
一个晶胞只含一个格点则称为简单格子，此时格点位于晶胞的八个顶角处；晶胞中含不只一个格点时称为复杂格子，其格点除了位于晶胞的八个顶角处外，还可以位于晶胞的体心（体心格子）、一对面的中心（底心格子）和所有面的中心（面心格子）。
倒格子是晶格经过傅里叶变换所得到的几何格子，其中倒格子基矢可以用公式（1）和（2）表示，其中2πρ是一个常数，a和b是正格子基矢，且b= a×a。
倒格子空间是正格子的倒易空间。
布里渊区是倒空间中由倒格矢的中垂面所围成的区域，其中第一布里渊区是倒格矢的中垂面所围成的最小区域，是倒空间中的对称性原胞。
结晶动力学avrami方程
结晶动力学Avrami方程1. 简介结晶动力学是研究物质从亚稳态向稳态转变的过程。
在材料科学、地球科学、化学工程等领域，结晶动力学的研究对于理解和控制材料的性能具有重要意义。
Avrami 方程是描述结晶过程中晶体生长速率与时间关系的数学模型，由Sergei Avrami于1939年提出。
2. Avrami方程的推导假设在结晶过程中，物质从初始状态开始，经过一段时间后形成了晶体。
Avrami 方程描述了这个过程中晶体形成的速率与时间的关系。
考虑一个简化模型，假设结晶是在均匀各向同性条件下进行的，并且每个结晶核都具有相同的生长速率。
此外，假设结晶是以立方体为单位进行生长，并且生长速率与已经形成的晶体数量成正比。
根据以上假设，可以得到Avrami方程：V=1−e−kt nV0其中，V表示已经形成的晶体数量，V0表示总共需要形成的晶体数量，k为结晶速率常数，t为时间，n为Avrami指数。
3. Avrami方程的物理意义Avrami方程的形式说明了晶体生长速率随时间的增加而减小。
方程中的指数n决定了晶体生长过程的性质。
当n=1时，Avrami方程变为：V=1−e−ktV0此时，Avrami方程描述了一维线性生长过程。
在这种情况下，晶体生长速率与时间成正比。
当n=2时，Avrami方程变为：V=1−e−kt2V0此时，Avrami方程描述了二维面状生长过程。
在这种情况下，晶体生长速率随时间的平方增加。
当n=3时，Avrami方程变为：V=1−e−kt3V0此时，Avrami方程描述了三维体积生长过程。
在这种情况下，晶体生长速率随时间的立方增加。
通过改变Avrami指数n的值，可以控制晶体生长过程的形态和速率。
4. Avrami方程在实际应用中的意义Avrami方程在材料科学和化学工程中具有广泛的应用。
通过实验测量晶体生长过程中已经形成的晶体数量和时间，可以拟合Avrami方程，从而确定结晶速率常数k和Avrami指数n。
晶体的状态方程
整理：侯柱锋 houzf@ 2005 年 8 月 13 日
摘 要
晶体的状态方程(Equation of State, EOS)在基础和应用科学中具有重要的意义。 比如平衡体积(V0 )， 体弹性模量(B0 )及它的一阶导数(B0 )这些可测的物理性质直接与晶体的状态方程有关。在高压下的状态 方程有好几种不同函数形式来描述， 比如Murnaghan方程、 Brich-Murnaghan(BM)方程和普适方程等。
参考文献
[1] F. D. Murnaghan, Proc. Natl. Acad, Sci. 30, 244 (1944). [2] F. Brich, Phys. Rev. B 71, 809 (1947). [3] F. Brich, J. Geophys. Res. 83, 1257 (1978). [4] T. Tsuchiya and K. Kawamura, J. Chem. Phys. 114, 10086 (2001). [5] P. Vinet, J. Ferrante, J. R. Smith and J. H. Rose, J. Phys. C: Solid State Phys. 19, L467 (1986). [6] P. Vinet, J. H. Rose, J. Ferrante, and J. R. Smith, J. Phys.: Condens. Matter 1, 1941 (1987). [7] J. P. Poirier, Introduction to the Physics of the Earth’s Interior (Cambridge University Press, 2000, 2nd ed.) [8] N. Sata, G. Shen, M. L. Rivers and S. Sutton, Phys. Rev. B 65, 104114 (2002).
固体物理教学课件：Chapt3-6
3、格律乃森方程：
由热力学定律可知：
∑ P =
−
∂F ∂V
T
∑ ( ) = − dU 0 −
dV
= − dU 0
∂kBT −
qs
ln(1 − e−ωs (q)/kBT )
dV
∂V
e−ωs (q)/kBT dωs q
1− e qs
−ωs (q)/kBT
dV
∑ = − dU 0 dV
−
qs
ωs (q) 1
∂U V (T ,V
∂T
)
V
= γ CV
CV : 晶体定容比热
=
−V
∂P ∂V
T
1 V
∂V ∂T
P
= κα
κ : 体积弹性模量
α : 热膨胀系数
考虑热力学关系：
∂P ∂V ∂T = −1 ∂V T ∂T P ∂P V
γ = καV 1-3之间
CV
关于热力学关系
∂P ∂V
π
−∞
a
1
∫ ∫ 分母 ≈
∞
e− fδ2
kBT (1 +
gδ3
)dδ
∞
= e− fδ2 kBT dδ
−∞
kBT
−∞
=
πkBT f
2
δ
3 4
g f2
kBT
> 0,
线膨胀系数=α
1= dδ a dT
3 gkB , 4 f 2a
更高次项展开，膨胀系数将依赖于温度
M2
V = Na
q = 2πh , Na
qa = 2π h ，与a无关
N
γ = − d ln ωs (q) = − 1 d ln ω2 (q)
碳酸钙和醋酸的离子反应方程式
碳酸钙和醋酸的离子反应方程式碳酸钙和醋酸反应是一个重要的化学反应，也是一个非常常见的化学反应。
碳酸钙和醋酸反应即碳酸钙（CaCO3）与醋酸（CH3COOH）反应，反应的中间物是水酸化钙（Ca（HCO3）2），反应式如下：1. 化学方程式：CaCO3 + 2CH3COOH = Ca（HCO3）2 + H2O + CO22. 离子反应：Ca2+ + 2HCO3- + 2CH3COO- = Ca2+ + 2H2O + 2CO32-3. 部分晶体方程式：CaCO3 (s) + 2CH3COOH (aq) = Ca（HCO3）2 (aq) + H2O (l) + CO2 (g)4. 物质平衡：K = [Ca2+].[HCO3-]2/[CH3COO-]2该反应可以进行分析，得到反应速率的定义、状态方程和部分晶体方程式，而实际的反应流程，是碳酸钙作为沉淀物，在溶液中存在于比较稳定的状态；当溶解在醋酸的酸性条件下时受影响，同时碳酸钙也能产生难溶盐水杨酸钙；由于水酸化钙的电离比较强，故溶液中的碳酸钙转化为水杨酸钙很快，而这一过程又伴随着二氧化碳、水的释放，所以这一化学反应又被称为气体反应。
该反应的速率取决于物质的浓度，越浓的溶液的反应速率越快；另外，反应速率会随着温度的升高而增加，不同物质的反应速率差距也比较大。
此外，由于碳酸钙物质具有结晶能力，溶解碳酸钙时会把碳酸钙物质转变为液体，从而影响碳酸钙溶解度和反应速率；采用醋酸溶解碳酸钙时，酸性容易与碳酸钙反应，而不容易与水解，从而使反应速率加快。
总之，碳酸钙和醋酸反应是一种重要的化学反应，可以激发出大量的化学能量，通过变化的溶液浓度、温度，以及醋酸和碳酸钙之间的电离，可以实现反应速度的大幅增加。
使用正确的反应条件，可以实现快速的反应。
gs状态方程
gs状态方程
GS状态方程，全称为Gibbs state equation，是描述物质状态变化的基本方程之一。
它通过描述物质的热力学性质和相互作用来揭示物质的状态。
GS状态方程的核心思想是熵增原理，即在一个孤立系统中，熵总是朝着增加的方向发展。
GS状态方程可以用来解释物质在不同条件下的相变行为。
例如，当温度升高时，晶体物质通常会变成液体，液体又会变成气体。
这种相变行为可以通过GS状态方程来解释。
根据GS状态方程，当温度升高时，物质的熵会增加，这会导致物质从一个有序的状态转变为一个无序的状态。
除了描述相变行为，GS状态方程还可以用来描述物质的热力学性质。
例如，通过GS状态方程，我们可以计算出物质的焓、熵和自由能等热力学量。
这些热力学量可以用来描述物质的稳定性和反应性。
通过对GS状态方程的研究，科学家们可以预测和控制物质的性质，从而开发出各种应用。
GS状态方程在化学、物理和材料科学等领域都有广泛的应用。
例如，在化学反应中，GS状态方程可以用来描述反应的平衡条件。
在材料科学中，GS状态方程可以用来研究材料的结构和性能。
在物理学中，GS状态方程可以用来解释物质的热力学行为和相变现象。
GS状态方程是描述物质状态变化的重要工具，它揭示了物质的热力
学性质和相互作用。
通过对GS状态方程的研究，我们可以深入理解物质的行为，并应用于各个领域。
这一方程的应用不仅推动了科学的发展，也为人类创造了丰富多样的生活。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1、状态方程：处于热力学平衡状态下均匀系统 状态参量之间的函数关系。例如理想气体状态 方程是指理想气体的状态参量(P，V、T)之间 的关系。
2、热膨胀：是指温度升高时，物体在压强不变 下发生长度、面积和体积增加的现象。对于气 体，由气体状态方程可知，压强不变情况下， 气体体积随温度长高而增加；对于液体和固体， 在平衡位置附近作热振动的粒子间的平均距离 随温度而改变，温度越高，距离越大。
P dU E ,其中 d ln 是格临爱森常数。
dV V
d lnV
三、晶体热膨胀现象
热膨胀：是指温度升高时，物体在压强不
变下发生长度、面积和体积增加的现象。
对于气体，由气体状态方程可知，压强不变情况 下，气体体积随温度长高而增加； 对于液体和固体，在平衡位置附近作热振动的粒 子间的平均距离随温度而改变，温度越高，距离 越大。
1 V0
( V T
)P
1 ( V )
V P
B
1
V ( P V
)T
V
(
2F V 2
)T
二、晶体状态方程——格林爱森状态方程
1、晶格自由能F（T，V） 自由能函数一般写成：
F=-KBTlnZ…………(1)
Ei
Z为配分函数， Z e kBT ......(2)
热膨胀示意图
U
3
Uf(rx))
rV00 V0 V
V
3. 0.6
dU 0
dU
dV 0
dV x
1.6
dU ( dV )V0
0
T增加时，E升高;
则( dU ) E 0;
dV V
从图中可见，这表 示体积必须发生一 定膨胀V ，才能 使图线达到一定的 正的斜率。
体热膨胀系数α的规律
ln 1 ln 1 ln H
2
2
lnV ln(2Na) ln(2N ) ln a
均为0。
d ln 1 d ln 1 d ln H
2
2
d lnV d ln(2Na) d ln(2N ) d ln a
d ln d ln
d lnV dV d lnV j dV
j dV
P dU
dV
j
1 2
j
e
j kBT
j
1
1 V
d ln j
d lnV
晶格平均振动能 E
格临爱森提出：它是表征ωj随V变化的量（无量纲）。 假设它近似对所有振动相同，可以得到格临爱森状态方程：
定的γ值一般在1-2之间。
（2）热膨胀原因分析
我们以一维双原子为例来分析产生热膨胀的原因。
对于一维双原子体系：
用H替代
2
M m Mm
1
1
4Mm (M m)2
sin2
aq
2
H
aq n , N n N
N2
2
V 2Na
（2）热膨胀原因分析
进行一泰般勒展V开V0 。比较小，所以可以在V0附近对
dU dV
dU dV
dU ( dV )V0
d 2U ( dV 2 )V0 V
高阶项
dU dV
E V
, ( dU dV
)V0
0
d 2U ( dV 2 )V0 V
E 或 V V V0
V0
(
d 2U dV 2
)V0
主要内容
前面用简谐近似讨论晶格振动对比热的 贡献。这一节主要讨论与非谐效应有关的热 膨胀问题并讨论计入非谐项后的状态方程。 主要内容有：
一、基本热力学关系式
二、晶体状态方程——格林爱森状态方程 三、晶体热膨胀现象
(1)格林爱森关系；(2)热膨胀原因分析。
一、基本热力学关系式
晶格热力学基本关系中，晶格自由能是最基 本的物理量，一旦求出晶格自由能F，则从：
dF dU d(TS) PdV SdT
式中，通过求
P F V T
可得到状态方程
f(P,V,T)=0。从状态方程可求出一些热力学参数
和弹性力学参数，如：
热力学参数和弹性力学参数
线膨胀系数 体膨胀系数 压缩系数 弹性模量
L
1 L0
L ( T )P
V
（1）格林爱森定律 （2）热膨胀原因分析
（1）格临爱森定律
格临爱森状态方程： P dU E
dT V
令P 0,则 dU E .
dV V
设V0为平衡晶格体积，则(
dU dV
） V0
0
分析：T升高时，
E
增大，则
dU dV
0
表明晶体体积要发生
一定的膨胀 V 。
描述体膨胀的物理量：晶体体胀系数α
( E ) V
体热膨胀系数α的规律
静止晶格的体弹模量K
0＝V0
(
d 2U dV 2
)V0
;
d( V )
则体胀系数
V0 dT
K0
1 V
E ( T )V0
CV
K 0V
CV 称格临爱森定律。
K 0V
表示当温度变化时，热膨胀系数近似与晶格热容量成比
例，对很多固体材料的测量证实了这一关系，由实验确
d lnV 2d ln a
（2）热膨胀原因分析
(
d
2U dr
(r
2
)
)a
U(a);
ln lnU(a);
d ln
d lnU(a) d lna 1
a
U(a )
U(a
)
a 2
U(a) U(a)
这里，U(r) U(a ) U(a) 1 U(a) 2 1 U(a) 3 ......
2
6
简谐近似
非谐效应
可见，实际热膨胀是由原子间非谐作用引起的。
当γ=0时，不发生热膨胀现象。
非谐作用和简谐近似的U(r)图
U
3
a
Uf(rx))
Vr
3.
0.6
x
1.6
(1)简谐近似的图线(虚线 ）：关于r=a对称；
(2)非谐作用使得U(r)不完全对称：
δ<0一侧，图线更陡斜——表明相互作用更强； δ>0一侧，图线更平缓——表明吸引作用减弱。
连加是对所有晶格的 能级Ei相加。
这里，Ei除包括原子处于格点位置时的平衡晶格的能 量U（V）外，还有各格波的振动能量，即：
Ei U (V )
j
(nj
1 )
2
j
..........
..(3)
(3)式代入(2)式
[U
3
N
(
n
j
1 2
)jBiblioteka ]jZ e
kBT
nj 0
格林爱森状态方程
U
1 2
j
n j j
Z e kBT e kBT [ e ] kBT
j
nj 0
F
kBT ln Z
F
U
Z e kBT
j
1 2
j
e kBT [
1 ] j
1 e kBT
U kBT
j
[1
j
j
ln(1 e kBT
)].........(4)
2 kBT…………即P138的（3-158）式
F
P
( V
)T
格林爱森状态方程
P dU
dV
j
1
( 2
j
) d j .........5()
dV
e kBT 1
d ln j d ln j dV 1 d j V V d j