实际流体恒定总流的伯努利方程讲解
浅析气体动力学原理——伯努利方程例解

浅析气体动力学原理——伯努利方程例解气体动力学作为一门研究物体运动的科学,是研究物理学的重要组成部分。
在气体动力学中有许多定律,伯努利方程是其中最基础也最重要的定律之一。
本文将对伯努利方程的原理及其在例题中的解法进行浅析。
一、伯努利方程原理伯努利方程(Bernoulli equation),又称为贝纳方程,是气体动力学的基本方程,由拉丁物理学家Daniel Bernoulli于1738年发现,他发现在一个恒定的系统中,当沿着系统上流动的流体(一般情况下是气体)改变速度和高度,其内能总量是不变的,这一定律叫做伯努利定律。
伯努利方程可以概括为:P +γV +gh = k(γ是气体的比容系数,V是气体流速,h是气体高度,P是气体压强,g是重力加速度,k是常数)式中,其中P +γV体现了气体的动能,gh表示气体的位能,两者之和即为气体的总能量,而k则表示该总能量在系统中是恒定的。
二、伯努利方程在例题中的解法1.设有一个气体在一定的容器中,容器的高度是 h1,而此时气体的压强为P1,流速为V1,则由伯努利方程可知:P1 +γV1 +gh1 = k2.气体流出容器时,留下来的气体高度为h2,压强为P2,流速为V2,由伯努利方程可知:P2 +γV2 +gh2 = k3.上面两公式代入可得:P1 +γV1 +gh1 = P2 +γV2 +gh24.两边中的P1,V1,h1分别消去可得:P2 =γ(V2 - V1) +(h2 - h1)5.此可以看出,当流体从一个容器流出到另一容器时,流体的压强受其高度的变化以及流体的流速变化的影响。
三、结论伯努利方程是气体动力学中重要的基础定律,它描述了在一定系统中流体运动时总能量保持不变的定律。
本文通过一个具体的例子,讲解了伯努利方程的原理及其在例题中的解法,从而使我们对伯努利方程有了更深的理解。
流體力學第四章伯努利方程

第四章 伯努利方程4.1 伯努利方程4.1.1 理想流体沿流线的伯努利方程1. 伯努利方程的推导将欧拉运动微分方程式积分可以得到流体的压力分布规律,但只能在特殊的条件下,不可能在任何的情况下都可求得其解,故我们需对流场作出如下假设:(1)理想流体(2)定常流动(3)质量力有势(4)不可压缩流体(5)沿流线积分在定常流动的条件下,理想流体的运动微分方程(欧拉运动微分方程)可以写成 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-∂∂+∂∂+∂∂=∂∂-z v v y v v x v v z p f z v v y v v x v v y p f z v v y v v x v v x p f z z z y z x z y z y y y x y x z x y x x x ρρρ111 (4.1) 将这个方程沿流线积分,如图4.1所示,可得到伯努利方程。
为此,将式(4.1)的第一式乘以x d 得x zv v x y v v x x v v x x p x f x z x y x x x d d d d 1d ∂∂+∂∂+∂∂=∂∂-ρ (1) 按照流线方程 zy x v z v y v x d d d == 将有,y v x v x y d d =,z v x v x z d d =故式(1)可写成x x x x x x x x x v v z zv v y y v v x x v v x x p x f d d d d d 1d =∂∂+∂∂+∂∂=∂∂-ρ (2) 式(4.1)的另外两式分别乘y d 、z d 后,作类似的代换,可得y y y v v y yp y f d d 1d =∂∂-ρ (3)z z z v v z zp z f d d 1d =∂∂-ρ (4) 将式(2)、(3)和式(4)相加,得 z z y y x x z y x v v v v v v z zp y y p x x p z f y f x f d d d )d d d (1d d d ++=∂∂+∂∂+∂∂-++ρ (5) p 的全微分可以表示为 dz zp dy y p dx x p dp ∂∂+∂∂+∂∂= 质量力有势,则必存在势函数U ,满足y f y f x f z zU y y U x x U U y y x d d d d d d d ++=∂∂+∂∂+∂∂=而 2/d d d d 2v v v v v v v z z y y x x =++式中等号右端的v 为平均速度。
流体的稳定流动伯努利方程

无热传导
理想流体假设中,流体被 视为无热传导的,即流体 的温度在整个流场中保持 一致。
流体的能量守恒原理
能量守恒
流体的能量守恒原理指出,在封闭系 统中,流体的总能量(包括动能和势 能)在流动过程中保持不变。
动能与势能转换
在流体的流动过程中,动能和势能之 间可以相互转换,但总能量保持不变 。
伯努利方程的推导过程
伯努利方程的重要性
01
描述流体稳定流动的规律
伯努利方程是流体力学中的基本方程,用于描述流体在稳定流动状态下
的压力、速度和密度等物理量的关系。
02 03
解决实际问题
在实际生产和生活中,许多问题都涉及到流体的流动,如管道输送、流 体机械、航空航天等。通过应用伯努利方程,可以解决这些实际问题, 提高生产效率和生活品质。
伯努利方程是流体力学中的基本方程,用于描述流体在稳 定流动状态下的压力、速度和位势之间的关系,是理解和 预测流体运动的关键。
广泛应用领域
伯努利方程在多个领域中都有应用,如航空航天、流体机 械、管道输送、气象学等,对于指导工程设计和优化流体 系统性能具有重要意义。
理论基石
作为流体力学的基础理论之一,伯努利方程为后续深入研 究流体动力学、湍流理论等提供了重要的理论支撑。
详细描述
流体静压强的计算公式为 P = ρgh,其中ρ为流体密度,g为重 力加速度,h为流体高度。该公式适用于计算液体在容器中的静 压强。
流体动压强的计算
总结词
流体动压强是指流体在运动状态下对物体表面产生的压力。
详细描述
流体动压强的计算公式为 P = ρv²/2,其中ρ为流体密度,v为流体速度。该公式适用于计算气体或液体在管道或 容器中的动压强。
理想流体和实际流体的贝努利方程

v1A1 v2A2 (一维稳定流动, const)
vA
d
4
2
vD
2
R
vD
vA d 2
8R
1.953m / s
管流伯努利方程式及应用
A-D列伯努利方程:
gH
PA
1 2
v
2 APDΒιβλιοθήκη 1 2v2 D
PA=0.8892×105 Pa
静压力平衡方程: gH PA PB PB=0.9873×105 Pa
2g
(管端处,u2=0)
又(见题图) u12 p2* p1 h
2g
u1 2hg
3.6 贝努利方程的应用
例3-3.求钢包出口处的金属液流速 解:将第一个断面选在钢液 断面1
上表面(自由表面),可以利用 z=0及v1≈0使方程简化。
断面2
第二个断面的选取要包含待求量。 列出断面1和断面2处的贝努利方 程,根据式(3.55) :
(3) 选好基准面,基准面原则上可以选在任何位置, 但选择得当,可使解题大大简化,通常选在管轴线的水 平面或自由液面,要注意的是,基准面必须选为水平面.
(4) 求解流量时,一般要结合一维流动的连续性方 程求解。伯努利方程的p1和p2应为同一度量单位,同 为绝对压强或者同为相对压强,p1和p2的问题与静力 学中的处理完全相同。
实际流体经流道流动的贝努利方程 用平均参量表示(推导过程略),结果为:
z1g
P1
1
v12 2
z2g
P2
2
v22 2
ghW
或
z1
P1
1
v12 2g
z2
P2
2
v22 2g
hW
水力学5.1(2、3)实际流体的动力学基础(N-S方程,能量方程)

水力坡度J: 当总水头线为直线时,
J hw l
当总水头线为曲线时, J dhw dH dl dl
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(2)测管水头线可沿程降 低或升高.为什么?
测管水头线坡度JP:
d(z p)
JP
dl
水力学中规定:所有沿 程下降的坡度为正,所 以式中有一负号.
5.3.3 实际流体恒定总流能量方程的意义
能量方程的几何意义:
(3)在流速不变的流段内, 测管水头线与总水头线 平行.为什么?
5.3.4 实际流体恒定总流能量方程的应用
能量方程的应用条件及注意事项: (1)必须是恒定流,且为不可压缩的均质流体.
(2)作用于流体上的质量力只有重力,所研究的流 体边界是静止的.
流速分布越均匀,α越接近于1. 流速分布越不均匀,α的值越大. 一般渐变流, α≈1.05~1.10
为简便,常常取α=1.0
5.3.2 实际流体恒定总流的能量方程
Q (z1i
p1i
)dQi
Q
u12i 2g
dQi
Q (z2i
p2i
)dQi
Q
u22i 2g
dQi
Q hw idQi
(3)第三类积分: Q hw dQ
5 实际(粘性)流体的动力学基础
实际(粘性)流体
仅有连续性方程远远不能解决实际 问题,如:作用力,能量问题等
本章主要任务:
给出实际(粘性)流体的运动微分方程 (N-S方程),在此基础上讨论元流和恒定 总流的伯努利方程(能量方程),动量方程 的推导以及它们的意义和应用
5 实际(粘性)流体的动力学基础
流体力学第三章伯努利方程及动量方程
0 p1 v12 0 p2 v22
2g
2g
28
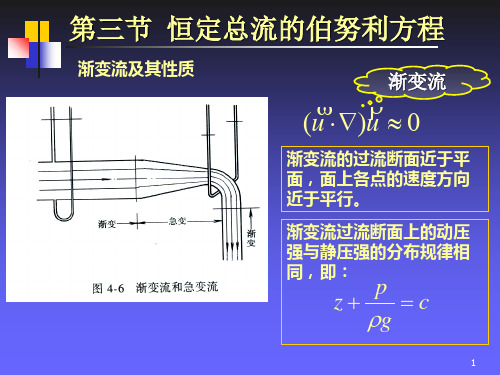
第三节 恒定总流的伯努利方程
p1 p2 v22 v12 h
2g 2g
连续性方程
v1
4
d12
v2
4
d
2 2
v2 v1
d1 d2
Z1
dQ
p1
Z1
dQ
p1
Z1
Q
9
第三节 恒定总流的伯努利方程
同理:
p2 Z2 dQ
p2
Z2
dQ
p2
Z2
dQ
p2
Z2
Q
10
第三节 恒定总流的伯努利方程
二、动能积分 u2 dQ u3 dA u3dA
Q 2g
A 2g
2g A
表单位时间通过断面的流体动 能
v
Q
udA
A
AA
u3dA u3dA
18
第三节 恒定总流的伯努利方程
19
第三节 恒定总流的伯努利方程
20
第三节 恒定总流的伯努利方程
总水头线和测压管水头线
总水头=位置水头+压强水2g
H1 H2 hw 或 H2 H1 hw
v2 H H p 2g
水力坡度: J dH dhw dl dl
p1 (Z1 Z2 ) p2
Z1
p1
Z2
p2
4
第三节 恒定总流的伯努利方程
Z1
p1
Z2
p2
均匀流过流断面上压强 分布服从水静力学规 律
Z p c
5
第三节 恒定总流的伯努利方程
渐变流:非严格均匀流,接近于均匀流 渐变流: 1)流线近似于平行直线。 2)惯性力忽略不计。 3)过流断面近似于平面。 4)过流断面上,压强分布可认为服从流体静力学规律。
流体力学【关于伯努利方程的应用】

工程流体力学综合报告学院:机械工程学院专业:机械工程班级:学号:学生姓名:任课老师:提交日期:2017年12月27 日关于伯努利方程的应用摘要“伯努利原理“是著名的瑞士科学家丹尼尔·伯努利在1726年提出的。
这是在流体力学的连续介质理论方程建立之前,水力学所采用的基本原理,其实质是流体的机械能守恒。
理想正压流体在有势彻体力作用下作定常运动时,运动方程(即欧拉方程)沿流线积分而得到的表达运动流体机械能守恒的方程。
即:动能+重力势能+压力势能=常数。
其最为著名的推论为:等高流动时,流速大,压力就小。
伯努利方程对于确定流体内部各处的压力和流速有很大意义,在水利、造船、航空等部门有着广泛的应用。
关键词:伯努利方程 公式及原理 应用 流体力学1 伯努利方程伯努利原理往往被表述为p+1/2ρv2+ρgh=C ,这个式子被称为伯努利方程。
式中p 为流体中某点的压强,v 为流体该点的流速,ρ为流体密度,g 为重力加速度,h 为该点所在高度,C 是一个常量。
它也可以被表述为p1+1/2ρv12+ρgh1=p2+1/2ρv22+ρgh2。
需要注意的是,由于伯努利方程是由机械能守恒推导出的,所以它仅适用于粘度可以忽略、不可被压缩的理想流体1.1 流线上的伯努利方程流线上的伯努利方程:g V g p z g V g p z C gv g p z 222222221112++=++=++ρρρ适于理想流体(不存在摩擦阻力)。
式中各项分别表示单位流体的动能、位能、静压能之差。
如果流动速度为0,则由伯努利方程可得平衡流体的流体静力学基本公式(C g p z =+ρ)。
1.2 总流的伯努利方程总流是无数元流的总和,将元流伯努利方程沿总流过流断面积分,即可推导出总流的伯努利方程,也即总流能量方程。
动能修正系数α为实际动能与按平均速度计算的动能的比值,α值反映了断面速度分布的不均匀程度。
由于气体的动力黏度值较小,过流断面速度梯度小,g V g p z g V g p z 222222221111αραρ++=++实际的气流运动的速度分布比较均匀,接近于断面平均流速。
伯努利流体动力学-概述说明以及解释

伯努利流体动力学-概述说明以及解释1.引言1.1 概述引言是一篇文章的开头部分,旨在为读者提供一个概述,引起读者的兴趣并引导他们进入后续内容的阅读。
本文将介绍伯努利流体动力学的相关概念和原理。
伯努利流体动力学是流体力学研究的重要领域之一。
流体动力学是研究流体运动规律和性质的学科,而伯努利原理是其中一个基本概念。
伯努利原理指出,在理想流体中,当流体在沿流线流动过程中速度增加时,压力会降低,而速度减小时,则压力增加。
这一原理可以通过数学公式来描述,即伯努利方程。
伯努利方程是伯努利原理的数学表达方式,它将流体动能、压力能和势能联系起来。
通过应用伯努利方程,可以分析流体在不同位置的速度、压力和高度等参数的关系,从而帮助解释和预测流体运动中的现象和现象背后的物理本质。
本文将探讨伯努利原理的基本概念、流体动力学的基本概念,以及阐述伯努利方程的应用。
通过深入了解伯努利流体动力学,可以对流体运动的原理和性质有更清晰的认识,并且可以为未来的研究提出新的方向和可能性。
在结论部分,我们将总结伯努利流体动力学的重要性,并展望未来的研究方向。
通过本文的研究,我们能够更好地理解和应用伯努利流体动力学的原理,为工程和科学领域的相关研究提供重要的理论基础。
总而言之,本文将以伯努利流体动力学为主题,介绍伯努利原理和伯努利方程的基本概念以及应用。
通过深入研究这一领域,我们可以更好地理解流体运动的本质和特性,为相关领域的研究和应用提供有益的借鉴和启示。
1.2文章结构1.2 文章结构本篇文章将围绕伯努利流体动力学展开讨论。
文章分为引言、正文和结论三个部分。
在引言部分,将首先对伯努利流体动力学进行概述,介绍其基本概念和重要性。
然后,阐述文章的结构和目的,以及对伯努利流体动力学的总结。
正文部分将详细介绍伯努利原理及其基本概念,以及流体动力学基本概念和伯努利方程。
通过对这些理论的深入讨论和分析,读者将能够全面了解伯努利流体动力学的原理和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
u2 dQ= u3dA= v3A=v2 Q
Q 2g
2g A
2g
2g
3.水头损失积分:
h' l12
dQ
Q
物理含义:表示单位时间内流体克服1-2流段的摩擦阻 力作功所损失的机械能
为了计算方便,设 hw 为单位重量流体
在两过流断面上的平均能量损失。
h' l12
——实际流体恒定总流的能量方程式, 也称之为恒定总流伯努利方程。
伯努利方程的目的:确立了恒定总流流动中势能和动能、 流速和压强相互转化的普遍规律。
(二)恒定总流能量方程式的应用 船吸现象
案例: 1912年秋季的某一天,当时世界上最大的远洋轮船—— “奥林匹克号”正航行在大海上,在离“奥林匹克号”100m的地方,有 一比它小得多的铁甲巡洋舰“豪克号”与它平行疾驶着,这时却发生 了一件意外的事情:小船好像被大船吸过去似的,完全失控,一个劲地 向“奥林匹克号”冲去,最后,“豪克号”的船撞在“奥林匹克号”的 船舷上,把“奥林匹克撞了个大洞。是什么原因造成这次事故呢?
5.两断面间没有分流或合流
18
假设两断面间有分流或合流的情况:
19
z1+
p1
g
+ 1 v12
2g
=z
+
2
p2
g
+ 2 v12
2g
+h
l1-2
z1+
p1
g
+ 1 v12
2g
=z
+
3
p3
g
+
3
v
2 3
2g
+h
l1-3
结论:对于断面有分支的流动,在列方程时,只需 计入所列断面间的能量损失,不需要考虑另一股分 支流的能量损失。
相互转化的普遍规律; 明确了方程中各项的物理意义; 应用该方程解释了生活中的一些物理现象。
(二).适用条件 1.恒定流
z1 p1g来自 1v122g
z2
p2
g
2v22
2g
hw
2.流体是不可压缩的
3.列方程的两个断面必须是渐变流的过流断面 (均匀流更没问题)
4.整个流段质量力只有重力,不受惯性力 的作用
u2 dQ= u3dA
Q 2g
2g A
物理含义:表示单位时间内通过断面的流体动能。
引入一个动能修正系数
( 是实际动能与按断面平均流速计算的动能之比)
u3dA u3dA
2g
A
v3dA
A
v3A
2g A
的物理意义:
流体流速分布均匀性的指标。
在工程中,通常取 1
工程流体力学 ——实际流体恒定总流的伯努利方程
1
船吸现象
案例: 1912年秋季的某一天,当时世界上最大的远洋轮船——“奥 林匹克号”正航行在大海上,在离“奥林匹克号”100m的地方,有一比 它小得多的铁甲巡洋舰“豪克号”与它平行疾驶着,这时却发生了一 件意外的事情:小船好像被大船吸过去似的,完全失控,一个劲地向 “奥林匹克号”冲去,最后,“豪克号”的船撞在“奥林匹克号”的船 舷上,把“奥林匹克撞了个大洞。是什么原因造成这次事故呢?
20
6.断面间无能量的输入和输出:
在实际工程中,有能量的输入和输出的情况还是 非常多的,比如:管道中有风机或者水泵就会有能量 的输入,如果管道中安装水轮机或汽轮机,就可以输 出能量。对这种情况只要把守恒关系建立起来就行了
( z1
p1
g
u12 2g
)
dQ
(z2
p2
g
u22 2g
) dQ
h' l12
dQ
?
元流
总流
元流 积 分 总流
元流是总流的一个微分流动
积分,得单位时间内通过总流两过流断面的能量关系:
Q
( z1
p1
g
u12 2g
)
dQ
Q
(z2
p2
g
u22 2g
p2
g
u22 2g
h'l1 ~
2
适用条件:恒定、不可压缩、质量力是重力的实际流动。
方程的物理含义与几何含义
z
p g u2 2g
z+ p + u 2 g 2g
物理意义 单位重量流体所具有的位能 单位重量流体所具有的压能 单位重量流体所具有的动能 单位重量流体所具有的总能量
(机械能)
h' l1 ~ 2
机械能的损失
z p
g
位能与压能之和称为势能, 从几何角度看,称之为测压管水头
几何意义 位置水头 压强水头 速度水头
总水头
水头损失
三、实际流体恒定总流的伯努利方程
(一)恒定总流能量方程式的推导
恒定元流能量方程
z1
p1
g
u12 2g
z2
p2
g
u22 2g
h'l1 ~
2
方程两端乘以重量流量dQ ,得单位时间内通过元流两过流断面 的能量关系:
是什么原因造成这次事故呢?
现象的解释
小实验:如果两手各拿一张薄纸,使它们之间的距离大约4-6厘米,然后 用嘴向着两张纸中间吹气,如图所示,纸张是向内靠还是向外飘动?想一想, 动手试试看
[例题]
如图所示管流,水箱中的水位保持恒定,
已知H、d、hW,试求通过流量Q。
[解]据1→2建立总流的伯努利方程:
)
dQ
Q
h' l12
dQ
重量流量
重量流量 重量流量
1.势能积分:
(z
Q
p )dQ g
物理含义:表示单位时间内通过断面的流体势能
如果断面是渐变流,服从静压强分布规律
p z C
g
(z
Q
p )dQ=(z g
p ) g
dQ=(z
Q
p ) g
Q
2.动能积分:
dQ
hw
Q
Q
(z
Q
p )dQ=(z g
p g
)Q
u2 dQ=v2 Q
2g
2g
h‘ l1-2
dQ=h w
Q
将上面三个积分项均除以 Q , 就得到了总流的能量方程式。
z1
p1
g
1v12
2g
z2
p2
g
2v22
2g
hw
是什么原因造成这次事故呢?
“奥林匹克号”与“豪克号”相撞事故示意图
小实验
小实验:如果两手各拿一张薄纸,使它们之间的距离大约4-6厘米,然后 用嘴向着两张纸中间吹气,如图所示,纸张是向内靠还是向外飘动?想一想, 动手试试看
知识回顾
实际流体恒定元流的伯努利方程
z1
p1
g
u12 2g
z2
z1
p1
g
1v12
2g
z2
p2
g
2v22
2g
hl1~2
H
00
0 0 v2 2g
hW
得
v
2g
H
hW
Q Av d 2
4
2g
H
hw
小结
z1
p1
g
1v12
2g
z2
p2
g
2v22
2g
hw
建立了恒定总流能量方程; 确立了总流流动中动能和势能、流速和压强
