基本初等函数2
函数的概念与基本初等函数2-1

素可无原象,即B中元素可有剩余.
4.若函数是由一些基本初等函数通过四则运算结合而成的,那么它的定义域是
各基本初等函数定义域的交集.对于含有字母的函数求定义域,或已知其定
义域求字母参数的取值范围,必须对字母的取值情况进行讨论.求给定函数 解析式的定义域往往归结为解不等式组的问题,在解不等式组时要细心,取 交集时可借助于数轴,并且要注意端点值或边界值的取舍. 5.求函数的值域,不但要重视对应法则的作用,而且要特别注意定义域对值域
集
映射 合B的 ,记作f :A→B.
思考:函数与映射有什么区别? 提示:函数是特殊的映射,映射不一定是函数.函数是从一个非空数集 到另一个非空数集的映射.映射是从一个非空集合到另一个非空集合
(这两个集合不一定是数集)的对应.
1.已知函数y=f(x),x∈[a,b],那么集合{(x,y)|y=f(x),x∈[a,b]}∩ {(x,y)|x=x0}中所含元素的个数是________. 解析:垂直于x轴的直线与函数的图象最多只有一个交点. 答案:0或1 2.下列方程对应的图形,其中不是函数图象的是________. ①x2+y2=1;②y= 答案:①③④ 3.函数y= 答案:[-1,1] 的定义域是________,值域是________. [0,1] ;③ ;④y2=4x2+1
确定函数定义域的原则
(1)当函数y=f(x)用列表法给出时,函数的定义域是指表格中实数x的集合;
(2)当函数y=f(x) 用图象法给出时,函数的定义域是指图象在x轴上的投影所覆盖的实数
的集合;
(3)当函数y=f(x)用解析式给出时,函数的定义域是指使解析式有意义的实数x的集合; (4)当函数y=f(x)由实际问题给出时,函数的定义域由实际问题的意义确定. (5)若已知函数f(x)的定义域为[a,b],其复合函数f(g(x))的定义域由不等式 a≤g(x)≤b解出.
1-2基本初等函数,常用经济函数

成本函数
成本是生产一定数量产品所需要的
各种生产要素投入的价格或费用总额,
y x 1.幂函数
(是常数)
y
y x2
1
(1,1)
y x
y x
o
1 y x
1
x
• 指数函数
年复利率5.5%,投资100元 1年后,100•1.055 2年后,100•(1.055) … …
n x 2
n年后, 100•(1.055)
复利提供了指数函数的一个例子y=P•a
y a x (a 0 且 a 1 )
3. 对数函数 (logarithmic function)
y loga x (a 0, a 1)
y ln x
y log a x
(1,0)
(a 1)
y log 1 x
a
• 对数函数的性质
a e
log a x
x, log a a x
x x
ln x
x, ln e x
4. 三角函数
正弦函数
y sin x
y sin x
余弦函数 y cos x
y cos x
正切函数 y tan x
y tan x
余切函数 y cot x
y cot x
• 恒等式
cos2 sin 2 1
cos( A B) cos A cos B sin A sin B sin( A B) sin A cos B cos A sin B
2_基本初等函数知识点小结

第二章 基本初等函数知识点小结一.【课标要求】1.指数函数(1)通过具体实例(如细胞的分裂,考古中所用的14C 的衰减,药物在人体内残留量的变化等),了解指数函数模型的实际背景;(2)理解有理指数幂的含义,通过具体实例了解实数指数幂的意义,掌握幂的运算。
(3)理解指数函数的概念和意义,能借助计算器或计算机画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点;(4)在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型 2.对数函数(1)理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;通过阅读材料,了解对数的发现历史以及对简化运算的作用;(2)通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点; 3.知道指数函数x a y =与对数函数x y alog =互为反函数(a >0,a ≠1)。
4.幂函数(1)了解幂函数的概念(2)结合函数y=x, ,y=x 2, y=x 3,y=x 21,y=x1的图象,了解它们的变化情况二.【要点精讲】1.指数与对数运算(1)根式的概念:①定义:若一个数的n 次方等于),1(*∈>N n n a 且,则这个数称a 的n 次方根。
即若a xn=,则x 称a 的n 次方根)1*∈>N n n 且,1)当n 为奇数时,n a 的次方根记作n a ;2)当n 为偶数时,负数a 没有n 次方根,而正数a 有两个n 次方根且互为相反数,记作)0(>±a a n②性质:1)a a nn =)(;2)当n 为奇数时,a ann=;3)当n 为偶数时,⎩⎨⎧<-≥==)0()0(||a a a a a a n。
(2).幂的有关概念①规定:1)∈⋅⋅⋅=n a a a a n ( N *;2))0(10≠=a a ; n 个 3)∈=-p aapp(1Q ,4)m a a anmnm,0(>=、∈n N *且)1>n②性质:1)r a a a a s r s r ,0(>=⋅+、∈s Q ); 2)r a a a s r s r ,0()(>=⋅、∈s Q ); 3)∈>>⋅=⋅r b a b a b a r r r ,0,0()( Q )。
基本初等函数2

龙文教育数学学科教师个性化辅导学案教师: 学生: 时间: 年 月 日 时段:课 题教学目标教学重点、难点教学方法教学内容【对数函数】对数其实是指数的逆过程。
指数函数是相同的底数a 被自乘x 次之后的结果;对数就是知道了这个结果和底数,求一下究竟自乘了多少次。
1、(1)定义:一般地,对于指数式a b =N,把数b 叫做以a 为底N 的对数,记作log a N,其中a 叫做对数的底数,N 叫做真数. (2)对数性质①零和负数没有对数,即N>0;②1的对数为0,即log a 1=0(a>0且a ≠1); ③底的对数等于1,即log a a=1(a>0且a ≠1).对数恒等式:log N a N(a 0a 1,N 0).a=>≠>且 ②log a a b =b(a>0,且a ≠1,b ∈R)(4)常用对数:通常将以10为底的对数叫做常用对数,N 的常用对数log 10N 简记为lgN.(5)自然对数:以无理数e=2.71828…为底的对数称为自然对数,N 的自然对数log e N 简记作lnN. 2、对数的运算性质如果a>0且a ≠1,M>0,N>0,那么()()()()a a a aa a n a a 1log (M N)log M log N;2log log M log N; 3log M nlog M n R .(4)log log (5)log log 1log (6)log log m n a a a b a b a MNnb b mb a N N b=+=-=∈=∙==2lg 2lg3111lg 0.36lg823+++ex:化简、求值:3、图象性质f(x)=log a x 对数函数的图象:经过点(1,0),且图象都在第一、四象限;都以y 轴为渐近线(当0<a<1时,图象向上无限接近y 轴;当a>1时,图象向下无限接近y 轴) 无论在x 轴的上侧还是下侧,底数随顺时针方向变大. *另记,作y=1,从左往右,底数从小到大。
高中数学 第一章 基本初等函数(II)1.3 三角函数的图象与性质 1.3.2 余弦函数、正切函数的
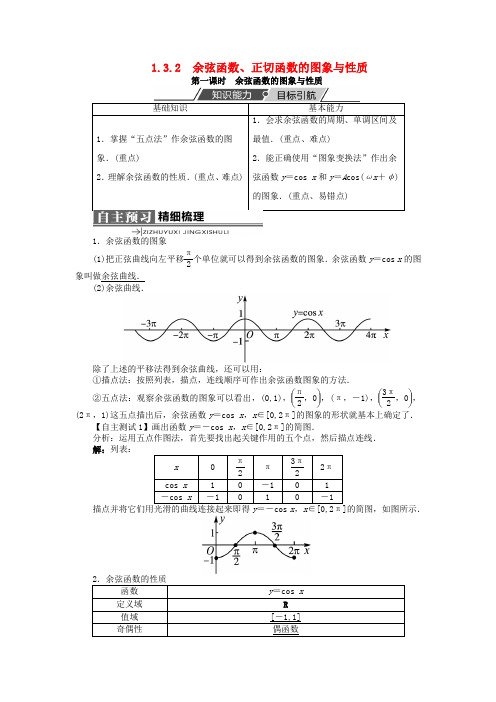
1.3.2 余弦函数、正切函数的图象与性质第一课时 余弦函数的图象与性质1.余弦函数的图象(1)把正弦曲线向左平移π2个单位就可以得到余弦函数的图象.余弦函数y =cos x 的图象叫做余弦曲线.(2)余弦曲线.除了上述的平移法得到余弦曲线,还可以用:①描点法:按照列表,描点,连线顺序可作出余弦函数图象的方法.②五点法:观察余弦函数的图象可以看出,(0,1),⎝ ⎛⎭⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎫3π2,0,(2π,1)这五点描出后,余弦函数y =cos x ,x ∈[0,2π]的图象的形状就基本上确定了.【自主测试1】画出函数y =-cos x ,x ∈[0,2π]的简图.分析:运用五点作图法,首先要找出起关键作用的五个点,然后描点连线. 解:列表:ω>0)的周期为T =2πω.今后,可以使用这个公式直接求这类函数的周期.【自主测试2-1】函数y =2cos x +1的最大值和最小值分别是( ) A .2,-2 B .3,-1 C .1,-1 D .2,-1 答案:B【自主测试2-2】已知函数f (x )=sin ⎝⎛⎭⎪⎫x -π2(x ∈R ),下列结论错误的是( )A .函数f (x )的最小正周期为2πB .函数f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上是增函数C .函数f (x )的图象关于直线x =0对称D .函数f (x )是奇函数解析:∵f (x )=sin ⎝⎛⎭⎪⎫x -π2=-cos x (x ∈R ),f (-x )=f (x ),∴函数f (x )是偶函数. 答案:D正弦函数与余弦函数的图象和性质的区别与联系(4)sin x +cos x =1题型一 用“五点法”作函数y =A cos(ωx +φ)的图象 【例题1】用“五点法”画出函数y =2cos 2x 的简图.分析:先找出此函数图象上的五个关键点,画出其在一个周期上的函数图象,再进行扩展得到在整个定义域内的简图.解:因为y =2cos 2x 的周期T =2π2=π,所以先在区间[0,π]上按五个关键点列表如下.然后把y =2cos 2x 在[0,π]上的图象向左、右平移,每次平移π个单位长度,则得到y =2cos 2x 在R 上的简图如下.反思在用“五点法”画出函数y =A cos(ωx +φ)的图象时,所取的五点应由ωx +φ=0,π2,π,3π2,2π来确定,而不是令x =0,π2,π,3π2,2π.题型二 三角函数的图象变换【例题2】函数y =sin 2x 的图象可由y =cos ⎝⎛⎭⎪⎫2x -π4的图象平移得到,若使平移的距离最短,则应( )A .向左平移π8个单位长度B .向右平移7π8个单位长度C .向左平移π4个单位长度D .向右平移π8个单位长度解析:y =cos ⎝ ⎛⎭⎪⎫2x -π4=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫2x -π4 =sin ⎝ ⎛⎭⎪⎫3π4-2x =-sin ⎝⎛⎭⎪⎫2x -3π4 =sin ⎝ ⎛⎭⎪⎫2x -3π4+π=sin ⎝ ⎛⎭⎪⎫2x +π4 =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +π8,故函数y =sin 2x 的图象可由y =cos ⎝⎛⎭⎪⎫2x -π4的图象向右平移π8个单位长度得到.故选D .答案:D反思一定要注意看清变换的顺序,即看清是以哪个函数图象作为基准. 题型三 函数的定义域问题【例题3】求函数y =36-x 2+lg cos x 的定义域.分析:首先根据函数解析式列出使函数有意义的条件不等式组,然后分别求解,最后求交集即可.解:要使函数有意义,只需⎩⎪⎨⎪⎧36-x 2≥0,cos x >0,即⎩⎪⎨⎪⎧-6≤x ≤6,2k π-π2<x <2k π+π2k ∈Z .利用数轴求解,如图所示:所以函数的定义域为⎣⎢⎡⎭⎪⎫-6,-3π2∪⎝ ⎛⎭⎪⎫-π2,π2∪⎝ ⎛⎦⎥⎤3π2,6. 反思利用数轴或者单位圆取解集的交集或并集非常简捷、清晰,但要注意区间的开闭情况.题型四 余弦函数的最值或值域【例题4】(1)求函数y =cos x ,x ∈⎣⎢⎡⎦⎥⎤-π3,2π3的值域;(2)求函数y =2+cos x2-cos x的最值;(3)求函数y =3cos 2x -4cos x +1,x ∈⎣⎢⎡⎦⎥⎤π3,2π3的值域.分析:(1)结合y =cos x 的图象在区间⎣⎢⎡⎦⎥⎤-π3,2π3上先增后减即可求解;(2)利用|cos x |≤1这一性质;(3)利用配方法,结合二次函数的性质求解.解:(1)∵y =cos x 在区间⎣⎢⎡⎦⎥⎤-π3,0上单调递增,在区间⎣⎢⎡⎦⎥⎤0,2π3上单调递减,∴y ma x =cos 0=1,y min =cos 2π3=-12,∴y =cos x 的值域为⎣⎢⎡⎦⎥⎤-12,1. (2)由y =2+cos x 2-cos x ,求得cos x =2y -1y +1.∵|cos x |≤1,∴⎪⎪⎪⎪⎪⎪2y -1y +1≤1,∴[2(y -1)]2≤(y +1)2.解得13≤y ≤3,∴y ma x =3,y min =13.(3)y =3cos 2x -4cos x +1=3⎝⎛⎭⎪⎫cos x -232-13,∵x ∈⎣⎢⎡⎦⎥⎤π3,2π3,∴cos x ∈⎣⎢⎡⎦⎥⎤-12,12, 从而当cos x =-12,即x =2π3时,y ma x =154.当cos x =12,即x =π3时,y min =-14.∴函数y =3cos 2x -4cos x +1的值域为⎣⎢⎡⎦⎥⎤-14,154.反思求函数的最值的方法有以下几种:(1)直接法.根据函数值域的定义,由自变量的取值范围求出函数值的取值范围. (2)利用函数的单调性.(3)利用函数的图象,转化为求函数图象上最高点和最低点的纵坐标的问题.(4)利用换元法,转化为一次函数、二次函数、指数函数、对数函数等基本初等函数问题.题型五 余弦函数图象的应用【例题5】求函数y =cos ⎝⎛⎭⎪⎫2x +π4的对称中心、对称轴方程、单调递减区间和最小正周期.分析:利用整体换元,设t =2x +π4,则问题转化为考查函数y =cos t 的相关性质.解:设t =2x +π4,则函数y =cos t 的图象如图所示.令t =k π(k ∈Z ),则2x +π4=k π(k ∈Z ).故x =k ·π2-π8(k ∈Z )即为所求的对称轴方程.令t =k π+π2(k ∈Z ),则2x +π4=k π+π2(k ∈Z ),则x =k ·π2+π8(k ∈Z ).故⎝ ⎛⎭⎪⎫k ·π2+π8,0(k ∈Z )即为所求的对称中心.当t ∈[2k π,2k π+π](k ∈Z )时,2x +π4∈[2k π,2k π+π](k ∈Z ),则x ∈⎣⎢⎡⎦⎥⎤k π-π8,k π+3π8(k ∈Z ). 故其单调递减区间为⎣⎢⎡⎦⎥⎤k π-π8,k π+3π8(k ∈Z ). ∵cos ⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫2x +π4+2π=cos ⎣⎢⎡⎦⎥⎤2x +π+π4, ∴最小正周期T =π.反思整体换元思想是解决较复杂三角函数问题常用的一种方法,它能将问题化归为对基本三角函数的考查.〖互动探究〗若将本例中的函数改为“y =⎪⎪⎪⎪⎪⎪cos ⎝⎛⎭⎪⎫2x +π4”呢? 解:设t =2x +π4,则问题转化为考查函数y =|cos t |,如图所示:解答过程同例题,可得无对称中心.令t =k ·π2(k ∈Z ),则2x +π4=k ·π2(k ∈Z ),∴对称轴为x =k ·π4-π8(k ∈Z );令t ∈⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z ), ∴2x +π4∈⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z ),则x ∈⎣⎢⎡⎦⎥⎤k ·π2-π8,k ·π2+π8故其单调递减区间为⎣⎢⎡⎦⎥⎤k ·π2-π8,k ·π2+π8(k ∈Z ).最小正周期T =π2.反思(1)若三角函数式子中带绝对值号,则通常通过观察图象得到周期和单调区间. (2)正弦函数y =sin x 和余弦函数y =cos x 取绝对值后,周期缩为原来的一半,即 ①y =|sin x |的周期为π; ②y =|cos x |的周期为π.1.下列说法不正确的是( )A .正弦函数、余弦函数的定义域是R ,值域是[-1,1]B .余弦函数当且仅当x =2k π(k ∈Z )时取得最大值1,当且仅当x =(2k +1)π(k ∈Z )时取得最小值-1C .正弦函数在每个区间⎣⎢⎡⎦⎥⎤π2+2k π,3π2+2k π(k ∈Z )上都是减函数 D .余弦函数在每个区间[2k π-π,2k π](k ∈Z )上都是减函数 答案:D2.下列函数中,周期为π,且在⎣⎢⎡⎦⎥⎤π4,π2上为减函数的是( ) A .y =sin ⎝ ⎛⎭⎪⎫2x +π2 B .y =cos ⎝ ⎛⎭⎪⎫2x +π2 C .y =sin ⎝ ⎛⎭⎪⎫x +π2 D .y =cos ⎝⎛⎭⎪⎫x +π2答案:A3.(2012·重庆期末)把函数y =cos ⎝⎛⎭⎪⎫2x +π3图象上所有点的横坐标缩短为原来的12倍(纵坐标不变),得到图象的解析式为( )A .y =cos ⎝ ⎛⎭⎪⎫x +π6B .y =cos ⎝ ⎛⎭⎪⎫x +π3C .y =cos ⎝ ⎛⎭⎪⎫4x +2π3D .y =cos ⎝⎛⎭⎪⎫4x +π3 答案:D4.若函数y =a cos x +b 的最小值为-12,最大值为32,则a =__________,b =__________.解析:由于y ma x =32,y min =-12,且-1≤cos x ≤1,则当a >0时,有⎩⎪⎨⎪⎧a +b =32,-a +b =-12,解得⎩⎪⎨⎪⎧a =1,b =12.当a <0时,有⎩⎪⎨⎪⎧-a +b =32,a +b =-12,解得⎩⎪⎨⎪⎧a =-1,b =12.综上,a =±1,b =12.答案:±1 125.函数y =|cos x |的单调增区间为________,单调减区间为________,最小正周期为________.解析:函数y =|cos x |的图象,如图所示.由图可知它的最小正周期为π.又因为在一个周期⎣⎢⎡⎦⎥⎤-π2,π2上,函数的增区间是⎣⎢⎡⎦⎥⎤-π2,0,减区间是⎣⎢⎡⎦⎥⎤0,π2.而函数的周期是k π(k ∈Z ),因此函数y =|cos x |的增区间是⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ),减区间是⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z ). 答案:⎣⎢⎡⎦⎥⎤k π-π2,k π(k ∈Z ) ⎣⎢⎡⎦⎥⎤k π,k π+π2(k ∈Z ) π 6.函数f (x )的定义域为[0,1],则f (cos x )的定义域是__________.解析:由已知0≤cos x ≤1,得2k π-π2≤x ≤2k π+π2(k ∈Z ).答案:⎣⎢⎡⎦⎥⎤2k π-π2,2k π+π2(k ∈Z ) 7.已知函数f (x )=3cos ⎝⎛⎭⎪⎫2x -π4,x ∈R . (1)用“五点法”画出函数f (x )在长度为一个周期的闭区间上的简图; (2)求函数f (x )的最大值,并求出取得最大值时自变量x 的取值集合; (3)求函数f (x )的单调增区间. 解:(1)列表:(2)当2x -π4=2k π(k ∈Z ),即x =k π+π8(k ∈Z )时,y ma x =3,此时x 取值的集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x =k π+π8,k ∈Z. (3)当2k π-π≤2x -π4≤2k π(k ∈Z )时,k π-3π8≤x ≤k π+π8,k ∈Z ,故函数f (x )的单调增区间为⎣⎢⎡⎦⎥⎤k π-3π8,k π+π8(k ∈Z ).。
基本初等函数知识总结

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数(y=C)(1)定义域: D(f)=(-∞,+∞)(2)值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0,C)在y轴上截距为C的直线(4 )图像:(5)周期性:常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T,f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义:形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数.(2)性质:在(0,+∞)内总有意义①当α>0时函数图像过点(0,0)和(1,1),在(0,+∞)内单调增加且无界②当α<0时函数图像过点(1,1),在(0,+∞)内单调减少且无界(3)图像:3.指数函数y=a^x(a>0且a≠1)(1)定义域:x∈R(2)值域:(0,+∞)(3)性质:①单调性:1.当0<a<1时,在(-∞,+∞)内单调减少 2.当a >1时,在(-∞,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(4)图像:①由指数函数y=a^x与直线x=1相交于点(1,a)可知:在y轴右侧,图像从下到上相应的底数由小变大。
②由指数函数y=a^x与直线x=-1相交于点(-1,1/a)可知:在y轴左侧,图像从下到上相应的底数由大变小。
③指数函数的底数与图像间的关系可概括的记忆为:在y轴右边“底大图高”;在y轴左边“底大图低” 如图:(5)运算法则:①②③④4.对数函数y=logax(a>0 且a≠1)(1)定义:如果a^x=N(a>0,且a ≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数一般地,函数y=logax(a>0,且a ≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数(2)定义域:(0,+∞),即x>0(3)值域:R(4)性质:①单调性:1.当0<a<1时,在(0,+∞)内单调减少 2.当a >1时,在(0,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(5)图像:【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式:5.三角函数⑴正弦函数y=sin x(1)定义:对边与斜边的比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ(K∈Z)时,Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:奇函数③对称性:对称中心是(Kπ,0),K ∈Z;对称轴是直线x=Kπ+π/2,K ∈Z④单调性:在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减⑤有界性:有界函数(6)图像:(2)余弦函数y=cos x(1)定义:邻边与斜边之比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ +π /2(K∈Z)时,Y取最大值1 2.当X=2Kπ +π (K∈Z)时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:偶函数③对称性:对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z④单调性:在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增⑤有界性:有界函数(6)图像:(3)正切函数y=tan x(1)定义:对边与邻边之比(2)定义域:{x∣x≠Kπ+π/2,K∈Z}(3)值域:R(4)最值:无最大值和最小值(5)性质:①周期性:最小正周期都是πT=π②奇偶性:奇函数③对称性:对称中心是(Kπ/2,0),K∈Z④单调性:在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增⑤有界性:无界函数(6)图像:(4)余切函数y=cot x(1)定义:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切。
2初等函数、经济中的常用函数
反正切函数的图象有何特性?
?
反正切函数图象关于原点对称,是奇函数; 是单调增函数;
arctan x ,是有界函数。
2
经济数学
1.基本初等函数 (6) 反三角函数
反余切函数:y arc cot x
反余切函数的图象有何特性?
?
是单调减函数;
0 arccot x ,是有界函数。
解:(1)y ln cos x
(2)y arctan x (3) y sin2 (ex ) (4) y tan(arcsin(x3 1))
经济数学
2. 复合函数 (3) 分解
例4 指出下列复合函数的复合过程
(1) y cos x2 ; (3) y e arccot x ;
(2) y arctan x ; (4) y ln arccos 1 x 。
解:(1) y cosu,u x2
(2)y arctan u ,u x (3)y eu,u v ,v arccot x (4)y ln u ,u arccos v,v w ,w 1 x
线性供应函数 Q c dp (c 0, d 0) 二次供应函数 Q a bp cp2 (a 0,b 0, c 0) 指数供应函数 Q Aebp ( A 0,b 0)
经济数学
2.3 经济中常用的函数
1.需求函数与供应函数 (1) 需求函数
市场对某种商品的需求量,主要受到该商品的价格的影响, 通常降低商品的价格会使需求量增加,提高商品的价格会使需求 量减少.在假定其它因素不变的条件下,市场需求量 Q 可视为该
反函数图象关于原点对称,是奇函数; 是单调增函数;
2020届高考数学命题猜想及专题练习--函数﹑基本初等函数的图像与性质2(含解析)
2020届高考数学命题猜想函数﹑基本初等函数的图像与性质2【考向解读】1.高考对函数的三要素,函数的表示方法等内容的考查以基础知识为主,难度中等偏下.2.对图象的考查主要有两个方面:一是识图,二是用图,即利用函数的图象,通过数形结合的思想解决问题.3.对函数性质的考查,则主要是将单调性、奇偶性、周期性等综合一起考查,既有具体函数也有抽象函数.常以选择题、填空题的形式出现,且常与新定义问题相结合,难度较大.【命题热点突破一】函数的性质及应用1.单调性:单调性是函数在其定义域上的局部性质.利用定义证明函数的单调性时,规范步骤为取值、作差、判断符号、下结论.复合函数的单调性遵循“同增异减”的原则.2.奇偶性:奇偶性是函数在定义域上的整体性质.偶函数的图象关于y轴对称,在关于坐标原点对称的定义域区间上具有相反的单调性;奇函数的图象关于坐标原点对称,在关于坐标原点对称的定义域区间上具有相同的单调性.3.周期性:周期性是函数在定义域上的整体性质.若函数在其定义域上满足f(a+x)=f(x)(a 不等于0),则其一个周期T=|a|.f x例1、【2017北京,文5】已知函数,则()(A)是偶函数,且在R上是增函数(B)是奇函数,且在R上是增函数(C)是偶函数,且在R上是减函数(D)是奇函数,且在R上是增函数【变式探究】已知函数()f x 是定义在R 上的周期为2的奇函数,当0<x <1时,()4xf x =,则= .【答案】-2【解析】因为函数()f x 是定义在R 上的周期为2的奇函数, 所以,所以,即(1)0f =,,所以.【变式探究】【2017课标1,文8】函数sin21cos xy x =-的部分图像大致为A .B .C .D .【变式探究】函数在[]2,2-的图像大致为(A)(B)(C)(D)【答案】D【感悟提升】(1)根据函数的解析式判断函数的图象,要从定义域、值域、单调性、奇偶性等方面入手,结合给出的函数图象进行全面分析,有时也可结合特殊的函数值进行辅助推断,这是解决函数图象判断类试题的基本方法.(2)研究函数时,注意结合图象,在解方程和不等式等问题时,借助图象能起到十分快捷的作用.【变式探究】(1)已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)-f(x 1)](x2-x1)<0恒成立,设a =f ⎝ ⎛⎭⎪⎪⎫-12,b =f(2),c =f(3),则a ,b ,c 的大小关系为( )A.c >a >bB.c >b >aC.a >c >bD.b >a >c(2)设函数f(x)=ex(2x -1)-ax +a ,其中a<1,若存在唯一的整数x0使得f(x0)<0,则a 的取值范围是( )A.⎣⎢⎢⎡⎭⎪⎪⎫-32e ,1B.⎣⎢⎢⎡⎭⎪⎪⎫-32e ,34C.⎣⎢⎢⎡⎭⎪⎪⎫32e ,34D.⎣⎢⎢⎡⎭⎪⎪⎫32e ,1 【解析】(1)由于函数f(x)的图象向左平移1个单位后得到的图象关于y 轴对称,故函数y =f(x)的图象本身关于直线x =1对称,所以a =f ⎝ ⎛⎭⎪⎪⎫-12=f ⎝ ⎛⎭⎪⎪⎫52,当x2>x1>1时,[f(x2)-f(x1)](x2-x1)<0恒成立,等价于函数f(x)在(1,+∞)上单调递减,所以b >a >c.选D.【高考真题解读】1. (2018年浙江卷)函数y=sin2x 的图象可能是A.B. C. D.【答案】D2. (2018年全国III 卷)函数的图像大致为A. AB. BC. CD. D【答案】D【解析】当时,,排除A,B.,当时,,排除C,故正确答案选D.3. (2018年全国卷Ⅱ)函数的图像大致为A. AB. BC. CD. D【答案】B4. (2018年天津卷)已知,则的大小关系为A. B. C. D.【答案】D【解析】由题意可知:,即,,即,,即,综上可得:.本题选择D选项.5. (2018年全国I卷)设函数,则满足的x的取值范围是A. B. C. D.【答案】D【解析】将函数的图像画出来,f x3.【2017北京,文5】已知函数,则()(A)是偶函数,且在R上是增函数(B )是奇函数,且在R 上是增函数 (C )是偶函数,且在R 上是减函数 (D )是奇函数,且在R 上是增函数 【答案】B【解析】,所以该函数是奇函数,并且3xy =是增函数,13xy ⎛⎫= ⎪⎝⎭是减函数,根据增函数−减函数=增函数,可知该函数是增函数,故选B. 4.【2017北京,文8】根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与MN 最接近的是(参考数据:lg3≈0.48)(A )1033 (B )1053 (C )1073 (D )1093 【答案】D5.【2017课标1,文9】已知函数,则A .()f x 在(0,2)单调递增B .()f x 在(0,2)单调递减C .y=()f x 的图像关于直线x=1对称D .y=()f x 的图像关于点(1,0)对称【答案】C 【解析】由题意知,,所以()f x 的图像关于直线1x =对称,故C 正确,D 错误;又(02x <<),由复合函数的单调性可知()f x在()0,1上单调递增,在()1,2上单调递减,所以A ,B 错误,故选C .1.【2016高考新课标3文数】已知432a =,254b =,1325c =,则( ) (A )b a c << (B )a b c << (C )b c a << (D )c a b << 【答案】A 【解析】因为,,所以b a c <<,故选A .2.【2016年高考北京文数】已知x ,y R ∈,且0x y >>,则( )A.110x y ->B.C. D.【答案】C3.【2016高考新课标1卷】函数在[]2,2-的图像大致为(A )(B )(C )(D )【答案】D【解析】函数f(x)=2x2–e|x|在[–2,2]上是偶函数,其图像关于y 轴对称,因为,所以排除A 、B 选项;当[]0,2x ∈时,有一零点,设为x ,当0(0,)x x ∈时,()f x 为减函数,当0(2)x x ,∈时,()f x 为增函数.故选D 。
第三章 基本初等函数 第2课时
第2课时 对数及对数的运算(预习案)一、学习目标:1.理解对数的概念,了解对数与指数的关系.2.理解和掌握对数的性质;对数式与指数式的关系.二、回归教材1.对数定义:一般地,如果 ,那么数x 叫做以a 为底N 的 ,记作 ,其中a 叫做对数的 ,N 叫做 .2. (1)当a >0,a ≠1时, ⇔N x 10log =;(2) 和 没有对数.(3)化指数式N a b=为对数式3.两个常用的结论:1log a = ,a a log = (a >0,且a ≠1).4.对数的运算性质如下:如果a >0,且a ≠1,M >0,N >0,那么: ()()N M a •log 1= ;(2)⎪⎭⎫ ⎝⎛N M a log = ;()n a M log 3= (n ∈R ). 5. 换底公式及对数恒等式:(1)b a log = ;(2)对数恒等式:三、基础自测1.对于a >0,且a ≠1,下列说法中正确的是( )①若,则N M a a log log =;②若N M a a log log =,则;③若22log log N M a a =,则M=N ;④若,则22log log N M a a =.A.①③B.②④C.②D.①②③④2.设2log 3=a ,则6log 28log 33-用a 表示的形式是( )A.a -2 ()213.a a B -- C.5a -2 2.a D -+3a -1 3.()x 32log log =0,则x =( )4.已知lg 2=a ,lg 3=b ,则lg 6= .5.3log 2·2log 3= .6.已知lg 2≈0.301 0,lg 3≈0.477 1,求lg 45.第2课时 对数及对数的运算(预习案)一、典例精析考向一:指数与对数的转化【例1】将下列指数式化为对数式,对数式化为指数式:(1)ln 10=2.303; (2)64126=-; (3)m⎪⎭⎫ ⎝⎛31=5.73; (4)16log 21=-4; (5)lg 0.01=-2;【例2】求下列各式中x 的值:()32log 164-=x ; ()68log 2=x ; (4)-2ln e =x ; ()()1lg log 63=x .考向二:换底公式与对数运算律的应用【例3】计算(1). (2)()()2log 2log 3log 3log 9384++【例4】用,表示下列各式:; .考向三: 对数式的化简与求值 【例5】求值:(1)(lg 5)2+lg 50·lg 2; (2)12lg 3249-43lg 8+lg 245(3)5log 177-二、当堂达标:1.2 log 510+log 50.25=( ).A .0B .1C .2D .42.已知a =log 0.70.8,b =log 1.10.9,c =1.10.9,则a ,b ,c 的大小关系是( ).A .a <b <cB .a <c <bC .b <a <cD .c <a <b 3.若log a 23>1,则a 的取值范围是________. 4. 若f (x )=ax -12,且f (lg a )=10,则a =________. 5. 若2a =5b =10,求1a +1b的值.6.求下列各式的值:;(2)lg 0.000 01;(3)ln . (4)lg 5+lg 2;三、高考链接:1.(2010·辽宁)设2a =5b =m ,且1a +1b=2,则m =( ). A.10 B .10 C .20 D .1002.(2018全国卷Ⅲ)设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+3.(2013浙江)已知为正实数,则A .B .C .D . 4.(2016年浙江) 已知1a b >>,若5log log 2a b b a +=,b a a b =,则a = ,b = . 5.(2015浙江)若4log 3a =,则22a a -+=_______.6.(2012北京)已知函数()lg f x x =,若()1f ab =,则22()()f a f b += .7.(2011天津)已知22log log 1a b +≥,则39a b+的最小值为__________. y x ,y x y x lg lg lg lg 222+=+lg()lg lg 222x y x y +=g y x yx lg lg lg lg 222+=•lg()lg lg 222xy x y =g。
高等数学第二节初等函数
x u f y
自变量
中间变量 因变量
例1.设y=f (u)=lgu, 而u=(x)=sinx.
则它们构成的复合函数为 y=f [(x)] = lgsinx.
例2.设y=f (u)=lg(u–2), u=(x)=sinx,能否构成
复合函数?
因u=sinx的值中,不能使y=lg(u-2)有意义, 所以 它们不能构成复合函数
税率(%) 3 10 20
写出个人月收入x (不大于12500元)元与应缴纳税款y元 之间的关系,当某人月收入为6500元时,应缴纳多少税款?
解: 依此可以列出下面的函数关系:
0,
0 x 3500
y
(x (x
-
3500) 3500)
都是初等函数。
y
3 3x tan 5x x3 sin x - 2-x
今后我们所讨论的函数,绝大多数都是初等函数。
四、函数关系举例
1.如何选择通信公司
小王买部手机想入网,他得知:中国联通130网的收费标准 是:月租费30元,每月来电显示6元,本地通话每分钟0.4元; 中国移动“神州行”储值卡的收费标准是:本地通话每分钟 0.6元,月租费和来电显示费全免,小王相拥有来电服务,请 问他如何选择?
第二节初等函数
一、基本初等函数 二、复合函数 三、初等函数 四、建立函数关系举例
一、基本初等函数
1 、常数函数 y C y
O
yc
x
函数定义域为R,只有一个函数值
1.1 函数
2、幂函数
y x y
y x2
1
(是常数)
y x y x
(1,1)
y 1 x
o1
x
随着而不同,但在(0, )中都有定义;经过点 (1,1), 在(0, )内当 0时,x为增函数; 0时,x为减函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数
1 若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(1,0)-
和(0,1),则( )
A 2,2a b ==
B 2a b ==
C 2,1a b ==
D a b ==2 已知x x f 26log )(=,那么)8(f 等于( )
A 34
B 8
C 18
D 21
3 函数lg y x =( )
A . 是偶函数,在区间(,0)-∞ 上单调递增
B . 是偶函数,在区间(,0)-∞上单调递减
C . 是奇函数,在区间(0,)+∞ 上单调递增
D 是奇函数,在区间(0,)+∞上单调递减
4 若函数)10(log )(<<=a x x f a 在区间]2,[a a 上的最大值
是最小值的3倍,则a 的值为( )
A 42
B 22
C 41
D 21
5 已知函数=-=+-=)(.)(.11lg )(a f b a f x x
x f 则若( )
A b
B b -
C b 1
D 1
b -
6 函数()log 1a f x x =-在(0,1)上递减,那么()f x 在(1,)+∞上(
)
A 递增且无最大值
B 递减且无最小值
C 递增且有最大值
D 递减且有最小值
二、填空题
1 若a x f x x lg 22)(-+=是奇函数,则实数a =_________
2 函数()
212()log 25f x x x =-+的值域是__________
3 已知1414log 7,log 5,a b ==则用,a b 表示35log 28=
4 设(){}1,,lg A y xy =, {}0,,B x y =,且A B =,则x = ;y =
5 计算:()()5log 22323-+
6 函数x x e 1e 1
y -=+的值域是__________ 三、解答题
1 比较下列各组数值的大小:
(1)3.37
.1和1.28.0;(2)7.03.3和8.04.3;(3)25log ,27log ,2398
2 解方程:(1)19
2327x x ---⋅= (2)649x x x +=
3 已知,3234+⋅-=x
x y 当其值域为[1,7]时,求x 的取值范围
4 已知函数()log ()x a f x a a =-(1)a >,求()f x 的定义域和值域;
参考答案
一、选择题
1 A
132311log 3log (2),log (2),2,8,,384
a a a a a a a a a a a a ======2 A log (1)0,a
b -=且log 1,2a b a b ===
3 D
令1666228(0),8(8)()log log x x x f f x x =>=====4 B 令()lg ,()lg lg ()f x x f x x x f x =-=-==,即为偶函数 令,0u x x =<时,u 是x 的减函数,即lg y x =在区间(,0)-∞上单调递减 5 B 11()lg lg ().()().11x x f x f x f a f a b x x
+--==-=--=-=--+则 6 A 令1u x =-,(0,1)是u 的递减区间,即1a >,(1,)+∞是u 的 递增区间,即()f x 递增且无最大值
二、填空题
1 110
()()22lg 22lg x x x x f x f x a a --+-=+++ 1(lg 1)(22)0,lg 10,10
x x a a a -=++=+== (另法):x R ∈,由()()f x f x -=-得(0)0f =,即1lg 10,10a a +==
2 (],2-∞- 22
25(1)44,x x x -+=-+≥ 而101,2<<()21122
log 25log 42x x -+≤=- 3 2a a b
-+ 141414143514log 28log 7log 5log 35,log 28log 35a b +==+= 141414141414141414
1log log (214)1log 21(1log 7)27log 35log 35log 35log 35a a b +⨯++--=====+ 4 1,1-- ∵0,0,A y ∈≠∴lg()0,1xy xy ==
又∵1,1,B y ∈≠∴1,1x x =≠而,∴1,1x y =-=-且
5 15
(
)
()323232log 5log 515
--++=== 6 (1,1)- x x e 1e 1y -=+,10,111x y e y y
+=>-<<- 三、解答题
1 解:(1)∵ 3.301.7 1.71,>= 2.100.80.81<=,∴ 3.31.7>1.28.0
(2)∵0.7
0.80.80.83.3 3.3,3.3 3.4<<,∴0.73.3<8.04.3 (3)8293log 27log 3,log 25log 5,==
332222233333log 2log log 3,log 3log log 5,22
====> ∴983log 25log 27.2<
< 2 解:(1)2(3)63270,(33)(39)0,330x x x x x ------⋅-=+-=+≠而
2390,33,x x ---==
2x =-
(2)22422()()1,()()103933
x x x x +=+-=
2
3
22()0,()33log x x x >=∴=则 3 解:由已知得143237,x x ≤-⋅+≤
即43237,43231x x x x ⎧-⋅+≤⎪⎨-⋅+≥⎪⎩得(21)(24)0(21)(22)0
x x x x ⎧+-≤⎪⎨--≥⎪⎩ 即021x
<≤,或224x ≤≤ ∴0x ≤,或12x ≤≤
4 解:0,,1x x
a a a a x -><<,即定义域为(,1)-∞; 0,0,log ()1x x x a a a a a a a ><-<-<,
即值域为(,1)-∞。
