动态电路的电路方程
合集下载
第3章3.2动态电路的方程及其解

第三章 动态电路
§3.2
动态电路的方程及其解
■
第 1页
§3.2 动态电路的方程及其解
描述动态电路的方程是微分方程。 描述动态电路的方程是微分方程。用一阶微分 微分方程 方程描述的电路常称为一阶电路 一般而言, 一阶电路。 方程描述的电路常称为一阶电路。一般而言,如果 电路中含有n个独立的动态元件 个独立的动态元件, 电路中含有 个独立的动态元件,则描述它的将是 n阶微分方程,该电路可称为 阶电路。 阶微分方程, 阶电路。 阶微分方程 该电路可称为n阶电路
• 动态电路方程的建立 • 微分方程的经典解法
▲
■
第 2页
一、动态电路方程的建立
1、依据:元件VAR,KCL和KVL列写方程; 依据:元件VAR,KCL和KVL列写方程; VAR 列写方程 uR 一阶电路举例: 2、一阶电路举例: R i S RC电路 t=0时开关 电路, 时开关S 例1:图RC电路,t=0时开关S闭 uC uS 讨论t>0时的电容电压u 。 t>0时的电容电压 合,讨论t>0时的电容电压 C(t)。 C t>0时 根据KVL KVL方程列出回 t>0时,根据KVL方程列出回 RC串联电路 uR + uC – uS = 0 路电压方程为 d uC d uC , uR = R i = RC 根据元件的VAR VAR, 根据元件的VAR,有 i = C 代入上式, 代入上式,整 理得
− 1 t RC +U S
uC (t) = (U0 −US ) e
,t ≥ 0
▲ ■ 第 11 页
3、结果分析
固有响应和强迫响应 暂态响应和稳态响应
− 1 t RC +U
uC (t) = (U0 −US ) e
§3.2
动态电路的方程及其解
■
第 1页
§3.2 动态电路的方程及其解
描述动态电路的方程是微分方程。 描述动态电路的方程是微分方程。用一阶微分 微分方程 方程描述的电路常称为一阶电路 一般而言, 一阶电路。 方程描述的电路常称为一阶电路。一般而言,如果 电路中含有n个独立的动态元件 个独立的动态元件, 电路中含有 个独立的动态元件,则描述它的将是 n阶微分方程,该电路可称为 阶电路。 阶微分方程, 阶电路。 阶微分方程 该电路可称为n阶电路
• 动态电路方程的建立 • 微分方程的经典解法
▲
■
第 2页
一、动态电路方程的建立
1、依据:元件VAR,KCL和KVL列写方程; 依据:元件VAR,KCL和KVL列写方程; VAR 列写方程 uR 一阶电路举例: 2、一阶电路举例: R i S RC电路 t=0时开关 电路, 时开关S 例1:图RC电路,t=0时开关S闭 uC uS 讨论t>0时的电容电压u 。 t>0时的电容电压 合,讨论t>0时的电容电压 C(t)。 C t>0时 根据KVL KVL方程列出回 t>0时,根据KVL方程列出回 RC串联电路 uR + uC – uS = 0 路电压方程为 d uC d uC , uR = R i = RC 根据元件的VAR VAR, 根据元件的VAR,有 i = C 代入上式, 代入上式,整 理得
− 1 t RC +U S
uC (t) = (U0 −US ) e
,t ≥ 0
▲ ■ 第 11 页
3、结果分析
固有响应和强迫响应 暂态响应和稳态响应
− 1 t RC +U
uC (t) = (U0 −US ) e
3-5 动态电路的输入-输出方程

电路原理
2
§35 动态电路的输入-输出方程
d 2uc (t ) R duc (t ) 1 1 u ( t ) us (t ) c 2 dt L dt LC LC
d 2 i (t ) R di (t ) 1 1 dus (t ) i (t ) 2 dt L dt LC L dt
§35 动态电路的输入-输出方程 输入
作为输入激励的电压或者电流简称输入。 —— f(t) 如:电压源、电流源
输出
作为待求响应的电压或者电流简称输出。 —— r(t) 如:待求响应,任意电压或电流
输入-输出方程
联系输入变量和输出变量之间关系的单一变量的微 分方程。
电路原理
§35 动态电路的输入-输出方程 列写输入-输出方程的依据 拓扑约束
电路原理
§35 动态电路的输入-输出方程
us(t)为输入,i(t)为输出
di(t ) Ri(t ) L uc (t ) us (t ) dt 2 dit d it duc t dus t R L 2 dt dt dt dt
d i(t ) R di(t ) 1 1 dus (t ) i(t ) 2 dt L dt LC L dt
电路中含有两个独立的储能元件,所列方程
为二阶常系数线性微分方程。
电路原理
§35 动态电路的输入-输出方程
两个独立的储能元件 二阶常系数线性微分方程
n个独立的储能元件 n阶微分方程
输入-输出方程的一般形式
d n r (t ) d n1r (t ) dr (t ) an1 a1 a0 r (t ) n n 1 dt dt dt d m f (t ) d m1 f (t ) df (t ) bm bm1 b1 b0 f (t ) m m1 dt dt dt
2
§35 动态电路的输入-输出方程
d 2uc (t ) R duc (t ) 1 1 u ( t ) us (t ) c 2 dt L dt LC LC
d 2 i (t ) R di (t ) 1 1 dus (t ) i (t ) 2 dt L dt LC L dt
§35 动态电路的输入-输出方程 输入
作为输入激励的电压或者电流简称输入。 —— f(t) 如:电压源、电流源
输出
作为待求响应的电压或者电流简称输出。 —— r(t) 如:待求响应,任意电压或电流
输入-输出方程
联系输入变量和输出变量之间关系的单一变量的微 分方程。
电路原理
§35 动态电路的输入-输出方程 列写输入-输出方程的依据 拓扑约束
电路原理
§35 动态电路的输入-输出方程
us(t)为输入,i(t)为输出
di(t ) Ri(t ) L uc (t ) us (t ) dt 2 dit d it duc t dus t R L 2 dt dt dt dt
d i(t ) R di(t ) 1 1 dus (t ) i(t ) 2 dt L dt LC L dt
电路中含有两个独立的储能元件,所列方程
为二阶常系数线性微分方程。
电路原理
§35 动态电路的输入-输出方程
两个独立的储能元件 二阶常系数线性微分方程
n个独立的储能元件 n阶微分方程
输入-输出方程的一般形式
d n r (t ) d n1r (t ) dr (t ) an1 a1 a0 r (t ) n n 1 dt dt dt d m f (t ) d m1 f (t ) df (t ) bm bm1 b1 b0 f (t ) m m1 dt dt dt
动态电路的方程及其初始条件
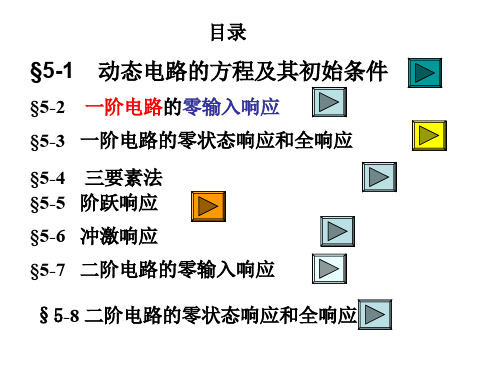
t=0
i
换路在 t=0 时刻进行 ,
Us
K
R
+
uC
C
–
-∞
0-
0
0+
+∞
原稳态 原稳态 换路 换路后初
终值
瞬间
始值
过渡 过程
新稳态
链接
RC电路
初始条件:为 t = 0+ 时 u , i 的值
动画
如在 t = t0 合上,则 t = t0+
二、换路定理
Switch Theorem
1. 电容 (cap acitor)
–
i
I 0e
R L
t
I 0e
L
t /
R
t 0
uL
L
di dt
t
RI 0e L / R
t 0
特征根 p = 由初始值
R L
i(0+)= I0
得:
A= i(0+)= I0
i(t)
I0e pt
I
0e
R L
t
令 = L/R , 一阶 RL 电路时间常数
[
]
+
- 10V
40kΩ
k iC
uCt = 0 时断开开关 k , 求
-
解: (1) 由 0- 电路求 uC(0-) (2) 由换路定律
+ 10kΩ
+
40kΩ
- 10V
iC
uC
-
+ i 10kΩ
- 10V
iC
iC(0+) ?
电路第七章

U s uC (0 ) 12 12 (3) i1 (0 ) 0 R1 4
i2 (0 )
uC (0 ) 12 1.5 A R2 8
iC (0 ) i1 (0 ) i2 (0 ) 1.5 A
例5: 图示电路,t=0时S由1扳向2, t < 0 时电路稳定。求初始值 i1(0+) 、 i2(0+)和uL(0+)。 Us 9 3A 解:(1) t<0时:i L (0 ) R1 3 (2) 0+等效电路。根据换路定律:
方程通解:uC (t ) A e A e
pt
t RC
uC ( t ) U 0 e
t RC
带入初始条件: A U 0
t RC
(t 0)
duC U 0 i C e dt R
( t 0)
4、参量图形分析t
uC (t)和i(t)从初始值按指数规律衰减 电容充放电分析: 1、t<0时充电,稳定后,uC=U0 。
第7章 一阶电路和二阶电路的时域分 析
7.1 动态电路的方程及其初始条件
7.2
7.3 7.4 7.5 7.7
一阶电路的零输入响应
一阶电路的零状态响应 一阶电路的全响应 二阶电路的零输入响应 一阶电路和二阶电路的阶跃响应
7.1 动态电路的方程及其初始条件
1. 动态电路
含有动态元件电容和电感的电路称动态电路。
例
电阻电路
i
+ i
(t = 0) R1 R2 0
i U S / R2
t 过渡期为零
us
i U S ( R1 R2 )
-
返 回
上 页
下 页
i2 (0 )
uC (0 ) 12 1.5 A R2 8
iC (0 ) i1 (0 ) i2 (0 ) 1.5 A
例5: 图示电路,t=0时S由1扳向2, t < 0 时电路稳定。求初始值 i1(0+) 、 i2(0+)和uL(0+)。 Us 9 3A 解:(1) t<0时:i L (0 ) R1 3 (2) 0+等效电路。根据换路定律:
方程通解:uC (t ) A e A e
pt
t RC
uC ( t ) U 0 e
t RC
带入初始条件: A U 0
t RC
(t 0)
duC U 0 i C e dt R
( t 0)
4、参量图形分析t
uC (t)和i(t)从初始值按指数规律衰减 电容充放电分析: 1、t<0时充电,稳定后,uC=U0 。
第7章 一阶电路和二阶电路的时域分 析
7.1 动态电路的方程及其初始条件
7.2
7.3 7.4 7.5 7.7
一阶电路的零输入响应
一阶电路的零状态响应 一阶电路的全响应 二阶电路的零输入响应 一阶电路和二阶电路的阶跃响应
7.1 动态电路的方程及其初始条件
1. 动态电路
含有动态元件电容和电感的电路称动态电路。
例
电阻电路
i
+ i
(t = 0) R1 R2 0
i U S / R2
t 过渡期为零
us
i U S ( R1 R2 )
-
返 回
上 页
下 页
3-5动态电路的输入-输出方程.

2 建立输入-输出方程的依据——两个约束关系
联接形式所确定的约束关系(KVL,KCL) 元件性质所确定的约束关系(VCR)(有微分关系) 所以输入-输出方程为微分方程,方程阶数等于电路 独立动态元件个数。
3 建立输入-输出方程的方法: 第二章的方法
例1 建立以uS(t)为输入,uC(t)为输出的
输入—输出方程 解:由KCL
un2
iS
1
11
LD
un1
( LD
R2 )un2
0
D 常量 0
CD 1 1 R1 LD
11ຫໍສະໝຸດ CD 1 11
LD 1
un2
R1 LD 1
iS 0
LD
LD R2
LD
LCD 2un2
( L R1
R2C )Du n2
(1
R2 R1
)un 2
R2iS
LC
动态电路在换路时使电路从一个稳定工作状态 转变为另一个稳定工作状态,这种转变需要时 间,要经过一个过程。
§3-5 动态电路的输入—输出方程
三、动态电路方程
输入f(t):电压源的uS(t);电流源的iS(t) 输出r(t):待求响应(response) (任意电压或电流)
1 输入-输出方程——联系f(t)、r(t)的方程
§3-5 动态电路的输入—输出方程
一、换路 换路不需要时间,一般以换路发生时刻作 为计时时刻,即 t=0 时换路
t=0- 表示换路前瞬间,与t=0的间隔→0 t=0+ 表示换路后瞬间,与t=0的间隔→0 二、动态电路 1.动态电路定义 (a) 具有动态元件(L、C、M)
(b) 具有换路 2.动态电路阶数 = 等于独立储能元件个数
联接形式所确定的约束关系(KVL,KCL) 元件性质所确定的约束关系(VCR)(有微分关系) 所以输入-输出方程为微分方程,方程阶数等于电路 独立动态元件个数。
3 建立输入-输出方程的方法: 第二章的方法
例1 建立以uS(t)为输入,uC(t)为输出的
输入—输出方程 解:由KCL
un2
iS
1
11
LD
un1
( LD
R2 )un2
0
D 常量 0
CD 1 1 R1 LD
11ຫໍສະໝຸດ CD 1 11
LD 1
un2
R1 LD 1
iS 0
LD
LD R2
LD
LCD 2un2
( L R1
R2C )Du n2
(1
R2 R1
)un 2
R2iS
LC
动态电路在换路时使电路从一个稳定工作状态 转变为另一个稳定工作状态,这种转变需要时 间,要经过一个过程。
§3-5 动态电路的输入—输出方程
三、动态电路方程
输入f(t):电压源的uS(t);电流源的iS(t) 输出r(t):待求响应(response) (任意电压或电流)
1 输入-输出方程——联系f(t)、r(t)的方程
§3-5 动态电路的输入—输出方程
一、换路 换路不需要时间,一般以换路发生时刻作 为计时时刻,即 t=0 时换路
t=0- 表示换路前瞬间,与t=0的间隔→0 t=0+ 表示换路后瞬间,与t=0的间隔→0 二、动态电路 1.动态电路定义 (a) 具有动态元件(L、C、M)
(b) 具有换路 2.动态电路阶数 = 等于独立储能元件个数
第三章 动态电路

无源元件
+ uC –
u/V
5V
iC 例:已知C=2F两端电压波形如下, C 求iC(t)=?
t/s
0 1 3 4
在0 t 1s时 : ic (t ) 2 5 10 A
在1 t 3s时 : ic (t ) 0
duC 解: iC ( t ) C dt
电容量 耐压值
3.电容的伏安关系 iC
dq( t ) 由于: iC ( t ) dt 而: q( t ) C uC ( t ) duC ( t ) 所以: iC ( t ) C dt
+ uc –
C
注:ic与uc为关联参考方向。
duC ( t ) 当ic与uc非关联时: iC ( t ) C dt
L (t0 ) L (t0 )
qC (t0 ) qC (t0 )
三、电容、电感的串联和并联 1、电容的串联
i C1 C2 + u +u1- +u22、电容的并联 i + u C1 C2 Cn +un+ u –
i Ceq
n 1 1 1 1 1 .... C eq C1 C 2 C 3 k 1 C k
瞬时功率:
diL (t ) p(t ) u L (t ) iL (t ) LiL (t ) dt 贮存的能量:
t t
diL ( ) wL (t ) p( )d L iL ( ) d d 1 2 1 2 Li L (t ) Li L () 2 2 当iL(-∞)=0时,电感吸收的能量为:
1 2 wL (t ) Li L (t ) 2
无源元件
第三章 动态电路分析

第3章
1. 动态电路
动态电路分析
3.1 动态电路的基本概念
含有动态元件电容和电感的电路称动态电路。 含有动态元件电容和电感的电路称动态电路。 动态元件电容 的电路称动态电路 当动态电路状态发生改变时(换路)需要 当动态电路状态发生改变时(换路) 特点 经历一个变化过程才能达到新的稳定状态。这 经历一个变化过程才能达到新的稳定状态。 过渡过程。 个变化过程称为电路的过渡过程 个变化过程称为电路的过渡过程。 电路结构、 换路 电路结构、状态发生变化 过渡过程产生的原因 电路内部含有储能元件L 电路内部含有储能元件 、C,电路在换路时能量发生 , 变化,而能量的储存和释放都需要一定的时间来完成。 变化,而能量的储存和释放都需要一定的时间来完成。 支路接入或断开 电路参数变化
③电感的初始条件
iL(0+)= iL(0-) ψL (0+)= ψL (0-)
换路瞬间,若电感电压保持为有限值, 则电感电流 换路瞬间,若电感电压保持为有限值, 磁链)换路前后保持不变。 (磁链)换路前后保持不变。
4. 换路定律
qc (0+) = qc (0-) uC (0+) = uC (0-)
表明
τ大
t
τ 大→过渡时间长; τ 小→过渡时间短 过渡时间长 过渡时间短 t 0 τ 2τ 3τ 5τ
uc =U0e
−
0
τ小
τ
t
U0 U0 e -1
U0 e -2
U0 e -3
U0 e -5
U0 0.368U0 0.135U0 0.05U0 0.007U0
电容电压衰减到原来电压36.8%所需的时间。工程上认 所需的时间。 电容电压衰减到原来电压 所需的时间 过渡过程结束。 为, 经过 3τ-5τ , 过渡过程结束。
1. 动态电路
动态电路分析
3.1 动态电路的基本概念
含有动态元件电容和电感的电路称动态电路。 含有动态元件电容和电感的电路称动态电路。 动态元件电容 的电路称动态电路 当动态电路状态发生改变时(换路)需要 当动态电路状态发生改变时(换路) 特点 经历一个变化过程才能达到新的稳定状态。这 经历一个变化过程才能达到新的稳定状态。 过渡过程。 个变化过程称为电路的过渡过程 个变化过程称为电路的过渡过程。 电路结构、 换路 电路结构、状态发生变化 过渡过程产生的原因 电路内部含有储能元件L 电路内部含有储能元件 、C,电路在换路时能量发生 , 变化,而能量的储存和释放都需要一定的时间来完成。 变化,而能量的储存和释放都需要一定的时间来完成。 支路接入或断开 电路参数变化
③电感的初始条件
iL(0+)= iL(0-) ψL (0+)= ψL (0-)
换路瞬间,若电感电压保持为有限值, 则电感电流 换路瞬间,若电感电压保持为有限值, 磁链)换路前后保持不变。 (磁链)换路前后保持不变。
4. 换路定律
qc (0+) = qc (0-) uC (0+) = uC (0-)
表明
τ大
t
τ 大→过渡时间长; τ 小→过渡时间短 过渡时间长 过渡时间短 t 0 τ 2τ 3τ 5τ
uc =U0e
−
0
τ小
τ
t
U0 U0 e -1
U0 e -2
U0 e -3
U0 e -5
U0 0.368U0 0.135U0 0.05U0 0.007U0
电容电压衰减到原来电压36.8%所需的时间。工程上认 所需的时间。 电容电压衰减到原来电压 所需的时间 过渡过程结束。 为, 经过 3τ-5τ , 过渡过程结束。
动态电路的概念

方程的通解 =方程的特解 + 对应齐次方程的通解 将电容C用数值为uc(0+)的电压源代替
C+ L +
(2) 再求其它电量初始值。 初始值:电路中各 u、i 在 t =0+ 时的数值。
t=0+:表示换路后的
1) 由t =0+的电路求其它电量的初始值; 即换路后电路中,
将电容C用数值为uc(0+)的电压源代替
以电容电压uC(t)为变量,列出图(b)所示电路的微分方程
由KVL可得
Ri+uc=US
Rd d u C tC u C U S (t 0)
方程的通解 =方程的特解 + 对应齐次方程的通解
即 u C (t) u C (t) u C (t)
特解u'C满足微分方程关系
R
CduC dt
uC
Us
对应齐次微分方程的通解 uC 满足
+-uC2 (0-)
R3
= —6×—2—0 = 10V 3+6+3
uC1(0+)= uC1(0-)= 5V uC2(0+)= uC2(0-)= 10V
t=0–的电路
9-3 三要素法
电路如图(a)所示,开关连接在1端为时已经很久,uC(0-)=U0。 t=0时开关倒向2端。t >0 时的电路如图 (b)所示。
态
t=0
t
新 稳 态
旧稳态 i=0, uC = 0
新稳态
i = 0, uC= U
K
+
_U
R
+
_U
Ri
uC
i
uC
过渡过程 : 旧稳态
新稳态
C+ L +
(2) 再求其它电量初始值。 初始值:电路中各 u、i 在 t =0+ 时的数值。
t=0+:表示换路后的
1) 由t =0+的电路求其它电量的初始值; 即换路后电路中,
将电容C用数值为uc(0+)的电压源代替
以电容电压uC(t)为变量,列出图(b)所示电路的微分方程
由KVL可得
Ri+uc=US
Rd d u C tC u C U S (t 0)
方程的通解 =方程的特解 + 对应齐次方程的通解
即 u C (t) u C (t) u C (t)
特解u'C满足微分方程关系
R
CduC dt
uC
Us
对应齐次微分方程的通解 uC 满足
+-uC2 (0-)
R3
= —6×—2—0 = 10V 3+6+3
uC1(0+)= uC1(0-)= 5V uC2(0+)= uC2(0-)= 10V
t=0–的电路
9-3 三要素法
电路如图(a)所示,开关连接在1端为时已经很久,uC(0-)=U0。 t=0时开关倒向2端。t >0 时的电路如图 (b)所示。
态
t=0
t
新 稳 态
旧稳态 i=0, uC = 0
新稳态
i = 0, uC= U
K
+
_U
R
+
_U
Ri
uC
i
uC
过渡过程 : 旧稳态
新稳态
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图7-18
解:对于图(a)所示RC串联电路,可以写出以下方程
uS (t) uR (t) uC (t) Ri(t) uC (t)
在上式中代入: 得到
i(t) C duC (t) dt
RC
duC (t) dt
uC
(t)=uS (t)
(7-21)
这是常系数非齐次一阶微分方程,图(a)是一阶电路。
uS
经过整理得到以下微分方程
LC
d 2 uC dt 2
L ( R1
R2C)
duC dt
(R1 R2 ) R1
uC
uS
(7 26)
这是常系数非齐次二阶微分方程,图示电路是二阶电路。
必作习题:第266~267页 习题七:7 – 9 、 7 – 13 2002年春节摄于成都人民公园
R1C
duC dt
uS
(1)
R1iL
R1C
duC dt
uC
0
( 2)
从式(2)得到
iL
C
duC dt
1 R1
uC
将iL(t)代入式(1)中
LC
d 2 uC dt 2
L R1
duC dt
(R1
R2 )C
duC dt
(
R1
R1
R2
)
uC
R1C
duC dt
R1R2 R1 R2
uoc
R2 R1 R2
uS
由图(b)电路得到与式7-25相同的微分方程。
例7-11 电路如图7-21所示,以uC(t)为变量列出电路的微分 方程。
图7-21
解:以iL(t)和iC(t)为网孔电流,列出网孔方程
L diL dt
(R1
R2 )iL
R1iC
动态电路的电路方程
含有储能元件的动态电路中的电压电流仍然 受到KCL、KVL的拓扑约束和元件特性VCR的约 束。一般来说,根据KCL、KVL和VCR写出的电 路方程是一组微分方程。
由一阶微分方程描述的电路称为一阶电路。 由二阶微分方程描述的电路称为二阶电路。 由n阶微分方程描述的电路称为n阶电路。
例7-8 列出图7-18所示电路的一阶微分方程。
对于图(b)所示RL并联电路,可以写出以下方程
iS (t) iR (t) iL (t) GuL (t) iL (t)
在上式中代入 :
uL(t)LdiL (t) dt
得到
GL
diL (t) dt
iL (t)=iS (t)
(7 22)
这是常系数非齐次一阶微分方程。图(b)是一阶电路。
uS uC
0
补充方程
iC
C
duC dt
得到以i1(t)和uC(t)为变量的方程
( R1
R2 )i1
R2C
duC dt
uS
(1)
R2i1
(R2
R3 )C
duC dt
uC
0
(2)
从式(2)中写出i1(t)的表达式
i1
( R2
R3 )C R2
duC dt
( R1+R2 )L R1 R2
diL dt
iL
uS R1
(7 24)
这是常系数非齐次一阶微分方程,图(a)是一阶电路。
例7-10 电路如图7-20(a)所示,以uC(t)为变量列出电路的微 分方程。
解一:列出网孔方程
图7-20
(RR1 2i1R2
)i1 R2iC (R2 R3 )iC
例7-9 电路如图7-19(a)所示,以iL为变量列出电路的微分 方程。
图7-19
解一:列出网孔方程
(
R1
R2 )i1
R2iL
uS
(1)
R2i1
L
diL dt
R2iL
0
(2)
由式(2)求得
i1
L R2
diL dt
iL
代入式(1)得到
( R1
R2 )L R2
uS
R1iL R1iC uC 0
L diL dt
(R1
R2 )iL
R1iC
uS
R1iL R1iC uC 0
代入电容的VCR方程
iC
C
duC dt
得到以iL(t)和uC(t)为变量的方程
L
diL dt
(R1 R2 )iL
diL dt
(R1
R2 )iL
R2iL
uS
整理
( R1
R2 )L R2
diL dt
R1iL
uS
(7 23)
图7-19
解二:将含源电阻单口用诺顿等效电路代替,得到图(b)电 路,其中
Ro
R1R2 R1 R2
iSC
uS R1
图7-19
图(b)电路与前面图(b)电路完全相同,直接引用式7- 22可以得到
1 R2
uC
将 i1(t)代入式(1),得到以下方程
( R3
R1R2 )C R1 R2
duC dt
uC
R2 R1 R2
uS
(7 25)
这是以电容电压为变量的一阶微分方程。
图7-20
解二:将连接电容的含源电阻单口网络用戴维宁等效电路 代替,得到图(b)所示电路,其中
Ro
R3
解:对于图(a)所示RC串联电路,可以写出以下方程
uS (t) uR (t) uC (t) Ri(t) uC (t)
在上式中代入: 得到
i(t) C duC (t) dt
RC
duC (t) dt
uC
(t)=uS (t)
(7-21)
这是常系数非齐次一阶微分方程,图(a)是一阶电路。
uS
经过整理得到以下微分方程
LC
d 2 uC dt 2
L ( R1
R2C)
duC dt
(R1 R2 ) R1
uC
uS
(7 26)
这是常系数非齐次二阶微分方程,图示电路是二阶电路。
必作习题:第266~267页 习题七:7 – 9 、 7 – 13 2002年春节摄于成都人民公园
R1C
duC dt
uS
(1)
R1iL
R1C
duC dt
uC
0
( 2)
从式(2)得到
iL
C
duC dt
1 R1
uC
将iL(t)代入式(1)中
LC
d 2 uC dt 2
L R1
duC dt
(R1
R2 )C
duC dt
(
R1
R1
R2
)
uC
R1C
duC dt
R1R2 R1 R2
uoc
R2 R1 R2
uS
由图(b)电路得到与式7-25相同的微分方程。
例7-11 电路如图7-21所示,以uC(t)为变量列出电路的微分 方程。
图7-21
解:以iL(t)和iC(t)为网孔电流,列出网孔方程
L diL dt
(R1
R2 )iL
R1iC
动态电路的电路方程
含有储能元件的动态电路中的电压电流仍然 受到KCL、KVL的拓扑约束和元件特性VCR的约 束。一般来说,根据KCL、KVL和VCR写出的电 路方程是一组微分方程。
由一阶微分方程描述的电路称为一阶电路。 由二阶微分方程描述的电路称为二阶电路。 由n阶微分方程描述的电路称为n阶电路。
例7-8 列出图7-18所示电路的一阶微分方程。
对于图(b)所示RL并联电路,可以写出以下方程
iS (t) iR (t) iL (t) GuL (t) iL (t)
在上式中代入 :
uL(t)LdiL (t) dt
得到
GL
diL (t) dt
iL (t)=iS (t)
(7 22)
这是常系数非齐次一阶微分方程。图(b)是一阶电路。
uS uC
0
补充方程
iC
C
duC dt
得到以i1(t)和uC(t)为变量的方程
( R1
R2 )i1
R2C
duC dt
uS
(1)
R2i1
(R2
R3 )C
duC dt
uC
0
(2)
从式(2)中写出i1(t)的表达式
i1
( R2
R3 )C R2
duC dt
( R1+R2 )L R1 R2
diL dt
iL
uS R1
(7 24)
这是常系数非齐次一阶微分方程,图(a)是一阶电路。
例7-10 电路如图7-20(a)所示,以uC(t)为变量列出电路的微 分方程。
解一:列出网孔方程
图7-20
(RR1 2i1R2
)i1 R2iC (R2 R3 )iC
例7-9 电路如图7-19(a)所示,以iL为变量列出电路的微分 方程。
图7-19
解一:列出网孔方程
(
R1
R2 )i1
R2iL
uS
(1)
R2i1
L
diL dt
R2iL
0
(2)
由式(2)求得
i1
L R2
diL dt
iL
代入式(1)得到
( R1
R2 )L R2
uS
R1iL R1iC uC 0
L diL dt
(R1
R2 )iL
R1iC
uS
R1iL R1iC uC 0
代入电容的VCR方程
iC
C
duC dt
得到以iL(t)和uC(t)为变量的方程
L
diL dt
(R1 R2 )iL
diL dt
(R1
R2 )iL
R2iL
uS
整理
( R1
R2 )L R2
diL dt
R1iL
uS
(7 23)
图7-19
解二:将含源电阻单口用诺顿等效电路代替,得到图(b)电 路,其中
Ro
R1R2 R1 R2
iSC
uS R1
图7-19
图(b)电路与前面图(b)电路完全相同,直接引用式7- 22可以得到
1 R2
uC
将 i1(t)代入式(1),得到以下方程
( R3
R1R2 )C R1 R2
duC dt
uC
R2 R1 R2
uS
(7 25)
这是以电容电压为变量的一阶微分方程。
图7-20
解二:将连接电容的含源电阻单口网络用戴维宁等效电路 代替,得到图(b)所示电路,其中
Ro
R3
