动态电路的输入输出方程
第3章3.2动态电路的方程及其解

§3.2
动态电路的方程及其解
■
第 1页
§3.2 动态电路的方程及其解
描述动态电路的方程是微分方程。 描述动态电路的方程是微分方程。用一阶微分 微分方程 方程描述的电路常称为一阶电路 一般而言, 一阶电路。 方程描述的电路常称为一阶电路。一般而言,如果 电路中含有n个独立的动态元件 个独立的动态元件, 电路中含有 个独立的动态元件,则描述它的将是 n阶微分方程,该电路可称为 阶电路。 阶微分方程, 阶电路。 阶微分方程 该电路可称为n阶电路
• 动态电路方程的建立 • 微分方程的经典解法
▲
■
第 2页
一、动态电路方程的建立
1、依据:元件VAR,KCL和KVL列写方程; 依据:元件VAR,KCL和KVL列写方程; VAR 列写方程 uR 一阶电路举例: 2、一阶电路举例: R i S RC电路 t=0时开关 电路, 时开关S 例1:图RC电路,t=0时开关S闭 uC uS 讨论t>0时的电容电压u 。 t>0时的电容电压 合,讨论t>0时的电容电压 C(t)。 C t>0时 根据KVL KVL方程列出回 t>0时,根据KVL方程列出回 RC串联电路 uR + uC – uS = 0 路电压方程为 d uC d uC , uR = R i = RC 根据元件的VAR VAR, 根据元件的VAR,有 i = C 代入上式, 代入上式,整 理得
− 1 t RC +U S
uC (t) = (U0 −US ) e
,t ≥ 0
▲ ■ 第 11 页
3、结果分析
固有响应和强迫响应 暂态响应和稳态响应
− 1 t RC +U
uC (t) = (U0 −US ) e
3-5 动态电路的输入-输出方程

2
§35 动态电路的输入-输出方程
d 2uc (t ) R duc (t ) 1 1 u ( t ) us (t ) c 2 dt L dt LC LC
d 2 i (t ) R di (t ) 1 1 dus (t ) i (t ) 2 dt L dt LC L dt
§35 动态电路的输入-输出方程 输入
作为输入激励的电压或者电流简称输入。 —— f(t) 如:电压源、电流源
输出
作为待求响应的电压或者电流简称输出。 —— r(t) 如:待求响应,任意电压或电流
输入-输出方程
联系输入变量和输出变量之间关系的单一变量的微 分方程。
电路原理
§35 动态电路的输入-输出方程 列写输入-输出方程的依据 拓扑约束
电路原理
§35 动态电路的输入-输出方程
us(t)为输入,i(t)为输出
di(t ) Ri(t ) L uc (t ) us (t ) dt 2 dit d it duc t dus t R L 2 dt dt dt dt
d i(t ) R di(t ) 1 1 dus (t ) i(t ) 2 dt L dt LC L dt
电路中含有两个独立的储能元件,所列方程
为二阶常系数线性微分方程。
电路原理
§35 动态电路的输入-输出方程
两个独立的储能元件 二阶常系数线性微分方程
n个独立的储能元件 n阶微分方程
输入-输出方程的一般形式
d n r (t ) d n1r (t ) dr (t ) an1 a1 a0 r (t ) n n 1 dt dt dt d m f (t ) d m1 f (t ) df (t ) bm bm1 b1 b0 f (t ) m m1 dt dt dt
电路理论习题库+参考答案

电路理论习题库+参考答案一、判断题(共100题,每题1分,共100分)1.欧姆定律可表示成U=RI,也可表示成U=-RI,这与采用的参考方向有关。
()A、正确B、错误正确答案:A2.非正弦周期信号分解后的傅里叶级数不一定是一个收敛的无穷三角级数()A、正确B、错误正确答案:B3.由于假定各节点电压的参考极性总是由独立节点指向参考节点,所以,各节点电压在相连电阻中引起的电流总是流出该节点的。
因此,节点电压方程的等式左边是各节点电压引起的流出相应节点的电流,而右边则是电流源和等效电流源注入节点的电流。
()A、正确B、错误正确答案:A4.电阻混联是指电阻连接中,既有串联又有并联()A、正确B、错误正确答案:A5.理想变压器反映阻抗的性质与负载阻抗的性质相反。
()A、正确B、错误正确答案:B6.三相电路是一种特殊类型的复杂电路,因而仍可采用一般复杂电路的分析方法对其进行分析和计算。
()A、正确B、错误正确答案:A7.支路分析法适用于分析支路数较少的电路()A、正确B、错误正确答案:A8.正弦电路中,若串联电路的总电压超前电流(电压、电流取关联参考方向),则此电路一定呈感性。
()A、正确B、错误正确答案:A9.造成系统误差的原因主要是操作者粗心大意。
()A、正确B、错误正确答案:B10.一个线性含源二端网络和其外部负载所构成的电路无唯一解时,此二端网络就可能无等效电源电路()A、正确B、错误正确答案:A11.电工指示仪表准确度的数字越小,表示仪表的准确度越低。
(A、正确B、错误正确答案:B12.对称三相电路Y-Y系统中不管是否含有高次谐波分量,U1=√3U()A、正确B、错误正确答案:B13.工程上将同向耦合状态下的一对施感电流的入端或出端定义为耦合电感的同名端()A、正确B、错误正确答案:A14.三相电路中,对称负载Y接无中线时,发生一相断路故障后,非断开相的相电压降低到电源线电压的一半。
()A、正确B、错误正确答案:A15.RLC串联电路的谐振,电源提供的无功功率为0,电路中无能量交换。
动态电路的方程及其初始条件
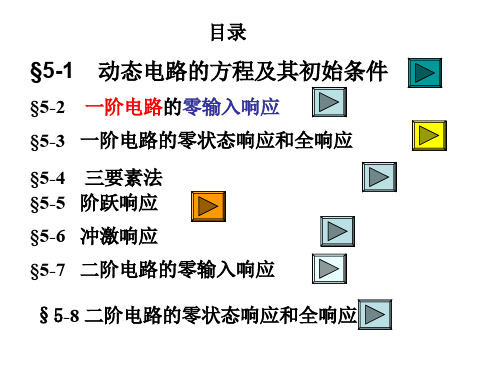
t=0
i
换路在 t=0 时刻进行 ,
Us
K
R
+
uC
C
–
-∞
0-
0
0+
+∞
原稳态 原稳态 换路 换路后初
终值
瞬间
始值
过渡 过程
新稳态
链接
RC电路
初始条件:为 t = 0+ 时 u , i 的值
动画
如在 t = t0 合上,则 t = t0+
二、换路定理
Switch Theorem
1. 电容 (cap acitor)
–
i
I 0e
R L
t
I 0e
L
t /
R
t 0
uL
L
di dt
t
RI 0e L / R
t 0
特征根 p = 由初始值
R L
i(0+)= I0
得:
A= i(0+)= I0
i(t)
I0e pt
I
0e
R L
t
令 = L/R , 一阶 RL 电路时间常数
[
]
+
- 10V
40kΩ
k iC
uCt = 0 时断开开关 k , 求
-
解: (1) 由 0- 电路求 uC(0-) (2) 由换路定律
+ 10kΩ
+
40kΩ
- 10V
iC
uC
-
+ i 10kΩ
- 10V
iC
iC(0+) ?
动态电路的电路方程

解:对于图(a)所示RC串联电路,可以写出以下方程
uS (t) uR (t) uC (t) Ri(t) uC (t)
在上式中代入: 得到
i(t) C duC (t) dt
RC
duC (t) dt
uC
(t)=uS (t)
(7-21)
这是常系数非齐次一阶微分方程,图(a)是一阶电路。
uS
经过整理得到以下微分方程
LC
d 2 uC dt 2
L ( R1
R2C)
duC dt
(R1 R2 ) R1
uC
uS
(7 26)
这是常系数非齐次二阶微分方程,图示电路是二阶电路。
必作习题:第266~267页 习题七:7 – 9 、 7 – 13 2002年春节摄于成都人民公园
R1C
duC dt
uS
(1)
R1iL
R1C
duC dt
uC
0
( 2)
从式(2)得到
iL
C
duC dt
1 R1
uC
将iL(t)代入式(1)中
LC
d 2 uC dt 2
L R1
duC dt
(R1
R2 )C
duC dt
(
R1
R1
R2
)
uC
R1C
duC dt
R1R2 R1 R2
uoc
R2 R1 R2
uS
由图(b)电路得到与式7-25相同的微分方程。
例7-11 电路如图7-21所示,以uC(t)为变量列出电路的微分 方程。
3-5动态电路的输入-输出方程.

联接形式所确定的约束关系(KVL,KCL) 元件性质所确定的约束关系(VCR)(有微分关系) 所以输入-输出方程为微分方程,方程阶数等于电路 独立动态元件个数。
3 建立输入-输出方程的方法: 第二章的方法
例1 建立以uS(t)为输入,uC(t)为输出的
输入—输出方程 解:由KCL
un2
iS
1
11
LD
un1
( LD
R2 )un2
0
D 常量 0
CD 1 1 R1 LD
11ຫໍສະໝຸດ CD 1 11
LD 1
un2
R1 LD 1
iS 0
LD
LD R2
LD
LCD 2un2
( L R1
R2C )Du n2
(1
R2 R1
)un 2
R2iS
LC
动态电路在换路时使电路从一个稳定工作状态 转变为另一个稳定工作状态,这种转变需要时 间,要经过一个过程。
§3-5 动态电路的输入—输出方程
三、动态电路方程
输入f(t):电压源的uS(t);电流源的iS(t) 输出r(t):待求响应(response) (任意电压或电流)
1 输入-输出方程——联系f(t)、r(t)的方程
§3-5 动态电路的输入—输出方程
一、换路 换路不需要时间,一般以换路发生时刻作 为计时时刻,即 t=0 时换路
t=0- 表示换路前瞬间,与t=0的间隔→0 t=0+ 表示换路后瞬间,与t=0的间隔→0 二、动态电路 1.动态电路定义 (a) 具有动态元件(L、C、M)
(b) 具有换路 2.动态电路阶数 = 等于独立储能元件个数
状态方程和输出方程

状态方程和输出方程状态方程和输出方程是系统理论中的重要概念,用于描述动态系统的行为。
状态方程描述了系统的状态如何随时间变化,而输出方程则描述了系统的输出如何由状态决定。
在这篇文章中,我们将详细介绍状态方程和输出方程的概念、推导方法和应用。
一、状态方程状态方程又称为状态空间方程或系统方程,用数学表示为:x(t)=A·x(t-1)+B·u(t)其中,x(t)为系统的状态向量,表示系统在其中一时刻的状态;A为状态转移矩阵,描述了系统的状态如何随时间变化;x(t-1)为系统在上一时刻的状态;B为输入矩阵,描述了外部输入信号如何影响系统的状态;u(t)为外部输入信号,表示系统在其中一时刻的输入。
状态方程的物理意义是描述系统的动态行为。
通过状态方程,我们可以了解系统的状态如何由前一时刻的状态和当前的输入决定。
状态方程是描述系统动态行为的基础,可以用于系统的建模、分析和控制。
推导状态方程的方法有两种:物理建模和数学建模。
物理建模是通过系统的物理原理和方程来推导状态方程;数学建模是通过对系统的输入输出进行数学分析,从而推导出状态方程。
物理建模适用于具有物理背景的系统,如机械系统、电路系统等;数学建模适用于所有类型的系统。
二、输出方程输出方程又称为观测方程或测量方程,用数学表示为:y(t)=C·x(t)其中,y(t)为系统的输出向量,表示系统在其中一时刻的输出;C为观测矩阵,描述了系统的输出如何由状态决定;x(t)为系统在其中一时刻的状态。
输出方程的物理意义是描述系统的输出如何由状态决定。
通过输出方程,我们可以了解系统的输出如何与系统的状态相关。
输出方程是描述系统的输出特性的关键,可以帮助我们理解系统的性能和行为。
推导输出方程的方法有直接测量和模型匹配。
直接测量是通过对系统的输出进行实际测量,从而得到输出方程;模型匹配是通过对系统进行数学建模,从而推导出输出方程。
直接测量适用于系统的输出直接可测量的情况;模型匹配适用于系统的输出无法直接测量或想要通过模型进行预测的情况。
《电路原理》(第2版) 周守昌 目录

第九章 拉普拉斯变换
§9-1 拉普拉斯变换 §9-2 拉普拉斯变换的基本性质 §9-3 进行拉普拉斯反变换的部分分式展开法 §9-4 线性动态电路方程的拉普拉斯变换解法
第十章 电路的复频域分析
§10-1 基尔霍夫定律的复复频域导纳 §10-3 用复频域模型分析线路动态电路 §10-4 网络函数
绪论
第一章 基尔霍夫定律和电阻元件
§1-1 电路和电路模型 §1-2 电流和电压的参考方向 §1-3 基尔霍夫定律 §1-4 电阻元件 §1-5 独立源 §1-6 受控源 §1-7 运算放大器 §1-8 支路分析法
第二章 电阻电路的分析
§2-1 线性电路的性质·叠加定理 §2-2 替代定理 §2-3 戴维宁定理 §2-4 诺顿定理 §2-5 有伴电源的等效变换 §2-6 星形电阻网络与三角形电阻网络的等效变换 §2-7 特勒根定理 §2-8 互易定理 §2-9 节点分析法 §2-10 回路分析法 §2-11 电源的转移
第三章 动态元件和动态电路导论
§3-1 电容元件 §3-2 电感元件 §3-3 耦合电感元件 §3-4 单位阶跃函数和单位冲激函数 §3-5 动态电路的输入— 输出方程 §3-6 初始状态与初始条件 §3-7 零输入响应 §3-8 零状态响应 §3-9 全响应
第四章 一阶电路与二阶电路
§4-1 一阶电路的零输入响应 §4-2 一阶电路的阶跃响应 §4-3 一阶电路的冲激响应 §4-4 一阶电路对阶跃激励的全响应 §4-5 二阶电路的冲激响应 §4-6 卷积积分及零状态响应的卷积计算法
第一章基尔霍夫定律和电阻元件11电路和电路模型12电流和电压的参考方向13基尔霍夫定律14电阻元件15独立源16受控源17运算放大器18支路分析法第二章电阻电路的分析21线性电路的性质叠加定理22替代定理23戴维宁定理24诺顿定理25有伴电源的等效变换26星形电阻网络与三角形电阻网络的等效变换27特勒根定理28互易定理29节点分析法210回路分析法211电源的转移第三章动态元件和动态电路导论31电容元件32电感元件33耦合电感元件34单位阶跃函数和单位冲激函数35动态电路的输入输出方程36初始状态与初始条件37零输入响应38零状态响应39全响应第四章一阶电路与二阶电路41一阶电路的零输入响应42一阶电路的阶跃响应43一阶电路的冲激响应44一阶电路对阶跃激励的全响应45二阶电路的冲激响应46卷积积分及零状态响应的卷积计算法第五章正弦电流电路导论51正弦电压和电流的基本概念52线性电路对正弦激励的响应正弦稳态响应53正弦量的相量表示法54基尔霍夫定律的相量形式55电路元件方程的相量形式56阻抗和导纳57阻抗的串联与并联第六章正弦电流电路的分析61正弦电流电路的相量分析62正弦电流电路中的功率63谐振电路64含有耦合电感元件的正弦电流电路65理想变量器第七章三相电路71对称三相电压72三相制的联接法73对称三相电路的计算74不对称三相电路的计算75三相电路中的功率第八章非正弦周期电流电路的分析81周期函数的傅里叶级数展开式82线性电路对周期性激励的稳态响应83非正弦周期电流和电压的有效值平均功率84傅里叶级数的指数形式85周期信号的频谱简介86对称三相电路中的高次谐波第九章拉普拉斯变换91拉普拉斯变换92拉普拉斯变换的基本性质93进行拉普拉斯反变换的部分分式展开法94线性动态电路方程的拉普拉斯变换解法第十章电路的复频域分析101基尔霍夫定律的复频域形式102电路元件的复频域模型复频域阻抗和复频域导纳103用复频域模型分析线路动态电路104网络函数附录非线性电路1非线性电阻元件及其约束关系2非线性电阻元件的串联和并联3非线性电阻电路的图解分析法4小信号分析法绪论返回
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
du C 1 + uC dt R1
将代入式(1)中,消去变量iL(t)得到仅以uC(t)为变量的微 分方程
LC d 2uC dt 2 + du du ( R + R2 ) L du C u C − R1C C = uS + ( R1 + R2 )C C + 1 dt dt R1 R1 dt
代入电容的VCR方程:
∴ RC
duC ( t ) + uC ( t ) = uS ( t ) dt
(a)电路的输入—输出方程
∴ GL
di L ( t ) + i L (t ) = i S (t ) dt
4
(b)电路的输入—输出方程
2009-10-21
2009-10-21
都是一个常系数非齐次一阶微分方程—一阶电路
(2)二阶电路 根据KVL和元件方程: uS(t) = uR(t) + uL(t) + uC(t) uR(t) =i ⋅R iC(t) = C⋅duC(t) /dt uL(t) = L⋅diL(t) /dt
d u ( t ) R duC ( t ) 1 1 得: C2 + + uC ( t ) = u S (t ) L dt LC LC dt
常系数非齐次二阶微分方程—二阶电路 (3)N阶电路—— 输入—输出方程是n阶微分方程的电路 方程的一般形式如书p109式(3-5-8)
2009-10-21 5 2009-10-21
6
1
§3.5 -§3.9
§3.5 -§3.9
§3.5 -§3.9
例:以uC(t)为变量列出电路的微分方程。
从式(2)得到iL(t)的表达式
iL = C
以iL(t)和iC(t)为网孔电流,列出网孔方程
d iL + ( R 1 + R 2 ) iL − R 1iC = u S dt − R 1iL + R 1iC + u C = 0 L
§3.5 -§3.9
一、几个概念 输入—作为激励的电压或电流称为输入(能量输 入)。 输出—作为待求响应的电压或电流称为输出。 单输入、单输出电路—只含有一个激励源和一个 输出变量的电路 。 输入-输出方程—电路的输入uS(t)(或iS(t))与 输出uC(t) (或iC(t))之间的单一变量的方程, 称为该电路的输入—输出方程。 二、动态电路的输入——输出方程 1 动态电路—含有动态元件(C,L)的电路
3
(a)所示RC电路,由KVL和元 件特性方程可写出以下方程: uS(t) = uR(t) + uC(t) = Ri(t) + uC(t) i(t) = C⋅duC(t) /dt
(b)所示RL电路,根据KVL和 元件特性可写出以下方程: iS(t) = iR(t) + iL(t) = Gu(t) + iL(t) u(t) = L⋅diL(t) /dt
常系数非齐次二阶微分方程
2009-10-21 8
2009-10-21
§3.5 -§3.9
作业:p109 p125
3-5-2 3-22
-21
9
2
§3.5 -§3.9
§3.5 -§3.9
如何评价? 激励 一个 系统 响应 输出
§3.5 -§3.9
§3.5 动态电路的输入—输出方程
主要内容: 什么是输入输出方程 动态电路输入—输出方程的 形式 敲击
输入
如何知道好坏? 声音
2009-10-21
1
2009-10-21
2
§3.5 -§3.9
2 动态电路的输入—输出方程 (1)一阶电路
iC = C
du C dt
(1) (2) 7
经过整理得到以下微分方程:
LC d 2uC dt 2 +( du ( R + R2 ) L + R2 C ) C + 1 u C = uS R1 dt R1 (7 − 26)
得到以iL(t)和uC(t)为变量的方程 :
du C diL + ( R1 + R 2 )i L − R1 C = uS dt dt du C − R1 i L + R1 C + uC = 0 dt L
2
§3.5 -§3.9
§3.5 -§3.9
i(t)
R
L
uR(t) uS(t)
uL(t) uC(t) C
几点说明: 对线性动态电路,输入—输出方程是常系数线性 微分方程。 原因:动态元件的u-i关系呈导数和积分关系; 动态电路也服从KL定律。 求解动态电路问题就变成解常系数线形微分方程 的数学问题。 电路的阶数不一定和电路中动态元件的个数一样 (因为动态元件的联接方式也有影响)。
