二自由度系统仿真
基于Matlab的二自由度系统模拟实验

基于Matlab 的两自由度振动系统模拟实验报告一、 实验目的1、 深入了解两自由度振动系统的模态正交性。
2. 掌握Matlab 编程基本语言和两自由度系统的响应模态求解方法。
二、 实验原理如图1所示的系统,设0=t 时,两个圆盘恰处于平衡位置, 设,221I I =2t t k k =。
图1 振动系统模型图设,,21θθ为21I I ,的转角,则21θθ,描述了系统的运动情况。
故该系统的自由度为两个。
当不考虑图示系统的阻尼和外界激励时,根据牛顿运动定律,其运动的微分方程为:[]⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎭⎬⎫⎩⎨⎧00][2121θθθθK M(1)其中[]⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=222100200I I I I M ,]⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--+=2222222212t t t t t t t t t k k k k k k k k k K 由[][]{}0)(=-u M ωK 2,可得频率方程如下:0002-22222222=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--I I k k k k t t t t ω (2)求解式(2)得2222122)22(22-2I k I k t t -==ω, 22222)22(I k t +=ω (3)系统振型为{}[]T 211=φ,{}[]T 212-=φ,其振型图如下:图2 系统振型图令{}{}⎥⎦⎤⎢⎣⎡-==Φ2211],[][21φφ, 则 ⎥⎦⎤⎢⎣⎡=ΦΦ10014][][][2I M T, ⎥⎥⎦⎤⎢⎢⎣⎡=ΦΦ22212004][][][ωωI K T (4)式(4)为振动系统的模态正交特性。
当考虑图1系统的外界激励时,即{}t F F F ωsin 21⎭⎬⎫⎩⎨⎧=时,其运动的微分方程为: []t F F K M ωθθθθsin ][212121⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎭⎬⎫⎩⎨⎧ (5)为了求出方程(5)的稳态解,可令⎭⎬⎫⎩⎨⎧Φ=⎭⎬⎫⎩⎨⎧2121][q q θθ,将⎭⎬⎫⎩⎨⎧Φ=⎭⎬⎫⎩⎨⎧2121][q q θθ代入式(5),同时方程两边同乘以T ][Φ,并利用振动系统的模态正交特性,有t I F F I F F q q qq ωωωsin )4/()2()4/()2(0022122121222121⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-+=⎭⎬⎫⎩⎨⎧⎥⎥⎦⎤⎢⎢⎣⎡+⎭⎬⎫⎩⎨⎧(6)利用式(6)很容易求得t I F F I F F q q Tωωωωωsin ))4/()2(,)4/()2((22222122122121---+=⎭⎬⎫⎩⎨⎧, 再由⎭⎬⎫⎩⎨⎧Φ=⎭⎬⎫⎩⎨⎧2121][q q θθ求得⎭⎬⎫⎩⎨⎧21θθ。
毕业设计-二自由度机器人的结构设计与仿真

二自由度机器人的结构设计与仿真学院:专业:姓名:指导老师:机械与车辆学院机械电子工程学号:职称:教授中国·XX二○一二年五月毕业设计诚信承诺书本人郑重承诺:本人承诺呈交的毕业设计《二自由度机器人的结构设计与仿真》是在指导教师的指导下,独立开展研究取得的成果,文中引用他人的观点和材料,均在文后按顺序列出其参考文献,设计使用的数据真实可靠。
本人签名:日期:年月日二自由度机器人的结构设计与仿真摘要并联机器人有着串联机器人所不具有的优点,在应用上与串联机器人形成互补关系。
二自由度并联机器人是并联机器人家族中的重要组成部分,由于结构简单、控制方便和造价低等特点,有着重要的应用前景和开发价值。
本论文研究了一种新型二自由度平移运动并联机构,该并联机构采用类五杆机构,平行四边形刚架结构来实现,可有效地消除铰链间隙,提高动平台的工作性能,同时有抵抗切削颠覆力矩的能力。
根据该二自由度平面机构的工作空间,利用平面几何的方法求得连杆的长度,并通过Pro/E软件进行仿真检验,并通过软件仿真的方式,优化连杆长度,排除奇异点,同时合理设计机械结构的尺寸,完成结构设计。
对该二自由度并联机器人,以Pro/E为平台,建立两自由度平移运动并联机器人运动仿真模型,验证了机构的实际工作空间和运动情况。
最后指出了本机构的在实际中的应用。
并使用AutoCAD软件进行了重要装置和关键零件的工程图绘制工作,利用ANSYS 软件分析了核心零件的力学性能。
研究结果表明,本文所设计的二自由度机器人性能良好、工作灵活,很好地满足了设计指标要求,并已具备了一定的实用性。
关键词:二自由度;并联机器人;仿真;结构设计;Pro/E2-DOF robot structure design and simulationAbstractParallel robot has a series of advantages of the robot does not have to form a complementary relationship between the application and the series robot. The 2-DOF parallel robot is an important part of the family of parallel robots. The structure is simple, convenient and cost control and low, with significant potential applications and the development value. In this thesis, a new 2- DOF translational motion parallel mechanism, the analogous mechanism for class five institutions, parallelogram frame structure, which can effectively eliminate the hinge gap and improve the performance of the moving platform, while resistance to cutting subvert the torque capacity.The working space of the 2-DOF planar mechanism, the use of plane geometry to obtain the length of the connecting rod, and the Pro/E software simulation test, and software simulation to optimize the connecting rod length, excluding the singular point, while the size of the rational design of mechanical structure, complete the structural design. And important equipment and key parts of the engineering drawings using AutoCAD software, using ANSYS software to analyze the mechanical properties of the core parts.The 2-DOF parallel robot to the Pro/E platform, the establishment of the 2-DOF of translational motion parallel robot simulation model to verify the organization's actual work space and movement. Finally, this institution in the practical application. The results show that the combination of good motor performance of the 2-DOF parallel robot,good to meet the index requirements, and already have a certain amount of practicality.Keywords: 2-DOF; parallel robot; simulation; structural design; Pro/E目录1前言 (1)1.1本课题的研究背景及意义 (1)1.1.1什么是机器人 (1)1.1.2机器人技术的研究意义 (1)1.2机器人的历史与发展现状 (2)1.2.1机器人的发展历程 (2)1.2.2机器人的主要研究工作 (3)1.2.3少自由度机器人的发展历程 (4)1.3本课题的研究内容 (5)2二自由度机器人系统方案设计 (7)2.1二自由度并联机器人机构简介 (7)2.2执行机构方案设计及分析 (7)3二自由度机器人的结构设计与运动分析 (8)3.1已知设计条件及参数 (8)3.1.1连杆机构自由度计算 (8)3.1.2五杆所能达到的位置计算 (8)3.2对机构主体部分的运动学逆解分析 (10)3.2.1位置分析 (10)3.2.2速度与加速的分析 (11)3.3受力分析 (12)4基于Pro/E软件环境下二自由度机器人的结构设计 (16)4.1 Pro/E软件简介 (16)4.2驱动元器件的选择 (17)4.2.1步进电机的选择 (17)4.2.2联轴器选择 (18)4.3平面连杆机构的结构参数确定 (19)4.4输入轴的设计 (20)4.5安装支架的参数确定 (21)5基于Pro/E软件环境下的机器人装配及动态仿真 (23)5.1虚拟装配过程 (23)5.1.1连杆机构的装配 (23)5.1.2安装支架的装配 (24)5.1.3完成二自由度机器人的最终装配 (24)5.2基于Pro/E软件环境下的动态仿真 (25)6基于AutoCAD软件环境下的机械结构设计 (31)6.1AutoCAD软件简介 (31)6.2平面连杆机构的结构设计 (32)6.3机架的结构部件图绘制 (33)6.4二自由度机器人工程图绘制 (34)7基于Ansys软件环境下的有限元分析 (36)7.1Ansys软件简介 (36)7.2对输入轴的有限元分析 (37)7.3对输入连杆的有限元分析 (37)8 总结与展望 (40)8.1课题研究工作总结 (40)8.2研究展望 (41)参考文献 (42)致谢 (44)附录(一) (45)附录(二) (52)1前言机器人技术是一门光机电高度综合、交叉的学科,它涉及机械、电气、力学、控制、通信等诸多方面。
[整理]matlab二自由度系统振动.
![[整理]matlab二自由度系统振动.](https://img.taocdn.com/s3/m/76298ee0c1c708a1284a4482.png)
利用Adams 和Matlab 对二自由度系统振动进行仿真与分析一、实验思想Adams 是一种可以对一些典型运动进行高效仿真的软件,本实验是利用Adams 对二自由度系统振动进行仿真及分析,再和理论公式对比,并用另外一种常见的仿真软件Matlab 的仿真结果进行对比,观察两者的差异,分析软件仿真产生差异的原因,加深对二自由度系统振动的理解。
二、二自由度系统振动分析固有频率取决于系统本身物理性质,而与初始条件无关。
对于二自由度的振动系统是有两种频率的简谐波组成的复合运动,这两个频率都是系统的固有频率。
主振型是当系统按固有频率作自由振动时,称为主振动。
系统作主振动时,任何瞬时各个运动坐标之间具有一定的相对比值,即整个系统具有确定的振动形态,称为主振型。
强迫振动是振动系统在周期性的外力作用下,其所发生的振动称为强迫振动,这个周期性的外力称为驱动力。
三、二自由度系统自由振动1.建立二自由度系统振动模型1)创建底座:先生成一个尺寸合适的长方体基体,再使用add to part 指令创建底座的侧壁。
2)使用new part 指令分别创建两个滑块,创建滑块时应注意滑块与滑块、滑块与侧壁之间的尺寸适当。
3)弹簧连接:分别用弹簧链接滑块、侧壁的中心点。
弹簧生成后,依次选中弹簧,在modify 选项中的stiffness and damping 下拉菜单中将damping coefficient 设置成no damping,即弹簧无阻尼。
添加约束:底座和地面固定,滑块和底座用滑动副连接。
弹簧刚度分别改为1、1、2(newton/mm)滑块质量分别为1.0 2.0滑块与机体滑动副的阻尼改为1.0E-0072.模型展示3.运动仿真结果设置x10=12经过Adams 运算后,滑块1、2 运动状态如图所示:4.matlab验证程序:k1=1000;k2=1000;k3=2000;m1=1;m2=2;a=(k1+k2)/m1;b=k2/m1;c=k2/m2;d=(k2+k3)/m2;[x1x2]=dsolve('D2x1+2000*x1-1000*x2=0','2*D2x2-1000*x1+3000*x2=0','x 1(0)=0.012','x2(0)=0','Dx1(0)=0','Dx2(0)=0','t')t1=0:0.01:2;;x1=subs(x1,'t',t1);x2=subs(x2,'t',t1);figureplot(t1,x1,'-');title('系统响应x(1)曲线');xlabel('时间/s');ylabel('位移/m');figureplot(t1,x2,'-');title('系统响应x(2)曲线');xlabel('时间/s');ylabel('位移/m');计算结果:5.结果分析存在差异的原因是Adams 仿真中并没有完全忽略摩擦力,而Matlab 计算时没有考虑摩擦,故存在差异,但是在允许范围内。
matlab二自由度车辆横摆角速度仿真代码

matlab二自由度车辆横摆角速度仿真代码摘要:一、引言二、Matlab 二自由度车辆横摆角速度仿真代码介绍1.二自由度车辆的定义2.Matlab 仿真代码的基本原理三、Matlab 二自由度车辆横摆角速度仿真实例1.仿真实验设置2.仿真实验结果四、结论正文:一、引言车辆动力学仿真是研究汽车行驶性能的重要方法,其中二自由度车辆模型是研究汽车操稳特性的基础。
Matlab 是一种广泛应用于科学计算和数据分析的编程语言,通过Matlab 可以方便地实现车辆动力学仿真。
本文将介绍一种基于Matlab 的二自由度车辆横摆角速度仿真代码。
二、Matlab 二自由度车辆横摆角速度仿真代码介绍1.二自由度车辆的定义二自由度车辆模型是指将车辆简化为两个自由度,即横摆角速度和侧偏角。
在这个模型中,悬架系统被忽略,整车简化为两轮,认为车轮在运动过程中不存在垂直振动。
二自由度车辆模型可以定量描述车辆质心位置、轮胎侧偏特性等影响车辆侧向运动的关键参数。
2.Matlab 仿真代码的基本原理Matlab 仿真代码通过建立车辆动力学模型,输入路面激励信号,计算出车辆的横摆角速度响应。
在这个过程中,需要考虑车辆的质量、轮胎刚度、悬挂刚度等因素。
通过改变这些参数,可以研究不同参数对车辆横摆角速度响应的影响。
三、Matlab 二自由度车辆横摆角速度仿真实例1.仿真实验设置在本例中,我们选取了一个二自由度车辆模型,输入路面激励信号为一个1rad 的转角。
车辆相关参数设置如下:车辆质量为1000kg,轮胎刚度为1000N/m,悬挂刚度为200N/m。
2.仿真实验结果通过Matlab 仿真,得到了车辆在路面激励信号作用下的横摆角速度响应。
从仿真实验结果可以看出,随着车辆质量的增加,横摆角速度响应减小;随着轮胎刚度的增加,横摆角速度响应减小;随着悬挂刚度的增加,横摆角速度响应增大。
四、结论通过Matlab 实现的二自由度车辆横摆角速度仿真代码,可以定量描述车辆在路面激励信号作用下的横摆角速度响应。
matlab仿真--二自由度机械臂动态仿真

机电系统的动力与运动的计算机仿真-----------基于二自由度两连杆平面机器人系统仿真马国锋梁应海周凯(武汉理工大学机电工程学院机械工程及自动化系)摘要:平面两连杆机器人(机械臂)是一种简单的两自由度的机械装置,其具有一定的复杂动力特性,对其的简单研究能够对机电系统和机器人有更好的学习了解和认识。
利用matlab仿真的快捷,简洁,以及可视化操作可以使其研究更方便,以及利用PID调节,使系统具有更好的时间响应性能。
关键词:matlab仿真PID控制调节平面机器人伺服直流电动机Abstract:The Planar two-link robot (Robot Arm) is a simple mechanical device of two degreesof freedom, it has complex dynamic characteristics. We can gain better learning and understandingfor Mechanical and Electrical systems and Robots only through studying it simply! Using thesuperior performance of MATLAB ,we can make the research more convenient ,besides ,we alsocan make the system have better performance in Time Response through the PID correction.0、引言随着科学技术的发展,利用计算机对控制系统进行仿真和分析,是研究控制系统的重要方法。
对控制系统进行仿真,首先应该建立系统模型,然后根据系统模型进行仿真,并充分的利用计算机作为工具进行数值求解。
Matlab是目前应用最为广泛的仿真语言之一。
第三章二自由度系统

二自由度系统振动 / 不同坐标系的运动微分方程
以汽车的二自由度振动模型为例
汽车板簧以上部分被简化成为一根刚性杆,具有质量m和绕质心 的转动惯量Ic。质心位于C 点。分别在A点和B点与杆相联的弹性 元件k1、k2为汽车的前,后板簧。
若系统有 n 个自由度,则各项皆为 n 维矩阵或列向量
二自由度系统振动 / 运动微分方程
式中:
[M
]
m11 m21
m12
m22
m1
0
0
m2
[K
]
k11 k 21
[C]
c11 c21
k12
k
22
k1 k2
k2
c12
c22
2 ET x1x1
2 ET x12
m1
m12
2 ET x1x2
2 ET x2x1
m21
0
m22
2ET x2x2
2 ET x22
m2
[M
]
m11 m21
m12
m22
m1
0
0
m2
二自由度系统振动 / 能量法
(t ) (t)
如同在单自由度系统中所定义的,在多自由度系统中 也将质量、刚度、位移、加速度及力都理解为广义的。
一种二自由度并联摇摆台运动分析与仿真

该摇 摆 台 的结 构 设 计 具 有 如 下特 点 : 动平 台具 有 三 条支 撑 腿 , 于 并 联 闭环 机 构 , 此 具 有 很 高 属 因 的支 撑 刚度 和 承 载 能 力 ; 外 , 于采 用 三 条 腿 并 此 由
当驱动液 压 缸 活 塞杆 , L 运 动 时 , 用 坐 和 采 标变 换法 可 以求解 运 动 平 台的 姿态 , 即舰 船 的横 摇 运动 和纵 摇运 动 。建 立 如 图 3所 示 的坐 标 系 , 中 其
以实现 既定规律 下运 动平 台的横摇和纵摇运 动, 完全满足“ 涅耳” 菲 光学助 降装置 的性 能测试要求。
关键词 “ 菲涅耳” 光学助 降装置 中图法分类号 T 1 32 ; H 1. 2
并联摇摆 台 文献标志码 A
横摇运动
纵摇运动
美 国现 代 大 型 航母 上都 安 装 有 “ 涅 耳 ” 学 菲 光 助 降装 置 , 图 1 示 , 如 所 为返航 着舰 的固定翼舰 载机 提供 3 5 ~ 。 . 。 4 的下 滑 角 , 助 飞行 员 进行 着 舰 。 由 辅 于航 母 的海 上 运 动 是 一 种 六 自 由度 的 随 机 复 杂 运
1 摇摆 台机构特点及 自由度分析
21 0 1年 5月 2 日收 到
第 9 山 讲师, 研究
1 1 机 构设 计特 点 .
方向: 航空机械工程。 -a:h5 308 i-m(o Emi wd8 35@sa 。・' l 8 c 3 n 1 1
联 支 撑运 动平 台 , 端 执 行 元 件 累 积 制 造 和装 配误 末
M =( 6—1 )X( 7—1 6— )+( 3+3× 3X1 2 1× 2+ )=
链, R表示转动副 , P表示移动副 , s表示球铰链 ) ,
基于MATLAB仿真的典型时滞系统的二自由度控制分析
Two De r e fFr e m nto g e s o e do Co r lAnay i lss Z HANG n, YI Yo g—s ng,HUANG Bi N n he An
( in x Api t nE gne n oe e eate t fE c i l n i e n ,Pnxa g3 7 2,C ia Ja g i p lai n ier gC lg ,D p r n o l tc gn r g ig i 3 0 c o i l m e ra E e i n 4 hn )
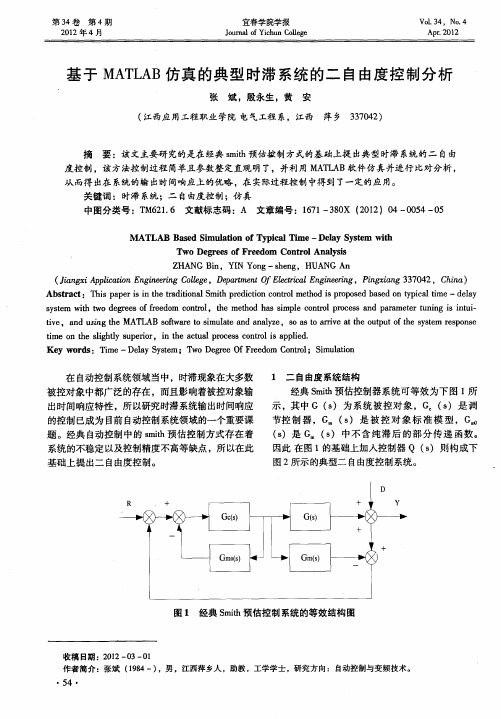
图 2 二 自 由度控 制 系统 结构 图
由 图 2可得 系统 的输 出为 :
Y s () ()+H () () ()= sR s o sD s 其 中,式 ( )为系统对给定值输入 的传递函 1
对象 () s 和控制器 Q s 可 以分别设计 ,从而让 () 系统 同时获得 良 的给定值动态响应特性和干扰值 好 动态响应特性 ,而不像传统 s i 控制那样在两种 mt h 响应特性之 间进行折中选择 ,并且使系统具有 比较
收稿 日期 :2 1 0 0 2— 3—0 1 作者简介 :张斌 ( 94一) 18 ,男 ,江西萍乡人 ,助教 ,工学学士 ,研究方向 :自动控制与变频技术 。
・
54 ・
第4 期
张 斌, 殷永生 ,黄
安 :基于 M T A 仿真 的典型时滞系统的二 自由度控制 分析 AL B
第 3 卷 4
从 而得 出在 系统的 输 出时间响应 上的优略 ,在 实际过程 控制 中得 到 了一定的 应用 。 关键 词 :时滞 系统 ;二 自由度 控制 ;仿真 中图分类 号 :T 6 16 文献标 志码 :A 文章 编号 :17 —30 (02 4 - 04- 5 M 2. 6 1 8X 2 1 )0 05 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二自由度系统仿真
传统的四轴客车的初始参数:
轴箱数 4*2=8个
摇枕数:2个
二系刚度以及阻尼:2*2=4侧
*8==40
*8==16
*8==120
*4==3.2
*4==1.2
*4==200
*4==120
=24000
2
原模型图:
垂向图横向
4ksz、4csz 4ksy、4csy
8kpy
8kpz、8cpz
简化图(简化为二自由度系统):
建立数学模型方程:
垂直:
横向:
将激励分离
并写成矩阵形式
垂向:
+ + =
横向:
+ +=垂直方向或横向振动都满足方程
+ + =
=
化简:
= *将其写成写成传递函数的形式
A=
Y方向的振动式同上
由此编制程序计算
原参数计算结果:
程序代码;
m=[24000,3000*2];
kz=[2,0.8];
ky=[5,0.3];
cz=[15,50];
cy=[0,30];
[Mz,Cz,Kz]=create_MCK(m,cz,kz);
[My,Cy,Ky]=create_MCK(m,cy,ky);
Wnz=getWn(Mz,Kz)
Wny=getWn(My,Ky)
[Z,Z1,Za,Z1a,w]=transfer_funVertical(Mz,Cz,Kz); [Y,Y1,Ya,Y1a,w]=transfer_funVertical(My,Cy,Ky);
对于原参数所计算得到的数据进行作图垂向频响函数
横向频响函数
探究参数对于频响函数的影响:
编制程序:
程序界面如下:
得到的有关结论:
说明在此我仅仅对于车体的垂向位移频响函数以及加速度频响函数进行讨论
考虑车辆垂向加速度传递函数的低频性能(即0-50rad/s)。
(人体在垂向的敏感频率为4-8Hz,32rad/s-
50rad/s)
根据推荐的优化方向,即在总静挠度不变的情况下,挠度的分配比为7:3(2.333)左右,二系的阻尼比为0.2-0.3。
根据此要求,我在界面上增加了控件。
并做了验证
其实,扰度比在1.5到2.5都不错
二系阻尼比变化:
如果提高一系阻尼可以是能量的分布向更高频率处分配(如果阻尼太大最终造成振动的能量无法耗散,全部集中在了高频部分)。
