2二维线性鉴别分析(2DLDA)
2 二维线性鉴别分析（2DLDA ）
2．1 实验原理
由上面的公式计算w G 和b G ，类似于经典的Fisher 准则，二维图像直接投影的广义Fisher 准则定义如下：
()T b T w X G X J X X G X
= 一般情况下w G 可逆，也就是根据1w b G G -计算本征值、本征向量，取最大的d 个本征值
对应的本征向量作为二维投影的向量组。
需要特别指出的是，尽管b G 和w G 都是对称矩阵，
但1w b G G -不一定是对称矩阵。
所以各投影轴之间关于w G 及t G 共轭正交，而不是正交。
本实验为简单起见，使用的为欧式距离。
2.2 实验过程
读取训练样本——〉求样本均值——〉求类内散布矩阵——〉特征值分解——〉对实验样本分类——〉计算分类正确率
2.3 实验结果分析
本实验中的类别数为40，每类的样本数为10，训练数为5，检测数为5。
实验的结果正确率为72%，结果正确率偏低。
2.4 matlab 代码
clear all;
t0=clock;
class_num = 40;
class_sample = 10;
train_num = 5;
test_num = 5;
scale = 1;
allsamples=[];%所有训练图像
gnd=[];
k=1;
path = ['C:\Documents and Settings\dongyan\桌面\模式识别\ORL\ORL\ORL'];
for i=1:class_num
for j =1:train_num
name =[path num2str(10*i+j-10,'%.3d') '.BMP' ];
[a,map]=imread(name,'bmp');
a = imresize(a,scale);
a=double(a);
ImageSize=size(a);
height=ImageSize(1);
width=ImageSize(2);
A=reshape(a,1,ImageSize(1)*ImageSize(2));
allsamples=[allsamples;A];
gnd(k)=i;
k=k+1;
end;
end;
trainData=allsamples;
sampleMean=mean(allsamples);%求所有图片的均值
[nSmp,nFea] = size(trainData);
classLabel = unique(gnd);
nClass = length(classLabel);
classmean=zeros(nClass,height*width);%求每类的均值
for i=1:nClass
index = find(gnd==classLabel(i));
classmean(i,:)=mean(trainData(index, :));
end
Gb=0;
Amean=reshape(sampleMean,height,width);%求类间散布矩阵Gb
for i=1:nClass
Aimean=reshape(classmean(i,:),height,width);
Gb=Gb+(Aimean-Amean)'*(Aimean-Amean);
end
Gw=0;%求类内散布矩阵
for i=1:nClass
for j=train_num*(i-1)+1:train_num*i
g=reshape((trainData(j,:)-classmean(i,:)),height,width);
Gw=Gw+g'*g;
end
end
invGw=inv(Gw);%求（Gw-1）*Gb
U=invGw*Gb;
[eigvu eigvet]=eig(U);%求特征值与特征向量
d=diag(eigvu);
[d1 index]=sort(d);
cols=size(eigvet,2);
for i=1:cols
vsort(:,i) = eigvet(:, index(cols-i+1) ); % vsort 是一个M*col阶矩阵，保存的是按降序排列的特征向量,每一列构成一个特征向量
dsort(i) = d( index(cols-i+1) ); % dsort 保存的是按降序排列的特征值，是一维行向量end %完成降序排列
for i=1:8
X(:,i)=vsort(:,i);%X表示投影轴
end
accu=0;%做测试，记录命中率
for i=1:class_num
for j =train_num+1:class_sample
name =[path num2str(10*i+j-10,'%.3d') '.BMP' ];
Image = double(imread(name));
Image = imresize(Image,scale);
testdata1=Image*X;
for k=1:class_num*train_num
juli(k)=norm(testdata1-reshape(trainData(k,:),height,width)*X);%计算图片与训练样本之间的距离，如果距离最小，认为测试图片与训练图片属于同一类
end;
[r t]=min(juli);
if fix((t-1)/train_num)==(i-1)
accu=accu+1;
end
end;
end;
accu=accu/(class_num*test_num);
accu
time1 = etime(clock,t0)。
基于双向2 DLDA与 LDA相结合的 SAR目标识别算法
基于双向2 DLDA与 LDA相结合的 SAR目标识别算法杨佐龙;王德功;胡朝军;尹辉;岳剑飞【期刊名称】《计算机应用与软件》【年(卷),期】2014(000)011【摘要】线性判决分析（ LDA）用于图像特征提取时，存在着损失二维空间结构信息、计算复杂度大的缺点。
二维线性判决分析（2DLDA）弥补了LDA的缺点，但2DLDA仅消除了图像各列间的相关性，所提取的图像特征维数仍然较大。
为解决上述问题，采用双向2DLDA与LDA相结合的特征提取算法对图像的行和列同时进行压缩，减少特征矩阵维数，降低计算量。
实验结果表明，所提出的SAR （ Synthetic Aperture Radar）图像目标识别方法有效地降低了图像数据维数，提高了识别率，并克服了方位角变化对识别结果的影响。
%Linear discriminant analysis ( LDA) has the disadvantages of information losses in regard to two-dimensional spatial structure and high computational complexity when applying to image feature extraction.Two-dimensional linear discriminant analysis (2DLDA) makes up the flaws of LDA.However, it only eliminates the pertinence between the columns of image, while the number of features extracted is still large.In order to solve the problems, we adopt a new feature extraction algorithm to compress the columns and rows of image simultaneously, which combines the bidirectional 2DLDA with LDA, thus reduces the number of feature matrix dimensions and decreases the calculation amount.Experimental results show that the SAR images recognition method presented in this paper effectively reducesimage dimensions numberand raises recognition rate, it also overcomes the impact on recognition result brought by the variation of target azimuth.【总页数】5页(P279-282,317)【作者】杨佐龙;王德功;胡朝军;尹辉;岳剑飞【作者单位】空军航空大学吉林长春 130022;空军航空大学吉林长春 130022;解放军94916部队江苏南京 210022;空军航空大学吉林长春 130022;解放军66347部队河北保定 071000【正文语种】中文【中图分类】TN957.52;TP391【相关文献】1.一种基于重采样双向2DLDA融合的人脸识别算法 [J], 李文辉;姜园媛;王莹;傅博2.一种用于SAR目标特征提取的I2DLDA方法 [J], 刘振;姜晖3.2DPCA+2DLDA和改进的LPP相结合的人脸识别算法 [J], 李球球;杨恢先;奉俊鹏;蔡勇勇;翟云龙4.两向2DLDA与SVM相结合的SAR图像识别 [J], 杨佐龙;王德功;胡朝军;王新超5.基于局部二元模式和重采样双向2DLDA的人脸识别算法 [J], 苏立明;王莹;姜园媛;李文辉因版权原因，仅展示原文概要，查看原文内容请购买。
《线性判别分析LDA》PPT课件
类别的原始数据，现在要求将数据从二维降维到一维。直接投影
到x1轴或者x2轴，不同类别之间 会有重复，导致分类效果下降。
右图映射到的直线就是用LDA方法计算得到的，可以看到，红色类
别和绿色类别在映射之后之间的距离是最大的，而且每个类别内
部点的离散程度是最小的（或者说聚集程度是最大的）。
5
2021/3/3
6
2021/3/3
LDA
要说明白LDA，首先得弄明白线性分类器(Linear Classifier)
：因为LDA是一种线性分类器。对于K-分类的一个分类问题，
会有K个线性函数：
权向量（weight vector） 法向量（normal vector）
阈值（threshold） 偏置（bias）
当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x 属于类别k。对于每一个分类，都有一个公式去算一个分值， 在所有的公式得到的分值中，找一个最大的，就是所属的分类 。
12
2021/3/3
么么么么方面 Sds绝对是假的
LDA
我们定义一个投影前的各类别分散程度的矩阵，这个矩阵看起 来有一点麻烦，其实意思是，如果某一个分类的输入点集Di里 面的点距离这个分类的中心店mi越近，则Si里面元素的值就越 小，如果分类的点都紧紧地围绕着mi，则Si里面的元素值越更 接近0.
7
2021/3/3
LDA
上式实际上就是一种投影，是将一个高维的点投影到一条高维 的直线上，LDA最求的目标是，给出一个标注了类别的数据集， 投影到了一条直线之后，能够使得点尽量的按类别区分开，当 k=2即二分类问题的时候，如下图所示：
红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过 原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和 蓝色的点被原点明显的分开了，这个数据只是随便画的，如果在高维 8的情况下，看起来会更好一点。下面我来推导一下二分类LDA问题的2021公/3/3 式：
线性判别分析
线性判别分析
线性判别分析(linear discriminant analysis，LDA)是对费舍尔的线性鉴别方法的归纳，这种方法使用统计学，模式识别和机器学习方法，试图找到两类物体或事件的特征的一个线性组合，以能够特征化或区分它们。
所得的组合可用来作为一个线性分类器，或者，更常见的是，为后续的分类做降维处理。
之前我们讨论的PCA、ICA也好，对样本数据来言，可以是没有类别标签y的。
回想我们做回归时，如果特征太多，那么会产生不相关特征引入、过度拟合等问题。
我们可以使用PCA来降维，但PCA没有将类别标签考虑进去，属于无监督的。
比如回到上次提出的文档中含有“learn”和“study”的问题，使用PCA后，也许可以将这两个特征合并为一个，降了维度。
但假设我们的类别标签y是判断这篇文章的topic是不是有关学习方面的。
那么这两个特征对y几乎没什么影响，完全可以去除。
Fisher提出LDA距今已近七十年，仍然是降维和模式分类领域应用中最为广泛采用而且极为有效的方法之一，其典型应用包括人脸检测、人脸识别、基于视觉飞行的地平线检测、目标跟踪和检测、信用卡欺诈检测和图像检索、语音识别等。
线性判别分析（LinearDiscriminantAnalysis，LDA）
线性判别分析（LinearDiscriminantAnalysis，LDA）⼀、LDA的基本思想线性判别式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher线性判别(Fisher Linear Discriminant ,FLD)，是模式识别的经典算法，它是在1996年由Belhumeur引⼊模式识别和⼈⼯智能领域的。
线性鉴别分析的基本思想是将⾼维的模式样本投影到最佳鉴别⽮量空间，以达到抽取分类信息和压缩特征空间维数的效果，投影后保证模式样本在新的⼦空间有最⼤的类间距离和最⼩的类内距离，即模式在该空间中有最佳的可分离性。
如下图所⽰，根据肤⾊和⿐⼦⾼低将⼈分为⽩⼈和⿊⼈，样本中⽩⼈的⿐⼦⾼低和⽪肤颜⾊主要集中A组区域，⿊⼈的⿐⼦⾼低和⽪肤颜⾊主要集中在B组区域，很显然A组合B组在空间上明显分离的，将A组和B组上的点都投影到直线L上，分别落在直线L的不同区域，这样就线性的将⿊⼈和⽩⼈分开了。
⼀旦有未知样本需要区分，只需将⽪肤颜⾊和⿐⼦⾼低代⼊直线L的⽅程，即可判断出未知样本的所属的分类。
因此，LDA的关键步骤是选择合适的投影⽅向，即建⽴合适的线性判别函数（⾮线性不是本⽂的重点）。
⼆、LDA的计算过程1、代数表⽰的计算过程设已知两个总体A和B，在A、B两总体分别提出m个特征，然后从A、B两总体中分别抽取出、个样本，得到A、B两总体的样本数据如下：和假设存在这样的线性函数（投影平⾯），可以将A、B两类样本投影到该平⾯上，使得A、B两样本在该直线上的投影满⾜以下两点：（1）两类样本的中⼼距离最远；（2）同⼀样本内的所有投影距离最近。
我们将该线性函数表达如下：将A总体的第个样本点投影到平⾯上得到投影点，即A总体的样本在平⾯投影的重⼼为其中同理可以得到B在平⾯上的投影点以及B总体样本在平⾯投影的重⼼为其中按照Fisher的思想，不同总体A、B的投影点应尽量分开，⽤数学表达式表⽰为，⽽同⼀总体的投影点的距离应尽可能的⼩，⽤数学表达式表⽰为，，合并得到求从⽽使得得到最⼤值，分别对进⾏求导即可，详细步骤不表。
2二维线性鉴别分析（2DLDA）
2二维线性鉴别分析（2DLDA）2 二维线性鉴别分析（2DLDA ）2．1 实验原理由上面的公式计算w G 和b G ，类似于经典的Fisher 准则，二维图像直接投影的广义Fisher 准则定义如下：()T b T w X G X J X X G X= 一般情况下w G 可逆，也就是根据1w b G G -计算本征值、本征向量，取最大的d 个本征值对应的本征向量作为二维投影的向量组。
需要特别指出的是，尽管b G 和w G 都是对称矩阵，但1w b G G -不一定是对称矩阵。
所以各投影轴之间关于w G 及t G 共轭正交，而不是正交。
本实验为简单起见，使用的为欧式距离。
2.2 实验过程读取训练样本——〉求样本均值——〉求类内散布矩阵——〉特征值分解——〉对实验样本分类——〉计算分类正确率2.3 实验结果分析本实验中的类别数为40，每类的样本数为10，训练数为5，检测数为5。
实验的结果正确率为72%，结果正确率偏低。
2.4 matlab 代码clear all;t0=clock;class_num = 40;class_sample = 10;train_num = 5;test_num = 5;scale = 1;allsamples=[];%所有训练图像gnd=[];k=1;path = ['C:\Documents and Settings\dongyan\桌面\模式识别\ORL\ORL\ORL'];for i=1:class_numfor j =1:train_numname =[path num2str(10*i+j-10,'%.3d') '.BMP' ];[a,map]=imread(name,'bmp');a = imresize(a,scale);a=double(a);ImageSize=size(a);height=ImageSize(1);width=ImageSize(2);A=reshape(a,1,ImageSize(1)*ImageSize(2));allsamples=[allsamples;A];gnd(k)=i;k=k+1;end;end;trainData=allsamples;sampleMean=mean(allsamples);%求所有图片的均值[nSmp,nFea] = size(trainData);classLabel = unique(gnd);nClass = length(classLabel);classmean=zeros(nClass,height*width);%求每类的均值for i=1:nClassindex = find(gnd==classLabel(i));classmean(i,:)=mean(trainData(index, :));endGb=0;Amean=reshape(sampleMean,height,width);%求类间散布矩阵Gbfor i=1:nClassAimean=reshape(classmean(i,:),height,width);Gb=Gb+(Aimean-Amean)'*(Aimean-Amean);endGw=0;%求类内散布矩阵for i=1:nClassfor j=train_num*(i-1)+1:train_num*ig=reshape((trainData(j,:)-classmean(i,:)),height,width);Gw=Gw+g'*g;endendinvGw=inv(Gw);%求（Gw-1）*GbU=invGw*Gb;[eigvu eigvet]=eig(U);%求特征值与特征向量d=diag(eigvu);[d1 index]=sort(d);cols=size(eigvet,2);for i=1:colsvsort(:,i) = eigvet(:, index(cols-i+1) ); % vsort 是一个M*col阶矩阵，保存的是按降序排列的特征向量,每一列构成一个特征向量dsort(i) = d( index(cols-i+1) ); % dsort 保存的是按降序排列的特征值，是一维行向量end %完成降序排列for i=1:8X(:,i)=vsort(:,i);%X表示投影轴endaccu=0;%做测试，记录命中率for i=1:class_numfor j =train_num+1:class_samplename =[path num2str(10*i+j-10,'%.3d') '.BMP' ];Image = double(imread(name));Image = imresize(Image,scale);testdata1=Image*X;for k=1:class_num*train_numjuli(k)=norm(testdata1-reshape(trainData(k,:),height,width)*X);%计算图片与训练样本之间的距离，如果距离最小，认为测试图片与训练图片属于同一类end;[r t]=min(juli);if fix((t-1)/train_num)==(i-1)accu=accu+1;endend;end;accu=accu/(class_num*test_num);accutime1 = etime(clock,t0)。
线性判别分析（LDA）
线性判别分析（LDA）说明：本⽂为个⼈随笔记录，⽬的在于简单了解LDA的原理，为后⾯详细分析打下基础。
⼀、LDA的原理LDA的全称是Linear Discriminant Analysis（线性判别分析），是⼀种supervised learning。
LDA的原理：将带上标签的数据（点），通过投影的⽅法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，⼀簇⼀簇的情况，相同类别的点，将会在投影后的空间中更接近。
因为LDA是⼀种线性分类器。
对于K-分类的⼀个分类问题，会有K个线性函数：当满⾜条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。
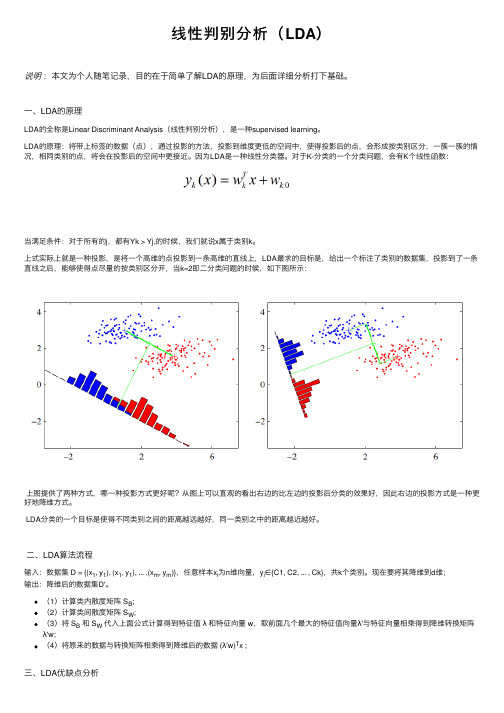
上式实际上就是⼀种投影，是将⼀个⾼维的点投影到⼀条⾼维的直线上，LDA最求的⽬标是，给出⼀个标注了类别的数据集，投影到了⼀条直线之后，能够使得点尽量的按类别区分开，当k=2即⼆分类问题的时候，如下图所⽰：上图提供了两种⽅式，哪⼀种投影⽅式更好呢？从图上可以直观的看出右边的⽐左边的投影后分类的效果好，因此右边的投影⽅式是⼀种更好地降维⽅式。
LDA分类的⼀个⽬标是使得不同类别之间的距离越远越好，同⼀类别之中的距离越近越好。
⼆、LDA算法流程输⼊：数据集 D = {(x1, y1), (x1, y1), ... ,(x m, y m)}，任意样本x i为n维向量，y i∈{C1, C2, ... , Ck}，共k个类别。
现在要将其降维到d维；输出：降维后的数据集D'。
（1）计算类内散度矩阵 S B;（2）计算类间散度矩阵 S W;（3）将 S B和 S W代⼊上⾯公式计算得到特征值λ和特征向量 w，取前⾯⼏个最⼤的特征值向量λ'与特征向量相乘得到降维转换矩阵λ'w;（4）将原来的数据与转换矩阵相乘得到降维后的数据 (λ'w)T x ;三、LDA优缺点分析LDA算法既可以⽤来降维，⼜可以⽤来分类，但是⽬前来说，主要还是⽤于降维。
一种基于图像隶属度的分块2DLDA人脸识别方法
时Ｌ ＤＡ不 一定具 有最 佳鉴 别性能 。因此 在小 样本情 况下 ，如何 抽取
然 后计算测试样本对每一类所有子块 的隶 属度 ，从大到小依次排 列为： （ 【 （， Ｑ １ ） （… ・ ２ ） ， （ ），分类原则是取每幅 人脸 图 ｘ ） 像 中隶 属度最 大的ｘ 个子 块 ：
人脸 识别 的研究 具有 巨大 的理论 意义和 应用 价值 ，它对 图象处 理 、模式识别 、计算机 视觉等领域的发展具有 巨大的推动作用 ，同时 在 生物特征认证 、视频 监控 、安全等各个领域也 有着非常广泛 的应用
ｌ
：
－ ｔ
… ‘ … ‘
ｌ｝ｌ ｌ － Ｂ ｚ Ｂ ｊ ２
Ｑ … ‘ ５）
ＬＡ Ｄ 人脸识 别方法仅适 用于类 内散布矩阵 的情 形 ， 实际应用 中 但 存在 着大量的典型的小样本 问题 ，类 内散布矩阵经常是 奇异的 。这是
因为 待识别的图像矢量 的维 数一般较高 ，而在实 际问题 中难以找到或 根本 不可能找到足够 多的训练 样本来保证类 内散布矩 阵的可逆性 ，这
技 术 创 新
缸 科 技 ２ １年第９ ０ ２ 期
一
种 基 于图像隶 属度 的分块２ ＤＡ ＤＬ 人脸识别 方法
苏 长 明
信息 科学与技术 学院 成 都学院 ６ ０ ０ 成 都 １１６
摘 要 有效地提取特 征和设计好 的分 类方法是人脸识 别的关键 ，本 文结合隶属度 函数提 出一种基 于图像 分块 的二维线性判别分 析识 别方 法。首先对人脸样本 图像等量划分 为若 干个子模 块 ，再直接对子模 块图像 矩阵进行二 维线性判 别分析提 取特征 ，得到子模块 低维特征 矩阵 ，最后算 出测试 图像 子模块相对 于训 练类对应子模块的 隶属度 ，选取几个隶属度最 大的于模块进 行权值叠加 ，被测试 图 像 最 终 归属 于 叠加 结 果 最 大 的 一 类 。 该 方 法 既 克服 了 小样 本 问题 又 具 有 更 人 性 化 的 分 类 设 计 。在 ＯＲＬ Ｆ ＲＥ －－ 数 据 库 上 的 实验 结 和 Ｅ Ｔ＆脸 果表 明，提 出的方法不仅 运算量小而且识别率也 明显优 于其 它方法。 关键词 二维线性判 别分析 人脸识 别 特征提取 隶属度
融合2DDCT、2DPCA和2DLDA的人脸识别方法
融合2DDCT、2DPCA和2DLDA的人脸识别方法廖正湘;陈元枝;李强【摘要】二维主分量分析(2DPCA)是人脸识别中的一种非常有效的特征提取方法.二维线性判别(2DLDA)方法具有很好的分类效果.在研究这两种理论的基础上提出一种基于2DDCT(二维离散余弦变换)与2DPCA+ 2DLDA相结合的人脸识别方法,并在0RL人脸库上分别对单一的方法与相融合的方法进行识别比较研究.实验结果表明,提出的方法不仅提高了识别率,而且减少了训练与分类时间.%Two-dimensional principal component analysis (2DPCA) is a very effective feature extraction method in face recognition; two-dimensional linear discriminant (2DLDA) method has very good classification results. In this paper, based on the study of these two theories, we propose a new face recognition method which is on the basis of integrating the two-dimensional discrete cosine transform (2DDCT) with 2DPCA and 2DLDA, and utilising the ORL database we carry out respectively the comparative study on recognitions with each single method and the integrated method. Experimental results show that the integrated method proposed in the paper improves the recognition rate, and it also reduces the training and classification time as well.【期刊名称】《计算机应用与软件》【年(卷),期】2012(029)009【总页数】4页(P237-239,288)【关键词】二维主分量分析;二维线性判别分析;特征提取;离散余弦变换【作者】廖正湘;陈元枝;李强【作者单位】桂林电子科技大学电子工程与自动化学院广西桂林541004;桂林电子科技大学电子工程与自动化学院广西桂林541004;桂林电子科技大学电子工程与自动化学院广西桂林541004【正文语种】中文【中图分类】TP391.410 引言人脸识别技术在身认证、视频监控等安防领域得到了广泛的应用，是生物特征识别系统中研究中的热门话题之一。
线性判别分析LDA与主成分分析PCA
基本思想
线性判别分析的基本思想是将高维的模式样本投 影到最佳鉴别矢量空间，以达到抽取分类信息和 压缩特征空间维数的效果。投影后保证模式样本 在新的子空间有最大的类间距离和最小的类内距 离，即模式在该空间中有最佳的可分离性。因此， 它是一种有效的特征抽取方法。使用这种方法能 够使投影后模式样本的类间散布矩阵最大，并且 同时类内散布矩阵最小。
基本思想
主成分分析所要做的就是设法将原来众多具 有一定相关性的变量，重新组合为一组新的 相互无关的综合变量来代替原来变量。通常， 数学上的处理方法就是将原来的变量做线性 组合，作为新的综合变量，但是这种组合如 果不加以限制，则可以有很多，应该如何选 择呢？
基本思想
如果将选取的第一个线性组合即第一个综合变量记为F1 ，自然希望它尽可能多地反 映原来变量的信息，这里“信息”用方差来测量，即希望Var(F1)越大，表示F1包 含的信息越多。因此在所有的线性组合中所选取的F1应该是方差最大的，故称F1为 第一主成分。如果第一主成分不足以代表原来p 个变量的信息，再考虑选取F2即第 二个线性组合，为了有效地反映原来信息,F1已有的信息就不需要再出现在F2中， 用数学语言表达就是要求Cov(F1 ,F2)=0，称F2为第二主成分，依此类推可以构造 出第三、四…第p 个主成分。
例子
举一个例子，假设我们对一张100*100像素的 图片做人脸识别，每个像素是一个特征，那 么会有10000个特征，而对应的类别标签y仅 仅是0，1值，1代表是人脸。这么多特征不仅 训练复杂，而且不必要特征对结果会带来不 可预知的影响，但我们想得到降维后的一些 最佳特征（与y关系最密切的），怎么办呢？
下面给出一个例子，说明LDA的目标：
可以看到两个类别，一个绿色类别，一个红色类 别。左图是两个类别的原始数据，现在要求将数 据从二维降维到一维。直接投影到x1轴或者x2轴， 不同类别之间 会有重复，导致分类效果下降。右 图映射到的直线就是用LDA方法计算得到的，可以 看到，红色类别和绿色类别在映射之后之间的距 离是最大的，而且每个类别内 部点的离散程度是 最小的（或者说聚集程度是最大的）。
判别分析模型研究及应用
判别分析模型研究及应用判别分析模型是一种统计分析方法，用于解决分类问题。
其主要目标是通过对已知分类的样本进行学习，得出一个分类函数，然后通过应用这个分类函数对未知样本进行分类。
判别分析模型在许多领域中都得到广泛的应用，例如医学诊断、金融风险评估、文本分类等。
判别分析模型主要包括线性判别分析（Linear Discriminant Analysis，简称LDA）和二次判别分析（Quadratic Discriminant Analysis，简称QDA）两种。
LDA 假设样本的特征在每个类别中的分布服从正态分布，且各个类别的协方差矩阵相同。
LDA通过计算每个类别的均值向量和协方差矩阵，然后基于贝叶斯决策理论计算后验概率，从而得到分类函数。
QDA则放松了协方差矩阵相同的假设，允许每个类别有不同的协方差矩阵。
判别分析模型的研究主要围绕以下几个方面展开。
首先，模型的建立和求解是研究的重点之一。
在模型建立过程中，需要根据实际问题选择适当的判别准则和优化方法，以提高模型的分类性能。
其次，特征选择和降维也是研究的热点。
由于判别分析模型的性能受样本维度的影响，因此特征选择和降维可以提高模型的准确性和效率。
另外，与其他机器学习方法的集成也是一个重要的研究方向。
判别分析模型与支持向量机、神经网络等机器学习方法相结合，可以提高分类性能，拓展模型的应用范围。
判别分析模型在实际应用中具有广泛的应用价值。
一方面，它可以用于医学诊断，帮助医生识别疾病并制定治疗方案。
例如，通过对病人的病历、症状和检测结果进行分析，可以建立一个判别分析模型，用于区分正常人和疾病人群。
另一方面，判别分析模型也可以用于金融风险评估。
通过对客户的个人信息、信用记录和财务状况进行分析，可以建立一个判别分析模型，用于预测客户是否有违约的风险。
此外，判别分析模型还可以用于文本分类。
通过对文本的词频、词义和句法等进行分析，可以建立一个判别分析模型，用于将文本分类到不同的主题或类别。