控制工程基础 第6章 控制系统的误差分析和计算
合集下载
控制工程基础6章
H(S) +
Xor(S)
+ N(S)
+
-
E(S)
G1(S)
G2(S)
X0(S)
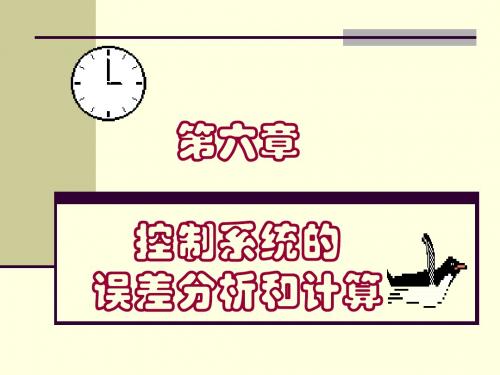
设xor (t )是控制系统希望的输出信号，而 xo (t ) 是实际的输出信号, 一般把二者之差定义为 误差信号，记做e(t), e(t) = xor (t ) - xo (t )
m(p) 是理想算子，是认为规 定的。一般情况下， m( s) =1/H(s)。
时的系统输出端的稳态误差。
1 2 例题：求下图所示系统 在1(t), t, 和 t 分别作用下的稳态误差 。 2
五、扰动引起的误差
+
G1(s) N(s) G2(s) Xo(s)
Xi(s) +
+
Y(s) H(s)
要想求稳态偏差，可以利用叠加原理，分别求
出给定信号Xi(s) 和N(s)单独作用时的偏差，然
2 2
对于0型系统，Ka=0，ess=
对于I型系统， Ka=0, ess=
对于II型系统， Ka=K, ess= 1/K 对于III型及以上系统， Ka= , ess= 0
0和I型系统不能跟踪单位斜坡输入，I I型系统能跟踪单 位斜坡输入但有静差，需要III型以上系统才能消除静差。
10 G 例：设有一非单位反馈控制系统， ( s) = s 1 H(s)=Kh，输入为单位阶跃。试求， Kh=1和0.1
结构形式 输入形 式
1 例：设单位反馈控制系统的 G( s) = ，输 2 Ts t 入信sint ， 2 试求系统的稳态误差。
为什么？ 因为：E(s) = s (s 2 2 )(s 1 ) T T 1 T s T 2 3 1 =- 2 2 2 2 2 2 2 2 1 T 1 s 2 T 1 s 2 T 1 s T 求拉式反变换 T
Xor(S)
+ N(S)
+
-
E(S)
G1(S)
G2(S)
X0(S)
设xor (t )是控制系统希望的输出信号，而 xo (t ) 是实际的输出信号, 一般把二者之差定义为 误差信号，记做e(t), e(t) = xor (t ) - xo (t )
m(p) 是理想算子，是认为规 定的。一般情况下， m( s) =1/H(s)。
时的系统输出端的稳态误差。
1 2 例题：求下图所示系统 在1(t), t, 和 t 分别作用下的稳态误差 。 2
五、扰动引起的误差
+
G1(s) N(s) G2(s) Xo(s)
Xi(s) +
+
Y(s) H(s)
要想求稳态偏差，可以利用叠加原理，分别求
出给定信号Xi(s) 和N(s)单独作用时的偏差，然
2 2
对于0型系统，Ka=0，ess=
对于I型系统， Ka=0, ess=
对于II型系统， Ka=K, ess= 1/K 对于III型及以上系统， Ka= , ess= 0
0和I型系统不能跟踪单位斜坡输入，I I型系统能跟踪单 位斜坡输入但有静差，需要III型以上系统才能消除静差。
10 G 例：设有一非单位反馈控制系统， ( s) = s 1 H(s)=Kh，输入为单位阶跃。试求， Kh=1和0.1
结构形式 输入形 式
1 例：设单位反馈控制系统的 G( s) = ，输 2 Ts t 入信sint ， 2 试求系统的稳态误差。
为什么？ 因为：E(s) = s (s 2 2 )(s 1 ) T T 1 T s T 2 3 1 =- 2 2 2 2 2 2 2 2 1 T 1 s 2 T 1 s 2 T 1 s T 求拉式反变换 T
第六章 控制系统误差分析与计算
23
6.3 综合分析
静态误差
提高系统的准确度，增加系统的抗干扰能力，必须增 大干扰作用点之前的回路的放大倍数K1，以及增加这 一段回路中积分环节的数目。 增加干扰作用点之后到输出量之间的放大系数K2，或 增加积分环节的数目，对减少干扰引起的误差是没有 好处的。
24
6.4
动态误差
系统的动态误差
6.1
2.系统偏差
误差的概念
系统误差e(t)与偏差ε(t)
系统偏差ε (t). E(s)是输入信号与反馈信号的差。 若输入信号xi(t)作为期望值，反馈信号b(t)作为实际 值。 则偏差： ε (t)= xi(t)- b(t) L变换： E(s)= Xi(s)- B(s) = Xi(s)-H(s) • Xo(s) ---(2)
系统误差：
E1(s) = Xor(s)- Xo(s) =Xi(s)/H(s)- Xo(s) =〔1/ H(s) - Gxi(s)〕•Xi(s)+（-GN(s)）•N(s) = Φ xi(s) •Xi(s)+Φ N(s) •N(s)
可见，系统的误差不仅与系统的结构和参数有关，而且 8 与系统的输入和干扰的特性有关。
前面讲的是静态误差，是一个静态值。即当 t→∞时系统误差的极限值。 E(S)逆变换，是一个时间的函数。
时间在t→∞是一个有限的变化过程。 实际控制系统的稳态误差往往表现为时间的函数，----即动态误差。
25
6.4
例：如图系统：
动态误差
动态误差实例
其误差传递函数为：
Φxi(s)= E(s)/ Xi(s)=1/[1+G(s)H(s)]
13
6.3
静态误差
与输入有关的静态偏差
第六章 控制系统的误差分析和计算
解
+
E ( s)
10 s
X o ( s)
e ( s ) =
1 1 s = = 1 + G ( s ) 1 + 10 s + 10 s s ess = lim si iXi (s) s →0 s + 10 1 Xi ( s) = s s 1 ess = lim si i =0 s →0 s + 10 s
K a = lim s 2 iG ( s )
s →0
对0型系统 型系统
K a = lim s 2 i
s →0
K 0 (Ta s + 1)(Tb s + 1) (Tm s + 1) =0 (T1s + 1)(T2 s + 1) (Tn s + 1)
对Ⅰ型系统
K a = lim s 2 i
s →0
K1 (Ta s + 1)(Tb s + 1) (Tm s + 1) s (T1s + 1)(T2 s + 1) (Tn s + 1)
=0
自动控制原理
对Ⅱ型系统
K2 (Ta s +1)(Tb s +1)(Tms +1) Ka = lim s i 2 = K2 s→0 s (T1s +1)(T2s +1)(Tn s +1)
2
所以， 就是Ⅱ 所以，静态加速度误差系数 Ka 就是Ⅱ型系统的开环放大倍 对于Ⅲ型或高于Ⅲ型的系统， 数 K 2 。对于Ⅲ型或高于Ⅲ型的系统， K a 才为 ∞ 。 在单位加速度输入下 型系统， 对0型系统， ess = ∞ 型系统 型系统， 对Ⅰ型系统，
这就是求去单位反馈系统稳态误差的方法
+
E ( s)
10 s
X o ( s)
e ( s ) =
1 1 s = = 1 + G ( s ) 1 + 10 s + 10 s s ess = lim si iXi (s) s →0 s + 10 1 Xi ( s) = s s 1 ess = lim si i =0 s →0 s + 10 s
K a = lim s 2 iG ( s )
s →0
对0型系统 型系统
K a = lim s 2 i
s →0
K 0 (Ta s + 1)(Tb s + 1) (Tm s + 1) =0 (T1s + 1)(T2 s + 1) (Tn s + 1)
对Ⅰ型系统
K a = lim s 2 i
s →0
K1 (Ta s + 1)(Tb s + 1) (Tm s + 1) s (T1s + 1)(T2 s + 1) (Tn s + 1)
=0
自动控制原理
对Ⅱ型系统
K2 (Ta s +1)(Tb s +1)(Tms +1) Ka = lim s i 2 = K2 s→0 s (T1s +1)(T2s +1)(Tn s +1)
2
所以， 就是Ⅱ 所以，静态加速度误差系数 Ka 就是Ⅱ型系统的开环放大倍 对于Ⅲ型或高于Ⅲ型的系统， 数 K 2 。对于Ⅲ型或高于Ⅲ型的系统， K a 才为 ∞ 。 在单位加速度输入下 型系统， 对0型系统， ess = ∞ 型系统 型系统， 对Ⅰ型系统，
这就是求去单位反馈系统稳态误差的方法
第6章 控制系统的误差分析和计算
H(s) H(s)
ess = lime(t ) = lims ⋅ E(s) = lims ⋅
t →∞ s→0 s→0
H(s)
ε (s)
H(s)
控制系统的误差分析和计算
输入及干扰引起的稳态误差计算 输入作用下的偏差传递函数及稳态偏差计算
1 ΦRε (s) = = R(s) 1+ G1(s)G2 (s)H(s)
满足由0<K<6，显然调整 值也无法使稳态误差小于 。 调整K值也无法使稳态误差小于 调整 值也无法使稳态误差小于0.1。
式中：K − 开环放大系数； ν − 积分环节个数； 控制系统的误差分析和计算 G0 (s) −开环传递函数去掉积分和比例环节； 输入及干扰引起的稳态误差分析
G 0 (0) = 1 ,
s→0
KP的大小反映了系统在阶跃输入下的稳态精度。KP越大， 的大小反映了系统在阶跃输入下的稳态精度。 越大， ess越小。所以说 P 反映了系统跟踪阶跃输入的能力。 越小。所以说K 反映了系统跟踪阶跃输入的能力。 稳态误差为零的系统称为无差系统,为有限值称有差系统。 稳态误差为零的系统称为无差系统,为有限值称有差系统。 无差系统 有差系统 在单位阶跃作用下, 的系统为有差系统, 在单位阶跃作用下,υ=0 的系统为有差系统, 系统为无差系统 为无差系统。 υ>=1 的系统为无差系统。
ν = 0 → Kν = lims ⋅ Gk (s) = 0 → ess−r = ∞
s→0
ν = 1 → Kν = lims ⋅ Gk (s) = K → ess−r = 1/ K
s→0
ν ≥ 2 → Kν = lims ⋅ Gk (s) = ∞ → ess−r = 0
s→0
Kυ的大小反映了系统在斜坡输入下的稳态精度。K υ越大， 的大小反映了系统在斜坡输入下的稳态精度。 越大， 斜坡输入下的稳态精度 ess越小。所以说 Kυ 反映了系统跟踪斜坡输入的能力。 越小。 反映了系统跟踪斜坡输入的能力。 斜坡输入的能力
ess = lime(t ) = lims ⋅ E(s) = lims ⋅
t →∞ s→0 s→0
H(s)
ε (s)
H(s)
控制系统的误差分析和计算
输入及干扰引起的稳态误差计算 输入作用下的偏差传递函数及稳态偏差计算
1 ΦRε (s) = = R(s) 1+ G1(s)G2 (s)H(s)
满足由0<K<6，显然调整 值也无法使稳态误差小于 。 调整K值也无法使稳态误差小于 调整 值也无法使稳态误差小于0.1。
式中：K − 开环放大系数； ν − 积分环节个数； 控制系统的误差分析和计算 G0 (s) −开环传递函数去掉积分和比例环节； 输入及干扰引起的稳态误差分析
G 0 (0) = 1 ,
s→0
KP的大小反映了系统在阶跃输入下的稳态精度。KP越大， 的大小反映了系统在阶跃输入下的稳态精度。 越大， ess越小。所以说 P 反映了系统跟踪阶跃输入的能力。 越小。所以说K 反映了系统跟踪阶跃输入的能力。 稳态误差为零的系统称为无差系统,为有限值称有差系统。 稳态误差为零的系统称为无差系统,为有限值称有差系统。 无差系统 有差系统 在单位阶跃作用下, 的系统为有差系统, 在单位阶跃作用下,υ=0 的系统为有差系统, 系统为无差系统 为无差系统。 υ>=1 的系统为无差系统。
ν = 0 → Kν = lims ⋅ Gk (s) = 0 → ess−r = ∞
s→0
ν = 1 → Kν = lims ⋅ Gk (s) = K → ess−r = 1/ K
s→0
ν ≥ 2 → Kν = lims ⋅ Gk (s) = ∞ → ess−r = 0
s→0
Kυ的大小反映了系统在斜坡输入下的稳态精度。K υ越大， 的大小反映了系统在斜坡输入下的稳态精度。 越大， 斜坡输入下的稳态精度 ess越小。所以说 Kυ 反映了系统跟踪斜坡输入的能力。 越小。 反映了系统跟踪斜坡输入的能力。 斜坡输入的能力
第六章 控制系统的误差分析与计算
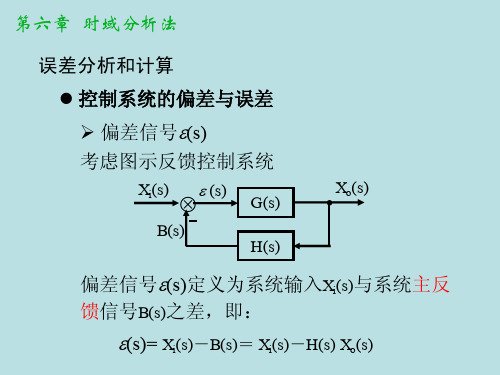
第三章 时域分析法 不同类型系统的稳态误差系数及稳态误差 0型系统
K (1s 1)( 2 s 1) ( m s 1) G( s) H ( s) (T1s 1)(T2 s 1) (Tnv s 1)
K p lim G(s) H (s) K
s0
ss
G (s) H (s) K ( 1s 1)( 2 s 1) ( m s 1) s 2 (T1s 1)(T2 s 1) (Tnv s 1)
1 0 1 K p
K p lim G(s) H (s)
s0
ss
Kv lim sG(s) H (s)
2 2
cost
T 2 2 T 1
2 2
sin t
而如果采用拉氏变换的终值定理求解，将得 到错误得结论：
Ts ess lim s 0 2 2 s 0 Ts 1 s
此例表明，输入信号不同，系统的稳态误差 也不相同。
第三章 时域分析法 稳态误差系数 稳态误差系数的概念 稳态位置误差（偏差）系数 单位阶跃输入时系统的稳态偏差
G ( s) H ( s) K (1s 1)( 2 s 1) ( m s 1) s v (T1s 1)(T2 s 1) (Tnv s 1) K ~ G ( s) v s
则： ss
sX i (s) lim (t ) lim s (s) lim t s0 s0 1 G( s) H ( s)
在单位加速度输入下的稳态误差为：
ess lim s
s0
1 Ts 1 X i ( s) lim s 3 s0 Ts 1 s 1 G( s)
第三章 时域分析法
控制系统的误差分析和计算
1 E s X i s 1 G s 1 e ss lim e t lim sE s lim s X i s t s0 s 0 1 G s
11
控制工程基础
第六章 控制系统的误差分析和计算
非单位反馈系统
1 X i s 1 G s H s
' '
( s) X or ( s) X o ( s) E ( s)
'
( s)
H ( s)
1 单位反馈系统H s 1，E s s E s s H ( s) H ( s) : 求稳态误差，应先求稳态偏差。
9
控制工程基础
n m
14
控制工程基础
第六章 控制系统的误差分析和计算
1、影响稳态误差的因素
G s K 1 s 1 2 s 1 v s T1 s 1T2 s 1
s 0
n m
e ss lim e ( t ) lim sE ( s )
t
输出量期望值的大小，即Xor(s)= Xi(s)，由此得到：
( s) Xi ( s) H ( s) X 0 ( s) X or (s) X 0 (s) E (s)
单位反馈控制系统的偏差函数(s)和误差函数E(s)是相等的。
7
控制工程基础
第六章 控制系统的误差分析和计算
对于非单位负反馈控制系统，其输入量间接反映了输出量 期望值的大小，根据等效规则转变为单位负反馈控制系统。
Xi s
s
× -
( s)
Y s
G s
Xo s
H s
机械工程控制基础控制系统的误差分析和计算
12
对单位阶跃输入，稳态误差为
ess
lim
s0
s 1
G
1
s
H (s)
1 s
1
G
1
0 H (0)
静态位置误差系数的定义：
Kp
lim G
s0
s
H (s)
G
0 H (0)
则
ess
1 1 Kp
13
对0型系统
Gs
K 1s 1 2s 1 T1s 1 T2s 1
Kp
lim
s0
K0 t1s 1t2s 1L T1s 1T2s 1L
Gs
K 1s 1 2s 1 T1s 1 T2s 1
Kv
lim
s0
s
K 1s 1 2s 1 T1s 1 T2s 1
0
16
对I型系统
Gs
K 1s 1 2s 1 s T1s 1 T2s 1
Kv
lim
s0
s
K 1s 1 2s 1 s T1s 1 T2s 1
K1
对II型系统
Gs
K 1s 1 2s 1 s2 T1s 1 T2s 1
ε(s) =Xi(s) - Y(s) Y(s)=H(s)Xo(s)
(s) 1
H (s)
p202
Xi (s)
X oi (s)
(s)
(s)
G1 ( s )
N(s)
＋ G2 (s)
Y (s)
H (s)
E(s)
1 H (s)
Xi (s)
X o (s)
ε(s) =Xi(s) - H(s)Xo(s)
1 (s)
t
s0
2. 利用终值定理计算系统的稳态误差：
第6章_控制系统的误差分析和计算_6.3干扰引起的稳态误差
N (s ) R (s ) E (s )
-
G1 = K1
+
G2 =
K2 s
C (s )
（2）扰动作用下的误差传递函数为 K2 − E(s) − K2 s ΦNE (s) = = = N(s) 1+ K K2 s + K1K2 1 s 当扰动输入为单位阶跃输入时，稳态误差为
essn
1 − K2 1 1 = lim s ⋅ Φ NE ⋅ = lim s ⋅ ⋅ =− s →0 s s →0 s + K1 K 2 s K1
N (s )
X i (s )
ε (s )
B (s )
-
G1 ( s )
+
H (s )
G2 (s)
X o (s )
（2）稳态误差的计算 ）
①给定作用下的偏差传递函数
N (s )
X i
X i (s )
-
G1 ( s )
+
H (s )
G2 (s)
X o (s )
ε (s )
ess = essr + essn 1 =− K1
（3）输入作用与扰动作用共同作用下的稳态误差为
N (s ) R (s ) E (s )
-
G1 =
K1 s
+
G2 =
K2 s
C (s )
（4）如果要求稳态误差为零，可以在G1中串联积分环节，令 K1 G1 = s 1 s2 1 essr = lim s ⋅ Φ RE ⋅ = lim s ⋅ 2 ⋅ =0 则有 s →0 s s →0 s + K1 K 2 s
④对于稳定的系统，采用拉氏变换的终值定理计算稳态偏差
控制系统的误差分析
6.2 输入引起的稳态误差
6.2.1 误差传递函数与稳态误差
先讨论单位反馈的控制系统，如图6-2所示。
Xi(s)X0(s)11 G G((ss))Xi(s)1GG (s()s)Xi(s) X i s
E(s)
G(s)
X o s
1G 1(s)Xi(s)
根据终值定理
图6-2 单位反馈系统
这就是求取输入引起的单位反馈系统稳态误差的方法。
ess
1 1Kp
1 1K
对于Ⅰ型或高于Ⅰ型以上系统
K p ls i0s K m ((T 1 1 s s 1 1 ))T (2 (2 s s 1 1 )) ((T m ns s 1 1 ) )
ess 0 可编辑ppt
6
(3) 静态速度误差系数Kv
当系统的输入为单位斜坡信号时r(t)=t·1(t)，即R(s)
误差定义为控制系统希望的输出量与实际的输出量之差，记
做e(t)，误差信号的稳态分量被称为稳态误差，或称为静态误差， 记作 。输入信号和反馈信号比较后的信号 也能反映系统误
差的大小，称之为偏差。应该指出，系统的误差信号e(t)与偏差 信号 ，在一般情况下并不相同(见图6-1)。
控制系统的误差信号的象函数是
essK1
对于Ⅱ型或Ⅱ型以上系统：
Kls i0m ssK ((T11ss 1 1))T ((22ss 1 1)) ((Tm nss 1 1))
ess0
可编辑ppt
，则有
7
(4) 静态加速度误差系数Ka
当系统输入为单位加速度信号时，即 r(t)1t21(t)R ,(s)1
2
s3
则系统稳态误差为
1
ess
lims s0 1G(s)
第六章 控制系统的误差分析
稳态误差系数和稳态误差
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
K ( i s 1)
m
0型系统的稳态误差
G (s)H(s) K ( i s 1) s
v m
(T s 1) V=0
i i 1
i 1 n v
K p lim G (s)H(s) lim
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
例1
ess lim s
s 0
1 (0.5s 1)(0.04s 1) R( s) lim s R( s ) s 0 (0.5s 1)(0.04s 1) 20 1 G( s) H ( s)
1 s
ess lim s
K j
20lg | G( jv ) H ( jv ) | 20lg | Kv / jv | 0dB
v Kv
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
• II型系统（稳态加速度误差系数）
低频段
G (s) H ( s)
K ( i s 1) s 2 (Ti s 1) i 1 2 a
t
1 '' e (0)r ' ' ( t ) 2!
1 1 1 r(t) r' (t) r' ' (t) k0 k1 k2 动态加速度误差系数
动态位置误差系数
动态速度误差系数
浙江理工大学机械与自动控制学院
控制工程基础
第六章 控制系统的误差分析
动态误差系数的长除法求取
s 0
第6章_控制系统的误差分析和计算_6.4减小系统误差的途径
Φ n ( s) = 0
G1 ( s )
即可以使得干扰信号N(s)所产生的输出信号C(s)=0，从而 N(s) C(s)=0 消除了干扰信号N(s)对输出信号C(s)的影响。 该系统由两个通道组成，属于复合控制系统。实际上，该 系统就是利用双通道原理，实现了对干扰信号N(s)的补偿作用。 一个通道是干扰信号N(s)直接到达相加点，另一个通道是干扰信 号N(s)经过Gc(s)G1(s)后到达同一个相加点。如果满足上述选择 Gc(s)G1(s)=-1，则从两个通道过来的干扰信号在此相加点处， 大小相等，方向相反，从而实现了干扰信号的全补偿。
《控制工程基础》 控制工程基础》
第6章 控制系统的误差分析和计算 6.4 减小系统误差的途径
为了减小系统误差，可以考虑以下途径： （1）反馈通道的精度对于减小系统误差至关 重要。反馈通道元部件的精度要高，避免在反馈通 道引入干扰。 （2）在系统稳定的前提下： 对于输入引起的误差，增大系统开环放大倍数 或提高系统型次，可以使之减小。 对于干扰引起的误差，在前向通道干扰点前加 积分器或增大放大倍数，可以使之减小。 （3）既要求稳态误差小，又要求良好的动态 性能，只靠加大开环放大倍数或串入积分环节不能 同时满足要求时，可以采用复合控制（顺馈）方法 对误差进行补偿。补偿的方式可分为按干扰补偿和 按输入补偿。
6.4.2 按输入补偿（顺馈补偿闭环控制） 按输入补偿（顺馈补偿闭环控制）
顺馈补偿闭环控制系统的典型结构如图所示，其中R(s) 是输入信号，C(s)是输出信号，E(s)是偏差，Gc(s)是顺馈补偿 通道传递函数。该系统由两个通道组成，属于复合控制系统。 一个通道是由G1(s)G2(s)组成的主控制通道，为闭环控制。另 一个通道是由Gc(s)G2(s)组成的顺馈补偿控制通道，为开环控 制。系统的输出不仅与系统的误差有关，而且还与补偿信号有 关。补偿信号所产生的作用，可以用来补偿原来的误差信号。
G1 ( s )
即可以使得干扰信号N(s)所产生的输出信号C(s)=0，从而 N(s) C(s)=0 消除了干扰信号N(s)对输出信号C(s)的影响。 该系统由两个通道组成，属于复合控制系统。实际上，该 系统就是利用双通道原理，实现了对干扰信号N(s)的补偿作用。 一个通道是干扰信号N(s)直接到达相加点，另一个通道是干扰信 号N(s)经过Gc(s)G1(s)后到达同一个相加点。如果满足上述选择 Gc(s)G1(s)=-1，则从两个通道过来的干扰信号在此相加点处， 大小相等，方向相反，从而实现了干扰信号的全补偿。
《控制工程基础》 控制工程基础》
第6章 控制系统的误差分析和计算 6.4 减小系统误差的途径
为了减小系统误差，可以考虑以下途径： （1）反馈通道的精度对于减小系统误差至关 重要。反馈通道元部件的精度要高，避免在反馈通 道引入干扰。 （2）在系统稳定的前提下： 对于输入引起的误差，增大系统开环放大倍数 或提高系统型次，可以使之减小。 对于干扰引起的误差，在前向通道干扰点前加 积分器或增大放大倍数，可以使之减小。 （3）既要求稳态误差小，又要求良好的动态 性能，只靠加大开环放大倍数或串入积分环节不能 同时满足要求时，可以采用复合控制（顺馈）方法 对误差进行补偿。补偿的方式可分为按干扰补偿和 按输入补偿。
6.4.2 按输入补偿（顺馈补偿闭环控制） 按输入补偿（顺馈补偿闭环控制）
顺馈补偿闭环控制系统的典型结构如图所示，其中R(s) 是输入信号，C(s)是输出信号，E(s)是偏差，Gc(s)是顺馈补偿 通道传递函数。该系统由两个通道组成，属于复合控制系统。 一个通道是由G1(s)G2(s)组成的主控制通道，为闭环控制。另 一个通道是由Gc(s)G2(s)组成的顺馈补偿控制通道，为开环控 制。系统的输出不仅与系统的误差有关，而且还与补偿信号有 关。补偿信号所产生的作用，可以用来补偿原来的误差信号。
自控原理-第6章 控制系统的误差分析与计算
esslt i e m (t)ls i0sm E (s)
偏差 ( t ) ：系统的输入 x i ( t ) 和主反馈信号 y ( t ) 之差。即
( t ) x i( t ) y ( t ) ( s ) X i( s ) Y ( s )
稳态偏差 s s ：当t→∞时的系统偏差。即
6.1 稳态误差的基本概念
自控控制理论
本课程与误差有关的概念都是建立在反馈控制系统基础 之上的。 稳态的定义：时间趋于无穷大（足够长）时的固定响应称 为控制系统的稳定状态，简称稳态。 稳态误差：当系统在特定类型输入信号作用下，达到稳态 时系统精度的度量。
说明：误差产生的原因是多样的，课程中只研究由于系统 结构、参量、以及输入信号的形式不同所引起的误差。
i1 n
0
(Tis1)
i1
I型系统的稳态误差
V=1
m
K ( is 1)
G(s)H (s)
i 1 nv
sv (Tis 1)
i 1
自控控制理论
Kplsi m 0G (s)H(s)
1
essp
1 Kp
0
K vlsi m 0sG (s)H (s)K
自控控制理论
例 : 设 单 位 反 馈 系 统 的 开 环 传 递 函 数 为 G (s)1,试 求 当 输 入 Ts
信 号 为 r(t)1t2时 ,控 制 系 统 的 稳 态 误 差 值 。 2
解:
e(s)
1 1G ( S )
S S 1/T
当
r(t)
稳态加速度 误差系数
自控控制理论
6.2.4 不同类型反馈控制系统的稳态误差系数
偏差 ( t ) ：系统的输入 x i ( t ) 和主反馈信号 y ( t ) 之差。即
( t ) x i( t ) y ( t ) ( s ) X i( s ) Y ( s )
稳态偏差 s s ：当t→∞时的系统偏差。即
6.1 稳态误差的基本概念
自控控制理论
本课程与误差有关的概念都是建立在反馈控制系统基础 之上的。 稳态的定义：时间趋于无穷大（足够长）时的固定响应称 为控制系统的稳定状态，简称稳态。 稳态误差：当系统在特定类型输入信号作用下，达到稳态 时系统精度的度量。
说明：误差产生的原因是多样的，课程中只研究由于系统 结构、参量、以及输入信号的形式不同所引起的误差。
i1 n
0
(Tis1)
i1
I型系统的稳态误差
V=1
m
K ( is 1)
G(s)H (s)
i 1 nv
sv (Tis 1)
i 1
自控控制理论
Kplsi m 0G (s)H(s)
1
essp
1 Kp
0
K vlsi m 0sG (s)H (s)K
自控控制理论
例 : 设 单 位 反 馈 系 统 的 开 环 传 递 函 数 为 G (s)1,试 求 当 输 入 Ts
信 号 为 r(t)1t2时 ,控 制 系 统 的 稳 态 误 差 值 。 2
解:
e(s)
1 1G ( S )
S S 1/T
当
r(t)
稳态加速度 误差系数
自控控制理论
6.2.4 不同类型反馈控制系统的稳态误差系数
控制系统的误差分析和计算
lim
s0
s1 1 G(s)
Xi (s)
这就是求取输入引起的单位反馈系统稳态误差的方法.需要注意 的是,终值定理只有对有终值的变量有意义.如果系统本身不稳定, 用终值定理求出的值是虚假的.故在求取系统稳态误差之前,通常 应首先判断系统的稳定性.
➢ 非单位反馈控制系统
输入引起的系统的偏差传递函数为:
(
s)
H
(
s)
1
G1
G2 s s G2 s
H
s
N
s
干扰引起的偏差为:
s
1
G2(s)H s G2 (s)G1sH
s
N
s
根据终值定理,干扰引起稳态偏差为:
ss
lim t
t
lim
s0
s s
则干扰引起稳态误差为:
ess
ss
H 0
例6-3 系统结构图如图6-8所示,当输入信号xi(t)=1(t),干扰N(t)=1(t)时,求系 统总的稳态误差ess.
输入信号和反馈信号比较后的信号ε(t)也能反映系统误差的大小,
称之为偏差.应该指出,系统的误差信号e(t)与偏差信号ε(t),在
一般情况下并不相同(见图6-1).
控制系统的方块图如图6-1所示.实线部分与实际系统有对应关系, 而虚线部分则是为了说明概念额外画出的.
控制系统的误差信号的象函数是 E(s) sXi s X o s
s0
1 s2
1 K
，
其中
K
lim sG(s)H (s) s0
,定义为系统静态
速度误差系数。 对于0型系统：
K
lim s s0
K (1s 1)( 2s 1) ( ms 1)
第六章 控制系统的误差分析和计算
设G1(s)=1,系统是一阶的,因此稳定.图6-9中,R是电动机电枢电阻,CM为力矩系 数,N是扰动力矩,干扰作用为一个常值阶跃干扰,故稳态偏差为
- K2Kc
ssls i0m s1TKM 1sK2K 1c
NR K2Kc NR CMs 1K1K2Kc CM
TMs1
则稳态误差为 essKscs1KK 1K 22Kc C NMR
差
es
s1
lims 1 s0 1K1
K2 s
10 s
- K2
再求干扰引起的稳态误差
ess2
lims s
s0
1K1
K2 s
1 1 s K1
所以,总误差为
11 esses1ses2 s0-K1K1
例6-4 某直流伺服电动机调速系统如图6-9所示,试求扰动力矩N(s)引起的稳态误 差.
解:首先应选择合适的G1(s)使系统稳定.Kc是测速负反馈系数,这是一个非单位反 馈的控制系统,先求扰动作用下的稳态偏差,再求稳态误差ess.
控制系统的方块图如图6-1所示.实线部分与实际系统有对应关系, 而虚线部分则是为了说明概念额外画出的.
控制系统的误差信号的象函数是 E ( s ) s X is X o s (6-1)
而
偏差信号的象函数是 (s) X is Y s (6-2)
考虑Xi(s)与Y(s)近似相等,且Y(s)=H(s)Xo(s),得
对于一个实际的控制系统,由于系统的结构、输入作用的类型 (给定量或扰动量)、输入函数的形式(阶跃、斜坡或抛物线)不同, 控制系统的稳态输出不可能在任何情况下都与输入量一致或相当, 也不可能在任何形式的扰动作用下都能准确地恢复到原平衡位置. 这类由于系统结构、输入作用形式和类型所产生的稳态误差称为 原理性稳态误差.
- K2Kc
ssls i0m s1TKM 1sK2K 1c
NR K2Kc NR CMs 1K1K2Kc CM
TMs1
则稳态误差为 essKscs1KK 1K 22Kc C NMR
差
es
s1
lims 1 s0 1K1
K2 s
10 s
- K2
再求干扰引起的稳态误差
ess2
lims s
s0
1K1
K2 s
1 1 s K1
所以,总误差为
11 esses1ses2 s0-K1K1
例6-4 某直流伺服电动机调速系统如图6-9所示,试求扰动力矩N(s)引起的稳态误 差.
解:首先应选择合适的G1(s)使系统稳定.Kc是测速负反馈系数,这是一个非单位反 馈的控制系统,先求扰动作用下的稳态偏差,再求稳态误差ess.
控制系统的方块图如图6-1所示.实线部分与实际系统有对应关系, 而虚线部分则是为了说明概念额外画出的.
控制系统的误差信号的象函数是 E ( s ) s X is X o s (6-1)
而
偏差信号的象函数是 (s) X is Y s (6-2)
考虑Xi(s)与Y(s)近似相等,且Y(s)=H(s)Xo(s),得
对于一个实际的控制系统,由于系统的结构、输入作用的类型 (给定量或扰动量)、输入函数的形式(阶跃、斜坡或抛物线)不同, 控制系统的稳态输出不可能在任何情况下都与输入量一致或相当, 也不可能在任何形式的扰动作用下都能准确地恢复到原平衡位置. 这类由于系统结构、输入作用形式和类型所产生的稳态误差称为 原理性稳态误差.
机械工程控制基础第六章控制系统的误差分析和计算PPT学习教案
6.4 减小系统误差的途径
(1) 反馈通道的精度对于减小系统误差至关重要。 反馈通道元部件的精度要高；避免在反馈通道
引入干扰。
(2) 在系统稳定的前提下， 对于输入引起的误差，增大系统开环放大倍数， 提高系统型次； 对于干扰引起的误差，在前向通道干扰点前加 积分器，增大放大倍数。
第37页/共50页
如下图为稳定系统，G1(s)中不包含纯微分环节。
第30页/共50页
n(t)＝at·1(t)
N
s
a s2
Xo s
G2 s
N s
1
1 s2
G1
s
G2
s
H
s
s2
s2G2 s G1 sG2 s
H
s
ess
lim
s0
s
Xo s N s
N
s
lim
s0
s
s2
G1
s2G2 s G2
s s
H
s
a s2
Ka
lim
s0
s2
Gs
对0型系统
Gs
K 1s 1 2s 1 T1s 1 T2s 1
Ka
lim
s0
s2
K 1s 1 2s 1 T1s 1 T2s 1
0
第18页/共50页
对I型系统
Gs
K 1s 1 2s 1 s T1s 1 T2s 1
Ka
lim s2
s0
K 1s 1 2s 1 s T1s 1 T2s 1
第2页/共50页
6-1 稳态误差的基本概念
e(t)=μ(t)xi(t) -xo(t)
Xoi (s) E(s) (s)
ε(t) = xi(t) - y(t)
控制工程基础 第6讲 控制系统的误差分析和计算
误差和偏差eshsxsgshs与输入相关的稳态误差单位阶跃输入单位速度输入单位加速度输入ii型系统例子单位反馈系统的开环传递函数为10011试求静态误差系数2当输入为时系统的稳态误差
第6讲 误差分析和计算
Lec.6 Error Analysis & Calculation
内容提纲
一、相关的基本概念 二、与输入相关的稳态误差 三、与干扰相关的稳态误差 四、减小误差的方法 五、反馈系统的抗干扰性
Xi(s) +
-
控制器
N(s) 被控对象
G1(s)
++
G2(s)
Xo(s)
测量机构
H(s)
Xo(s) = Xo1(s) + Xo2(s)
G1(s)·G2(s)
=
·Xi(s)
1+G1(s)·G2(s)·H(s)
G2(s) +
·N(s)
1+G1(s)·G2(s)·H(s)
设计反馈控制系统时满足：
| G1(s) ·H(s) | >> 1 | G1(s) ·G2(s) ·H(s) | >> 1
减小误差的方法
▪ 提高反馈通道部件的精度 ▪ 增大系统开环增益，提高系统的型次 ▪ 前馈补偿（干扰和输入）
按干扰前馈补偿
N s
Xi s E s+ +
+-
Gn s
+
G1 s +
G2 s
Xos
Gn
s
1
G1
s
按输入前馈补偿
Gr s
+
Es +
+
Xi s -
G s
第6讲 误差分析和计算
Lec.6 Error Analysis & Calculation
内容提纲
一、相关的基本概念 二、与输入相关的稳态误差 三、与干扰相关的稳态误差 四、减小误差的方法 五、反馈系统的抗干扰性
Xi(s) +
-
控制器
N(s) 被控对象
G1(s)
++
G2(s)
Xo(s)
测量机构
H(s)
Xo(s) = Xo1(s) + Xo2(s)
G1(s)·G2(s)
=
·Xi(s)
1+G1(s)·G2(s)·H(s)
G2(s) +
·N(s)
1+G1(s)·G2(s)·H(s)
设计反馈控制系统时满足：
| G1(s) ·H(s) | >> 1 | G1(s) ·G2(s) ·H(s) | >> 1
减小误差的方法
▪ 提高反馈通道部件的精度 ▪ 增大系统开环增益，提高系统的型次 ▪ 前馈补偿（干扰和输入）
按干扰前馈补偿
N s
Xi s E s+ +
+-
Gn s
+
G1 s +
G2 s
Xos
Gn
s
1
G1
s
按输入前馈补偿
Gr s
+
Es +
+
Xi s -
G s
六章控制系统误差分析
如下图为稳定系统，G1(s)中不包含纯微分环节。
n(t)＝a·1(t)
N s a
s
X os
G 2s
N s
1
1 s
G
1
s
G
2
s
H
s
s
sG 2 s G1sG 2sH
s
e ss
lim
s 0
s
X os N s
N
s
lim
s 0
s
s
sG 2 s G1sG 2sH
s
a s
0
同理，如果反馈控制系统对前向通道的扰动是一 个斜坡函数，那么只要保证系统稳定的前提下，在扰 动作用点前有二个积分器，就可以消除斜坡扰动引起 的稳态误差。
对II型系统 Gss K 2T 1 1s s 1 1T2 2s s 1 1
Kalsi m 0s2sK 2T1 1ss 1 1T2 2ss 1 1 K
单位加速度输入时，
11
11
esslsi m 0s1G ss3lsi m 0s2G sK a
对0型系统
ess
1 Ka
1 0
对I型系统 对II型系统
ess
可利用叠加原理，分别求出每个量作用
情况下的偏差，然后相加求出。
例 某系统如下图所示，当
x it t1 t, n t 0 .5 1 t
时作用时， e s s 值为多少？
N s
+ s 10
+
1 XO s
XI s -
0.1s 1 +
ss 4
解: 根据劳斯判据该系统稳定。
单位反馈系统的偏差即为误差。
补偿的方式可分为按干扰补偿和按输入补偿。
n(t)＝a·1(t)
N s a
s
X os
G 2s
N s
1
1 s
G
1
s
G
2
s
H
s
s
sG 2 s G1sG 2sH
s
e ss
lim
s 0
s
X os N s
N
s
lim
s 0
s
s
sG 2 s G1sG 2sH
s
a s
0
同理，如果反馈控制系统对前向通道的扰动是一 个斜坡函数，那么只要保证系统稳定的前提下，在扰 动作用点前有二个积分器，就可以消除斜坡扰动引起 的稳态误差。
对II型系统 Gss K 2T 1 1s s 1 1T2 2s s 1 1
Kalsi m 0s2sK 2T1 1ss 1 1T2 2ss 1 1 K
单位加速度输入时，
11
11
esslsi m 0s1G ss3lsi m 0s2G sK a
对0型系统
ess
1 Ka
1 0
对I型系统 对II型系统
ess
可利用叠加原理，分别求出每个量作用
情况下的偏差，然后相加求出。
例 某系统如下图所示，当
x it t1 t, n t 0 .5 1 t
时作用时， e s s 值为多少？
N s
+ s 10
+
1 XO s
XI s -
0.1s 1 +
ss 4
解: 根据劳斯判据该系统稳定。
单位反馈系统的偏差即为误差。
补偿的方式可分为按干扰补偿和按输入补偿。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
C0 (s)
N (s)
R(s) B(s)
(s)
-
G1 ( s )
+ G2 (s)
H (s)
e(s) -
C(s)
(b)
误差
C0(s) (s) N(s)
R(s)
1 H(s)
R1(s) C0(s)
E1(s(s))H(s)
E(s)
G1(s)
G2(s) C(s)
(c)
e(s) -+ (s)
H (s)
E(s)
因为偏差 (s) R(s) B(s) H (s)C0 (s) H (s)C(s) H (s)e(s)
这里 R(s) H (s)C0 (s) 是基于控制系统在理想工作情况下
(s) 0 得到的。
即当控制系统的偏差信号 (s) 0 时，该控制系统无调节控制
作用，此时的实际输出信号C(s)就是希望输出信号 C0 (s) 。
G(s)H(s)
i1 nv
sv (Tis 1)
i1
（4）稳态误差系数和稳态误差的总结 （系统在控制信号作用下）
此表概括了0型、Ⅰ型和Ⅱ型反馈控制系统在不同输入信号作用下的
稳态误差。在对角线上，稳态误差为有限值；在对角线以上部分，
稳态误差为无穷大；在对角线以下部分，稳态误差为零。由此表可
以得如下结论：
何改变系统结构?
(s)
- G1 K1
解：（1）给定作用下的误差传递函数为
RE (s)
(s)
R(s)
1
1
K1
K2 s
s s K1K2
当给定输入为单位阶跃输入时，稳态误差为
N (s)
+
G2
K2 s
C(s)
essr
lim s0
s RE
1 s
lim s0
s
s s K1K2
1 s
0
R(s) (s)
(1) 同一个系统，如果输入的控制信号不同，其稳态误差也不同。
(2) 同一个控制信号作用于不同的控制系统，其稳态误差也不同。
(3) 系统的稳态误差与其开环增益有关，开环增益越大，系统的稳态
误差越小；反之，开环增益越小，系统的稳态误差越大。
(4)注意区分稳态偏差与稳态误差的区别,
只有单位反
馈系统,
影响稳态误差的因素： ·给定作用下的稳态误差与外作用有关。对同一系统 加入不同的输入，稳态误差不同。 ·与时间常数形式的开环增益有关；开环增益K↑，稳 态误差↓，但同时系统的稳定性和动态特性变差。 ·与积分环节的个数有关。积分环节的个数↑，稳态 误差↓，但同时系统的稳定性和动态特性变差。
求得 ssx 后,再按下式求出
m
K (is 1)
K p lim G(s)H (s) lim
s0
s0
i 1 n
K
(Tis 1)
i 1
单位阶跃信号输入
m
K(is 1)
Kv
lim sG(s)H(s)
s0
lim s
s0
i1 n
0
(Tis 1)
1 essv K v
i1
单位斜坡信号输入 m
K(is 1)
减小和消除稳态误差方法： ·提高系统的开环增益。 ·增加系统开环传递函数中积分环节的个数。 但是这两种方法会降低系统的稳定性。 由此可见，对稳态误差的要求往往与系统的稳定性和动态特 性的要求是矛盾的。 因此，系统的稳定性、准确性与快速性之间的关系是相互关 联和相互矛盾的。
线性系统在多个信号共同作用下总的稳态偏差（误 差），等于多个信号单独作用下的稳态偏差（误差） 之和。
0型系统:
GsH s
K0 1s 1 2s 1 m s 1 T1s 1T2s 1Tn s 1
I型系统:
GsH s
K11s 1 2s 1 m s 1 sT1s 1T2s 1Tn1s 1
II型系统:
GsH s
K 2 1s 1 2s 1 m s 1 s 2 T1s 1T2 s 1Tn2 s 1
稳态的定义：时间趋于无穷大（足够长）时的稳定响 应称为控制系统的稳定状态，简称稳态。
稳态误差：当系统在特定类型输入信号作用下，达到 稳态时系统精度的度量。
说明：误差产生的原因是多样的，我们只研究由于系 统结构、参量、以及输入信号的形式不同所引起的误 差。
误差及稳态误差的定义
系统误差 e(t) ：输出量的希望值 c0 (t)和实际值c(t) 之差。即
1 s
0
ess essr essn 0
6.4 减小系统误差的途径
（1）前馈补偿闭环控制（按干扰补偿）
Gc(s) N(s)
R(s) E(s) G1(s)
-
C(s) G2(s)
（2）顺馈补偿闭环控制（按输入补偿）
Gc(s) R(s) E(s)
G1(s) -
C(s) G2(s)
作业
❖ 习题6-11② 扰Leabharlann 作用下的偏差传递函数C(s)
B(s)
N (s) G2 (s)
+
H (s)
(s) 1
G1 ( s )
NE (s)
(s)
N (s)
G2 (s)H (s) 1 G1(s)G2 (s)H (s)
③ 给定和扰动同时作用下的偏差表达式
(s) RE (s)R(s) NE (s)N(s)
R(s)
6.2.2 稳态误差系数
（1）系统的“型”的概 念闭环系统的开环传递函数一般可以表示为:
m
K ( is 1)
G(s)H (s)
i 1 n
s (Tis 1)
i 1
定义： 当ν=0时，称为0型系统，没有积分环节； 当ν=1时，称为I型系统，有1个积分环节； 当ν=2时，称为II型系统，有2个积分环节； 依次类推。
e(t) c0 (t) c(t)
系统稳态误差 ess ：当t→∞时的系统误差，用 ess 表示。即
ess
lim e(t )
t
lim
s0
s e(s)
系统偏差 E(s) ：系统的输入 r(t) 和主反馈信号b(t) 之差。即
(t) r(t) b(t)
系统稳态偏差 ss：当t→∞时的系统偏差，用 ss表示。即
稳态误差=跟随误差+扰动误差
ess= esr+ esn
稳态误差的计算
N (s)
R(s) (s) G1(s)
+ G2 (s)
B(s) -
H (s)
C(s)
① 给定作用下的偏差传递函数
R(s)
- C(s)
B(s)
H (s)
G2 (s)
(s) G1 ( s )
RE (s)
(s)
R(s)
1
1 G1(s)G2 (s)H (s)
ss
lim (t)
t
lim s (s)
s0
对单位反馈系统，给定作
C0 (s)
e(s)
N (s)
用 r(t) 即为输出量的希望
值， r(t) c0 (t) ，误差 ess
等于偏差 ss，即 ss ess
R(s) (s) G1(s) + B(s) -
(a)
-
G2 (s) C(s)
对非单位反馈系统，给定
- G1 K1
N (s)
+
G2
K2 s
C(s)
（2）扰动作用下的误差传递函数为
NE (s)
(s)
N (s)
K2
s
1
K1
K2 s
K2 s K1K2
当扰动输入为单位阶跃输入时，稳态误差为
essn
lim s0
s NE
1 s
lim
s0
s
K2 s K1K2
1 s
1 K1
（3）输入作用与扰动作用共同作用下的稳态误差为
（2）稳态误差系数的概念
➢单位阶跃输入
R(s) 1 s
定义：
essss
lim s s0 1
1 G(s)H (s)
1 s
1
lim
1 G(s)H (s)
1 1 K
p
稳态位置 误差系数
s0
➢单位斜坡输入
R(s) 1 s2
定义： 稳态速度
e
ssss
lim
s0
s
1
1 G(s)H(s)
1 s2
1 lim sG(s)H(s)
出量的变化率是“速度”，但是，对于误差分析所 得到的结论同样适用于输出量为其它物理量的系统。 例如在温度控制中，上述的“位置”就表示温度， “速度”就表示温度的变化率，等等。因此，对于 “位置”、“速度”等名词应当作广义的理解。
6.3 干扰引起的稳态误差
稳态误差分类：
跟随误差：表示系统能以什么精度跟随系统输入信号的变 化，用esr表示。 扰动误差：表示系统在扰动信号作用下系统偏离平衡点的情 况，用esn表示。 同样要注意稳态偏差与稳态误差的区别, 有 只有对单位反馈系统
s0
1 Kv
误差系数
➢单位抛物线输入
R(s) 1 s3
定义： 稳态加速度
esss
lim
s0
s
1
1 G(s)H(s)
1 s3
1 lim s2G(s)H(s)
s0
1 Ka
误差系数
（3）不同类型反馈控制系统的稳态误差系数
0型系统的稳态误差
V=0
m
K(is 1)
G(s)H(s) i1 nv sv (Tis 1) i1
ess
essr
essn
1 K1
（4）如果要求稳态误差