有理数复习一
有理数复习(1)——有理数相关概念

生活中的应用
8.老师想利用周末时间对班上6位同学进行家访. 六位同学家住在一条东西走向笔直的大道旁。 如果规定向东为正,向西为负,老师驾车的行程如下 (单位:千米)+5 , -4, -12 , -1, -3 , +10. (1)出发地记为0,老师到达最后一位同学家时, 你能求出老师的具体位置吗? (2)若汽车耗油量为0.1升/千米,这次家访 共耗油多少升?
知识提升
9.已知a,b,c为有理数,且它们在数 轴上的位置如图所示. a 0 b c (1) 试判断,a,b,c的正负性;
a<0, b>0, c>0
(2)化简: ① |a|= -a ; |b|= b ;③|c|= ② |-a|= -a ; |b+c|= b+c ;
c
;
去绝对值符号: 1.先判断绝对值符号里面的数或式子的正负 2.再利用绝对值的性质去绝对值符号。
拓展延伸
1.如图所示,数轴上点A与点B之间的距离用 AB表示,
若A,B两点分别表示-2与5,则 AB = 7 。 若A,B两点在数轴上分别表示2与5,则 AB = 3 。 若A,B两点分别表示-2与-5,则 AB = 3 。 根据上述结论回答下列问题: (2)如果点M表示-4,点N表示x,且 NM = 6, 那么x等于多少?
(2)你能把以上有理数在数轴上表示出来吗?
-3 -2 -1 O 1 2 3
例1 (2)在数轴上表示出下列各数:
-3
-2
-1
O
1
2
3
归纳:
1. 数轴上原点右侧的数是正数,原点左侧的数是负数。 2.数轴上表示的有理数中,右边的数大于左边的数。 3. 数轴上在(原点)原点两侧,到原点距离相等的两个数 互 相反数 4. 数轴上一个数到原点的距离,叫做这个数的绝对值
有理数的概念复习1

有理数的概念复习1、已知0>a ,0<b ,b a <,用“<”符号把a ,a -,b ,b -连接起来的式子为2、一个点从数轴的原点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是_________.3、数轴上与原点的距离是2个单位长度的点表示的数是________.到-3距离5个单位长度的点表示的数是_________.数轴上-1.5与+3.2之间的距离是_________.4、若一个数的绝对值为2,则这个数是_______;2.绝对值不大于2的非负整数为______绝对值不大于3的整数有_________.绝对值不大于3的非负整数________.绝对值小于10的所有的整数的和是 ,积是 .5、在数轴上,把表示3的点移动5个单位,则与此位置相对应的数是 。
6、到原点的距离不大于3的整数有 个,它们是:大于-4.5的非正整数有____个,大于-7.6且小于2.9的整数有___个。
7、数轴上,若A 、B 表示互为相反数,A 在B 的右侧,并且这两点的距离为8,则这两点所表示的数分别是_______和_______.8、已知 |a|=3,那么a = ;已知82=-x ,则x 的值为 ,绝对值大于1而不大于3的整数是 。
9、若023=-+-y x , y — x =________。
若3=a ,2=b ,则b a +的值为_________. 如果6=m ,2=n ,m n n m -=-,那么=m ,=n . 若8=a ,3=b ,且0>a ,0>b ,则=-b a ________,当52<<-x 时,化简25+--x x =_____________.10、若a a -= ,则 a 的取值范围是( )A 、0>a B 、0<a C 、0≥a D 、0≤a11、若|a+b|=-(a+b ),正确的是( )(A )a+b<0 (B )a+b ≤0(C )a+b=0 (D )a+b>012、若a a >-,那么( ) (A )0≥a (B )0>a (C )0<a (D )0≠a13、若23=a ,37=b ,则b a +的值是( ) (A )623 (B )65- (C )623或65- 14、高度每增加1千米,气温就下降2°C ,现在地面气温是10°C ,那么7千米的高空的气温是_____________.15、某粮店出售的三种品牌的面粉袋上分别标有质量为(25±0.1)kg,(25±0.2)kg, (25±0.3)kg的字样,从中任意拿出两袋,它们的质量最多相差____________.16、若│a│=4,b是绝对值最小的数,c是最大的负整数, a+b-c=_____________.17、写出下列各数的精确度1)43.8____________(2)32.4亿_____________ (3)6×104 ________________(4)6.00×107 ___________18、32、5亿(用科学记数法表示)=_________________________.346700000(科学计数法)=____________________19、把下列各数填入相应的集合里.-6,8,│-3.5│,+│-13│,-3.14,0,|+558|,34,-│-45│,|-0.75|.整数集合:{ …};正数集合:{ …};负分数集合:{ …};正分数集合:{ …};非正数集合:{ …};非负数集合:{ …};非正整数集合:{ …}。
6有 理 数 复 习---概念

3、并根据数轴指出:
1 1 (1)所有大于-2 而小于2 的整数. 2 2
(2) 大于-4的负整数有几个? (3) 小于4的正整数有几个? (4) 大于-4且小于4的整数有几个?
• 4、 (1)-3的相反数是____ 3 ; 4的相反数是____. -4 • (2)-(-8)的相反数是 -8 ; • (3)+(-6)是 6 的相反数; • (4)若-x=1,则x= -1 . -a-b • (5)a+b的相反数表示为______; -a+b a-b的相反数表示为________ 2 个, • (6)到原点的距离是2的点有__ 2、-2 这些点所表示的数是______
4 5
• 请谈谈这节课的收获!
C B c A -4 -3 -2 -1 0 1 2 3 4
(3)、将C点向左移动4个单位长度后, C点表示的数比B点表示的数大 多少?
在数轴上有三个点A、B、C,回答下列 问题:
C B A -4 -3 -2 -1 0 1 2 3 4
(4)、怎样移动A、B、C中的两个点, 才能使三个点表示的数相同? 有几种移动方法?
a-b (4) 若a 0, b0,则 a - b ____ a-b (5) 若a 0, b0,则 - a b ____
(6) 若a 0, b0,则 a - b - a b 2a-2b ___
10、 • (1)绝对值等于3的数有 2 个, 它们是3、-3; 无数 • (2)绝对值等于本身的数有 个, 它们是非负数 _______; • (3)①若│a│=3,则a= 3 . ②若│-a│=3,则a= 3 . 5、 1 ③若│a-2│=3,则a=____ 3 4 (4)比较大小: ___ 〉
• 5、已知:a、b在数轴上的位置 如图所示,在数轴上做出他们的 相反数.并用“〈”将这四个数连 接起来.
有理数复习课教案

有理数复习(一)初一级主备人(李青)教学目标:知识点一:正负数的意义具有相反意义的量 1.下列语句中,含有相反意义的两个量是()A. 盈利 1 千元和收入 2 千元 B. 上升 8 米和后退 8米C.存入 1 千元和取出 2 千元D.超过 2 厘米和上涨 2 厘米2.如果零上 6。
c 记作 +3,则这个问题中,基准是()A. 零上 3 。
cB.零下 3。
CC. 0D. 以上都不对3.上升 9 记作 +9,那么上升 6 又下降 8 后记作正负数的概念判断题 :①不带“-”号的数都是正数②带“ +”号的数都是正数③如果 a 是正数,那么- a 一定是负数④不存在既不是正数,也不是负数的数⑤一个有理数不是正数就是负数⑥0℃表示没有温度知识点二:有理数的分类1._____________统称整数,试举例说明。
2._____________统称分数,试举例说明。
3._____________统称有理数。
4.有理数的分类表:把下列各数填在相应额大括号内:1,- 0.1,-789,25,2∏, 0,-20, -3.14, 200%, 6/7正整数集{负整数集{正分数集{⋯}⋯}⋯}负分数集{⋯}正有理数集{⋯}负有理数集{⋯}自然数集{⋯}有理数集{⋯}非负整数集{⋯}有限小数、无限循环小数都是分数判断:(1)整数一定是自然数()(2)自然数一定是整数()填空:最小的自然数是__,最大的负整数是__,最小的正整数是__,最大的非正数是__。
知识点三:数轴、相反数、绝对值数轴是一条直线数轴是一条直线1.__________________________叫数轴。
-3–2–1012341)在数轴上表示的数,右边的数总比左边的数大;2)正数都大于0,负数都小于0;正数大于一切负数;3)所有有理数都可以用数轴上的点表示。
-3–2–1012341.两个有理数表示较大的数的点离原点的距离较近()2.与原点的距离为三个单位的点有__个,他们分别表示的有理数是__和 __。
有理数总复习1

零 负有理数
[基础练习] 1☆把下列各数填在相应额大括号内: 1,-0.1,-789,25,0,-20,-3.14,-590,6/7 正整数集{ …}; 正有理数集{ …}; 负有理数集{ …};负整数集{ …}; 自然数集{ …}; · 正分数集{ …} 负分数集{ …} 2☆ 某种食用油的价格随着市场经济的变化涨落,规定上 涨记为正,则-5.8元的意义是 ;如果这种油 的原价是76元,那么现在的卖价是 。
6、计算
1 1 1 1 1 1 1 1 1 1 ........ 2 2 3 3 4 4 5 9 10
7.有理数大小的比较
1)可通过数轴比较: 在数轴上的两个数,右边的数 总比左边的数大; 正数都大于0,负数都小于0; 正数大于一切负数; 2)两个负数,绝对值大的反而小。 即:若a<0,b<0,且︱a︱>︱b︱, 则a < b.
4.相反数
只有符号不同的两个数, 其中一个是另一个的相反数。 1)数a的相反数是-a
(a是任意一个有理数);
2)0的相反数是0. 3)若a、b互为相反数,则a+b=0.
-4
-2 2 4
-4 -3 –2 –1
0
1
2
3
4
• [基础练习] • 1☆-5的相反数是 ;-(-8)的相反数是 ; - [+(-6)]=________;0的相反数是 ; a的相反数 是 ; 1 的相反数的倒数是______________ ; 8 • 2☆若a和b是互为相反数,则a+b=( ) A. –2a B .2b C. 0 D. 任意有理数 • 3★(1)如果a=-13,那么-a=______; (2)如果-a=-5.4,那么a=______; (3)如果-x=-6,那么x=______; (4)-x=9,那么x=______. • 4★★已知a、b都是有理数,且|a|=a,|b|=-b,则ab是 ( ) A.负数; B.正数; C.负数或零; D.非负数
有理数重难点复习

2 (1)把一个大于10的数记成的形式,其中a是整数位只有一位的数,这种记数法叫做科学记数法。 (2)一个近似数,从左边第一个不是0的数字起,到精确到的数位止,所有的数字,都叫做这个数的有效数字。 (3)近似数就是与实际数非常接近的数。 四. 考点分析 对负数意义的理解,绝对值的代数和几何意义,有理数的分类,相反数和倒数的概念,科学记数法,有效数字等都是中考命题的热点,考查学生对概念的把握能力。 【典型例题】 例1. 判断正误 (1)a一定是正数;(2)一定是负数; (3)一定大于0;(4)0是正整数。 分析:本题主要考查对负数意义的理解 (1)由字母表示数的意义可知,a可是任意的数,既可以是正数,还可以是负数或0,故不正确。 (2)由上题可知,当a是负数或0时,是正数或0,故不正确。 (3)是的相反数,但a可以是一个负数,故不正确。 (4)由定义可知0不是正数也不是负数,不正确。 例2. 若,且x、y都是整数,请写出符合条件的x、y的值。 分析:本题是开放性问题,利用绝对值的几何意义和数轴解决问题,即x对应在数轴上的点到原点的距离,与y对应在数轴上的点到原点的距离之和为3。 解:由题意知,x对应在数轴上的点到原点的距离与y对应在数轴上的点到原点的距离之和为3。 从数轴上可以看出,x、y可以取的数应为从-3到3之间的整数。 ∴(1)当x=-3时,y=0 (2)当x=-2时,y=1 (3)当x=-1时,y=2 (4)当x=0时,y=3 (5)当x=1时,y=-2 (6)当x=2时,y=-1 (7)当x=3时,y=0 例3. 数a、b、c在数轴上的位置如图所示,化简。 分析:本题考查数轴上的数的大小及绝对值的代数意义 解:由上图可知 ∴
第一章有理数复习
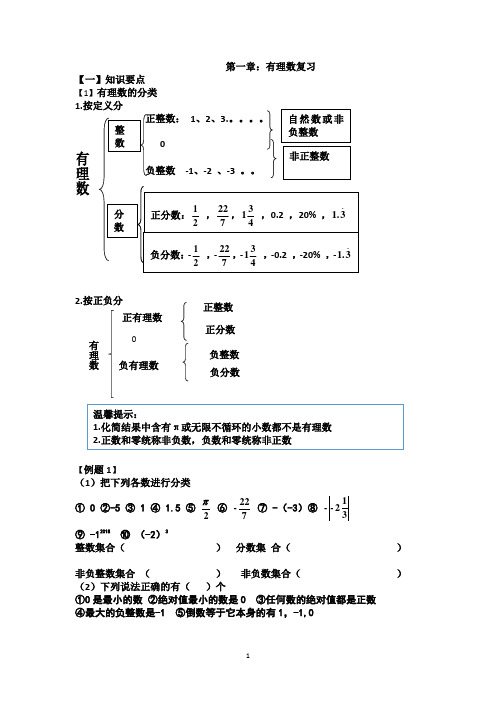
第一章:有理数复习【一】知识要点 【1】有理数的分类 1.2.按正负分【例题1】(1)把下列各数进行分类 ① 0 ②-5 ③ 1 ④ 1.5 ⑤2 ⑥ 722- ⑦ -(-3)⑧ 312--⑨ -12018 ⑩ (-2)3整数集合( ) 分数集 合( )非负整数集合 ( ) 非负数集合( ) (2)下列说法正确的有( )个①0是最小的数 ②绝对值最小的数是0 ③任何数的绝对值都是正数 ④最大的负整数是-1 ⑤倒数等于它本身的有1,-1,0有理数正有理数负有理数温馨提示: 1.化简结果中含有π或无限不循环的小数都不是有理数 2.正数和零统称非负数,负数和零统称非正数 正整数正分数 负整数 负分数有理数【2】相关概念1.数轴:规定了原点、正方向、单位长度的一条直线2.相反数:3.绝对值①几何定义:一个数a 的绝对值就是数轴上表示这个数a 的点离开原点的距离,绝对值越大离原点越远②代数定义:⎩⎨⎧≤-≥=)0()0(a a a a a (注意0)4.倒数:若两个数的积是1,那么这两个数互为倒数5.科学计数法6.近似数和有效数字7.数的大小比较方法:数轴上从左到右依次递增,数轴上的点与实数..是一一对应 ①代数定义:只有符号不同......的两个数叫做相反数 ②几何定义:数轴上在原点的两旁,到原点距离相等的两个点代表的数互为相反数③求一个数或式子的相反数,就在它的前面加上‘-’④a 的相反数是-a ,a-b 的相反数是-(a-b )=b-a,a+b 的相反数是-(a+b)=-a-b (注意括号),相反数等于它本身的只有0 ⑤性质:若a,b 互为相反数,则a+b=0,或a=-b 1、非负数的绝对值等于它本身,非正数的绝对值是它的相反数 2、绝对值符号去掉规律:非负数各项不变号,非正数各项都变号 3、一个数的绝对值(或者平方)等于正数.............,那么这个数有两个..①a,b 互为倒数 ab=1②倒数等于它本身只有±1,切记0没有倒数形式:ax10n (a 是整数位数只有一位的数,n 是整数), 当a ≥10时,n=原数整数位数-1 , 当a <1时,n=-(原数第一个非0数字前所有0的个数) ①保留近似数的方法有:四舍五入法、进一法、去尾法 ②近似数可以用计数单位或科学计数法表示 ③有效数字是从左边第一个不是零的数字起以后的所有数字都是这个数的有效数字 ④通过测量得到的数都是近似数 ①差法 ②数轴法 ③两个负的绝对值法 ④平方法 ⑤商法8.非负数性质【例题2】正负数应用(1)如果提高10分表示+10分,那么下降8分表示____,不升不降用___表示. (2)巴黎与北京的时间差为-7时(正数表示同一时刻比北京时间早的时数),如果北京时间是7月2日14:00,那么巴黎时间是()A. 7月2日21时B. 7月2日7时C. 7月1日7时D. 7月2日5时 (3)某项科学研究,以45分钟为1个时间单位,并记每天上午10时为0,10时以前记为负,10时以后记为正,例如9:15记为-1,10:45记为1等等,依此类推,上午7:45应记为【例题3】数轴、相反数、绝对值、倒数、非负数应用(1)已知 a ,b 互为相反数,c ,d 互为倒数,m-1的绝对值是2,则m dccd b a -+-+222=(2)在数轴上到表示-1的点的距离为7个单位长度的点有_____个,它们表示27(4)绝对值不大于2的整数有________,它们的和是 ,积是 ((6)已知|x|=4,|y|=2且y <0,则x+y 的值为(7) ①π-14.3=②20171-2018131-4121-311-21++++。
有理数全章复习(按知识点分类复习)

第一章 有理数全章复习考点一:用正负数表示相反意义的量1、 七年级一班某次数学测验的平均成绩为80分,数学老师以平均成绩为基准,记作0,把小龙、小聪、小梅、小莉、小刚这五位同学的成绩简记为+10,–15,0,+20,–2.问这五位同学的实际成绩分别是多少分2、如果规定收入为正,支出为负.收入500 元记作500元,那么支出237元应记作( ) A .-500元B .-237元C .237元D .500元3.有4包真空小包装火腿,每包以标准克数〔450克〕为基准,超过的克数记作正数,不足的克数记作负数,以下数据是记录结果,其中表示实际克数最接近标准克数的( )A .+2B .-3C .+3D .+44.某商店出售三种不同品牌的大米,米袋上分别标有质量如下表:现从中任意拿出两袋不同品牌的大米,这两袋大米的质量最多相差 ( )A .B .C .D .考点二:有理数的分类1、_______、_______和_________成为整数,__________和__________统称为分数。
___________和_________统称为有理数。
练习稳固:1、在–2,+3.5,0,32-,–0.7,11中.负分数有……………………〔 〕 A 、l 个 B 、2个 C 、3个 D 、4个2、不超过3)23(-的最大整数是………………………………………〔 〕 A 、–4 B –3 C 、3 D 、43.在数8.3、-4、0、-〔-5〕、+6、-|-10|、1中,正数有____ 个; 4、以下说法中正确的个数有 ( )①一个有理数不是整数就是分数 ②一个有理数不是正数就是负数 ③一个整数不是正的,就是负的 ④一个分数不是正的,就是负的A 1B 2C 3D 45、在数+8.3,-4,-0.8,0,90,-|-24|中,__________是正数,____________不是整数。
6、比132-大而比123小的所有整数的和为 __________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正数集合{
1 5
,3.2,+3.07,+4,+170
,
98,0.31
,π
…}
负数集合{-3,
-1
2 3
,
-2005
…}
整数集合{-3,0,+4,-2005, 98
…}
正分有数理集数合集{ 15合,{315.2,,3-.21,23+,3+.037.0,+74,,++117700,,
0.31 …} 98,0.31…}
A. 1 B. -1 C. 0 D.不存在
2.下列结论正确的是 ( B )
A. -a一定是负数 B. -|a|一定是非正数 C. |a|一定是正数 D. |a|一定是负数
3.下列说法正确的是( C )
A.正数与负数统称为有理数 B.带负号的数是负数 C.正数一定大于0 D.最大的负数是-1
巩固提高: 请选择
题组一:
1、如果向东走7km记作+7km,那么-5km表
示 向西走5km 。
2、
3 5
的相反数是 5
ห้องสมุดไป่ตู้
3 5
3 ,绝对值是 5 ,
倒数是 3
。
3、相反数是它本身的数是 0 ,绝对值是它本
身的数是非负数,倒数是它本身的数是±1 。
4、数轴上,到表示-2的点的距离是5的点所表
示的数是 -7或3 。
5、比较大小:(-3+π) >-9,
题组三:
2.53×108 百分位 6.8万(6.8×104) 3、近似数8.305×105精确到了 百 位, 它有 4 个有效数字,这些有效数字 分别是 8、3、0、5 .
典例解析:
例1:有理数a、b、c在数轴上的位置如图 所示,化简|b-a|+|b+c|-|a-c|.
ab
0c
典例解析:
例2:设符号(a,b)表示a,b两数中较小的 一个,符号[x,y]表示两数中较大的一个。 试求(-1,3)+[-4,(-2,-7)]的值。
B
B 6.两个非零数的和为零,则它们的商为(B )
A. 0 B. -1 C.+1 D.不能确定
巩固提高: 请填空
1.若|x|=7,则x为 ±7 . 2.若|a|=a 则a为 非负数 .
3.绝对值小于4且大于或等于1的所有整数 的积等于 -36 .
4.用<、>、=号填空:
-0.02 < 1, -3.14 <
典例解析:
例3:学校、家、书店依次坐落在一条东西 走向的大街上,学校在家的西边20米,书店 在家的东边100米,张倩同学从家里出发, 向东走了50米,接着又向东走了 -70米,
(1)此时张倩的位置在何处?(画出示意图)
(2)她爸爸一天上上午开着三轮车,从家里 出发,给这条路上的店铺送大米,向东为正,向 西为负,行车里程(单位:米)依先后次序记录 如下: +390,+150,+100,+250,-410,-450,-200,-250。 如果三轮车每千米耗油1.1升,他将最后一车 大米送达目的地时共耗油多少升?
巩固提高:
判断正误
1.一个数的相反数一定比原数小.( × )
2. |a|=|b|, 则a=b . ( × )
3.如果两个有理数不相等,那么这两个有
理数的绝对值也不相等.( × )
4. |-2.7|>|-2.6|
(√ )
5.若a+b=0,则a,b互为相反数. ( √ )
巩固提高: 请选择
1.相反数是它本身的数是( C )
4 5
<
57.
6、化简:+[-(-6)]= 6 , -|+(-5)|= -5 .
7、若|x+3|+(y-2)2=0,则(x+y)2008= 1 .
8、如图,a<b,a-b < 0, a+b < 0.
a -1
0 b1
题组二:
……
把下列各数填在相应的集合中
--320,0515,,+ 1730.2,,98-,1230.3,10,,π+3. .07,+4,
-(
3 4
)
= -[+(-0.75)]
22 7
,
5.数轴上表示-5和-14的两点之间的距离 是9。
巩固提高: 请填空
6.若a、b互为相反数,c、d互为倒数,则
?a ? b ?3 ? 3 ?cd ?的值为 -3 。
7.计算1-2+3-4+5-6+……+2001- 2002=-1001 。
2019 SUCCESS
POWERPOINT
2018 年12月12日星期三 16
2019 SUCCESS
THANK YOU
2018 年12月12日星期三 17
