计量经济学 第6章
计量经济学第六章自相关

计量经济学第六章自相关自相关是计量经济学中一种重要的现象,它指的是一个变量与其自己在过去时间点上的相关性。
自相关在实证研究中十分常见,对经济学家来说,了解和掌握自相关性质是至关重要的。
1. 引言自相关作为计量经济学的一项基础概念,是经济学研究中不可或缺的一个重要方法。
自相关性的存在通常会引起回归结果的偏误,而忽略自相关性可能导致估计不准确的结果。
因此,探讨自相关性的性质和应对方法是计量经济学的重点之一。
2. 自相关的定义和表示自相关是指一个变量与其自身在过去时间点上的相关性。
假设我们有一个时间序列数据集,其中变量yt表示一个时间点上的观测值,t表示时间索引。
自相关系数可以通过计算观测值yt与其在过去某一时间点上的观测值yt-k(k为时间滞后期数)的相关性来得到。
数学上,自相关系数可以用公式表示为:ρ(k) = Cov(yt, yt-k) / (σ(yt) * σ(yt-k))其中,ρ(k)表示第k期的自相关系数,Cov表示协方差,σ表示标准差。
3. 自相关性的性质自相关性具有以下几个性质:3.1 一阶自相关性一阶自相关性是指变量值yt与前一期的观测值yt-1之间的相关性。
一阶自相关系数ρ(1)通常用来检验时间序列数据是否存在自相关性。
若ρ(1)大于零且显著,则表明存在正的一阶自相关性;若ρ(1)小于零且显著,则表明存在负的一阶自相关性。
3.2 高阶自相关性除了一阶自相关性,时间序列数据还可能存在高阶自相关性。
高阶自相关性是指变量值yt与过去第k期的观测值yt-k之间的相关性。
通过计算不同滞后期的自相关系数ρ(k),可以了解数据在不同时间跨度上的自相关性情况。
3.3 异方差自相关性异方差自相关性是指时间序列数据中的方差不仅与自身相关,还与过去观测值的相关性有关。
异方差自相关性可能导致在回归分析中的标准误差失效,从而产生无效的回归结果。
因此,在处理存在异方差自相关性的数据时要采取合适的修正方法。
4. 自相关性的检验方法在实证研究中,经济学家通常使用多种方法来检验数据中的自相关性,常用的方法包括:4.1 Durbin-Watson检验Durbin-Watson检验是一种常用的检验自相关性的方法,其基本思想是通过检验误差项的相关性来判断自相关是否存在。
计量经济学第6章假设检验

i1
n
或直接取自输出结果2.2.1中的方差分析部分“回归分析(行) F(列)”(399.09999)。(见表2.4.4)
有时S(回归系数的标准差,有时也记为 S e )也可不写;t统计 量右上角*的表示显著性水平的大小,**一般表示在显著性水平 1%下显著,*一般表示在显著性水平5%下显著,无*表示5%下 不显著。
b1
L xx L yy
n
( x x ) ( y y ) 其 中 x y
i 1
L
n
L xx
L
yy
n
i 1
( xi x )2
i 1
( yi y )2
为x与y的简单线性相关系数,简称相关系数。它表示x和y的线 性相 关关系的密切程度。其取值范围为|r| 1,即-1 r 1。 当r=-1时,表示x与y之间完全负相关; 当r=1时,表示x与y之间完全正相关; 当r=0时,表示x与y之间无线性相关关系,即说明x与y可 能无相关关系或x与y之间存在非线性相关关系。 5、四种检验的关系 前面介绍了t检验、拟合优度( )检验、 F检验和相关 R 2 系数(r)检验,对于一元线性回归方程来说,可以证 明,这四种检验:
第二步:计算F统计量 因为ESS=1602708.6 (计算过程见表2.4.3) 或直接取自输出结果 2.2.1中的方差分析部分“回归分析(行) SS(列)”(1602708.6)。
ˆ= RSS ( yi y )2 40158.071 (计算过程见计算表2.3.3) 或直接取
第六章计量经济学

第六章 虚拟变量的回归模型第一部分 学习目标和要求本章主要介绍虚拟变量的基本概念及其应用。
需要掌握并理解以下内容:(1) 虚拟变量的基本概念、虚拟变量分别作为解释变量和被解释变量的情形、虚拟变量回归模型的类型和解释变量个数选取规则; (2) 定量变量与不同数量定性变量(一对一、一对多和多对多)虚拟变量模型; (3) 应用虚拟变量改变回归直线的截距或斜率; (4) 分段线性回归;(5) 应用虚拟变量检验回归模型的结构稳定性、传统判别结构稳定性的方法及存在的缺陷、虚拟变量法比较两个回归方程的结构方法。
第二部分 练习题一、解释下列概念:1.虚拟变量2.方差分析模型(ANOV A ) 3.协方差模型(ANOCV A ) 4.基底5.级差截距系数 6.虚拟变量陷阱二、简要回答下列问题:1.虚拟变量在线性回归模型中的作用是什么?举例说明。
2.回归模型中虚拟变量个数的选取原则是什么?为什么?3.如果现在有月度数据,在对下面的假设进行检验时,你将引入几个虚拟变量? A) 一年中的每月均呈现季节性波动趋势;B) 只有双数月份呈现季节性波动趋势。
4.如果现在让你着手检验上海和深圳两个股票市场在过去5年内的收益率是否有显著差异,如何使用虚拟变量进行?三、考虑如下模型:12i i i Y D u ββ=++其中,i D 对前20个观察值取0,对后30个观察值取1。
已知2()300i Var u =。
(1) 如何解释1β和2β? (2) 这两组的均值分别是多少?(3) 已知12()15Cov ββ∧∧+=-。
如何计算12()ββ∧∧+的方差?四、考虑如下模型:12i i i i Y D X u ααβ=+++ 其中Y 代表一位大学教授的年薪; X 为从教年限; D 为性别虚拟变量。
考虑定义虚拟变量的三种方式:(1)D 对男性取值1,对女性取值0; (2)D 对女性取值1,对男性取值2; (3)D 对女性取值1,对男性取值-1;对每种虚拟变量定义解释上述回归模型。
南开大学计量经济学第6章自相关

经济模型中最常见的是一阶自回归形式。
T
ut ut1
依据 OLS 公式,模型 ut = 1 ut -1 + vt 中1 的估计公式是
aˆ1
=
t=2 T
。
ut12
t=2
若把 ut, u t-1 看作两个变量,则它们的相关系数是 ˆ =
T
ut ut1
t=2
。
T
T
ut 2
u t 1 2
(2)样本容量T
21 1.22 1.42 1.13 1.54 1.03 1.67 0.93 1.81 0.83 1.96
22 1.24 1.43 1.15 1.54 1.05 1.66 0.96 1.80 0.86 1.94 (3)原回归模型中解 23 1.26 1.44 1.17 1.54 1.08 1.66 0.99 1.79 0.90 1.92 释变量个数k(不包括
《Econometrics》 《计量经济学》
攸频
nkeconometrics126 南开大学经济学院数量经济研究所
第六章 自相关
Autocorrelation
§6.1 基本概念、类型及来源 §6.2 自相关的后果 §6.3 自相关的检验(DW检验、LM检验) §6.4 自相关的修正(GLS) §6.5 案例
同理,Cov(ut, ut - s) = s Var(ut)
自相关的表现形式
§6.1.3 自相关的来源
(1)惯性 大多数经济时间数据都有一个明显的特点,即
具有惯性。 如:经济周期
棘轮效应
(2)设定偏误:模型中遗漏了显著的变量
例如:如果对羊肉需求的正确模型应为
Yt=b0+b1X1t+b2X2t+b3X3t+ut
计量经济学第六章

Simultaneous-Equations Model 第一节 联立方程模型概述 第二节 联立方程模型的结构式和简化式 第三节 联立方程模型的识别 第四节 联立方程模型的参数估计 第五节 联立方程模型的应用与检验
第一节 联立方程模型概述
一、联立方程模型的提出 例:研究某一商品的需求问题。
山东经济学院统计与数学学院计量经济教研室
Y1t Y 2t Y= M Ygt
注意: 注意:
X1t X 2t X= M Xkt
u1t u 2t U= M ugt
1. 矩阵 是可逆的,以保证联立方程模型有唯一解。 矩阵B是可逆的,以保证联立方程模型有唯一解。 是可逆的 2. 矩阵 和Γ 往往是稀疏矩阵,即存在大量的零元素。 矩阵B和 往往是稀疏矩阵 即存在大量的零元素。 是稀疏矩阵, 3. 一般情况下,β11=β22=…=βgg=1,以说明因变量系数为 。 一般情况下, ,以说明因变量系数为1。 4. Xt的第一个元素通常为 ,以说明 个外生变量中含常数项。 的第一个元素通常为1,以说明k个外生变量中含常数项 个外生变量中含常数项。
山东经济学院统计与数学学院计量经济教研室
例:一个简单的宏观经济系统
由国内生产总值Y、居民消费总额 、投资总额I和政府消 由国内生产总值 、居民消费总额C、投资总额 和政府消 费额G等变量构成简单的宏观经济系统 等变量构成简单的宏观经济系统。 费额 等变量构成简单的宏观经济系统。 将政府消费额G由系统外部给定, 将政府消费额G由系统外部给定,其他变量互相影响并互 为因果。 为因果。
• 在联立方程模型中,内生变量既作为被解释变量, 在联立方程模型中,内生变量既作为被解释变量, 又可以在不同的方程中作为解释变量。 又可以在不同的方程中作为解释变量。
伍德里奇---计量经济学第6章部分计算机习题详解(STATA)
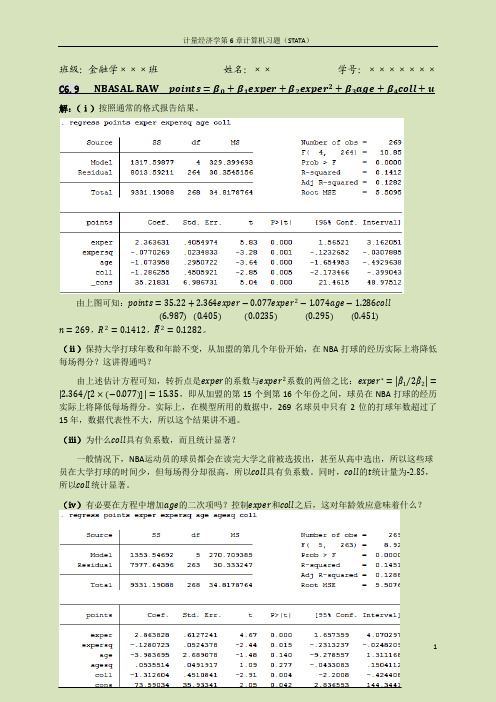
班级:金融学×××班姓名:××学号:×××××××C6.9 NBASAL.RAW points=β0+β1exper+β2exper2+β3age+β4coll+u 解:(ⅰ)按照通常的格式报告结果。
由上图可知:points=35.22+2.364exper−0.077exper2−1.074age−1.286coll6.9870.4050.02350.295 (0.451)n=269,R2=0.1412,R2=0.1282。
(ⅱ)保持大学打球年数和年龄不变,从加盟的第几个年份开始,在NBA打球的经历实际上将降低每场得分?这讲得通吗?由上述估计方程可知,转折点是exper的系数与exper2系数的两倍之比:exper∗= β12β2= 2.364[2×−0.077]=15.35,即从加盟的第15个到第16个年份之间,球员在NBA打球的经历实际上将降低每场得分。
实际上,在模型所用的数据中,269名球员中只有2位的打球年数超过了15年,数据代表性不大,所以这个结果讲不通。
(ⅲ)为什么coll具有负系数,而且统计显著?一般情况下,NBA运动员的球员都会在读完大学之前被选拔出,甚至从高中选出,所以这些球员在大学打球的时间少,但每场得分却很高,所以coll具有负系数。
同时,coll的t统计量为-2.85,所以coll统计显著。
(ⅳ)有必要在方程中增加age的二次项吗?控制exper和coll之后,这对年龄效应意味着什么?增加age的二次项后,原估计模型变成:points=73.59+2.864exper−0.128exper2−3.984age+0.054age2−1.313coll35.930.610.05 2.690.05 (0.45)n=269,R2=0.1451,R2=0.1288。
古扎拉蒂《计量经济学基础》第6章
倒数模型
Yi
1
2(
1 Xi
)
ui
这一模型的特点:关于参数是线性的,但关
于变量是非线性的,所以从回归的角度看,这是
一个线性回归模型;当X趋于无穷大时,1/X趋于0,
而 Y则趋于β2。
一个例子:菲利普斯曲线
其中Y为通胀变化率,X为失业率,上半部 (较陡)表明,当失业率低于自然失业率时, 失业的单位变化(下降)引起的工资的变化率 (通胀)上升,其速度快于对应的在失业率高 于自然失业率时,失业的同样变化所引起的工 资下降(下半部较上半部平缓)。
yt 1 2 xt ut (绝对变化) R 2 0.67 ln yt 1 2 xt u(t 相对变化) R2 0.8
对数-线性模型
Yi 1 2 ln X i ui
X 变化一个百分比,Y的绝对变化量
2
Y X / X
Y
2 X
/
X
含义:Y的绝对变化(Y)等于2乘以X的相对变化。
(参数线性)
Yi
X e 2 ui 1i
ln Yi
ln 1
2
ln
Xi
ui
(参数线性)
Yi
X 2 1i
ui
ln Yi
ln(
1
X
i
2
ui )
(参数非线性)
运用OLS估计,假定:ln ui ~ i.i.d.N (0, 2 )
因此,在检验残差是否为正态时时,是对估计的残差 lnˆ ui
进行诊断,而不是对原始的残差。
要点与结论 1.有时一个回归模型并不明显包含截距项。 这样的模型被称为过原点回归。虽然估计这种模型 的代数方法很简单,但应小心使用这些模型。对于 这种模型,残差和是非零的;此外,通常计算的r2 不一定有意义。除非有很强的理论原因,否则还是 在模型中明显地引入一个截距为好。 2.因为单位和尺度是回归系数赖以解释的关 键,所以用什么单位和尺度来表达回归子和回归元 是很重要的。在经验研究中,研究者不仅要注明数 据的来源,还要声明变量是怎样度量的。
《计量经济学》第六章精选题及答案
第六章自相关二、问答题1、那些原因可以造成自相关;2、存在自相关时,参数的OLS估计具有哪些性质;3、如何检验是否存在自相关;4、当存在自相关时,如何利用广义差分法进行参数估计;5、当存在自相关时,如何利用广义最小平方估计法进行参数估计;6、异方差与自相关有什么异同;三、计算题1、证明:当样本个数较大时,)d。
≈-1(2ρα2、通过D-W检验,判断下列模型中是否存在自相关,显著性水平%5=(1)样本大小:20;解释变量个数(包括常数项):2;d=0.73;(2)样本大小:35;解释变量个数(包括常数项):3;d=3.56;(3)样本大小:50;解释变量个数(包括常数项):3;d=1.87;(4)样本大小:80;解释变量个数(包括常数项):6;d=1.62;(5)样本大小:100;解释变量个数(包括常数项):5;d=2.41;3、假定存在下表所示的时间序列数据:请回答下列问题:(1)利用表中数据估计模型:t t t x y εββ++=10;(2)利用D-W 检验是否存在自相关?如果存在请用d 值计算估计自相关系数ρ;(3)利用广义差分法重新估计模型:'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。
第三部分 参考答案二、问答题1、那些原因可以造成自相关?答:造成自相关的原因大致包括以下六个方面:(1)经济变量的变化具有一定的倾向性。
在实际的经济现象中,许多经济变量的现值依赖于他的前期值。
也就是说,许多经济时间序列都有一个明显的相依性特点,这种现象称作经济变量所具有的惯性。
(2)缺乏应有变量的设定偏差。
(3)不正确的函数形式的设定错误。
(4)蛛网现象和滞后效应。
(5)随机误差项的特征。
(6)数据拟合方法造成的影响。
2、存在自相关时,参数的OLS 估计具有哪些性质?答:当存在自相关,即I D ≠ΩΩ=,)(2σε时,OLS 估计的性质有:(1)βˆ是观察值Y 和X 的线性函数;(2)βˆ是β的无偏估计;(3)βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ;(4)βˆ不是β的最小方差线性无偏估计;(5)如果nX X n Ω'∞→lim存在,那么βˆ是β的一致估计;(6)2σ 不是2σ的无偏估计;(7)2σ不是2σ的一致估计。
计量经济学习题第6章多重共线性
计量经济学习题第6章多重共线性第6章多重共线性⼀、单项选择题1、当模型存在严重的多重共线性时,OLS估计量将不具备()A、线性B、⽆偏性C、有效性D、⼀致性2、经验认为某个解释与其他解释变量间多重共线性严重的情况是这个解释变量的VIF()A、⼤于B、⼩于C、⼤于5D、⼩于53、模型中引⼊实际上与解释变量有关的变量,会导致参数的OLS估计量⽅差()A、增⼤B、减⼩C、有偏D、⾮有效4、对于模型y t=b0+b1x1t+b2x2t+u t,与r12=0相⽐,r12=0.5时,估计量的⽅差将是原来的()A、1倍B、1.33倍C、1.8倍D、2倍5、如果⽅差膨胀因⼦VIF=10,则什么问题是严重的()A、异⽅差问题B、序列相关问题C、多重共线性问题D、解释变量与随机项的相关性6、在多元线性回归模型中,若某个解释变量对其余解释变量的判定系数接近于1,则表明模型中存在( )A 异⽅差B 序列相关C 多重共线性D ⾼拟合优度7、存在严重的多重共线性时,参数估计的标准差()A、变⼤B、变⼩C、⽆法估计D、⽆穷⼤8、完全多重共线性时,下列判断不正确的是()A、参数⽆法估计B、只能估计参数的线性组合C、模型的拟合程度不能判断D、可以计算模型的拟合程度⼆、多项选择题1、下列哪些回归分析中很可能出现多重共线性问题()A、资本投⼊与劳动投⼊两个变量同时作为⽣产函数的解释变量B、消费作被解释变量,收⼊作解释变量的消费函数C、本期收⼊和前期收⼊同时作为消费的解释变量的消费函数D、商品价格、地区、消费风俗同时作为解释变量的需求函数E、每亩施肥量、每亩施肥量的平⽅同时作为⼩麦亩产的解释变量的模型2、当模型中解释变量间存在⾼度的多重共线性时()A、各个解释变量对被解释变量的影响将难以精确鉴别B、部分解释变量与随机误差项之间将⾼度相关C、估计量的精度将⼤幅度下降D、估计对于样本容量的变动将⼗分敏感E、模型的随机误差项也将序列相关3、下述统计量可以⽤来检验多重共线性的严重性()A、相关系数B、DW值C、⽅差膨胀因⼦D、特征值E、⾃相关系数4、多重共线性产⽣的原因主要有()A、经济变量之间往往存在同⽅向的变化趋势B、经济变量之间往往存在着密切的关联C、在模型中采⽤滞后变量也容易产⽣多重共线性D、在建模过程中由于解释变量选择不当,引起了变量之间的多重共线性E、以上都正确5、多重共线性的解决⽅法主要有()A、保留重要的解释变量,去掉次要的或替代的解释变量B、利⽤先验信息改变参数的约束形式C、变换模型的形式D、综合使⽤时序数据与截⾯数据E、逐步回归法以及增加样本容量6、关于多重共线性,判断错误的有()A、解释变量两两不相关,则不存在多重共线性B、所有的t检验都不显著,则说明模型总体是不显著的C、有多重共线性的计量经济模型没有应⽤的意义D、存在严重的多重共线性的模型不能⽤于结构分析7、模型存在完全多重共线性时,下列判断正确的是()A、参数⽆法估计B、只能估计参数的线性组合C、模型的判定系数为0D、模型的判定系数为1三、简述1、什么是多重共线性?产⽣多重共线性的原因是什么?2、什么是完全多重共线性?什么是不完全多重共线性?3、完全多重共线性对OLS估计量的影响有哪些?4、不完全多重共线性对OLS估计量的影响有哪些?5、从哪些症状中可以判断可能存在多重共线性?6、什么是⽅差膨胀因⼦检验法?四、判断(1)如果简单相关系数检测法证明多元回归模型的解释变量两两不相关,则可以判断解释变量间不存在多重共线性。
计量经济学-第六章:联立方程计量经济模型
It
2122Yt1
23Gt
v2t
Yt 3132Yt133Gtv3t
3.简化式模型的矩阵表示
Ct 1112Yt113Gtv1t
It
2122Yt1
23Gt
v2t
Yt 3132Yt133Gtv3t
C t
Y It Yt11 Nhomakorabea12
13
21
22
23
31
32
33
1
X
Y G
t
结构式模型的导出的结果:
C Itt001100 1 1001111112( 111 1 21)11YYt t1111111 111G Gttu11ut111t 1uu1212tt111u2u21tt Yt 10 1011121Yt11111Gt 1u1 t 1 u2t1
而简化式模型的一般表示:
Ct 1112Yt113Gtv1t
Ct 0 1Yt u1t It 0 1Yt 2Yt1 u2t
Yt Ct It Gt
◇联立方程模型中方程、变量及其属性 方程包括:随机方程、确定性方程 按变量性质:内生变量、外生变量 按因果关系:解释变量、被解释变量 内生变量:是随机变量,内生变量之间相互影响, 内生变量还受到外生变量的影响 外生变量:是确定性变量,对内生变量产生影响 先决变量:外生变量、滞后内生变量
2.模型的一般表示方法 对于联立方程模型,可描述为: g个内生变量(g个方程),内生变量用向量Y表示; k个先决变量,先决变量用向量X表示; 则结构式模型矩阵表示为:
参数矩阵为:
U
◇写出下列简单宏观计量经济模型的矩阵形式:
Ct 0 1Yt u1t It 0 1Yt 2Yt1 u2t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 1 ˆ) ( X X ) Var( 如果仍用 来估计 ,显然这种估
计是有偏的,不一致的。建立在这样一 ˆ ) 的t检验与F检验可能产生严重的 个 Var( 误导,得出错误的结论。
6.2 异方差
3、异方差的判断 1)残差序列分析. A、不存在异方差
Y
6.2 异方差
B、存在异方差,残差方差随y的增大而 增大。
6.3 自相关
或者表示为:
yt * 1xt * t
其中: yt * yt yt 1, 0 (1 ), xt * xt xt 1 , 上式的回归为最佳线性、无偏的一致估 计。
6.3 自相关
6、例:自相关的处理. 中国宏观消费分析1952-1993,其中X 为国民收入,y为居民消费。
6.2 异方差
一个实例:货币供给增长率对GNP的影 响。
5000 4000
GNP
3000
2000
1000 500
1000
1500 M2
2000
2500
3000
6.2 异方差
Estimation Equation: GNP = C(1) + C(2)*M2
结果:
异方差检验:
结果:
Y
6.2 异方差
缺点:在样本期太短时无法判断。
6.2 异方差
2)异方差检验 Park异方差检验步骤: A、回归方程,得方程得残差序列。 B、取残差序列的平方,再估算一个方程:
ˆi ln X i vi ln u C、如果 值统计显著,说明数据存在
2
异方差。
6.3 自相关
6.3 自相关
DW检验的缺陷: 1)只能检验残差的一阶自相关。 2)当解释变量中出现被解释变量的滞后 变量时,DW不再适用。
6.3 自相关
5、自相关的处理。
残差自相关的结构已知——广义差分法。 ut ut 1 t 如果残差一阶自相关:
以一元回归为例,原回归为:
其中 v j 为随机误差。
6.1 多重共线性
2、多重共线性的后果 ˆ (X 估计值的表达式为: X )1 X Y,其中:
1 1 X 1 x11 x21 xn1 x1 j x2 j xnj x1k x2 k xnk
6.1 多重共线性
6.2 异方差
1、异方差的产生 学习模型,随学习时间的增加,其行为 的误差减少。(方差减少) 储蓄行为模型,随收入的增加,个人如 何支配他们的收入有更大的选择,有人 可以选择较多的储蓄,有人也可以选择 较少的储蓄,从而,收入越高,储蓄的 差异越大。(方差增大)
6.2 异方差
Y
0
X
Xi
Xj
消费支出与收入和财富的关系。其中Y表示消费支出、 X1表示收入,X2表示财富。
6.1 多重共线性
回归方程:Y = C(1) + C(2)*X1 + C(3)*X2 回归结果:
6.1 多重共线性
回归结果的拟合程度非常高,但系数的 斜率没有一个通过了显著性检验,但方 程的总体系数检验的F统计量又非常高, 说明X1、X2斜率至少有一个不为0。
计量经济学 第6章
多重共线性、异方差和自相关
6.1 多重共线性
1、多重共线性的产生 回归模型的部分解释变量之间存在线性 关系,即某个解释变量可以表示为另外 解释变量的线性组合。
6.1 多重共线性
完全的多重共线性,解释变量之间存在准确的 线性关系,有: x j 1x1 2 x2 j 1 x j 1 j 1 x j 1 k xk 欠完全的多重共线性,解释变量之间高度相关, 但又非完全相关,有: x j 1x1 2 x2 j 1x j 1 j 1x j 1 k xk v j
6.3 自相关
3、自相关的影响。
E(uiu j ) 0 由于模型假定随机误差项非自相关, 现 E(uiu j ) 0 ,则误差向量的方差协方差矩阵为:
11 12 21 22 Var (u ) T1 T 2 1T 2T 2I TT
,误差 表现为一种系统性变化的特征,造成自 相关。
6.3 自相关
2)忽略了模型的滞后效应。 如在消费模型中,消费不仅仅依赖于当期的收 入水平,由于消费者不会轻易改变他们的消费 习惯,因此他们的消费支出还依赖于前期的消 费支出,既有:
消费t=0+1收入t+2消费t-1+ut
如果忽略了滞后项,则模型的误差项由于滞后 变量对当前变量的影响而反映出一种系统性变 化的特征,具有自相关。
DW
2 ˆ ˆ ( u u ) t t 1 t 2 2 ˆ u t t 1 T T
其中T为样本容量。
6.3 自相关
ˆ t 依赖于解释变量,因此DW统计 由于 u 量与t统计量及F统计量的检验不同,没 有唯一的临界值可以用来检验一阶自相 关假设,DW给出上限 du 与下限 d L 两个 临界值。
6.2 异方差
当假定不成立时,有:
11 12 21 22 Var (u ) T1 T 2 1T 2T 2 I TT
当误差向量u的方差协方差矩阵的对角线上的元素不相 等时,说明该时间序列存在异方差。非对角线上的元 素表示误差向量的协方差,若非对角线上的元素不为0, 表示误差项自相关。
判断:各回归元系数均不显著,F检验接受回归元 系数为0的原假设,说明不存在异方差。
6.3 自相关
1、自相关的定义: 序列中的观测值之间的相关。
如果某个回归模型的残差存在类似如下 关系:
ut ut 1 t
其中 E(t ) 0, E(i j ) 0 ,说明残差序列 存在(一阶)自相关。
6.2 异方差
如果存在异方差,最小二乘估计仍具有无偏性 与一致性,但估计量不再是最优的,不满足最 小方差性。估计量的分布受到影响。
ˆ ) E[( ˆ )( ˆ )] Var ( E[( X X ) 1 X uuX ( X X ) 1 ] ( X X ) 1 X E (uu) X ( X X ) 1 ] ( X X ) 1 X X ( X X ) 1 ]
6.2 异方差
White异方差检验 White异方差检验思想:以两变量为例, 若原始的回归为
Yt 1 2 X 2t 3 X 3t ut
检验就以扩展的回归式为基础:
ˆt2 1 2 X 2t 3 X 3t 4 X 2t 2 5 X 3t 2 6 X 2t X 3t ut u
GCDAN vs. GW Y 120 100 80
GCDAN
40 20 0 0 1000 2000 3000 4000
6.2 异方差
2、异方差的后果 模型的假定条件给出的Var(u)是一个对角矩阵,各 误差项不相关,误差项的协方差为0,
2 0 2 2 Var (u ) I 2 0
6.3 自相关
DW ˆ (u
t 2 T t
ˆt 1 ) 2 u
2 ˆ u t t 1 2 t
T
ˆ u
t 2
T
ˆt 1 2 u ˆt u ˆt 1 u
2 t 2 t 2 2 ˆ u t t 1 T
T
T
ˆ u
t 2
T
2 t
ˆt 2 u ˆt u ˆt 1 u
25000
2 t 2 t 2
T
T
ˆ u
t 1
T
2(1
ˆu ˆ u
t 2 T
T
t t 1 2 t
2 t
ˆ u
t 1
) 2(1 )
6.3 自相关
其中 为 u t 与 ut 1 相关系数的估计
1 1
6.3 自相关
DW检验: H 0 : 0 ,( u t 一阶非自相关)
yt 0 1xt ut
(1 )
6.3 自相关
则在时刻t-1有: yt 1 0 1xt 1 ut 1 (2) (1)式减去(2)式乘以 ,有:
yt yt 1 (0 0 ) (1 xt 1xt 1 ) (ut ut 1 ) 0 (1 ) 1 ( xt xt 1 ) t
6.2 异方差
White异方差检验的输出结果给出了F统计量以 2 及自由度为扩展回归式中回归因子个数的 分 布。 判断:1、如果回归系数都不显著,则认为不 存在异方差,如果有任何一个回归的系数显著, 则认为该模型存在异方差。2、F统计量及 分 布在设定的显著水平接受原假设,即所有的回 归原系数为0,则认为不存在异方差。 2
6.1 多重共线性
4、多重共线性的判断 2 R 1) 高而显著的t值少。 2)解释变量之间高度相关 3) 估计量对数据小小的变化也会非常敏 感。
6.1 多重共线性
6、多重共线性的处理 1)根据先验信息重新设立模型。 2)去掉一个高度共线性的变量。 3)对原始序列做一阶差分。 4)增加数据进行回归。
如果第j个解释变量可以表示为其他解释变量的 线性组合,则X矩阵可以化简为:
