理论力学7-2
理论力学习题及答案1-7整理

第1章静力分析习题1.是非题(对画√,错画×)1-1.凡在二力作用下的约束称为二力构件。
()1-2.在两个力作用下,使刚体处于平衡的必要条件与充分条件式这两个力等值、反向、共线。
()1-3.力的可传性只适用于一般物体。
()1-4.合力比分力大。
()1-5.凡矢量都可以用平行四边形法则合成。
()1-6.汇交的三个力是平衡力。
()1-7.约束力是与主动力有关的力。
()1-8.作用力与反作用力是平衡力。
()1-9.画受力图时,对一般的物体力的可沿作用现任以的滑动。
()1-10. 受力图中不应出现内力。
()2.填空题(把正确的答案写在横线上)1-11.均质杆在A、B两点分别于矩形光滑槽接触,并在如图所示情况下平衡。
A点的受力方向为,B点的受力方向为。
1-12.AB杆自重不计,在5个已知力作用下处于平衡,则作用于B点的四个力的合力F R的大小F R= ,方向沿。
题1-11图F3R题1-12图3. 简答题1-13.如图所示刚体A、B自重不计,在光滑斜面上接触。
其中分别作用两等值、反向、共线的力F1和F2,问A、B是否平衡?若能平衡斜面是光滑的吗?1-14.如图所示,已知A点作用力F,能否在B点加一力使AB杆平衡?若能平衡A点的力F的方向应如何?1-15.如图所示刚架AC和BC,在C 处用销钉连接,在A、B处分别用铰链支座支承构件形成一个三铰拱。
现将作用在杆BC上的力F沿着其作用线移至刚体AC上。
不计三铰刚架自重。
试问移动后对A、B、C约束反力有没有影响?为什么?1-16.在刚体上的加上任意个的平衡力系,能改变原来力系对刚体的作用吗?但对于变形体而言又是如何?1-17.为什么说二力平衡条件、加减平衡力系原理和力的可传性等只能适用于刚体?1-18.如何区分二力平衡力和作用力与反作用力?1-19.为什么受力图中不画内力?如何理解?1-20.如何判定二力体或者二力杆?(a)(c)(d) (e)(g)(h)题1-21图题1-13图题1-14图题1-15图4.受力分析题1-21.画出下列标注字母物体的受力图,未画重力的各物体其自重不计,所有接触面均为光滑接触。
理论力学第七章

例题
点的复合运动
例 题 7-1
3. 速度分析。
绝对速度va:va=OA · =r ω ,方 ω 向垂直于OA,沿铅垂
方向向上。
牵连速度ve:ve为所要求的未知量, 方向垂直于O1B 。 相对速度vr:大小未知,方向沿摇杆 O1B 。 应用速度合成定理
va ve vr
13
例题
点的复合运动
2. 运动分析。 绝对运动-以O为圆心的圆周运动。 相对运动-沿杆BC直线运动。 牵连运动-平动。
24
ω0
O
30
C
例题
点的复合运动
例 题 8-10
3. 速度分析。
α
ω
60
绝对速度va:va = ω0 r,垂直于OA向下。
D A E 牵连速度ve: ve= vB,垂直于BD向右下。
B
vr vB v a
a
a
n ae sin 30 cos 30
2 3o l r 3l
所以杆BD的角加速度
t ae l
2 3 o r (l r )
3l 2
27
例题
点的复合运动
习题课
28
第七章
一、基本概念
点的合成运动习题课
1.一个动点,两个坐标系,三种 运动 2.速度合成定理
v2 B
v1
30
vr 与 va 的夹角 ve
60
M
β
ve sin 60 46 12 arcsin vr
va
vr
18
§7-3点的加速度合成定理
先分析 k’ 对时间的导数。
' drA rA rO k vA e rA dt ' ' drO dk e (rO k ) dt dt 因为 v drO r O e O dt
理论力学第七章摩擦课件

>>摩擦力与摩擦角
当物体A保持静止并且临界状态为先滑动时,只要保证所有主动
外力的合力与公法线的夹角小于等于摩擦角m,则无论外力多大,
全约束反力总可以与其形成平衡,而不会滑动。这种现象称为自锁 现象。如果主动力合力的作用线位于摩擦锥以外,则无论力多小, 物体都不能保持平衡。
7.2 考虑摩擦时物体系统的平衡
F
F4
b cos h sin a cos
W 2
1m cos20 2m sin20 200 kN
1.8m cos30
2
104 .2kN
综合以上四个结果,可得系统保持平衡时,拉力F的取值范围为
40.2 kN F1 F F4 104 .2 kN
>> 考虑摩擦时物体系统的平衡
例7-4 等厚均质矩形体A和B,如图7.14 所示。A重20kN,A与铅垂墙间是光 滑的,A与B和B与水平固定面间的摩 擦系数均为fs。试求系统平衡时fs至 少应为多大?B的重量W2至少应为多 少?
(2) 当物体处于向上滑动的临界状态时,摩擦力方向与图(b)所示的 摩擦力方向相反。
F
F2
sin cos
f f
cos sin
W
sin 20 0.2 cos 20 200 kN cos30 0.2 sin 30
109 .7 kN
(3) 当物体处于绕O点翻倒的临界状态时,此时有:x=0
Fy 0 FNB W 0 (c)
求解可得:
FNB
W cos 2 s in
Fs
W cos 2 s in
>> 考虑摩擦时物体系统的平衡
(2)这属于平衡的临界状态。首先
求角度的最小值,此时梯子的受力
理论力学第七章

B
M2
M
B
vr
M
va ve
A
M1
A
由各速度的定义:
MM va lim Dt 0 Dt
MM 1 ve lim Dt 0 Dt
M 1M MM 2 vr lim lim Dt 0 Dt 0 Dt Dt
理论力学
中南大学土木工程学院
28
va ve vr
wOC
C
va ve vr
ve va sin q v sin q
wOC
ve v sin q OA a
ab v sin q a
ve va
O
q
v A B
vr
vC OC wOC
理论力学
中南大学土木工程学院
38
[例]水平直杆AB在半径为r的固定圆环上以匀速u竖直下落。 求套在该直杆和圆环交点处的小环M的速度。 解:以小环M为动点,动系取在AB杆上, 动点的速度合成矢量图如图。 A 由图可得:
摆动推杆 凸轮机构
理论力学
中南大学土木工程学院
6
§7-1 绝对运动
绝对轨迹 绝对速度 va 绝对加速度 aa t n 或 aa ,aa ,
点的合成运动概念
动 点
点的运动
相对运动
相对轨迹 相对速度 v r 相对加速度 ar 或 art ,arn,
动系相对于定系的运动
定 系
固结于地面上的坐标系
(不需要画出)
中南大学土木工程学院
14
绝对加速度:aa
相对加速度:ar
牵连加速度:ae
理论力学
中南大学土木工程学院
15
动点:AB杆上的A点 动系:偏心轮
理论力学第七版答案_哈工大编_高等教育出版社出版
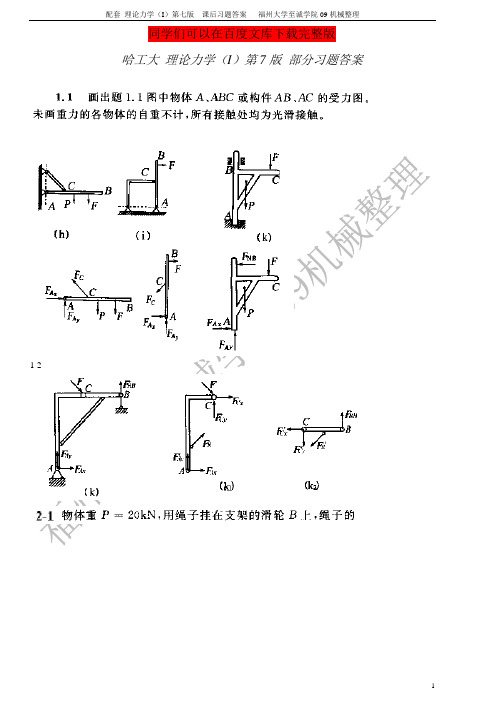
哈工大理论力学(I)第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1(i,j), 1-2(e,k)2-3, 2-6, 2-14,2-20, 2-306-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-2410-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4,15,16,1813-11,13-15,13-166-2 图6-2示为把工件送入干燥炉内的机构,叉杆OA=1.5 m在铅垂面内转动,杆AB=0.8 m,A端为铰链,B端有放置工件的框架。
在机构运动时,工件的速度恒为0.05 m/s,杆AB始终铅垂。
设运动开始时,角0=?。
求运动过程中角?与时间的关系,以及点B的轨迹方程。
10-3 如图所示水平面上放 1 均质三棱柱 A ,在其斜面上又放 1 均质三棱柱 B 。
两三棱柱的横截面均为直角三角形。
三棱柱 A 的质量为 mA 三棱柱 B 质量 mB 的 3 倍,其尺寸如图所示。
设各处摩擦不计,初始时系统静止。
求当三棱柱 B 沿三棱柱 A 滑下接触到水平面时,三棱柱 A 移动的距离。
11-4解取A、B 两三棱柱组成 1 质点系为研究对象,把坐标轴Ox 固连于水平面上,O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用,且开始时系统处于静止,故系统质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置(如图b 所示)在x 方向坐标分别为当棱柱B 接触水平面时,如图c所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示,均质杆AB,长l,直立在光滑的水平面上。
理论力学(第七版)思考题答案

理论力学思考题答案1-1 (1)若F 1=F 2表示力,则一般只说明两个力大小相等,方向相同。
(2)若F 1=F 2表示力,则一般只说明两个力大小相等,方向是否相同,难以判定。
(3)说明两个力大小、方向、作用效果均相同。
1-2 前者为两个矢量相加,后者为两个代数量相加。
1-3 (1)B 处应为拉力,A 处力的方向不对。
(2)C 、B 处力方向不对,A 处力的指向反了。
(3)A 处力的方向不对,本题不属于三力汇交问题。
(4)A 、B 处力的方向不对。
1-4 不能。
因为在B 点加和力F 等值反向的力会形成力偶。
1-5 不能平衡。
沿着AB 的方向。
1-7 提示:单独画销钉受力图,力F 作用在销钉上;若销钉属于AC ,则力F 作用在AC 上。
受力图略。
2-1 根据电线所受力的三角形可得结论。
2-2不同。
2-3(a )图和(b )图中B 处约束力相同,其余不同。
2-4(a )力偶由螺杆上的摩擦力和法向力的水平分力形成的力偶平衡,螺杆上的摩擦力与法向力的铅直方向的分力与N F 平衡。
(b )重力P 与O 处的约束力构成力偶与M 平衡。
2-5可能是一个力和平衡。
2-6可能是一个力;不可能是一个力偶;可能是一个力和一个力偶。
2-7一个力偶或平衡。
2-8(1)不可能;(2)可能;(3)可能;(4)可能;(5)不可能;(6)不可能。
2-9主矢:''RC RA F F =,平行于BO ;主矩:'2C RA M aF =,顺时针。
2-10正确:B ;不正确:A ,C ,D 。
2-11提示:OA 部分相当一个二力构件,A 处约束力应沿OA ,从右段可以判别B 处约束力应平行于DE 。
3-13-2 (1)能;(2)不能;(3)不能;(4)不能;(5)不能;(6)能。
3-3 (1)不等;(2)相等。
3-4 (1)'()B Fa =-M j k ;(2)'RC F =-F i ,C Fa =-M k 。
理论力学练习册及答案
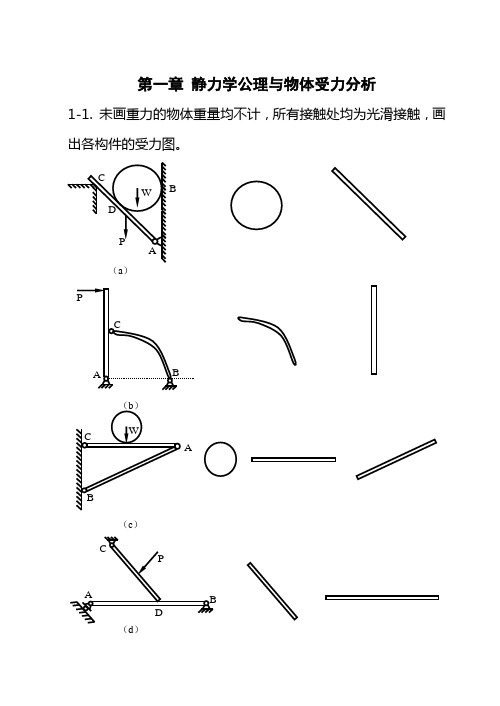
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解:将力系向A点简化,并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋,
作用点为:
3-2.已知A(1,0,1),B(0,1,2)(长度单位为米),F= kN。求力F对x、y、z轴的矩?
解:
3-3.如图所示,长方体边长为a、b、c,力F沿BD,试计算力F对AC轴之矩MAC(F)
解:力F对C点的矩为:
4-3.置于铅垂面内的均质正方形簿板重P= 100kN,与地面间的摩擦系数f= 0.5,欲使簿板静止不动,求作用在点A的力F的最大值?
4-4.折梯放在水平地面上,其两脚与地面的摩擦系数分别为fA= 0.2,fB= 0.6,折梯一边AC的中点D上有一重为P= 500N的重物,折梯重量不计,问折梯能否平衡?如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1.在如图所示中,已知ω、。在图上标示出A、B两的速度、加速度。
6-2.在如图所示的平面机构中,半径为r的半圆盘在A和B处与杆铰接,已知 , ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3.在如图所示的平面机构中,齿轮1紧固在杆AC上, ,齿轮1与半径为r2的齿轮2啮合,齿轮2可绕O2轴转动,。设 , ,试确定 时,轮2的角速度和角加速度。
解:动点取曲柄OA上A点,
第七章---理论力学

= −kv ,
v t =0 = v0 ,
求: x=x(t)
C LY
系 列 一
活塞作直线运动,取坐标轴Ox如图 解:1 活塞作直线运动,取坐标轴 如图
2
由
dv = −kv a= dt
dυ
υ
= − kdt
得
dv = − k t dt ∫v0 v ∫0
v
v = −kt, v = v0e −kt ln v0
3
由
dx = = −v0 e− kt v dt
v0 ( −kt ) x = x0 + 1 − e k
C LY
系 列 一
§7-5 自然法
以点的轨迹作为一条曲线形式的坐标轴来确定动点位置的方 以点的轨迹作为一条曲线形式的坐标轴来确定动点位置的方 轨迹作为一条曲线形式的坐标轴来确定动点 法叫自然坐标法 自然坐标法。 法叫自然坐标法。 一、弧坐标,自然轴系 弧坐标,
C LY
系 列 一
点都作直线运动, 轴如图所示。 解:A,B点都作直线运动,取ox轴如图所示。 点都作直线运动 轴如图所示 运动方程
xA = b + rsin ϕ = b + rsin ω +θ) ( t
xB = r sin ϕ = r sin ω +θ) ( t
B点的速度和加速度 点的速度和加速度
知 O C C t 已 : C = AC = B = l, M = a,ϕ =ω
求:① M 点的运动方程 ② 轨迹 ③ 速度 ④ 加速度
C LY
系 列 一
已知: 已知: C = AC = B = l, M = a,ϕ =ωt O C C 求:x=x(t), y=y(t)。 作曲线运动, 解:点M作曲线运动,取坐标系 作曲线运动 取坐标系xoy 运动方程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
M M '
rM z '
r'
O' x'
k ' rO ' i '
j'
y'
O
y
UNIVERSITY OF JINAN
第七章 点的合成运动
1. 动系做平移时 i 0, j 0, k 0
' k ' 0 2 x' i ' y ' j ' z
ve vr va ro
vB ve r O l l l
UNIVERSITY OF JINAN
第七章 点的合成运动
绝对加速度 相对加速度
n 2 aa aa O r
方向由A指向O
ar ?
n e 2 e
方向水平
2 O r2
v 牵连加速度 a l
l
方向由B指向D
v R vr aa R R 2 v R 2 r 2vr R
2 a 2
UNIVERSITY OF JINAN
第七章 点的合成运动
加速度合成定理(Theorem of composition of accelerations)
1. 动系做平移时
aa ae ar
2. 两个不相关的物体,求二者的相对速度。 根据题意, 选择所求相对运动速度的点为动点, 动系 固结于另一物体上。
UNIVERSITY OF JINAN
第七章 点的合成运动
3. 相对于运动物体在运动的物体上有一动点,求该点的绝 对运动。则取该点取为动点,动系固结于另一个运动物体 上。
UNIVERSITY OF JINAN
UNIVERSITY OF JINAN
第七章 点的合成运动
解:1、 动点:滑块A
动系:O1B杆
绝对运动:圆周运动 相对运动:直线运动(沿O1B) 牵连运动:定轴转动(绕O1轴) 2 、速度
va ve vr r
√
大小
? ?
√
rl vr va cos 2 2 l r
由于量较多,一般用解析法求解,即由合矢量投影定理: 投影于x轴:
a a a a arx arx
t ax n ax t ex n ex
t
n
UNIVERSITY OF JINAN
第七章 点的合成运动
y
C
n a
O a
O
A
ae
O
a
ar
D
t a
[例7-5]曲柄导杆机构中,已知:OA=R, 绕轴O转动的角速度为O,角加速度为 O,,求此时导杆加速度 解:A为动点,动系与导杆固结 x
t ae ?
方向垂直DB
UNIVERSITY OF JINAN
第七章 点的合成运动
v aa a r , a l t n aa ae ae ar
n a 2 O n e
2 e
2 O r2
l
t a 假设 ae r 指向如图,将上式向y轴投影
t aa sin 300 ae cos300 aen sin 300
设圆盘以匀角速度绕固定轴O顺时针转动,同时圆盘上有一 动点M,在半径为R的圆槽内以大小不变的相对速度vr顺时针作 圆周运动,那么M点对于静参考系的绝对加速度应该是多少? 动系固连于圆盘上,随同圆 盘一起转动 相对加速度大小: ar vr2 / R 牵连加速度大小:ae =R2 绝对加速度大小 va R vr
aa ae ar aC
UNIVERSITY OF JINAN
第七章 点的合成运动
牵连运动为平移时:
aa ae a r
t n a a a
注意: 点做曲线时加速度有两个分量
t n t n t n ∴一般式可写为: aa aa ae ae ar ar
方向 √
r 2 ve va sin 2 2 l r
ve ve r 2 1 2 2 2 2 O1 A l r l r
UNIVERSITY OF JINAN
第七章 点的合成运动
3、加速度 aa ae ar aC n t n aa ae ae ar aC
O
a
ar
D
t a
ae R O sin R 2 O cos
方向如图所示
UNIVERSITY OF JINAN
第七章 点的合成运动
[例7-5]平面机构中曲柄OA=r,以匀角速度O 转动。套管A可沿 BC杆滑动。BC=DE,BD=CE=l。求图示位置时杆BD的角速度 和角加速度 解:A点为动点,BC为动系 (平移坐标系) va = rO 做速度平行四边形
A
UNIVERSITY OF JINAN
2. 动系做定轴转动时
aa ae ar aC
aC 2e vr
称为科氏加速度 (Coriolis acceleration)
UNIVERSITY OF JINAN
第七章 点的合成运动
证明 思路
rM rO r '
r ' xi ' yj ' z k '
大小 2 r 方向
?
12 O1 A
?
21vr
√
√
√
√
√
沿 x 轴投影
n t aax a ' e aC
a a aC 2ω1vr ω r cos
t e n ax ' 2
2 2 2 2 rl l r a rl (l r ) 2 1 3 2 2 2 2 2 2 2 2 O1 A l r l r l r
UNIVERSITY OF JINAN
第七章 点的合成运动
【练习】已知:OC=e , CA=r , (匀角速度) 求:图示位置CA竖直时AB的速度。
300
va e
300
v AB
3 ve e () 2
UNIVERSITY OF JINAN
第七章 点的合成运动
§7-3, §7-4 点的加速度合成定理
z
M M '
rM rM
注意 : (1) M ' 是动系里的点, 其相对坐标x' , y ' , z ' 是不变的, 而M是动点,相对于动系和定 系坐标在变化。 (2)单位矢量i ' , j ' , k ' 对于平移 坐标系是常矢量,对转动坐标 x 系则是变矢量。
UNIVERSITY OF JINAN
rM z '
r'
O' x'
k ' rO ' i '
j'
y'
O
y
第七章 点的合成运动
rM r r M M rO r ' r x'i ' yj ' z k ' rM r r O'
d 2 rM aa 2 dt rO xi y j z k xi y j z k 2( xi y j z k ) 2 d rM xi yj zk ae r O dt 2 x ~2 d r i j k ar 2 x y z dt
相对加速度ar=? 方向铅直
牵连加速度 ae=?方向水平
UNIVERSITY OF JINAN
第七章 点的合成运动
y
C
n a
O
O a
A
ae
n t aa aa ae ar
应用合矢量投影定理,将个加速度 矢量向x轴投影 x
t n aa sin aa cos ae
D
ω
ω
C
aC 2 0 ( // v2 )
UNIVERSITY OF JINAN
第七章 点的合成运动
例7-6 刨床的急回机构如图所示。曲柄OA的一端A与 滑块用铰链连接。当曲柄OA以匀角速度ω绕固定轴O转动 时,滑块在摇杆O1B上滑动,并带动杆O1B绕定轴O1摆动。 设曲柄长为OA=r,两轴间距离OO1=l。 求:摇杆O1B在如图所示位置时的角速度和角加速度。
aa ae ar
2. 动系做定轴转动时
dk ' k ' k' dt
dr v r dt d i ' ' i ' y ' j ' z ' k ' 2 x i i ' dt 2 x ' i ' y ' j ' z 'k ' d j ' j' j' 2 vr dt
t e 2
UNIVERSITY OF JINAN
第七章 点的合成运动
练习:如图所示凸轮机构中,凸轮以匀角速度ω绕水平O轴 转动,带动直杆AB沿铅直线上、下运动,且O,A,B 共线。 凸轮上与点A接触的为 A ' ,图示瞬时凸轮上点 A ' 曲率半径为 ρA ,点 A 的法线与 OA夹角为θ,OA=l。 ' 求:该瞬时AB的速度及加速度。
科氏加速度大小
aC 2e vr sin
方向垂直于 e 和 vr 指向按右手法则确定
