工程的温度应力计算
混凝土温度应力计算方法
混凝土温度应力计算方法一、前言混凝土结构在施工和使用过程中，由于温度变化和变形等原因，产生的应力可能会对结构的稳定性和安全性产生影响。
因此，对混凝土温度应力的计算和控制是非常重要的。
本文旨在介绍混凝土温度应力的计算方法，包括温度应力的基本概念、计算公式、影响因素、计算过程等内容。
希望能够为混凝土结构的设计和施工提供参考。
二、温度应力的基本概念温度应力是指混凝土结构由于温度变化而产生的内部应力。
当混凝土受到温度变化的影响时，其体积会发生变化，从而引起内部应力的产生。
温度应力的大小与混凝土的热膨胀系数、温度变化量、混凝土的限制程度等因素有关。
温度应力的计算是基于温度变化量和混凝土的热膨胀系数进行的。
温度应力的计算公式如下：σ = α × ΔT × E其中，σ为温度应力，α为混凝土的热膨胀系数，ΔT为温度变化量，E为混凝土的弹性模量。
三、影响因素温度应力的大小受到多种因素的影响，主要包括以下几个方面：1. 温度变化量温度变化量是影响温度应力大小的重要因素。
温度变化量越大，温度应力就越大。
因此，在混凝土结构的设计和施工过程中，需要对温度变化量进行充分的考虑和控制。
2. 混凝土的热膨胀系数混凝土的热膨胀系数是指在单位温度变化下混凝土体积发生的变化量。
混凝土的热膨胀系数与混凝土的配合比、水胶比、骨料种类、骨料粒径、混凝土龄期等因素有关。
不同的混凝土配合比和龄期对应的热膨胀系数也不同。
3. 混凝土的限制程度混凝土的限制程度是指混凝土在受到约束时所能发生的变形程度。
混凝土的限制程度越小，混凝土受到的温度应力就会越大。
因此，在混凝土结构的设计和施工过程中，需要对混凝土的限制程度进行充分的考虑和控制。
4. 混凝土的弹性模量混凝土的弹性模量是指混凝土在受到外力作用时，单位应力下所发生的应变量。
混凝土的弹性模量与混凝土的配合比、水胶比、骨料种类、骨料粒径、混凝土龄期等因素有关。
不同的混凝土配合比和龄期对应的弹性模量也不同。
附录四 坝体混凝土温度和温度应力计算
附录四 坝体混凝土温度和温度应力计算—、温度计算1.坝体混凝土的初期温度计算(有内热源的温度场计算) (1)计算目的：坝体混凝土的初期温度计算目的，主要是确定基础块混凝土(或靠近老混凝土块的混凝土)中的最高温度T ，以便控制基础温差，最高温度T 可按下式计算：r j T T T += (附79)式中 T j ——混凝土的浇筑温度(℃，以下均同)，或称入仓温度； T r ——混凝土因水化热和其他原因产生的最高温升。
(2)混凝土的浇筑温度计算：η)(o q o j T T T T -+= (附80)式中 T o ——混凝土的拌和(即出机口)温度(忽略拌和中的热量损失或热量流入影响)； T q ——混凝土浇筑时的平均气温；η——考虑混凝土在拌和、装卸、运输、转运和浇筑过程中热量损失或倒罐的系数。
在一般的现场条件下，η=0.2～0.3，当运距较长，转运手续较多以及采用人工方法浇筑时，η =0.4～0.5。
混凝土的拌和温度按下述公式计算：i i ii i o C W T C W T ∑∑=(附81)式中 W i ——每立米混凝土中各种原材料的重量，kg/m 3； C i ——混凝土各种原材料的比热，kcal/(kg ·℃)； T i ——混凝土各种原材料的温度。
注：①在公式(附81)中未考虑骨料含水率的影响，当骨料含水率较大，不宜忽略时，应在公式中加以考虑。
②当在混凝土拌和中加入冰屑时，应考虑冰的潜热(80kcal/kg)和有效利用系数0.7～0.8。
③应考虑混凝土拌和时，拌和机发出的机械热，在没有实测资料情况下，可用350kcal 。
④在缺乏具体资料时，各种原材料的比热C 可按附表16采用。
附表16(3)混凝土的温升计算：混凝土入仓后的温升T r ，主要由水化热引起，此外混凝土入仓温度T j 和气温T q 的温差；浇筑块顶面(有时顶面加侧面)和冷却水管的散热以及基岩的吸热作用也对T r 有一定的影响。
大体积混凝土温度应力实用计算方法及控制工程实例
大体积混凝土温度应力实用计算方法及控制工程实例随着建筑工程的不断推进，大体积混凝土的使用越来越广泛。
然而，在大体积混凝土的施工过程中，其内部产生的温度差异会导致产生应力，从而影响混凝土的力学性能和使用寿命。
因此，如何控制大体积混凝土的温度应力，成为了工程师们研究的重点。
本文将围绕“大体积混凝土温度应力实用计算方法及控制工程实例”进行阐述，分步骤探究其实现方法。
步骤一：温度应力计算公式的推导大体积混凝土的温度应力可通过以下公式进行计算：σ =EαΔT，其中，σ表示温度应力，E表示混凝土的弹性模量，α表示混凝土的热膨胀系数，ΔT表示混凝土各处的温度差异。
在实际施工过程中，根据测量数据，可以计算出混凝土各部位的温差，进而根据上述公式计算出温度应力。
步骤二：温度应力控制的方法针对大体积混凝土的温度应力，可以采用以下措施进行控制：1.采用低热化水泥。
低热化水泥的热释放较低，可以减少混凝土内部的温度差异，从而降低温度应力。
2.增加混凝土中的纤维材料含量。
纤维材料可以改善混凝土的韧性和抗裂性能，从而有效地减小温度应力。
3.采取降温措施。
在混凝土浇注后，可以采用冷却设备等技术，将混凝土表面降温，从而减少混凝土内部的温度差异。
步骤三：大体积混凝土温度应力控制工程实例以某大规模混凝土建筑施工为例，为了控制混凝土的温度应力，采取了以下措施：1.采用低热化水泥，减少混凝土的热释放，降低温度应力。
2.增加混凝土中的纤维材料含量，提高混凝土的韧性和抗裂性能。
3.在混凝土浇注后，采用冷却设备对混凝土表面进行降温处理，控制混凝土内部的温度差异。
通过实际施工效果的观察和测量，发现混凝土的温度应力得到了较好的控制，施工质量得到了有效保障。
综上所述，控制大体积混凝土的温度应力，是建筑工程中不可忽视的重要环节。
通过正确计算温度应力，选用合适的控制措施，可以有效地提高混凝土的力学性能和使用寿命。
工程的温应力计算
一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（0.0+2.4+6.4+11.9+17.0+20.9+24.4+25.2+22.1+16.9+9.2+3.5）/12=13.3。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。
温度应力计算
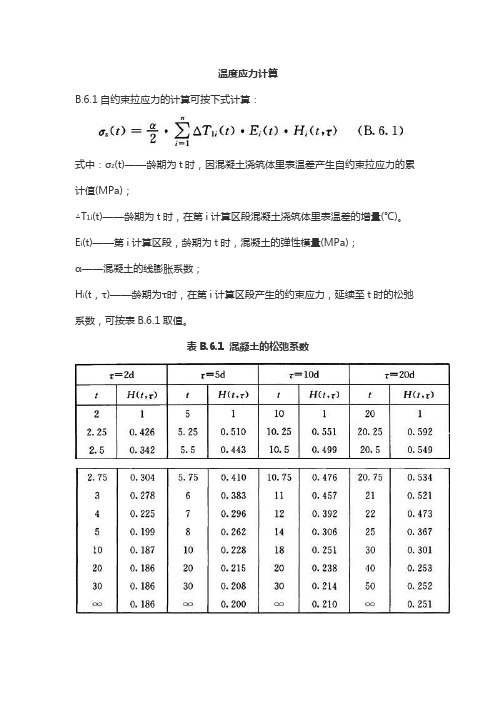
温度应力计算B.6.1自约束拉应力的计算可按下式计算：式中：σz(t)——龄期为t时，因混凝土浇筑体里表温差产生自约束拉应力的累计值(MPa)；△T1i(t)——龄期为t时，在第i计算区段混凝土浇筑体里表温差的增量(℃)。
E i(t)——第i计算区段，龄期为t时，混凝土的弹性模量(MPa)；α——混凝土的线膨胀系数；H i(t，τ)——龄期为τ时，在第i计算区段产生的约束应力，延续至t时的松弛系数，可按表B.6.1取值。
表B.6.1 混凝土的松弛系数注：τ为龄期，H(t，τ)为在龄期为τ时产生的约束应力，延续至t时的松弛系数。
B.6.2混凝土浇筑体里表温差的增量可按下式计算：式中：j——为第i计算区段步长(d)。
B.6.3在施工准备阶段，最大自约束应力可按下式计算：式中：σzmax——最大自约束应力(MPa)；△T1max——混凝土浇筑后可能出现的最大里表温差(℃)；E(t)——与最大里表温差△T1max相对应龄期t时，混凝土的弹性模量(MPa)；H(t，τ)——在龄期为τ时产生的约束应力，延续至t时(d)的松弛系数。
B.6.4外约束拉应力可按下式计算：式中：σx(t)——龄期为t时，因综合降温差，在外约束条件下产生的拉应力(M Pa)；△T2i(t)——龄期为t时，在第i计算区段内，混凝土浇筑体综合降温差的增量(℃)。
μ——混凝土的泊松比，取0.15；R i(t)——龄期为t时，在第i计算区段，外约束的约束系数。
L——混凝土浇筑体的长度(mm)；H——混凝土浇筑体的厚度，该厚度为块体实际厚度与保温层换算混凝土虚拟厚度之和(mm)；C x——外约束介质的水平变形刚度(N／mm3)，可按表B.6.4取值。
表B.6.4 不同外约束介质的水平变形刚度取值(10-2N／mm3)。
工程的温度应力计算
工程的温度应力计算温度应力是指由于温度变化引起的物体内部的应力。
在工程领域中，温度应力的计算对于材料的选择、结构设计和工程的安全性评估都具有重要意义。
本文将介绍温度应力的计算方法以及常见的应用案例。
温度应力的计算方法主要有两种：线性热弹性法和非线性热塑性法。
线性热弹性法是一种基于线性弹性理论的计算方法，适用于温度变化幅度较小、材料线性弹性行为较好的情况。
该方法的基本步骤如下：1.确定温度应变：根据温度变化情况和材料的线膨胀系数，计算出温度应变。
2.确定材料的弹性模量：根据材料的力学特性和温度，选择适当的弹性模量。
3.计算温度应力：根据线性弹性理论，利用得到的温度应变和弹性模量，计算出温度应力。
非线性热塑性法是一种基于材料的非线性力学行为的计算方法，适用于温度变化幅度较大、材料非线性行为较明显的情况。
该方法的基本步骤如下：1.确定温度应变：根据温度变化情况和材料的热膨胀系数，计算出温度应变。
2.确定材料的本构关系：根据材料的热塑性行为，选择适当的本构关系。
3.进行有限元分析：利用有限元分析软件，建立模型并进行计算。
4.计算温度应力：根据模型的计算结果，得到温度应力。
温度应力的计算在工程中有许多应用案例。
以下是一些常见的案例：1.管道的热应力计算：管道在运行过程中由于温度变化会产生应力，如果应力超过材料的强度极限，就会导致管道的破裂。
因此，计算管道的热应力是管道工程设计的重要环节。
2.钢结构的温度应力计算：钢结构在夏季高温和冬季低温的环境中，由于温度变化会产生应力，如果应力过大，就会引起结构的变形和破坏。
因此，计算钢结构的温度应力是钢结构工程设计的重要内容。
3.复合材料的热应力计算：复合材料由于材料的组分不同，在温度变化时会产生不同的热应力。
对于复合材料的设计，需要计算不同温度下的热应力，以保证材料的安全性。
4.太阳能电池板的温度应力计算：太阳能电池板在太阳光的照射下会发生温度变化，如果温度应力过大，就会影响电池板的性能和寿命。
大体积混凝土温度应力实用计算方法及控制工程实例
大体积混凝土温度应力实用计算方法及控制
工程实例
大体积混凝土的温度应力主要由于混凝土内部温度梯度不均匀所
引起，温度应力大小与混凝土的水泥含量、骨料类型、孔隙结构以及
环境温度等因素有关。
计算温度应力可采用以下公式：σ=αEΔT+(1-ν)αmΔT，其中，σ为温度应力，α为混凝土的线膨胀系数，E为混凝土的弹性模量，
ν为混凝土的泊松比，αm为混凝土的平均线膨胀系数，ΔT为混凝土内部温度差。
控制大体积混凝土的温度应力，可采取以下措施：
1. 使用高性能混凝土材料，降低混凝土线膨胀系数；
2. 对混凝土的成分、配合比等进行优化设计，降低混凝土内部温度梯度；
3. 控制施工环境的温度和湿度，提高混凝土的早期强度和抗裂性能；
4. 采用降温措施，如水帘喷淋、冷却剂等，降低混凝土的温度。
实际工程中，可通过对混凝土施工过程进行监控和管控，以及采
用温度预应力技术等措施，有效控制大体积混凝土的温度应力。
例如，在某大型桥梁工程中，采用了温度预应力技术，并通过建立温度控制
模型对施工过程进行精细化监控，成功地控制了混凝土的温度应力，
确保了施工质量和结构安全。
混凝土构件温度应力的计算原理
混凝土构件温度应力的计算原理
混凝土构件在使用过程中会受到温度的影响，由于混凝土的热膨胀系
数很小，因此在温度变化时会产生较大的应力。
在设计混凝土构件时，需要考虑温度应力的影响，以保证结构的安全性和可靠性。
温度应力的计算原理可以分为以下几个方面：
1.热膨胀系数的确定
混凝土的热膨胀系数是指单位温度变化时混凝土的长度、面积或体积
的变化量与原长度、面积或体积的比值。
热膨胀系数的大小与混凝土
的配合比、骨料种类、水胶比、水泥品种等因素有关。
一般情况下，
混凝土热膨胀系数的取值范围在10×10^-6/℃~15×10^-6/℃之间。
2.温度应力的计算公式
温度应力的计算公式为σ=αEΔT，其中σ为混凝土构件的温度应力，
α为混凝土的热膨胀系数，E为混凝土的弹性模量，ΔT为温度变化量。
在实际计算中，需要考虑温度应力的分布情况和混凝土构件的几何形状，一般采用有限元法或者解析法进行计算。
3.温度应力的控制
为了保证混凝土构件在使用过程中不会发生温度开裂或者温度变形过大的情况，需要采取一定的控制措施。
一方面可以采用降低混凝土的热膨胀系数的方法，比如在混凝土中添加一定比例的矿渣粉、粉煤灰等掺合料，或者采用高强度、高模量的混凝土。
另一方面可以采取降低温度应力的方法，比如增加混凝土构件的截面尺寸、采用预应力或者钢筋混凝土等方法。
总之，混凝土构件的温度应力计算是一个复杂的问题，需要考虑多种因素的综合影响。
只有通过科学的计算和合理的控制措施，才能够保证混凝土结构的安全性和可靠性。
混凝土结构的温度应力分析方法
混凝土结构的温度应力分析方法一、概述混凝土结构在使用过程中会受到温度的影响，温度变化会引起混凝土内部的应力变化，进而影响结构的稳定性和安全性。
因此，在混凝土结构的设计和施工中，需要考虑温度应力的影响。
本文将介绍混凝土结构的温度应力分析方法。
二、温度应力产生原因温度变化会引起混凝土内部的温度变化，从而引起混凝土内部的体积变化。
当混凝土受到约束时，体积变化会引起内部应力的变化，从而产生温度应力。
温度应力的大小与混凝土的线膨胀系数、温度变化量、混凝土的约束程度等因素有关。
三、温度应力分析方法1. 温度应力计算公式根据基本力学原理，可以得到混凝土结构的温度应力计算公式：σ = αΔT E其中，σ为温度应力，α为混凝土的线膨胀系数，ΔT为温度变化量，E为混凝土的弹性模量。
2. 温度应力分析步骤（1）确定温度变化量在进行温度应力分析前，首先需要确定温度变化量。
通常情况下，可以根据气象资料和历史数据来确定设计温度范围。
（2）确定混凝土的线膨胀系数混凝土的线膨胀系数是影响温度应力大小的关键因素之一。
一般情况下，可以根据混凝土的配比和试验数据来确定混凝土的线膨胀系数。
（3）确定混凝土的约束程度混凝土的约束程度也是影响温度应力大小的关键因素之一。
混凝土的约束程度越大，温度应力就越大。
一般情况下，可以根据混凝土的结构形式和施工方式来确定混凝土的约束程度。
（4）计算温度应力根据上述公式和确定的参数，可以计算出混凝土结构在温度变化下的应力分布情况。
四、温度应力分析案例以下是一个混凝土结构的温度应力分析案例：假设某混凝土结构的线膨胀系数为1.2×10^-5/℃，设计温度范围为-10℃~30℃，混凝土的约束程度为中等程度。
根据上述参数，可以计算出该混凝土结构在温度变化下的应力分布情况。
（1）确定温度变化量根据设计温度范围，温度变化量为40℃。
（2）确定混凝土的线膨胀系数已知混凝土的线膨胀系数为1.2×10^-5/℃。
混凝土结构温度应力计算技术规程
混凝土结构温度应力计算技术规程一、引言混凝土结构在使用过程中受到外部环境和内部荷载的影响，会产生温度应力。
温度应力是混凝土结构设计中必须考虑的因素。
本文将详细介绍混凝土结构温度应力的计算方法和技术规程。
二、温度应力的计算温度应力的计算可以通过以下公式进行：$$\sigma_t = \alpha(T - T_0)$$其中，$\sigma_t$表示温度应力，$\alpha$表示混凝土线膨胀系数，$T$表示混凝土温度，$T_0$表示混凝土的参考温度，一般为20℃。
在实际计算中，需要考虑混凝土的温度分布，因此需要将混凝土分成若干个部分进行计算。
具体计算方法如下：1. 将混凝土结构分成若干块，每块的尺寸要足够小，以保证温度分布的准确性。
2. 对于每块混凝土，计算其所受到的温度变化量，即$\Delta T = T - T_0$。
3. 计算每块混凝土的温度应力，即$\sigma_t = \alpha \Delta T$。
4. 将每块混凝土的温度应力合并，得到整个结构的温度应力。
合并时需要考虑混凝土的相互作用，具体方法见下文。
三、温度应力的调整在实际计算中，由于混凝土的温度分布不均匀，可能会产生一些局部的过大应力。
为了避免这种情况的发生，需要对温度应力进行调整。
具体方法如下：1. 对于局部应力过大的区域，可以采用降温的方法进行调整。
降温的方法包括增加通风、喷水等。
2. 对于整体应力过大的情况，可以采用结构的增强措施进行调整。
增强措施包括增加钢筋、增加混凝土厚度等。
四、温度应力的合并在实际计算中，需要将每块混凝土的温度应力合并，得到整个结构的温度应力。
合并时需要考虑混凝土的相互作用，具体方法如下：1. 对于相邻的混凝土块，应力的合并可以采用叠加原理进行。
即将相邻块的应力相加，得到它们合并后的应力。
2. 对于不相邻的混凝土块，应力的合并需要考虑它们之间的相互作用。
一般采用有限元分析等方法进行计算。
五、温度应力的设计在设计混凝土结构时，需要考虑温度应力的影响。
第十五章工程结构温度应力计算方法
图15.2 砖混组合体胀缩变形关系图
图15.3 墙板边界变形条件的建立 注：1. 顶板；2. 墙体；3. 底板。
第十五章 工程结构温度应力计算方法
砖混结构温度应力实用计算方法
将钢筋混凝土顶板与墙体分离，放松相互之间的约束力，则顶板及墙 体在温差及干湿影响下，其自由应变量分别为 c1 ac (T1 T ) c1 (15-1) (15-2) 根据变形协调条件，墙与板接触面纤维的应变方程如图15.2所示 c1 b1 ec1 eb1 (15-3) 同样，将钢筋混凝土底板与上、下层墙体分离，则有 (15-4) c 2 ac (T3 T ) c 2
(15-9)
e 从而得 (15-10) bhE 2Z E Ac1 ( Ac 2 ) ——钢筋混凝土顶(底)板的断面积； 式中： Zc1 (Zc 2 )——钢筋混凝土顶(底)板的断面系数； Zb ——墙体的断面系数； b ——墙体厚度； Eb ( Ec ) ——砖砌体(混凝土)弹性模量； b1 ( b 2 ) ——砖砌体顶(底)边沿纤维应力； c1 ( c 2 ) ——混凝土顶(底)板边沿纤维应力。
2. 考虑墙板底面嵌固，对Q1、Q2的修正 考虑墙板底面嵌固时，在力偶作用下不发生弯 曲变形，从而不产生水平应力，只产生竖向应 力 y 。如图15.5所示。根据墙体在力偶作用下 的变形趋势和工程实例中水平包角缝和水平鼓 起缝的实际情况，又可假定竖向应力 y 作线性 分布，即在热胀情况下，最大竖向应力 [( y )max ]x0 产生于墙板的对称轴；在冷缩情况下，最大竖 [( y )max ]x a 产生于墙的两肩。 15.13 向应
a
图15.4 墙板放松法计算温度应力图
顶板边沿应变 底板内应力 底板应变
温度应力计算·
施工配合比（kg/m3）二．温度计算（1）绝热温升Tmax′＝WQ/γC(1-e-mt) Tmax′---绝热温升Q-----水泥水化热Q=377x103J/KgC-----砼比热C=0.96X103J/(Kg.℃)γ-----砼重度γ=2400Kg/M3W-----每立方米水泥重量260 Kg/M3m-----热影响系数,m=0.43+0.0018QTmax′=260X377X103/0.96X103X2400(1-e-1.10X3) =44℃Tmax=8℃+44℃=52℃(12℃为入模温度)相应也可以建立绝热温度见公式:Tmax′＝WQ/γCxε+F/50F-----粉煤灰用量ε――――不同浇筑块的热系数Tmax′＝260X377X103/Tmax=8+55=63℃取Tmax＝63℃三. 温应力计算1.将砼的收缩随时间的进程换算成当量温度计算：Ty(t)= εy(t)/αα=1x10-5砼线膨胀系数εy(t)=ε0M1M2M3······M10(1-e0.01t)Ty(t)------当量温度εy(t)----任意时间的收缩(mm/mm)M1-----水泥品种为普通水泥,取1.0M2-----水泥细度为4000孔，取1.35M3-----骨料为石灰石，取1.00M4-----水灰比为0.52,取1.64M5-----水泥浆量为0.2,取1.00M6------自然养护30天，取0.93M7------环境相对湿度为50%,取0.54M8------水里半径倒数为0.4,取1.2M9------机械振捣，取1.00M10------含筋率为8%,取0.9ε0--ε∞---最终收缩，在标准状态下ε0=3.24X10-4εy(30)=1.01x10-4Ty(30)=10.1℃εy(27)=0.92 x10-4Ty(27)=9.2℃εy(24)=0.83 x10-4Ty(24)=8.3℃εy(21)=0.73 x10-4 Ty(21)=7.3℃εy(18)=0.64 x10-4Ty(18)=6.4℃εy(15)=0.54 x10-4Ty(15)=5.4℃εy(12)=0.439 x10-4 Ty(12)=4.39℃εy(9)=0.335 x10-4 Ty(9)=3.35℃εy(6)=0.226 x10-4 Ty(6)=2.26℃εy(3)=0.114 x10-4 Ty(3)=1.14℃计算中心温度当量温差:△T6=2.26-1.14=1.12℃△T9=3.35-2.26=1.09℃△T12=4.39-3.35=1.04℃△T15=5.4-4.39=1.01℃△T18=6.4-5.4=1.0℃△T21=7.3-6.4=0.9℃△T24=8.3-7.3=1.0℃△T27=9.2-8.3=0.9℃△T30=10.1-9.2=0.9℃2.计算中心温度砼基础施工时处于散热条件，考虑上下表面及侧面的散热条件,当体积厚达3m时,,散热影响系数取0.97；当中心浇筑完第四天后，水化热达峰值。
(整理)温度场和温度应力计算
附计算书3：温度场和温度应力计算一、温度场计算计算以本工程1.2m 厚底板为例，用差分法计算底板28d 水化热温升曲线。
计算中各参数的取值如下：W ——每m 3胶凝材料用量，440kg/ m 3；Q ——胶凝材料水化热总量（kJ/kg ）；，本例采用实测值260kJ/kg ；c ——混凝土的比热，取1.0kJ/ (kg ∙C )；ρ——混凝土的质量密度，取2400kg/ m 3；α——导温系数，取0.0035m 2/h ；m ，取0.5。
混凝土的入模温度取10C ，地基温度为18C ，大气温度为18C 。
温度场计算差分公式如下：1,1,,1,,222(21)2n k n kn k n kn k T T t t T aT a T x x -+++∆∆=∙--+∆∆∆ （B.4.2-1）⑴试算t ∆、x ∆，确定2x t∆∆α。
取t ∆ = 0.5天 = 12小时，x ∆ = 0.4m ，即分3层 则412625.04.0120035.022≈=⨯=∆∆x t α，可行。
代入该值得出相应的差分法公式为k k n kn k n k n T T T T T ∆+⋅++⋅=+-+,,1,11,475.02525.0⑵画出相应的计算示意图，并进行计算。
底板厚1.2m ，分3层，每层0.4m ，相应的计算示意如下图。
从上至下各层混凝土的温度分别用1T 、2T 、3T 表示，相应k 时刻各层的温度即为k T ,1、k T ,2、k T ,3。
混凝土与大气接触的上表面边界温度用0T 表示，与地基接触的下表面边界温度用0'T 表示。
k = 0，即第05.00=⋅=∆⋅t k 天， 上表面边界0T ，取大气温度，0T = 18C 各层混凝土温度取入模温度，即0,1T =0,2T = 0,3T = 10C下表面边界0'T ，取地基温度，0'T = 18C ；k = 1，即第5.05.01=⋅=∆⋅t k 天，温升=-⋅⋅⋅=-=∆⋅⋅-⋅-⋅-∆⋅⋅-∆⋅-⋅-)(24000.1260440)(5.015.05.0)11(5.0)1(max 1e e e eT T t k m tk m10.544C上表面边界温度0T ，散热温升为0，始终保持不变，0T = 18C第一层混凝土温度1,1T ，见计算图示中方框1，1,1T 的边界为0T 和0,2T ，在0,1T 的基础上考虑温升1T ∆，即C T T T T T 644.22475.02525.010,10,201,1=∆+⋅++⋅=第二层混凝土温度1,2T ，见计算图示中方框2，1,2T 的边界为0,1T 和0,3T ，在0,2T 的基础上考虑温升1T ∆，即C T T T T T 544.20475.02525.010,20,30,11,2=∆+⋅++⋅=m m m第三层混凝土温度1,3T ，见计算图示中方框3，1,3T 的边界为0,2T 和0'T ，在0,3T 的基础上考虑温升1T ∆，即2,003,13,010.5250.47522.6442T T T T T C'+=+⋅+∆=︒下表面边界温度0'T ，需要考虑散热温升2/1T ∆，所以需每一步都需进行修正。
工程的温度应力计算
一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（+++++++++++）/12=。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。
工程的温度应力计算
一、温差效应理论1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：1，施工阶段最低或最高温度（T2）选取：A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（+++++++++++）/12=。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。
温度应力计算
温度应力计算第四节温度应力计算一、温度对结构的影响1 温度影响（1）年温差影响指气温随季节发生周期性变化时对结构物所引起的作用。
假定温度沿结构截面高度方向以均值变化。
则12t t t -=?12t t t -=?该温差对结构的影响表现为：对无水平约束的结构，只引起结构纵向均匀伸缩；对有水平约束的结构，不仅引起结构纵向均匀伸缩，还将引起结构内温度次内力；（2）局部温差影响指日照温差或混凝土水化热等影响。
A ：混凝土水化热主要在施工过程中发生的。
混凝土水化热处理不好，易导致混凝土早期裂缝。
在大体积混凝土施工时，混凝土水化热的问题很突出，必须采取措施控制过高的温度。
如埋入水管散热等。
B ：日照温差是在结构运营期间发生的。
日照温差是通过各种不同的传热方式在结构内部形成瞬时的温度场。
桥梁结构为空间结构，所以温度场是三维方向和时间的函数，即： ),,,(t z y x f T i =该类三维温度场问题较为复杂。
在桥梁分析计算中常采用简化近似方法解决。
假定桥梁沿长度方向的温度变化为一致，则简化为二维温度场，即： ),,(t z x f T i =进一步假定截面沿横向或竖向的温度变化也为一致，则可简化为一维温度场。
如只考虑竖向温度变化的一维温度场为：),(t z f T i =我国桥梁设计规范对结构沿梁高方向的温度场规定了有如下几种型式：2 温度梯度f（z，t）（1）线性温度变化梁截面变形服从平截面假定。
对静定结构，只引起结构变形，不产生温度次内力；对超静定结构，不但引起结构变形，而且产生温度次内力；（2）非线性温度变化梁在挠曲变形时，截面上的纵向纤维因温差的伸缩受到约束，从而产。
生约束温度应力，称为温度自应力σ0s对静定结构，只产生截面的温度自应力；对超静定结构，不但产生截面的温度自应力，而且产生温度次应力；二、基本结构上温度自应力计算1 计算简图23 ε和χ的计算三、连续梁温度次内力及温度次应力计算采用结构力学中的力法求解。
温度应力计算公式
温度应力计算公式温度应力是物体在受到温度变化时产生的应力。
当物体处于不均匀温度场中时，由于物体不同部分的膨胀系数不同，就会产生应力，这种应力称为温度应力。
温度应力的大小与物体材料的热膨胀系数、温度变化量以及物体内部的约束情况有关。
温度应力的计算可以使用线性热弹性材料的温度应力公式：\[ \sigma = \alpha \cdot E \cdot \Delta T \]其中，\[ \sigma \] 是温度应力，\[ \alpha \] 是物体的热膨胀系数，\[ E \] 是杨氏模量，\[ \Delta T \] 是温度变化量。
这个公式的前提是物体只受到温度的影响，没有其他外力作用。
如果物体还受到其他外力作用，需要考虑这些外力的影响。
在计算温度应力时，可以采用以下几个步骤：1.确定物体的几何形状和材料性质，包括热膨胀系数和杨氏模量。
这些参数可以通过实验或者查阅相关资料获得。
2.确定温度变化量。
温度应力的计算需要知道物体的初始温度和最终温度之间的差值。
3. 将参数带入温度应力公式，计算出温度应力的数值。
注意单位的一致性，热膨胀系数一般以 \( 1/\text{℃} \) 为单位，杨氏模量一般以 \text{帕斯卡}（\text{Pa}）为单位，温度变化量一般以摄氏度为单位，温度应力的单位为帕斯卡（\text{Pa}）。
温度应力的计算公式可以通过引入热力学和弹性力学的知识推导得到。
在温度变化时，由于物体不同部分的温度不同，就会引起物体的体积膨胀或者收缩。
这种膨胀或者收缩会引起内部的应力分布，从而产生温度应力。
需要注意的是，温度应力只是物体在受到温度变化时产生的瞬时应力，不会一直存在。
一旦温度变化停止，温度应力就会消失。
温度应力的计算方法还有其他的一些公式，比如复杂几何形状的物体可以使用有限元方法进行计算。
不同的方法适用于不同的情况，根据具体的问题选择适合的计算方法。
总之，温度应力的计算是热力学和弹性力学的应用，通过使用温度应力公式，可以计算出物体在受到温度变化时产生的应力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、温差效应理论
1，局部温差不对整体结构产生影响，只考虑整体温差。
2，出现温差时梁板等水平构件变形受到竖向构件的约束而产生应力，同时竖向构件会受到相应的水平剪力。
3，使用阶段由于外围有幕墙，屋顶有保温，首层室外楼板也有覆土或其他面层，且室内有空调，常年的温度较为稳定，可不考虑使用阶段的温差效应，只考虑施工阶段的温差效应。
二、温差取值
对于温差T1-T2，即施工阶段基准温度T1-施工后保温围护前的最低或最高温度T2：
1，施工阶段最低或最高温度（T2）选取：
A，对地下室构件，即使地下水位较高，回填土也会在地下室施工完成不久后封闭，温度变化对结构影响很小很缓慢，可考虑地区季节性平均温度变化（地下结构一般从设置后浇带、尽早回填等措施来降低温差的影响，一般不需要计算）。
B，对地上结构，可以认为完全暴露在室外。
可能达到的最低和最高温度可取当地最近十年的历史最低、最高气温（一般参考荷载规范里的基本气温数据，比如青岛地区为-9/33度）。
2，施工阶段基准温度（T1）选取：
结构在后浇带合拢前各部分面积较小，温度效应可以忽略不计。
因此后浇带浇注时的温度作为温差效应里的基准温度T1。
当工程进展顺利，地上各层结构的合拢时间可以精确到季节甚至月
份时候，这里的基准温度可取当季或当月的近十年平均气温。
当施工进度无法掌握时，基准温度可取近十年月平均气温值T1=（0.0+2.4+6.4+11.9+17.0+20.9+24.4+25.2+22.1+16.9+9.2+3.5）/12 =13.3。
因此一般适当控制后浇带合拢温度时，基准温度T1可按15度进行计算：降温温差T1-T2=15-（-9）=24℃；当计算地上结构升温温差时，升温温差T1-T2=15-33=18℃。
只有当地上结构一层顶合拢日期距屋面合拢的日期超过一年时，最大负温差和最大正温差才会共存在一个工程中，因正温差主要产生压应力，所以温度效应仍是按最大负温差来控制。
探讨：对于有后浇带的工程，在满足至少两个月的条件下是否可将后浇带浇注时间限定在温度较低的月份，至少避开最高的月份夜间浇筑，这样计算最大负温差时的基准温度（T1）会降低，相应最大负温差也会减小。
三、混凝土长期收缩的影响
根据王梦铁的《工程结构裂缝控制》中相关计算公式和表格。
混凝土收缩是一个长期的过程，影响最终收缩量的因素有水泥成分、温度、骨料材质、级配、含泥量、水灰比、水泥浆量、养护时间、环境温度和气流场、构件的尺寸效应、混凝土振捣质量、配筋率、外加剂等。
由于竖向构件的约束，水平构件的混凝土收缩会产生拉应变，这种应变可以和混凝土因温度变化产生的应变等效，可用产生等量应变的温度差（当量温差）计入混凝土收缩效应的影响。
参考王梦铁的《工程结构裂缝控制》中的相关计算方法，混凝土收缩应变的形式和发展与混凝土龄期密切相关，任意时间t （天数）时混凝土已完成的收缩应变为：)1(1024.3)1(1024.3)(01.042101.04t n t y e M M M e t -----⨯≈⋅⋅⋅-⨯=ε
其中M M 为各种修正系数，各修正系数的取值和对应的影响因素见下表：
表8.3.1 计算混凝土收缩的修正系数
时间无限长即整个龄期混凝土的收缩徐变应变为401.041024.3)1(1024.3)(-∞--⨯=-⨯=∞e y ε
这样，任意时间t （天数）时混凝土剩余未完成的收缩应变为：
混凝土收缩的应变量可等同于混凝土在一定负温差下产生的收缩应变量，混凝土温差应变为T y ∆⋅=αε，其中α为混凝土线膨胀系数，α =1×10-5/℃
因此混凝土剩余未完成的收缩应变当量负温差为 t y e T 01.04.32/-⨯==∆αε。
（1）假设结构后浇带在施工2个月后浇注，则结构剩余未完成的收缩应变当量负温差为8.174.32/6001.060=⨯==∆⨯-e T y αε℃；
（1）假设结构后浇带在施工6个月后浇注，则结构剩余未完成的收缩应变当量负温差为4.54.32/18001.0180=⨯==∆⨯-e T y αε℃；
计算时的总温差为季节温差与收缩当量温差相叠加，如果结构后浇带在施工6个月后封闭，则降温温差为24+5.4=29.4℃；升温温差18-5.4=12.6℃。
四、计算操作
采用PMSAP 软件对整体模型进行温差和收缩效应分析，楼板采用弹性膜模拟，分层对整个平面内的节点施加相应的温差作用进行计算。
楼板应
力不考虑梁及其翼缘对其的分担作用
【1）为考虑砼的徐变应力松弛，砼构件的温度内力可
以乘以折减系数0.3，钢构件不折减；2）温度效应的组合贡献：可以取组合值系数0.7乘以分项系数1.2=0.84；3）为考虑砼构件裂缝引起的刚度退化，砼构件的刚度（即混凝土弹性模量）可以乘以折减系数0.85，钢构件不折减。
】
从计算结果中可以读出楼板最大主拉应力值σMPa （局部应力引起的裂缝对整个结构的影响不大，可不考虑），也可读出相应楼板温度配筋面积。
则需要配置双层双向温度筋的单层每延米钢筋面积：As=钢筋抗拉强度标准值楼板厚度）混凝土抗拉强度标准值（楼板应力x 2x 1000
x -，如C30混凝土
（ftk=2.02MPa ），三级钢（fyk=400MPa ），楼板厚度150mm ，楼板温度应力
4.62MPa （拉力），则楼板单侧每米钢筋面积
As=
00
4x250x1000
1x
.01
2-
62
.4）
（=489mm2，即需要另外附加的楼板温度钢筋为双层10@150（524 mm2）可满足要求。
至于温度效应引起的压力，混凝土自身抗压强度基本可以抵消，不再另行计算。