1112立方根
实用的平方根表立方根表.pdf

,检查合同的履行情况;
4.5.4 保管法人代表授权委托书、合同专用章,并按编号归口使用;
4.5.5 建立合同管理台帐,对合同文本资料进行编号统计管理;
4.5.6 组织对法规、制度的学习和贯彻执行,定期向有关领导和部门报告工作;
4.5.7 在总经理领导下,做好合同管理的其他工作,
4.6 工程技术部:专职合同管理员及材料、燃料供应部兼职合同管理员履行以下职责:
4.2 工程部:是发电厂建设施工安装等工程合同签订管理部门;负责签订管理基建、安装、人工技术的工程合同。
4.3 经营部:是合同签订管理部门,负责管理设备、材料、物资的订购合同。
4.5 合同管理部门履行以下职责:
4.5.1 建立健全合同管理办法并逐步完善规范;
4.5.2 参与合同的洽谈、起草、审查、签约、变更、解除以及合同的签证、公证、调解、诉讼等活动,全程跟踪和检查合同的履行质量; 4.5.3 审查、登记合同对方单位代表资格及单位资质,包括营业执照、经营范围、技术装备、信誉、越区域经营许可等证件及履约能力(必要时要求对方提供担保)
立方根 √3 1 = 1 √ 2 = 1.260 √ 3 = 1.442 √ 4 = 1.587 √ 5 = 1.710 √ 6 = 1.817 √ 7 = 1.913 √8 = 2 √ 9 = 2.080 √ 10 = 2.154 √ 11 = 2.224 √ 12 = 2.289 √ 13 = 2.351 √ 14 = 2.410 √ 15 = 2.466 √ 16 = 2.520 √ 17 = 2.571 √ 18 = 2.621 √ 19 = 2.668 √ 20 = 2.714
平方根 √1=1 √2= 1.414 √3= 1.732 √4=2 √5= 2.236 √6= 2.449 √7= 2.646 √8= 2.828 √9=3 √10=3.162 √11 = 3.317 √12 = 3.464 √13 = 3.606 √14 = 3.742 √15 = 3.873 √16 = 4 √17 = 4.123 √18 = 4.243 √19 = 4.359 √20 = 4.472
1112立方根课件

问题:要糊一只体积为 216 ㎝3
的正方体纸盒,它的每一条棱长是多少?
在这个实际问题中,提出了一个怎样的计算问题? 与上节课所学相联系,你能抽象一个什么概念?
我们发现:
如果一个数的立方等于 a,那么这个数就 叫做a的立方根。
即如果 x3 =a,那么x就是a的立方根。
你能说说立方根的性质吗?
(2)64的平方根的立方根是 __±_2_
(3)一个数的立方根是它本身,这个数 是_-1_、__0_、_1_
2.若 a ? b ? 2 与 a ? b ? 1 互为相反数,
求3 22a ? 2b 的值.
(1)立方根的特征 正数有立方根吗?如果有,有几个?
负数呢? 零呢? 一个正数有一个正的立方根; 一个负数有一个负的立方根, 零的立方根是零。
平方根 立方根
被开方数必须是非负数 被开方数可正可负
正数有两个平方根
任何一个数的立方根 都只有一个
试一试
1.选择题:
(1)下列语句正确的是( A )
A. 64 的立方根是2
B.-3是27的负立方根
C.
125 的立方根是 ? 5
216
6
D. (?1)2 的立方根是 -1
(2)如果一个数的平方根与立方根相等,
(1)正数有一个立方根,仍为正数。 (2)0的立方根是 0。 (3)负数有一个立方根,仍为负数。
由此我们发现:
任何一个数都有立方根,且只有一个立方根。
立方根的表示方法:
数a的立方根记作: 3 a
读作:“三次根号 a” a称为被开方数, 3称为根指数,不能省略 求一个数的立方根的运算,叫做开立方。
这样的数有 ( A )
A.1个 B.2个 C.3个 D.无数个
1112 立方根-2021-2022学年八年级数学上册同步教学辅导讲义(华师大版)

11.1.1平方根基础知识1、一般地,如果一个数x 的立方等于a ,即3x a =,那么这个数x 就叫做a 的立方根,也叫做a 的三次方根.2、通过立方根的定义可以看出:所有的数都有立方根。
一个正数只有一个正的立方根;一个负数只有一个负的立方根;0的立方根是0.注意平方根和立方根的这个差别。
3、立方根的表示方法:数a 读作“三次根号a ”.要注意,这里的根指数“3”不能省略.4、规律:被开方数每移动2位小数,算术平方根的结果向相应方向移动一位。
被开方数每移动3位小数,立方根的结果向相应方向移动一位。
例题例1.计算下列各数的立方根:(1)125;(2)-0.064;(3)-6.【答案】(1)5;(2)-0.4;(3)【分析】如果一个数x 的立方等于a ,那么x 是a 的立方根,根据此定义求解即可.【详解】解:(1)∵35125=,,即125的立方根是5;(2)∵()30.4=0.064-,0.4-,即-0.064的立方根是-0.4;(3)∵(3=6-,-6的立方根是【点睛】此题主要考查了求一个数的立方根,解题时应先找出所要求的这个数是哪一个数的立方.由开立方和立方是互逆运算,用立方的方法求这个数的立方根.注意一个数的立方根与原数的性质符号相同.例2.求下列各式的值:(1) (2) (3) 【答案】(1)-5;(2)0.4;(3)45-【分析】(1)根据立方根的运算法则进行计算即可;(2)根据立方根的运算法则进行计算即可;(3)根据立方根的运算法则进行计算即可.【详解】解:5;0.4;45. 【点睛】本题考查了立方根,掌握求立方根的方法是解题关键.练习1.8的立方根等于( )A .﹣2B .2C .±2 D2.-8的立方根是( )A .2B .2-C .12-D .3.下列说法正确的是( )A .1的立方根是±1B .-1的平方根是-1C .4的算术平方根是±2D .5是 25的算术平方根 4.下列计算正确的是( )A 2±B 2-C 3D 0.12 5.下列说法正确的是( )A .64的平方根是8B .-16的立方根是-4C .只有非负数才有立方根D .-3的立方根是6.实数27的立方根是___.7=_____.8.方程31402x +=的解是________.92.872_______. 10.按要求填写下列各数:①倒数是它本身的数是_________.②相反数是它本身的数是_________.③绝对值是它本身的数是_________.④平方是它本身的数是_________.⑤平方根是它本身的数是_________.⑥算术平方根是它本身的数是_________.⑦立方是它本身的数是_________.⑧立方根是它本身的数是_________.11.若实数m 的平方根是421a +和6a -,b 的立方根是2-,求3m a b ++的算术平方根.12.计算:21(1)2--.13x y +的值.14.已知:a 与2b 互为相反数,-a b 的算术平方根是3.(1)求a 、b 的值;(2)若20a c +,求13c d +-的立方根.15.求下列各式中x 的值.(1)225169=x ;(2)3460-=x .参考答案1.B【分析】根据立方根的定义,进行计算即可.【详解】∵328,∴8的立方根是2.故选:B.【点睛】本题主要考查了立方根的定义,解题的关键是熟练掌握立方根的定义.2.B【分析】利用立方根的定义解答.【详解】解:∵(-2)3=-8,∴-8的立方根是-2.故选:B.【点睛】本题考查了立方根,熟练掌握立方根的定义是解题的关键.3.D【分析】根据立方根、平方根以及算术平方根的定义进行选择即可.【详解】解:A. 1的立方根是1,故选项A说法错误;不符合题意;B.负数没有平方根,故选项B说法错误,不符合蛱;C. 4的算术平方根是2,故选项C说法错误,不符合题意;D. 5是25的算术平方根,说法正确,符合题意;故选:D.【点睛】本题考查了立方根、平方根以及算术平方根的定义,掌握立方根、平方根以及算术平方根的定义并记牢固是解题的关键.4.B【分析】根据算术平方根、立方根的概念逐一进行分析判断即可.【详解】A .2=,故A 答案错误;B.2=-,故B 答案正确;C . C 答案错误;D . 1.2,故D 答案错误;故选:D【点睛】本题考查了算术平方根、立方根,特别注意:(1)非负数a 的算术平方根a 有双重非负性:①被开方数a 是非负数;②算术平方根a 本身是非负数.(2)求一个非负数的算术平方根与求一个数的平方互为逆运算,在求一个非负数的算术平方根时,可以借助乘方运算来寻找.5.D【分析】根据平方根和立方根的定义逐项判断即可得.【详解】A 、64的平方根是8±,则此项说法错误,不符题意;B 、因为()346416-=-≠- ,所以16-的立方根不是4-,此项说法错误,不符题意; C 、任何实数都有立方根,则此项说法错误,不符题意;D =3-的立方根是 故选:D .【点睛】本题考查了平方根和立方根,熟练掌握定义是解题关键.6.3.【分析】如果一个数x 的立方等于a ,那么x 是a 的立方根,根据此定义求解即可.【详解】解:∵3的立方等于27,∴27的立方根等于3.故答案为3.【点睛】本题考查了立方根的定义,属于基础题型,熟知立方根的概念是解题的关键.7.-6【分析】分别根据立方根、算术平方根的定义及绝对值的性质解答即可.【详解】=---=--=-.24246故答案为:-6.【点睛】本题考查了立方根、算术平方根及绝对值,熟记立方根、二次根式及绝对值的性质是解答本题的关键.x=-8.2【分析】方程整理后,利用立方根定义求出解即可.【详解】方程整理得:x3=-8,开立方得:x=-2.故答案为:x=-2【点睛】本题考查了立方根,熟练掌握立方根的定义是解本题的关键.9.13.33【分析】根据立方根的性质,即可解答.【详解】1.333≈,⨯,1.33310=13.33故答案为:13.33.【点睛】本题考查了立方根,解决本题的关键是熟记立方根的性质.10.±1;0;非负数;0,1;0;0,1;1,0,-1;-1,0,1【分析】根据平方根、立方根的定义,可得答案.【详解】解:①倒数是它本身的数是±1, ②相反数是它本身的数是 0,③绝对值是它本身的数是 非负数,④平方是它本身的数是 0,1,⑤平方根是它本身的数是 0,⑥算术平方根是它本身的数是 0,1,⑦立方是它本身的数是 1,0,-1,⑧立方根是它本身的数是-1,0,1,故答案为:±1,0,非负数,0,1;0;0,1;1,0,-1;-1,0,1. 【点睛】本题考查了实数的性质,利用平方根、立方根是解题关键.11.8【分析】根据平方根的定义可得421a ++6a -=0,解方程可求出a 的值,即可得出m 的值,根据立方根得定义可得b 的值,根据算术平方根的定义即可得答案.【详解】∵实数m 的平方根是421a +和6a -,∴42160a a ++-=,解得:3a =-.∴69a -=-,∴2(9)81m =-=.∵b 的立方根是2-,∴3(2)8b =-=-,∴3813(3)864m a b ++=+⨯--=,∴3m a b ++的算术平方根为8.【点睛】本题考查平方根、算术平方根、立方根的定义及解一元一次方程,一个正实数的平方根有两个,它们互为相反数;其中正的平方根叫做算术平方根;熟练掌握定义是解题关键.12.12.【分析】先计算有理数的乘方、立方根与算术平方根、化简绝对值,再计算有理数的加减运算即可得.【详解】 解:原式11(2)22-=++-, 12=. 【点睛】本题考查了有理数的乘方、立方根与算术平方根、化简绝对值等知识点,熟练掌握各运算法则是解题关键.13.1.【分析】根据相反数及立方根的性质列出方程即可求解.【详解】∴3x -7+3y +4=0∴3(x y +)=3,∴x y +=1.【点睛】此题主要考查代数式求值,解题的关键是熟知立方根的性质与相反数的定义. 14.(1)6a =,3b =-;(2)-2【分析】(1)根据题意列出方程组可得答案;(2)根据非负数的性质得到c ,d 的值,代入计算,再求立方根即可.【详解】解:(1)由题意得:209a b a b +=⎧⎨-=⎩, 解得:6a =,3b =-.(2)由非负数的性质可得:200a c b d +=⎧⎨-=⎩, 即12030c d +=⎧⎨--=⎩, 12c ∴=-,3d =-. ∴143183c d +-=---=-, ∴13c d +-的立方根是-2. 【点睛】本题考查立方根和算术平方根,掌握求立方根和算术平方根的方法是解题关键. 15.(1)135=±x ;(2)4x = 【分析】(1)根据解方程的方法和平方根的定义可以解答本题;(2)根据解方程的方法和立方根的定义可以解答本题.【详解】解:(1)225169=x216925x = 135x =或135x =-; (2)3460-=x364x =4x =【点睛】本题考查立方根、平方根、解方程,解答本题的关键是明确它们各自的计算方法.。
实用的平方根表立方根表
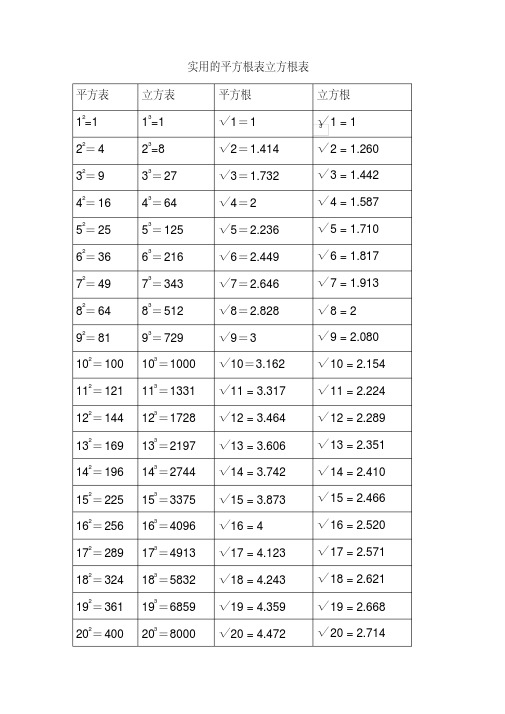
3 实用的平方根表立方根表平方表立方表平方根立方根12=1 13=1 √1=1 √1 = 1 22=4 23=8 √2=1.414 √2 = 1.260 32=9 33=27 √3=1.732 √3 = 1.442 42=16 43=64 √4=2 √4 = 1.587 52=25 53=125 √5=2.236 √5 = 1.710 62=36 63=216 √6=2.449 √6 = 1.817 72=49 73=343 √7=2.646 √7 = 1.913 82=64 83=512 √8=2.828 √8 = 2 92=81 93=729 √9=3 √9 = 2.080 102=100 103=1000 √10=3.162 √10 = 2.154 112=121 113=1331 √11 = 3.317 √11 = 2.224 122=144 123=1728 √12 = 3.464 √12 = 2.289 132=169 133=2197 √13 = 3.606 √13 = 2.351 142=196 143=2744 √14 = 3.742 √14 = 2.410 152=225 153=3375 √15 = 3.873 √15 = 2.466 162=256 163=4096 √16 = 4 √16 = 2.520 172=289 173=4913 √17 = 4.123 √17 = 2.571 182=324 183=5832 √18 = 4.243 √18 = 2.621 192=361 193=6859 √19 = 4.359 √19 = 2.668 202=400203=8000√20 = 4.472√20 = 2.7143√0 = 0(表示根号0等于0,下平方根表立方根表√1 = 1√2 = 1.414√3 = 1.732√4 = 2√5 = 2.236√6 = 2.449√7 = 2.646√8 = 2.828√9 = 3√10 = 3.162√11 = 3.317√12 = 3.464√13 = 3.606√14 = 3.742√15 = 3.873√16 = 4√17 = 4.123√18 = 4.243√19 = 4.359√20 = 4.472其中专业理论知识内容包括:保安理论知识、消防业务知识、职业道德、法律常识、保安礼仪、救护知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.1 平方根与立方根
2.立方根
【教学目标】:
1.了解立方根的概念,能够用根号表示一个数的立方根; 2.能用类比平方根的方法学习立方根及开立方运算,并区分立方根与平方根的不同。
【重点】:立方根的概念和求法。
【难点】:立方根与平方根的区别。
一、知识回顾
解:设这种包装箱的边长为x m,则
因为2733=,所以
二、新知导入
1.立方根的概念:
一般地,如果一个数的立方等于a ,这个数就叫做a 的立方根(也叫做三次方根).
用式子表示,如果a x =3,那么x 叫做a 的立方根.数a 的立方根用符号“3
a ”表示,
读作“三次根号a ”,其中a 是被开方数,3是根指数(注意:根指数3不能省略).
例如: 表示27的立方根,
3
27- 表示-27的立方根
想一想:
如:33
=27 则把3叫做27的立方根,即 ,
2.开立方:求一个数的立方根的运算,叫做开立方.开立方与立方也是互为逆运算,因此求一个数的立方根可以通过立方运算来求.
因为823=,所以8的立方根是
因为 ,所以0.125的立方根
因为
,所以0的立方根是 因为 ,所以-8的立方根是 因为 ,所以
27
8
的立方根是 【总结归纳】 正数的立方根是____________,
负数的立方根______________,0的立方根______________, 任何数都有_________立方根.
①正数的平方根有 个,且 。
正数的立方根有 个,是 数。
②负数 平方根,负数的立方根有 个,是 数 ③0的平方根是
,0的立方根是
例1、求下列各数的立方根。
(1)8 (2)0.001 (3)-27 (4)0
例2 求下列各式的值:
三、知识总结
①因为38-= ,-38= 所以 因为327-= ,327-= 所以327
仔细观察,你能得出什么结论:_______ __
即求负数的立方根,可以先求出这个负数的绝对值的立方根,再取其相反数。
②求下列各数的值,并找规律
结论:对于任何数a 都有
③
3
641)(3
001.02-)
(3
64
27-(3)
(4)
3
27
10
2
3
27
( )3=0.125 ( )3=0 ( )3= - 8 ( )3=
27
8
=
332=-33)2(=
-3
3)3(=
3
3
4=
3
30()
=3383=()=3327()=-3327()=
3
3
结论:对于任何数a 都有
1.若为,则x x 0
183
=+( )
A .-
21 B .2
1
± C .21 D .-41 2.16的平方根与-8
的立方根之和是( )
A .0
B .-4
C .0或-4
D .4 3.如果a a =3
,那么a 是( )
A .±1
B .1,0
C .±1,0
D .以上都不对 4.64的立方根是 平方根是_______。
5、若
()12513=-x ,则x=
6、立方根等于自己本身的数有_________
7.若10m -<<,且n ,则m 、n 的大小关系是( ).
A .m n >
B .m n <
C .m n =
D .不能确定 8.27- ).
A .0
B .6
C .-12或6
D .0或-6
9、若164
=x ,则x= ;若813=n ,则n= ;
10、若3x x =,则x= ;若x x -=2
,则x ;
11、当x 时,13-x 有意义;当x 时,325+x 有意义;
12、若0|2|1=-++y x ,则x+y= ; 13、计算:
381264
27
3292531+-+= ;
14、求下列各数的立方根 ⑴001.0-, ⑵8
33, ⑶3
)4(-
15、求下列各式中的x 的值 ⑴02163
=-x
, ⑵64)5(3=+x , ⑶8)12
1(3=+x
16、计算题
(1)、49.0381003⨯-⨯ (2)、9
144
20045243⨯⨯⨯
17、若332321--y x 与互为相反数,求y
x
21+的值
18、已知2
3
2
a -1a -1=,求a 的值。
