有限元讲义弹性力学平面问题有限单元法(四结点四边形等参元-八结点曲线四边形等参元-问题补充)分析
平面问题的有限单元法.ppt

5.3.3 单元分析 (略)
对三角形单元,建立结点位移与结点力之间的转换关系。
vm
m
um
vvi
Vm
(a)
i ui m
Um
Vj
j
Uj
e
Vi
i Ui
(b)
结点位移
ui
vi
qe
u
v
j j
um
vm
• 结点力
•
平面应力问题
平面应变问题
y
平面
应力
问题
0
y
t/2
t/2
z x
ͼ 1-10
厚度为 t 的很薄的均匀木板。只在边缘上受到平行于板面且 不沿厚度变化的面力,同时,体力也平行于板面且不沿厚度变化。
以薄板的中面为xy面,以垂直于中面的任一直线为Z轴。由于 薄板两表面上没有垂直和平行于板面的外力,所以板面上各点均 有:
3) 对于现在的单元插值函数是线性的,在单元内部及单元的 边界上位移也是线性的,可由节点上的位移唯一确定。由于 相邻的单元公共节点的节点位移相等,因此保证了相邻节点 在公共边界上位移的连续性。
• 选择单元位移函数时,应当保证有限元法解答的收 敛性,即当网格逐渐加密时,有限元法的解答应当收敛 于问题的正确解答。因此,选用的位移模式应当满足下 列条件:
Ui
Vi
ui*
vi*
uj*
vj*
um*
vm*
Uj Vj
Um
q* eTFe
Vm
28
根据虚功原理,得
q* eT Fe * T tdxdy
第四章 弹性力学平面问题的有限单元法

(i, j,m)
22
如果注意到(4-1)式,则(4-11)式可写成
S i i S j j S m m
从(4-13)、(4-14)式可以看出, S 中的元素都是常量,所以每 个单元中的应力分量也是常量。因而,相邻单元将具有不同的应 力和应变。这样,越过公共边界,从一个单元到另一个与它相邻 的单元,应力和应变的值都将有突变,但是位移是连续的(参阅 下节),常应变单元的这些性质实际上都是由于选取线性的位移 模式所造成的。
(f)
式(e)和式(f)可以看出单元内部位移是由节点位移表示的
14
如令
1 Ni (ai bi x ci y ) , 2
位移模式(e)、(f)就可以写成
(i, j,m)
(4-4)
u N i ui N j u j N m u m v N i vi N j v j N m vm
yi yj ym
的面积,
(4-2)
等于三角形 i , j , m
, j,m
为使求得面积的值不致成负值,结点 i 转向,如图所示。
的次序必须是逆时针
13
将(d)式代入(b)式中的第一式,并稍加整理得
u
其中
1 (ai bi x ci y ) ui (a j b j x c j y ) u j 2 (am bm x cm y ) um
。
15
例1
求图示的三角形单元的形函数
三角形单元
16
二 单元的应变
有了单元的位移模式,就可以利用平面问题的几何方程
u x x v y y xy u v y x
平面四边形4结点等参有限单元法

有限元程序设计平面四边形4结点等参有限单元法程序设计1、程序功能及特点a.该程序采用四边形4节点等参单元,能解决弹性力学的平面应力应变问题。
b.前处理采用网格自动划分技术,自动生成单元及结点信息。
b.能计算受集中力、自重体力、分布面力和静水压力的作用。
c.计算结点的位移和单元中心点的应力分量及其主应力。
d.后处理采取整体应力磨平求得各个结点的应力分量。
e.算例计算结果与ANSYS计算结果比较,并给出误差分析。
f.程序采用Visual Fortran 5.0编制而成。
2、程序流程及图框图2-1程序流程图图2-2子程序框图其中,各子程序的主要功能为:INPUT――输入原始数据HUAFEN――自动网格划分,形成COOR(2,NP),X,Y的坐标值与单元信息CBAND――形成主元素序号指示矩阵MA(*)SKO――形成整体刚度矩阵[K]CONCR――计算集中力引起的等效结点荷载{R}eBODYR――计算自重体力引起的等效结点荷载{R}eFACER――计算分布面力引起的等效结点荷载{R}eDECOP――支配方程LU三角分解FOBA――LU分解直接解法中的回代过程OUTDISP――输出结点位移分量STRESS――计算单元应力分量OUTSTRE――输出单元应力分量STIF――计算单元刚度矩阵FDNX――计算形函数对整体坐标的导数TiiyNxN⎥⎦⎤⎢⎣⎡∂∂∂∂,=i1,2,3,4。
FUN8――计算形函数及雅可比矩阵[J]SFUN ――应力磨平-单元下的‘K’=NCN‘SCN――应力磨平-单元下的右端项系数‘CN‘SUMSKN――应力磨平-单元下的右端项集成到总体的‘P‘SUMSTRS――应力磨平-单元下的集成到总体的‘K‘GAUSTRSS――高斯消元求磨平后的应力3、输入数据及变量说明当程序开始运行时,按屏幕提示,键入数据文件的名字。
在运行程序之前,根据程序中INPUT需要的数据输入建立一个存放原始数据的文件,这个文件的名字为INDAT.DAT。
弹性力学平面问题的有限单元法

(c)
深梁(离散化结构)
14
§6.2 有限单元法的概念
例如:将深梁划分为许多三角形单元,这
些单元仅在角点用铰连接起来。
图(c)与图( a)相比,两者都是离散 化结构;区别是,桁架的单元是杆件,而 图(c)的单元是三角形块体(注意:三角 形单元内部仍是连续体)。
15
§6.2 有限单元法的概念
2.单元分析
f y )T 。
f y )T 。
T
面力: f ( f x 应变:
应力:
位移函数: d (u ( x, y ) , v( x, y )) 。
ε (ε x ε y γxy )T 。 σ (σ x σ y τ xy )T 。
F ( Fix Fiy Fjx Fjy )T 。
T δ ( u v u v ) 。 结点位移列阵: i i j j
5.本章介绍平面问题的FEM 仅叙述按位移求解的方法。 且一般都以平面应力问题来表示。
7
§6.1 基本量和基本方程的矩阵表示
采用矩阵表示,可使公式统一、简洁, 且便于编制程序。 本章无特别指明,均表示为平面应力 问题的公式。
8
§6.1 基本量和基本方程的矩阵表示
基本物理量: 体力: f ( f x
25
§6.3 单元的位移模式与解答的收敛性
1 ~ 6
xi , yi ,及ui , vi ,。
将式(a)按未知数 ui , vi , 归纳为:
u N i ui N j u j N m u m , v N i vi N j v j N m vm。
或用矩阵表示为:
结点力列阵:
9
§6.1 基本量和基本方程的矩阵表示
最新平面四边形4结点等参有限单元法

有限元程序设计平面四边形4结点等参有限单元法程序设计1、程序功能及特点a.该程序采用四边形4节点等参单元,能解决弹性力学的平面应力应变问题。
b.前处理采用网格自动划分技术,自动生成单元及结点信息。
b.能计算受集中力、自重体力、分布面力和静水压力的作用。
c.计算结点的位移和单元中心点的应力分量及其主应力。
d.后处理采取整体应力磨平求得各个结点的应力分量。
e.算例计算结果与ANSYS计算结果比较,并给出误差分析。
f.程序采用Visual Fortran 5.0编制而成。
2、程序流程及图框图2-1程序流程图图2-2子程序框图其中,各子程序的主要功能为:INPUT――输入原始数据HUAFEN――自动网格划分,形成COOR(2,NP),X,Y的坐标值与单元信息CBAND――形成主元素序号指示矩阵MA(*)SKO――形成整体刚度矩阵[K]CONCR――计算集中力引起的等效结点荷载{R}eBODYR――计算自重体力引起的等效结点荷载{R}eFACER――计算分布面力引起的等效结点荷载{R}eDECOP――支配方程LU三角分解FOBA――LU分解直接解法中的回代过程OUTDISP――输出结点位移分量STRESS――计算单元应力分量OUTSTRE――输出单元应力分量STIF――计算单元刚度矩阵FDNX――计算形函数对整体坐标的导数TiiyNxN⎥⎦⎤⎢⎣⎡∂∂∂∂,=i1,2,3,4。
FUN8――计算形函数及雅可比矩阵[J]SFUN ――应力磨平-单元下的‘K’=NCN‘SCN――应力磨平-单元下的右端项系数‘CN‘SUMSKN――应力磨平-单元下的右端项集成到总体的‘P‘SUMSTRS――应力磨平-单元下的集成到总体的‘K‘GAUSTRSS――高斯消元求磨平后的应力3、输入数据及变量说明当程序开始运行时,按屏幕提示,键入数据文件的名字。
在运行程序之前,根据程序中INPUT需要的数据输入建立一个存放原始数据的文件,这个文件的名字为INDAT.DAT。
西工大-有限元试题(附答案)
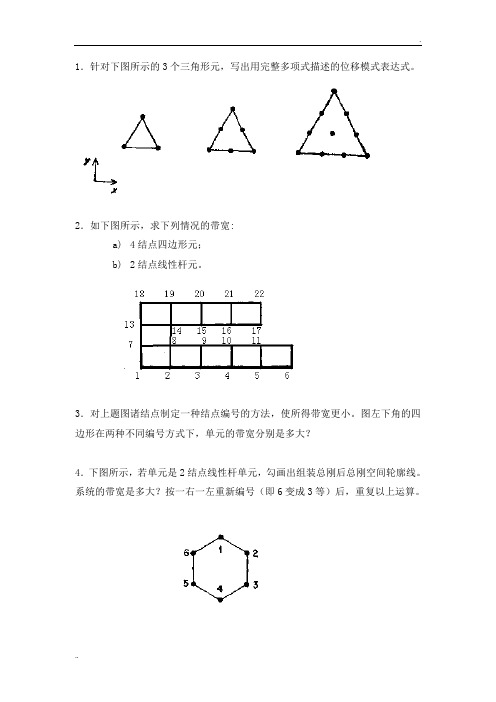
1.针对下图所示的3个三角形元,写出用完整多项式描述的位移模式表达式。
2.如下图所示,求下列情况的带宽:a)4结点四边形元;b)2结点线性杆元。
3.对上题图诸结点制定一种结点编号的方法,使所得带宽更小。
图左下角的四边形在两种不同编号方式下,单元的带宽分别是多大?4.下图所示,若单元是2结点线性杆单元,勾画出组装总刚后总刚空间轮廓线。
系统的带宽是多大?按一右一左重新编号(即6变成3等)后,重复以上运算。
5. 设杆件1-2受轴向力作用,截面积为A ,长度为L ,弹性模量为E ,试写出杆端力F 1,F 2与杆端位移21,u u 之间的关系式,并求出杆件的单元刚度矩阵)(][e k6.设阶梯形杆件由两个等截面杆件○1与○2所组成,试写出三个结点1、2、3的结点轴向力F 1,F 2,F 3与结点轴向位移321,,u u u 之间的整体刚度矩阵[K]。
7. 在上题的阶梯形杆件中,设结点3为固定端,结点1作用轴向载荷F 1=P ,求各结点的轴向位移和各杆的轴力。
8. 下图所示为平面桁架中的任一单元,y x ,为局部坐标系,x ,y 为总体坐标系,x 轴与x 轴的夹角为 。
(1) 求在局部坐标系中的单元刚度矩阵 )(][e k (2) 求单元的坐标转换矩阵 [T];(3) 求在总体坐标系中的单元刚度矩阵 )(][e k9.如图所示一个直角三角形桁架,已知27/103cm N E ⨯=,两个直角边长度cm l 100=,各杆截面面积210cm A =,求整体刚度矩阵[K]。
10. 设上题中的桁架的支承情况和载荷情况如下图所示,按有限元素法求出各结点的位移与各杆的内力。
11. 进行结点编号时,如果把所有固定端处的结点编在最后,那么在引入边界条件时是否会更简便些?12. 针对下图所示的3结点三角形单元,同一网格的两种不同的编号方式,单元的带宽分别是多大?13. 下图所示一个矩形单元,边长分别为2a 与2b ,坐标原点取在单元中心。
弹性力学_第7章_平面问题的有限单元法

(d* )T p {ε* }T σdxdy {δ* }T F L
5. 建立有限单元法的基本方程: 在各个节点处,列出内力和外力的平衡方程,就得到有限 单元法的总体劲度方程
Kδ FL
其中:K FL
— 总体劲度矩阵, — 位移列阵,各个节点的位移, — 荷载列阵,将荷载化为节点力列阵
《弹塑性力学》课件
内容提要 平 面 问 题 的 有 限 单 元 法
2012/5/10
§7-1 §7-2 §7-3 §7-4 §7-5 §7-6 §7-7
基本量及基本方程的矩阵表示 有限单元法的概念 单元的位移模式与解答的收敛性 单元的应变列阵和应力列阵 单元的结点力列阵与劲度矩阵 载荷向结点移置 等效节点荷载 结构的整体分析 节点平衡方程组
有限单元法的基本解题步骤为: 1. 划分单元; 2. 建立位移模式。即建立单元内任一点位移与节点位移之间的 关系,设三角形单元三个节点的位移分别为:(ui,vi), (uj,vj), (um,vm),三角形单元任何一点的位移 u 与 v用结点位移表示。 ui ui 结点位移列阵 v u [ N , N , N ] i i j m u j δi u j um 人为设计 δe δ j δ v j 的表达式。 v i m u m v [ N i , N j , N m ]v j v m v m 这种表示是人为设计的,每种单元都有不同表示方法,本 课程仅讲三结点三角形单元。
2 56
1、有限元法(Finite Element Method)
简称FEM,是弹性力学的一种近似解法。 首先将连续体变换为离散化结构,然后再利用分片插值技术与虚功原 理或变分方法进行求解。
弹性力学有限元法详解

x
4
i1 4
Ni ( ,)xi
y
i1
Ni ( ,) yi
总体坐标系适用于整体结构,局部坐标系只适用于具体某个 单元。
常用的对于平面问题还有八节点等参元,空间问题有八节 点空间等参元,二十节点等参元等 。
第18页,共40页。
3.2 连续体离散化
5.轴对称单元
对于回转结构,如果约束条件和载荷都对称于回转轴,其 应力、应变和位移也都对称于回转轴线,这类应力应变问题称 为轴对称问题 ,通常用柱坐标来描述应力、应变和位移,单元 为实心圆环体,仅截面不同
1
2
ai
(1
0
)
ai (1 0 ) ai (1 0 )
1
2
ai
(1
0
)
(i, j,l,m)
对于平面应变问题:
E
E 1 2
1
第29页,共40页。
3.3 单元分析
2. 单元分析
由虚功原理得:
Fe
K e BT DBdxdyt A
BT DBdxdyt δe
A
Fe Keδe
单元刚度矩阵可分块表示为:
第10页,共40页。
3.2 连续体离散化
3. 薄板弯曲单元和薄板单元
A. 薄板弯曲单元
l
θxi
i
θyi
wi
m
j
四边形弯 曲单元
四边形单元有四个节点,每个节点有三个自由度,主要承 受横向载荷和绕水平轴的弯矩。
第11页,共40页。
3.2 连续体离散化
3.薄板弯曲单元和薄板单元
A. 薄板弯曲单元
m
θxi
对于平面应变问题:
E
E 1 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.6 四结点四边形单元(The four-node quadrilateral element)前面介绍了四结点的矩形单元其位移函数:xy y x U 4321αααα+++=xy y x V8765αααα+++=为双线性函数,应力,应变在单元内呈线性变化,比常应力三角形单元精度高。
但它对边界要求严格。
本节介绍的四结点四边形等参元,它不但具有较高的精度,而且其网格划分也不受边界的影响。
对任意四边形单元(图见下面)若仍直接采用前面矩形单元的位移函数,在边界上它便不再是线性的(因边界不与x,y 轴一致),这样会使得相邻两单元在公共边界上的位移可能会出现不连续现象(非协调元),而使收敛性受到影响。
可以验证,利用坐标变换就能解决这个问题,即可以通过坐标变换将整体坐标中的四边形(图a )变换成在局部坐标系中与四边形方向无关的边长为2的正方形。
正方形四个结点i,j,m,p 按反时钟顺序对应四边形的四个结点i j m p 。
正方形的1-=η 和 1=η 二条边界,分别对应四边形的i ,j 边界和p,m 边界;ξ=-1和ξ=+1分别对应四边形的i ,p 边界和j ,m 边界。
如果用二组直线等分四边形的四个边界线段,使四边形绘成一个非正交网格,那么该非正交网格在正方形上对应着一个等距离的规则网格(见图a, b )。
当然, 局部坐标上的A 点与整体坐标的A 点对应。
一、四结点四边形等参单元的形函数及坐标变换由于可以将整体坐标下的四边形单元变换成局部坐标下的正方形单元,对于这种正方形单元,自然仍取形函数为: ξηαηαξαα2321+++=U ξηαηαξαα8765+++=V引入边界条件,即可得位移函数:∑=ijmpi i U N Ui ijmpi V N V ∑==写成矩阵形式:{}{}[]{}ee p i p i ed N d N N N N V U f =⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=000 式中形函数:()()()ηηξξηξi i i N ++=1141, ()p m j i ,,,按照等参元的定义,我们将坐标变换式亦取为: p p m m j j i i i ijmpi x N x N x N x N x N x +++==∑p p m m j j i i i ijmpi y N y N y N y N y N y +++==∑ ()162-- 式中形函数N 与位移函数中的完全一致。
可以验证,利用坐标变换式(2-6-1),可以把整体坐标系中的任意四边形单元(图a )变换成在局部坐标系中与四边形对应的边长为2的正方形。
因此可以将上述位移函数和形函数用于任意四边形单元,并将形函数中的ξ,η理解为任意四边形单元的局部坐标。
这样由位移函数可以得到单元各点的位移。
在四条边界上分别有ξ=±和η=±1,故边界上的位移呈线性变化,位移的连续性可得到保证。
于是,我们可以理解为:任意四边形单元是从基本的正方形单元变换过来的实际单元。
因此又称正方形单元为母体单元,或基本单元。
例题:为了加深理解,现考察实际单元为矩形单元的坐标变换,在2.4节中,我们定义局部坐标与整体坐标的关系是:()01x x a-=ξ ()01y y b -=η式中(x 0 , y 0 )为局部坐标原点。
由上第一式()01x x a-=ξ得:()()j i i j x x x x x a x ++-=+=21210ξξ 将其重新组合:()()j i x x x ξξ++-=121121()()()()()()()()p m j i x x x x ηξηξηξηξ+-++++-++--=1141114111411141 对照2.4中的形函数表达式,便知:p p m m j j i i x N x N x N x N x +++= 自然同理可得: p p m m j j i i y N y N y N y N y +++=由此知,矩形单元可以看作是四结点四边形单元的特例,自然,它也是等参元。
《有限元法概论》(第二版)P 172 中,是这样解释等参元的基本概念和推导方法的:图形变换四结点正方形(母元) 图形变换 四结点四边形(等参元) (ξ-η平面内) ───→ (x,y 平面内)进行图形变换的关键是进行图形结点坐标之间的变换:正方形结点坐标 坐标变换 四边形结点坐标 (ξi ,ηi ) ────→ (x,y) i=i,j,m,p i=i,j,m,p为了实现上述结点坐标之间的变换,可利用母元的形函数,得出(ξ,η)和(x,y)之间的坐标变换式。
图形变换具有如下性质:1. 母元中的坐标线对应于等参元的直线;2. 四结点正方形母元对应于四个结点可以任意布置的直边四边形等参元;3. 变换式(2-6-1)能保证相邻等参元的边界位移彼此协调。
二、几何矩阵[B]已知单元的应变与结点位移之间的关系是:{}{}d N N N N x y y xp i pi ⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=0000 ε ()262-- 形函数矩阵[N]只是局部坐标ξ,η的显函数,为求形函数对整体坐标x,y 的偏导数,必须用复合函数求导公式:ξξξ∂∂∂∂+∂∂∂∂=∂∂yy N x x N N i i i ηηη∂∂∂∂+∂∂∂∂=∂∂yy N x x N N i i i ()362-- 或写成: []⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧∂∂∂∂y N x N J N N i i i i ηξ ()a 362--式中: []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=ηηξξx yx yx J ()b 362-- 称为雅可比矩阵,而把它的行列式称为雅可比行列式。
把式(2-6-1)代入[J]得:[]⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=∑∑∑∑p pm mj j i ip m j ip m j iijmp i i ijmpii ijmp i i ijmp iiy x y x y x y x N N N N N N N N y N xNy N x N J ηηηηξξξξηηξξ 将形函数 ()()ηηξξi i i N ++=1141 ()p m j i ,,, 代入,分别对ξ,η求偏导,即可得到四结点四边形等参元的雅可比矩阵:[]⎥⎦⎤⎢⎣⎡++++=ξβξβηβηβB A B A J 432141 ()562--式中常数记为: ∑=ijmp i i i x A ηξ ∑=ijmpi i i y B ηξ∑=ijmpi i x ξβ1 ∑=ijmpi i y ξβ2∑=ijmpi i x ηβ3 ∑=ijmpi i y ηβ4该雅可比矩阵的逆:[]()()⎥⎦⎤⎢⎣⎡++-+-+=-ηβξβηβξβA A B B JJ 1324141 雅可比行列式:()()()()[]ξβηββηβηβA A A J ++-++=3241161()()()[]ηββξββββββ34213241161B A A B -+-+-=可以证明,如果四结点四边形的四个内角都小于180°的话,雅可比行列式|J|大于零,其逆阵[J]-1是存在的。
换句话说,为了使上述等参元能保持较好的精度,整体坐标系下所划分的任意四边形单元必须是凸四边形,即任意内角都不能大于180°。
四边形也不能太歪斜,否则会影响其精度。
利用雅可比的逆矩阵,即可求出整体坐标系下形函数的偏导数:[][]()()),,,(111141p m j i i i i i i i i i i J N N J y N x N ⎭⎬⎫⎩⎨⎧++=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧∂∂∂∂=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧∂∂∂∂--ξξηηηξηξ ()662-- 求出全部偏导,即代回(2-6-2)右侧,即可得到几何矩阵[B], [B]是ηξ,的函数,即:[][]⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∂∂∂∂∂∂∂∂=x N y N x N y N x N y N y N y N y N x N x N x N N x yy x B p p j j ii p j i pj i 0000000将(2-6-6)代入即可获得[B], [B]是ηξ,的函数。
三、单元刚度矩阵获得[B]后,便可由单刚的一般表达式:[][][][]⎰⎰=dxdy B D B t K T求出四结点四边形的单元刚度矩阵。
在按上述公式作积分运算时,必须把面积元dxdy变换成ηξdd,图a上的面积元abdc的面积等于矢量→ab与矢量→ac的矢量积的模,即微元→→⨯=acabdA沿ξ轴对应于dξ的矢量增量是:→→→∂∂+∂∂=jdyidxabξξξξ沿η轴对应于η的矢量增量是:→→→∂∂+∂∂=jdyidxacηηηη式中→→ji,是坐标x,y的单位矢,注意到:=⨯=⨯→→→→jjii1=⨯→→ji则有:⎪⎭⎫⎝⎛∂∂+∂∂⨯⎪⎭⎫⎝⎛∂∂+∂∂=→→→→jdyidxjdyidxdAηηηηξξξξηξηξηξηξddJjiddxyyx=⨯⎪⎪⎭⎫⎝⎛∂∂∂∂-∂∂∂∂=→→因此刚度矩阵的积分式:[][][]⎰⎰--=1111ηξdtdJDBK T()762--在计算单元刚度矩阵[K]中元素时,由于被积函数中出现了雅可比行列式,使得它用解析法很难求其积分,故常采用高斯数值积分法.四、数值积分1.一维数值积分()⎰ba d F ξξ基本思想:构造一个多项目式()ξψ,使在i ξ(i=1,2……n)上有 ()()i i F ξξψ= , 然后用近似函数()ξψ的积分()⎰ba d ξξψ来近似原被积函数()ξF 的积分()⎰ba d F ξξ。
iξ称为积分点或取样点,积分点i ξ的数值和位置决定了()ξψ近似()ξF 的程度,亦即决定数值积分的精度。
对于n 个积分点,按照积分点位置的不同选择,通常采用两种不同的数值积分方法,Newton-Cotes 积分和高斯积分方案。
二者方法基本相同,只是前者的积分点ξi 是等间距分布,而后者不是等间距分布。
高斯积分的积分点位置由下述方法确定:① 定义n 次多项式()()()()n P ξξξξξξξ---= 21 ② 由下列条件确定n 个积分点位置()⎰=bai d P 0ξξξ 11,0-=n i由上二式可见,()ξP有以下性质:① 在积分点上()0=i P ξ;② 多项式()ξP 与1210 ... ,,,-n ξξξξ在(a, b )域内正交。
由此可见n 个积分点的位置ξi 是在求积域(a, b )内与1210 ... ,,,-n ξξξξ正交的n 次多项式()ξP 构成方程()⎰=bai d P 0ξξξ的解。
