单纯形法的表格解法
第三节 单纯形法

θi 32.5 40 25
5 7. 5
注意:单纯形法中, 注意:单纯形法中, 1.每一步运算只能用矩阵初等行 1.每一步运算只能用矩阵初等行 变换; 变换; 2.表中第3列的数总应保持非负 2.表中第 表中第3 (≥ 0); 3.当所有检验数均非正(≤ 0) 3.当所有检验数均非正 当所有检验数均非正( 得到最优单纯形表。 时,得到最优单纯形表。
8
1.初始单纯形表: 1.初始单纯形表: 初始单纯形表
CB XB b b1 b2 ┇ bm f
m
cn+1 xn+1 cn+2 xn+2 ┇ ┇ cn+m xn+m m -z
c1 x1 a11 a21 ┇ am1 σ1
… … … … ┇ … …
cn xn a1n a2n ┇ amn σn
m
cn+1 xn+1 1 0 ┇ 0 m 0
-z
15
在最优单纯形表中,非基变量的检验数不 在最优单纯形表中, 是正数,于是得到最优解为X 是正数,于是得到最优解为X*=(15,10,0,0,45)T 最优目标值为z =32500。注意到非基变量x 最优目标值为z*=32500。注意到非基变量x4 的检验数是0 如果选x 为进基变量, 的检验数是0,如果选x4为进基变量,迭代 还可以进行下去,但是最优值不会增大, 还可以进行下去,但是最优值不会增大, 而只有最优解改变,这就是多解的情况。 而只有最优解改变,这就是多解的情况。 下面再迭代一步,如表2 所示。 下面再迭代一步,如表2-9所示。
19
解:单纯形法求解过程如下表。 单纯形法求解过程如下表。
CB XB
0 0 0 -z 7 0 0 -z x1 x6 x7 x5 x6 x7
使用表格形式的单纯形方法

使用表格形式的单纯形方法本文档将通过表格形式介绍单纯形方法的主要概念和步骤,包括初始表格、基变量、非基变量、基可行解、目标函数、最优解、灵敏度分析、稳定性分析、对偶问题和对偶解等方面。
一、初始表格初始表格是单纯形方法的起点,通常由系数矩阵和约束条件组成。
系数矩阵的每一行对应一个约束条件,每一列对应一个变量。
初始表格的最后一列通常为价值列,用于衡量每个基变量的目标函数值。
二、基变量和非基变量在初始表格中,基变量是指位于基可行解中的变量,而非基变量则是指未位于基可行解中的变量。
基变量和非基变量的区分是单纯形方法的关键之一。
三、基可行解基可行解是指满足所有约束条件的解,其中基变量被定义为位于基可行解中的变量。
在单纯形方法中,基可行解是寻找最优解的起点。
四、目标函数目标函数是指要最小化或最大化的函数,它通常由基变量的线性组合构成。
目标函数在单纯形方法中用于衡量每个基可行解的质量,最优解即为目标函数值最小的基可行解。
五、最优解最优解是指满足所有约束条件且目标函数值最小的解。
在单纯形方法中,最优解是寻找基可行解的终点。
六、灵敏度分析灵敏度分析是指分析目标函数值对基变量的敏感程度。
在单纯形方法中,灵敏度分析用于确定最优解的稳定性。
七、稳定性分析稳定性分析是指分析最优解是否稳定。
在单纯形方法中,稳定性分析用于确定最优解是否受基变量值变化的影响。
八、对偶问题对偶问题是指与原问题相对应的问题。
在单纯形方法中,对偶问题用于分析原问题的约束条件和目标函数的性质。
九、对偶解对偶解是指满足对偶问题的解。
在单纯形方法中,对偶解用于确定最优解的性质和约束条件的可行性。
运筹学单纯形法的计算步骤

b2
0… 0
a2,m+1
…
a2n
2
…
…
…
…
cm xm
bm
0… 1
am,m+1
…
amn
m
-z -z 值 0 … 0
m+1
…
n
XB 列——基变量, CB 列——基变量的价值系数(目标函数系数) cj 行——价值系数,b 列——方程组右侧常数 列——确定换入变量时的比率计算值
下面一行——检验数, 中间主要部分——约束方程系数
(4).根据max(j > 0) =k,拟定xk为换入变量,按 规则计算 =min{bi/aik\aik>0}
可拟定第l行旳基变量为换出变量。转入下一步。
(5).以 alk 为主元素进行迭代(即用高斯消去法或称为旋转变 换),把 xk 所对应的列向量变换为(0,0,…,1,…,0)T,将
XB 列中的第 l 个基变量换为 xk,得到新的单纯形表,返回(2)。
b
x1
x2
x3
x4
x5
2 x1 2 0 x4 8 3 x2 3
1
0
1
0 -1/2 -
0 0 -4 1 (2 ) 4
0 1 0 0 1/4 12
-z
-13
0
0 -2
0 1/4
X(2)=(2,3,0,8,0)T, z2 =13
cj
2 30 0 0
CB XB
b
x1
x2
x3
x4
x5
2 x1 4 0 x5 4 3 x2 2
量,给出第一阶段的数学模型为:
min = x6+x7
x1-2x2+x3+x4
单纯形法的表格解法

只用非基变量来表示目标函数,这只要在约束等式中通过移项等处理就可 以用非基变量来表示基变量,然后用非基变量的表示式代替目标函数中基 变量,这样目标函数中只含有非基变量了,或者说目标函数中基变量的系 数都为零了。此时目标函数中所有变量的系数即为各变量的检验数,把变 量xi的检验数记为σi。显然所有基变量的检验数必为零。在本例题中目标 函数为50x1+100x2。由于初始可行解中x1,x2为非基变量,所以此目标函 数已经用非基变量表示了,不需要再代换出基变量了。这样我们可知 σ1=50,σ2=100,σ3=0,σ4=0,σ5=0。
向量为 pj j 1, 2,L ,n 则
z j cB1,L , cBm pj cB pj ,
其中,(cB)是由第1列第m行各约束方程中的基变量相应的目标函数依 次组成的有序行向量。
单纯形法的表格形式是把用单纯形法求出基本可行解、检验其最优性、
迭代某步骤都用表格的方式来计算求出,其表格的形式有些像增广矩阵,
n
bi aij xj. i 1, 2,L , m
j m1
把以上的表达式带入目标函数,就有
m
n
z c1x1 c2 x2 L cn xn ci xi c j x j
i 1
j m 1
其中:
n
n
z0
c j z j x j z0 j x j
j m 1
j m 1
.
§1 单纯形法的基本思路和原理
非基变量:与非基向量pj相应的变量xj叫非基变量,非基变量有n-m个。 由线性代数的知识知道,如果我们在约束方程组系数矩阵中找到一个
单纯形法求解线性规划的步骤

单纯形法求解线性规划的步骤1>初始化将给定的线性规划问题化成标准形式,并建立一个初始表格,它最右边的单元格都是非负的(否则无解),接下来的m列组成一个m*m的单元矩阵(目标行的单元格则不必满足这一条件),这m列确定了初始的基本可行解的基本变量,而表格中行用基本变量来表示2>最优化测试如果目标行的所有单元格都是非负的(除了最右列中代表目标函数值的那个单元格),就可以停止了,该表格代表了一个最优解,它的基本变量的值在最右列中,而剩下的非基本变量都为03>确定输入变量从目标行的前n个单元格中选择一个负的单元格(选择绝对值最大的那个)该单元格所在的列确定的输入变量及主元列4>确定分离变量对于主元列的每个正单元格,求出θ比率(如果主元格的单元格为负或为0,说明该问题是无解的,算法终止),找出θ比率最小的列,改行确定了分离变量和主元行5>建立下一张表格将主元行的所有单元格除以主元得到新的主元行,包括主元行在内的每一行,要减去改行主元列单元格和新主元行的成绩(除主元行为1外,这一步将主元列的所有单元格变成0).把主元列的变量名进行代换,得到新的单纯形表,返回第一步为求简单在本程序中,需要自己建立标准矩阵(比如加入松弛变量等工作需要用户自己完成),程序的输入有两种方式:1:指定行和列,由用户自行输入每一个元素 SimpleMatrix(introw=0,int col=0);2:直接在主程序中初始化一个二维数组,然后利用构造函数 SimpleMatrix(introw,int col,double **M) 来初始化和处理(本程序所用的实例用的是这种方法)程序中主要的函数以及说明~SimpleMatrix();销毁动态分配的数组.用于很难预先估计矩阵的行和列,所以在程序中才了动态的内存分配.需要重载析构函数bool Is_objectLine_All_Positive(); //判断目标行是否全部为非负数,最后一列不作考虑这个函数用来判断是否已经存在最优解bool Is_MainCol_All_Negative(int col);//判断主元列是否全部为负数或零这个函数用来判断线性规划是否是无解的bool Is_column_all_Positive(int col); //判断col列中是否全部为正(不包括目标行)用来判断线性规划是否存在最优解,因为如果最后一列如果有负数的化,就无解了,算法终止int InColumn(); //确定输入变量用来判断主元所在的列int DepartRow(int col); //确定分离变量(寻找主元)用来确定主元所在的行void MainItem_To_1(int row,int col); //将主元所在的行做处理,使主元变为1void SubMatrixLine(int row1,int row2,intcol);//将矩阵的其他行做处理,矩阵的两行相减这个函数是在主元行已经做处理以后调用,目的是是矩阵的其他行主元列的元素变成0.其中row2为主元所在的行,col为主元所在的列,row1为要处理的行void PrintAnswer(); //输出矩阵的最优解int GetRows(); //返回矩阵的行数int GetCols(); //返回矩阵的列数double GetItem(int row,int col); //返回矩阵第row行,第col列的元素源代码//SimpleMatrix.h#ifndef SIMPLEMATRIX_H_#define SIMPLEMATRIX_H_class SimpleMatrix{public:SimpleMatrix(int row=0,int col=0);SimpleMatrix(int row,int col,double **M);~SimpleMatrix();bool Is_objectLine_All_Positive(); //判断目标行是否全部为非负数,最后一列不作考虑 bool Is_MainCol_All_Negative(int col);//判断主元列是否全部为负数或零bool Is_column_all_Positive(int col); //判断col列中是否全部为正(不包括目标行)int InColumn(); //确定输入变量int DepartRow(int col); //确定分离变量(寻找主元)void MainItem_To_1(int row,int col); //将主元所在的行做处理,使主元变为1void SubMatrixLine(int row1,int row2,int col);//将矩阵的其他行做处理,矩阵的两行相减 void PrintAnswer(); //输出矩阵的最优解int GetRows(); //返回矩阵的行数int GetCols(); //返回矩阵的列数double GetItem(int row,int col); //返回矩阵第row行,第col列的元素private:int rowLen; //标准矩阵的行数int colLen; //标准矩阵的列数double **data; //一个二维数组,指向标准矩阵的数据成员void init(int rows,int cols); //动态分配一个rows行,cols列的二维数组};#end if//SimpleMatrix.cpp#include <iostream>#include <cmath>#include "SimpleMatrix.h"using namespace std;void SimpleMatrix::init(int rows,int cols){if(rows>0&&cols>0){rowLen=rows;colLen=cols;data = new double *[rows];for (int i=0;i<rows;i++){data[i]=new double[cols];}}elsecout<<"矩阵的行.列数不合法"<<endl;}SimpleMatrix::SimpleMatrix(int row,int col){init(row,col);for(int i=0;i<rowLen;i++){cout<<"请输入矩阵中第"<<i+1<<"行的系数"<<endl; for(int j=0;j<colLen;j++)cin>>data[i][j];}}SimpleMatrix::SimpleMatrix(int row,int col,double **M) {rowLen=row;colLen=col;init(row,col);for (int i=0;i<row;i++)for(int j=0;j<col;j++){data[i][j]=*((double*)M+col*i+j); ;}}SimpleMatrix::~SimpleMatrix(){if(colLen*rowLen != 0 ){for(int i=rowLen-1;i>=0;i--){if (data[i]!=NULL)if (data!=NULL)delete[] data;}}bool SimpleMatrix::Is_objectLine_All_Positive(){for(int i=0;i<colLen-1;i++)if(data[rowLen-1][i]<0)return false;return true;}bool SimpleMatrix::Is_MainCol_All_Negative(int col) {for(int i=0;i<rowLen;i++)if(data[i][col]>0)return false;return true;}bool SimpleMatrix::Is_column_all_Positive(int col) {for(int i=0;i<rowLen-1;i++){if(data[i][col-1]<0)return false;}return true;}int SimpleMatrix::InColumn(){int count=0;for(int i=0;i<colLen-1;i++){int temp=GetItem(rowLen-1,i);if(temp>=0){count++;}elsebreak;}double maxItem=fabs(GetItem(rowLen-1,count)); int index_col;for(i=0;i<colLen-1;i++){double temp=GetItem(rowLen-1,i);if(temp<0){maxItem=fabs(temp);index_col=i;}}}return index_col;}int SimpleMatrix::DepartRow(int col){int index_row;int count=0;for(int i=0;i<rowLen;i++){if(data[i][col]<0)count++;elsebreak;}double minItem=data[count][colLen-1]/data[count][col]; index_row=count;double temp;for(i=0;i<rowLen-1;i++){temp=data[i][col];if(temp>0){temp=data[i][colLen-1]/temp;if(temp<minItem){minItem=temp;index_row=i;}}}return index_row;}void SimpleMatrix::MainItem_To_1(int row,int col){double temp=GetItem(row,col);//double temp=data[row-1][col-1];for (int i=0;i<colLen;i++){data[row][i]/=temp;}}void SimpleMatrix::SubMatrixLine(int row1,int row2,int col) {double temp=GetItem(row1,col);//double temp=data[row1-1][col-1];double*tempLine=new double[colLen];for(int i=0;i<colLen;i++){tempLine[i]=data[row2][i];}for(i=0;i<colLen;i++){data[row1][i]=data[row1][i]-temp*tempLine[i];}delete[]tempLine;}int SimpleMatrix::GetRows(){return rowLen;}int SimpleMatrix::GetCols(){return colLen;}double SimpleMatrix::GetItem(int row,int col){return data[row][col];}void SimpleMatrix::PrintAnswer(){//先确定单位矩阵中1的位置for (int i=0;i<GetRows();i++)for (int j=0;j<GetRows();j++){if(1==data[i][j]){int index_col=j;cout<<"x"<<index_col+1<<"="<<data[i][colLen-1]<<" ";}}cout<<endl;cout<<"取得最优解,并且最优值为"<<data[rowLen-1][colLen-1];}//单纯形法.cpp#include <iostream>#include "SimpleMatrix.h"using namespace std;int main(){double M[4][7]={{5,3,1,1,0,0,9},{-5,6,15,0,1,0,15},{2,-1,1,0,0,-1,5},{-10,-15,-12,0,0,0,}}; SimpleMatrix Matrix(4,7,(double **)M);if(Matrix.Is_column_all_Positive(5)) //判断是否存在最优解{bool p=Matrix.Is_objectLine_All_Positive(); //判断主元列是否全部为正,确定是否已经取得最优解 while(!p){int col=Matrix.InColumn(); //确定主元所在的行if(Matrix.Is_MainCol_All_Negative(col)) //确定线性规划的解是否为无解的{cout<<"线性规划问题是无界的,没有最优解"<<endl;exit(EXIT_FAILURE);}else{int mainRow=Matrix.DepartRow(col); //确定主元所在的行Matrix.MainItem_To_1(mainRow,col); //将主元所在的行做变换,使主元变成1int i=0;while(i<Matrix.GetRows()){if(i!=mainRow){Matrix.SubMatrixLine(i,mainRow,col); //处理矩阵中其他的行,使主元列的元素为0i++;}else{i++;}}}for(int i=0;i<Matrix.GetRows();i++) //输出变换以后的矩阵,判断是否正确处理{for (int j=0;j<Matrix.GetCols();j++){cout<<Matrix.GetItem(i,j)<<" ";}cout<<endl;}p=Matrix.Is_objectLine_All_Positive();}Matrix.PrintAnswer();}elsecout<<"线性规划无解"<<endl;return0;}。
线性规划的单纯形法表格方法
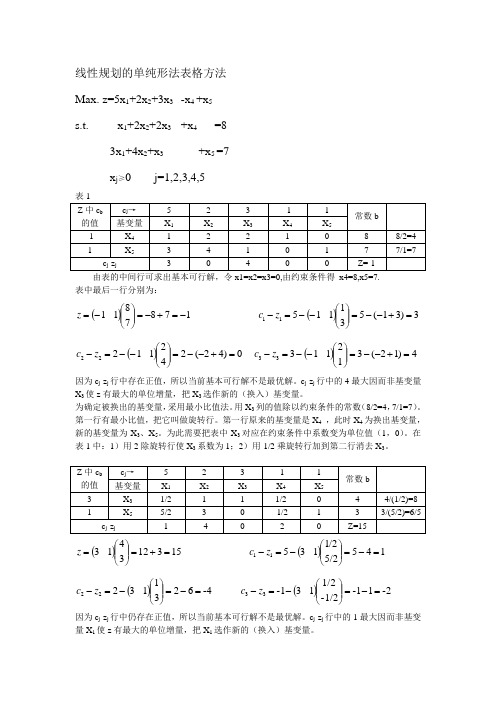
线性规划的单纯形法表格方法 Max. z=5x 1+2x 2+3x 3 -x 4 +x 5 s.t. x 1+2x 2+2x 3 +x 4 =8 3x 1+4x 2+x 3 +x 5 =7 x j ≥0 j=1,2,3,4,5表1由表的中间行可求出基本可行解,令x1=x2=x3=0,由约束条件得 x4=8,x5=7. 表中最后一行分别为:()1787811-=+-=⎪⎪⎭⎫ ⎝⎛-=z ()3)31(53111511=+--=⎪⎪⎭⎫ ⎝⎛--=-z c ()0)42(24211222=+--=⎪⎪⎭⎫ ⎝⎛--=-z c ()4)12(31211333=+--=⎪⎪⎭⎫⎝⎛--=-z c 因为c j -z j 行中存在正值,所以当前基本可行解不是最优解。
c j -z j 行中的4最大因而非基变量X 3使z 有最大的单位增量,把X 3选作新的(换入)基变量。
为确定被换出的基变量,采用最小比值法。
用X 3列的值除以约束条件的常数(8/2=4,7/1=7)。
第一行有最小比值,把它叫做旋转行。
第一行原来的基变量是X 4 ,此时X 4为换出基变量,新的基变量为X 3、X 5。
为此需要把表中X 3对应在约束条件中系数变为单位值(1,0)。
在表1中:1)用2除旋转行使X 3系数为1;2)用-1/2乘旋转行加到第二行消去X 3。
()153123413=+=⎪⎪⎭⎫ ⎝⎛=z ()1455/2/2113511=-=⎪⎪⎭⎫ ⎝⎛-=-z c ()-4623113222=-=⎪⎪⎭⎫ ⎝⎛-=-z c ()-21-11/2-21/13-133=-=⎪⎪⎭⎫⎝⎛-=-z c 因为c j -z j 行中仍存在正值,所以当前基本可行解不是最优解。
c j -z j 行中的1最大因而非基变量X 1使z 有最大的单位增量,把X 1选作新的(换入)基变量。
为确定被换出的基变量,采用最小比值法。
用X 1列的值除以约束条件的常数(4/(1/2)=8,3/(5/2)=6/5)。
单纯形表解法
Max Z =2x1+3x2. x1+2x2≤84x1≤164x2≤12x1,x2≥0先化为标准形式Max Z =2x1+3x2+0x3+0x4+0x5. x1+2x2+x3 =84x1+x4=164x2 +x5=12x1 , x2 , x3 , x4 , x5 ≥0成立初始单纯性表x3 , x4 , x5 为基变量,x1 , x2 为非基变量,令x1 =x2=0 则-z0=0,z0=0因为σ1>0,σ2>0,故X(0)=(0,0,8,16,12)T不是最优解σ1<σ2,应选择x2为进基变量。
θ列:8/2=4 > 12/4=3,应选择x5为离基变量。
如此就能够够确信主元素【4】进行基变换(第三行/4,第一行-2*第三行,第四行-3*第三行)可得下表:x2 , x3 , x4为基变量,x1 , x5为非基变量,令x1 , x5=0X(1)=(0,3,2,16,0)T Z1=9因为σ1>0,故这也不是最优解选择x1作为进基变量θ列:2/1=2 < 16/4=4,应选择x3为离基变量确信主元素【1】进行基变换(第二行-4*第一行,第四行-2*第一行)可得下表:x 1,x 2,x 4为变量,x 3,x 5为非基变量,令x 3,x 5=0 X (2)=(2,3,0,8,0)T Z 2=13 因为σ5>0,故这也不是最优解 选择x 5作为进基变量θ列:8/2=4 < 3/(1/4)=12,应选择x 4为离基变量 确信主元素【2】进行基变换(第二行/2,第一行+第二行/2,第三行-第二行/4,第四行-第二行/4)可得下表:x 1 , x 2 , x 5 为基变量,x 3 , x 4 为非基变量,令x 3 =x 4=0X(3)=(4,2,0,0,4)T Z3=14因为σ3<0,σ4<0,故X(3)=(4,2,0,0,4)T是最优解。
单纯形法表的解题步骤
单纯形法表的解题步骤单纯形法表结构如下:j c →对应变量的价值系数i θB Cb Xb1x 2x 3x " j x基变量的价值系数基变量 资源列θ规则求的值j σ检验数①一般形式若线性规划问题标准形式如下:123451231425max 23000284164120,1,2,5j z x x x x x x x x x x x x x j =++++++=⎧⎪+=⎪⎨+=⎪⎪≥=⎩"取松弛变量345,,x x x 为基变量,它对应的单位矩阵为基。
这样就得到初始可行基解:()()00,0,8,16,12TX =。
将有关数字填入表中,得到初始单纯形表,如表1-1所示:表 1-1 ()()00,0,8,16,12TX =j c →2 3 0 0 0i θB C b X b1x 2x 3x 4x 5x0 3x 8 1 2 1 0 0 4 04x16 4 0 0 1 0 -5x12 0 [4] 0 0 1 3j σ2 3 0 0 0若检验数均未达到小于等于0,则对上表进行调整。
选择上表中检验数最大的列,该列对应的非变量为入基变量;再应用θ规则该列对应的各基变量对应的θ值,选出其中最小的一行,该行对应的基变量为出基变量。
修改单纯形表,对各行进行初等变换,确保基变量组成的矩阵为单为矩阵。
修改后的单纯形表如表1-2所示:表 1-2 ()()10,3,2,16,0TX =检验数12,0σσ>,则进行继续调整,调整后的单纯形法表如表1-3所示:表 1-3 ()()22,3,0,8,0TX =表1-3中, 50σ>,则继续进行调整,调整结果如表1-4所示:表 1-4 ()()34,2,0,0,4TX =检验数0j σ≤,这表示目标函数值已不可能再增大,于是得到最优解:()()3*4,2,0,0,4TX X ==*14z =②带人工变量现有线性规划问题:12312312313123min 321142321,,0z x x x x x x x x x x x x x x =−++−+≤⎧⎪−++≥⎪⎨−+=⎪⎪≥⎩ 将上述线性规划问题用大M 法求解,在约束条件中加入松弛变量4x ,剩余变量5x ,人工变量6x ,7x 得到:1234567123412356137min 300211423210,1,2,,7j z x x x x x Mx Mx x x x x x x x x x x x x x j =−++++++−++=⎧⎪−++−+=⎪⎨−++=⎪⎪≥=⎩"其中,M 是一个任意大的正数。
第3章05-单纯形表法
第3章05单纯形表法同学们大家好,前面我们讲了单纯形法的原理,它的整个过程看似很复杂,但实际上,单纯形法的全部计算过程,可以简单地在一张类似增广矩阵的表格上进行,这种表格我们称为单纯形表,所以,今天我们就来学习线性规划模型的单纯形表法。
给定一个可行基,可以画出一张单纯形表。
单纯形表的行标是n个变量以及右端项b,列标是m个基变量以及检验数行σ。
所以,用矩阵的形式把它表示出来,就如下表所示我们注意到,像B,所以,是与原方程组等价的。
最后一行是检验数C-C B B-1A,右下角是-C B B-1b,它恰好是这个基B所对应的可行解的目标函数值的相反数。
用单纯形表法求解线性规划模型时,有下面的步骤:单纯形表法求解线性规划问题的步骤:Step1.转换一般的线形规划模型为标准型,并写出A,b,C。
Step2找初始基本可行解,写出B,B-1,X B,C B。
Step3计算单纯形表中的各矩阵B-1A,B-1b,C-C B B-1A,-C B B-1b,并构造初始单纯形表。
Step4判断基本最优解。
Step5换基迭代,返回Step4。
第一步是将一般的线性规划模型转化为标准形,并写出约束矩阵A,右端项b,以及价值向量C。
第二步,找初始的基本可行解。
根据上一讲单纯形法的原理,你要注意的是,我们总是从约束矩阵A里面选一个单位阵出来作为初始基,在右端项非负的条件下,这样选出来的单位阵一定是可行基,也就是找到了初始的基本可行解。
而如果约束矩阵A中没有单位阵,我们将会通过引入人工变量构造出一个单位阵,这种构造方法我们将在后面进行详细介绍。
初始基选出来之后,我们就能写出B,B-1,以及基变量X B和基变量所对应的价值向量C B。
第三步,计算B-1A,B-1b,C-C B B-1A,-C B B-1b,这样就可以把初始单纯形表写出来。
第四步,判断当前的基本可行解是不是最优解?按照我们上一讲介绍的单纯形法的原理,如果检验数行中所有的检验数都小于等于0,当前的基本解就是最优解;如果有一个非基变量的检验数是正的,而且它所对应A中的列的项都小于等于0,那么这个时候是无界解。
线性规划-单纯形法
选x2为入基变量。
2. 出基变量的确定
要在原来的3个基变量s1,s2,s3中确定一个出基变量 如果把s3作为出基变量,则新的基变量为x2,s1,s2,
x2 +s1=300,
bj 350 125 350 125
s3
zj
0
2
-2M
1
-M
0
M
0
M
1
0
0
600
300
0 -M -M
σj=cj-zj
-2+2M -3+M -3+M -M 0
0
0
-475M
cB a1 1 x1 -M -2
x1
x2
s1
s2
s3
a1
a2
-2
0 1
-3
1 0
0
-1 0
0
1 -1
0
0 0
-M -M
1 0 -1 1
x1 10
3 5 5 10
x2 9
2 5 6 9
x3 4
4 1 3 4
x4 6
2 3 1 6
x5 0
1 0 0 0
x6 0
0 1 0 0
x7 0
0 0 1 0
bj
bj/aj1
70 70/3 60 60/5 25 25/5
0
σj=cj-zj
cB x5 x6 x1 0 0 10
x1 10
0 0 1 0
z1 z0 j x j
jJ
x j≥ 0 j ≤0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
§1 单纯形法的基本思路和原理
在本例题中我们就找到了一个基是单位矩阵。
1 0 0
B2 0 1 0
0 0 1
通过例1的求解来介绍单纯形法: 在加上松弛变量之后我们可得到标准型如下:
目标函数: max 50x1+100x2 约束条件:x1+x2+s1=300,
2x1+x2+s2=400, x2+s3=250.
xj≥0 (j=1,2),sj≥0 (j=1,2,3)
.
§1 单纯形法的基本思路和原理
它的系数矩阵 , 1 1 1 0 0
.
§1 单纯形法的基本思路和原理
一般来说判断一个基是否是可行基,只有在求出其基本解以后,当其基本解 所有变量的解都是大于等于零,才能断定这个解是基本可行解,这个基是可行 基。那么我们能否在求解之前,就找到一个可行基呢?也就是说我们找到的一个 基能保证在求解之后得到的解一定是基本可行解呢?由于在线性规划的标准型中 要求bj都大于等于零,如果我们能找到一个基是单位矩阵,或者说一个基是由单位 矩阵的各列向量所组成(至于各列向量的前后顺序是无关紧要的事)例如,
都小
j
于等于零时,可知 j xj 是一个小于等于零的数,要使z
jJ
的值最大,显然 j xj 只有为零。我们把这些xj取为非基 jJ
变量(即令这些xj的值为零),所求得的基本可行解就使目标 函数值最大为z0。
**对于求目标函数最小值的情况,只需把 j≤0改为 j≥0
.
§1 单纯形法的基本思路和原理
.
§1 单纯形法的基本思路和原理
我们把确定出基变量的方法概括如下:把已确定的入基变量在各约束方 程中的正的系数除以其所在约束方程中的常数项的值,把其中最小比值所 在的约束方程中的原基变量确定为出基变量。这样在下一步迭代的矩阵变 换中可以确保新得到的bj值都大于等于零。
在本例题中约束方程为
x1 x2 s1 300, 2x1 x2 s2 400, x2 s3 250.
B3 1 0 0
1 0 1
非基变量x1,s2为零。这时约束方程就变为基变量的约束方程:
.
§1 单纯形法的基本思路和原理
x2+s1=300, x2=400, x2+s3=250. 求解得到此线性规划的一个基本解: x1=0,x2=400,s1=-100,s2=0,s3=-150 由于在这个基本解中s1=-100,s3=-150,不满足该线性规划s1≥0, s3≥0的约束条件,显然不是此线性规划的可行解,一个基本解可以是 可行解,也可以是非可行解,它们之间的主要区别在于其所有变量的解 是否满足非负的条件。我们把满足非负条件的一个基本解叫做基本可行 解,并把这样的基叫做可行基。
§2 单纯形法的表格形式
迭代 基变
次数 量
cB
x1
x2
s1
50 100 0
ቤተ መጻሕፍቲ ባይዱs2
s3
0
0
比值
b
Bi/ai2
s1
0
s2
0
0
s3
0
1
1
1
2
1
0
0
1
0
0
0
1
0
0
1
zj
j cj zj
0
00
50 100 0
0
0
0
0
300
300/1
400
400/1
250
250/1
z=0
• 按照线性规划模型在表中填入相对应的值,如上表所示; • 在上表中有一个m*m的单位矩阵,对应的基变量为s1,s2,s3; • 在 z2=z0j行*1中+0填*1入+0第*1j列=0与,c所B列在中zi行对中应的的第元2素位相数乘填相入加0;所得的值,如 • 在 j c j z j 行中填入cj-zj所得的值,如 1 50 0 50 ; • z表示把初始基本可行解代入目标函数求得的目标函数值,即b列*cB列; • 初始基本可行解为s1=300,s2=400,s3=250,x1=0,x2=0; • 由于250/1最小,因此确定s3为出基变量; • 由 在于列的2 交 汇1 处0,为因主此元确,定这x里2为是入a32基=1变,量在。表出中基画变圈量以所示在区行别,。入基变量所
而其计算的方法也大体上使用矩阵的行的初等变换。以下用单纯形表格来
求解第二章的例1。
max 50x1+100x2+0·s1+0·s2+0·s3. x1+x2+s1=300, 2x1+x2+s2=400, x2+s3=250,
x1, x2, s1, s2, s3≥0. 把上面的数据填入如下的单纯形表格
.
的基变量s3为出基变量,这样可知x2,s1,s2为基变量,x1,s3为非基变量。 令非基变量为零,得
x2+s1=300, x2+s2=400, x2=250. 求解得到新的基本可行解x1=0,x2=250,s1=50,s2=150. 这时目标函数值为
50x1+100x2=50×0+100×250=25000。 显然比初始基本可行解x1=0,x2=0,s1=300,s3=250时的目标函数值为0要好 得多。
n
bi aij xj. i 1, 2,L , m
j m1
把以上的表达式带入目标函数,就有
m
n
z c1x1 c2 x2 L cn xn ci xi c j x j
i 1
j m 1
其中:
n
n
z0
c j z j x j z0 j x j
j m 1
j m 1
m
z0 cibi , j c j z j ;
a1 j
i1 m
z j ciaij c1a1 j c2a2 j L
i 1
cmamj
c1, c2 ,L
, cm
a2
j
M
amj
c1, c2 ,L , cm p j .
§2 单纯形法的表格形式
上面假设x1,x2,…xm是基变量,即第i行约束方程的基变量正好是xi,而 经过迭代后,基将发生变化,计算zj的式子也会发生变化。如果迭代后的 第i行约束方程中的基变量为xBi,与xBi相应的目标函数系数为cBi,系数列
在第一次找可行基时,所找到的基或为单位矩阵或为由单位矩阵的各 列向量所组成,称之为初始可行基,其相应的基本可行解叫初始基本可行 解。如果找不到单位矩阵或由单位矩阵的各列向量组成的基作为初始可行 基,我们将构造初始可行基,具体做法在以后详细讲述。
.
§1 单纯形法的基本思路和原理
二、 最优性检验 所谓最优性检验就是判断已求得的基本可行解是否是最优解。
单纯形法
• §1 单纯形法的基本思路和原理 • §2 单纯形法的表格形式 • §3 求目标函数值最小的线性规划的问题的
单纯形表解法 • §4 几种特殊情况
主讲人:
.
§1 单纯形法的基本思路和原理
单纯形法的基本思路:从可行域中某一个顶点开始,判断此顶点是否是最优 解,如不是,则再找另一个使得其目标函数值更优的顶点,称之为迭代,再判断此 点是否是最优解。直到找到一个顶点为其最优解,就是使得其目标函数值最优的 解,或者能判断出线性规划问题无最优解为止。
.
§1 单纯形法的基本思路和原理
非基变量:与非基向量pj相应的变量xj叫非基变量,非基变量有n-m个。 由线性代数的知识知道,如果我们在约束方程组系数矩阵中找到一个
基,令这个基的非基变量为零,再求解这个m元线性方程组就可得到唯一
的解了,这个解我们称之为线性规划的基本解。
在此例中我们不妨找到了 1 1 0 为A的一个基,令这个基的
.
§1 单纯形法的基本思路和原理
• 2.最优解判别定理
对于求最大目标函数的问题中,对于某个基本可行解,
如果所有检验数 j ≤0,则这个基本可行解是最优解。下面
我们用通俗的说法来解释最优解判别定理。设用非基变量
表示的目标函数为如下形式
z z0 j xj
由于所有的xj的取值范围为大jJ 于等于零,当所有的
A ( p1, p2 , p3 , p4 , p5 ) 2 1 0 1 0 0 1 0 0 1
其中pj为系数矩阵A第j列的向量。A的秩为3,A的秩m小于此方程组的变 量的个数n,为了找到一个初始基本可行解,先介绍以下几个线性规划的 基本概念。 基: 已知A是约束条件的m×n系数矩阵,其秩为m。若B是A中m×m阶非 奇异子矩阵(即可逆矩阵),则称B是线性规划问题中的一个基。 基向量:基B中的一列即称为一个基向量。基B中共有m个基向量。 非基向量:在A中除了基B之外的一列则称之为基B的非基向量。 基变量:与基向量pi相应的变量xi叫基变量,基变量有m个。
向量为 pj j 1, 2,L ,n 则
z j cB1,L , cBm pj cB pj ,
其中,(cB)是由第1列第m行各约束方程中的基变量相应的目标函数依 次组成的有序行向量。
单纯形法的表格形式是把用单纯形法求出基本可行解、检验其最优性、
迭代某步骤都用表格的方式来计算求出,其表格的形式有些像增广矩阵,
xj 0. j 1, 2,L , n
以下用 xi i 1, 2,L , m 表示基变量,用 xj j m 1, m 2,L , n
表示非基变量。
.
§2 单纯形法的表格形式
把第i个约束方程移项,就可以用非基变量来表示基变量xi, xi bi a x i,m1 m1 a x i,m2 m2 L ai,n xn
