二叉排序树 求树的深度 各个结点的深度
二叉排序树

9
第9章
第三节
二、二叉排序树(插入)
查找
动态查找表
二叉排序树是一种动态查找表
当树中不存在查找的结点时,作插入操作
新插入的结点一定是叶子结点(只需改动一个 结点的指针) 该叶子结点是查找不成功时路径上访问的最后 一个结点的左孩子或右孩子(新结点值小于或 大于该结点值) 10
第9章
第三节
查找
19
在二叉排序树中查找关 键字值等于37,88,94
3
第9章
第三节
查找
动态查找表
二、二叉排序树(查找函数)中结点结构定义 二叉排序树通常采用二叉链表的形式进行存 储,其结点结构定义如下:
typedef struct BiNode { int data; BiNode *lChild, *rChild; }BiNode,*BitTree;
4
第9章
第三节
查找
动态查找表
2、二叉排序树的定义 定义二叉排序树所有用到的变量 BitTree root; int
//查找是否成功(1--成功,0--不成功) //查找位置(表示在BisCount层中的第几个位置
BisSuccess;
int
int
BisPos;
BisCount;
//查找次数(相当于树的层数)
7
第9章
第三节
查找
动态查找表
二、二叉排序树(查找函数)
else { BisSuccess = 0; root=GetNode(k);//查找不成功,插入新的结点}
} BiNode * GetNode(int k) { BiNode *s; s = new BiNode; s->data = k; s->lChild = NULL; s->rChild = NULL; return(s);}
二叉排序树

②若*p结点只有左子树,或只有右子树,则可将*p的左子 树或右子树直接改为其双亲结点*f的左子树,即: f->1child=p->1child(或f->1child=p->rchild); free(p); *f
F *p P P1
*f
F
*f
F *p P
*f
F
Pr
P1
Pr
③若*p既有左子树,又有右子树。则:
-1 0
47
-1
47
47
0
31 69
69
25
0
47
0
25
0
47
-1 0
31
0
69
0
40
69
40
69
0
25 76
40
76
(a)
AL、BL、BR 都是空树
(b) AL、BL、BR 都是非空树
LR型调整操作示意图
2
A
-1
0
C
AR C BL CL CR AR
0 0
B BL CL S
B
A
CR
(a) 插入结点*s后失去平衡
31
0 0 -1
31
0 1
28
0
25
0 0
47
0
25
-1
47
0
25
0
31
0
16 0
28
16
28
0
16 30
30
47
(c) LR(R)型调整
RL型调整操作示意图
A B C A BR CR B BR
AL
C
AL
CL CR
详解平衡二叉树
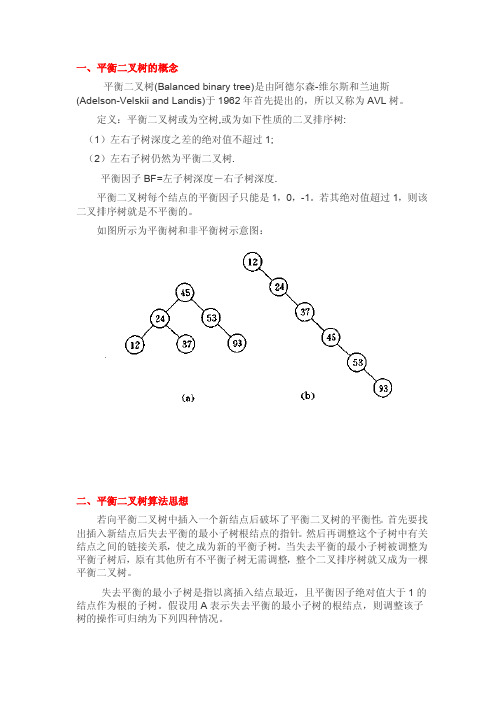
一、平衡二叉树的概念平衡二叉树(Balanced binary tree)是由阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出的,所以又称为AVL树。
定义:平衡二叉树或为空树,或为如下性质的二叉排序树:(1)左右子树深度之差的绝对值不超过1;(2)左右子树仍然为平衡二叉树.平衡因子BF=左子树深度-右子树深度.平衡二叉树每个结点的平衡因子只能是1,0,-1。
若其绝对值超过1,则该二叉排序树就是不平衡的。
如图所示为平衡树和非平衡树示意图:二、平衡二叉树算法思想若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。
首先要找出插入新结点后失去平衡的最小子树根结点的指针。
然后再调整这个子树中有关结点之间的链接关系,使之成为新的平衡子树。
当失去平衡的最小子树被调整为平衡子树后,原有其他所有不平衡子树无需调整,整个二叉排序树就又成为一棵平衡二叉树。
失去平衡的最小子树是指以离插入结点最近,且平衡因子绝对值大于1的结点作为根的子树。
假设用A表示失去平衡的最小子树的根结点,则调整该子树的操作可归纳为下列四种情况。
1)LL型平衡旋转法由于在A的左孩子B的左子树上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行一次顺时针旋转操作。
即将A的左孩子B向右上旋转代替A作为根结点,A向右下旋转成为B的右子树的根结点。
而原来B的右子树则变成A的左子树。
(2)RR型平衡旋转法由于在A的右孩子C 的右子树上插入结点F,使A的平衡因子由-1减至-2而失去平衡。
故需进行一次逆时针旋转操作。
即将A的右孩子C向左上旋转代替A作为根结点,A向左下旋转成为C的左子树的根结点。
而原来C的左子树则变成A的右子树。
(3)LR型平衡旋转法由于在A的左孩子B的右子数上插入结点F,使A的平衡因子由1增至2而失去平衡。
故需进行两次旋转操作(先逆时针,后顺时针)。
即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置,然后再把该D结点向右上旋转提升到A结点的位置。
2016年考研核心题型【数据结构部分】【第4章 树与二叉树】

其余的 b 和 c 结点都各有一个前驱结点和后继结点。
那么,将 d 右指针域(初始为空)调整并指向其后继结点 b。将 b 结点的左指针域调整
指向其前驱结点 d,因为 b 的右指针域不为空,所以线索化过程中不需要调整。c 的左右指
针域都为空,令其左指针域指向其前驱结点 b,右指针域指向其后继结点 a。
有在已知前序遍历序列或者后序遍历序列的情况下,又知道中序遍历序列,才能唯一确定
一棵二叉树。
遍历一棵二叉树,要使得前序遍历序列和后序遍历序列刚好相反,那么必须保证每一
个结点都只有一个孩子结点。故而,二叉树的高度为 4。那么,在前序遍历序列为 1、2、3、
4,后序遍历序列为 4、3、2、1 的情况下,该二叉树第 1、2、3、4 层的结点依次为 1、2、
【解析】对于某一种遍历顺序对应的线索化,只需写出对应的遍历序列,然后修改空
指针域分别指向该遍历序列的前驱和后继即可。例如,本题中的二叉树的后序遍历可得到
序列 d、b、c、a。那么,d 是第一个元素,没有前驱,所以其左指针域原来为空,线索化时
亦为空;a 是最后一个元素,但是其左右孩子都不为空,所以不需要考虑该结点的线索化;
24
13
53
37
90
48
图 4.4 插入新的结点 48 之后,我们沿着叶子结点 48 往根节点的路径上,查找第一个不平衡 的结点。显然,24 是第一个不平衡的结点,其左子树的高度为 1,右子树的高度为 3。图中 的粗线部分,即需要旋转的部分。 那么,造成了什么类型的不平衡呢?我们这样判断:53 是 24 右孩子(R),37 是 24 的左孩子(L),所以是 RL 型不平衡。于是,先把结点 24 的右孩子 53 的左孩子 37 向右上 方旋转到原来 53 的位置,再将 37 向左上旋转到 24 的位置,24 被旋转下来。成了如图 4.5 所示的样子。
二叉排序树

就维护表的有序性而言,二叉排序树无须移 动结点,只需修改指针即可完成插入和删 除操作,且其平均的执行时间均为O(lgn), 因此更有效。二分查找所涉及的有序表是 一个向量,若有插入和删除结点的操作, 则维护表的有序性所花的代价是O(n)。当 有序表是静态查找表时,宜用向量作为其 存储结构,而采用二分查找实现其查找操 作;若有序表里动态查找表,则应选择二 叉排序树作为其存储结构。
if(q->lchild) //*q的左子树非空,找*q的左子 树的最右节点r. {for(q=q->lchild;q->rchild;q=q->rchild); q->rchild=p->rchild; } if(parent->lchild==p)parent->lchild=p>lchild; else parent->rchild=p->lchild; free(p); /释放*p占用的空间 } //DelBSTNode
下图(a)所示的树,是按如下插入次序构成的: 45,24,55,12,37,53,60,28,40,70 下图(b)所示的树,是按如下插入次序构成的: 12,24,28,37,40,45,53,55,60,70
在二叉排序树上进行查找时的平均查找长度和二叉树的形态 有关: ①在最坏情况下,二叉排序树是通过把一个有序表的n 个结点依次插入而生成的,此时所得的二叉排序树蜕化为 棵深度为n的单支树,它的平均查找长度和单链表上的顺 序查找相同,亦是(n+1)/2。 ②在最好情况下,二叉排序树在生成的过程中,树的形 态比较匀称,最终得到的是一棵形态与二分查找的判定树 相似的二叉排序树,此时它的平均查找长度大约是lgn。 ③插入、删除和查找算法的时间复杂度均为O(lgn)。 (3)二叉排序树和二分查找的比较 就平均时间性能而言,二叉排序树上的查找和二分查找 差不多。
数据结构二叉排序树

05
13
19
21
37
56
64
75
80
88
92
low mid high 因为r[mid].key<k,所以向右找,令low:=mid+1=4 (3) low=4;high=5;mid=(4+5) div 2=4
05
13
19
low
21
37
56
64
75
80
88
92
mid high
因为r[mid].key=k,查找成功,所查元素在表中的序号为mid 的值
平均查找长度:为确定某元素在表中某位置所进行的比 较次数的期望值。 在长度为n的表中找某一元素,查找成功的平均查找长度:
ASL=∑PiCi
Pi :为查找表中第i个元素的概率 Ci :为查到表中第i个元素时已经进行的比较次数
在顺序查找时, Ci取决于所查元素在表中的位置, Ci =i,设每个元素的查找概率相等,即Pi=1/n,则:
RL型的第一次旋转(顺时针) 以 53 为轴心,把 37 从 53 的左上转到 53 的左下,使得 53 的左 是 37 ;右是 90 ,原 53 的左变成了 37 的右。 RL型的第二次旋转(逆时针)
一般情况下,假设由于二叉排序树上插入结点而失去 平衡的最小子树的根结点指针为a(即a是离插入结点最 近,且平衡因子绝对值超过1的祖先结点),则失去平衡 后进行调整的规律可归纳为下列四种情况: ⒈RR型平衡旋转: a -2 b -1 h-1 a1
2.查找关键字k=85 的情况 (1) low=1;high=11;mid=(1+11) / 2=6
05
13
19
21
东北大学历年初试考研真题分享
21115
196
3314
186
5、(方向移动,试举例说明之。快速排序中有没有这种现象?
二、(15分)设有一个由正整数组成的无序(向后)单链表,编写完成下列功能的算法:
1、找出最小值结点,且打印该数值;
2、若该数值是奇数,则将其与直接后继结点的值交换;
3、若该数值是偶数,则将其直接后继结点删除;
三、(14分)解答下列问题:
1、(4分)将算术表达式((a+b)+c*(d+e)+f)*(g+h)转化为二叉树;
2、(10分)假设一个仅包含二元运算符的算术表达式以链表形式存储在二叉树b1中,写出计算该表达式值的算法。
四、(21分)解答下列问题:
1、(5分)画出有向图十字链表存储结构中头接点和表结点的结点结构。
5、设有1000个无序的元素,希望用最大的速度挑选出其中前十个最大的元素,在以下的方法中采用哪一种最好?为什么?(3分)
(快速排序,归并排序,堆排序,基数排序,shell排序)
二、(10分)两个正数序列A=a1,a2,a3,…..am和B=b1,b2,b3,…bn已经存入两个单链表中,设计一个算法,判别序列B是否是序列A的子序列。
(1)、构造出散列函数;(3分)
(2)、计算出等概率情况下查找成功的平均查找长度;(3分)
(3)、计算出等概率情况下查找失败的平均查找长度;(3分)
4、判别一下序列是否为堆,若不是,则把他调整为堆。
(1)(100,86,48,73,35,39,42,57,66,21)(4分)
(2)(12,70,33,65,24,56,48,92,86,33)(4分)
(4)在m阶B一树中每个结点上至少┌m/2┐有个关键字最多m有个关键字。
《数据结构与算法设计》树-习题
• 已知二叉树 – 先序序列为:ABCDEF – 中序序列为:CBAEDF • 请画出该二叉树。
A
B
C E
D
F
9
A
D
10
• 已知二叉树 – 中序序列为:ABCEFGHD – 后序序列为:ABFHGEDC • 请画出该二叉树。 – 中序:LDR A – 后序:LRD A B C E F G H D A B F H G E D C
swap(b->rchild );
}
交换左右子树
15
• 请指出下列函数的功能
void preserve(BiTNode *b, ElemType a[], int n){
static int i = 0; if(b != NULL) { preserve(b->lChild, a,n); a[i++] = b->data;
preserve(b->rChild, a,n);
} }
得到二叉树b的中序遍历序列,结果放在数组a中
16
2005考研试题
根据______可以唯一地确定一棵二叉树。 A. 先序遍历和后序遍历 B. 先序遍历和层次遍历 C. 中序遍历和层次遍历 D. 中序遍历和后序遍历
D. 中序遍历和后序遍历
所有分支结点的度为2的二叉树称为正则二叉树,试 用二叉链表做存储结构,编写一递归函数int FormalTree(Bitree t),判断二叉树是否为正则二叉树。 int FormalTree(Bitree t) { if (t == NULL) return 1; if ((t->lchild == NULL) && (t->rchild == NULL)) return 1; if ((t->lchild == NULL) || (t->rchild == NULL)) return 0; return (FormalTree(t->lchild)) && (FormalTree(t->rchild)); }
2014第一学期数据结构复习题
7数据结构复习题一、填空题(1)若已知一个栈的输入序列为1 ,2, 3 ,...n ,其输出序列为p1,p2,p3,....pn。
若p1=n,则pi为n-i+1。
(2) 在单循环链表中,指针p 所指结点为最后一个结点的条件是p->link==first。
(3)具有32有结点的完全二叉树的深度为 6 。
(4) L是带有头结点的单链表的头指针,第一个元素结点的指针是 first 。
(5)从逻辑关系上讲,数据结构主要分为两大类,它们是线性结构和非线性结构。
(6)有序表中元素为1,2,3,4,5,6,7,8,9.11采用二分查找方法进行查找,共有 2 个元素的查找长度为2。
(7)从无向图中的某个顶点出发,进行一次广度优先搜索,即可访问图的每个顶点,则该图一定是连通图。
(8)归并排序的时间复杂性为O(nlog2n)。
(9) 在一个长度为n的顺序表中删除第m个元素时,需向前移动n-m个元素。
(10) 多维数组实际上是由__一维数组的扩展实现的。
(11) 链接存储的特点是利用__指针___来表示数据元素之间的逻辑关系。
(12) 后缀表达式“4 5 * 3 2 + -”的值为__ 15______。
(14) 一个算法的复杂性可分为_ 时间 ___复杂性和空间复杂性。
(16) 在一棵树中,叶结点没有后继结点。
(17)(18) 在单链表中,指针p 所指结点为最后一个结点的条件是p->next=NULL。
(19) 栈是一种限定在表的一端进行插入和删除的线性表,又被称为后进先出的线性表。
(20) 设图G=(V,E),V={1,2,3,4}, E={<1,2>,<1,3>,<2,4>,<3,4>,<2,3>},从顶点1出发,对图G进行广度优先搜索的序列有___2 __种。
(21)已知一棵度为3的树有2个度为1的结点,3个度为2的结点,4个度为3的结点,则该树中有_____ 12_______ 个叶子的结点。
二叉树
平衡树——特点:所有结点左右子树深度差≤1排序树——特点:所有结点―左小右大字典树——由字符串构成的二叉排序树判定树——特点:分支查找树(例如12个球如何只称3次便分出轻重)带权树——特点:路径带权值(例如长度)最优树——是带权路径长度最短的树,又称Huffman树,用途之一是通信中的压缩编码。
1.1 二叉排序树:或是一棵空树;或者是具有如下性质的非空二叉树:(1)若左子树不为空,左子树的所有结点的值均小于根的值;(2)若右子树不为空,右子树的所有结点均大于根的值;(3)它的左右子树也分别为二叉排序树。
例:二叉排序树如图9.7:二叉排序树的查找过程和次优二叉树类似,通常采取二叉链表作为二叉排序树的存储结构。
中序遍历二叉排序树可得到一个关键字的有序序列,一个无序序列可以通过构造一棵二叉排序树变成一个有序序列,构造树的过程即为对无序序列进行排序的过程。
每次插入的新的结点都是二叉排序树上新的叶子结点,在进行插入操作时,不必移动其它结点,只需改动某个结点的指针,由空变为非空即可。
搜索,插入,删除的复杂度等于树高,期望O(logn),最坏O(n)(数列有序,树退化成线性表).虽然二叉排序树的最坏效率是O(n),但它支持动态查询,且有很多改进版的二叉排序树可以使树高为O(logn),如SBT,AVL,红黑树等.故不失为一种好的动态排序方法.2.2 二叉排序树b中查找在二叉排序树b中查找x的过程为:1. 若b是空树,则搜索失败,否则:2. 若x等于b的根节点的数据域之值,则查找成功;否则:3. 若x小于b的根节点的数据域之值,则搜索左子树;否则:4. 查找右子树。
[cpp]view plaincopyprint?1.Status SearchBST(BiTree T, KeyType key, BiTree f, BiTree &p){2. //在根指针T所指二叉排序樹中递归地查找其关键字等于key的数据元素,若查找成功,3. //则指针p指向该数据元素节点,并返回TRUE,否则指针P指向查找路径上访问的4. //最好一个节点并返回FALSE,指针f指向T的双亲,其初始调用值为NULL5. if(!T){ p=f; return FALSE;} //查找不成功6. else if EQ(key, T->data.key) {P=T; return TRUE;} //查找成功7. else if LT(key,T->data.key)8. return SearchBST(T->lchild, key, T, p); //在左子树继续查找9. else return SearchBST(T->rchild, key, T, p); //在右子树继续查找10.}2.3 在二叉排序树插入结点的算法向一个二叉排序树b中插入一个结点s的算法,过程为:1. 若b是空树,则将s所指结点作为根结点插入,否则:2. 若s->data等于b的根结点的数据域之值,则返回,否则:3. 若s->data小于b的根结点的数据域之值,则把s所指结点插入到左子树中,否则:4. 把s所指结点插入到右子树中。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ls[i] =0; rs[i] = 0;//每次进栈的新结点,其左子树和右子树均为访问
num++;if(max <=num) max =num;
}
if(( T->left ==NULL && T->right && rs[i] ==0 ) || (ls[i] ==1 && T->right&& rs[i] ==0 ) )
{
tree T = p; int i; tree q[100]; i =1; q[0]= T;int k ; k = 0;
int rs[100];int ls[100]; int j; int num =1; int max=1;
for(j=0; j<100 ;j++)
{
rs[j] =0;ls[j] =0;
//printf("\n");
AllTreeDepth(p);
printf("\n");
}
else { tmp = T; T= T->left; sign =0;}
if(T ==NULL && sign == 1) { tmp ->right = q;}
if(T ==NULL && sign == 0) { tmp ->left = q;}
}
}
int TreeDepth(tree p)//统计"根“的深度
printf("结点值为%d的深度:%d\n",q[i]->data,TreeDepth(q[i]));
}
if(( T->left ==NULL && T->right && rs[i] ==0 ) || (ls[i] ==1 && T->right&& rs[i] ==0 ) )
{
T = T->right;
{
q[i] = T;
printf("结点值为%d的深度:%d\n",q[i]->data,TreeDepth(q[i]));
}
while(T->left && ls[i] == 0)
{
T =T->left;
ls[i] = 1;
i++; q[i] = T;k++;
ls[i] =0; rs[i] = 0;
p->data = num; p->left =NULL; p->right =NULL;
int i;
for(i=1; i<=4;i++)
{scanf("%d",&num); InsertTree(p,num);}
printf("\n");
printf("树的深度为:%d\n",TreeDepth(p));
{
tree T = p; int i; tree q[100]; i =1; q[0]= T;int k ; k = 0;
int rs[100];int ls[100]; int j;
for(j=0; j<100 ;j++)
{
rs[j] =0;ls[j] =0;
}
while( i != 0)
{
if(i==1 && k == 0)
#include <stdio.h>
#include <stdlib.h>
typedef struct Tree
{
int data;
struct Tree *left;
struct Tree *right;
}*tree;
void InsertTree(tree p,int num)
{
tree T; T = p; int i; int sign;
||(T->right ==NULL && ls[i] == 1 ) ||( rs[i] ==1&& ls[i] == 1 ) )
{
iபைடு நூலகம்-; k++; num--;
T = q[i];
}
}
return max;
}
void AllTreeDepth(tree p)//所有“结点”的深度,利用“每个结点“重新作为”根“,重复运用”求根的深度“函数则可…
}
while( i != 0)
//采取先序遍历的方法,依次进栈、出栈(进栈的数目最大值则为:根的深度)
{
if(i==1 && k == 0)
{
q[i] = T;
}
while(T->left && ls[i] == 0)
{
T =T->left;ls[i] = 1;//访问了当前结点的左结点,则标记Ls[i]=1;
||(T->right ==NULL && ls[i] == 1 ) ||( rs[i] ==1&& ls[i] == 1 ) )
{
i--; k++;
T = q[i];
}
}
}
void main()
{
tree p =NULL; int num; scanf("%d",&num);
p =(tree) malloc( sizeof(struct Tree) );
rs[i] =1;
k++;
i++;q[i] = T;
ls[i] =0; rs[i] = 0;
printf("结点值为%d的深度:%d\n",q[i]->data,TreeDepth(q[i]));
}
if( (T->left ==NULL && rs[i] == 1 ) ||(T->left ==NULL && T->right == NULL)
{
T = T->right; rs[i] =1;//访问了当前结点的右结点,则标记Rs[i]=1;
k++;i++;q[i] = T;
ls[i] =0; rs[i] = 0;
num++;if(max <=num) max =num;
}
if( (T->left ==NULL && rs[i] == 1 ) ||(T->left ==NULL && T->right == NULL)
i=0; tree q,tmp;
q =(tree ) malloc( sizeof(struct Tree) );
q->data = num; q->left =NULL; q->right =NULL;
while(T)
{
if(num > T->data ) { tmp = T; T= T->right;sign =1;}
