矩阵理论研究生课程大作业
考博必备 研究生矩阵理论课后答案矩阵分析所有习题共73页

3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
矩阵论大作业

“矩阵论”课程研究报告科目:矩阵理论及其应用教师:姓名:学号:专业:机械设计及理论类别:上课时间: 2013年2月至2013年5月考生成绩:阅卷评语:阅卷教师(签名)利用矩阵论相关知识求解传动轴固有频率的有限元分析法摘要:在结构力学中,求解结构自由振动的固有频率是十分重要的内容。
本文通过对某机器传动轴各个单元进行单元刚度矩阵、单元质量矩阵等特性分析,再把各个单元的特性矩阵组集起来组成结构的总刚度矩阵、总质量矩阵,从而形成结构的自由振动方程式。
最后利用矩阵论相关知识求解自由振动方程式的广义特征值,并通过广义特征值与固有频率的关系求得传动轴的固有频率。
正文一、问题描述已知某机器传动轴两端固定,其传动轴受扭长度L为1500mm,传动轴的横截面积是环形,其外径D为50mm,内径d为45mm,弹性模量E为52。
利2.110/N mm用矩阵论及有限元分析法求解传动轴的固有频率。
二、方法简述1.建立传动轴的有限元分析模型由于传动轴两端固定,采用平面梁单元分析该传动轴。
考虑到本次计算是手算,为了简化计算,将该传动轴划分为(1)、(2)两个单元,共1、2、3三个结点。
由于该结构中一个结点有两个自由度,故总共有1、2、3、4、5、6六个自由度。
建立有限元分析模型及各个部分编号如图1所示。
图1 传动轴有限元分析模型2.平面梁单元的单元刚度矩阵由《机械结构有限元分析》[1]中形状函数N 的构造方法可知,对于该结构的平面梁单元,它有两个节点,四个自由度,采用自然坐标系,通过构造计算可得单元的形函数为()()()()v iiv j j N N N N N θθ⎡⎤=⎣⎦23232332(132)(2)(32)()ξξξξξξξξξ⎡⎤=-+-+--⎣⎦ (1)其中,i j 为结点编号,v 为结点位移,θ为结点转角,xlξ=,l 为梁单元的长度。
平面梁单元的单元刚度矩阵T lk E I B B d x=⎰ (2) 其中E 为弹性模量,I 为惯性矩。
中科院矩阵分析与应用大作业

中科院矩阵分析与应用大作业1. 研究背景矩阵是数学领域中的重要概念之一,它在各个领域中都有广泛的应用。
在计算机科学中,矩阵常常用于图像处理、计算机视觉等领域;在数据分析中,矩阵则被用来描述数据之间的关系。
因此,深入研究矩阵的相关算法和应用,对于提高计算机科学和数据分析领域的研究水平具有重要意义。
2. 研究目的本次研究的主要目的是掌握矩阵分析的基本概念和相关算法,并将其应用于实际问题中,进一步提高对于矩阵分析的理解和应用能力。
3. 研究内容3.1 矩阵分解矩阵分解是矩阵分析中的一项重要任务,它将一个矩阵分解成为多个小的矩阵,从而更方便的进行处理。
常见的矩阵分解算法有:1.奇异值分解(SVD)2.QR分解3.LU分解4.特征值分解3.2 矩阵重构矩阵重构是指将矩阵进行转换、组合等操作,旨在从不同的角度探索和发现矩阵的内在规律。
常见的矩阵重构算法有:1.矩阵乘法2.矩阵转置3.矩阵拼接4.矩阵切片3.3 矩阵应用矩阵在各个领域的应用非常广泛,下面列举几个常见的应用场景:1.图像处理:将图像转化成为矩阵,对其进行矩阵分解、矩阵重构等操作,从而实现图像降噪、图像识别等功能。
2.推荐系统:利用矩阵分解的方法将原始数据转化为矩阵,再对其进行推荐系统的处理,从而为用户提供更好的推荐服务。
3.聚类分析:将大量数据转化为矩阵,从而利用聚类算法对其进行分析,发现数据之间的关系,进一步深入研究数据的内在规律。
4. 研究通过对于矩阵分解、矩阵重构、矩阵应用等领域的研究,我们可以得到以下:1.奇异值分解、QR分解、LU分解、特征值分解等矩阵分解算法各有优缺点,在实际应用中应该根据具体情况选用不同的算法。
2.矩阵乘法、矩阵转置、矩阵拼接、矩阵切片等矩阵重构算法可以帮助我们从不同的角度分析和处理矩阵,从而深入研究矩阵的内在规律。
3.矩阵在图像处理、推荐系统、聚类分析等领域有着广泛的应用,掌握矩阵分析算法可以帮助我们更好地解决实际问题。
研究生矩阵理论课后答案4,5章习题
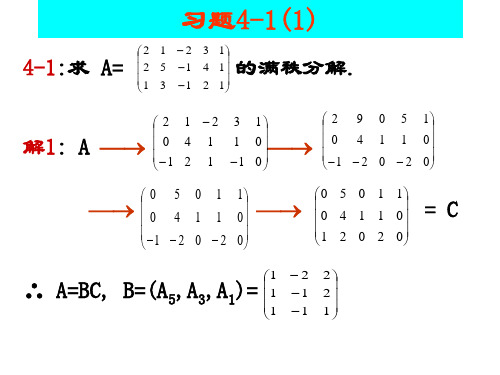
2 1 − 2 3 1 0 4 1 1 0 −1 2 1 −1 0
0 5 0 1 1 0 4 1 1 0 −1 −2 0 −2 0
→
1 1 1 −2 −1 −1
0 5 0 1 1 0 4 1 1 0 1 2 0 2 0
同一向量的三种范数之间的大小关系 习题#5-4:对n维线性空间的任意向量x成 习题#5维线性空间的任意向量x #5
‖x‖∞ ≤‖x‖2 ≤‖x‖1 ≤ n‖x‖∞ ≤ n‖x‖2 ≤ n‖x‖1 ≤ n2‖x‖∞ ≤ …
立
证: |,…,|x ‖x‖∞= max{|x1|, ,|xn|} ≤(Σi=1n|xi|2)1/2 = ‖x‖2 |+…+|x ≤((|x1|+ +|xn|)2)1/2 = ‖x‖1 |,…,|x ≤ n max{|x1|, ,|xn|} = n‖x‖∞
习题#5是正定矩阵,x ,x∈ 习题#5-6A∈Cn×n是正定矩阵,x∈Cn #5
是向量范数. •证明:‖x‖=(x*Ax)1/2 是向量范数. 证明:‖x‖=(x
解1:因A是正定Hermite矩阵A,故存在可逆矩阵B 是正定Hermite矩阵A,故存在可逆矩阵B Hermite矩阵A,故存在可逆矩阵 使得A=B B.则 的上述表示式可写为: 使得A=B*B.则x的上述表示式可写为: (Bx)) ‖x‖=(x*Ax)1/2 =((Bx)*(Bx))1/2 =‖Bx‖2 其中‖‖ 是向量2 范数.再注意可逆矩阵B 其中‖‖2 是向量2-范数.再注意可逆矩阵B的性 Bx=0,即可直接推出非负性 即可直接推出非负性. 质:x=0 ⇔ Bx=0,即可直接推出非负性. ‖kx‖=‖B(kx)‖2=|k|‖Bx‖2=|k|‖x‖ 推出齐次性;三角不等式则由下式推出: 推出齐次性;三角不等式则由下式推出: ‖x+y‖=‖B(x+y)‖2≤‖Bx‖2+‖By‖2
研究生矩阵论课后习题答案(全)习题二

习题二1 2 (1)J 1 2 2 20 0 0 0 0 2(2)0 ( 1)2 02 0 03 2 2 3 2 1 (3)4 235 322422343 6(4) 0611 3 3 1 22解:( 1) 对矩阵 作初等 变换1 2c 1 c31 22 21 0 0c 22c 1 0c3 c 10 0(1) 则该矩阵为 Sm ith 标准型为1.化下列矩阵为 Smith 标准型: 20 0 02 2 323 4;11 222 00 00 01212r3r 02 2r11001 0c 3 c2 r 1( 1)0,0 0( 1)( 1)2)矩阵的各阶行列式因子为 D 4( )4( 1)4,D 3( )( 1)2( 1)2,D 2( ) ( 1),D 1( ) 1,从而不变因子为 1)4() D 3() D 2()1),d 4()D 4() D 3()2(1)1 0 0 (1)0 00 0(3)对矩阵作初等变换3 2 2 3 2 1 22 3 4 235 3 2234 242 147 263r 2 r1片(22)「32 1 2247 2 632q ( 2)03 °? ( 2)C3213213q ( 1)°2321 0H ( 25) r 2r 1 ( 1)0 d i ( ) 1阳)D 2^-)( D i () 故该矩阵的Smith 标准型为 故该矩阵的Smith 标准型为0 0 0 0 (1) 02 20 ( 1)3 2 2 21 22 C 1 03“4 2 3 322222 2 12 245 010 2 1 2 245 0 10 0 1 2 245 01 010 10 01 0r 1r 31C 30 1 010 (1)2(111(1)2( 1)(4)对矩阵作初等变换2 3 01143 62 2 C l2 C52 2 062 0 C2 3C 32 01 010 110 3 31223 3 12 20 10 01C 1 3C 2 02 2 「2 2r 10 C 3 2C 220 C 3 C 1211 0 010 00 0110 1 01 0「12C30 0 0 02C1C40 2C 40 0C2C50 01 0 0 0 00 0 01 00 10 0 00 00 1在最后的形式中,可求得行列式因子11;(2);1 01;(32 1 0(1) 0 2 11 0 0 00 1 0 00 0 10 0 0 (1)0 0 0 02•求下列矩阵的不变 :因子:故该矩阵的Smith 标准形为0 0 02( 1)D 5( ) 3( 1)2,D 4()1),D 3() D 2( ) D !( ) 1, D 4()1),d 5() D 5()D 4() 2( 1)于是不变因子为0 0 15 4 3 20 0 1 20 1 2 0(4) 1 2 0 0.2 0 0 0解:1)该矩阵的右上角的 2 阶子式为 1,故(D1( ) D2( ) 1,而D3( ) ( 2)3,所以该矩阵的不变因子为d1( ) d2( ) 1,d3( 2) ( 2)2;(2)当0由于时,D4( ) ( )4,D3( ) () 2,D2( ) D1( ) 1,故不变因子为d1( ) d2( ) 1,d3( )()2,d4( ) ( )2当0 时,由于D4( ) [( )2 2] ,且该矩阵中右上角的 3 阶子式为2( ),且( 2( ),D4( )) 1,则 D 3( ) 1,故 D 2( ) D 1( ) 1 ,所以该 矩阵的不变因子为22 d 1( ) d 2( ) d 3( ) 1, d 4( ) [()22];3)该 矩阵的右上角的 3 阶子式为 1,故D 1( ) D 2( )D 3( ) 1,而D 4 ( ) 4233 245 ,所以该矩阵的不变因子为d 1( ) d 2( ) d 3( )1, d 4( ) 4 2 3 3 2 45;(4)该矩阵的行列式因子为D 1( ) D 2( )D 3()1,D 4( ) ( 2)4,所以该矩阵的不变因子为d 1( ) d 2( )d 3()41, d 4( ) ( 2)4 .3.求下列 矩阵的初等因子:3231(1)2323 2 32;2(2)3222 1 22 1232 2 2 1 222解:(1)该矩阵的行列式因子 为D 1( ) 1 ,D 2()2( 1)( 1)2 ,故初等因子为1,( 1)2;故不变因子为(2) 该矩阵的行列式因子为D 1( )1,D 2(1)( 1)2, d 1( ) 1,d 2( ) ( 1)( 1),解:( 1)设该矩阵为 A ,则1 0 0E A 0 10,0 0(1)2( 3)故 A 的初等因子为(1)2( 3),则 A 的 Jordan 标准形为300 0 1 1 0 0 12)设该矩阵为 A ,则1 0 0EA0 1 0,0 0( 1)3故 A 的初等因子为( 1)3 , 从而 A 的 Jordan 标准形为110 0 1 1 ; 00113 16 16 4 52 3 731)5 76 ;(2) 2 2 1; ( 3) 2 5 26871 1 14 1031 2 3 41 1 10 33 0 1 2 3 4) 3 3 3 ;(5) 18 6 ;(6)0 0 1 22 2 221410 0 0 0 14.求下列矩阵的 Jordan 标准形:1 0 0EA 0 1 00 0 (1)( 2 1) 故A 的初等因子为1i ,i,,从而A 的 Jordan 标准形为1 0 00 i 0 J0 0 i(4)设该矩阵为A ,则1 0 0E A 0 0,0 0 2故A 的初等因子为2从而A 的 Jordan 标准形为0 0 00 0 1 J0 0 0(5)设该矩阵为A,则1 0 0EA 0 1 00 0( 1)2故A 的初等因子为,( 1)2,从而A 的 Jordan 标准形为(6)设该矩阵为A ,则E A该矩阵的各阶行列式因子为D i ( ) D 2( 则不变因子为d i ( ) d 2(故初等因子为0 01 1 ;0 0112 3 41 230 1 21)D 3() 1,D 4()( 1)4,)d 3( ) 1,d 4() ( 1)4,(1)4,110 0 0 110 00 1 1.0 0 0 1故A 的特征值为11, 5.则A 的Jordan 标准形为5•设矩阵属于特征值 1 1的特征向量为 1 (1,0,0) T,求 A 的 Jordan 标准形 J,并求相似变换矩阵P ,使得 1P 1AP J .解 :(1) 求 A 的 Jordan 标准形 J .2111 00IA2 1 20 101120 ( 1)故其初等因子为1,(1)2,故 A 的 Jordan 标准形1 0 0J0 1 1.0 0 1(2)求相似变换矩阵 P . 考虑方程组属于2 35 的特征向量为 设P [ 1, 2, 3] 则 A P P 1.,故A 5 P 5P 16.设矩阵A2(2,1,2)T , 3(1, 2,1)T.12 1 1 0 0 01 2 , 0 5 0 , 02 10 0 5441 4 54 3 54 1440 3 54 4 54440 4 54 3 542 1 1 2 1 2 ,11 1 x1(I A)X 0, 即2 2 2 x2 0,11 1 x3解之 ,得1 0X1 0 ,X2 1.1 1其通解为k1k1X1 k2 X2=k2Jk1 k2其中k i,k2为任意常数考虑方程组1 11 x1 k12 22 x2 k211 11 x3k1 k21 1 1 k1 1 1 1 k12 2 2 k2 0 0 0 2k1 k21 1 1 k1 k2 0 0 0 2k1 k2 故当2k1 k2 0 时,方程组有解 .取k1 1,k2 2 ,解此方程组 ,得X3 01则相似变换矩阵1 0 0P [X1,X2,X3] 0 1 01 1 17•设矩阵试计算2A8 3A5A A2 4I .解:矩阵A的特征多项式为f A() I A 3 2 1, 由于2 83 54 2 4 ( 3 202 1)f( ) (24 3710)其中f( ) 2 5 4 3 5 29 14.且A3 2A I O, 故证明:设矩阵A的特征多项式为f A() I A n na1 1 na22 L an 1a n3 48 262A8 3A5 A4 A2 4I=24A2 37A 10I 0 95 610 61 34 8•证明:任意可逆矩阵A的逆矩阵A 1可以表示为A的多项式则A n a1A n 1a2A n 2 L a n 1A a n I O, 即A(A n1 a1A n 2 區n 3a?A L a n 1I) a n I , 因为A可逆,故a n ( 1)n A 0,则11n 1 n 2 n 3A(A a i A a ?A L a n J)a n9•设矩阵2 1A,1 3试计算(A 45A 36A 26A 8I) 1.解:矩阵A 的特征多项式为f A ( ) | I A 257,则A 2 2A 7I O ,而故143211111 21(A 5A 6A 6A 8I) (A I )-23 1 1解:矩阵A 的特征多项式为f A ( ) I A (1)( 1)( 2),则设由 f (1) 0, f( 1) 0, f (2) 0,得a b c 1, a b c 1,2n4a2b c 2 .解之,得7)( 21)1,10.已知3阶矩阵A 的三个特征值为11,2,试将A 2n表示为A 的二次式.2n2f( )g( ) a bc ,a 3(22n 1),b °,c£(22n 4), 33因此A 2n aA bA cI -(22n 1)A 2 ^(22n 4)I 3 3(3) n 阶单位阵I n 的最小多项式为 m() ⑷因为3 1 14 2 2 (1) 0 2 0 ;( 2)5 7 5 1 1 16 7 4a 。
研究生矩阵理论课后答案第6-7章

求矩阵的Jordan标准形与变换矩阵 求矩阵的Jordan标准形与变换矩阵 Jordan
由行列式因子定不变因子和初等因子:( :(参看 ①由行列式因子定不变因子和初等因子:(参看 0 λ − 2 0 第二章有关定义及结果). ).如 第二章有关定义及结果).如 λE-A= −1 λ −1 −1 )=λ行列式因子:D 行列式因子:D1(λ)=1; D2(λ)=λ-2;
第六章 矩阵函数
•矩阵函数一般定义:矩阵函数是从Cm×n到Cu×v的一 矩阵函数一般定义:矩阵函数是从C 个对应规则f:C 使对每个x 个对应规则f:Cm×n→Cu×v,使对每个x∈Cm×n,都 对应于唯一 f(x)∈ 唯一的 对应于唯一的f(x)∈Cu×v. 例如:det:C ,det(A)∈ 例如:det:Cn×n→C1×1,∀A∈Cn×n,det(A)∈C1×1; ,f(A)=2Af:Cn×n→Cn×n,∀A∈Cn×n,f(A)=2A-E∈Cn×n. 矩阵函数的概念十分广泛, •矩阵函数的概念十分广泛,其应用也相应地十分 广泛. 广泛. 我们仅限于讨论从C •我们仅限于讨论从Cn×n到自身的函数 f:Cn×n→Cn×n. 特别更限于最简单的矩阵多项式函数和由矩阵 矩阵多项式函数和由 特别更限于最简单的矩阵多项式函数和由矩阵 幂级数定义的矩阵函数. 幂级数定义的矩阵函数.
0 1 1 1 0 0 1 0 −1
. P -1=
0 1 0 1 −1 1 0 1 − 1
2 0 0 2 0 0 0 A − 2E = 1 1 1 − 2 = 1 −1 1 1 −1 3 2 1 −1 1 0 0 x = 1 , ( A − 2E)x = 1 1 1 1 0 z = 0 , ( A − 2E)z = 1 −1 1 0 00 −1 1 1 = 0 −1 1 1 0 0 1 −1 1 0 = 0 −1 1 −1
研究生矩阵论课后习题答案(全)习题一

i =1 j =1 n n
成的线性空间的一组基,该线性空间的维数是
n(n + 1) . 2
② 令 Gij = Eij − E ji (i < j ) , 则 Gij 是 反 对 称 矩 阵 , 易 证
解
(1)设 Eij 是第 i 行第 j 列的元素为 1 而其余元素全为 0 的 n 阶方阵.
①令 Fij = ⎨
⎧ Eii , i = j , 则 Fij 是对称矩阵, 易证 F11 ,L , F1n , F22 , L , F2 n , ⎩ Eij + E ji , i ≠ j
L , Fnn 线 性 无 关 , 且 对 任 意 n 阶 对 称 矩 阵 A = (aij ) n×n , 其 中 aij = a ji , 有
1(1 − 1) 2 a ) = ( a, b) 2
= k o ( a, b) + l o ( a, b) = k o α + +l o α ;
⑧ k o (α ⊕ β ) = k o (a + c, b + d + ac)
k (k − 1) (a + c) 2 ) 2 k (k − 1) 2 k (k − 1) 2 = (ka + kb, (kb + a ) + (kd + c ) + (ka)(kc)) 2 2 k (k − 1) 2 k (k − 1) 2 = (ka, kb + a ) ⊕ (kc, kd + c ) 2 2 = (k (a + b), k (b + d + ac) +
矩阵大作业

(由于图形是利用工程制图软件 CAXA 完成的,所以比较粗陋。上边是机翼模型,下边 是其简化模型。图中标注部分的长度均为������⁄2,两个质点的集中质量均为������,左边质点的位 移设为������1,右边质点位移设为������2,方向均向上。) 基本术语
=
1 2
[������̇1
������̇2] [���0���1
���0���2] [������������̇̇12]
U
=
1 2
[������1
������2] [������������1211
������������1222] [������������12]
将动能、势能代入拉格朗日方程,即可得到二自由度系统的运动方程:
矩阵特征值与特征向量在振动力学中 求解多自由系统阵型的应用
报告人信息 姓名:侯怡鑫 学号:20153113019 组序:5 组 学院:航空航天学院
摘要 工程中的动力系统基本都包含多个自由度,对于多自由度系统的振动求解问题需要用到
微分方程组的求解,而矩阵作为一个强有力的数学工具,在这方面发挥着重要的作工程模型,运用矩阵论的理论知识求解 微分方程组,再结合初始条件与边界条件,最终确定出系统各阶振动形态。 题目内容
固有频率:系统在自身物理性质确定的情况下,振动的频率是固定的,不随外界条件改 变,称之为固有频率。多自由度系统的自由度数目对应着固有频率的个数,最小的固有频率 为该系统的基频。
主振型:多自由度系统中,每一个固有频率都对应着一个单自由度的振动,当该振动的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
研究生“矩阵论”课程课外作业
姓名:学号:
学院:专业:
类别:组数:
成绩:
人口迁移问题和航班问题
(重庆大学 机械工程学院,机械传动国家重点实验室)
摘要:随着人类文明的进程,一些关于数学类的问题越来越贴近我们的生活,越发觉得数学与我们息息相关。
本文将利用矩阵理论的知识对人口迁移问题和航班问题进行分析。
人口迁移问题
假设有两个地区——如南方和北方,之间发生人口迁移。
每一年北方50%的人口迁移到南方,同时有25%的南方人口迁移到北方,直观上可由下图表示:
问题:如果这个移民过程持续下去,北方的人会不会全部都到南方?如果会请说明理由;如果不会,那么北方的最终人口分布会怎样?
解 设n 年后北方和南方的人口分别为n x 和n y , 我们假设最初北方有0x 人,南方有0y 人。
则我们可得,1=n 时,一年后北方和南方的人口为
⎩⎨⎧+=+=0
010
0175.05.025.05.0y x y y x x (1-1)
将上述方程组(1-1)写成矩阵的形式
⎪⎪⎭
⎫ ⎝⎛=⎪⎪⎭⎫
⎝⎛0011y x A y x
其中 ⎥⎦
⎤
⎢⎣⎡=75.05.025.05.0A
2=n 时,两年后北方和南方的人口为
⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛0021122y x A y x A y x
依次类推下去,n 年后北方和南方的人口为
⎪⎪⎭
⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛00y x A y x n n n (1-2) N S 0.5 0.25 0.5 0.75
现在只需求出n A 就可得出若干年后北方和南方的人口数。
下面将使用待定系数法[1]求n A
)1)(25.0(25
.025.125
.05.0)75.0)(5.0(75
.05.025
.05
.02--=+-=⨯---=----=
-λλλλλλλλλA E
所以 1,25.021==λλ
矩阵A 的最小多项式为 )1)(25.0()(--=λλλm 设A a E a A n 10+= 由此可得方程组
⎩⎨⎧=+=+125.025.01010a a a a n
解方程组得
⎪⎪⎩⎪⎪⎨⎧-=+-=75.025.0175.025.025.010n n
a a 所以
⎥⎦
⎤⎢⎣⎡+⨯--⨯+=-++-=+=++11
1025.05.025.05.05.025.025.025.05.025.075.0175
.025.0175.025.025.0n n n n n
n n
A
E A a E a A 所以由式(1-2),我们得到n 年后北方和南方的人口
北方:01
075.025.025.075.025.05.025.0y x x n n n +-+⨯+=
南方:01
075
.025.05.075.025.05.05.0y x y n n n +++⨯-=
当∞→n 时,得
)(3
1
)75.025.025.075.025.05.025.0(lim lim 0001
0y x y x x n n n n n +=-+⨯+=+∞→∞→
()000103
2
75.025.05.075.025.05.05.0lim lim y x y x y n n n n n +=⎪⎪⎭⎫
⎝⎛++⨯-=+∞∞→∞→ 由上面计算可以得到,如果移民过程持续下去,北方的人不会全部都到南方。
最终北方的人口是移民前南北人口之和的1/3。
南方人口是北方人口的两倍。
结论
本文论述的南北方人口迁移问题是一个比较理想化的问题,但还是有一些实际的参考价值,通过本问题的演算过程,我们可以推论,若一个地区有人口迁出(迁出率<1),那么只要有人口迁入,则该地区始终有人口住居。
航班问题
一家航空公司经营A 、B 、C 、D 和H 五个城市的航线业务,其中H 为中心城市。
各个城市间的路线见图1。
图 1
假设你想从A 城市飞往B 城市,因此要完成这次路线,至少需要两个相连的航班,即A →H 和H →B 。
如果没有中转站的话,就不得不要至少三个相连的航班。
那么问题如下: (1)从A 到B ,有多少条路线刚好是三个相连的航班; (2)从A 到B ,有多少条路线要求不多于四个相连的航班。
解 为了方便计算,设1、2、3、4、5分别代表A 、B 、C 、D 、H 五个城市。
令()ij a A =,其中ij a 表示i 城市到j 城市单连航班的路线条数()5,4,3,2,1,=j i ,若1=ij a 表示i 城市到j 城市的单连航班有1条,若0=ij a 表示i 城市到j 城市的单连航班有0条[2]。
则表示i 城市到j 城市单连航班的路线条数用矩阵A 表示为
⎥⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎣⎡=01111
1001011000
100011010
0A 令()
2A b B ij ==,则ij b 表示i 城市到j 城市两个相连航班的路线条数
⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢
⎢⎣⎡==411111*********
11211121112A B
令()
3A c C ij ==,则ij c 表示i 城市到j 城市三个相连航班的路线条数
⎥⎥⎥
⎥⎥⎥⎦
⎤
⎢⎢⎢⎢⎢⎢⎣⎡==45555
5232252223
53222522323
A C
令()
4A d D ij ==,则ij c 表示i 城市到j 城市四个相连航班的路线条数
⎥⎥⎥
⎥⎥
⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎣⎡==209999
9877797877
9778797
7784A D
(1)由上面的计算可得,12c 代表从A 到B 刚好是三个相连的航班路线条数。
所以,从A 到B ,有3条路线刚好是三个相连的航班。
(2)要求从A 到B ,不多于四个相连的航班路线条数,即是要把单个相连、两个相连、三 个相连和四个相连的全部航班路线条数加起来。
即 11731012121212=+++=+++d c b a
所以,从A 到B ,有11条路线不多于四个相连的航班。
参考文献
[1]李新,何传江.矩阵理论及其应用[M].重庆:重庆大学出版社,2005.8:117-120 [2]同济大学数学系.工程数学.线性代数[M].北京:高等教育出版社,2007.5:30-37。
