武汉理工大物实验-谐振法测电感
大学物理实验谐振频率测量实验报告

大学物理实验谐振频率测量实验报告一、实验目的1、了解谐振电路的基本原理和特性。
2、掌握测量谐振频率的方法。
3、学会使用实验仪器进行数据测量和分析。
二、实验原理在一个由电感 L、电容 C 和电阻 R 组成的串联谐振电路中,当外加交流电源的频率等于电路的谐振频率时,电路中的电流达到最大值,此时电路呈现纯电阻性。
谐振频率$f_0$ 的计算公式为:$f_0 =\frac{1}{2\pi\sqrt{LC}}$在实际测量中,由于电阻的存在,谐振曲线不是理想的尖锐峰值,而是有一定的带宽。
我们可以通过测量不同频率下的电流值,绘制出谐振曲线,从而确定谐振频率。
三、实验仪器1、信号发生器2、示波器3、电感线圈4、电容箱5、电阻箱四、实验步骤1、按照电路图连接好实验仪器,组成串联谐振电路。
将电感线圈、电容箱和电阻箱串联连接,信号发生器的输出端连接到电路的输入端,示波器的两个通道分别测量电路的输入电压和电流。
2、调节电容箱的电容值和电阻箱的电阻值,使其达到预定的值。
3、打开信号发生器,设置起始频率和终止频率,并逐渐改变频率,每次改变频率后,记录示波器上显示的电流值。
4、绘制出频率与电流的关系曲线,即谐振曲线。
5、从谐振曲线中找出电流最大值所对应的频率,即为谐振频率。
五、实验数据记录与处理1、实验中所使用的电感值 L =______ H,电容值 C =______ F,电阻值 R =______ Ω。
2、以下是不同频率下测量得到的电流值:|频率(Hz)|电流(A)||||| 500 | 012 || 600 | 015 || 700 | 018 || 800 | 021 || 900 | 025 || 1000 | 030 || 1100 | 035 || 1200 | 040 || 1300 | 045 || 1400 | 050 || 1500 | 055 |3、根据以上数据,绘制出频率与电流的关系曲线,如下所示:(此处插入手绘或使用软件绘制的曲线图片)从曲线中可以看出,电流最大值出现在频率约为______ Hz 处,因此,本次实验测量得到的谐振频率为______ Hz。
谐振电路的测试实验

谐振电路的测试实验
实验目的: 一 、 实验目的 :
1、 通过实验进一步的了解串联谐振和并联谐振发生的条件及其特征 。 、
2、 观察谐振电路中电压 、 电流随频率变化的现象并测出谐振曲线 。
实验原理: 二 、 实验原理 :
300
400
450
480
503
520
550
600
700
800
-------
-------
-------
----
----
-------
-------
-------
-------
?
-------
五、 误差分析
理论 : Q = 实验 : Q′ =
ω0 L
R
U L0 Us
相对误差 : γ Q =
Q′ − Q 100 × 1并联谐振 : U s =3V(RMS)
ω0 =
f0 =
1 CR 2 1− = L LC 1 2π LC 1−
1 LC
CR 2 1 = L 2π LC
参数: 三 、 LC 参数 :
1
~
33 组: L=0.1 H
C=1 μ F
四 、 实验记录
电感的直流电阻 : r=
回路电阻 : R=
频率 f( Hz) 200 ( ) I 串 联 ( mA) ) 串联 U C (V) U L (V) I 并 联 ( mA) ) -------
mV mV
函 数 发 生 器
RN = 1Ω
r us(t) C L
函 数 发 生 器
RN = 1Ω
大学物理实验谐振频率测量实验报告

谐振频率测量【实验目的】1.通过实验进一步了解串联谐振与并联谐振发生的条件及其特征。
2.观察谐振电路中电压,电流随频率变化的现象并测定谐振曲线。
3. 了解谐振现象在生活和工业中的应用。
【实验仪器】 1. 函数信号发生器; 2. 示波器;3. RLC 串联谐振电路板;4. 导线若干。
【实验原理】由电感和电容元件串联组成的二端口网络见图1所示。
记二端网络中的电感为L,电阻为R,电容为C ,输入电压为U ,电阻两端的电压为R U ,电感两端的电压为L U ,电容两端的电压C U 。
则该网络的等效阻抗为1()Z R j L Cωω=+-(1) 它是电源频率的函数。
要使该网络发生谐振时,其端口电压与电流同相位,即1/0L C ωω-=,从而得到谐振角频率为0ω=01/(2f π=,见图2所示。
电路谐振时的感抗0L ω或容抗01Cω为特性阻抗ρ,特性阻抗ρ与电阻R 的比值为品质因数Q ,即0LQ RRωρ===当电路谐振时阻抗最小,如果端口电压U 保持稳定,那么电路中的电流将达到最大值,RMAX U U I Z R==,仅与电阻的阻值有关,与电感和电容的值无关,电感电压与电容电压数值相等相位相反,电阻电压等于总电压。
电感或电容电压是输入电压的Q 倍,即图1R 、L 、C 串联电路图2串联谐振电路的电流s )-1L C R U U QU QU === (2)在一般情况下,RLC 串联电路中的电流是电源频率的函数,即()()UI Z j ωω====3)图3连接图图4 RLC 谐振电路板【实验步骤】1.按照图3所示,连接好电路。
连接信号发生器的A 通道,红色连接在RLC 谐振电路板的正极“VCC ”,黑色在RLC 谐振电路板的负极(“GND ”),RLC 谐振电路板如图4所示。
2.示波器的地端连接在RLC 谐振电路板的负极(“GND ”),信号端连接在电阻的另一端。
3.以中心频率为中心,左右各记录5各以上的点。
谐振法测互感

谐振法测互感系数摘要:实验主要是操作者自己动手自制2个参数不同的线圈,利用谐振法分别测出其电感系数,再测出互感系数。
关键词:电感线圈、自感系数、互感、互感系数、谐振频率①电感线圈是用绝缘导线扰之而成的电磁感应元件。
当线圈中有电流通过时,线圈中就会产生磁场。
当线圈中电流发生变化时,其周围的磁场也产生相应的变化,此变化的磁场可使线圈自身产生电动势,这就是自感。
两个电感线圈互相靠近时,一个电感线圈的磁场变化影响另一个线圈,这种影响就是互感。
自感系数的大小主要取决于电感线圈的匝数、绕制方法、有无磁芯及磁芯的材料等等。
线圈匝数越大,绕制的越密,磁芯导磁率越大,则自感系数也越大。
本实验的重点是自制线圈。
第一个线圈用0.5毫米直径的漆皮导线,1.5厘米半径的塑料管,绕制。
紧密缠绕,共绕10层,每层100匝,有效长度4.4厘米。
另一个线圈是用0.3毫米直径的漆皮导线,1.5厘米半径的塑料管,紧密缠绕,共绕10层,每层100匝,有效长度6.8厘米,缠绕后为防止线圈松动,用透明胶布将其缠绕固定。
由于线圈是由人手工缠绕,在第二层开始,线圈缠绕不够紧密,并且出现不同层次之间掺和,导致漏磁。
实验过程中尝试过加入铁芯,但由于铁芯形状大小与塑料管形状不和,无法很好的贴合,因此实验现象不明显,没有采用。
实验电路图如下:测单个线圈自感系数:测互感系数:按电路图连结各元件,在将线圈接入电路前,去掉接头处漆皮。
选取电容为0.1微法,电阻为3000欧姆,电源电压10伏调节电源输出频率,当达到谐振频率时,电压和电流相位重合,根据公式L= ,找到谐振频率即算出自感系数。
分别将两个线圈连入电路,找出谐振频率算出自感系数。
将两线圈串连入电路,找出此时的谐振频率,算出这时的电感。
再将其中一个线圈反向接入电路,找出谐振频率算出电感。
根据正向接入时L01=L1+L2+2M,反向接入时L02=L1+L2-2M,得出M=(L01-L02)/4。
实验数据及处理合,其中包含输出信号频率不好控制的因素,选取定点效果最明显的两个点进行记录。
用谐振法测电感
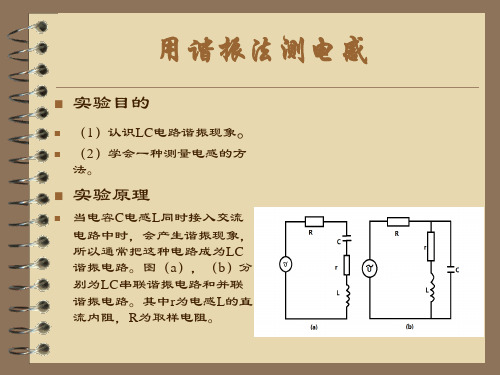
最大,Z并两端电压有最大值。 R上电压UR与Z并上电压Uz并同相 在实验中可用适当的方法测出电路谐振时的频率 条件下,根据 可计算出电感 1
f0 = 2π LC
f 0 。在电容C已知的
1 (2πf 0 ) 2 C
L=
实验仪器
标准电容箱 待测电感(标准电感箱) 电阻箱 信号发生器 双踪示波器
实验要求
2 2 0
0
0
实验原理
2并联谐振
对图(b)所示的LC并联电路,可求得
Z= r 2 + (ωL) 2 (1 − ω 2 LC ) 2 + (ωCr ) 2
Z= L/C r 2 + (ωL − 1 2 ) ωC
接近谐振时,
ω 2 = ω02 =
当
1 LC,即
ω0 L =
1 ωC
时,Z并=L/rC,LC并联电路谐振。此时阻抗
(1)明确实验原理,拟定测量方案,画出实验电路图,作出数据 记录表。 (2)根据实验室提供的元器件,选择适当的测量参数。 (3)列出验步骤,进行测量与数据处理,得出实验结果。
(1)
利用幅值的四种方法 串联中1示波器并联到电感和电容一侧, 则当 时阻抗达最小示波器 1
ω0 L = ω0 C
峰值达最小时的频率是此时的谐振频率 2示波器并联到R两端,则当峰值达最大 时的频率为谐振频率 并联中 1示波器并联到电感和电容一侧,当示波 器上的峰值达最大时为谐振频率 2示波器并联到R两端时,峰值达最小时 为谐振频率
对上图的(a)所示的LC串联电路, 阻抗和相位关系可用矢量图表示如下 图(c) 由图可知
z = zr2 +(zL − zc )2 = r2 +(ωL− 1 2 ) ωC
武汉理工大物实验-谐振法测电感
算出L的平均值。
还可以用相位差的方法
表格
(1)
(2)
在串联中,可以选择R=50 电感可以选择7mH 在并联中,可以选择R=1000 电感也可以选
择7mH
(3)
步骤:
串联电路:按电路图(a)连接好电路,R,L值设好后 调好示波器中的正弦波,改变电容C的值,寻找幅值最 小时对应的f 值,记录到表格中。
实验原理
1.串联谐振
对上图的(a)所示的LC串联电路, 阻抗和相位关系可用矢量图表示如下 图(c)
由图可知
z
zr2 (zL zc )2
r2 (L 1 )2 C
式中 w为正弦电压U的圆频( 2f0 )
当 2 Z=r,
02
1 LC
,即
实验仪器
标准电容箱 待测电感(标准电感箱) 电阻箱 信号发生器 双踪示波器
实Hale Waihona Puke 要求 (1)明确实验原理,拟定测量方案,画出实验电路图,作出数据 记录表。
(2)根据实验室提供的元器件,选择适当的测量参数。 (3)列出实验步骤,进行测量与数据处理,得出实验结果。
(1)
C
当
,即 2
02
1 LC
0
L
1 C
时,Z并=L/rC,LC并联电路谐振。此时阻抗
最大,Z并两端电压有最大值。
R上电压UR与Z并上电压Uz并同相
在实验中可用适当的方法测出电路谐振时的频率 f0 。在电容C已知的
谐振法测电感(教案)
二、实验原理
1 RLC串联谐振电路:
RLC串联电路和向量计算如图(a)、(b)所示。
电路总阻抗
Z =
1 R + ωL − ωC
2
2
(1)
二、实验原理
电路电流
I = U = Z R U
2
(2)
2
1 + ωL − ωC
电流与信号源电压之间的相位差 ϕ = − arctan
ωL − 1 / ωC
R
(3)
对于所研究的电路,保持信号源输出电压幅度一定,以上各 参数都将随信号源频率ω的改变而变化。由式3不难看出,当信号源ห้องสมุดไป่ตู้的频ω满足 ωL =
1 条件时,电路总阻抗Z=R为最小值,而此时回路 ωC R
电流为最大值 I max = U ,相位差φ=0,即称电路谐振。
三、实验仪器
标准电容箱,待测电感(标准电感箱),电阻箱,信号发生器, 双踪示波器。
四、预习要求
每一位同学都要查阅相关参考资料。 在熟知RLC谐振电路基础上写出一份完整的设计性实验报告。 实验报告要求:明确实验原理,拟定实验测量方案,画出实验电路图, 列出实验步骤,作出实验数据记录表及数据处理方法。
五、评分标准
预习(40%),课堂操作(40%)报告(20%)
谐 振 法 测 电 感( 教
案)
一、实验目的
(1)研究RLC电路的交流谐振特性。 (2)利用RLC电路的谐振特性测电感。
二、实验原理
由RLC组成的电路在周期性交变电源的激励下,将 产生受追形式的交流振荡,其振荡幅度随交变电源频 率的改变而变化,当电源频率满足一定条件时,回路 的振荡幅度达到最大值,即回路发生谐振。谐振时, 电路的特性也因RLC电路的串联或并联的形式不同而展 现出不同的结果,分别讨论如下。
谐振法测电感数据处理
谐振法测电感数据处理一.并联法测电感并联时:电感二7mH 电阻=50Q电容的平均值:C 平=ECi/6= (1. 00+0. 80+0. 75+0. 70+0. 65+0. 60) /6=0. 75 uF 频率的平均值:fo平二EfOi/6二(1. 90+2. 15+2. 25+2. 32+2. 40+2. 46)/6二2. 25 kHz 电感的平均值:L 平=ELi/6二(7. 02+7. 06+6. 88+6. 93+6. 97+6. 98)/6二6. 98 mH A 类不确定度:A=E (Li-L平)"2/(n-l)/n]P.5={[ (7. 02-6. 98)边+(7・ 06-6.98)‘2+(6. 98-6. 88) + (6.98-6.93厂2+ (6. 98-6. 87厂2+(6. 98-6. 98厂2]/30厂0・ 5=0. 07mH拓展不确定度:S二2*A=0. 14mH (K二2)则电感为L二L 平±S=6. 98 ±0. 14mH误差计算W二(6. 98-7) /7H00%二-0.28%二.串联法测电感电容的平均值:C 平=ECi/6= (1. 00+0. 80+0. 75+0. 70+0. 65+0. 60) /6=0. 75 uF 频率的平均值:fo 平二E fOi/6二(1. 98+2. 23+2. 35+2. 47+2. 39+2. 53) /6二2. 33 kHz 电感的平均值:L 平二XLi/6二(6. 94+7. 02+6. 87+6. 96+6. 98+6. 80)/6二6. 94 mH A 类不确定度:A={[E (Li-L 平)"2 / (nT)/n] "}0. 5二= [(6. 94-6. 94厂2+(7・ 02-6. 98厂2+(6. 87-6. 94厂2+(6. 96-6. 94) "2+(6. 98-6. 94厂2+(6. 80-6. 94厂2]/30厂0. 5 二0.14mH拓展不确定度:S二A*2二0. 14*2=0. 28mH (K二2)则电感为L=L平土S=6. 94 ±0. 28误差计算W二(6. 94-7) /7*100%二-0.86%三.李萨育图形串联法电容的平均值:C Y=ECi/6= (1. 00+0. 80+0. 75+0. 70+0. 65+0. 60) /6=0. 75 uF 频率的平均值:fo 平=Ef0i/6= (1. 91+2. 12+2. 20+2. 27+2. 36+2. 46) /6=2. 22 kHz 电感的平均值:L 平=ELi/6=(6. 99+7. 05+6. 99+7. 06+7. 09+6. 98)/6二7. 04 mH A类不确定度:A={[E (Li-L 平)"2/(n-l)/n]“}0.5= {[(7. 04-6. 99厂2+(7. 04-7. 05厂2+(7. 04-6. 99) "2+(7. 04-7. 06厂2+(7. 04-7. 09) "2+(7. 04-6. 98)^21/30)^0. 5 二0. 02mH 拓展不确定度:S二A*2二0. 02*2二0. 04mH (K二2)则电感为:L=L 平土S=7. 00 ±0. 04 mH误差计算:W= (7. 04-7) /7*100%=0. 57%四.李萨育图形并联法电容的平均值:C T=ECi/6= (1. 00+0. 80+0. 75+0. 70+0. 65+0. 60) /6=0. 75 uF 频率的平均值:foT=Ef0i/6= (1. 89+2. 19+2. 17+2. 33+2. 38+2. 23) /6=2. 23 kHz电感的平均值:L T=ELi/6=(7. 10+6. 61+7. 18+6. 67+6. 89+7. 16)/6二6. 93 mHA 类不确定度:S={[E (Li-L 平)"2/(n-l)/n]"}0.5= [(6. 93-7. 10) "2+(6. 93-6. 61) "2+(6. 93-7. 18) ^2+(6. 93-6・ 67厂2+(6・ 93-6. 89厂2+(6. 93-7. 16)^21/30)^0. 5 二0.02mH拓展不确定度:S二A*2二0. 02*2二0. 04mH (K二2)则电感为:L二L 平±S=6. 93±0. 0.04 mH误差计算:W= (6. 93-7) /7*100%二一 1.00%四.电源电感电压的测量串联电容:C=0. luF五.分析和结论在上面四种处理方法中,误差最小的是并联法测电感,其值为-0. 28%o不确定度最小的也是并联测电感法,其值为0. 14mHo串联法测电感显然误差过大, 其值为-0. 86%,不确定度也很大其值为0. 28mHo这两种方法中,并联法显然比串联法更精确。
谐振法测电感实验报告
谐振法测电感实验报告
实验目的:
通过谐振法测量电感的大小。
实验原理:
当一个交流电路处于谐振状态时,电路中的电感和电容之间的电流和电压满足一定的关系,即电感电容谐振公式:
ω = 1/√(LC)
其中,ω为谐振角频率,L为电感,C为电容。
实验仪器:
1.信号发生器
2.电感L
3.电容C
4.示波器
5.电阻
6.电压表
7.电流表
实验步骤:
1.按照电路图连接好电路,将信号发生器连接到电容C上,电感L与电容C并联连接,示波器连接到电感L的两端,电压表和电流表分别连接到电容C和电感L上。
2.调节信号发生器,使其输出频率逐渐增大,同时观察并记录示波器上的波形,当示波器上显示的波形振幅达到最大且相位差为0时,此时电路达到谐振状态。
3.记录此时的频率f0,电流表和电压表的读数(电流表的读数
为电感L上的电流值,电压表的读数为电容C上的电压值)。
4.改变电容C或电感L的值,重新进行调节,得到新的谐振频率f1、电流表和电压表的读数。
5.依次改变电容C或电感L的值,重复步骤4,得到多组数据。
6.根据公式ω = 1/√(LC),计算得到电感L的估计值。
实验结果:
根据实验数据计算得到的电感L的估计值为xxH。
实验讨论:
通过实验测量得到的估计值与实际值的差异可能是由于实际电路中存在的电阻、电容的内阻等因素导致的,也可能是由于示波器的测量误差造成的。
在实际操作中,还需要注意保持电路的稳定性,避免外界干扰对测量结果的影响。
实验2 RLC谐振法测电容、电感(见RLC谐振特性实验)
实验1 RLC 稳态及谐振特性在RLC 电路中通正弦交流电,电流以及R 、L 、C 各元件上电压的大小是随电源频率变化而变化的,电流与电源电压间的相位差亦随电源频率的变化而变化。
一、基本教学要求1.研究交流信号在RLC 串联电路中的相频和幅频特性,了解RLC 电路的应用。
2.学习测量两个波形相位差的方法; 3.掌握RLC 电路的谐振特点; 二、实验原理1 RC 电路)1(CjR I U ω-=••; C j R Z ω1-=电阻R 两端的电压为:2)1(1CR UIR U R ω+==电容C 两端的电压为 2)(1C R U CI U Cωω+==电压相量•U 落后于电流相量•I 的相位差为 CR ωϕ1arctan =相频特性:在R ,C ,U 都保持不变的条件下,回路中的总电压与总电流间的相位差ϕ随ω的增加而趋于零,随ω的减少而趋于2/π-。
幅频特性:在R ,C ,U 都保持不变的条件下,电容电压和电阻电压的幅度C U 和R U 都将随ω的变化而变化,在低频时电源电压主要降落在电容C 上;在高频时,电源电压主要降落在电阻R 上。
2 RL 电路)(L j R I U ω+=•• , L j R Z ω+=由相量图可知电阻R 两端的电压为: 2)(1RLU IR U R ω+==电感两端的电压为:2)(1LRULIULωω+==电压相量•U超前于电流相量•I的相位差为:RLωϕarctan=相频特性:在R、L、U都保持不变的情况下,总电压与总电流之间的相位差ϕ随ω的增加而逐渐增大,趋于2/π,随ω的减小而趋于零。
幅频特性:在R,L,U都保持不变的情况下,电阻和电感上的电压RU和LU都随ω的变化而变化,当角频率ω增加时,回路电流i减小、电阻上压降RU将减小,而电感上压降LU将增大。
RL电路与RC电路的性质是相反的,这两类电路是一对对偶电路。
3.RLC串联电路)1(CjLjRIUωω-+=••,)1(CLjRZωω-+=回路电流22)1(CLRUIωω-+=电压相量•U与电流相量•I的相位差为:RCLωωϕ/1arctan-=相频特性:当CLωω1=时,0=ϕ,总电压•U与电流•I同相位,犹如电路中只有纯电阻元件,此时称电路发生了谐振,此频率称为谐振频率:LCfπ21=当CLωω1>时,0>ϕ,总电压•U超前于电流•I。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
串联中1示波器并联到电感和电容一侧,
则当
0
L
1 0C
时阻抗达最小示波器
峰值达最小时的频率是此时的谐振频率
2示波器并联到R两端,则当峰值达最大 时的频率为谐振频率
并联中
1示波器并联到电感和电容一侧,当示波 器上的峰值达最大时为谐振频率
2示波器并联到R两端时,峰值达最小时 为谐振频率
条件下,根据
f0
2
1 LC
可计算出电感
1
L (2f0)2C
实验仪器
标准电容箱 待测电感(标准电感箱) 电阻箱 信号发生器 双踪示波器
实验要求
(1)明确实验原理,拟定测量方案,画出实验电路图,作出数据 记录表。
(2)根据实验室提供的元器件,选择适当的测量参数。 (3)列出实验步骤,进行测量与数据处理,得出实验结果。
算出L的平均值。
实验原理
1.串联谐振
对上图的(a)所示的LC串联电路, 阻抗和相位关系可用矢量图表示如下 图(c)
由图可知
zzr2(zLzc)2r2(L1C)2
式中 w为正弦电压U的圆频( 2f0 )
当 2 02 Z=r,
1 LC
,即
0
L
1 0C
时,
LC串联电路谐振。此时阻抗最小, Z串两端电压有最小值,R上电压 UR与Z串上电压Uz串同相。
实验原理
2并联谐振
对图(b)所示的LC并联电路,可求得
Z
r2(L)2 (12LC)2(C)r2
接近谐振时, Z L/C
r2 (L 1 )2 C
当
2
02
1
LC,即
0
L
1 C
时,Z并=L/rC,LC并联电路谐振。此时阻抗
最大,Z并两端电压有最大值。
R上电压UR与Z并上电压Uz并同相
在实验中可用适当的方法测出电路谐振时的频率 f 0 。在电容C已知的
还可以用相位差的方法
表格
(1)
(2)
在串联中,可以选择R=50 电感可以选择7mH 在并联中,可以选择R=1000 电感也可以选
择7mH
(3)
步骤:
串联电路:按电路图(a)连接好电路,R,L值设好后 调好示波器中的正弦波,改变电容C的值,寻找幅值最 小时对应的f 值,记录到表格中。
并联电路:按电路图(b)连接好电路,R,L值设好后 调好示波器中的正弦波,改变电容C的值,寻找幅值最 大时对应的f 值,记录到表格中。
武汉理工大学大学物理实验
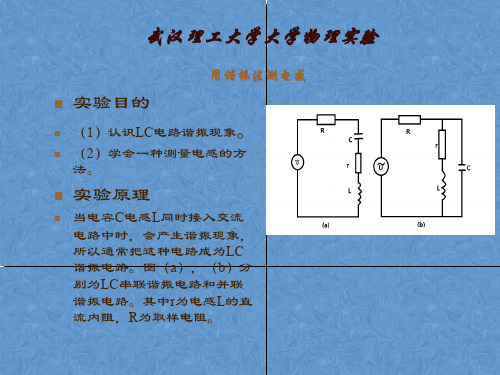
用谐振法测电感
实验目的
(1)认识LC电路谐振现象。
(2)学会一种测量电感的方 法。
实验原理
当电容C电感L同时接入交流 电路中时,会产生谐振现象, 所以通常把这种电路成为LC 谐振电路。图(a),(b)分 别为LC串联谐振电路和并联 谐振电路。其中r为电感L的直 流内阻,R为取样电阻。
