几何变换之旋转(点题资料)
中考数学专题复习旋转类几何变换
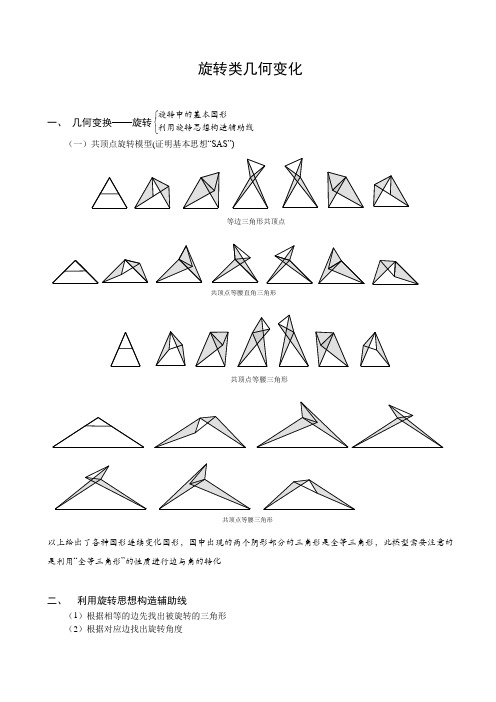
旋转类几何变化一、几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩（一）共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形，图中出现的两个阴影部分的三角形是全等三角形，此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二、利用旋转思想构造辅助线（1）根据相等的边先找出被旋转的三角形（2）根据对应边找出旋转角度（3）根据旋转角度画出对应的旋转的三角形三 、 旋转变换前后具有以下性质：（1）对应线段相等，对应角相等 （2）对应点位置的排列次序相同（3）任意两条对应线段所在直线的夹角都等于旋转角θ．考点一 旋转与最短路程☞考点说明：旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题，同时与旋转有关路程最短的问题，比较重要的就是费马点问题，涉及费马点问题，视学生程度进行选择性讲解。
【例1】 如图，四边形ABCD 是正方形，ABE ∆是等边三角形，M 为对角线BD 上任意一点，将BM 绕点B逆时针旋转60︒得到BN ，连接AM 、CM 、EN ． ⑴求证：AMB ENB ∆∆≌⑵①当M 点在何处时，AM CM +的值最小；②当M 点在何处时，AM BM CM ++的值最小，并说明理由； ⑶当AM BM CM ++的最小值为31+时，求正方形的边长．ENMDCB A【例2】 阅读下列材料对于任意的ABC ∆，若三角形内或三角形上有一点P ，若PA PB PC ++有最小值，则取到最小值时，点P 为该三角形的费马点。
①若三角形内有一个内角大于或等于120︒，这个内角的顶点就是费马点②若三角形内角均小于120︒，则满足条件120APB BPC APC ∠=∠=∠=︒时，点P 既为费马点 解决问题：⑴如图，ABC ∆中，三个内角均小于120︒，分别以AB 、AC 为边向外作等边ABD ∆、ACE ∆，连接CD 、BE 交于点P ，证明：点P 为ABC ∆的费马点。
专题32 几何变换之旋转模型--2024年中考数学核心几何模型重点突破(学生版)
专题32几何变换之旋转模型【理论基础】1.旋转的概念：将一个图形绕一个定点转动一定的角度，这样的图形运动称为图形的旋转，定点称为旋转中心，旋转的角度称为旋转角.2.旋转三要素：旋转中心、旋转方形和旋转角度.3.旋转的性质(1)对应点到旋转中心的距离相等；(2)两组对应点分别与旋转中心连线所成的角度相等.注：图形在绕着某一个点进行旋转的时候，既可以顺时针旋转，也可以逆时针旋转.4.旋转作图：在画旋转图形时，首先要确定旋转中心，其次确定图形的关键点，再将这些关键点沿指定的方向旋转指定的角度，然后连接对应的部分，形成相应的图形.具体步骤如下：(1)连接图形中的每一个关键点与旋转中心；(2)把连线按要求(顺/逆时针)绕旋转中心旋转一定的角度(旋转角)；(3)在角的一边上截取关键点到旋转中心的距离，得到各点的对应点；(4)连接所得到的对应点.5.旋转中的全等变换.(1)等腰直角三角形中的半角模型(2)正方形中的半角模型6.自旋转模型：有一组相邻的线段相等，可以通过构造旋转全等.(1)60º自旋转模型(2)90º自旋转模型(3)等腰旋转模型(4)中点旋转模型(倍长中线模型)7.共旋转模型(1)等边三角形共顶点旋转模型(2)正方形共顶点旋转模型8.旋转相似【例1】如图，在Rt△ABC中，AB＝AC，D，E是斜边BC上两点，且∠DAE＝45°，将△ADC 绕点A顺时针旋转90°后，得到△AFB，连接EF．下列结论：①△AED≌△AEF；②∠FAD ＝90°，③BE+DC＝DE；④∠ADC+∠AFE＝180°．其中结论正确的序号为（）A．①②③B．②③④C．①②④D．①③④【例2】如图，点E 为正方形ABCD 外一点，∠AEB ＝90°，将Rt △ABE 绕A 点逆时针方向旋转90°得到△ADF ，DF 的延长线交BE 于H 点，若BH ＝7，BC ＝13，则DH ＝_____．【例3】如图，ADE △由ABC △绕点A 按逆时针方向旋转90°得到，且点B 的对应点D 恰好落在BC 的延长线上，AD ，EC 相交于点P ．(1)求∠BDE 的度数；(2)F 是EC 延长线上的点，且DF PF =．①判断CDF ∠和DAC ∠的数量关系，并证明；②求证：EP PC PF CF=．一、单选题1．如图，P 是等边三角形ABC 内一点，将△ACP 绕点A 顺时针旋转60°得到△ABQ ，若PA＝2，PB ＝4，PC =，则四边形APBQ 的面积为（）A ．B ．C ．D ．2．如图，在ABC 中，AB AC =，若M 是BC 边上任意一点，将ABM 绕点A 逆时针旋转得到ACN △，点M 的对应点为点N ，连接MN ，则下列结论不一定成立的是（）A ．AM AN=B ．AMN ANM ∠=∠C ．CA 平分BCN ∠D ．MN AC⊥3．如图，在平面直角坐标系中，△ABC 中点A 的坐标是(3，4)，把△ABC 绕原点O 逆时针旋转90︒得到A B C ''' ，则点A ′的坐标为（）A ．(4，－3)B ．(－4，3)C ．(－3，4)D ．(－3，－4)4．如图，O 是边长为1的等边ABC 的中心，将AB 、BC 、CA 分别绕点A 、点B 、点C 顺时针旋转()0180αα︒<<︒，得到AB '、BC '、CA '，连接A B ''、B C ''、A C ''、OA '、OB '．当A B C '''V 的周长取得最大值时，此时旋转角α的度数为（）A ．60°B ．90°C ．120°D ．150°5．如图，正方形ABCD 的边长为4，30BCM ∠=︒，点E 是直线CM 上一个动点，连接BE ，线段BE 绕点B 顺时针旋转45°得到BF ，连接DF ，则线段DF 长度的最小值等于（）A ．424B ．222C ．2623D ．2636．如图，在ABC 中，90C ∠<︒，30B ∠=︒，10AB =，7AC =，O 为AC 的中点，M 为BC 边上一动点，将ABC 绕点A 逆时针旋转角()0360αα︒<≤︒得到AB C ''△，点M 的对应点为M '，连接OM '，在旋转过程中，线段OM '的长度的最小值是（）A ．1B ．1.5C ．2D ．37．如图，矩形ABCD 中，3AB =，BC ＝3，P 为矩形内一点，连接PA ，PB ，PC ，则PA ＋PB ＋PC 的最小值是（）A ．233+B ．25C ．233+D 218．如图，在平面直角坐标系中，等腰直角△OAB 位置如图，∠OBA =90°，点B 的坐标为（1，0），每一次将△OAB 绕点O 逆时针旋转90°，同时每边扩大为原来的2倍，第一次旋转得到△OA 1B 1，第二次旋转得到△OA 2B 2，…，以此类推，则点A 2022的坐标是（）A ．(22022，22022)B ．(-22021，22021)C ．(22021，-22021)D ．(-22022，-22022)二、填空题9．如图，在正方形ABCD 中，点M 是AB 上一动点，点E 是CM 的中点，AE 绕点E 顺时针旋转90°得到EF ，连接DE ，DF ．给出结论：①DE =EF ；②∠CDF =45°；③若正方形的边长为2，则点M 在射线AB 上运动时，CF ．其中结论正确的是____．10．如图，四边形ABCD ，AB ＝3，AC ＝2，把△ABD 绕点D 按顺时针方向旋转60°后得到△ECD ，此时发现点A 、C 、E 恰好在一条直线上，则AD 的长为__________.11．在△ABC 中，∠C ＝90°，AB ＝5，把△ABC 绕点C 旋转，使点B 落在射线BA 上的点E 处（点E 不与点A ，B 重合），此时点A 落在点F ，联结FA ，若△AEF 是直角三角形，且AF ＝4，则BC ＝_____．12．如图，在四边形ABCD 中，60ADC ∠=︒，30ABC ∠=︒，且AD CD =，连接BD ，若2AB =，BD =BC 的长为______．13．已知，⊙O 的直径BC ＝，点A 为⊙O 上一动点，AD 、BD 分别平分△ABC 的外角，AD 与⊙O 交于点E ．若将AO 绕O 点逆时针旋转270°，则点D 所经历的路径长为_____．（提示：在半径为R 的圆中，n °圆心角所对弧长为180R n π）14．如图，在正方形ABCD 中，M ，N 分别是AB ，CD 的中点，P 是线段MN 上的一点，BP 的延长线交4D 于点E ，连接PD ，PC ，将DEP 绕点P 顺时针旋转90︒得GFP ，则下列结论：CP GP =①，tan 1CGF ∠=②；BC ③垂直平分FG ；④若4AB =，点E 在AD 边上运动，则D ，F ______．15．已知⊙O 的半径为4，A 为圆内一定点，AO ＝2．M 为圆上一动点，以AM 为边作等腰△AMN ，AM ＝MN ，∠AMN ＝108°，ON 的最大值为_____________．16．如图，在矩形ABCD 中，AB ＝3，BC ＝4，将矩形ABCD 绕点C 按顺时针方向旋转α角，得到矩形A ′B ′CD ′，B ′C 与AD 交于点E ，AD 的延长线与A ′D ′交于点F ．当矩形A 'B 'CD '的顶点A '落在CD 的延长线上时，则EF ＝_____．三、解答题17．如图，在平面直角坐标系中△ABC 的三个顶点都在格点上，点A 的坐标为（2，2），请解答下列问题：(1)画出△ABC 绕点B 逆时针旋转90°后得到△A 1B 1C 1，并写出点A 1的坐标；(2)画出和△A 1B 1C 1关于原点O 成中心对称的△A 2B 2C 2，并写出点A 2的坐标；(3)在（1）的条件下，求BC 在旋转过程中扫过的面积．18．如图，在△ABC 中，点E 在BC 边上，AE ＝AB ，将线段AC 绕A 点旋转到AF 的位置，使得∠CAF ＝∠BAE ，连接EF ，EF 与AC 交于点G ．(1)求证：EF ＝BC ；(2)若63ABC ∠︒＝，25ACB ∠︒＝，求∠FGC 的度数．19．如图，正方形ABCD 中，=45°MAN ∠，MAN ∠绕点A 顺时针旋转，它的两边分别交BC 、DC （或它们的延长线）于点M 、N ．(1)如图1，求证：MN BM DN =+；(2)当=6AB ，5MN =时，求CMN 的面积；(3)当MAN ∠绕点A 旋转到如图2位置时，线段BM 、DN 和MN 之间有怎样的数量关系？请写出你的猜想并证明．20．阅读下面材料：小岩遇到这样一个问题：如图1，在正三角形ABC 内有一点P ，且PA ＝1，PB PC ＝2，求∠APB 的度数；小岩是这样思考的：如图2，利用旋转和全等的知识构造AP C '△，连接PP '，得到两个特殊的三角形，从而将问题解决．(1)请你回答：图1中∠APB 的度数等于____；（直接写答案）参考小岩同学思考问题的方法，解决下列问题：(2)如图3，在正方形ABCD 内有一点P ，且PA =1PB =，PD =APB 的度数；(3)如图4，在正六边形ABCDEF 内有一点P ，若∠APB ＝120︒，直接写出PA ，PB 和PF 的数量关系．21．在ABC 中，90C ∠=︒，30BAC ∠=︒，点D 是CB 延长线上一点（30ADC ∠>︒），连接AD ，将线段AD 绕点D 顺时针旋转60°，得到线段DE ，连接EC ．(1)依题意，补全图形；(2)若2BD BC ==，求CE 的长．(3)延长EC 交AB 于F ，用等式表示线段CE CF ，之间的数量关系，并证明．22．在△ABC 中，∠ACB =90°，BC =AC =2，将△ABC 绕点A 顺时针方向旋转60°至AB C ''△的位置．(1)如图1，连接C C '与AB 交于点M ，则CC '=_____，BC '=_____；(2)如图2，连接BB '，延长CC '交BB '于点D ，求CD 的长．23．如图，在等腰Rt △ABC 中，将线段AC 绕点A 顺时针旋转()090αα︒<<︒，得到线段AD ，连接CD ，作∠BAD 的平分线AE ，交BC 于E ．(1)①根据题意，补全图形；②请用等式写出∠BAD 与∠BCD 的数量关系．(2)分别延长CD 和AE 交于点F ，①直接写出∠AFC 的度数；②用等式表示线段AF ，CF ，DF 的数量关系，并证明．24．如图，已知抛物线经过点()1,0A -，()3,0B ，()0,3C 三点，点D 是直线BC 绕点B 逆时针旋转90︒后与y 轴的交点，点M 是线段AB 上的一个动点，设点M 的坐标为()0m ,，过点M作x 轴的垂线交抛物线于点E ，交直线BD 于点F ．(1)求该抛物线所表示的二次函数的解析式；(2)在点M运动过程中，若存在以EF为直径的圆恰好与y轴相切，求m的值；ΔA O C，点A、O、C的对应点(3)连接AC，将AOC∆绕平面内某点G旋转180︒后，得到111ΔA O C的两个顶点恰好落在分别是点1A、1O、1C，是否存在点G使得AOC∆旋转后得到的111抛物线上，若存在，求出G点的坐标；若不存在，请说明理由．。
考点15 旋转变换(解析版)
旋转变换通常结合全等三角形探索角的数量关系，线段与线段之间的位置关系与数量关系，经常作为作为中等偏难一点的题型出现．★★★○○○○旋转的性质有：①旋转角是对应点与旋转中心所连线段的夹角是旋转角；②旋转前后的图形全等；③对应点到旋转中心的距离相等．如图，△ABC绕点O逆时针方向旋转∠AOA′到△A′B′C′的位置，则①旋转角是∠AOA′＝∠BOB′＝∠COC′；②△ABC≌△A′B′C′；③OA＝OA′，OB＝OB′，OC＝OC′．1.注意旋转的三要素：旋转中心，旋转方向，旋转角；2.抓住旋转只是改变图形的位置，不改变图形的形状和大小，即旋转前后的图形全等；3.能够用旋转解题的图形的基本特征是有公共端点且相等的两条线段，这个公共端点往往会是旋转中心．例1.如图，将Rt△ABC（其中∠B＝35°，∠C＝90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C，A，B1在同一条直线上，那么旋转角等于( )A. 55°B. 70°C. 125°D. 155°【答案】C例2.如图，点P为定角∠AOB的平分线上的一个定点，且∠MPN与∠AOB互补，若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：（1）PM＝PN恒成立；（2）OM＋ON 的值不变；（3）四边形PMON的面积不变；（4）MN的长不变，其中正确的个数为（）A. 4B. 3C. 2D. 1【答案】B学科@网【精细解读】因为角平分线上的点到角的两边的距离相等，所以存在着隐性的有公共端点的相等线段的特征，故可考虑过点P作∠AOB的两边的垂线，再结合旋转的性质求解．如图作PE⊥OA于E，PF⊥OB于F．例3.如图1，在△ABC中，∠ACB＝90°，点P为△ABC内一点.（1）连接PB，PC，将△BCP沿射线CA方向平移，得到△DAE，点B，C，P的对应点分别为点D、A、E，连接CE.①依题意，请在图2中补全图形；②如果BP⊥CE，BP＝3，AB＝6，求CE的长．（2）如图3，以点A为旋转中心，将△ABP顺时针旋转60°得到△AMN，连接P A、PB、PC，当AC＝3，AB＝6时，根据此图求P A＋PB＋PC的最小值．【答案】（1）33（2）37∵△BCP沿射线CA方向平移，得到△DAE，∴BC∥AD且BC＝AD，∵∠ACB＝90°，∴四边形BCAD是矩形，∴CD＝AB＝6，∵BP＝3，∴DE＝BP＝3，∵BP⊥CE，BP∥DE，∴DE⊥CE，∴在Rt△DCE中，22--；CE=CD DE=369=27=33（2）证明：如图所示，1.把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是 ( )A. 6B. 6C. 3D. 3＋3【答案】A【解析】试题解析：连接BC′，∵旋转角∠BAB′＝45°，∠BAD′＝45°，∴B在对角线AC′上，∵B′C′＝AB′＝3，在Rt△AB′C′中，AC′＝，∴BC′＝3－3，在等腰Rt△OBC′中，OB＝BC′＝3－3，在直角三角形OBC′中，OC′＝（3－3）＝6－3，∴OD′＝3－OC′＝3－3，∴四边形ABOD′的周长是：2AD′＋OB＋OD′＝6＋3－3＋3－3＝6．故选A．2.两个全等的三角尺重叠放在△ACB的位置，将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置，使点A恰好落在边DE上，AB与CE相交于点F．已知∠ACB＝∠DCE＝90°，∠B＝30°，AB＝8cm，则CF ＝_________cm．【答案】233.如图，菱形ABCD中，边长为2，∠B＝60°，将△ACD绕点C旋转，当AC（即A′C）与AB交于一点E，CD（即CD′）同时与AD交于一点F时，点E，F和点A构成△AEF．试探究△AEF的周长是否存在最小值，如果不存在，请说明理由；如果存在，请计算出△AEF周长的最小值.【答案】2＋3（每道试题10分，总计100分）1.如图，在□ABCD中，AE⊥BC于点E，以点B为中心，取旋转角等于∠ABC，把△BAE顺时针旋转，得到△BA′E′，连接DA′，若∠ADC＝60°，∠ADA′＝50°，则∠DA′E′的大小为（）A. 130°B. 150°C. 160°D. 170°【答案】C【解析】根据平行四边形对角相等、邻角互补，得∠ABC＝60°，∠DCB＝120°，再由∠A′DC＝10°，可运用三角形外角求出∠DA′B＝130°，再根据旋转的性质得到∠BA′E′＝∠BAE＝30°，从而得到答案．解：∵四边形ABCD是平行四边形，∠ADC＝60°，∴∠ABC＝60°，∠DCB＝120°，∵∠ADA′＝50°，∴∠A′DC＝10°，∴∠DA′B＝130°，∵AE⊥BC于点E，∴∠BAE＝30°，∵△BAE顺时针旋转，得到△BA′E′，∴∠BA′E′＝∠BAE＝30°，∴∠DA′E′＝∠DA′B＋∠BA′E′＝160°．故选C．学科@网2.如图，中，，，将绕点顺时针旋转得到，当点、、三点共线时，旋转角为，连接，交于点．下面结论：①为等腰三角形；②；③；④中，正确的是（）A. ①③④B. ①②④C. ②③④D. ①②③④【答案】B3.三角板ABC中，∠ACB＝90°，∠B＝30°，AC＝3，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（）A. 32πB.433πC. 2πD. 3π【答案】C4.如图，将△ABC绕点B逆时针旋转60°得到△A′C′B，且BC＝2，那么CC′的长是___________.【答案】2；【解析】试题解析：∵△ABC绕点B逆时针旋转60°得到△A′C′B，∴BC＝BC′＝2，∠CBC′＝60°，∴△BCC′为等边三角形，∴CC′＝BC＝BC′＝2.学科@网5.如图，在△ABC中，∠ACB＝90°，∠ABC＝60°，AB＝12cm，将△ABC以点B为中心顺时针旋转，使点C 旋转到AB边延长线上的点D处，则AC边扫过的图形（阴影部分）的面积是_____cm2．（结果保留π）．【答案】36π6.在Rt△ABC中，∠C＝90°，AC＝1，BC＝，点O为Rt△ABC内一点，连接AO、BO、CO，且∠AOC＝∠COB＝∠BOA＝120°，则OA＋OB＋OC＝__________．【答案】7【解析】试题解析：∵∠ACB＝90°，AC＝1，BC＝，∴tan∠ABC＝，∴∠ABC＝30°，∵△AOB绕点B顺时针方向旋转60°，∴∠A′BC＝∠ABC＋60°＝30°＋60°＝90°，∴A′B⊥CB，∵∠ACB＝90°，AC＝1，∠ABC＝30°，∴AB＝2AC＝2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B＝AB＝2，BO＝BO′，A′O′＝AO，∴△BOO′是等边三角形，∴BO＝OO′，∠BOO′＝∠BO′O＝60°，∵∠AOC＝∠COB＝∠BOA＝120°，∴∠COB＋∠BOO′＝∠BO′A′＋∠BO′O＝120°＋60°＝180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C＝，∴OA＋OB＋OC＝A′O′＋OO′＋OC＝A′C＝．7.如图，⊙P的半径为5，A、B是圆上任意两点，且AB＝6，以AB为边作正方形ABCD（点D、P在直线AB两侧）．若AB边绕点P旋转一周，则CD边扫过的面积为____．【答案】9π8.如图，四边形ABCD是正方形，△ADF按顺时针方向旋转一定角度后得到△ABE，若AF＝4，AB＝7.（1）旋转中心为______；旋转角度为______；（2）DE的长度为______；（3）指出BE与DF的位置关系如何？并说明理由.【答案】（1）A，90°；（2）3；（3）BE⊥DF，理由见解析.9.如图（1），已知△ABC中，∠BAC＝90°，AB＝AC，AE是过A的一条直线，且B、C在A、E的异侧，BD ⊥AE于D，CE⊥AE于E（1）试说明：BD＝DE＋CE．（2）若直线AE绕A点旋转到图（2）位置时（BD＜CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果；（3）若直线AE绕A点旋转到图（3）位置时（BD＞CE），其余条件不变，问BD与DE、CE的关系如何？请直接写出结果，不需说明理由．【答案】（1）证明见解析；（2）DE＝BD＋CE；（3）DE＝BD＋CE．10.（1）探究：如图，四边形ABCD 中，已知AB AD =， 90BAD ∠=︒，点E F 、分别在边BC CD 、上， 45EAF ∠=︒；①如图1，若B ADC ∠∠、都是直角，把ABE 绕点A 逆时针旋转90︒至ADG ，使AB 与AD 重合，则能证得EF BE DF =+，请写出推理过程；②如图2，若B D ∠∠、不是直角，则当B D ∠∠、满足数量关系 时，仍有EF BE DF =+；（2）拓展：如图3，在ABC 中， 90BAC ∠=︒， 22AB AC ==，点D E 、均在边BC 上，且45DAE ∠=︒，若1BD =，求DE 的长．【答案】（1）①证明见解析； ②当∠B ＋∠ADC ＝180°时，EF ＝BE ＋DF ；(2) DE ＝53. 【解析】试题分析: （1）①根据旋转的性质得出AE ＝AG ，∠BAE ＝∠DAG ，BE ＝DG ，求出∠EAF ＝∠GAF ＝45°，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF ＝GF ，即可求出答案；②根据旋转的性质得出AE ＝AG ，∠B ＝∠ADG ，∠BAE ＝∠DAG ，求出C 、D 、G 在一条直线上，根据SAS 推出△EAF ≌△GAF ，根据全等三角形的性质得出EF ＝GF ，即可求出答案；（2）根据等腰直角三角形性质好勾股定理求出∠ABC ＝∠C ＝45°，BC ＝4，根据旋转的性质得出AF ＝AE ，∠FBA ＝∠C ＝45°，∠BAF ＝∠CAE ，求出∠F AD ＝∠DAE ＝45°，证△F AD ≌△EAD ，根据全等得出DF ＝DE ，设DE ＝x ，则DF ＝x ，BF ＝CE ＝3−x ，根据勾股定理得出方程，求出x 即可．②当∠B ＋∠ADC ＝180°时，EF ＝BE ＋DF ；把△ACE 旋转到ABF 的位置，连接DF ，则∠F AB ＝∠CAE .∵∠BAC ＝90°，∠DAE ＝45°，∴∠BAD ＋∠CAE ＝45°，又∵∠F AB ＝∠CAE ，∴∠F AD ＝∠DAE ＝45°，则在△ADF 和△ADE 中， AD AD FAD DAE AF AE =⎧⎪∠=∠⎨⎪=⎩，∴△ADF ≌△ADE ，∴DF ＝DE ，∠C ＝∠ABF ＝45°，∴∠BDF ＝90°，∴△BDF 是直角三角形，∴222BD BF DF +=，∴222BD CE DE +=． ∵∠BAC ＝90°，AB ＝AC ＝22，∴BC ＝4，∵BD ＝1，∴DC ＝3，EC ＝3－DE ，∴()2213DE DE +-=，解得DE ＝53．学科@网____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________ ____________________________________________________________________________________________。
九年级(初三)《旋转》知识点及练习(带答案)
旋转一.知识框架二．知识概念1.旋转：在平面内，将一个图形绕一个图形按某个方向转动一个角度，这样的运动叫做图形的旋转。
这个定点叫做旋转中心，转动的角度叫做旋转角。
（图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动，其中对应点到旋转中心的距离相等，对应线段的长度、对应角的大小相等，旋转前后图形的大小和形状没有改变。
）2.旋转对称中心：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角（旋转角小于0°，大于360°）。
3．中心对称图形与中心对称：中心对称图形：如果把一个图形绕着某一点旋转180度后能与自身重合，那么我们就说，这个图形成中心对称图形。
中心对称：如果把一个图形绕着某一点旋转180度后能与另一个图形重合，那么我们就说，这两个图形成中心对称。
4.中心对称的性质：关于中心对称的两个图形是全等形。
关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
关于中心对称的两个图形，对应线段平行（或者在同一直线上）且相等。
一、精心选一选 (每小题3分，共30分)1．下面的图形中，是中心对称图形的是（）A．B．C．D．2．平面直角坐标系内一点P （－2,3）关于原点对称的点的坐标是 （ ）A ．（3，－2）B ． (2,3）C ．（－2，－3）D ． (2，－3）3．3张扑克牌如图1所示放在桌子上，小敏把其中一张旋转180º后得到如图（2）所示，则她所旋转的牌从左数起是（ ）A ．第一张B ．第二张C ．第三张D ．第四张 4．在下图右侧的四个三角形中，不能由△ABC 经过旋转或平移得到的是（ ）5．如图3的方格纸中，左边图形到右边图形的变换是（ ） A ．向右平移7格B ．以AB 的垂直平分线为对称轴作轴对称，再以AB 为对称轴作轴对称C ．绕AB 的中点旋转1800，再以AB 为对称轴作轴对称D ．以AB 为对称轴作轴对称，再向右平移7格6．从数学上对称的角度看，下面几组大写英文字母中，不同于另外三组的一组是（ ）A ．A N E GB ．K B X NC ．X I H OD ．Z D W H7．如图4，C 是线段BD 上一点，分别以BC 、CD 为边在BD 同侧作等边△ABC 和等边△CDE,AD 交CE 于F ，BE 交AC 于G ，则图中可通过旋转而相互得到的三角形对数有( )． A ．1对B ．2对C ．3对D ．4对8．下列这些复杂的图案都是在一个图案的基础上，在“几何画板”软件中拖动一点后形成的，它们中每一个图案都可以由一个“基本图案”通过连续旋转得来，旋转的角度是（ ）A ︒30B ︒45C ︒60D ︒909．如图5所示，图中的一个矩形是另一个矩形顺时针方向旋转90°后形成的个数是（ ） A ．l 个B ．2个C ．3个D ．4个ABCABCDCDE图4图5图图1210．如图6，ΔABC 和ΔADE 都是等腰直角三角形，∠C 和∠ADE 都是直角，点C 在AE 上，ΔABC 绕着A 点经过逆时针旋转后能 够与ΔADE 重合得到图7，再将图23—A —4作为“基本图形”绕 着A 点经过逆时针连续旋转得到图7.两次旋转的角度分别为（ ）A ．45°，90°B ．90°，45°C ．60°，30°D ．30°，60 二、耐心填一填（每小题3分，共24分）11．关于中心对称的两个图形，对称点所连线段都经过 ，而且被_____________平分.12．在平行四边形、矩形、菱形、正方形、等腰梯形这五种图形中，既是轴对称图形，又是中心对称图形的是_____________．13．时钟上的时针不停地旋转，从上午8时到上午11时，时针旋转的旋转角是_____________． 14．如图8，△ABC 以点A 为旋转中心，按逆时针方向旋转60°，得△AB ′C ′，则△ABB ′是 三角形.15．已知ａ＜0，则点Ｐ（ａ2，－ａ＋3）关于原点的对称点Ｐ1在第＿＿＿象限16．如图9，△COD 是△AOB 绕点O 顺时针方向旋转40°后所得的图形，点C 恰好在AB 上，∠AOD ＝90°，则∠D 的度数是 ．17．如图10，在两个同心圆中，三条直径把大圆分成相等的六部分，若大圆的半径为2，则图中阴影部分的面积是＿＿＿.18．如图,四边形ABCD 中，∠BAD=∠C=90º，AB=AD ，AE ⊥BC 于E ，若线段AE=5，则S 四边形ABCD＝ 。
中考数学几何旋转经典例题
旋转知识点归纳知识点1:旋转的定义及其有关概念在平面内，将一个图形绕一个定点O 沿某个方向转动一个角度，这样的图形运动称为旋转，定点O 称为旋转中心，转动的角称为旋转角;如果图形上的点P 经过旋转到点P ',那么这两个点叫做这个旋转的对应点. 如图1,线段AB 绕点O 顺时针转动090得到B A '',这就是旋转,点O 就是旋转中心,A AO B BO '∠'∠,都是旋转角. 说明: 旋转的范围是在平面内旋转，否则有可能旋转为立体图形，因此“在平面内”这一条件不可忽略.决定旋转的因素有三个:一是旋转中心;二是旋转角;三是旋转方向. 知识点2:旋转的性质由旋转的定义可知，旋转不改变图形的大小和形状，这说明旋转前后的两个图形是全等的.由此得到如下性质：⑴经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度，对应点的排列次序相同. ⑵任意一对对应点与旋转中心的连线所成的角都是旋转角. ⑶对应点到旋转中心的距离相等. ⑷对应线段相等，对应角相等.例1 、如图2，D 是等腰Rt △ABC 内一点，BC 是斜边，如果将△ADB 绕点A 逆时针方向旋转到△C D A '的位置，则ADD '∠的度数是（ ）ＤＡ．25Ｂ．30Ｃ．35Ｄ．45知识点3:旋转作图1.明确作图的条件:(1)已知旋转中心;(2)已知旋转方向与旋转角.2.理解作图的依据:(1)旋转的定义: 在平面内，将一个图形绕一个定点O 沿某个方向转动一个角度的图形变换叫做旋转;(2)旋转的性质:经过旋转,图形上的每一点都绕旋转中心沿相同的方向转动了相同的角度,任意一对对应点与旋转中心的连线所组成的角都是旋转角,对应点到旋转中心的距离相等.3.掌握作图的步骤:(1)分析题目要求,找出旋转中心、旋转角；（2）分析图形，找出构成图形的关键点；（3）沿一定的方向，按一定的角度，通过截取线段的方法，找出各个关键点；（4）连接作出的各个关键点，并标上字母；（5）写出结论.'图1D图2例2 如图3，小明将△ABC 绕O 点旋转得到△C B A '''，其中点C B A '''、、分别是A 、B 、C 的对应点.随即又将△ABC 的边AC 、BC 及旋转中心O 擦去(不留痕迹),他说他还能把旋转中心O 及△ABC 的位置找到,你认为可以吗?若可以,试确定旋转中心及的位置;如不可以,请说明理由.解：连接A A '，B B ',分别作A A '，B B '的垂直平分线，相交于O 点，则O 点即为旋转中心.再作C '关于点的对应点,连接,则的位置就确定了.如图4所示.评注:旋转角相等及对应点到旋转中心的距离相等是解决这类问题的关键.考点4:钟表的旋转问题钟表的时针与分针每时每刻都以轴心为旋转中心作旋转运动,其中时针12小时旋转一周,则每小时旋转,301236000=这样时针每分钟旋转;5.00分针每小时旋转一周,则每分钟旋转.66036000=例3 从1点到1点25分,分针转了多少度角?时针转了多少度角?1点25分时时针与分针的夹角是多少度?A图3'解读生活中的旋转一.旋转及其基本性质1.旋转的概念在平面内,将一个图形绕一个定点沿着某个方向转动一个角度,这样的图形运动称为旋转,这个定点称为旋转中心,转动的角称为旋转角.2.旋转的基本性质(1)旋转前后两个图形的对应点到旋转中心的距离相等;(2)对应点与旋转中心的连线所成的角彼此相等.3.理解旋转中的不变量图形旋转的主要因素是旋转的方向和旋转的角度,图形在旋转过程中,图形中的每一点都按同样的方向旋转了相同的角度.图形在旋转后点的位置改变,但线段的长度不变,对应点到旋转中心的距离不变,每对对应点与旋转中心连线所成的角都相等.总结:旋转过程中,每一个点都绕旋转中心沿相同的方向旋转了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.二.旋转前后两个图形的比较图形是由点组成的,图形中的主要元素有线段和角,也有一些其他可度量的元素,所以从这两个方面加以分析.旋转的特点有以下几个方面:(1)旋转前后两个图形的形状和大小没有发生改变,位置发生了改变;(2)对应线段相等，对应角相等;(3)每对对应点与旋转中心连线所成的角都是相等的，它们都是旋转角.三.旋转作图1.旋转作图的依据是:图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,对应点到旋转中心的距离相等.2.旋转作图的条件(1)图形原来所在的位置;(2)旋转中心;(3)图形旋转的方向;(4)图形的旋转角度.3.旋转作图的具体步骤为:(1)分析题目的要求,找出旋转中心、旋转角；(2)分析所作的图形，找出构造图形的关键点；(3) 沿一定的方向，按一定的角度，通过攫取线段的方法，旋转各个关键点。
2020中考数学复习--专题03 几何变换之旋转的性质
G
D
P
C
E
A
B
【分析】特殊的菱形旋 转特殊的角度必然得到其他特殊的图形． 连接 DE，易证△PDE 是等腰直角三角形，∵AB =2，∴ AC 2 3 ，
F
G
D
P
C
E
A
B
∵ AE AB 2 ，∴ CE 2 3 2 ，∴ PE 3 1 ，∴ PD 3 1 ．
3.（2018·陇南）如图，点 E 是正方形 ABCD 的边 DC 上一点，把 ADE 绕点 A 顺时针旋转 90 到 ABF 的位置，若四边形 AECF 的面积为 25， DE 2 ，则 AE 的长为( )
时针旋转得到 ADE ，使得点 D 落在 AC 上，则 tanECD 的值为 ．
E
A
C
D
B
【分析】对应边相等求线段长，即可得所求角的正切值． 由题意得：A D=AB=5，E N=CB=12， ∴CD=AC-AD=13-5=8， ∴ tan ECD 12 3 ．
82
2.（2019·内江）如图，在△ABC 中，A B=2，B C=3.6，∠B=60°，将△ABC 绕点 A 顺时 针旋转得到△ADE ，当点 B 的对应点 D 恰好落在 BC 边上时，则 CD 的长为( )
过点 B 作 BH ⊥AB 交 AB 于 H 点，则 A H=4，BH=1，∴ BC 1 ．
C'
D D'
B' C
A
HB
2.（2019·梧州）如图，在菱形 ABCD 中， AB 2 ，BAD 60 ，将菱形 ABCD 绕点 A 逆 时针方向旋转，对应得到菱形 AEFG ，点 E 在 AC 上， EF 与CD 交于点 P ，则 DP 的长 是．
专题22 几何三大变换问题之旋转问题(压轴题)
《中考压轴题》专题22：几何三大变换问题之旋转（中心对称）问题一、选择题1.如图，已知△ABC 中，∠C=90°，AC=BC=，将△ABC 绕点A 顺时针方向旋转60°到△AB′C′的位置，连接C′B ，则C′B 的长为A ．22-B ．32C ．31-D ．12.如图，△AOB 为等腰三角形，顶点A 的坐标为（2，5），底边OB 在x 轴上．将△AOB 绕点B 按顺时针方向旋转一定角度后得△A'O'B ，点A 的对应点A'在x 轴上，则点O'的坐标为A ．（203，103）B ．（163，453）C ．（203，453）D ．（163，43）3.在平面直角坐标系中，函数y=x 2﹣2x （x≥0）的图象为C 1，C 1关于原点对称的图象为C 2，则直线y=a （a 为常数）与C 1、C 2的交点共有A.1个B.1个或2个C.个或2个或3个D.1个或2个或3个或4个4.如图，矩形ABCD 的长为6，宽为3，点O 1为矩形的中心，⊙O 2的半径为1，O 1O 2⊥AB 于点P ，O 1O 2=6．若⊙O 2绕点P 按顺时针方向旋转360°，在旋转过程中，⊙O 2与矩形的边只有一个公共点的情况一共出现A ．3次B ．4次C ．5次D ．6次5．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使得点A′恰好落在AB上，则旋转角度为A．30°B．60°C．90°D．150°6.如图所示，在直角坐标系中放置一个边长为1的正方形ABCD，将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动，当点A离开原点后第一次落在x轴上时，点A运动的路径线与x轴围成的面积为A．122π+B．12π+C．1π+D．3-7.如图，直线y=2x与双曲线2yx=在第一象限的交点为A，过点A作AB⊥x轴于B，将△ABO绕点O旋转90°，得到△A′B′O，则点A′的坐标为A．（1.0）B．（1.0）或（﹣1.0）C．（2.0）或（0，﹣2）D．（﹣2.1）或（2，﹣1）8.如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置，则旋转角是A．45°B．60°C．90°D．120°9.如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（）A．△ABC绕点C顺时针旋转90°，再向下平移3B．△ABC绕点C顺时针旋转90°，再向下平移1 C．△ABC绕点C逆时针旋转90°，再向下平移1D．△ABC绕点C逆时针旋转90°，再向下平移3二、填空题1.如图，△ABC绕点A顺时针旋转45°得到△A'B'C'，若∠BAC=90°，AB=AC=2，则图中阴影部分的面积等于.2.如图，在在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB=90°，直角边AO在x轴上，且AO=1．将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1，且A1O=2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2，且A2O=2A1O…，依此规律，得到等腰直角三角形A2014OB2014，则点A2014的坐标为．3.如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P1，此时AP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2=1+2；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3=2+2；…，按此规律继续旋转，直至得到点P2014为止．则AP2014=．4.如图，在平面直角坐标系xOy中，已知点M0的坐标为（1，0），将线段OM0绕原点O逆时针方向旋转45°，再将其延长到M1，使得M1M0⊥OM0，得到线段OM1；又将线段OM1绕原点O逆时针方向旋转45°，再将其延长到M2，使得M2M1⊥OM1，得到线段OM2；如此下去，得到线段OM3，OM4，OM5，…根据以上规律，请直接写出OM2014的长度为．5.如图，将等边△ABC绕顶点A顺时针方向旋转，使边AB与AC重合得△ACD，BC的中点E的对应点为F，则∠EAF的度数是．6.如图，已知∠AOB=90°，点A绕点O顺时针旋转后的对应点A1落在射线OB上，点A绕点A1顺时针旋转后的对应点A2落在射线OB上，点A绕点A2顺时针旋转后的对应点A3落在射线OB上，…，连接AA1，AA2，AA3…，依次作法，则∠AA n A n+1等于度．（用含n的代数式表示，n为正整数）7.如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图（2），则图（2）中四边形OGCF与△OCH面积的比为．8.如图在坐标系中放置一菱形OABC，已知∠ABC=60°，OA=1．先将菱形OABC沿x轴的正方向无滑动翻转，每次翻转60°，连续翻转2014次，点B的落点依次为B1，B2，B3，…，则B2014的坐标为．9.如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（53，0），B（0，4），则点B2014的横坐标为．10.通过对课本中《硬币滚动中的数学》的学习，我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程（如图①）．在图②中，有2014个半径为r的圆紧密排列成一条直线，半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位，则动圆C自身转动的周数为．11．如图，△COD是△AOB绕点O顺时针旋转40°后得到的图形，若点C恰好落在AB上，且∠AOD的度数为90°，则∠B的度数是．=上一点P（1，1），C为y轴上一点，连接PC，线段PC绕点12.如图，平面直角坐标系中，已知直线y xP顺时针旋转900至线段PD，过点D作直线AB⊥x轴。
专题2：几何旋转变换
专题2：几何旋转变换1、如图1，△ABC是等腰直角三角形，四边形ADEF是正方形，D、F分别在AB、AC边上，此时BD=CF，BD⊥CF 成立．（1）当正方形ADEF绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，BD=CF成立吗？若成立，请证明；若不成立，请说明理由．（2）当正方形ADEF绕点A逆时针旋转45°时，如图3，延长BD交CF于点G．①求证：BD⊥CF；②当AB=4，BG的长．2、在锐角△ABC中，AB=4，BC=5，∠ACB=45°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．（1）如图1，当点C1在线段CA的延长线上时，求∠CC1A1的度数；（2）如图2，连接AA1，CC1．若△ABA1的面积为4，求△CBC1的面积；（3）如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是点P1，求线段EP1长度的最大值与最小值．3、如图，在平面直角坐标系xOy中，AB⊥x轴于点B，AB=3，tan∠AOB=34，将△OAB绕着原点O逆时针旋转90°，得到△OA1B1；再将△OA1B1绕着线段OB1的中点旋转180°，得到△OA2B1，抛物线y=ax2+bx+c（a≠0）经过点B、B1、A2．（1）求抛物线的解析式．（2）在第三象限内，抛物线上的点P在什么位置时，△PBB1的面积最大？求出这时点P的坐标．（3）在第三象限内，抛物线上是否存在点Q，使点Q到线段BB1Q的坐标；若不存在，请说明理由．【答案】1、解：（1）BD=CF成立。
理由如下：∵△ABC是等腰直角三角形，四边形ADEF是正方形，∴AB=AC，AD=AF，∠BAC=∠DAF=90°。
∵∠BAD=∠BAC﹣∠DAC，∠CAF=∠DAF﹣∠DAC，∴∠BAD=∠CAF。
在△BAD和△CAF中，∵AB=AC，∠BAD=∠CAF，∴△BAD≌△CAF（SAS）。