几何变换之旋转
中考数学专题复习旋转类几何变换
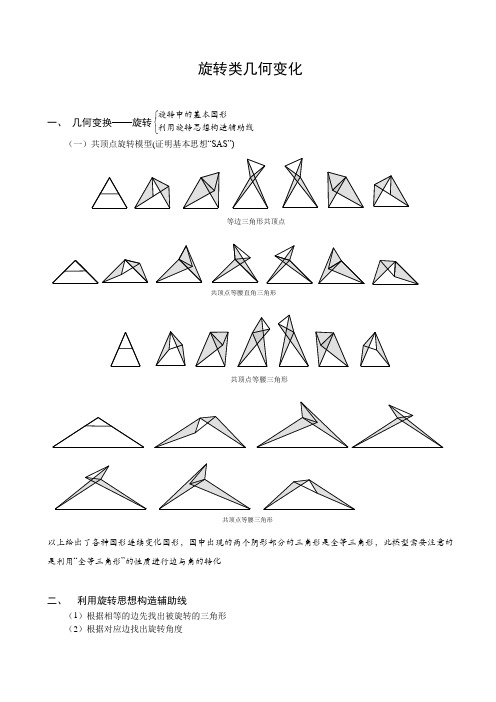
旋转类几何变化一、几何变换——旋转旋转中的基本图形利用旋转思想构造辅助线⎧⎨⎩(一)共顶点旋转模型(证明基本思想“SAS”)等边三角形共顶点共顶点等腰直角三角形共顶点等腰三角形共顶点等腰三角形以上给出了各种图形连续变化图形,图中出现的两个阴影部分的三角形是全等三角形,此模型需要注意的是利用“全等三角形”的性质进行边与角的转化二、利用旋转思想构造辅助线(1)根据相等的边先找出被旋转的三角形(2)根据对应边找出旋转角度(3)根据旋转角度画出对应的旋转的三角形三 、 旋转变换前后具有以下性质:(1)对应线段相等,对应角相等 (2)对应点位置的排列次序相同(3)任意两条对应线段所在直线的夹角都等于旋转角θ.考点一 旋转与最短路程☞考点说明:旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题,涉及费马点问题,视学生程度进行选择性讲解。
【例1】 如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B逆时针旋转60︒得到BN ,连接AM 、CM 、EN . ⑴求证:AMB ENB ∆∆≌⑵①当M 点在何处时,AM CM +的值最小;②当M 点在何处时,AM BM CM ++的值最小,并说明理由; ⑶当AM BM CM ++的最小值为31+时,求正方形的边长.ENMDCB A【例2】 阅读下列材料对于任意的ABC ∆,若三角形内或三角形上有一点P ,若PA PB PC ++有最小值,则取到最小值时,点P 为该三角形的费马点。
①若三角形内有一个内角大于或等于120︒,这个内角的顶点就是费马点②若三角形内角均小于120︒,则满足条件120APB BPC APC ∠=∠=∠=︒时,点P 既为费马点 解决问题:⑴如图,ABC ∆中,三个内角均小于120︒,分别以AB 、AC 为边向外作等边ABD ∆、ACE ∆,连接CD 、BE 交于点P ,证明:点P 为ABC ∆的费马点。
初中数学旋转的知识点

《初中数学旋转知识点全解析》在初中数学的学习中,旋转是一个重要的几何变换概念。
它不仅在数学知识体系中占据着关键地位,也为我们解决各种几何问题提供了有力的工具。
一、旋转的定义在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转。
这个定点称为旋转中心,转动的角称为旋转角。
如果图形上的点 P 经过旋转变为点P′,那么这两个点叫做这个旋转的对应点。
例如,时钟的指针围绕时钟的中心旋转,风车的叶片绕着中心轴旋转等,都是生活中常见的旋转现象。
二、旋转的性质1. 对应点到旋转中心的距离相等。
即旋转前后,图形上任意一点到旋转中心的距离始终保持不变。
例如,在一个正三角形绕其中心旋转的过程中,三角形的三个顶点到旋转中心的距离始终相等。
2. 对应点与旋转中心所连线段的夹角等于旋转角。
旋转过程中,对应点与旋转中心连接形成的线段之间的夹角大小与旋转角相等。
比如,一个矩形绕其对角线的交点旋转一定角度,任意一对对应点与旋转中心所连线段的夹角都等于旋转角。
3. 旋转前后的图形全等。
经过旋转,图形的形状和大小都不会发生改变。
无论旋转角度是多少,旋转后的图形与旋转前的图形完全相同。
例如,一个圆绕其圆心旋转任意角度,得到的图形仍然是与原来一样的圆。
三、旋转的三要素1. 旋转中心旋转中心是图形旋转时所围绕的那个定点。
它决定了图形旋转的位置。
不同的旋转中心会导致图形的旋转结果不同。
2. 旋转方向旋转方向分为顺时针和逆时针两种。
明确旋转方向对于准确描述和进行旋转操作至关重要。
3. 旋转角度旋转角度是指图形绕旋转中心转动的角度大小。
旋转角度的不同会使图形的位置发生不同程度的变化。
四、旋转的应用1. 解决几何问题在证明三角形全等、相似等问题时,常常可以通过旋转图形,使分散的条件集中起来,从而找到解题的思路。
例如,对于两个有公共顶点的等腰三角形,可以通过旋转其中一个三角形,使它们的对应边重合,进而证明全等。
2. 设计图案利用旋转可以设计出各种美丽的图案。
几何形的旋转和对称变换

几何形的旋转和对称变换几何形的旋转和对称变换是数学中常见的概念和技巧。
通过旋转和对称变换,我们可以改变几何形的位置和形状,展现出不同的视觉效果和特性。
本文将介绍旋转和对称变换的定义、性质以及在实际问题中的应用。
一、旋转变换旋转变换是指将几何形绕某个点或某条直线旋转一定角度,从而改变形状和位置。
1. 定义设点A(x, y)绕点O(a, b)逆时针旋转θ度,则旋转后点A的坐标为A’(x', y')。
根据旋转变换的定义,有以下公式:x' = a + (x-a)cosθ - (y-b)sinθy' = b + (x-a)sinθ + (y-b)cosθ2. 性质- 旋转变换不改变几何形的大小。
- 旋转变换保持直线上的点的相对位置关系。
- 旋转角度可以是正数或负数,正数表示逆时针旋转,负数表示顺时针旋转。
3. 应用旋转变换在计算机图形学、机器人学和物理学等领域有广泛的应用。
在设计制图中,旋转变换可以用于生成各种艺术效果、模拟物体的运动轨迹等。
在机器人学中,旋转变换可以应用于机器人的路径规划和姿态控制。
在物理学中,旋转变换可以用于分析刚体的运动和转动。
二、对称变换对称变换是指将几何形围绕着某个轴线或中心对称,从而保持形状不变或形状镜像对称。
1. 定义- 轴对称:如果一个几何形上的任意一点到轴的距离和该点的镜像到轴的距离相等,那么这个几何形关于该轴对称。
常见的轴对称有水平轴对称、垂直轴对称和斜对称。
- 中心对称:如果一个几何形上的任意一点关于某个点对称后仍然位于几何形上,那么这个几何形关于该点中心对称。
中心对称即是以某个点为中心,投影方向相反的对称。
2. 性质- 对称变换保持几何形的面积和周长不变。
- 轴对称保持几何形的形状相同,而中心对称保持几何形的形状镜像对称。
- 轴对称和中心对称可以叠加使用,得到更复杂的变换效果。
3. 应用对称变换在几何学、物理学和图像处理等领域具有重要的应用。
空间几何的旋转和旋转变换

空间几何的旋转和旋转变换空间几何中的旋转是指空间中一点围绕某一固定点旋转一定角度所形成的图形变换。
在空间几何中,旋转是一种非常重要的变换,它不仅广泛应用于数学、物理学等领域,也是3D图形学中的一个重要概念。
本文将对空间几何中的旋转和旋转变换进行探讨。
一、空间几何的旋转1.1 旋转的定义首先,我们需要明确什么是空间几何的旋转。
在空间几何中,旋转是指将空间中的任意一点A绕某一固定点O旋转一定角度后,所形成的新点A',即:A' = R(A)其中,R(A)表示将点A绕点O进行一定角度的旋转所得到的新点。
在这个过程中,极角和极径都会发生改变。
1.2 旋转的性质空间几何中的旋转具有以下特点:1、旋转是保持距离和角度不变的变换;2、旋转是一种可逆变换,即旋转一次可以得到一一对应的变换;3、在空间中,旋转操作可围绕任何轴进行,但绕不同轴旋转所得到的变换结果是不同的。
二、空间几何的旋转变换旋转变换是指将一个点绕着一个轴旋转一个角度。
旋转变换在实际应用中非常广泛,在制造业、航空航天等领域都有着重要的作用。
2.1 旋转变换的定义在空间几何中,旋转变换是指将空间中的任意一点A绕某一固定轴L旋转一定角度后,所形成的新点A',即:A' = R(A,α ,L)其中,R表示旋转变换,α表示旋转角度,L表示旋转轴。
2.2 旋转变换的性质旋转变换具有以下特点:1、旋转变换是保持距离和角度不变的变换;2、旋转变换是一种可逆变换,即旋转一次可以得到一一对应的变换;3、在空间中,旋转变换可围绕任何轴进行。
三、应用举例旋转变换广泛应用于制造业、航空航天、计算机图形学等领域。
以下是一些应用举例:3.1 机械加工在机械加工领域,旋转变换被广泛应用于三轴数控加工中。
通过旋转变换,可以实现工件在各个面上的加工,从而大大提高了加工质量和效率。
3.2 航空航天在航空航天领域,旋转变换被应用于飞机的飞行姿态控制。
通过调整飞机的俯仰、横滚和偏航角度,可以达到控制飞机飞行方向的目的。
旋转平移翻折的几何变换与性质

旋转平移翻折的几何变换与性质旋转、平移和翻折是几何中常见的基本变换方式,它们在空间和平面几何中发挥着重要的作用。
本文将介绍旋转平移翻折的几何变换及其性质,推导其数学表达式,并通过具体的实例来说明其应用。
一、旋转变换旋转是指将平面或空间中的图形按照一定角度绕着旋转中心进行旋转的操作。
对于平面上的点(x, y),其绕原点逆时针旋转θ度后的新坐标可以由以下公式计算得出:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,x'和y'分别表示旋转后点的坐标,θ为旋转角度。
二、平移变换平移是指将平面或空间中的图形沿着指定的方向和距离进行移动的操作。
平移变换可以用一个向量来表示。
对于平面上的点(x, y),其平移(dx, dy)后的新坐标可以由以下公式计算得出:x' = x + dxy' = y + dy其中,(dx, dy)为平移向量,x'和y'分别表示平移后点的坐标。
三、翻折变换翻折是指将平面或空间中的图形沿着指定的轴进行对称的操作。
对于平面上的点(x, y),其关于直线y=k翻折后的新坐标可以由以下公式计算得出:x' = xy' = 2k - y其中,(x', y')为翻折后点的坐标,k为翻折轴的位置。
以上是旋转、平移和翻折的几何变换的数学表达式。
下面将通过实例说明它们在几何问题中的应用。
实例一:旋转变换假设有一张平面上的三角形ABC,顶点分别为A(1, 2),B(3, 4)和C(5, 6)。
现在需要将该三角形绕原点顺时针旋转60度,求旋转后各顶点的坐标。
根据旋转变换的公式,旋转角度θ=60°,原点为旋转中心,可以计算得出旋转后的各顶点坐标为:A'(1*cos60° - 2*sin60°, 1*sin60° + 2*cos60°) = (0.5, 2.598)B'(3*cos60° - 4*sin60°, 3*sin60° + 4*cos60°) = (-1.133, 4.330)C'(5*cos60° - 6*sin60°, 5*sin60° + 6*cos60°) = (1.333, 7.464)实例二:平移变换假设有一条直线L,其方程为y = 2x - 1。
初中几何旋转知识点总结

初中几何旋转知识点总结一、基本概念1. 旋转的基本概念旋转是一种平移,比如将一张纸围绕桌子中心旋转,不移动位置但是角度改变。
可以定义一个点O为旋转中心,角度为θ,则旋转变换R(O,θ)将点P绕点O旋转θ度。
2. 旋转的表示方法通常用旋转中心和旋转的角度来表示一个旋转变换,如R(O,θ)表示以点O为旋转中心,按照角度θ进行旋转变换。
3. 旋转的方向根据旋转的角度正负可以表示旋转的方向,当角度为正时,表示顺时针旋转;当角度为负时,表示逆时针旋转。
二、旋转的性质1. 旋转中心的不变性对于任意一个固定的点P,在平面上做旋转变换后,点P相对于旋转中心O的距离不变,即OP'=OP。
2. 旋转中心的互易性两点围绕各自为中心的旋转之后,它们的连接线也围绕旋转后的两个点为中心进行旋转。
3. 旋转的对称性对于一个平面图形,绕着一个点做旋转变换之后,原来的平面图形与旋转后的图形具有对称性。
4. 旋转的组合性对于两个旋转变换R(O1,θ1)和R(O2,θ2),它们的组合旋转变换是R(O1,θ1) ◦R(O2,θ2)=R(O1O2,θ1+θ2),即先以O2为中心旋转θ2度,再以O1为中心旋转θ1度,等效于以点O1O2为中心旋转θ1+θ2度。
三、旋转的定理1. 旋转角度的性质(1)相等角度的旋转等效于一次旋转;(2)逆时针旋转θ度等效于顺时针旋转360-θ度;(3)旋转360度等效于不旋转。
2. 旋转的运动规律旋转的运动规律由旋转角度的规律和旋转方向的规律组成,它描述了一个点或者平面图形在旋转中的变化规律。
3. 旋转的应用(1)旋转的应用:如地球自转产生了昼夜交替、太阳绕地球公转产生了四季交替等;(2)旋转对称性:通过旋转对称性,可以简化问题的解决和推理过程。
四、常见问题解析1. 旋转的基本操作(1)绕平面上任一点旋转θ度的变换,可以用旋转矩阵R来表示,即对任意点(A, B),有(A', B') = R(A, B)。
几何形的旋转平移和对称变换
几何形的旋转平移和对称变换几何形的旋转、平移和对称变换几何形的旋转、平移和对称变换是几何学中的基础概念和操作,它们在数学和实际应用中都扮演着重要的角色。
通过这些变换,我们可以改变和调整图形的位置、方向和形状,使得几何问题的解决变得更加灵活和方便。
本文将对几何形的旋转、平移和对称变换进行详细介绍。
1. 旋转变换旋转变换是指沿着一个固定点旋转图形一定的角度。
在平面几何中,我们通常以原点为中心,按照逆时针方向旋转来描述旋转变换。
旋转变换可以保持图形的大小和形状不变,只改变其方向和位置。
常见的旋转角度有90度、180度和360度。
旋转变换的数学表示式为:x' = x*cosθ - y*sinθy' = x*sinθ + y*cosθ其中,(x, y)是旋转前的点的坐标,(x', y')是旋转后的点的坐标,θ是旋转的角度。
2. 平移变换平移变换是指将图形沿着平行于坐标轴的方向移动一定的距离。
平移变换只改变图形的位置,保持其大小、形状和方向不变。
平移变换可以用向量来表示,其中向量的分量表示图形在x轴和y轴上的位移。
平移变换的数学表示式为:x' = x + dxy' = y + dy其中,(x, y)是平移前的点的坐标,(x', y')是平移后的点的坐标,(dx, dy)是平移的距离。
3. 对称变换对称变换是指将图形绕着某个轴线或某个点进行翻转,使得图形在变换前后保持镜像对称关系。
常见的对称变换有关于x轴、y轴和原点的对称。
对称变换的数学表示式为:关于x轴对称:(x, y) -> (x, -y)关于y轴对称:(x, y) -> (-x, y)关于原点对称:(x, y) -> (-x, -y)4. 综合应用几何形的旋转、平移和对称变换在许多领域有着广泛的应用,如建筑设计、计算机图形学、机器人学等等。
通过这些变换,我们可以灵活地处理图形的位置和形状,满足不同需求的设计和计算要求。
专题22 几何三大变换问题之旋转问题(压轴题)
《中考压轴题》专题22:几何三大变换问题之旋转(中心对称)问题一、选择题1.如图,已知△ABC 中,∠C=90°,AC=BC=,将△ABC 绕点A 顺时针方向旋转60°到△AB′C′的位置,连接C′B ,则C′B 的长为A .22-B .32C .31-D .12.如图,△AOB 为等腰三角形,顶点A 的坐标为(2,5),底边OB 在x 轴上.将△AOB 绕点B 按顺时针方向旋转一定角度后得△A'O'B ,点A 的对应点A'在x 轴上,则点O'的坐标为A .(203,103)B .(163,453)C .(203,453)D .(163,43)3.在平面直角坐标系中,函数y=x 2﹣2x (x≥0)的图象为C 1,C 1关于原点对称的图象为C 2,则直线y=a (a 为常数)与C 1、C 2的交点共有A.1个B.1个或2个C.个或2个或3个D.1个或2个或3个或4个4.如图,矩形ABCD 的长为6,宽为3,点O 1为矩形的中心,⊙O 2的半径为1,O 1O 2⊥AB 于点P ,O 1O 2=6.若⊙O 2绕点P 按顺时针方向旋转360°,在旋转过程中,⊙O 2与矩形的边只有一个公共点的情况一共出现A .3次B .4次C .5次D .6次5.如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转至△A′B′C,使得点A′恰好落在AB上,则旋转角度为A.30°B.60°C.90°D.150°6.如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为A.122π+B.12π+C.1π+D.3-7.如图,直线y=2x与双曲线2yx=在第一象限的交点为A,过点A作AB⊥x轴于B,将△ABO绕点O旋转90°,得到△A′B′O,则点A′的坐标为A.(1.0)B.(1.0)或(﹣1.0)C.(2.0)或(0,﹣2)D.(﹣2.1)或(2,﹣1)8.如图,E、F分别是正方形ABCD的边AB、BC上的点,BE=CF,连接CE、DF.将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置,则旋转角是A.45°B.60°C.90°D.120°9.如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是()A.△ABC绕点C顺时针旋转90°,再向下平移3B.△ABC绕点C顺时针旋转90°,再向下平移1 C.△ABC绕点C逆时针旋转90°,再向下平移1D.△ABC绕点C逆时针旋转90°,再向下平移3二、填空题1.如图,△ABC绕点A顺时针旋转45°得到△A'B'C',若∠BAC=90°,AB=AC=2,则图中阴影部分的面积等于.2.如图,在在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2014OB2014,则点A2014的坐标为.3.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+2;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+2;…,按此规律继续旋转,直至得到点P2014为止.则AP2014=.4.如图,在平面直角坐标系xOy中,已知点M0的坐标为(1,0),将线段OM0绕原点O逆时针方向旋转45°,再将其延长到M1,使得M1M0⊥OM0,得到线段OM1;又将线段OM1绕原点O逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2;如此下去,得到线段OM3,OM4,OM5,…根据以上规律,请直接写出OM2014的长度为.5.如图,将等边△ABC绕顶点A顺时针方向旋转,使边AB与AC重合得△ACD,BC的中点E的对应点为F,则∠EAF的度数是.6.如图,已知∠AOB=90°,点A绕点O顺时针旋转后的对应点A1落在射线OB上,点A绕点A1顺时针旋转后的对应点A2落在射线OB上,点A绕点A2顺时针旋转后的对应点A3落在射线OB上,…,连接AA1,AA2,AA3…,依次作法,则∠AA n A n+1等于度.(用含n的代数式表示,n为正整数)7.如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为.8.如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为.9.如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(53,0),B(0,4),则点B2014的横坐标为.10.通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为.11.如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是.=上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点12.如图,平面直角坐标系中,已知直线y xP顺时针旋转900至线段PD,过点D作直线AB⊥x轴。
数学实验,由静变动——《几何三大变换之旋转》教学案例
数学实验,由静变动——《几何三大变换之旋转》教学案例发布时间:2022-11-20T18:23:04.310Z 来源:《基础教育参考》2022年11月作者:陈玉伦谢维锶[导读]陈玉伦谢维锶珠海市凤凰中学 519000中图分类号:G626.5 文献标识码:A 文章编号:ISSN1672-1128(2022)11-091-04数学实验是为了帮助学生建构某种几何理论,或检验某个几何猜想,或解决某类几何问题,借助于多媒体PC上的几何画板、平板软件上的几何画板等技术手段或者设计的具体实物教具,通过对实验素材进行实际操作来理解、解释或建构几何概念、定理或结论的学习活动。
旋转变换在初中几何中占有重要的地位,常在压轴题中出现。
旋转的定义及性质并不难理解,难的是有些几何题的题干没有提到旋转,直接求解有时会困难重重,若采用旋转,则可以得到一些新的特殊图形、特殊关系,利用这些图形和关系,能使问题迎刃而解,为同学们解题时提供思路。
一、设计简述【教学目标】1.回顾旋转变换的定义、性质等相关知识,利用旋转的性质解决相关问题。
2.通过数学实验,探索旋转变换的适用条件,经历将已知条件转换为待求目标,利用旋转找到解决问题的途径。
3.体验利用几何变换解决问题的优势,提高空间想象能力。
【教学过程】(一)知识回顾观看动画,回顾旋转的定义、性质,同时,学生通过每个小组发放的ipad,打开其中的软件,如动态几何画板等,在平板中画出相应的图形,通过不同的选择,在数学实验报告学案上填写出相应的数据,分析,归纳出旋转的基本性质。
(1)旋转的定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形变换称为旋转,这个定点称为旋转中心,转动的角称为旋转角。
(2)旋转的性质:①对应点到旋转中心的距离相等;②对应点与旋转中心所连线段的夹角等于旋转角;③旋转前、后的图形全等,即旋转前后图形的大小和形状没有改变。
(二)利用旋转图形的性质解决问题一些题已直接告知旋转变换的信息,直接利用旋转的性质来解决问题即可,接下来向同学们介绍两种常见考点。
九年级数学旋转的知识点
九年级数学旋转的知识点九年级数学中,旋转是一个重要的几何变换,它在解决各种几何问题中起着重要的作用。
本文将介绍九年级数学中旋转的基本概念、性质以及相关例题,以帮助同学们更好地理解和掌握这一知识点。
1. 旋转的基本概念旋转是指在平面内,绕着一个点旋转图形,使得图形在平面上转动。
旋转可以分为顺时针旋转和逆时针旋转两种。
常用的表示方法是以旋转中心为原点,旋转角度为正,顺时针旋转为负。
2. 旋转的性质(1)旋转是一个保角变换,即旋转前后的两条线段之间的夹角相等。
(2)旋转是一个保距变换,即旋转前后的两条线段的长度相等。
(3)旋转不改变图形的对称性,即旋转前后的图形具有相同的对称性。
3. 点、线和图形的旋转(1)点的旋转:点的旋转只是将一个点绕旋转中心旋转一定角度,并保持距离不变。
(2)线的旋转:线的旋转是通过将线段的两个端点绕旋转中心旋转一定角度,并保持线段长度不变。
(3)图形的旋转:图形的旋转是将整个图形绕旋转中心旋转一定角度,并保持图形的形状和大小不变。
4. 旋转的变换规律(1)旋转180度:一个图形绕旋转中心旋转180度后,得到的图形与原图关于旋转中心对称。
(2)旋转90度或270度:一个图形绕旋转中心旋转90度或270度后,得到的图形与原图关于旋转中心垂直对称。
(3)旋转360度:一个图形绕旋转中心旋转360度后,得到的图形与原图完全相同。
5. 旋转的应用举例(1)构造一个正方形:通过旋转一个合适的线段,可以构造一个正方形。
(2)判断图形是否重合:通过判断图形旋转一周后是否与原图形重合,可以判断两个图形是否重合。
(3)辅助解题:在解决一些几何问题时,通过对图形进行旋转可以得到一些有用的信息。
通过以上的介绍,希望同学们对九年级数学中旋转的知识点有了更深入的了解。
在学习和应用中,同学们可以灵活运用旋转的性质和规律,解决各种几何问题。
同时,建议同学们多做练习,加深对旋转的理解和运用能力。
祝大家在数学学习中取得更好的成绩!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例1】 如图,在Rt ABC ∆中,AB AC AD BC =⊥,,垂足为D .E F 、分别是CD AD 、上的点,且CE AF =.如果62AED ∠=︒,那么DBF ∠=__________.FCBA【答案】28︒【例2】 E 、F 分别是正方形ABCD 的BC 、CD 边上的点,且BE CF =.求证:AE BF ⊥.PFEDCBA【答案】在ABE ∆和BCF ∆中AB BCABE BCF BE CF =⎧⎪∠=∠⎨⎪=⎩∴ABE BCF ∆∆≌ ∴BAE CBF ∠=∠ ∵90BAE AEB ∠+∠=︒ ∴90CBF AEB ∠+∠=︒ ∴AE BF ⊥【例3】 E 、F 、G 分别是正方形ABCD 的BC 、CD 、AB 边上的点,GE EF ⊥,GE EF =.求证:BG CF BC +=.GA BC DEF【例4】 如图,矩形ABCD 中,E 是AD 上一点,CE EF ⊥交AB 于F 点,若2DE =,矩形周长为16,且CE EF =,求AE 的长.EDCBF A【答案】∵FE EC ⊥,∴90AEF DEC ∠+∠=︒.∵90AEF AFE ∠+∠=︒, ∴AFE DEC ∠=∠.在三角形AFE 与DEC ∆中,FE CE =,90A D ∠=∠=︒,AFE DEC ∠=∠,∴AFE DEC ∆∆≌. ∴AE DC =.∵矩形周长为16, ∴8AD DC +=. ∵AD AE DE =+,∴且2DE =.∴28AE DE =-.即3AE =【例5】 如图,已知ABC ∆中,90ABC AB BC ∠=︒=,,三角形的顶点在相互平行的三条直线123l l l ,,上,且12l l ,之间的距离为2,23l l ,之间的距离为3,则AC 的长是______.CBAl 3l 2l 1【答案】【例6】 两个全等的30︒、60︒的三角板ADE 、BAC ,如右下图所示摆放,E 、A 、C 在一条直线上,连结BD .取BD 的中点M ,连结ME 、MC ,试判断EMC ∆的形状,并说明理由.ME DCBA【解析】判断EMC ∆是等腰直角三角形.理由:如图,连结AM .DMBCA E∵30DAE ∠=︒,60BAC ∠=︒,∴90DAB ∠=︒ ∵ADE BAC ∆∆≌,∴AD AB =又∵M 是BD 的中点,∴AM DM BM == ∴45ADM MAB ∠=∠=︒∴6045105EDM EDA ADM ∠=∠+∠=︒+︒=︒ ∴4560105MAC MAB BAC ∠=∠+∠=︒+︒=︒ ∴EDM MAC ∠=∠∵ED CA =,∴EDM CAM ∆∆≌ ∴EM CM =,DME AMC ∠=∠而90DME EMA ∠+∠=︒,∴90AMC EMA ∠+∠=︒ 即90EMC ∠=︒,∴EMC ∆是等腰直角三角形.【例7】 已知等腰直角三角形ABC ,C ∠为直角,M 为BC 的中点.CD AM ⊥.求证:AMC DMB ∠=∠.求证:AMC DMB ∠=∠.MDCBA【例8】 如图所示,已知在等腰直角三角形ABC 中,BAC ∠是直角,D 是AC 上一点,AE BD ⊥,AE 的延长线交BC 于F ,若A D B F D C ∠=∠,求证:D 是AC 的中点.F EDCBA【答案】过C 作CH 垂直于AC 交AF 延长线于H 点;易证ABD AHC ∆∆≌,HC AD =;进而证明FHC FDC ∆∆≌,得到HC CD =,则D 为AC 中点.H F EDCBA【例9】 如图所示,在等边ABC ∆中,DE BC ∥,O 为ADE ∆的中心,M 为BE 的中点,求证OM CM ⊥.【答案】如图所示,延长OM 至点N ,使OM MN =,连接OA 、OE 、OC 、BN 、CN .M CBAED ON MCB AED O因为OM NM =,BM M E =,OME NMB ∠=∠, 故BMN ∆≌EMO ∆,则BN EO =,OEM NBM ∠=∠. 因为DE BC ∥,则DEB CBE ∠=∠,OED CBN ∠=∠.因为O 为ADE ∆的中心,则OA OE BN ==,30OAE OED CBN ∠=∠=︒=∠. 因为AC BC =,故AOC ∆≌BNC ∆,从而OC CN =. 因为OM MN =,故OM CM ⊥.【点评】如果具备三角形相似的知识,我们就可以采取下面的解法. 如图所示,取AE 的中点N ,连接MN 、OA 、ON 、OC .因为O 为ADE ∆的中心,故30OAN ∠=︒,2OA ON =. 因为AN NE =,BM EM =,故2AB MN AC ==. 因为ON AC ⊥,MN AB ∥,故60MNE ∠=︒,因为30ONM ∠=︒,故O A C ∆∽ONM ∆,OMN OCN ∠=∠,则O 、M 、C 、N 四点共圆.因为ON AC ⊥,故OM CM ⊥.【例10】 已知P 为等腰直角ABC ∆的斜边AB 上任意一点,PE 、PF 分别为AC 、BC 之垂线,垂足为E 、F .M 为AB 之中点.则E 、M 、F 组成等腰直角三角形.MP F EC BA【答案】解法一:如图,连接CM ,则CM 为AB 之中线,亦为AB 之高.PMBA F EC∴90CMA ∠=︒.∵90PEC PFC ECF ∠=∠=∠=︒, ∴ECFP 为矩形,故PE CF =. 又∵45A ∠=︒,∴AEP ∆为等腰直角三角形,∴AE PE =.∴AE CF =. 又∵CM AM =,45MCF A ∠=∠=︒, ∴AEM CFM ∆∆≌,∴AME CMF ∠=∠,EM FM =. ∵90CME AME ∠+∠=︒,∴90CME CMF ∠+∠=︒,即90EMF ∠=︒. ∴EM F ∆为等腰直角三角形. 解法二:如图,由M 作ME AC '⊥,MF BC '⊥,则显然由于M 为AB 之中点,AC BC =,AC BC ⊥,PMBA F E C F'E'Q∴ME CF ''为正方形,故M E M F ''=. 又设M E '交PF 于Q , 则∵PE AC ⊥,PF BC ⊥,∴90EPF C ∠=∠=︒.而90PEE EE Q ''∠=∠=︒. ∴EE QP '为矩形,故EE PQ '=. 同理FF QM '=.又∵PF AC ∥,∴45QPM A ∠=∠=︒. ∴PQM ∆为等腰直角三角形, ∴PQ QM =,故EE FF ''=.又M E M F ''=,90EE M FF M ''∠=∠=︒.∴EEMFFM ''∆∆≌, ∴EM E FM F ''∠=∠,EM FM =. 又90E MF FMF ''∠+∠=︒, ∴90E MF EME ''∠+∠=︒.即90EMF ∠=︒,故M EF ∆为等腰直角三角形.解法三:如图,延长FM 到Q ,使MQ FM =,连接AQ .PMBA F EC Q∵AM BM =,∴A 、F 、B 、Q 4点组成平行四边形. ∴AQ FB =,AQ FB ∥. 又∵BC AC ⊥,∴AQ AC ⊥, ∴90QAE FCE ∠=∠=︒.又∵PF BC ⊥,45B ∠=︒,∴FP FB =.同理EP AE =. ∵ECFP 为矩形,∴FP CE =,EP CF =,故AB .而CM AB ⊥, ∴AQ CE =,AE CF =. ∴Rt Rt AEQ CFE ∆∆≌.∴EQ FE =,AQE CEF ∠=∠,QEA EFC ∠=∠. ∵90AQE QEA ∠+∠=︒, ∴90CEF QEA ∠+∠=︒.故PFQF= ∴FEQ ∆为等腰直角三角形.而M 为底边之中点,所以EM F ∆亦为等腰直角三角形.解法四:如图,连接CM ,则因为M 为AB 之中点,所以CM AB ⊥,CM 平分ACB ∠,即45MCB ∠=︒.由F 向MB 引垂线FQ ,向CM 引垂线FF ',显然F FQM'为矩形.则FF MQ '=.PM BA FECF'Q又∵CF F '∆为等腰直角三角形,CF '. 又∵PE AC ⊥,PF BC ⊥,AC BC ⊥, ∴ECFP为矩形,故EP CF ==.于是在Rt EPF ∆和Rt MQF ∆中,PF FB ==,PF QF =EPMQ= ∴PF EPQF MQ=,∴EPF MQF ∆∆∽,故EFP MFQ ∠=∠. 又∵45PFM MFQ ∠+∠=︒,∵45PFM EFP ∠+∠=︒,即PF BF =. 同理45FEM ∠=︒,EM F ∆为等腰直角三角形. 解法五:如图,连接CP 、CM .PMBA F EC∵PF BF =,ABC ∆为等腰直角三角形, ∴45BPF BCM ∠=∠=︒.∴P 、C 、F 、M 4点共圆.∴CMF CPF ∠=∠.又∵CPF CEF ∠=∠,∴CEF CMF ∠=∠,∴E 、C 、F 、M 4点共圆. ∴45MEF MCF ∠=∠=︒,45MFE MCE ∠=∠=︒,∴iEMF 是等腰直角三角形.【例11】 长方形ABCD 中,4AB =,7BC =,BAD ∠的角平分线交BC 于点E ,EF ED⊥交AB 于F ,则EF =_________.FEDCB A【解析】由4AB =,AE 平分BAD ∠可知4BE AB CD ===. 由基本图可知BEF CDE ∆∆≌,故EF DE =又7BC =,4BE =,故3CE =.由勾股定理可知,5DE =. 从而可知5EF =. 【答案】5【例12】 如图,设ABC ∆和CDE ∆都是正三角形,且62EBD ∠=︒,则AEB ∠ 的度数是( )A .124︒B .122︒C .120︒D .118︒图1ADBCE【答案】分析 既然题目这样问,说明这两个角之间必然能找到一定的联系.解 易知ACE BCD ∠=∠,AEC BDC ∆∆≌,于是EAC DBC ∠=∠,从而EBD CBD CBE EAC CBE ∠=∠+∠=∠+∠, 在考虑到360EAC AEC ACE CEB ECB EBD ∠+∠+∠+∠+∠+∠= ,有:3606062360BEC AEC AEB ∠+∠=--=-∠ 从而122AEB ∠= ,选B 。
【例13】 已知:BD CE 、是ABC ∆的高,点P 在BD 的延长线上,BP AC =,点Q 在CE 上,CQ AB =,求证:⑴AP AQ =;⑵AP AQ ⊥.PDQCBEA【答案】如图,设CE 交BD 于F .⑴ 由BD CA ⊥,CE AB ⊥,知90BEF CDF ∠=︒=∠.而BFE CFD ∠=∠, 故ABD QCA ∠=∠.由已知,有AB QC =,BP CA =,从而ABP QCA ∆∆≌, 即有AP AQ =.⑵ 由⑴可得AQC PAB ∠=∠,而 90AQC QEA QAE QAE ∠=∠+∠=︒+∠. PAB PAQ QAE ∠=∠+∠.从而可得90PAQ ∠=︒,即AP AQ ⊥.【例14】 如图,ABC ∆的边BC 在直线l 上,AC BC ⊥,且AC BC =;EFP ∆的边FP 也在直线l 上,边EF 与边AC 重合,且EF FP =.⑴ 在图1中,请你通过观察、测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;⑵ 将EFP ∆沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连结AP ,BQ .猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想; ⑶ 将EFP ∆沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长线于点Q ,连结AP ,BQ .你认为⑵中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.图⑴lPC (F )B A (E )图⑵Q ←lPFE C B A图⑶←QAEB CF Pl4321A B C EFPlQN lPFCBEAQ【答案】(1)AB AP =;AB AP ⊥.(2)BQ AP =;BQ AP ⊥.①由已知,得EF EP EF FP =⊥,,∴45EPF ∠=︒. 又∵AC BC ⊥,∴45CQP CPQ ∠=∠=︒.∴CQ CP =. 在Rt BCQ ∆和Rt ACP ∆中,90BC AC BCQ ACP CQ CP =∠=∠=︒=,,,∴Rt Rt BCQ ACP ∆∆≌,∴BQ AP =. ②如图,延长BQ 交AP 于点M . ∵Rt Rt BCQ ACP ∆∆≌,∴12∠=∠. 在Rt BCP △中,1390∠+∠=︒,又34∠=∠,∴241390∠+∠=∠+∠=︒.∴90QMA ∠=︒.∴BQ AP ⊥. (3)成立.①∵45EPF ∠=︒,∴45CPQ ∠=︒.又∵AC BC ⊥,∴45CQP CPQ ∠=∠=︒.∴CQ CP =. 在Rt BCQ ∆和Rt ACP ∆中,90BC AC BCQ ACP CQ CP =∠=∠=︒=,,,∴Rt Rt BCQ ACP ∆∆≌.∴BQ AP =.②如图,延长QB 交AP 于点N ,则PBN CBQ ∠=∠. ∵Rt Rt BCQ ACP ∆∆≌,∴BQC APC ∠=∠. 在Rt BCQ ∆中,90BQC CBQ ∠+∠=︒, ∴90APC PBN ∠+∠=︒.∴90PNB ∠=︒. ∴BQ AP ⊥.【例15】ABC ∆中,D 为BC 中点,DE BC ⊥交BAC ∠的平分线于点E ,EF AB ⊥于F EG AC ⊥于G .求证:BF CG =.EGF DC BADE 垂直平分BC ,∴BE CE =,AE 平分BAC ∠,EF AB ⊥,EG AC ⊥,∴EF EG =,又90BFE CGE ∠=∠=︒,∴Rt BEF ∆≌Rt CEG ∆(HL ),∴BF CG =,【例16】 如图,在正方形ABCD 中,M 是AB 的中点,,MN MD BN CBE ⊥∠平分,E 为AB的延长线上一点.求证:MD MN =.NM EDCB A【答案】取AD 的中点P ,连接MP ,证明PMD BNM ∆∆≌,于是MD MN =.【例17】 如图,点M 为正方形ABCD 的边AB 上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,MD 与MN 有怎样的数量关系?N CDE B M A NCDEB M A【答案】猜测DM MN =.在AD 上截取AG AM =,∴DG MB =,∴45AGM = ∠∴135DGM MBN ==︒∠∠,∴ADM NMB =∠∠, ∴DGM MBN ∆∆≌,∴DM MN =.【例18】 如图,点M 为正方形ABCD 的边AB (或BA )延长线上任意一点,MN DM ⊥且与ABC ∠外角的平分线交于点N ,此时MD 与MN 有何数量关系?并加以证明.CD NEM B A【答案】猜测MD MN =,延长AD 至点P ,使DP BM =,连结PM .P CDNEM B A∵DC AM ∥, ∴CDM DMA =∠∠, ∴PDM BMN =∠∠, 而45APM NBM ==︒∠∠, ∴PDM BMN ∆∆≌, ∴MD MN =【例19】 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=︒,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系?NEB M A D【答案】猜测DM MN =.过点M 作MG BD ∥交AD 于点G ,AG AM =,GNEB M A D∴GD MB =又∵120ADM DMA +∠= ∠,120DMA NMB += ∠∠ ∴ADM NMB =∠∠,而120DGM MBN == ∠∠,∴DGM MBN ∆∆≌,∴DM MN =.【例20】 已知,ABC ∆中,3AB =,120BAC ∠=︒,1AC =,D 为AB 延长线上一点,1BD =,点P 在BAC ∠的平分线上,且满足PAD ∆是等边三角形. ⑴ 求证:BC BP =; ⑵ 求点C 到BP 的距离.CB P DAEDC BA【答案】⑴ 解法一:连结PC∵11AC BD ==,,∴AC BD =, ∵120BAC ∠=︒,AP 平分BAC ∠, ∴1602CAB BAC ∠=∠=︒,∵PAD ∆是等边三角形,∴60PA PD D =∠=︒,, ∴CAB D ∠=∠,∴PAC PDB ∆∆≌, ∴PC PB APC DPB =∠=∠,, ∴60APC APB DPB APB BPC DPA ∠+∠=∠+∠∠=∠=︒,, ∴PBC ∆是等边三角形,BC BP =.解法二:作BM PA ∥交PD 于M ,证明PBM BCA ∆∆≌, 证明过程略.MADP B CNFEAD PBC⑵ 解法一:作CE PB ⊥于E ,PF AB ⊥于F . ∵31AB BD ==,,∴4AD =, ∵PAD ∆是等边三角形,PF AB ⊥,∴12sin602DF AD PF PD ===⋅︒=,∴1BF DF BD BP =-=,∴sin 60sin 60CE BC BP =⋅︒=⋅︒, 即点C 到BP. 解法二:作BN DP ⊥于N , ∴12DN =,72NP DP DN =-=,BN =,∴BP =以下同解法一.【例21】 如图,已知ABC ∆和ADE ∆都是等边三角形,B 、C 、D 在一条直线上,试说明CE与AC CD +相等的理由.EDCBA【答案】∵AC AB =,CAE BAD ∠=∠,AE AD =∴AEC ADB ∆∆≌ ∴CE BD =又∵BD BC CD AC CD =+=+ ∴CE AC CD =+【例22】 如图,在四边形ABCD 中, AD BC ∥,点E 是AB 上一个动点;若60B ∠=︒,AB BC =,且60DEC ∠=︒,判断AD AE +与BC 的关系并证明你的结论.EDCB A【答案】过点E 作EF BC ∥交AC 于F .F ABC DE∵60AB BC B =∠=︒,,∴ABC ∆是等边三角形, 由EF BC ∥易知,AEF ∆也是等边三角形, ∴60AE FE AEF AFE BE CF =∠=∠=︒=,,, ∵AD BC ∥,∴180120EAD B ∠=︒-∠=︒,且120EFC ∠=︒, ∵60DEC AEF ∠=∠=︒,∴AED FEC ∠=∠, ∴()ASA AED FEC ∆∆≌,∴AD FC BE ==, ∴AB AE BE AE AD =+=+,∴BC AD AE =+.【例23】 已知,在ABC ∆中,ACB ∠为锐角,D 是射线BC 上一动点(D 与C 不重合),以AD为一边向右侧作等边ADE ∆(C 与E 不重合),连接CE .⑴ 若ABC ∆为等边三角形,当点D 在线段BC 上时(如图1所示),则直线BD 与直线CE 所夹锐角为 度;⑵ 若ABC ∆为等边三角形,当点D 在线段BC 的延长线上时(如图2所示),你在⑴中得到的结论是否仍然成立?请说明理由; ⑶ 若ABC ∆不是等边三角形,且BC AC >(如图3所示).试探究当点D 在线段BC上时,你在⑴中得到的结论是否仍然成立?若成立,请说明理由;若不成立,请指出当ACB ∠满足什么条件时,能使⑴中的结论成立,并说明理由.图1FED C B A图2B C D F AE图3B CFAGEDF CBA【答案】⑴ 60︒;⑵ 成立.∵ABC ∆是等边三角形,∴60AB AC BAC =∠=︒,, ∵ADE ∆是等边三角形,∴60AD AE DAE =∠=︒,, ∴BAD CAE ∠=∠,∴()SAS BAD CAE ∆∆≌, ∴60ACE ABD ∠=∠=︒, ∵120ACD ∠=︒,∴60ECF ∠=︒, 即直线BD 与直线CE 所夹锐角为60︒.⑶ 原结论不成立.当60ACB ∠=︒时,才能使⑴中的结论成立. 当60ACB ∠=︒时,在BC 上取一点G ,使得CG AC =, 则AGC ∆是等边三角形,∴60AG AC GAC =∠=︒,, ∵ADE ∆是等边三角形,∴60AD AE DAE =∠=︒,, ∴GAD CAE ∠=∠,∴()SAS GAD CAE ∆∆≌, ∴60ACE AGD ∠=∠=︒,∴180180606060ECF ACG ACE ∠=︒-∠-∠=︒-︒-︒=︒. ∴当60ACB ∠=︒时,能使⑴中的结论成立.【例24】 如图,等边三角形ABC ∆与等边DEC ∆共顶点于C 点.求证:AE BD =.DECBA【答案】∵ABC ∆是等边三角形,∴60ACB ∠=︒,AC BC =.∴60BCD DCA ∠+∠=︒,同理60ACE DCA ∠+∠=︒,DC EC =.∴BCD ACE ∠=∠ 在BCD ∆与ACE ∆ 中,BC AC BCD ACE DC EC =⎧⎪∠=∠⎨⎪=⎩∴BCD ACE ∆∆≌,∴BD AE =.【例25】 如图,ABD ∆和CED ∆均为等边三角形,AC BC =,AC BC ⊥.若BE =CD = .图6DECB A【解析】易知CDB ∆≌CDA ∆≌EDB ∆,从而BC AC BE ==2AB =,由CDA CDB ∠=∠知CD 是ABD ∆一条高的一部分,1.1.【例26】 如图,B ,C ,E 三点共线,且ABC ∆与DCE ∆是等边三角形,连结BD ,AE 分别交AC ,DC 于M ,N 点.求证:CM CN =.NMEDCBA【答案】∵ABC ∆与DCE ∆都是等边三角形∴BC AC =,CD CE =及60ACB DCE ∠=∠=︒ ∵B ,C ,E 三点共线∴180BCD DCE ∠+∠=︒,180BCA ACE ∠+∠=︒ ∴120BCD ACE ∠=∠=︒ 在BCD ∆与ACE ∆中BC AC BCD ACE DC EC =⎧⎪∠=∠⎨⎪=⎩∴BCD ACE ∆∆≌, ∴CAN CBM ∠=∠∵120BCD ACE ∠=∠=︒,60BCM NCE ∠=∠=︒ ∴60ACD ∠=︒ 在BCM ∆与ACN ∆中60BC AC BCM ACN CBM CAN =⎧⎪∠==︒⎨⎪∠=∠⎩∴BCM ACN ∆∆≌,∴CM CN =.【例27】 如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.请你证明:(1)AN BM =; (2)DE AB ∥;(3)CF 平分AFB ∠.M D NEC BFA【答案】此图是旋转中的基本图形.其中蕴含了许多等量关系.60MCN ∠= 与三角形各内角相等,及平行线所形成的内错角及同位角相等; 全等三角形推导出来的对应角相等… 推到而得的:AFC BFC ∠=∠;AN BM =,CD CE =,AD ME =,ND BE =; AM CN ∥,CM BN ∥;DE AB ∥ACN MCB ∆∆≌,ADC MCE ∆∆≌,NDC BEC ∆∆≌; DEC ∆为等边三角形.(1)∵ACM ∆、CBN ∆是等边三角形, ∴MC AC =,CN CB =,ACN MCB ∠=∠ ∴ACN MCB ∆∆≌,∴AN BM =(2)由ACN MCB ∆∆≌易推得NDC BEC ∆∆≌,所以CD CE =,又60MCN ∠= , 进而可得DEC ∆为等边三角形.易得DE AB ∥. (3)过点C 作CG AN ⊥于G ,CH BM ⊥于H ,G M H DNEC BF A由ACN MCB ∆∆≌,利用AAS 进而再证BCH NCD ∆∆≌,可得AFC BFC ∠=∠,故CF 平分AFB ∠.【例28】 如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形,D 是AN 中点,E是BM 中点,求证:CDE ∆是等边三角形.M DNECBA【答案】∵ACN MCB ∆∆≌,∴AN BM =,ABM ANC ∠=∠又∵D 、E 分别是AN 、BM 的中点,∴BCE NCD ∆∆≌,∴CE CD =,BCE NCD ∠=∠ ∴60DCE NCD NCE BCE NCE NCB ∠=∠+∠=∠+∠=∠= ∴CDE ∆是等边三角形【例29】 如下图,在线段AE 同侧作两个等边三角形ABC ∆和CDE ∆(120ACE ∠<°),点P与点M 分别是线段BE 和AD 的中点,则CPM ∆是( )PMBC DEAA .钝角三角形B .直角三角形C .等边三角形D .非等腰三角形【答案】易得ACD BCE ∆∆≌.所以BCE ∆可以看成是ACD ∆绕着点C 顺时针旋转60︒而得到的.又M 为线段AD 中点,P 为线段BE 中点,故CP 就是CM 绕着点C 顺时针旋转60°而得.所以CP CM =且,60PCM ∠=°,故CPM ∆是等边三角形,选C .【例30】 已知:如图,点C 为线段AB 上一点,ACM ∆、CBN ∆是等边三角形.CG 、CH分别是ACN ∆、MCB ∆ 的高.求证:CG CH =.HG NM CBA【答案】由ACN MCB ∆∆≌,利用AAS 进而再证BCH NCD ∆∆≌,可得到CG CH =.【例31】 平面上三个正三角形ACF ,ABD ,BCE 两两共只有一个顶点,求证:EF 与CD平分.FE DCBA【答案】连接DE 与DFFE DCBA∵DBA EBC ∠=∠,BAD CAF ∠=∠ ∴DBE ABC ∠=∠,BAC DAF ∠=∠ ∴在DBE ∆与ABC ∆中 DB AB DBE ABC BE BC =⎧⎪∠=∠⎨⎪=⎩∴(SAS)DBE ABC ∆∆≌ ∴DE CA FC == 在D FA ∆与BCA ∆中 DA BA DAF BAC AF AC =⎧⎪∠=∠⎨⎪=⎩∴(SAS)DFA BCA ∆∆≌ ∴DF BC EC == ∴DECF 为平行四边形, ∴EF ,CD 互相平分.【例32】 已知:如图,ABC ∆、CDE ∆、EHK ∆都是等边三角形,且A 、D 、K 共线,AD DK =.求证:HBD ∆也是等边三角形.EKHCDBA【答案】连接CH 交AD 于点M ,连接BE BM ,, HE由CDE HEK ∆∆,均为等边三角形,可证得EDK ECH ∆∆≌ ∴DK CH =,CHE DKE ∠=∠ ∴60HME HEK ∠=∠=︒于是A M B C ,,,四点共圆,B M H D ,,,四点共圆, ∴HCB DAB BDA BHC ∠=∠∠=∠,∴BDA BHC ∆∆≌∴BH BD =,60HBD ∠=︒ ∴BHD ∆为等边三角形【例33】 如图,四边形ABCD 、DEFG 都是正方形,连接AE 、CG .求证:AE CG =.G FE DCBA【关键词】2008年怀化市中考 【解析】【答案】∵ADC EDG ∠=∠∴CDG ADE ∠=∠ 在CDG ∆和ADE ∆中CD AD CDG ADE DG DE =⎧⎪∠=∠⎨⎪=⎩∴CDG ADE ∆∆≌ ∴AE CG =【例34】 以ABC ∆的两边AB AC ,为边向外作正方形ABDE ACFG ,,求证:CE BG =,且CE BG ⊥.GOFEDCB A【答案】易证AEC ABG ∆∆≌,故ACE AGB ∠=∠,又A C A G ⊥,AOG BOC ∠=∠,故C E BG ⊥.【例35】 如图,在△ABC 外面作正方形ABEF 与ACGH ,AD 为△ABC 的高,其反向延长线交FH 于M ,求证:(1)BH CF =;(2)M F M H =GHM FED CBA【答案】证明△ABH ≌△AFC ;(1)作FP MD P ⊥于,HQ MD Q ⊥于, 先证△AFP ≌△BAD ,△ACD ≌△HAQ , 再证△FPM ≌△HQM【例36】 如图1,若ABC ∆和ADE ∆为等边三角形,M N ,分别EB CD ,的中点,易证:CD BE =,AMN ∆是等边三角形.(1)当把ADE ∆绕A 点旋转到图2的位置时,CD BE =是否仍然成立?若成立请证明,若不成立请说明理由;(2)当AD E ∆绕A 点旋转到图3的位置时,AMN ∆是否还是等边三角形?若是,请给出证明,并求出当2AB AD =时,ADE ∆与ABC ∆及AMN ∆的面积之比;若不是,请说明理由.图1N M E DC BA图2A BC DEMN 图3A BCDE MN【答案】(1)CD BE =.理由如下:∵ABC ∆和ADE ∆为等边三角形∴AB AC =,AE AD =,60BAC EAD ∠=∠=︒∵60BAE BAC EAC EAC ∠=∠-∠=︒-∠,60DAC DAE EAC EAC ∠=∠-∠=︒-∠, ∴BAE DAC ∠=∠, ∴ABE ACD ∆∆≌∴CD BE =(2)AMN ∆是等边三角形.理由如下: ∵ABE ACD ∆∆≌, ∴ABE ACD ∠=∠.∵M N 、分别是BE CD 、的中点, ∴1122BM BE CD CN === ∵AB AC =,ABE ACD ∠=∠, ∴ABM ACN ∆∆≌. ∴AM AN MAB NAC =∠=∠,.∴60NAM NAC CAM MAB CAM BAC ∠=∠+∠=∠+∠=∠=︒ ∴AMN ∆是等边三角形. 设AD a =,则2AB a =. ∵AD AE DE AB AC ===,, ∴CE DE =.∵ADE ∆为等边三角形, ∴12060DEC ADE ∠=︒∠=︒,,∴30EDC ECD ∠=∠=︒, ∴90ADC ∠=︒∴在Rt ADC ∆中,AD a =,30ACD ∠=︒, ∴CD =. ∵N 为DC 中点,∴DN =,∴AN ==. ∵ADE ∆,ABC ∆,AMN ∆为等边三角形, ∴()2227:2:1:4:4:16:74ADE ABC AMNS S S a a ⎫===⎪⎪⎝⎭∶∶ 解法二:AMN ∆是等边三角形.理由如下: ∵ABE ACD ∆∆≌,M 、N 分别是BE 、CN 的中点,∴AM AN NC MB ==,. ∵AB AC =,∴ABM ACN ∆∆≌,∴MAB NAC ∠=∠,∴60NAM NAC CAM MAB CAM BAC ∠=∠+∠=∠+∠=∠=︒ ∴AMN ∆是等边三角形设AD a =,则AD AE DE a ===,2AB BC AC a ===易证BE AC ⊥,∴BE ==,∴EM = ∴AM == ∵ADE ∆,ABC ∆,AMN ∆为等边三角形∴()2227:2:1:4:4:16:74ADE ABC AMNS S S a a ⎫===⎪⎪⎝⎭∶∶。
