5-2平面简谐波的波动方程详解
右行波的波动方程。
波速与介质的关系 通过波在介质中传播的动 力分析，再与波动方程相 比较，可得波的传播速度 的大小只取决于介质的弹 力与质元惯性。
2 y 2 x A 2 cos t 2 x u u 由上两式有:
e.g.流体中的纵波（如声波） K u , K是体积模量
是无声波时的流体 2 y 1 2 m y 2 RT pV 2 2 理想气体中的纵波(声波)速 x u t Mm
10
x
u t
x 五、波动微分方程
y x A sin t t u y x A sin t x u u 2 y x 2 A cos t 2 t u
x 由 y A cos t u
1
3.
§5-2 平面简谐波的波动方程(波函数) y0 A cos(t 0 ) 横波
纵波
y
二. 简谐波（harmonic waves) 波源作简谐振动
平面简谐波: （plane harmonic waves） 三.平面简谐波的波动方程 波动方程的一般表示：
O
u
p
X
x
y yt , x ----波函数
p点的相位超前于O点相位： x 2x u 则： p点的运动方程，
也就是左行波的波方程. x y( x , t ) A cos[ ( t + ) 0 ] u
7
四、波动方程的物理意义 1. x = x 0 (常数)
y( t ) A cos(t
表示在 t 1 时刻的波形
波的动力学微分方程 波速与介质的关系 通过波在介质中传播的动 力分析，再与波动方程相 比较，可得波的传播速度 的大小只取决于介质的弹 力与质元惯性。
第5章 习题解答
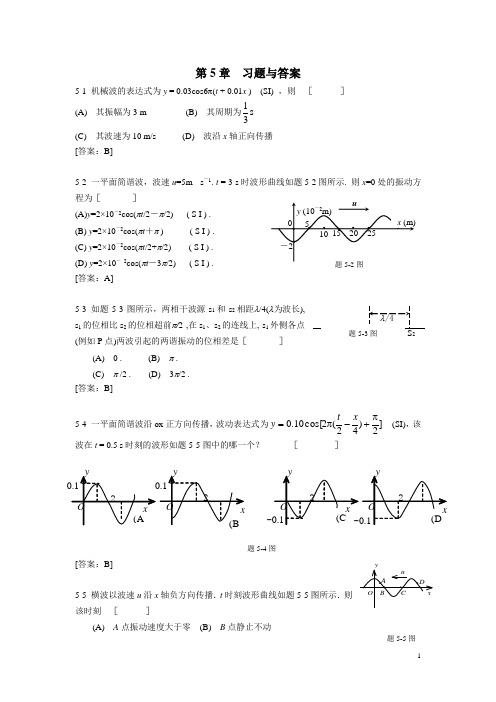
第5章 习题与答案5-1 机械波的表达式为y = 0.03cos6π(t + 0.01x ) (SI) ，则［ ］ (A) 其振幅为3 m(B) 其周期为s 31(C) 其波速为10 m/s (D)波沿x 轴正向传播 [答案：B]5-2 一平面简谐波，波速u =5m · s －1. t = 3 s 时波形曲线如题5-2图所示. 则x =0处的振动方程为［ ］(A)y =2×10－2cos(πt /2－π/2) ( S I ) . (B) y =2×10－2cos(πt ＋π ) ( S I ) . (C) y =2×10－2cos(πt /2+π/2) ( S I ) .(D) y =2×10－ 2cos(πt －3π/2) ( S I ) .[答案：A]5-3 如题5-3图所示，两相干波源s 1和s 2相距λ/4(λ为波长), s 1的位相比s 2的位相超前π/2 ,在s 1、s 2的连线上, s 1外侧各点(例如P 点)两波引起的两谐振动的位相差是［ ］(A) 0 . (B) π . (C) π /2 . (D) 3π/2 . [答案：B]5-4 一平面简谐波沿ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形如题5-5图中的哪一个？ ［ ］[答案：B]5-5 横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如题5-5图所示．则该时刻 ［ ］(A) A 点振动速度大于零 (B) B 点静止不动ux (m)y (10－2m)· · · · · · · 0 51015 20 25 －2题5-2图题5-4图题5-5图-(C) C 点向下运动 (D) D 点振动速度小于零 [答案：D]5-6 一平面简谐波沿x 轴正方向传播，t = 0 时刻的波形如题5-6图所示，则P 处质点的振动在t = 0时刻的旋转矢量图是［ ］[答案：A]5-7 一简谐波沿x 轴正方向传播，t = T /4时的波形曲线如题5-7图所示．若振动以余弦函数表示，且此题各点振动的初相取-π 到π 之间的值，则 ［ ］ (A) O 点的初相为00=φ(B) 1点的初相为π-=211φ(C) 2点的初相为π=2φ (D) 3点的初相为π-=213φ [答案：D]5-8 在驻波中，两个相邻波节间各质点的振动［ ］(A) 振幅相同，相位相同 (B) 振幅不同，相位相同 (C) 振幅相同，相位不同 (D) 振幅不同，相位不同 [答案：B]5-9 一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：［ ］(A) 它的动能转化为势能. (B) 它的势能转化为动能.(C) 它从相邻的一段质元获得能量其能量逐渐增大. (D) 它把自己的能量传给相邻的一段质元，其能量逐渐减小. [答案：D]ωS A O ′ωSA O ′ωωSAO ′(A)(B)(C)(D)S题5-6图5-10 一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是__________，波长是__________，频率是__________，波的传播速度是__________。
平面简谐波的波动方程.ppt
0 ]
任意一质点为坐标原点的波动方程
一平面波在介质中以速度u=20m/s沿直线传播，
已知A的振动方程为
yA 3cos(4，写t)出分别以
A、B点为坐标原点的波动方程。
8m 5m 9m
u
C BA
D
x
解：已知u=20m/s，ω=4π，
T 2 0.5s
A点
yA 3cos(4 t)
（1）O点振动方程
yO
0.1cos(200
t
3 2
以O点为原点的波动方程 y 0.1cos[200
) (
t
x) 400
3 2
]
（2）写出距原点为2m处的质点P的振动方程及以此点为
原点的波动方程；
解：(2)由波动方程可得P (x=2m )处的振动方程：
yP
0.1cos[200 (t
对同一质点，相邻两个时刻位相差为：
(t2
t1)
2
T
t
时间周期性
时间周期性
y
t T
对同一质点，相邻两个时刻位相差为：
(t2
位移差与位相差
t1)
2
T
t
Δt T 2T 3T 4T 5T … Δφ 2π 4π 6π 8π 10π …
6.2 平面简谐波的波动方程
2、波动方程物理意义_3
2、波动方程物理意义_行波
例题
x ut
由图可知：x 处 t 时刻振动状态经Δt ，传播到x+Δx 处；即 t 时刻x 处 振动状态与t +Δt 时刻x+Δx 处振动状态完全相同。
第二节 平面简谐波的波动方程
解： 由题意 波长 周期
u 0.40 m
T 1 8105 s
（1）原点处质点的振动表达式
y0 A cost 0.1103 cos(25103 t) m
（2）波函数
y Acos(t x)
u
0.1103
cos
即
y
Acos t
2 x1
上式代表x1处质点在其平衡位置附近以角频率
作简谐运动。
y
A
O
t
上页 下页 返回 退出
t 一定:令t=t1，则质点位移y 仅是x 的函数。
即
y
A
cos
t1
2 x
以y为纵坐标、x 为横坐标，得到一条余弦曲线，
它是t1时刻波线上各个质点偏离各自平衡位置的位移 所构成的波形曲线(波形图)。
y
u
A
x
上页 下页 返回 退出
沿波线方向，任意两点x1、x2的简谐运动相位差为：
2
1
2
x2 x1
2
x
x、t 都变化:
实线：t1 时刻波形；虚线：t2 时刻波形
y
u
o
x
x1 x
上页 下页 返回 退出
y
u
当t=t1时，y
A
cos
t1
0.5
M1
M2
0.4
0.2
a
0
b
0.2 10 20 30 40 50 60 70
大学物理学课件-平面简谐波规律
y 波形曲线
0
t = t0
x
大学物理学
章目录 节目录 上一页 下一页
5.2 平面简谐波规律
3、如x、t 均变化，波函数表示波形沿传播方向
的运动情况
t 时刻，x处质点的相位
(t x )
u
t 时t 刻， x 处 质Δx点的相位
dWk
1 2
A2 2
sin
2
(t
x u
)dV
2) 介质元的弹性势能：
dW p
1 2
k(dy
)2
dW p1 2来自A2 2sin2(t
x u
) dV
dWk
3) 介质元的总能量：
dW
dWk
dWp
A2 2
sin2
(t
x u
)
dV
大学物理学
章目录 节目录 上一页 下一页
5.2 平面简谐波规律
dW
dWk
dWp
(t
1)] 8
在下列情况下试求波函数(设波速为u)：
(1) 以 A 为原点； (2) 以 B 为原点；
x1
x
BA
(3) 若u沿x 轴负向，以上两种情况又如何？
解: (1)在x轴上任取一点P ，
该点振动方程为：
yp
Acos[4π
(t
x u
1)] 8
x1
u
x
BA P
波函数为： y(x,t) Acos[4π (t x 1)] u8
y Acos[t kx ]
k 2
大学物理学
章目录 节目录 上一页 下一页
第二节 平面简谐波波动方程
§ 9.2 平面简谐波的波动方程一、平面简谐波波动方程简谐波：如果波源和介质中的各质点都持续地作简谐振动，这种波称为简谐波。
平面简谐波：波面为平面的简谐波。
平面简谐波也称为一维简谐波，其表达式也称波函数(wave function)沿+x 方向传播的一维简谐波 (波速u ，振动角频率为ω)，假设媒质无吸收(质元振幅均为A )介质中任一质点（坐标为 x ）相对其平衡位置的位移（坐标为 y ）随时间的变化关系，即 称为波动方程。
设O 点处质点的振动方程为波线上坐标为x 的任意点P 处质点的振动方程振动从O 点传到P 点所需的时间为t 时刻点 P 的振动与 t-x/u 时刻点O 的振动状态相同，只是落后了Δt 点P 振动方程 式中称上式为沿x 轴正向传播的平面简谐波的波动方程(,)y x t cos O y A tω=(,)P y f x t ==？x t u∆=cos ()P xy A t uω=-2πων=u λν=xo任一点p参考点a波速u波方程的其它表示式讨论：（1）如果原点的初相位不为零设：点O振动方程则：波动方程为（2）如果平面简谐波沿x轴负方向传播则P点处质点相位比O点处质点的相位超前波动方程为二、波动方程的物理意义由从几方面讨论1 当x 一定时(设x =x0，即考察波线上某一点x0) 给出x =x0处质点的振动方程即x0处质元的振动表达式，表示x处的质点在各个不同的时刻位移随时间的变化情况，由它画出的曲线是x0处质元的振动曲线。
2 当t一定时(设t = t0，即在某一时刻t0)，给出t= t0时刻各质点的位移y分布情况反映t0时刻各不同x处质元的位移状况，即同一时刻x轴上各个质点离开它们平c o s2π()xy A tνλ=-[]c o sOy A tωϕ=+c o s[2π()]xy A tνϕλ=-+c o s[2π()]xy A tνϕλ=++c o s[2π()]xy A tνϕλ=-+()y y t=()y y x=c o s[2π()]xy A tνϕλ=-+2c o s()y A t xπωλ=-c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=++⎢⎥⎣⎦c o s()xy A tuωϕ⎡⎤=-+⎢⎥⎣⎦衡位置的位移分布，由它画出的曲线即t 0时刻的波形曲线。
平面简谐波的运动方程
(310-2 ) cos(4πt - x )
5
u
8m 5m 9m
C
B oA
Dx
20
5-2 平面简谐波的波函数
(2) 以 B 为坐标原点，写出波动方程
yA y(5,t ) (310-2 ) cos(4 π t )
t0 x0
y 0, v y 0 - π
t
2
y cos[2π( t - x ) - π ] (m) 2.0 2.0 2
cos(t - x - )
2
O
y
A
18
5-2 平面简谐波的波函数
例2 一平面简谐波以速度u 20 m s-1
沿直线传播，波线上点 A 的简谐运动方 程
yA 310-2 cos(4 π t); ( y, t单位分别为m，s).
5
yC
y(-13,t )
(310-2 ) cos[4 π t
13 π] 5
yD
y(9,t )
( 3 10-2
)cos[4 π t
-
9 5
π]
u
yA (310 -2 )co1s(04mπ t )
8m 5m 9m
C
B oA
Dx
22
5-2 平面简谐波的波函数
(3) 写出传播方向上点C、D的运动方程
5-2 平面简谐波的波函数
5.2.1 平面简谐波的运动方程--波函数 一、波长 波的周期和频率 波速
1 波长
波传播方向上相邻两振动状态完全相同
的质点间的距离（一完整波的长度）.
Ay
u
O
x
-A
平面简谐波的波动方程
y
u
t 时刻
tt时刻
O
xx
x
从t时到t+∆x时 : 波线上各质点的相位均向前传播 ∆x 即:
xu t （行波）
例1 已知波动方程如下，求波长、周期和波速.
y ( 5 c) c m π [ o 2 (s - .) 1 t5 ( 0 .0 0 c- 1 s ) m 1 x ].
t
u
a 2 t2 y 2 A co (t su x )[ ]
严格区分两种速度(波速和振动速度)
波速(相速)
u
T
v y A si (n t x [ ) ]
t
u
二 波动方程的物理意义
y A co ( t x ) s ] [A c2 o π ( t s x ) [ ]
y co ( t x s ) u [ ] c2 o ( t s T x ) [] m
u2
222
2）求t1 .0 s波形图.
y 1 .0 co 2π (st[x)π ] m 2 .02 .0 2
t 1 .0 s
波形方程
y1.0coπsπ (x) m 2
1.0siπ nx)( m
波形图为 y / m
pO
2π
x
p 2 π x 2 π T x u u x ypA co ts (p)
点 P 振动方程
ypAcos(tu x)
如果原点的 初相位不为零
y A
u
x0,0 O A
x
点 O 振动方程 y O A co t s)(
波 yAco(st [x)]u沿x轴正向
动 方
yAco(st [u x)]u沿 x轴负向
u
T
平面简谐波
解 根据题意设波源的振动方程为
y
0.01cos
200
t
x 400
0
vy00
0 0
即0.021csoins00
0 0
0
2
故
y
0.01cos
200
t
x 400
2
（1）B 和A 两点之间的振动相位差为
200
t
2 400
2
200
t
1 400
2
2
（2）以B 为坐标原点时有
t x
T
(t, x) (t t, x x)
x ut
讨论：如图简谐 波以余弦函数表示，
求 O、a、b、c 各点
振动初相位.
(π ~ π )
t =0 A y
Oa
A
A
O
y o π
O
A
O
y
a
π 2
O A
u
b c
A
y
y
t=T/4
x
b 0
c
π 2
讨论
1.同一波线上两个不同点的振动相位差
x 2 x
程、2）波函数。
2 y(102 m)
22
o
2
yo
t(s)
2 102 cos(2π t )m
4
A
oA2 y
π
3
t 0,x 0 y A 2 v 0
波函数
y 2 102 cos[2π( t x ) π ]m 44 3
x 0.5m 处质点的振动方程
y 1.0cos(π t π)m
y
y/m
3
1.0
3*
2
4
物理学14-平面简谐波的波函数与波动方程
若波源（原点）振动初位相不为零 y0 A cos( t 0 )
x y A cos[ (t ) 0 ] u
或
t x y A cos[ 2 ( ) 0 ] T 2x y A cos[ 2t ) 0 ] 2 y A cos[ (ut x) 0 ] A cos[ k (ut x) 0 ]
y
O
u
x
x
p
x O点振动状态传到p点需用 t u t 时刻p处质点的振动状态重复
y
O
u
x
x
p
x t 时刻O处质点的振动状态 u
x p点的振动方程： y A cos ( t ) u 沿x轴正向传播的平面简谐波的波动方程
沿着波传播方向，各质点的振动依次落后于波源振动 x 为p点的振动落后与原点振动的时间 u x 沿x轴负向传播的 y A cos ( t ) 平面简谐波的波动方程 u
在时间t内整个波形沿波的 传播方向平移了一段距离x
y
O
u
t
t t
x x
x
可见，波函数y(x,t)反映了波形的传播。 它描述的是在跑动的波，这种波被称为 行波（travelling wave）
三、平面波的波动微分方程
x y A cos[ ( t ) 0 ] u
求t 的二阶导数
2x0
若x0= 则 x0处质点落后于原点的位相为2
为x0处质点落后于原点的位相
是波在空间上的周期性的标志
同一波线上任意两点的振动位相差 x2 x1 x 2 1 2 2
பைடு நூலகம்
2、如果给定t，即t=t0 则y=y(x) Y x y A cos[ ( t 0 ) 0 ] u 表示给定时刻波线上各质 O 点在同一时刻的位移分布 ，即给定了t0 时刻的波形
平面简谐波的波动方程
x0 y A cos t 0 u
2.如果给定t，即 t t0 ，则y 只是x 的 函数, 这时波动方程表示在给定时刻波线 上各振动质点的位移分布，即给定了 t 0 时 刻的波形。
x y A cos t0 0 u
t y A cos 2 T
x 0
y A cos(t kx 0 )
三、波动方程的物理意义 x y A cos t0 0 u
1.如果给定
设沿x轴正向传播
是时间t
x ，即 x x0 ，则质点位移y 仅 的函数，表示质点在 x0处的振动方程：
平面简谐波的波动方程
一 平面简谐波概念
1、定义：作简谐运动的波源在均匀的、无吸
收的介质中传播、波面为平面的波动，称为 平面简谐波.
2、平面简谐波的特点：传播时，介质中各质
点振动的方向、振幅、频率与波源的振动方 向、振幅和频率相同。
一些复杂的波可视为若干个平面简谐波的叠加。
二、波动方程的推导
设有一沿 x 轴正方向传播的平面简谐波，波速为 u 。 如图，则O点处质点的振动方程为：
uT , k 2 , 所以：
x 0
t y A cos 2 T
y A cos(t kx 0 )
P点是任意的，这样我们就得到了波
动方程的三种表达式：
y A cos t
x 0 u
y
o
x
3.如果x 和t都变化，则波动方程表示波线 上各质点在不同时刻的位移，反映了波形的 传播。
y
t1时刻的波形
t1 t 时刻的波形
平面简谐波的波动方程
方程表示距原点为x 处的质元在不同时刻
的位移. y-t 曲线称之为位移时间曲线.
y
o
t
T
如果t 给定，则y 只是x 的函数, 这时波 动方程表示在给定时刻波射线上各振动质 元的位移，即给定时刻的波形图.
y
o
x
如果x 和t 都变化，则波动方程表示波射 线上各振动质元在不同时刻的位移，即波形 的传播.
2
x u
质元因变形而具有的势能等于动能
即dEp dEk 质元的总能量为
dE dEp dEk
( dV )A2 2 sin2 t x
u
2. 能量密度
为定量的反映能量在媒质中的分布和 随时间的变化情况, 引入能量密度的概念.
单位体积内的能量称为能量密度.
w dE dV
平面简谐波的能量密度为
yB
0.01cos
200
t
2 400
2
0.01cos
200
t
3
2
因此以B 为坐标原点的波动方程为
y
0.01cos
200
t
x 400
3
2
y
u
o
x
3. 有一沿x 轴正向传播的平面简谐波，在 t =0时的波形图如图中实线所示. 问：（1）
原点o 的振动相位是多大？（2）如果振幅为 A、圆频率为、波速为u ，请写出波动方程.
t1时刻的波形 t1 t时刻的波形 y
o
x1 x ut
x
u
由图可见t1时刻x1处的振动状态与t1+t 时 刻x1+x 处的振动状态完全相同，即相位相 同.
t1
x1 u
t1
t
x1
52平面简谐波讲解
A 2
cos
t
x u
信息学院 物理教研室
例题:某潜水艇的声纳发出的超声波为平面简谐
波，其振幅为 A 1.2103 m，频率 5.0104 Hz ，波
长 2.85102 m，波源振动的初相 0，求:
(1)该超声波的波函数；
t
x
3
4 u
2
Acos
t
x u
y
y
u
O
P x(x)
信息学院 物理教研室
(2):
v
y t
A
sin
t
x u
2
A sint
2
2、负向波的波函数
若波动向x轴负向传播，则:
y
B点比O点早起振 t x
u
所以: yB (t) yO (t t)
O x
则:
y( x、t)
Acos
t
x u
B
x
x轴负向传播的平面简谐波的波动方程
信息学院 物理教研室
x轴正向传播的波动方程
y( x、t)
信息学院 物理教研室
例题:一平面余弦波，波线上各质元振动的振幅
和角频率分别为A和，波沿 x 轴正向传播，波
速为u，设某一瞬时的波形如图，并取图示瞬时
为计时零点。 (1)在O点和P点各有一观察者，试
平面简谐波波动方程课件
非线性波动方程中，非线性项对 波形的变化和传播速度有重要影响。Fra bibliotek孤波的形成
在非线性波动中，孤波是一种特殊 的波形，其波形不会弥散或消失， 而是以固定的速度和形状传播。
稳定性分析
非线性波动方程的解的稳定性可以 通过线性稳定性分析来研究。
色散波动方程
色散现象
色散现象是指波在传播过程中， 不同频率的波速度不同，导致波
行波法
方法概述
介绍行波法的原理和适用 范围。
行波法的步骤
详细阐述行波法的实施步 骤，包括利用行波法求解 波函数和能流密度等物理 量。
行波法的优缺点
分析行波法的优点和缺点 ，如直观性强但计算量较 大。
04
平面简谐波波动方程的应用
在声波传播中的应用
声波的传播特性
平面简谐波波动方程可以描述声 波在空气或其他介质中的传播特 性，包括声波的传播速度、振幅 、频率等参数。
波动方程的形式
介绍平面简谐波波动方程 的一般形式，以及方程的 变量和参数。
求解方法的选取
根据波动方程的特点，选 取适合的求解方法。
分离变量法
方法概述
介绍分离变量法的原理和适用范围。
分离变量法的步骤
详细阐述分离变量法的实施步骤，包括对时间的积分和对空间的积 分。
分离变量法的优缺点
分析分离变量法的优点和缺点，如计算量较大但精度较高。
根据简化的波动方程，可以得 出平面简谐波的波动方程。
平面简谐波的波动方程描述了 波在平面上的传播规律，其中 包含了波的振幅、频率、相位 等参数。
通过求解平面简谐波的波动方 程，可以得到任意时刻波在平 面上的分布情况。
03
平面简谐波波动方程的求解
平面简谐波的波动方程三种形式
一、平面简谐波的概念平面简谐波是一种特殊的波动现象，它具有特定的波动方程和波动特性。
简谐波的振幅随时间以正弦或余弦函数变化，具有周期性和频率性，是物理学中常见的一种波动形式。
二、平面简谐波的波动方程1. 时间域的波动方程在时间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。
2. 空间域的波动方程在空间域内，平面简谐波的波动方程可以表示为：\[y(x,t) = A\sin(kx - \omega t + \phi)\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。
3. 复数形式的波动方程在复数形式下，平面简谐波的波动方程可以表示为：\[y(x,t) = A\cos(kx - \omega t + \phi) = \Re(Ae^{i(kx - \omega t + \phi)})\]其中，y表示波动的位移，A表示振幅，k表示波数，ω表示角频率，φ表示初相位。
三、不同形式的波动方程之间的关系1. 时间域的波动方程和空间域的波动方程时间域的波动方程和空间域的波动方程在形式上是相似的，都可以表示为简谐波的位移随时间和空间的变化而发生正弦或余弦函数的周期性振荡。
它们之间通过变量的不同而具有不同的物理意义，但是描述的是同一种波动现象。
2. 复数形式的波动方程和实数形式的波动方程在复数形式下，简谐波的波动方程可以更加简洁地描述，通过复数的指数函数形式可以很方便地进行波动的运算和分析。
复数形式的波动方程和实数形式的波动方程是等价的，可以相互转化，但在不同的数学和物理背景下有着不同的应用优势。
四、平面简谐波的应用领域平面简谐波作为一种特殊的波动形式，广泛应用于物理学、工程学、生物学等领域。
它在声学、光学、电磁学、机械振动、信号传输等方面有着重要的应用价值，可以用来描述和分析各种复杂的波动现象。
大学物理 第五章 波动
y
u
o
Px
x
O点简谐运动方程：y0 Acos(t 0)
由P 点的振动得到波动表示式：
y( x,
t)
Acos[(t
x u
)
0
]
y
( x, t )
Acos[2 ( t
T
x
)
0
]
沿 x轴正向，波线上
各质点的振动时间和 相位依次超前。
17
2. 波动方程
y Acost x u 0
求 x 、t 的二阶偏导数
移。即表示振动状态的传播，给出波形随时间而变化的
情况。
y
u
A
t 时刻波形
0 t+t 时刻波形
行
x x x x 波
x=u t
23
请指出你认为是对的答案 以波速 u 沿 x 轴逆向传播的简谐波 t 时刻的波形如下图
A B
A B
C
D
C
D
(1) A点的速度大于零；
v 振动速度
y t
(2) B点静止不动；
4
u
S
P
x x0
x
x
解： 2
xSP
2
(x
x0
)
S
(t
)
t
3
p (t) S (t)
t
3
2
(x x0)
y( x, t )
Acos[
t
3
2
(x
x0 )]
b点比a点的相位落后：
2 x
重要结论！
19
例:已知
ys
(t
)
A
cos(
t
平面简谐波波动详细介绍课件
=
−ω
x b
−
x a
=
−π
−
π
b
a
u 32
相同n,因为（x − x )〈λ
b
a
→ u = 0.84ms −1
波动方程 y(x, t) = 0.1cos(7πt − 7π x − 17 π ) (m) 23
0.84 3
练习
#1a1101001d
一沿x 轴正向传播的平面简
谐波在t=0 时刻的波形图如
图， O点的振动曲线为
本次课教学重点和要求
理解波长、周期、频率、波速等概念的含意; 掌握波长、周期、频率、波速之间的关系. 掌握由质点的谐振动方程或某时刻的简谐波波 形曲线 等已知条件建立简谐波波动方程的方法 掌握平面简谐波波动方程的物理意义
1
一 机械波的产生和传播
波动的一般概念 波动（简称波） 机械波，电磁波．．．
1 、机械波产生的条件: 波源；介质
2
2、两种基本类型： 横波和纵波
横波：质点振动方向与波的传播方向相垂直的波. （仅在固体中传播）
¾ 特征：具有交替出现的波峰和波谷.
纵波：质点振动方向与波的传播方向互相平行的波. （可在固体、液体和气体中传播）
¾ 特征：具有交替出现的密部和疏部.
3
3 波阵面和波射线
波阵面
球面波
波前 波线
波前
平面波
2
x
2
原点处：
原点振动方程：y0 (t)
=
π
A cos( 2
t
+
ϕ 0
)
Q
x
=
0;t
y
=
2时
t=2s
φ = 2kπ + 3π
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
u 沿 x 轴正向 u 沿 x 轴负向
第5章 机械波
5–2 平面简谐波的波动方程 平面简谐波波函数的其它形式
大学物理学 （第3版）
t y A cos[2 π( T
y A cos[2 t
y A cos[ 2
2 x
x ) 0 ] λ
0 ]
(ut x) 0 ] A cos[k (ut x) 0 ]
x y A cos (t ) (沿x轴负向传播) u
第5章 机械波
5–2 平面简谐波的波动方程 如果原点的
大学物理学 （第3版）
A
O
y
u
初相位不为零
x
x 0, 0 0 A
点 O 振动方程
y0 A cos(t 0 )
波 函 数
x y A cos[ (t ) 0 ] u x y A cos[ (t ) 0 ] u
2 y G 2 y 2 t x2 2 y E 2 y 2 t x 2
G为切变模量
固体内弹性平面纵波
E为杨氏模量
张紧柔软线绳上传播横波
2 y T 2 y 2 t x 2
T为线绳所受张力，为线密度:单位长度线绳的质量
第5章 机械波
5–2 平面简谐波的波动方程 2、波速 固体中弹性横波 固体中弹性纵波 张紧软绳中横波
x0 x0 2 π u λ
y ( x, t ) y ( x, t T ) （波具有时间的周期性）
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
波线上各点的简谐运动图
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
(2) 当 t t0 一定时，位移y只是坐标x的函数.
2 π 波矢 k
第5章 机械波
5–2 平面简谐波的波动方程 讨论 和
大学物理学 （第3版）
t x y A cos 2π ( ) (向x 轴正向传播 , π ) T x y A cos (t ) (向x 轴负向传播 , π ) u 2）平面简谐波的波函数为 y A cos(Bt Cx)
5–2 平面简谐波的波动方程
大学物理学 （第3版）
一 平面简谐波的波动方程 介质中任一质点（坐标为 x）相对其平衡位置的 位移（坐标为 y）随时间的变化关系，即 y ( x, t ) 称 为波函数.
y y ( x, t )
各质点相对平 衡位置的位移
波线上各质点 平衡位置
简谐波：在均匀的、无吸收的介质中，波源作 简谐运动时，在介质中所形成的波. 平面简谐波：波面为平面的简谐波.
x y A cos[ (t0 ) 0 ] u
称为t0时刻的波形方程.
同一质点在相邻两个 时刻的振动位相差为
t2 t1 (t2 t1 ) 2π T
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
(3)若t，x均变化，波函数表示波形沿传播方向的运 动情况（行波）.
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
以速度u 沿
x 轴正向传播的
平面简谐波 . 令 原点O 的初相为 零，其振动方程 时间推 迟方法
yO A cos t
yO A cos t
点O 的振动状态
t-x/u时刻点O 的运动
第5章 机械波
x P点在t时刻的振动方程 y A cos (t ) u
x t u
点P
t 时刻点 P 的运动
5–2 平面简谐波的波动方程
大学物理学 （第3版）
波动方程
y A
O
u
x
P
*
x y A cos (t ) u
A
x
点 O 振动方程
yo A cos t x 0 , 0
x P点的振动超前O点的振动，超前的时间为 u
点 P 振动方程
大学物理学 （第3版）
u
b
t=T/4
c
( π ~ π ) A o π O y
O
A
x
O
A b 0 y
π c 2
A
y
π a 2
A
O
yห้องสมุดไป่ตู้
第5章 机械波
5–2 平面简谐波的波动方程
大学物理学 （第3版）
*三 波动微分方程与波速
1、波动微分方程 弹性媒质中横波
大学物理学 （第3版）
u G / u// E / u T /
G为切变模量 E为杨氏模量
T为线绳所受张力，为线密度:单位长度线绳的质量
流体中纵波
第5章 机械波
u// B /
B为流体的体变模量
5–2 平面简谐波的波动方程
y 0.1cos
大学物理学 （第3版）
例5.1 已知波动方程为 25t x ，其中 10 x，y的单位为m，t的单位为s，求(1)振幅、波长、 周期、波速；(2)距原点为8m和10m两点处质点振动 的位相差；(3)波线上某质点在时间间隔0.2s内的位 相差. 解 (1)
1）给出下列波函数所表示的波的传播方向 x 0 点的初相位.
式中 A, B, C 为正常数，求波长、波速、波传播方 向上相距为 d 的两点间的相位差.
y A cos(Bt Cx)
2π T B
2π C
第5章 机械波
B u T C
t x y A cos 2 π ( ) T
x t时刻： y ( x) A cos[ (t ) 0 ] u x t t时刻： y ( x) A cos[ (t t ) 0 ] u y(t t , x x) y(t , x)
第5章 机械波
5–2 平面简谐波的波动方程 y 讨论：如图简谐 t =0 A 波以余弦函数表示， 求 O、a、b、c 各点 a O 振动初相位.
2 π d
dC
5–2 平面简谐波的波动方程
大学物理学 （第3版）
二
波动方程的物理意义
(1) 当x=x0为给定值时， 波函数表示该点的简谐运 动方程，并给出该点与点 O 振动的相位差.
x0 x0 y (t ) A cos( t 0 ) A cos( t 2 0 ) u