圆幂定理
圆幂的定理
圆幂的定理
圆幂定理是几何学中的一条定理，它描述了一个点与一个圆之间的关系。
具体来说，圆幂定理说明了如果有一条直线通过一个点P，与一个圆相交于点M和点N，那么这个点P到圆的两个切线段PM和PN的长度的乘积等于点P到圆心O的距离的平方减去圆的半径的平方，即可以表示为PM * PN = PO^2 - r^2。
圆幂定理可以推广到两个圆相交的情况下，即如果有两个圆分别为圆A和圆B，并且它们相交于点M和点N，那么点M和点N到这两个圆心的线段的乘积等于这两个圆心到点M和点N的距离的乘积，即可以表示为MA * MB = NA * NB。
这个式子即为圆A关于圆B的圆幂定理。
圆幂定理有许多应用，其中一个重要的应用是求解圆的切线长度。
通过圆幂定理，可以求解出切线与切点之间的关系，进而解决与圆切线相关的几何问题。
圆幂定理逆定理
圆幂定理逆定理
圆幂定理是一个经典的几何定理，它描述了一个点和圆之间的关系。
具体而言，如果一个点P在圆的外部，则它到圆的两个切点的距离的乘积等于它到圆心的距离的平方减去圆的半径的平方。
如果一个点P在圆的内部，则圆的半径的平方减去它到圆心的距离的平方等于它到圆的两个切点的距离的乘积。
圆幂定理的逆定理是指，如果给定一个点P和两条相交的直线AB和CD，使得AP·BP=CP·DP，则这个点P在由ABCD组成的圆上。
这个定理的证明可以通过构造圆心角相等来完成。
圆幂定理和它的逆定理在几何证明中经常被使用，它们可以帮助我们解决很多和圆相关的问题。
在学习几何知识的过程中，深入理解这些定理的含义和证明方法是非常重要的。
- 1 -。
圆幂定理
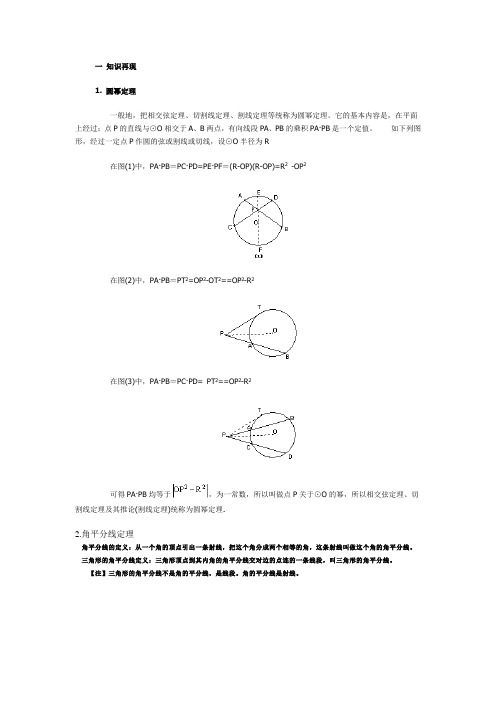
一知识再现1. 圆幂定理一般地，把相交弦定理、切割线定理、割线定理等统称为圆幂定理。
它的基本内容是，在平面上经过；点P的直线与⊙O相交于A、B两点，有向线段PA、PB的乘积PA·PB是一个定值。
如下列图形，经过一定点P作圆的弦或割线或切线，设⊙O半径为R在图(1)中，PA·PB＝PC·PD=PE·PF＝(R-OP)(R-OP)=R2-OP2在图(2)中，PA·PB＝PT2=OP2-OT2==OP2-R2在图(3)中，PA·PB＝PC·PD= PT2==OP2-R2可得PA·PB均等于，为一常数，所以叫做点P关于⊙O的幂，所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理.2.角平分线定理角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。
三角形的角平分线定义：三角形顶点到其内角的角平分线交对边的点连的一条线段，叫三角形的角平分线。
【注】三角形的角平分线不是角的平分线，是线段。
角的平分线是射线。
■拓展：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。
■定理1：在角平分线上的任意一点到这个角的两边距离相等。
■逆定理：在一个角的内部（包括顶角），且到这个角的两边距离相等的点在这个角的角平分线上。
■定理2：三角形一个角的平分线分对边所成的两条线段与这个角的两邻边对应成比例，如：在△ABC 中，BD 平分∠ABC ，则AD ：DC=AB ：BC 3.平行线分线段定理定理 三条平行线截两条直线，所得的对应线段成比例.二 例题讲解例1如图4AB 是⊙O 的弦，P 是AB 上一点，AB = 10cm ，P A : PB = 2 : 3，OP = 5cm ，则⊙O 的半径等于 ．解析：设⊙O 的半径为R ．∵AB = 10cm ，P A : PB = 2 : 3，∴PA = 4 cm ，PB = 6 cm ． 由相交弦定理，得P A ·PB = PC ·PD = R 2－OP 2，即4×6 = R 2－52． 所以，R = 7． 故⊙O 的半径等于7 cm ． 例2．如图5，已知P AC 为⊙O 的割线，连接PO 交⊙O 于B ，PB = 2，OP = 7，P A= AC ，则P A 的长为（ ）A ．7B ．23C ．14D ．32解析：延长PO 交⊙O 于D ．∵PB = 2，OP = 7，∴OB = 5，即PC = 12． 由切割线定理的推论，得 P A ·AC = PB ·PC ． ∵P A = AC ，∴2 P A 2 = 2×12． 所以，P A = 23．故应选B ．一、“四心”分类讨论1、外心三解形三条垂直平分线的交点叫做三角形的外心，即外接圆圆心。
圆幂定理洋葱数学
圆幂定理洋葱数学
【实用版】
目录
1.圆幂定理的概念与背景
2.圆幂定理的内容
a.相交弦定理
b.切割线定理
c.割线定理
3.圆幂定理的应用与意义
4.总结
正文
一、圆幂定理的概念与背景
圆幂定理是一个总结性的定理，它包含了相交弦定理、切割线定理和割线定理及其推论。
这些定理在几何学中具有重要的地位，尤其是在处理与圆相关的问题时，它们为我们提供了很多有用的信息。
二、圆幂定理的内容
1.相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
2.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆焦点的两条线段长的比例中项。
3.割线定理：从圆外一点引两条割线与圆分别交于 A、B、C、D，则有 PA·PB=PC·PD。
三、圆幂定理的应用与意义
圆幂定理在解决一些与圆相关的几何问题时，具有非常重要的作用。
例如，在解决相交弦定理、切割线定理和割线定理的问题时，我们可以利用圆幂定理来简化问题。
此外，圆幂定理还可以帮助我们更好地理解圆的性质，从而加深对几何学的认识。
四、总结
圆幂定理是一个涵盖了相交弦定理、切割线定理和割线定理及其推论的总结性定理，它在解决与圆相关的几何问题中具有重要意义。
圆幂定理及其证明
圆幂的定义假设平面上有一圆O，其半径为R,有一点P在圆O外，则ＯP＾2-Ｒ＾2即为P 点到圆O的幂;若Ｐ点在圆内，则圆幂为Ｒ^２-OP^２;综上所述,圆幂为|OＰ^2-R＾2｜。
圆幂恒大于或等于零。
圆幂的由来过任意在圆O外的一点P引一条直线L１与一条过圆心的直线Ｌ2,Ｌ1与圆交于Ａ、Ｂ（可重合,即切线）,L2与圆交于C、Ｄ。
则PA·PB＝PC·PＤ。
若圆半径为r,则PC·ＰD=(ＰO-r）·（PO+r)=PＯ^2－r^２＝|ＰＯ^2－r^２| (要加绝对值,原因见下）为定值。
这个值称为点P到圆O的幂。
(事实上所有的过P点与圆相交的直线都满足这个值）若点P在圆内，类似可得定值为r^２-PO^２=|PO＾2－r＾2|故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差，而过这一点引任意直线交圆于A、B,那么ＰA·ＰB等于圆幂的绝对值。
圆幂定理定理内容过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于Ａ、B(可重合,即切线）,L2与圆交于C、D(可重合），则有。
[１］圆幂定理的所有情况考虑经过P点与圆心O的直线，设PO交⊙O与Ｍ、N,R为圆的半径,则有圆幂定理的证明图Ⅰ：相交弦定理。
如图，AB、ＣD为圆O的两条任意弦。
相交于点P，连接AB、BＤ,由于∠Ｂ与∠D同为弧AC所对的圆周角，因此由圆周角定理知：∠B＝∠D,同理∠A=∠C,所以。
所以有:,即:图Ⅱ:割线定理。
如图,连接AD、ＢC。
可知∠B=∠D，又因为∠Ｐ为公共角,所以有,同上证得图Ⅲ：切割线定理。
如图，连接AＣ、AD。
∠ＰAC为切线PA 与弦AC组成的弦切角,因此有∠ＰAC=∠D,又因为∠P为公共角，所以有易证图Ⅳ:PＡ、PC均为切线,则∠PAO=∠ＰCO=直角,在直角三角形中:ＯC=OA＝R，PO为公共边,因此所以PA=ＰＣ,所以综上可知,是普遍成立的。
证明完毕。
圆中的重要模型-圆幂定理模型(学生版)
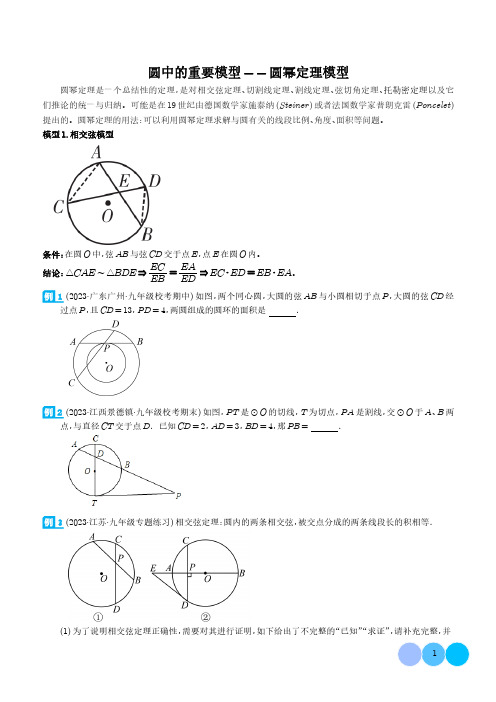
圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner)或者法国数学家普朗克雷(Poncelet)提出的。
圆幂定理的用法：可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件：在圆O中，弦AB与弦CD交于点E，点E在圆O内。
结论：△CAE∼△BDE⇒ECEB=EAED⇒EC⋅ED=EB⋅EA。
1(2023·广东广州·九年级校考期中)如图，两个同心圆，大圆的弦AB与小圆相切于点P，大圆的弦CD经过点P，且CD=13，PD=4，两圆组成的圆环的面积是．2(2023·江西景德镇·九年级校考期末)如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD=2，AD=3，BD=4，那PB=．3(2023·江苏·九年级专题练习)相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．(1)为了说明相交弦定理正确性，需要对其进行证明，如下给出了不完整的“已知”“求证”，请补充完整，并写出证明过程．已知：如图①，弦AB，CD交于点P，求证：．(2)如图②，已知AB是⊙O的直径，AB与弦CD交于点P，且AB⊥CD于点P，过D作⊙O的切线，交BA的延长线于E，D为切点，若AP=2，⊙O的半径为5，求AE的长．模型2.双割线模型条件：如图，割线CH与弦CF交圆O于点E和点G。
结论：△CEG∼△CHF⇒ECCH=CGCF⇒EC⋅FC=GC⋅HC4(2023·浙江·九年级假期作业)如图：PAB、PCD为⊙O的两条割线，若PA∙PB=30，PC=3，则CD的长为()A.10B.7C.510D.35(2023·四川成都·九年级校考阶段练习)如图，PAB为⊙O的割线，且PA=AB=3，PO交⊙O于点C，若PC=2，则⊙O的半径的长为．6(2022·河南洛阳·统考一模)我们知道，直线与圆有三种位置关系：相交、相切、相离．当直线与圆有两个公共点(即直线与圆相交)时，这条直线就叫做圆的割线．割线也有一些相关的定理．比如，割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等．下面给出了不完整的定理“证明一”，请补充完整．已知：如图①，过⊙O 外一点P 作⊙O 的两条割线，一条交⊙O 于A 、B 点，另一条交⊙O 于C 、D 点．求证：PA ⋅PB =PC ⋅PD ．证明一：连接AD 、BC ，∵∠A 和∠C 为BD 所对的圆周角，∴．又∵∠P =∠P ，∴，∴．即PA ⋅PB =PC ⋅PD ．研究后发现，如图②，如果连接AC 、BD ，即可得到学习过的圆内接四边形ABDC ．那么或许割线定理也可以用圆内接四边形的性质来证明．请根据提示，独立完成证明二．证明二：连接AC 、BD ，模型3.切割线模型条件：如图，CB 是圆O 的切线，CA 是圆O 的割线。
圆幂定理证明
圆幂定理证明
引言：
圆幂定理又称华罗庚公式，它表明在多项式中，二次项、四次项等次项的系数可以从非二次项的系数中求出来，它最早由科学家英国自然哲学家华罗庚在16世纪完成。
圆幂定理的性质：当z的n次幂展开时(z的n次幂为z的n个相同的因子)，各项系数满足公式：a（n）=（ -1）^( n-1 ) / ( n - 1 )! * 求和（k= 0到 n-1） [n^k 开始 * a （k）]，其中 n 称作次数，k 称作幂数。
证明：
首先，假设z的n次幂有如下公式：z^n = a0 +a1z+...+an-1zn-1 + anzn
我们分类讨论，首先当n为偶数时，如：
z^2 =a0+a1z+a2z^2
因为每一项的系数都是可以由未知系数a0,a1,a2求出来，即：
a0 = ( -1 )^ 1 / 1! * 求和（k= 0到 1） [2^k * a（k）]
当n为奇数时，如：
通过上述两种情况的分析，当n为任意正整数时，它们满足的条件都是一样的，即：a（n）=（ -1）^( n-1 ) / ( n - 1 )! * 求和（k= 0到 n-1） [n^k * a（k）]，其中n 称作次数，k 称作幂数。
圆幂定理 证明 知乎
圆幂定理证明知乎
圆幂定理是指在一个平面内，对于一个点P和两个相交的
圆C1和C2，如果从P到C1的两个切线分别与C2相交于A
和B，那么PA*PB等于P到两个切点的线段长度的乘积。
证明圆幂定理可以分为以下几个步骤：
步骤1：证明PA*PB的值与P到两个切点的线段长度的乘积
有关。
假设P到C1的两个切点分别为X和Y，那么根据相似三角
形的性质，可以得到△PAX∽△PYB。
因此，可以得到
PA/PY=PX/PB，即PA*PB=PX*PY。
步骤2：证明PX*PY等于P到C1和C2的切线之间的距离的
平方。
设P到C1和C2的切线之间的距离为d，那么可以得到
△PAX∽△PYB，因此可以得到PX/PY=AX/YB。
又因为AX=PY，YB=PX，所以可以得到PX*PY=AX*YB=d^2。
综上所述，可以得到PA*PB=d^2，即圆幂定理成立。
这是圆幂定理的证明过程的一个简单描述，具体的证明过
程可能会涉及到更多的几何推理和性质的运用。
圆幂定理逆定理
圆幂定理逆定理一、什么是圆幂定理逆定理圆幂定理是解决圆与直线之间的关系问题的重要定理，它描述了一个点与一个圆之间的幂的关系。
而圆幂定理逆定理则是对圆幂定理的逆向描述，即给定一个点与一个圆的幂，可以确定该点在圆上的位置。
二、圆幂定理逆定理的表述圆幂定理逆定理可以表述为：给定一个点P和一个圆O，若点P到圆O的距离等于该点P到圆心O的距离，那么点P一定在圆O上。
三、圆幂定理逆定理的证明1. 证明思路要证明圆幂定理逆定理，我们可以采用反证法。
假设点P在圆O外，即P到圆心O 的距离大于P到圆O的距离。
然后我们可以通过构造辅助线段，利用圆幂定理进行推导，最终得出矛盾，证明假设错误。
2. 证明过程步骤一：假设点P在圆O外假设点P在圆O外，即P到圆心O的距离大于P到圆O的距离。
步骤二：构造辅助线段构造线段PA和线段PB，使得线段PA与线段PB相交于点P，并且线段PA与圆O相切。
步骤三：利用圆幂定理推导根据圆幂定理，可以得到以下关系：•PA * PB = PO^2 - r^2其中，PA表示线段PA的长度，PB表示线段PB的长度，PO表示点P到圆心O的距离，r表示圆O的半径。
步骤四：计算距离根据题设条件，P到O的距离等于PO的距离，即PA = PO。
步骤五：代入计算将步骤四的结果代入步骤三的等式中，得到：•PA * PB = PO^2 - r^2•PO * PB = PO^2 - r^2•PB = PO - r^2 / PO步骤六：化简计算由于PO的长度大于r，所以PO - r^2 / PO的值大于0。
而PB表示线段PB的长度，根据几何性质，PB的长度必须大于0。
但根据步骤五的计算结果，PB的长度等于PO - r^2 / PO，这与PB的长度必须大于0相矛盾。
步骤七：得出矛盾由于步骤六得出了矛盾，假设点P在圆O外的假设被推翻。
因此，点P一定在圆O 上。
3. 证明结论根据上述证明过程，可以得出结论：给定一个点P和一个圆O，若点P到圆O的距离等于该点P到圆心O的距离，那么点P一定在圆O上。
圆幂定理大总结
圆幂定理大总结
圆幂定理是一个总结性的定理，它是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论的统一与归纳。
根据两条与圆有相交关系的线的位置不同，有以下定理：
1.相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。
2.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交
点的两条线段长的比例中项。
3.割线定理：从圆外一点P引两条割线与圆分别交于A、B、C、D，则有 P
A P
B = P
C P
D 。
如需证明圆幂定理，可参考以下步骤：
1.设两条与圆相交的线段分别为PA和PB，P为交点。
由相交弦定理，有
PA PB = PC PD （式（1））。
2.设另一条与圆相交的线段为PC，与圆交于点D。
由切割线定理，有 PD^2 = PA * PB
（式（2））。
3.将式（2）代入式（1），得 PA PB = PA PB。
这个等式显然成立，所以圆幂定
理得证。
希望以上信息对您有帮助，如果需要更详细的解释和证明，可以查阅相关的数学书籍或者咨询数学专家。
圆幂定理浙教版八年级上册
圆幂定理浙教版八年级上册摘要：一、圆幂定理简介1.圆幂定理的定义2.圆幂定理的意义二、圆幂定理的推导1.圆幂定理的数学表达式2.圆幂定理的推导过程三、圆幂定理的应用1.利用圆幂定理求解相关问题2.圆幂定理在日常生活中的应用四、圆幂定理与相关知识的联系1.圆幂定理与相似三角形2.圆幂定理与三角函数正文：一、圆幂定理简介圆幂定理，又称圆的幂定理或圆的面积公式，是指一个关于圆面积与半径平方之间关系的数学定理。
这一定理在解决与圆相关的几何问题时具有重要意义，也是学习圆的面积计算、圆的周长计算等知识的基础。
二、圆幂定理的推导圆幂定理的数学表达式为：πr = 2πr·h，其中r 为圆的半径，h 为圆心到圆上任意一点的距离。
推导过程如下：1.在一个圆中，连接圆心与圆上任意一点，得到一个直角三角形。
2.这个直角三角形的斜边就是圆的半径r，高就是圆心到圆上任意一点的距离h。
3.根据勾股定理，直角三角形的斜边平方等于两直角边平方和，即r = h + (r-h)。
4.将上式化简得到r = 2h - 2hr + r，即r = 2πr·h。
三、圆幂定理的应用1.利用圆幂定理求解相关问题：例如，已知圆的半径r，可以求解圆的面积；已知圆的面积和半径，可以求解圆的周长等。
2.圆幂定理在日常生活中的应用：例如，在建筑设计中，需要计算圆形结构的面积和周长；在机械制造中，需要根据圆幂定理来确定零件的尺寸等。
四、圆幂定理与相关知识的联系1.圆幂定理与相似三角形：当两个圆的半径成比例时，它们的面积也成比例。
这表明圆幂定理与相似三角形有密切的联系。
2.圆幂定理与三角函数：在解决与圆相关的三角问题时，可以利用三角函数与圆幂定理相互转换，简化问题的求解过程。
圆中的重要模型-圆幂定理模型(解析版)
圆中的重要模型--圆幂定理模型圆幂定理是一个总结性的定理，是对相交弦定理、切割线定理、割线定理、弦切角定理、托勒密定理以及它们推论的统一与归纳。
可能是在19世纪由德国数学家施泰纳(Steiner )或者法国数学家普朗克雷(Poncelet )提出的。
圆幂定理的用法：可以利用圆幂定理求解与圆有关的线段比例、角度、面积等问题。
模型1.相交弦模型条件：在圆O 中，弦AB 与弦CD 交于点E ，点E 在圆O 内。
结论：△CAE ∼△BDE ⇒EC EB =EA ED⇒EC ⋅ED =EB ⋅EA 。
1(2023·广东广州·九年级校考期中)如图，两个同心圆，大圆的弦AB 与小圆相切于点P ，大圆的弦CD 经过点P ，且CD =13，PD =4，两圆组成的圆环的面积是．【答案】36π【分析】连接AC ，BD ，OP ，OA ，先根据切线的性质定理和垂径定理证出PA =PB ，再证明△APC ∽△DPB ，得到AP DP =CP BP，代入数据求得AP =BP =6，最后根据圆环的面积公式进行计算即可求解．【详解】解：如图，连接AC ，BD ，OP ，OA ，∵大圆的弦AB 与小圆相切于点P ，∴OP ⊥AB ，∴PA =PB ，OA 2-OP 2=AP 2，∵CD =13，PD =4，∴PC =13-4=9，∵∠BAC =∠BDC ，∠C =∠B ，∴△APC ∽△DPB ，∴AP DP =CP BP ，即AP 4=9BP，解得：AP =BP =6(负值舍去)，∴圆环的面积为：π⋅OA 2-π⋅OP 2=π⋅AP 2=36π，故答案为：36π．【点睛】此题综合运用了切线的性质定理、垂径定理、勾股定理、圆周角定理、圆环的面积公式，分别求出大圆和小圆的半径是解题的关键．2(2023·江西景德镇·九年级校考期末)如图，PT是⊙O的切线，T为切点，PA是割线，交⊙O于A、B两点，与直径CT交于点D．已知CD=2，AD=3，BD=4，那PB=．【答案】20.【分析】连接AC，BT，AT，易证∆CAD~∆BTD，得到TD=6，易证：∆BTP~∆TAP，得：TP2=AP⋅BP，设PB=x，则AP=x+7，TP2=(x+7)⋅x，PD=x+4，根据勾股定理，即可求解.【详解】连接AC，BT，AT，∵∠CAD=∠BTD，∠ADC=∠TDB，∴∆CAD~∆BTD，∴CD BD =ADTD，即：24=3TD∴TD=6，∵PT是⊙O的切线，T为切点，∴∠BTP+∠BTD=90°，∵CT是直径，∴∠CAD+∠TAP=90°∵∠CAD=∠BTD，∴∠BTP=∠TAP，∵∠P=∠P，∴∆BTP~∆TAP，∴TPAP =BPTP，即：TP2=AP⋅BP，设PB=x，则AP=x+7，TP2=(x+7)⋅x，PD=x+4，∵在Rt∆DPT中，DT2+PT2=PD2，∴62+(x+7)x=(x+4)2，解得：x=20，故答案是：20.【点睛】本题主要考查相似三角形的判定和性质定理与圆的性质的综合，根据题意，添加辅助线，构造相似三角形，是解题的关键.3(2023·江苏·九年级专题练习)相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．(1)为了说明相交弦定理正确性，需要对其进行证明，如下给出了不完整的“已知”“求证”，请补充完整，并写出证明过程．已知：如图①，弦AB，CD交于点P，求证：．(2)如图②，已知AB是⊙O的直径，AB与弦CD交于点P，且AB⊥CD于点P，过D作⊙O的切线，交BA的延长线于E，D为切点，若AP=2，⊙O的半径为5，求AE的长．【答案】(1)PA ⋅PB =PC ⋅PD ，证明见解析(2)103【分析】(1)先证明△ACP ∽△DBP ，再利用相似的性质即可；(2)利用(1)可知PA ⋅PB =PC ⋅PD ，求出PD ，再证明△OPD ∼△DPE ，利用相似的性质求出PE ，求差即可得到AE 的长．【详解】(1)求证：PA ⋅PB =PC ⋅PD ．证明：连接AC 、BD ．如图①．∵∠A =∠D ，∠C =∠B ．∴△ACP ∽△DBP ．∴AP PD =PC BP．∴PA ⋅PB =PC ⋅PD ．(2)解：∵AP =2，OA =5，PB =10-2=8．由(1)可知PA ⋅PB =PC ⋅PD ．∴PC ⋅PD =16．∵AB ⊥CD ，AB 是⊙O 的直径，PC =PD ，PD =4．连接OD ．如图②．∵DE 为切线．∴∠EDO =90°．∵∠1+∠2=90°．∠E +∠2=90°．∴∠1=∠E ．∴△OPD ∼△DPE ．∵OP PD =PD PE，∴OP ⋅PE =PD ⋅PD ．∴16=3PE ，PE =163．又∵AP =2．∴AE =163-2=103．【点睛】本题考查了圆的相关性质，三角形相似的判定与性质，严格的逻辑思维和严密的书写过程是解题的关键．模型2.双割线模型条件：如图，割线CH 与弦CF 交圆O 于点E 和点G 。
圆幂定理
圆幂定理是对相交弦定理、切割线定理及割线定理（切割线定理推论）以及它们推论统一归纳的结果。
切线），L2与圆交于C、D（可重合），则有PA·PB=PC·PD。
问题1相交弦定理：圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明：连结AC，BD，由圆周角定理的推论，得∠A=∠D，∠C=∠B。
∴△PAC∽△PDB∴PA/PD=PC/PB∴PA·PB=PC·PD问题2割线定理：从圆外一点P引两条割线与圆分别交于A.B.C.D 则有PA·PB=PC·PD，当PA=PB，即直线AB重合，即PA切线时得到切线定理PA^2=PC·PD证明：（令A在P、B之间，C在P、D之间）∵ABCD为圆内接四边形∴∠CAB+∠CDB=180°又∠CAB+∠PAC=180°∴∠PAC=∠CDB∵∠APC公共∴△APC∽△DPB∴PA/PD=PC/PB∴PA·PB=PC·PD切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT^2=PA·PB（切割线定理）推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言：∵PBA、PDC是⊙O的割线∴PD·PC=PA·PB（切割线定理推论）问题3过点P任作直线交定圆于两点A、B，证明PA·PB为定值（圆幂定理）。
证：以P为原点，设圆的方程为(x-xO)^2+(y-yO)^2=a①过P的直线为x=k1ty=k2t则A、B的横坐标是方程(k1t-xO)^2+(k2t-yO)^2=r^2即(k1^2+k2^2)t^2-2(k1xO+k2yO)t+xO^2+yO^2-r^2=0的两个根t1、t2。
由韦达定理t1t2=(xO^2+yO^2-^2)/(k1^2+k2^2)于是PA·PB=√((k1t1)^2+(k2t1)^2)√((k1t2)^2+(k2t2)^2)=(√(k1^2+k2^2))^2|t1||t2|=k1^2+k2^2|(xO^2+yO^2-r^2)/(k1^2+k2^2)|=|(xO^2+yO^2-r^2)|为定值，证毕。
圆幂定理
圆幂定理圆幂定理就是对相交弦定理、切割线定理及割线定理(切割线定理推论)以及它们推论统一归纳的结果。
ﻩﻩﻩﻩ圆幂=PO^2-Ｒ^2(该结论为欧拉公式)所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
切割线定理:从圆外一点引圆的切线与割线,切线长就是这点到割线与圆交点的两条线段长的比例中项。
割线定理:从圆外一点P引两条割线与圆分别交于Ａ、B;C、D,则有PA·PB=PＣ·PＤ。
线),L2与圆交于C、D(可重合),则有ＰA·PB=PC·PD。
问题１相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的乘积相等。
证明:连结AC,BD,由圆周角定理的推论,得∠A=∠Ｄ,∠C=∠B。
∴△ＰAＣ∽△PDＢ∴ＰＡ/PD=PC/ＰＢ∴PＡ·PB=PC·PＤ问题２割线定理:从圆外一点Ｐ引两条割线与圆分别交于Ａ、B.C、D 则有PA·PB=PC·PD,当ＰA=ＰB,即直线AＢ重合,即ＰA切线时得到切线定理PA^2=PC·PD证明:(令A在P、B之间,Ｃ在P、D之间)∵ＡBCＤ为圆内接四边形∴∠CAB+∠CDB=１80°又∠ＣAB＋∠PAC=180°∴∠PＡC=∠CＤB∵∠APC公共∴△AＰC∽△DPＢ∴PＡ/PD=PC/PB∴PA·PB=ＰC·PＤ切割线定理:从圆外一点引圆的切线与割线,切线长就是这点到割线与圆交点的两条线段长的比例中项几何语言:∵PＴ切⊙O于点T,PBA就是⊙O的割线∴PT＾2=PA·ＰB(切割线定理)推论从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言:∵PＢA、PDC就是⊙O的割线∴PD·PC=PA·PＢ(切割线定理推论)问题3过点Ｐ任作直线交定圆于两点A、B,证明PA·PB为定值(圆幂定理)。
圆幂定理切割线定理
圆幂定理切割线定理圆幂定理和切割线定理是圆的基本定理之一，它们在几何学中有着广泛的应用。
圆幂定理是指在一个圆内，如果有两条相交的直线，那么它们所构成的四个交点的乘积相等。
而切割线定理则是指在一个圆内，如果有一条切线和一条割线相交，那么它们所构成的线段的乘积等于切点到圆心的距离的平方。
圆幂定理的证明可以通过相似三角形和勾股定理来完成。
假设有两条相交的直线AB和CD，它们分别与圆O相交于点E、F、G、H。
我们可以通过相似三角形来证明EF×GH=AE×EB=CF×FD。
首先，我们可以得到三角形AEO和CFD相似，因为它们都是直角三角形，且∠AEO=∠CFD。
因此，我们可以得到AE/CF=EO/FD。
同理，我们可以得到BE/DF=EO/FD。
将这两个式子相乘，我们可以得到AE×EB/CF×FD=EO²/FD²。
同样的，我们可以得到CE×ED/BF×FB=EO²/FD²。
将这两个式子相乘，我们可以得到EF×GH=AE×EB=CF×FD。
因此，圆幂定理得证。
切割线定理的证明也可以通过相似三角形和勾股定理来完成。
假设有一条切线AB和一条割线CD，它们分别与圆O相交于点E、F、G、H。
我们可以通过相似三角形来证明AE²=EF×EB。
首先，我们可以得到三角形AEO和EFB相似，因为它们都是直角三角形，且∠AEO=∠EFB。
因此，我们可以得到AE/EF=EO/EB。
将这个式子平方，我们可以得到AE²/EF²=EO²/EB²。
因为EF×EB=EF²+EB²，所以我们可以得到AE²=EF×EB。
因此，切割线定理得证。
圆幂定理和切割线定理在几何学中有着广泛的应用。
例如，在解决圆的切线和割线问题时，我们可以利用切割线定理来求出线段的长度。
圆幂定理的内容
圆幂定理的内容以下是 7 条关于圆幂定理的内容：1. 嘿，你知道吗？圆幂定理可有意思啦！就好比有两个点，在圆外和圆内的情况那可是大不同哦！比如说，有一个圆，点A 在圆外，点B 在圆内，那它们到圆的关系就像一场有趣的较量呢，这就是圆幂定理在起作用呀！比如你看，点 A 到圆的切线长和割线长之间的关系，是不是很神奇？2. 哎呀呀，圆幂定理啊，就像是一把神奇的钥匙！打开了圆与点之间奇妙关系的大门！想象一下，在一个大大的圆里，点 C 离圆很近，点 D 离圆稍远，它们的存在是不是让圆变得更加丰富多彩啦？就好像生活中的不同角色一样。
比如计算一下点 C 和点 D 到圆的各种距离，就能深深感受到圆幂定理的魅力啦！3. 哇塞，圆幂定理真的超有趣的！可以把圆和点的关系变得清晰明了。
举个例子呀，你看那个圆，还有点 E 和点 F 在它周围，就像好朋友围着它一样。
这种关系下，圆幂定理就像一个指挥家，指挥着它们之间距离的变化呢！比如观察点 E 和点 F 到圆的割线和交点的情况，神奇吧？4. 嘿哟，圆幂定理可不是一般的厉害！它能让我们看到圆和点那些隐藏的联系呢！好比一个舞台，圆是主角，点G 和点H 是配角，它们相互配合。
比如实际算一下点 G 和点 H 与圆相关的一些长度或数量，你就会惊叹，原来圆幂定理这么牛啊！5. 哇哦，圆幂定理呀！它就像一个神秘的魔法！可以让圆和点之间发生很多意想不到的事情呢！比如说有个圆，点 I 和点 J 在它身边，它们的故事可精彩啦！通过圆幂定理，我们能知道点 I 和点 J 对圆产生了怎样的影响。
就像在探索一个奇妙的世界，不是吗？比如试着分析一下它们到圆的某些线段长度，绝对让你大开眼界！6. 哈哈，圆幂定理真的让人大开眼界呀！就像一道亮光，照亮了圆和点的复杂关系。
想象一下，圆K，还有点L 和点M 在旁边，它们相互作用呢！用圆幂定理去理解这些关系，就好像解开一个谜团一样刺激！比如观察他们在圆上产生的一些变化情况，怎能不让人着迷？7. 圆幂定理呀，那可真是太重要啦！它可是连接圆与点的重要桥梁呢！无论是在数学世界里还是在我们的实际生活中，都有着不可忽视的作用呀！当真的去探索和应用它的时候，你会发现它的魅力无穷无尽！就像很多数学定理一样，看似普通，实则蕴含着巨大的能量呢！。
园幂定理
圆幂定理相交弦定理、切割线定理、割线定理统称为圆幂定理．圆幂定理实质上是反映两条相交直线与圆的位置关系的性质定理，其本质是与比例线段有关．相交弦定理: 在图(1)中⊙O的两条弦AB，CD相交于点P，则PA·PB＝PC·PD切割线定理: 在图(2)中 PAB为⊙O的割线；PT为⊙O的切线，则PA·PB＝PT2割线定理：在图(3)中，PAB、PCD为⊙O的两条割线，则PA·PB＝PC·PD 相交弦定理、切割线定理、割线定理有着密切的联系，主要体现在：1．用运动的观点看，切割线定理、割线定理是相交弦定理另一种情形，即移动圆内两条相交弦使其交点在圆外的情况；2．从定理的证明方法看，都是由一对相似三角形得到的等积式．熟悉以下基本图形、基本结论：以上定理形式虽然不同，但实质相同，它们是相互统一的.【例题求解】练习1 已知P 为⊙O 外一点，OP 与⊙O 交于点A ，割线PBC 与⊙O 交于点B ，C ，且PB ＝BC.如果OA ＝7，PA ＝2，求PC 的长.练习2 如图7-175，⊙O 和⊙O ′都经过点A 和B ，PQ 切⊙O 于P ，交⊙O ′于Q ，M ，交AB 的延长线于N.求证：PN 2＝NM ·NQ.【例1】 如图，PT 切⊙O 于点T ，PA 交⊙O 于A 、B 两点，且与直径CT 交于点D ，CD=2，AD=3，BD=6，则PB= ． (成都市中考题)思路点拨 综合运用圆幂定理、勾股定理求PB 长．注：比例线段是几何之中一个重要问题，比例线段的学习是一个由一般到特殊、不断深化的过程，大致经历了四个阶段： (1)平行线分线段对应成比例； (2)相似三角形对应边成比例；(3)直角三角形中的比例线段可以用积的形式简捷地表示出来； (4)圆中的比例线段通过圆幂定理明快地反映出来．【例2】 如图，在平行四边形ABCD 中，过A 、B 、C 三点的圆交AD 于点E ，且与CD 相切，若AB=4，BE=5，则DE 的长为( ) (全国初中数学联赛题)A ．3B ．4C ．415D ．516思路点拨 连AC ，CE ，由条件可得许多等线段，为切割线定理的运用创设条件． 注：圆中线段的算，常常需要综合相似三角形、直角三角形、圆幂定理等知识，通过代数化获解，加强对图形的分解，注重信息的重组与整合是解圆中线段计算问题的关键．【例3】 如图，△ABC 内接于⊙O ，AB 是∠O 的直径，PA 是过A 点的直线，∠PAC=∠B ．(1)求证：PA 是⊙O 的切线；(2)如果弦CD 交AB 于E ，CD 的延长线交PA 于F ，AC=8，CE ：ED=6：5， AE ：BE=2：3，求AB 的长和∠ECB 的正切值． (北京市海淀区中考题)思路点拨直径、切线对应着与圆相关的丰富知识．(1)问的证明为切割线定理的运用创造了条件；引入参数x、k处理(2)问中的比例式，把相应线段用是的代数式表示，并寻找x与k的关系，建立x或k的方程．【例4】如图，P是平行四边形AB的边AB的延长线上一点，DP与AC、BC分别交于点E、E，EG是过B、F、P三点圆的切线，G为切点，求证：EG=DE(四川省竞赛题) 思路点拨由切割线定理得EG2=EF·EP，要证明EG=DE，只需证明DE2=EF·EP，这样通过圆幂定理把线段相等问题的证明转化为线段等积式的证明．注：圆中的许多问题，若图形中有适用圆幂定理的条件，则能化解问题的难度，而圆中线段等积式是转化问题的桥梁．需要注意的是，圆幂定理的运用不仅局限于计算及比例线段的证明，可拓展到平面几何各种类型的问题中．【例5】如图，以正方形ABCD的AB边为直径，在正方形内部作半圆，圆心为O，DF切半圆于点E，交AB的延长线于点F，BF＝4．求：(1)cos∠F的值；(2)BE的长． (成都市中考题)思路点拨解决本例的基础是：熟悉圆中常用辅助线的添法(连OE，AE)；熟悉圆中重要性质定理及角与线段的转化方法．对于(1)，先求出EF，FO值；对于(2)，从△BE F∽△EAF，Rt△AEB入手．拓展练习：1．如图，PT是⊙O的切线，T为切点，PB是⊙O的割线，交⊙O于A、B两点，交弦CD于点M，已知CM=10，MD=2，PA=MB=4，则PT的长为．2．如图，PAB、PCD为⊙O的两条割线，若PA=5，AB=7，CD=11，则AC：BD= ．3．如图，AB是⊙O的直径，C是AB延长线上的一点，CD是⊙O的切线，D为切点，过点B作⊙O的切线交CD于点F，若AB=CD=2，则CE= ．4．如图，在△ABC 中，∠C=90°，AB=10，AC=6，以AC 为直径作圆与斜边交于点P ，则BP 的长为( )A ．6．4B ．3．2C ．3．6D ．85．如图，⊙O 的弦AB 平分半径OC ，交OC 于P 点，已知PA 、PB 的长分别为方程024122=+-x x 的两根，则此圆的直径为( )A ．28B ．26C ．24D ．226．如图，⊙O 的直径Ab 垂直于弦CD ，垂足为H ，点P 是AC 上一点(点P 不与A 、C 两点重合)，连结PC 、PD 、PA 、AD ，点E 在AP 的延长线上，PD 与AB 交于点F ，给出下列四个结论：①CH 2=AH ·BH ；②AD ＝AC ：③AD 2=DF ·DP ；④∠EPC=∠APD ，其中正确的个数是( )A ．1B ．2C ．3D ．4 7．如下图，BC 是半圆的直径，O 为圆心，P 是BC 延长线上一点，PA 切半圆于点A ，AD ⊥BC 于点D ．(1)若∠B=30°，问AB 与AP 是否相等?请说明理由； (2)求证：PD ·PO=PC ·PB ；(3)若BD ：DC=4：l ，且BC ＝10，求PC 的长．8．如上图，已知PA 切⊙O 于点A ，割线PBC 交⊙O 于点B 、C ，PD ⊥AB 于点D ，PD 、AO 的延长线相交于点E ，连CE 并延长交⊙O 于点F ，连AF ． (1)求证：△PBD ∽△PEC ；(2)若AB=12，tan ∠EAF=32，求⊙O 的半径的长．⌒⌒⌒9．如上图，已知AB 是⊙O 的直径，PB 切⊙O 于点B ，PA 交⊙O 于点C ，PF 分别交AB 、BC 于E 、D ，交⊙O 于F 、G ，且BE 、BD 恰哈好是关于x 的方程0)134(622=+++-m m x x (其中m 为实数)的两根．(1)求证：BE=BD ；(2)若GE ·EF=36，求∠A 的度数．10．如图，△ABC 中，∠C=90°，O 为AB 上一点，以O 为圆心，OB 为半径的圆 与AB 相交于点E ，与AC 相切于点D ，已知AD=2，AE=1，那么BC= ．11．如图，已知A 、B 、C 、D 在同一个圆上，BC=CD ，AC 与BD 交于E ，若AC=8，CD=4，且线段BE 、ED 为正整数，则BD= ．12．如图，P 是半圆O 的直径BC 延长线上一点，PA 切半圆于点A ，AH ⊥BC 于H ，若PA=1，PB+PC=a (a >2)，则PH=( )A ．a2B ．a 1C ．2aD ．3a13．如图，△ABC 是⊙O 的内接正三角形，弦EF 经过BC 的中点D ，且EF ∥AB ， 若AB=2，则DE 的长为( )A ．21 B ．215- C ．23D ．114．如图，已知AB为⊙O的直径，C为⊙O上一点，延长BC至D，使CD=BC，CE⊥AD于E，BE交⊙O于F，AF交CE于P，求证：PE=PC． (太原市竞赛题)15．已知：如图，ABCD为正方形，以D点为圆心，AD为半径的圆弧与以BC为直径的⊙O相交于P、C两点，连结AC、AP、CP，并延长CP、AP分别交AB、BC、⊙O 于E、H、F三点，连结OF．(1)求证：△AEP∽△CEA；(2)判断线段AB与OF的位置关系，并证明你的结论；(3)求BH:HC (四川省中考题)16．如图，PA、PB是⊙O的两条切线，PEC是一条割线，D是AB与PC的交点，若PE=2，CD=1，求DE的长．(国家理科实验班招生试题)。
圆幂定理与角平分线
圆幂定理与角平分线
圆幂定理和角平分线是几何学中重要的概念，它们在解决几何问题和证明定理时起着关键作用。
首先，让我们来谈谈圆幂定理。
圆幂定理是几何学中的基本定理之一，它描述了一个点到圆的切线上的两个切点之间的乘积与该点到圆心的距离的平方之间的关系。
具体来说，如果一个点P到圆的距离为d，点P到圆的切线上的两个切点分别为A和B，那么PAPB=d^2。
这个定理在解决与圆相关的问题时非常有用，可以帮助我们计算未知的长度或者证明几何关系。
接下来，让我们来讨论角平分线。
角平分线是指将一个角分成两个相等的角的线段。
在一个三角形中，如果一条线段从一个顶点到对边的中点，并且与对边的另一条边相交，那么这条线段就是该三角形的一个角平分线。
角平分线具有许多重要性质，例如角平分线定理指出，角平分线将对边分成的两条线段的比等于另外两条边的比。
这个定理在解决三角形内角平分线相关的问题时非常有用，可以帮助我们推导出许多几何关系和定理。
综上所述，圆幂定理和角平分线都是几何学中重要的概念，它
们在解决几何问题和证明定理时都发挥着关键作用。
对于圆幂定理，它描述了点到圆的切线上的两个切点之间的乘积与该点到圆心的距
离的平方之间的关系；对于角平分线，它是将一个角分成两个相等
的角的线段，并且具有许多重要的性质和定理。
在实际问题中，我
们可以通过运用这两个概念来解决各种与圆和三角形相关的几何问题，从而加深对几何学的理解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆幂定理：过一个定点P的任何一条直线 圆幂定理：过一个定点P的任何一条直线 与圆相交， 与圆相交，则这点到直线与圆的交点的两 =d 条线段的乘积为定值 O P − r . （等于点P到圆心的距离与半径的平方差 等于点 到圆心的距离与半径的平方差 的绝对值） 的绝对值）
2 2
已知： 是 的直径CB的延长线上的一点 已知：P是⊙O的直径 的延长线上的一点， 的直径 的延长线上的一点， PA和⊙O相切于 ，若PA＝15，PB＝5。 相切于A， 和 相切于 ＝ ， ＝ 。 的值；（ （1）求tan∠ABC的值；（ ）弦AD使 ） ∠ 的值；（2） 使 的长。 ∠BAD＝∠P，求AD的长。 ＝ ， 的长
圆幂定理
我们把圆的切线上某一点与切点之间 的线段的长叫做这点到圆的切线长 这点到圆的切线长。 的线段的长叫做这点到圆的切线长。
A
O·
P
B
切线与切线长的区别与联系： 切线与切线长的区别与联系： （1）切线是一条与圆相切的直线； 切线长是指切线上某一点与切点间的线段的长。 （2）切线长是指切线上某一点与切点间的线段的长。
A
O P B D C
E
证明：（1）连结AB
A
O P B D C
∵PA切⊙O于A,∴∠PAB＝∠AEB
E
∴PA＝PD （2）由切割线定理,
又PA＝PD，PC＝2PD 由相交弦定理， BD·DC＝AD·DE
已知在Rt△ 已知在 △ABC中，∠C＝90°，∠A的外 中 ＝ ° 的外 角平分线交BC的延长线于 的延长线于D交 角平分线交 的延长线于 交△ABC的外接 的外接 圆O于E，DF切⊙O于F， 于 ， 切 于 ， 求证： 求证： AB ⋅ AC＝DF －DA 。
A
圆幂定理求AE·ED的值 的值 圆幂定理求 即等于r 即等于 2-OE2
C 连接CD正相似，可得AE与ED的比
O B P
E
3; 4 1 0
D
如图已知： 外一点， 如图已知：点C是⊙O外一点，过C作⊙O的 是 外一点 作 的 切线CB和 ，切点分别为B、 ， 切线 和CD，切点分别为 、D，连BO并延 并延 长交⊙ 于点 于点E， 的延长线于A， 长交⊙O于点 ，交CD的延长线于 ，若 的延长线于
C P A O B P C A O B
D
运动观点看本质
• • • • • 切线长定理 相交弦定理 相交弦定理推论 切割线定理 割线定理
本质一样 圆幂定理
几个定理得统一
相交弦定理 C B A •P D PA•PB=PC•PD PA²=PC•PD PA=PC 割线定理 切割线定理 切线长定理
PA•PB=PC•PD
B
• 相交弦定理推论 如果弦与直径垂直相交， 那么弦的一半是它分直径所成的两条线段的 比例中项。 2
PC = PA·PB
• 如图，PAB和PCD是⊙O的 两条割线。 求证：PA·PB＝PC·PD
D C P A B O
PA·PB＝PC·PD ＝
• 切割线定理推论（割线定理） 从圆外一 点引圆的两条割线，这一点到每条割线与圆 的交点的两条线段长的积相等。
2 2
E
连接BE，证明三角形 ABE与三角形ACD相似
A O D C F
B
提 供了新的方法。 供了新的方法。
A
• 相交弦定理 圆内的两条相交 弦，被交点分成的两条线段长 的积相等。
D
O
C
P
B
PA·PB=PC·PD
• 切割线定理 从圆外一点引圆的 切线和割线，切线长是这点到割 线与圆交点的两条线段长的比例 中项。
T O
PT2= PA·PB
P A B
A P C O
D
• 如图，CD是弦，AB是直 径，CD⊥AB，垂足为P。 求证：PC2＝PA·PB
切线长定理 从圆外一点引圆的两条切线，它 从圆外一点引圆的两条切线， 们的切线长相等， 们的切线长相等，圆心和这一点的连线平分两 B 条切线的夹角。 条切线的夹角。
。
O
1 2
A
P
几何语言: 几何语言 PA、PB分别切⊙O于A、B 、 分别切 分别切⊙ 于 、 PA = PB ∠1=∠2 ∠
反思：切线长定理为证明线段相等、角相等 切线长定理为证明线段相等、 线段相等
统一叙述为：过一点P（无论点P在圆内 还是在圆外） 在圆内， 统一叙述为：过一点 （无论点 在圆内，还是在圆外） 的两条直线，与圆相交或相切（ 的两条直线，与圆相交或相切（把切点看成两个重合 交点” 于点A、 、 、 ， 的“交点”）于点 、B、C、D，PA•PB=PC•PD 。
(1)经过⊙O内或外一点 作两条直线交⊙O于 经过⊙ 内或外一点 作两条直线交⊙ 于 内或外一点P作两条直线交 经过 A,B,C,D四点 得到了如图所示的六种不同情 四点,得到了如图所示的六种不同情 四点 在六种情况下,PA,PB,PC,PD四条线段在 况.在六种情况下 在六种情况下 四条线段在 数量上满足的关系式可用同一个式子表示.请 数量上满足的关系式可用同一个式子表示 请 先写出这个式子，然后只就图②给予证明； 先写出这个式子，然后只就图②给予证明；
• 如图，在⊙O中，P是弦AB上一点，OP⊥PC， PC交⊙O于C。求证：PC2＝PA·PB
C A D P O B
• 如图，两个以O为圆心的同心圆，AB切大圆于B， AC切小圆于C，交大圆于D、E。AB=12，AO=15， AD=8，求两圆的半径。
B
A D C
O
E
• 如图，⊙O和⊙O′都经过点 A、B，PQ切⊙O于P，交 ⊙O ′于Q、M，交AB的延 长线于N。 求证：PN2＝NM·NQ
Q
A
O' M
O B N P
• 如图，C为AB的中点， BCDE是以BC为一边的正方 形，以B为圆心，BD为半径 的圆与AB及其延长线相交于 H、K。 求证：AH·AK=2AC2。
DELeabharlann AH CB
K
学会用半径加减或加减半径
• 如图，已知PAB是⊙O的割线，PO＝14cm， PA＝4cm，AB＝16cm。求⊙O的半径。
A
A
(P) D O B C P A
A P
D D
A
C
C
P
C
B
D O
D
P C
O
D
O
O
P
B
P
C
(D) O
BC
O
B
A (B)
A (B)
PA⋅ PB＝r －OP (P在圆内 )
2 2
PA⋅ PB＝OP －r (P在圆外 )
2 2
PA⋅ PB＝OP －r =0(P在圆上 )
2 2
定 值 OP − r 称 做 点 P对 圆 O的 " 幂 "
∠C 1 ＝ ，求m的值。 AD＝m·AE，且 tan 的值。 ＝ ， 的值 2 3
A E D
连接OD
3
O
B
C
如图， 切 如图，PA切⊙O于A，割线 于 ，割线PBC交⊙O于B、 交 于 、 C两点，D为PC的中点，且AD延长线交 两点， 为 的中点 的中点， 两点 延长线交 2 BE ＝DE ⋅ EA。 ⊙O于E，又 于 ， 求证：（ ） 求证：（1）PA=PD； ：（ ； 2 （ 2 ）2BD ＝AD ⋅ DE。