次指数平滑法算例
二次曲线、指数曲线、季节指数
（三）季节变动预测法
季节变动预测法是根据历史数据中所 包含的季节变动规律性，对预测目标的 未来状况作出预测的方法。
1、季节变动的特点和衡量指标
（1）季节变动及其特点
季节变动的循环周期为一年，而且在 一年中随着季节的更替呈现有规律的变 动。
（2）衡量指标
季节指数（%）=历年同季平均数/全时期总 平均数×100%
合计 1849.87 2058.17 1302.25 2008.20 7218.49 1804.62
全年比率平均法：
例：某商店2000-2004年分季销售资料, 用全年比率平均法测算季节指数。
历年各季的比率（%）=各季的数值 / 相应 度 年份
一季 度
二季 度
年度
1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
合计
某企业近年营业额不同α值的指数平滑法对照表
α=0.3
α=0.5
营业额 指数平滑值 绝对误差 指数平滑值 绝对误差
(260)
262
260.60
257
259.52
252
季度 一季度 二季度 三季度 四季度 合计
年份
（1） （2） （3） （4） （5） （6）
2000 25.55 26.64 22.46 25.35 100.00
2001 22.48 30.35 17.86 29.31 100.00
2002 26.78 24.65 19.66 28.91 100.00
1992
(262)
1993 262 262.00
1994 257 258.50
时间序列挖掘-预测算法-三次指数平滑法(Holt-Winters)
摘要: 所有移动平均法都存在很多问题。
它们都太难计算了。
每个点的计算都让你绞尽脑汁。
而且也不能通过之前的计算结果推算出加权移动平均值。
移动平均值永远不可能应用于现有的数据集边缘的数据，因为它们的窗口宽度是有限 ...所有移动平均法都存在很多问题。
它们都太难计算了。
每个点的计算都让你绞尽脑汁。
而且也不能通过之前的计算结果推算出加权移动平均值。
移动平均值永远不可能应用于现有的数据集边缘的数据，因为它们的窗口宽度是有限的。
这是一个大问题，因为数据集边缘的变动形态一般都是我们最感兴趣的部分。
类似地，移动平均法也不能应用于现有数据集的范围之外。
其结果是，它们对预测毫无用处。
幸运的是，有一种很简单的计算方案能够避免所有这些问题。
它叫指数平滑法(exponential smoothing)或Holt-Winters法。
指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列。
术语“Holt-Winters法”有时特指三次指数平滑法。
所有的指数平滑法都要更新上一时间步长的计算结果，并使用当前时间步长的数据中包含的新信息。
它们通过“混合”新信息和旧信息来实现，而相关的新旧信息的权重由一个可调整的拌和参数来控制。
各种方法的不同之处在于它们跟踪的量的个数和对应的拌和参数的个数。
一次指数平滑法的递推关系特别简单：其中，是时间步长i上经过平滑后的值，是这个时间步长上的实际(未平滑的)数据。
你可以看到是怎么由原始数据和上一时间步长的平滑值混合而成的。
拌和参数可以是0和1之间的任意值，它控制着新旧信息之间的平衡：当接近1时，我们就只保留当前数据点(即完全没有对序列进行平滑)；当接近0时，我们就只保留前面的平滑值(也就是说整个曲线都是平的)。
为何这个方法被称为“指数”平滑法？要找出答案，展开它的递推关系式即可知道：从这里可以看出，在指数平滑法中，所有先前的观测值都对当前平滑值产生了影响，但它们所起的作用随着参数的幂的增大而逐渐减小。
一次指数平滑和二次指数平滑
一次指数平滑和二次指数平滑好啦，今天咱们聊聊一次指数平滑和二次指数平滑，听起来可能有点高大上，其实呢，没啥可怕的，咱们就把它当成生活中的小玩意儿，轻轻松松来搞定。
说到平滑，大家可能会想到那种光滑的山坡，或者是顺滑的奶油蛋糕，心里都是美滋滋的感觉。
但是这里的平滑呢，更多的是在说数据处理，尤其是在预测和分析的时候，真的是个好帮手。
先说说一次指数平滑，听名字就觉得挺神秘的吧。
它就是在时间序列数据中，帮助咱们减少那些吵闹的波动，像个热心的朋友，把那些起伏不定的数字拉得更平稳。
你看，比如说咱们每天的气温，可能今天突然降温，明天又回暖，这样的数据变化可让人晕头转向。
用一次指数平滑的时候，咱们给最近的观测值更大的权重，就像亲戚家来了一位小明星，大家都特别关注他，老一辈儿的事儿就暂时不提了。
这种方法简单易懂，最重要的是，能让你在快速变化的环境中，抓住那些重要的趋势，跟着感觉走，准没错。
再说到二次指数平滑，这可就有点意思了，听起来像是升级版的平滑。
它不仅关注最近的数据，还关注数据的变化趋势。
想象一下，你在跟朋友聊八卦，朋友说“我觉得这个明星最近可能会大火”，这就是一种趋势的判断。
二次指数平滑就像在为你的预测加了一层保护罩，让你不光知道现在的情况，还能对未来的变化做出更准确的判断。
这样一来，预测就不是简单的跟风，而是能够提前一步，掌握主动权，简直是“先知”级别的存在。
举个例子，假如你在做销售，每天的数据都在变化。
一次指数平滑帮你看到现在的销量，二次指数平滑则能让你预判下个月的趋势。
你可以根据这些数据做出决策，是增加库存，还是调整促销策略。
想想看，少了那些波动，心里就踏实多了，不至于像个无头苍蝇到处乱撞，反而可以根据数据指引，稳扎稳打，像个老练的棋手。
这两种方法其实就像生活中的道理。
你在忙碌的工作中，难免会碰到不确定的事情。
有时候像过山车，起伏不定，让人心情忐忑不安。
这时候，运用一次和二次指数平滑，就能让你更理性地看待这些变化。
指数平滑法计算模板
1、指数平滑法产生背景：2、指数平滑法的基本理论 ：3、指数平滑法的基本公式：St=ayt+(1-a)S t-1式中:St--时间t 的平滑值；yt--时间t 的实际值S t-1--时间t-1的平滑值a--平滑常数，其取值范围为[0,1]4、一次移动平滑计算示例：时间序号（t ）0123456789101112131415销售量（y t ）10158201016182022242026272929a=0.111.010.911.311.011.911.712.112.713.414.315.315.716.817.818.919.9a=0.311.010.712.010.813.612.513.514.916.418.119.919.921.723.325.026.2a=0.511.010.512.810.415.212.614.316.118.120.022.021.023.525.327.128.11）2）3）4）5、二次移动平滑计算示例：权重a=0.9年份t 财政收入1次移动平滑2次移动平滑a tb tT T+t023*********.40198423635.2434.56198534039.5239.0340.02 4.4744.49198644847.1546.3447.967.3155.28198755453.3252.6254.01 6.2860.29198866261.1360.2861.987.6669.65198977069.1168.2370.007.9577.95199087675.3174.6076.026.3782.39指数平滑法理论及计算公式指数平滑法是移动平均法中的一种，其特点在于给过去的观测值不一样的权重，即较近期观测值的权数比较远期观测值的权数要大。
根据平滑次数不同，指数平滑法分为一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权数，新数据给予较大的权数，旧数据给予较小的权数。
指数平滑法应用案例
Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和，且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展，其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。
①一次指数平滑法设时间序列为，则一次指数平滑公式为：式中为第 t周期的一次指数平滑值；为加权系数，0＜＜1。
为了弄清指数平滑的实质，将上述公式依次展开，可得：由于0＜＜1，当→∞时，→0，于是上述公式变为：由此可见实际上是的加权平均。
加权系数分别为，，…，是按几何级数衰减的，愈近的数据，权数愈大，愈远的数据，权数愈小，且权数之和等于1，即。
因为加权系数符合指数规律，且又具有平滑数据的功能，所以称为指数平滑。
用上述平滑值进行预测，就是一次指数平滑法。
其预测模型为：即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时，使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时，用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此，也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为，则二次指数平滑的计算公式为：若时间序列从某时期开始具有直线趋势，且认为未来时期亦按此直线趋势变化，则与趋势移动平均类似，可用如下的直线趋势模型来预测。
式中t为当前时期数；T为由当前时期数t到预测期的时期数；为第t+T期的预测值；为截距，为斜率，其计算公式为：③三次指数平滑法若时间序列的变动呈现出二次曲线趋势，则需要用三次指数平滑法。
移动平均法、指数平滑法例题
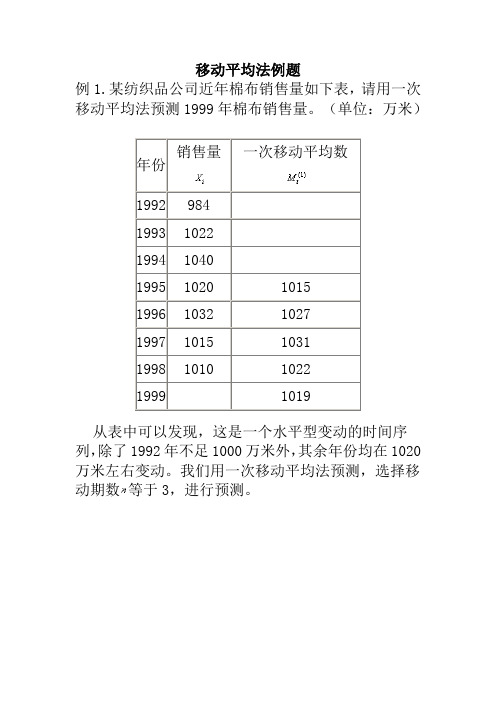
移动平均法例题例1.某纺织品公司近年棉布销售量如下表，请用一次移动平均法预测1999年棉布销售量。
（单位：万米）销售量一次移动平均数年份1992 9841993 10221994 10401995 1020 10151996 1032 10271997 1015 10311998 1010 10221999 1019从表中可以发现，这是一个水平型变动的时间序列，除了1992年不足1000万米外，其余年份均在1020万米左右变动。
我们用一次移动平均法预测，选择移动期数等于3，进行预测。
该纺织品公司1999年棉布销售量预测值为1019万米。
指数平滑预测法指以某种指标的本期实际数和本期预测数为基础，引入一个简化的加权因子，即平滑系数，以求得平均数的一种指数平滑预测法。
它是加权移动平均预测法一种变化。
平滑系数必须呈大于0、小于1，例如0.1、0.4、0.6等其计算公式：下期预测数=本期实际数×平滑系数+本期预测数×（1-平滑系数）上列公式是从下列公式演变而成：下期预测数=本期预测数+ 平滑系数（本期实际数- 本期预测数）这个公式的含义是：本期预测数上加上一部分用平滑系数调整过的本期实际数与本期预测数的差，就可求出下期预测数。
一般说来，下期预测数常介乎本期实际数与本期预测数之间。
平滑系数的大小，可根据过去的预测数与实际数比较而定。
差额大，则平滑系数应取大一些；反之则取小一些。
平滑系数愈大则近期倾向性变动影响愈大；反之，则近期的倾向性变动影响愈小，愈平滑种预测法简便易行，只要具备本期实际数、本期预测数和平滑系数三项资料，就可预测下期数。
某种产品销售量的平滑系数为0.4 ，1996年实际销售量31万件，预测销售量33万件则1997年预测销售量：1997年预测销售量= 31万件×0.4+33万件×（1-0.4）=32.2万件。
指数平滑法应用案例
Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和，且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展，其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。
①一次指数平滑法设时间序列为，则一次指数平滑公式为：式中为第t周期的一次指数平滑值；为加权系数，0＜＜1。
为了弄清指数平滑的实质，将上述公式依次展开，可得：由于0＜＜1，当→∞时，→0，于是上述公式变为：由此可见实际上是的加权平均。
加权系数分别为，，…，是按几何级数衰减的，愈近的数据，权数愈大，愈远的数据，权数愈小，且权数之和等于1，即。
因为加权系数符合指数规律，且又具有平滑数据的功能，所以称为指数平滑。
用上述平滑值进行预测，就是一次指数平滑法。
其预测模型为：即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时，使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时，用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此，也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为，则二次指数平滑的计算公式为：若时间序列从某时期开始具有直线趋势，且认为未来时期亦按此直线趋势变化，则与趋势移动平均类似，可用如下的直线趋势模型来预测。
式中t为当前时期数；T为由当前时期数t到预测期的时期数；为第t+T期的预测值；为截距，为斜率，其计算公式为：③三次指数平滑法若时间序列的变动呈现出二次曲线趋势，则需要用三次指数平滑法。
指数平滑法.
一、一次指数平滑法
1. 预测模型 y1, y2 , , yt , 已知时间序列为： 数平滑的基本公式为：
(1) t (1) t 1
,一次指
S yt (1 )S (1) ˆ ˆ y (1 )Y ˆ Yt 1 St 即，Y t 1 t t
二次指数平滑法
二次指数平滑数学模型：
ˆ a bT Y t T t t
(1) t (2) t
T 1, 2,3,
at 2 S S (1) (2) bt 1 ( St St )
算例
例题：某地1983年至1993年财政入的资料如下，试用指数平 滑法求解趋势直线方程并预测1996年的财政收入。
算例
于是，得t=11时预测模型为
ˆ 11T a11 b11T c11T 2 706.2 98.4T 4.4T 2 Y
预测2007年和2008年的产品销售量为：
ˆ 2007 = Y ˆ 12 =706.2 98.4 1 4.4 12 =809 Y （万台） ˆ 2008 = Y ˆ 13 =706.2 98.4 2 4.4 2 2 =920.6 Y （万台）
算例
解：（1）确定初始值 因为观察期为9小于20,取时间序列的前三项数 据的平均值作为初始值
S
(1) 0
y1 y2 y3 4000 4700 5000 4566.67(万元) 3 3
算例
（2）选择平滑系数α，计算各年一次指数平滑 值
这里分别取α=0.1、α=0.6和α=0.9计算各年一次 指数平滑值
指 数 平 滑 法
指数平滑法
指数平滑法是一种特殊的加权移动平均法，其加 权的特点是对离预测期近的历史数据给予较大的 权数，对离预测期远的历史数据给予较小的权数， 权数由近到远按指数规律递减，所以，这种方法 被称为指数平滑法。
指数平滑法实验
指数平滑法实验实验目的：掌握用指数平滑法对时序的平滑过程并进行相关的预测。
实验内容：指数平滑法知识准备：指数平滑法是另一种计算时间序列长期趋势的方法，是加权平均的一种特殊形式。
指数平滑法是布朗(Robert G..Brown)所提出，是在移动平均法基础上发展起来的一种时间序列分析预测法，是最常用的一种预测方法，特别适用于中短期预测。
1、单指数平滑法单指数平滑通常适用于不可预测的向上或向下趋势的预测。
设观测序列,为加权系数，其计算公式如下：(0<a<1)(43)现对（43）式进行递推，则（43）式可写成：(44)（44）式表明是全部历史数据的加权平均，加权系数分别为，,，…；由于加权系数呈指数函数衰减，加权平均又能消除或减弱随机干扰的影响，所以（43）式称为指数平滑。
根据实践经验，a的实际取值范围一般以0.1~0.3之间为宜。
如何进一步确定a的最佳取值，通常要结合理论分析和模型对比的方法来进行。
单指数平滑的预测公式如下：(45)2、双指数平滑双指数平滑是对一次指数平滑的再平滑，当观测数据有清楚的趋势并可能包括未来向上运动预测的信息时采用此法预测。
其表达式如下：(46)其中，(47)(48)其中：0<a<1，是单指数平滑序列，是二次指数平滑序列。
双指数平滑的预测公式如下：另外，由于指数平滑公式是递推计算公式，所以必须确定初始值。
初始值实质上是序列起始点之前所有历史数据的加权平均值，但在实际工作中，由于获得历史数据多少的不同，往往采用经验方法来确定。
因而可以通过在最初预测时，选择较高的值来减少由初始值选择不当所造成的预测偏差，从而使预测模型调整到当前水平。
Holt-Winters法也是指数平滑中的一种，它适用于对具有季节影响的线性增长趋势的序列进行预测。
这种方法计算截距（常数项）、趋势系数（斜率）和季节影响的各个递推值。
其可分为乘法、加法及无季节模型。
3、Holt-Winters乘法模型这种方法适用于序列具有线性趋势和乘法季节变化。
一次指数平滑法计算公式
一次指数平滑法计算公式一次指数平滑法是一种常用的时间序列预测方法，它在数据分析和预测领域有着广泛的应用。
先来说说一次指数平滑法的计算公式吧，公式是这样的：$S_{t} =\alpha Y_{t} + (1 - \alpha)S_{t - 1}$ 。
这里面，$S_{t}$ 表示第 t 期的平滑值，$Y_{t}$ 是第 t 期的实际值，$\alpha$ 是平滑系数，取值范围在0 到 1 之间，$S_{t - 1}$ 则是第 t - 1 期的平滑值。
给您举个例子来说明一下这个公式怎么用。
我之前在一家小超市工作，老板让我预测下个月某种饮料的销量。
我就收集了过去几个月这种饮料的销售数据。
假设第一个月卖了100 瓶，第二个月卖了120 瓶，平滑系数$\alpha$ 我先取 0.3 。
那么第一个月的平滑值$S_{1}$ 就等于第一个月的实际销量100 瓶。
到了第二个月，按照公式，$S_{2} = 0.3×120 + (1 - 0.3)×100 = 36 + 70 = 106$ 瓶。
然后第三个月实际卖了 110 瓶，那第三个月的平滑值$S_{3} =0.3×110 + (1 - 0.3)×106 = 33 + 74.2 = 107.2$ 瓶。
就这样依次计算下去，就能得到一系列的平滑值，通过对这些平滑值的分析，就可以对未来的销量做出一定的预测。
在实际应用中，平滑系数$\alpha$ 的选择很关键。
如果$\alpha$ 比较大，比如 0.8 ，那么新的数据在平滑值中的权重就比较大，预测结果对最新的变化反应更迅速，但可能会比较波动；如果$\alpha$ 比较小，比如 0.1 ，那么过去的数据在平滑值中的权重就大，预测结果相对更稳定，但可能对新的变化反应较慢。
比如说，如果最近市场上突然出现了对这种饮料的负面新闻，导致销量短期内大幅下降。
这时候如果我们用较大的$\alpha$ ，就能更快地在预测中反映出这种变化，及时调整采购和销售策略。
指数平滑模型公式
指数平滑模型公式1. 一次指数平滑法。
- 设时间序列为y_1,y_2,·s,y_t,·s，一次指数平滑公式为：S_t^(1)=α y_t+(1 - α)S_t - 1^(1)- 其中S_t^(1)为第t期的一次指数平滑值；y_t为第t期的实际观测值；α为平滑系数，0<α<1；S_t - 1^(1)为第t - 1期的一次指数平滑值。
当t = 1时，S_1^(1)=y_1（即初始值等于第一个观测值）。
2. 二次指数平滑法。
- 首先进行一次指数平滑得到S_t^(1)，然后在此基础上进行二次指数平滑，公式为：S_t^(2)=α S_t^(1)+(1 - α)S_t - 1^(2)- 其中S_t^(2)为第t期的二次指数平滑值，S_t - 1^(2)为第t - 1期的二次指数平滑值。
当t = 1时，S_1^(2)=S_1^(1)（初始值等于一次指数平滑的初始值）。
3. 三次指数平滑法（用于非线性趋势预测）- 在二次指数平滑基础上进行三次指数平滑，公式为：S_t^(3)=α S_t^(2)+(1 - α)S_t - 1^(3)- 其中S_t^(3)为第t期的三次指数平滑值，S_t - 1^(3)为第t - 1期的三次指数平滑值。
当t = 1时，S_1^(3)=S_1^(2)（初始值等于二次指数平滑的初始值）。
- 在得到S_t^(1)、S_t^(2)、S_t^(3)后，可以根据具体的预测模型进行预测，例如对于三次指数平滑法的预测模型（以线性趋势为例）：- ŷ_t + m=a_t + b_tm + c_tm^2- 其中m为预测期数，a_t = 3S_t^(1)-3S_t^(2)+S_t^(3)，b_t=(α)/(2(1 - α)^2)[(6 - 5α)S_t^(1)-2(5 - 4α)S_t^(2)+(4 - 3α)S_t^(3)]，c_t=(α^2)/(2(1 - α)^2)(S_t^(1)-2S_t^(2)+S_t^(3))。
指数平滑法
指数平滑法应用案例Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和，且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展，其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同，指数平滑法分为：一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是：预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权。
①一次指数平滑法设时间序列为，则一次指数平滑公式为：式中为第 t周期的一次指数平滑值；为加权系数，0＜＜1。
为了弄清指数平滑的实质，将上述公式依次展开，可得：由于0＜＜1，当→∞时，→0，于是上述公式变为：由此可见实际上是的加权平均。
加权系数分别为，，…，是按几何级数衰减的，愈近的数据，权数愈大，愈远的数据，权数愈小，且权数之和等于1，即。
因为加权系数符合指数规律，且又具有平滑数据的功能，所以称为指数平滑。
用上述平滑值进行预测，就是一次指数平滑法。
其预测模型为：即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时，使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时，用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此，也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为，则二次指数平滑的计算公式为：若时间序列从某时期开始具有直线趋势，且认为未来时期亦按此直线趋势变化，则与趋势移动平均类似，可用如下的直线趋势模型来预测。
式中t为当前时期数；T为由当前时期数t到预测期的时期数；为第t+T期的预测值；为截距，为斜率，其计算公式为：③三次指数平滑法若时间序列的变动呈现出二次曲线趋势，则需要用三次指数平滑法。
指数平滑法
实验二：时间序列平滑预测法一、实验目的根据所给的数据，采用适当的时间序列平滑预测法，来实现对原序列的趋势进行平滑，从而对未来某现象做出预测二、实验内容利用时间序列平滑预测法对某商品销售进行预测或商品的供应量进行预测三、实验步骤下表为某市自来水历年供应量，请选择合适的方法对下一期的自来水供应量进行预测，并说明选择该方法的理由。
一：根据上表数据做出散点图如下:|*供*星f 1U 石n-ooo 1:11:11:11:1oID42_l18642i —IIiIX根据上图可以看出：从1993后时间序列具有明显的线性变化趋势，为了避免利用移动平均法预测有趋势的数据时产生的误差，所以不宜采用一次移动平均法及一次指数线性二次指数平滑法才能满足预测模型的要求二次曲线指数平滑法的计算过程如下：(1)计算t时期的单指数平滑值s(1):tS⑴=o x+(1-a)S⑴ttt—1(2)计算t时期的双指数平滑值s⑵：tS⑵=a S⑴+(1—a)S⑵ttt—1(3)计算t时期的三重指数平滑值s⑶：tS⑶=a S⑵+(1—a)S(3)ttt—1(4)计算t时期的水平值A:tA=3S⑴一3S⑵+S(3)tttt(5)计算t时期的线性增量B:ta2B=[(6-5a)S⑴一(10-8a)S⑵+(4-3a)S⑶]t(1—a)2ttt(6)计算t时期的抛物线增量C：ta2C=(S(i)—2S⑵+S⑶)t(1一a)2ttt(7)预测m时期以后，即(t+m)时期的数值F:t+mF=A+Bm+—Cm2t+mtt2t其中，m是正整数，二次曲线指数平滑法的初始值依赖于两个时期的观测值x和x。
12已矢口X和X，假设:S(1)=S(2)=S⑶=x。
121111根据表中的数据可知：各个时期的供水量变化很大，所以乂的值要选择大一些，本题选择的a=0.5和a=0.8同时把第一期的值作为预测一次二次的初始预测值，所以其计算结果如下根据所给的数据，选取了三个不同的a值对该模型进行预测，具体计算数值通过计算机计算如下：(1)取二次曲线指数平滑法预测某市的供水量a=0.5时供水量(10序年份万吨) S(1)tS(2)t 1 19919.98 19.98 19.2 1991 29.56 24.77 22.383 19920.96 22.865 22.4 1993 12.94 17.903 20.265 19931.95 24.926 22.6 1995 36.16 30.543 26.577 19943.76 37.152 31.s⑶t19.98AtBtCtt+m21.18 28.363 5.39 1.221.22.634 -0.9 -0.5 34.21.08 14.004 -6.2 -1.5 21.4521.84 28.834 6.27 1.58 7.0 24.236.127 8 1.61 35.8928.03 43.906 8.95 1.46 44.F(m=1)1234□5TS910111Z131415时序(t)—观测值—预测值系列孑QOOC-C-O-oO-649-O-86421111$翌崔8 1997 56.86 47.006 39.43 33.73 56.451 12.3 1.87 53.9 1998 75.06 61.033 50.23 41.98 74.383 17.2 2.55 69.64 11999 82.12 71.576 60.9 51.44 83.459 13.7 1.2192.83 11 2000 96.04 83.808 72.36 61.9 96.255 13.9 1 97.76 12001 99.93 91.869 82.11 72.01 101.28 8.88 -0.4 11013 2002 115.5 103.68 92.9 82.45 114.81 11.6 0.34 110 12003 124.3 113.99 103.4 92.95 124.59 10.7 0.05 12615 2004 119.29 116.64 110 101.5 121.29 1.72 -1.9 135.3 12005 138.13127.39118.7110.1136.128.830.06122 12006145帛rh 自*水穴縉垦观测但-坝测但1-3(2)取a 二0.8二次曲线指数平滑法预测某市的供水量a 二0.8供水量(10 S (1) S (2) S⑶ A BC时序 年份 万吨)t t tt ttF (m =1)1 19919.98 19.98 19.919.9t +m2 19929.56 27.64 26.124.829.417.6 4.903 1992 20.96 22.3 23.06 23.42 21.14 -15.1 -6.37 49.59 4 19912.94 14.81 16.417.812.-17.-4.1 2.85 1994 31.95 28.52 26.11 24.46 31.7 34.92 12.18 -6.29 6 19936.16 34.63 32.931.236.311.10.17 72.7 7 1996 43.76 41.93 40.13 38.35 43.76 12.08 0.344 47.61 8 19956.86 53.87 51.148.556.822.5 3.0956.9 1998 75.06 70.82 66.88 63.22 75.04 32.3 4.431 80.91 119982.12 79.86 77.274.482.211.1-3.410911 2000 96.04 92.8 89.7 86.65 95.97 21.42 0.957 91.68 120099.93 98.5 96.794.710 4.68-4.111713 2002 115.5 112.1 109 106.2 115.4 25.05 3.368 102.6 1200124.3 121.9 119.116.124.14.9-0.914215 2004119.29119.8119.7119.1119.4—12.3—8.07138.8 16 2005138.13134.5131.5129137.930.917.507103.1 17 2006172.5某市自来水供给量观测值与预测値oooooooooooOT-舰测值-预测值系列廿1-4通过比较图1-2、1-3和1-4,我们可以看出当―0.5，预测线拟合的数值更接近真实的观测值，而当—0.8时，预测值与实际观测值偏差较大，故选取平滑常数^=0.5，来对某市的自来水供水量进行逐年预测。
二次平滑指数预测例题
二次平滑指数预测例题预测是企业决策过程中的重要环节之一。
准确的预测可以帮助企业做出更好的决策，提高效率和竞争力。
其中，二次平滑指数预测是一种常用的预测方法，下面将通过一个实例来解释如何使用二次平滑指数预测方法来做出准确的预测。
假设某企业想要预测下个季度的销售额，已知过去五个季度的销售额数据如下：季度 | 销售额Q1 | 100Q2 | 110Q3 | 120Q4 | 130Q5 | 140首先，我们将给出二次平滑指数预测中需要使用的参数。
主要有两个参数，分别是平滑系数和趋势系数。
平滑系数用于平滑过去的销售数据，趋势系数用于反映销售额的趋势走向。
根据实际情况选择适当的参数值可以提高预测的准确性。
在本例中，我们选择平滑系数为0.8，趋势系数为0.2。
接下来，我们按照以下步骤进行预测计算：1. 首先，首次预测的平滑值和趋势值需要初始化。
我们将第一个季度的销售额作为首次预测值，因此初始化平滑值为100，趋势值为10（第二个季度的销售额减去第一个季度的销售额）。
2. 接下来，我们可以通过以下公式来计算二次平滑指数预测值：平滑值 = 平滑系数 * 实际销售额 + (1-平滑系数) * (首次预测的平滑值 + 首次预测的趋势值)趋势值 = 趋势系数 * (平滑值 - 首次预测的平滑值) + (1-趋势系数) * 首次预测的趋势值预测值 = 平滑值 + 预测的季度数 * 趋势值根据这些公式，我们可以得到以下的预测结果：Q6预测值 = 0.8 * 140 + 0.2 * (100 + 10) = 128Q7预测值 = 0.8 * 128 + 0.2 * (140 - 100) = 129.2Q8预测值 = 0.8 * 129.2 + 0.2 * (128 - 100) = 128.483. 重复以上步骤，直到预测出所需的期数为止。
在本例中，我们可以继续按照以上公式计算出Q9、Q10等季度的销售额预测值。
通过以上的计算过程，我们可以得到下个季度销售额的预测值为128.48。
第7章4指数平滑法
4 3100 1940 1160 1160 1345600 1894 1206 1206 1454436 1967 1133 1133 1283689
5 1750 2056 -306 306 93636 2497 -747 747 558009 2987 -1237 1237 1530169
6 1550 2026 -476 476 226576 2123 -573 573 328329 1874 -324 324 104976
一、一次指数平滑法
设时间序列： X tX 1,X 2,...,X t,...,X n
一次指数平滑值计算公式为：
St(1)Xt(1)St( 11 )
其中：
S (1) t
第t期的一次指数平滑值
Xt 第t期的观测值
加权系数，0 1
指数平滑如何克服移动平均的不足？
St(1 )X t(1)St( 1 1 ) S t( 1 1 )X t 1 (1 )S t( 1 ) 2
……
S 1 (1 )X 1(1)S0 (1 )
迭代可得，
St(1)Xt(1)Xt1(1)2Xt2... ＋ (1-) tS0 (1)
S(1) t
Xt(1)Xt1(1)2Xt2...
＋ (1-) tS0 (1)
权系数为： ， （ 1 - ） ， （ 1 - ） 2 ， . . .
按指数几何级数衰减，符合指数规律，又具有平滑 数据的作用，因此称为指数平滑法。
2
825 720.7 689.4 752.0 13.4 676.0
3
774 736.7 703.6 769.8 14.2 765.4
4
716 730.5 711.7 749.3 8.1 784.0
指数平滑法——精选推荐
指数平滑法时间序列分解⼤量时间序列的观测样本表现出趋势性、季节性和随机性，或者三者中的其⼀或其⼆。
于是，我们认为每个时间序列，都可以分为三个部分的叠加其中，T是趋势项，S是季节项，R是随机项。
上述公式表现了趋势项和季节项是累加的，实际应⽤场景中，趋势项和季节项可能是累乘的，时间序列可以分解为如下公式实际应⽤中，随机项R的期望为0，没有规律，并且绝对值不⼤。
所以在应⽤场景中我们往往省略掉R，R称作噪声。
预测公式如下或⼀次指数平滑法线性回归算法中，每个经验点的权重是⼀致的，即很早以前的经验数据也可能对预测数据有较⼤的影响。
很多实际场景中，未来⼀段时间的趋势可能和在最近⼀段时间的趋势关系更加紧密。
⽐如⼩明去年数学考试成绩⼀直不及格，今年连续多次考试90多分，预测⼩明下⼀次数学考试的成绩，情理上90多分的可能性更⾼。
采⽤传统的线性回归算法，预测结果可能是70多分。
指数平滑法认为越⽼的经验数据对趋势的影响越⼩。
我们假定时间t的观测值为y(t)，时间t的预测值为S(t)，则时间t+1的预测值S(t+1)为a的取值范围(0, 1)，a越⼤，最近时间点的观测值对预测值的影响越⼤。
假设我们有t个经验数据，根据上述⼀次指数平滑公式，预测值S(t + n) = S(t + 1)，预测值不具备趋势。
⼆次指数平滑我们对⼀次指数平滑值再进⾏指数平滑，可以获得趋势。
⼆次指数平滑法的预测模型为：式中：分别为时间t和时间t - 1的⼆次指数平滑值。
三次指数平滑⼆次指数模型是线性的，对于⾮线性趋势预测我们可以使⽤三次指数平滑法。
公式如下Holt-Winters算法对于具有周期性的趋势预测，我们可以使⽤Holt-Winters算法。
累乘性Holt-Winters公式如下其中，alpha，beta，gamma取值范围为(0, 1)，分别表⽰全局因⼦，趋势因⼦，周期性因⼦中最近时间点数据对预测数据的影响程度。
y为经验数据，L为周期。
表⽰使⽤t时间点的估计值预测t+m时间点的值。
实验二：指数平滑法新
实验二：指数平滑法一、实验目的Part A:一次指数平滑法1根据时间序列数据散点图，熟悉一次指数平滑法适用条件的判断；2熟悉应用一次指数平滑法进行相应预测；3熟悉一次指数平滑法预测精度的分析及其最优平滑系数α的确定；Part B:二次指数平滑法1根据时间序列数据散点图，熟悉二次指数平滑法适用条件的判断；2熟悉应用二次指数平滑法进行相应预测；3熟悉二次指数平滑法预测精度的分析及其最优平滑系数α的确定；二、实验内容及实验过程Part A问题描述某商场在过去1-12周的某冰箱销售量统计数据如表1所示。
（1）试分析统计数据，选择合适的模型来估计下周产品销售量。
（2）平滑系数α=0.2，S0(1)=（X1+X2）/2采用一次指数平滑法进行预测，并分析其预测精度。
（3）何选择合适的平滑系数α，使预测精度较高？实验过程步骤1：绘制过去12周冰箱销售量的“XY散点图”，如图。
从散点图可以看出，冰箱销售量走势基本沿水平方向变化且无季节影响，因而可以使用一次指数平滑法进行预测。
步骤2：计算一次指数平滑预测值。
方法1：公式法取最初2期的观测值作为初始值，即在单元格C2中输入51。
平滑系数取α=0.2，单元格C3中输入一次指数平滑值，即“=0.2*B3+0.8*C2”,如图。
将单元格C3的内容复制到单元格区域C4: C14，得一次指数平滑值，如图在单元格D3输入“=C2”,并将单元格D3的内容复制到单元格区域D14，得一次指数平滑值，如图。
方法2：指数平滑数据分析模块法Excel的数据分析工具也提供了简单方便的指数平滑预测模块。
首先，在单元格B2中输入S0(1)的值“51”，并选择“指数平滑”数据分析。
点击Excel【工具】菜单下的【数据分析】子菜单，打开“数据分析”对话框，从“分析工具”列表中选择“指数平滑”，如图，并点击[确定]按钮。
参数指数平滑设置。
在“指数平滑”对话框中，“输入区域”选择原始数据所在的单元格区域“B2:B14”，“阻尼系数”中输入“0.8”,表示平滑系数a=0.2，“输出区域”选择单元格“C2”，如图，点击[确定]按钮，如图。
三次指数平滑法公式
三次指数平滑法公式三次指数平滑法是一种用于预测未来数值的时间序列分析方法。
它是一种对时间序列数据进行平滑处理的技术，可以用来预测未来的趋势。
在实际应用中，三次指数平滑法通常用于处理带有趋势和季节性的时间序列数据，以便更准确地预测未来的数值变化。
三次指数平滑法的公式可以表示为：\[F_{t} = \alpha \cdot Y_{t} + (1-\alpha) \cdot (F_{t-1} + T_{t-1}) \\T_{t} = \beta \cdot (F_{t} - F_{t-1}) + (1-\beta) \cdot T_{t-1} \\S_{t} = \gamma \cdot (Y_{t} - F_{t}) + (1-\gamma) \cdot S_{t-m}\]其中，\(F_{t}\)是在时刻\(t\)的预测值，\(Y_{t}\)是在时刻\(t\)的观测值，\(T_{t}\)是在时刻\(t\)的趋势值，\(S_{t}\)是在时刻\(t\)的季节性调整值，\(\alpha\)、\(\beta\)和\(\gamma\)是平滑系数，\(m\)是季节性的周期。
三次指数平滑法的计算过程包括以下几个步骤：1. 初始化参数：选择初始的平滑系数\(\alpha\)、\(\beta\)和\(\gamma\)，以及初始的预测值\(F_{1}\)、初始的趋势值\(T_{1}\)和初始的季节性调整值\(S_{1}\)。
2. 计算预测值：根据上面的公式，计算在时刻\(t\)的预测值\(F_{t}\)。
3. 计算趋势值：根据上面的公式，计算在时刻\(t\)的趋势值\(T_{t}\)。
4. 计算季节性调整值：根据上面的公式，计算在时刻\(t\)的季节性调整值\(S_{t}\)。
5. 更新参数：根据实际的观测值\(Y_{t}\)和预测值\(F_{t}\)来更新平滑系数\(\alpha\)、\(\beta\)和\(\gamma\)。
二次指数平滑法预测我国连锁餐饮业营业额
二次指数平滑法预测我国连锁餐饮业营业额1147622 金珊【目的】"民以食为天"，中国餐饮业连续12年来两位数迅猛增长，2002年的营业额首次突破5000亿元，占到了GDP的5.1%。
餐饮业的发展被认为有四大因素：个人消费兴起、餐饮业差异化增强、产品创新、经营模式连锁化。
连锁经营对营业额的提升作用是最为显著的，仔细分析数字就会发现，中国的连锁餐饮业还有巨大的发展空间。
连锁经营对营业额的提升作用原因在于中国餐饮业的连锁程度还很低。
据统计，前100强餐饮业企业的营业额不到270亿元，只占6.5%。
例如北京现有各类餐饮企业超过3万，常常是今天这家餐馆开张，明天另一家餐馆就关门。
频频发生的重迭更张，正是中餐企业发展水平低的具体体现。
在中餐企业长期在低水平发展阶段停滞不前的同时，以麦当劳、肯德基为代表的洋快餐，以及日本料理、韩国烧烤等外来餐饮却在我国市场遍地开花。
有关资料显示，目前麦当劳的单店平均营业额竟是中式快餐单店的160倍，肯德基在中国市场一年的销售额已超过20亿元。
随着更多投资者被市场发展吸引加入，以及理性消费时代的来临，未来餐饮业竞争将更多的表现为品牌的竞争。
是否拥有著名的品牌，将直接决定餐饮企业的生存和发展。
综观国外餐饮企业的发展，无一不是依靠其雄厚的品牌实力开展全球化经营的。
反观我们的餐饮企业，大都缺乏品牌，消费者大多跟风，新开的餐厅就蜂拥而至，过了热度期就相对萧条，形不成固定的客流量。
即便是我们认为的知名企业，无论是经营规模、市场占有额，还是品牌知名度等方面，和国际知名品牌都有较大差距。
面对全球经济一体化的机遇和挑战，我们的餐饮要想参与国际竞争，品牌就显得尤为重要了。
综合以上原因，本文结合统计学原理作业需要的条件下采用二次指数平滑法预测我国接下来几年的连锁营业额，旨在了解我国目前连锁餐饮市场发展动态，把握连锁餐饮行业消费现状与趋势，为企业制定市场策略提供一些参考。
【数据】本文所采用分析数据均来自《中国统计年鉴—2012》我国连锁餐饮业营业额年份营业额（亿元）2005 454.362006 563.752007 640.002008 860.912009 879.322010 955.422011 1120.39【方法】指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测。