立体几何求体积

- 1 -

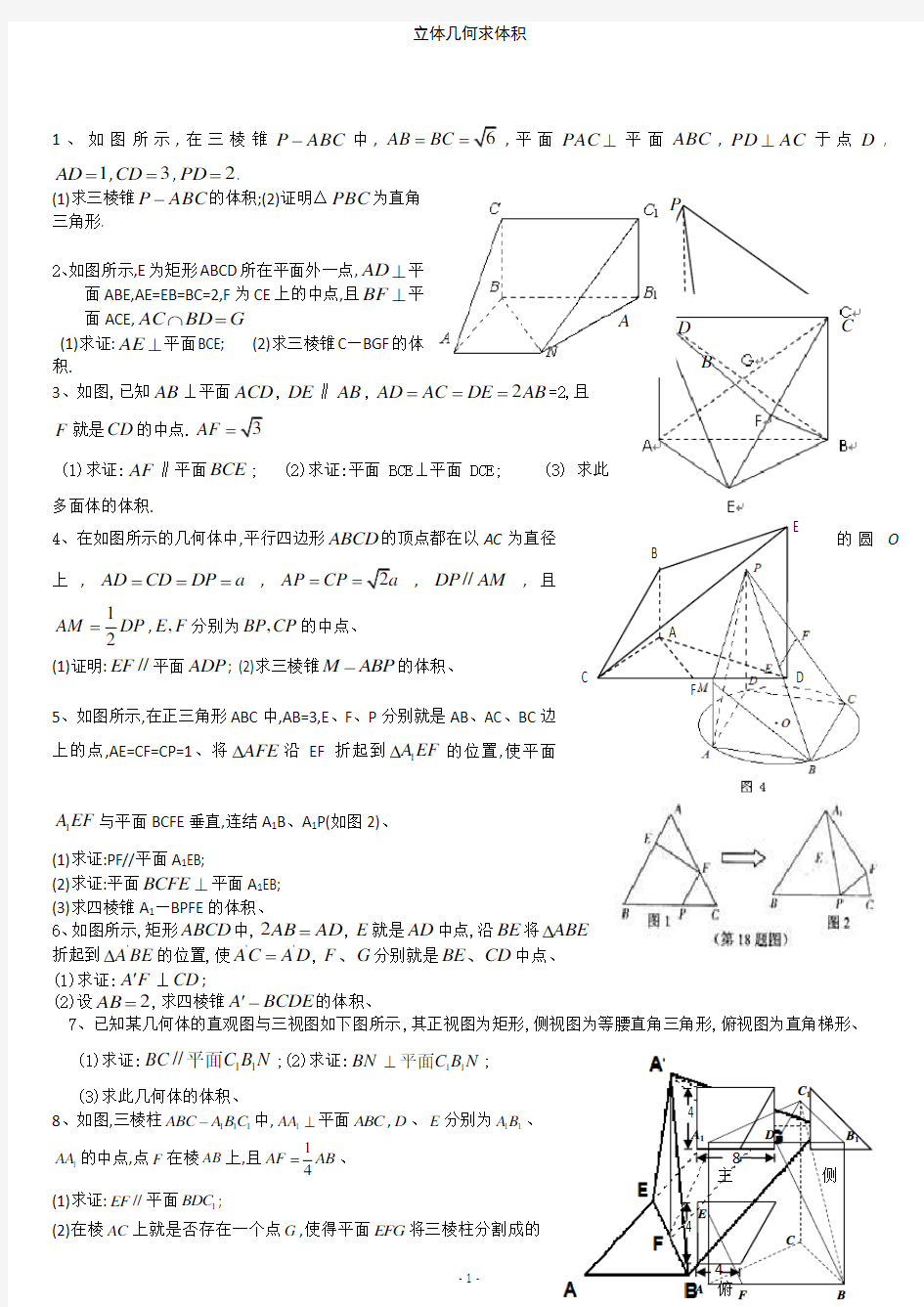
1、如图所示,在三棱锥ABC P -中,6AB BC ==,平面⊥PAC 平面ABC ,AC PD ⊥于点D ,

1AD =,3CD =,2=PD .

(1)求三棱锥ABC P -的体积;(2)证明△PBC 为直角

三角形.

2、如图所示,E 为矩形ABCD 所在平面外一点,⊥AD 平

面ABE,AE=EB=BC=2,F 为CE 上的中点,且⊥BF 平面ACE,G BD AC =?

(1)求证:⊥AE 平面BCE; (2)求三棱锥C —BGF 的体积.

3、如图,已知AB ⊥平面ACD ,DE ∥AB ,2AD AC DE AB ====2,且

F 就是CD 的中点.3AF =

(1)求证:AF ∥平面BCE ; (2)求证:平面BCE ⊥平面DCE; (3) 求此多面体的体积.

4、在如图所示的几何体中,平行四边形ABCD 的顶点都在以AC 为直径的圆O

上,

AD CD DP a ===,2AP CP a ==,//DP AM ,且

1

2

AM DP =

,,E F 分别为,BP CP 的中点、 (1)证明://EF 平面ADP ; (2)求三棱锥M ABP -的体积、

5、如图所示,在正三角形ABC 中,AB=3,E 、F 、P 分别就是AB 、AC 、BC 边上的点,AE=CF=CP=1、将AFE ?沿EF 折起到1A EF ?的位置,使平面

1A EF 与平面BCFE 垂直,连结A 1B 、A 1P(如图2)、

(1)求证:PF//平面A 1EB;

(2)求证:平面BCFE ⊥平面A 1EB; (3)求四棱锥A 1—BPFE 的体积、 6、如图所示,矩形ABCD 中,AD AB =2,E 就是AD 中点,沿BE 将ABE

?折起到'

A BE ?的位置,使''AC A D =,F G 、分别就是BE CD 、中点、

(1)求证:F A '⊥CD ;

(2)设2=AB ,求四棱锥BCDE A -'的体积、

7、已知某几何体的直观图与三视图如下图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形、 (1)求证:N B C BC 11//平面;(2)求证:BN 11C B N ⊥平面; (3)求此几何体的体积、

8、如图,三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 、E 分别为11A B 、1AA 的中点,点F 在棱AB 上,且1

4

AF AB =、

(1)求证://EF 平面1BDC ;

(2)在棱AC 上就是否存在一个点G ,使得平面EFG 将三棱柱分割成的

A

B

C

D

E

F

B

P

A

C

D 84

主侧

俯

4

4

D

E

C

C 1

A 1

B 1

A

- 2 -

两部分体积之比为1：15,若存在,指出点G 的位置;若不存在,说明理由、 9.已知梯形ABCD 中//AD BC ,2

π

=

∠=∠BAD ABC ,42===AD BC AB ,E 、F 分别就是AB 、CD 上的

点,//EF BC ,x AE =.沿EF 将梯形ABCD 翻折,使平面AEFD ⊥平面EBCF (如图).G 就是BC 的中点. (1)当2=x 时,求证:BD ⊥EG ;

(2)当x 变化 时,求三棱锥D BCF -的体积()f x 的函数式.